Abstract
This paper aims to assess the return and downside risk of a decumulation portfolio established at the retirement age of a senior, with a determined lifetime horizon differentiated by the sex of the citizen. To measure the portfolio’s return and downside risk, two ratios conditioned by seniors’ risk attitude towards portfolio failure are employed: the downside Sortino ratio and the downside risk–return ratio. Unlike other research in the field, this manuscript provides three portfolio compositions catering to different senior investment profiles: aggressive, moderate, and conservative. Additionally, it offers a decumulation horizon conditioned by the sex-specific life expectancy of the individual, instead of offering different scenarios for conducting a sensitivity analysis. Lastly, this study was conducted across three socioeconomically distinct countries: the US, Spain, and Japan. The results clearly demonstrate that both sex and nationality significantly influence the selection of the optimal decumulation portfolio composition aimed at exhausting funds by the senior’s demise.
1. Introduction
When a senior citizen undertakes planning the decumulation process of an accumulated capital fund upon retirement, their foremost concern is that this planning does not result in failure. In essence, they aim to be able to make periodic withdrawals until the end of their lifetime, with the final withdrawal completely exhausting the fund accumulated at retirement.
Achieving this objective is nearly impossible due to various factors influencing such planning. Since Markowitz’s modern portfolio theory, established in 1952, that investment diversification is an effective method for risk management (Markowitz 1952), numerous studies have focused on two main areas: determining the most suitable portfolio composition for individuals and identifying the optimal metrics for measuring associated risks. This study specifically focuses on research aimed at jointly measuring the return and risk of portfolios designed for seniors at retirement age, with a focus on decumulation strategies over their expected lifespan.
The initial studies in this field conducted by Bengen (1994) focused on estimating the generally acceptable sustainable withdrawal rate (henceforth, SWR) for the senior cohort, where the percentage of periodic capital withdrawal (typically monthly) from the accumulated retirement fund was estimated. These studies gave rise to the well-known “4% rule”1 regarding the SWR. Subsequently, Bengen (2001) and Pye (2000) investigated more precisely the determination and magnitude of this SWR, considering various portfolio compositions and updating the values related to the return and risk of the financial assets composing them, as well as the range of calendar years included in the study. Although most of the research initially focused on the US market and population, Blanchett et al. (2016) conducted their research for the UK market and population.
Subsequent contributions adjusted the SWR to the needs of seniors, as in the cases of Blanchett et al. (2012, 2016). Additionally, Clare et al. (2022), Drew and Walk (2015), and Estrada (2018b) optimised the magnitude of the sustainable withdrawal. Moreover, there are authors whose research has disagreed with the generally accepted “4% rule” for the SWR, such as Finke et al. (2013), Frank et al. (2011), Guyton (2004), Guyton and Klinger (2006), Pfau (2011), and Suarez et al. (2015). These studies have also focused on the US market and population, using historical data and considering hypothetical periods regarding individuals’ life expectancy. Taking these contributions to academia by various researchers as a reference and baseline, our work extends their investigations to the Spanish population, considering sex2-specific differences in the life expectancy among individuals in this country to estimate the probability of successful portfolio management during decumulation—an issue not addressed in the previously cited works.
Other studies in the literature, such as those by Suarez et al. (2015), Blanchett (2007), Spitzer et al. (2008), and Frank and Blanchett (2010), among others, examined dynamically adjusting the SWR to mitigate decumulation failures of the accumulated fund from retirement age until their demise, adapting it in response to market fluctuations. However, these contributions also overlooked the influence of sex and differing life expectancies in their application to the study. References to the potential inclusion of life expectancy in the context of decumulating senior portfolios can be found in the works by Ho et al. (1994) and Clare et al. (2022), and in relation to decumulating pension funds rather than capital in the work by Hyams et al. (2022).
In the realm of assessing return and risk metrics for assets comprising a senior’s decumulation portfolio at retirement and aimed at overseeing and managing financial planning for sustainable consumption over their life expectancy, the literature is scarce. Noteworthy contributions include the studies by Betzuen and Betzuen (2023a, 2023b). Concurrently, the studies by Sortino and Van Der Meer (1991), Sharpe et al. (2007), Blanchett (2007), and Estrada (2018a, 2021) focused on risk-return measures, deemed crucial for seniors due to their comprehensive consideration of the impact of both variables. In this vein, the study by Estrada (2021) specifically extended the analysis to a wide range of countries and included very broad historical periods since 1900. However, it did not explore the impact of sex on determining the SWR.
In this regard, our study employs calculations based on the contemporary market and demographic data, excluding the impact of epidemics and world wars, which, in our view, may distort the sought result. To this end, our calculations focus on a decumulation timeframe closely aligned with current conditions, integrating data pertaining to the returns and risk of the most up-to-date financial assets available.
Furthermore, a substantial body of literature illustrates the asymmetry in individuals’ concerns regarding the potential failure of decumulation portfolios. These studies conclude that individuals do not equally weigh the failure being due to a shortfall, where the fund is depleted before the pre-established time horizon, versus due to an excess, where there is surplus capital at the end of the portfolio’s estimated useful life (Kahneman and Tversky 1979). Specifically, Kahneman et al. (1991) and Ang et al. (2004), among others, argue that seniors are particularly apprehensive about failure due to a shortfall, commonly referred to as downside risk in the literature.
In light of this evidence, our manuscript exclusively uses a metric that not only measures the portfolio’s return but also measures its downside risk. Additionally, we consider it necessary to explore various portfolio compositions tailored to different risk profiles, including risk-averse, moderate, and risk-seeking strategies. Furthermore, we extend our analysis to encompass the time horizon aligned with the actuarial life expectancy of each citizen, differentiated by sex, across the US, Spanish, and Japanese populations.
The results obtained clearly demonstrate that sex-specific incidence and future life expectancy are significant and determining factors in planning decumulation strategies for retirement capital across the studied countries. We believe that this contribution significantly enriches the academic literature in this domain.
Based on the aforementioned reasons, the aim of this study is to jointly measure and assess both the return and downside risk through two metrics: the downside Sortino ratio and the risk-adjusted return ratio. This approach enables informed financial planning decisions for senior citizens’ decumulation portfolios, ensuring that the depletion of accumulated funds aligns with their projected life expectancy.
2. Methodology
As mentioned at the outset of this article, few issues are as critical for a senior citizen as the proper management of decumulating their retirement portfolio. Selecting the optimal decumulation strategy involves several key decisions, including the choice of appropriate financial assets to include in the portfolio, determining their percentage composition, and establishing the decumulation time horizon, among other considerations.
Throughout this methodological section, we will address these decision points, providing comprehensive solutions and clearly and concisely detailing the steps taken in the development of our research.
2.1. Construction of the Databases
To achieve the stated objective, we needed to construct two databases—one containing the returns of stocks and long-term government bonds from the US, Spain, and Japan, and another encompassing the sex-differentiated life expectancy for each of these countries, serving as the decumulation horizon for portfolios tailored to individual risk profiles. The selection of these three countries was based on their significant foresight, social, and economic differences, as well as the accessibility of their demographic and economic–financial data.
The obtained results enable comparisons among the countries and offer highly relevant conclusions.
Regarding the data related to the returns of the financial assets composing the portfolios, we used the annual real-term data from the publications of Dimson et al. (2002, 2023)3. Historical data show us different annual returns4; they are usually higher for stocks than for long-term government bonds, but they also imply greater risks for stocks compared to long-term government bonds. Therefore, it is necessary to study both financial asset classes in the constitution of a retirement capital, always aiming for the effectiveness of the portfolio decumulation strategy. Concerning the different portfolio compositions considered in our study, which address the three risk profiles of a senior citizen5 mentioned previously, we included the following:
- The risky portfolio, or 100/0 portfolio, corresponding to a risk-seeking profile, where the first member signifies a 100% investment in stocks and 0% in long-term government bonds.
- The moderate portfolio, or 70/30 portfolio, corresponding to a moderate risk profile, where there is a 70% investment in stocks and a 30% in long-term government bonds.
- The conservative portfolio, or 50/50 portfolio, corresponding to a risk-averse profile, where the investment is equally divided between stocks and long-term government bonds.
We believe that this type of differentiation in portfolio composition concerning the risk profiles of seniors is reasonable, as pointed out by Fong et al. (2021). The data related to the returns of financial assets, sourced from Dimson et al. (2002, 2023), are grouped into series, which are constituted, as previously mentioned, with the return rates corresponding to stocks and long-term government bonds, staggered by overlapping periods displaced by one year each time. Since our study focuses on future estimation, we selected a data collection period excluding anomalies in returns and volatility, such as world wars and major epidemics, as previously mentioned. Therefore, we limited our information collection to the period from 1960 to 2022. Using these data, we obtained the statistical values corresponding to the mean and standard deviation of the financial magnitudes using classical formulas.
To determine the decumulation horizon of a senior’s portfolio, which is determined by their life expectancy at retirement, we refer to the Human Mortality Database (n.d.), which is internationally renowned and freely accessible upon registration. It can be accessed at the following website: https://www.mortality.org/ (accessed 15 January 2024). This database provides the required information, differentiating the sex of the individual, their country of origin, and the calendar years from 1960 to 2022.
Once the data were collected and refined, we were positioned to perform the calculations corresponding to the different sections outlined below.
2.2. Measurement of Portfolio Return and Risk
Regarding the measurement of portfolio return and risk and addressing seniors’ concerns about the potential downside failure of the decumulation portfolio, we chose to employ the two aforementioned ratios, defined as follows.
2.2.1. The Downside Sortino Ratio
This ratio measures the risk-adjusted performance of a financial asset or portfolio, focusing on the downside risk. As such, it captures and quantifies the asymmetric risk attitude towards potential failures in seniors’ decumulation portfolios. The downside Sortino ratio (DSTR, hereafter) is especially useful for those investors who prioritise the protection of their portfolios against market downturns, as in the case of seniors, as already pointed out and highlighted by Kahneman and Tversky (1979).
The formula for the DSTR is given by Equation (1):
where
: the return of the portfolio;
E(): the estimated return of the portfolio;
: the risk-free return or benchmark return;
: the semi-deviation of the portfolio with respect to the benchmark return.
The semi-deviation of the portfolio concerning a reference return (or downside semi-deviation) measures the volatility of returns below a specific benchmark and considers returns that are either zero6 or negative, but never positive.
For its measurement, we used the following Equation (2):
where
: the return of a security at the time j;
: the risk-free return or benchmark return;
n: the number of elements in the chain7.
The interpretation of this ratio is that the higher the result, the better the portfolio’s performance concerning its inherent risk. However, it is crucial not to fixate solely on downside volatility when analysing the return-risk profile of a portfolio. This tendency is common among risk-averse investors who prioritise capital preservation. Such investors favour a high DSTR, as it signifies greater protection against downturns in returns. Nevertheless, this cautious approach may lead to missed opportunities for substantial gains during favourable market conditions. In essence, these investors may sacrifice potential upward gains in exchange for reduced volatility.
2.2.2. The Downside Risk-Adjusted Return Ratio
As mentioned in the introductory section, there are different perspectives regarding how individuals perceive the failure of a decumulation portfolio, whether in terms of shortfall or excess. Given that this study focuses on shortfall failure of a portfolio, it is important to note that such failure should also be measured by its magnitude, specifically by the number of shortfall years.
While the DSTR assumes risk-adjusted performance, the ratio presented next aligns specifically with the objective of this study. By using this ratio, we diverge somewhat from the interpretations presented in Sharpe et al. (2007) and Sortino and Van Der Meer (1991) and move closer to those in Blanchett (2007) and Estrada (2018a). This is the downside risk-adjusted return ratio (DRARR, hereafter).
Blanchett (2007) proposed a measure for evaluating retirement strategies called the “success to variability ratio”, defined as the ratio between the failure rate and the portfolio’s volatility. For Blanchett (2007), the standard deviation is one of the most common measures in risk assessment. However, their ratio measure heavily penalises aggressive strategies, which are also the most volatile. Estrada (2000, 2018a), on the other hand, argue that seniors’ concern about downside outcomes should be considered in the metric chosen for evaluating the risk–return profile.
We believe that the ratio should be built by including in the numerator the probable value of shortfall withdrawals and surplus withdrawals, and in the denominator, the value of downside risk. In accordance with this consideration, we have evaluated both dispositions.
We propose constructing the ratio by incorporating into the numerator the probable value of shortfall withdrawals and surplus withdrawals, and in the denominator, the measure of downside risk. Following this approach, we assessed both scenarios by calculating the number of dispositions consumed in cases of shortfall failure and the number of withdrawals that would be consumed in cases of surplus failure.
The most probable value of the dispositions to be consumed by the senior was calculated using Equation (3):
where
E(d): the most probable value of the drawdowns;
: the failure rate8;
ND: the number of years drawn down in the shortfall failed strategies9;
NE: the number of years drawn down in the surplus failed strategies10.
This result constitutes the numerator of the DRARR.
For the denominator, we used a formula for calculating downside volatility following the Sortino approach. The downside volatility was determined by Equation (4):
where
SSDp: the downside volatility of the portfolio;
: the failure rate;
ND: the number of years drawn down in the shortfall failed strategies;
n: the number of elements in the chain.
As can be observed, the stipulated period duration is taken as the benchmark instead of the most probable value of the drawdowns. This is because, as noted by Fong et al. (2021) and Estrada (2000), the senior citizen will reference the average life expectancy at retirement, that is, the duration of the stipulated period in the design of the portfolio planning. As mentioned before, the desired value is provided by the DRARR, obtained as the ratio between the most probable value of the drawdowns and the downside volatility of the portfolio as it is determined by Formula (5):
where
E(d): the most probable value of the drawdowns;
SSDp: the downside volatility of the portfolio.
3. Results
Throughout this section, we first offer the results obtained using the DSTR, and then present the results obtained after application of the DRARR.
3.1. Findings Regarding the Use of the DSTR
3.1.1. Case Study of a US Citizen
The DSTR delivered superior results in the first half of the calendar period under consideration for male subjects. Additionally, it yielded comparable outcomes across all three types of portfolios. However, this trend did not persist in the second half of the calendar period, where the DSTR showed superior results for female subjects.
Furthermore, it is interesting to observe the trend in ratio behaviour, which exhibits a more consistent level in the latter part compared to the former (Figure 1).
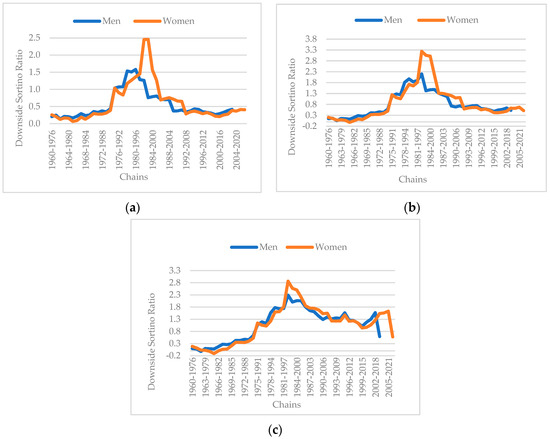
Figure 1.
(a) The DSTR for US men and women for an aggressive portfolio (100/0). (b) The DSTR for US men and women for a moderate portfolio (70/30). (c) The DSTR for US men and women for a conservative portfolio (50/50). Source: authors.
As can be observed, the ratio is positive throughout the entire study horizon, indicating that the portfolio generates value per unit of risk assumed. It is also evident that, based on the results, this ratio favours more conservative portfolios. Moreover, we notice that the ratio evolves more steadily in the second half compared to the first half, where the slope of the ratio’s evolution is quite steep. However, the DSTR shows negative results, especially for the female population, and over several years.
3.1.2. Case Study of a Spanish Citizen
The DSTR provided better results in the first half of the calendar period considered for the case of men. Furthermore, it offered similar results for all three types of portfolios. However, this was not the case in the second half of the calendar period, where the DSTR gave better results for the female sex. On the other hand, it is interesting to observe the behaviour trend of the ratio, which is much more level in the second part compared to the first (Figure 2).
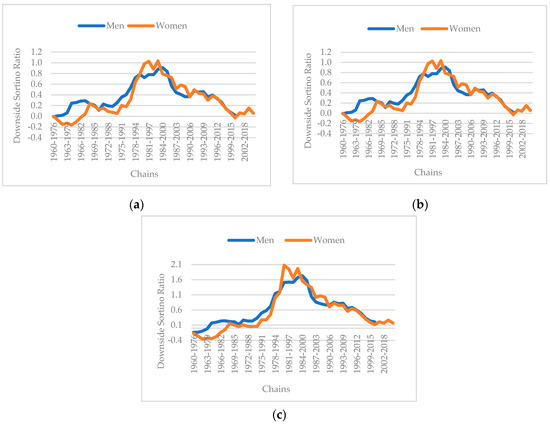
Figure 2.
(a) The DSTR for Spanish men and women for an aggressive portfolio (100/0). (b) The DSTR for Spanish men and women for a moderate portfolio (70/30). (c) The DSTR for Spanish men and women for a conservative portfolio (50/50). Source: authors.
As can be seen, the ratio is positive throughout the horizon under study, which means that the portfolio generates value per unit of risk assumed. It can also be seen that, in view of the results, this ratio is in favour of rather conservative portfolios.
3.1.3. Case Study of a Japanese Citizen
The DSTR produced distinctly different results when analysing the decumulation portfolios of the Japanese population. Specifically, there is no clear separation between the calendar periods; instead, a generally declining trend in the ratio’s magnitude is observed throughout almost the entire calendar period, except perhaps in the last quarter of the sample period. Additionally, we note that in the declining segments, the ratio yielded more favourable results for females compared to males. Conversely, the results are reversed in the segments where the ratio is increasing. Lastly, we would like to highlight that, for Japan, the ratio only shows negative results during the years from approximately 1988 to 1993. These are the periods when stock returns in Japan were negative, which significantly impacted the risky portfolios (Figure 3).
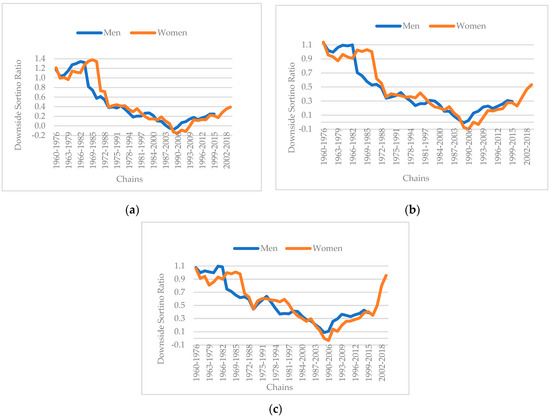
Figure 3.
(a) The DSTR for Japanese men and women for an aggressive portfolio (100/0). (b) The DSTR for Japanese men and women for a moderate portfolio (70/30). (c) The DSTR for Japanese men and women for a conservative portfolio (50/50). Source: authors.
Based on the above results, we can assert that differentiating the decumulation horizon concerning sex plays a significant role in the outcomes obtained using the DSTR.
3.2. Findings Regarding the Use of DRARR
The results presented in the following tables address the main objective of this study, which was to determine whether sex influences the selection and composition of a retirement investment portfolio, and if so, whether it shows a clear and consistent trend to facilitate decision-making for any citizen of a country.
Table 1 presents the results corresponding to the probable value of a portfolio, the downside semi-deviation of the portfolio risk, and the downside risk-adjusted return ratio (DRARR) of the portfolio. Clear differences in the magnitude between females and males are evident, but the decision criterion is nearly identical. The DRARR ratio favours moderately risky portfolios. Regarding portfolio performance, the results favour males, primarily due to their lower life expectancy. Additionally, we observe that while the probable values of default and excess returns exhibit a consistently decreasing trend, the same does not apply to risk, which in this study, was measured by downside semi-deviation.

Table 1.
DRARR results for US citizens.
Table 2 presents the results for the Spanish population. The findings indicate better portfolio performance for males. The evolution of the ratio is quite consistent, showing a preference for more risky portfolios. The lower magnitude of the ratio for females is attributed not only to their higher life expectancy but also to greater portfolio volatility. We note that the trend of the ratio does not align between the male populations of the US and Spain.

Table 2.
DRARR results for Spanish citizens.
Table 3 presents the results for the Japanese population. The results continue to show better portfolio performance for males compared to females. However, in this case, the gap is considerably smaller than in the Spanish and especially the US citizens.

Table 3.
DRARR results for Japanese citizens.
Most notably, the portfolio that yields the best performance is not the riskiest one, unlike in the previous countries, but the most conservative, particularly for males.
In summary, we generally observe better performance for males, favoured by lower life expectancy and lower downside semi-deviation of the portfolios. Additionally, while the expected returns are slightly higher for females, this advantage does not offset the greater risk undertaken by their portfolios.
Possibly, the most striking aspect, in light of the results presented in Table 3, is the remarkably low magnitude of the downside semi-deviation for US men. This is particularly notable when compared to the results for men from the other two countries and women from the US itself. We provide an explanation using two scenarios.
First, when comparing the downside semi-deviation results between US men and men from other countries, we found that the downside semi-deviation was influenced by the failure rate and the number of years withdrawn of failed portfolios, with life expectancy playing a significant role in gender comparisons. For US men, the failure rate generally decreased with an increased proportion to long-term government bonds, except in the 70/30 portfolio, which exhibited the lowest SSDp value. In contrast, Spain demonstrated a higher failure rate than the US, with only a slight decrease observed in conservative portfolios. However, the average number of years withdrawn of failed portfolios increased marginally, leading to higher SSDp values than those observed in the US. Similarly, Japan presented a higher failure rate, with SSDp values distinctly exceeding those of the US. Overall, the lower SSDp values observed in the US can be attributed to a reduced impact from the failure rate and shorter life expectancy.
Secondly, when comparing the downside semi-deviation results between US men and women, we found that portfolios held by US women exhibited higher SSDp values than those of US men, primarily due to higher failure rates and longer life expectancy.
4. Discussion
Throughout this section, we synthesise the most significant contributions of our study in relation to other authors in the field and with respect to our predefined research objective.
To the best of our knowledge, there is no other work in the literature that has methodologically considered the impact of the following specific factors, given that decumulation portfolios are aimed at a senior population:
- Limiting the range of calendar years for obtaining portfolio returns and risks to a more recent range of calendar years, covering the period of 1960–2022 for each type of portfolio and country under study.
- Using real returns, not nominal returns, for each portfolio and country under study.
- Establishing the time horizon of the decumulation portfolio as the expected life expectancy of the senior, differentiated by gender and for each country under study.
When comparing our results and findings with those discussed in the literature, we found that most works refer to portfolio theory in general and the accumulation process in particular. This process is conducted during the working life of the individual. However, few works have focused on the decumulation process of a portfolio upon retirement.
These works have various lines of research, and few have used any kind of measure or metric that provides results to optimally choose the best decumulation portfolio for seniors. Normally, they seek a ratio that sheds some light on this choice.
Thus, we refer to the works of Estrada (2018a), who utilised a range of return data spanning the period from 1900 to 2014, whereas our study employed data from 1960 to 2022. The broader time frame, which encompasses the 1919 epidemic and the two world wars, was deliberately excluded in our analysis, as we focused on more recent dates. This distinction leads to significant differences between his results and ours. Furthermore, Estrada (2018a) considered a 30-year time horizon, whereas our research determined the time horizon based on the expected mathematical survival of senior citizens post-retirement, differentiated by gender and for each of the countries under study.
Moreover, the studies by Blanchett (2007), Stout and Mitchell (2006), among others, considered life expectancy, but did not incorporate a risk-adjusted return metric, as we have in our work. Specifically, Blanchett (2007) presented his results in tabular form, applying various sensitivity hypotheses for each age and life expectancy horizon. However, unlike our approach, he did not adjust for the actual expected survival of senior citizens.
Authors adhering to the Sharpe ratio (Sharpe et al. 2007) produced results that are not comparable to ours, as their methodology incorporates standard deviation as a measure of portfolio risk, encompassing both upward and downward deviations symmetrically. In contrast, our work focuses specifically on downside deviations, aligning with the risk aversion typically exhibited by senior citizens.
Authors who followed the Sortino ratio, particularly in its downside form (Sortino and Van Der Meer 1991), included in the numerator the profit margins derived from portfolio returns. In our study, we incorporated the likely value of disbursements that a senior might obtain from portfolios that fail, both in terms of shortfall and surplus.
Recent studies on individuals’ financial behaviour indicate much greater concern regarding failure due to shortfall than excess in relation to investments made or to be made (Kahneman and Tversky (1979)). Such behaviour cannot be captured through the use of standard deviation, as envisaged in the Sharpe ratio, which reflects symmetric risk behaviour in investments.
For this reason, we believe that using semi-standard deviation represents a more appropriate measure of these preferences, particularly the use of downside semi-deviation.
To enhance this metric, we introduced a ratio we have termed DRARR as a reference metric for a senior citizen at retirement age when selecting the optimal portfolio. We found that the portfolio indicated by this metric does not always correspond to the most or least risky one but is clearly influenced by the senior’s sex and nationality, as evidenced in Table 1, Table 2 and Table 3 and explained in their respective sections.
While the general trend of the probable value and downside semi-deviation is towards a reduction as the portfolio composition becomes less risky, this is not the case when tracking the DRARR values.
In this regard, for the US population, the ratio favours intermediate-risk portfolios as optimal, whereas for the Spanish case, it leans towards slightly riskier portfolios, especially for females. This is not observed in the Japanese population, where we found a clear divergence by sex. Thus, the metric indicates the most conservative portfolio as optimal for males and the most aggressive for females, possibly due, among other factors, to their higher life expectancy.
Consequently, the final conclusion is that it is not advisable to unify the decision-making process using a single reference value of the DRARR ratio for both sexes, as it leads, in some cases, to different optimal portfolio selections.
From the results presented in this study, it is evident that this latter ratio is much more comprehensive than the Sortino ratio (Sortino and Van Der Meer 1991). In addition, it clearly demonstrates the impact of sex, life expectancy, and nationality on the outcomes, aspects not addressed in the literature that provide added value for decision-making in managing different decumulation portfolios tailored to client specifications.
Based on our methodological contribution and the results obtained, although not the focus of this research, we believe that the use of indicators based on sensitivity measures (beta coefficients) in both the conventional and downside framework would provide a valuable contribution to the literature. Therefore, we have identified it as a future line of research.
Finally, we would not like to conclude this section without mentioning the limitations faced by this study, including the challenge of obtaining sample data with the necessary rigor and officiality required for research. Due to the lack of uniformity in the publication of data related to returns of various assets across different countries by different official sources, we relied on the sample presented in Dimson et al. (2002, 2023); however, these data do not always align with the other published literature.
To partially overcome this limitation, we used only real values of returns. Possibly, using nominal values would have resulted in different outcomes in some cases.
Author Contributions
Conceptualisation, A.J.B.Á. and A.B.Z.; methodology, A.J.B.Á. and A.B.Z.; software, A.J.B.Á. and A.B.Z.; validation, A.J.B.Á. and A.B.Z.; formal analysis, A.J.B.Á. and A.B.Z.; investigation, A.J.B.Á. and A.B.Z.; resources, A.J.B.Á. and A.B.Z.; data curation, A.J.B.Á. and A.B.Z.; writing—original draft preparation, A.J.B.Á. and A.B.Z.; writing—review and editing, A.J.B.Á. and A.B.Z.; visualization, A.J.B.Á. and A.B.Z.; supervision, A.J.B.Á. and A.B.Z.; project administration, A.J.B.Á. and A.B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The database used in this paper is published on the Human Mortality Database website for academic or research purposes under free registration and is available online at www.mortality.org (accessed on 20 February 2024).
Acknowledgments
We would like to thank the University of the Basque Country UPV/EHU, Research Group ECISE (GIU 21/025) for their support in the editing of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Notes
| 1 | The “4% rule,” first published by Bengen (1994), consists of applying an initial 4% withdrawal rate on the amount accumulated in the senior’s portfolio at the time of retirement. The application of this initial 4% decumulation rate on the accumulated amount of the portfolio results in the amount to be withdrawn by the senior in the first year of decumulation. |
| 2 | Following the “Sex and Gender Equity in Research—SAGER—guidelines” this manuscript uses the term “sex” referring to the biological attribute of the senior citizen. |
| 3 | Regarding the index used, Dimson et al. (2002) in Chapter 3 of their publication describe in detail the design of an exclusive, self-constructed index, created from various sources and covering different calendar year ranges for the period 1900–2000. Moreover, the Dimson et al. (2002) publication contains specific chapters that detail the sources, and the calendar year ranges considered for each of the countries included in their research. Chapter 26 focuses on Japan, Chapter 29 on Spain, and Chapter 33 on the United States. Subsequent publications by the Credit Suisse Research Institute under the title “Credit Suisse Global Investment Returns Yearbook”, by authors Elroy Dimson, Paul Marsh, and Mike Staunton, provide annual updates to the data for all the countries covered in their research. |
| 4 | When considering the range of assets for portfolio construction, the works of Dimson et al. (2002, 2023) provide annual returns for stocks and long-term government bonds in various countries and the global market. These returns are real, meaning they are adjusted for each nation’s inflation, expressed in local currencies, and encompass both capital gains/losses and income from dividends or coupons. |
| 5 | The decumulation portfolio construction does not consider the differing risk propensities between men and women. |
| 6 | This manuscript considers that the risk-free return or benchmark return is equal to “0”. |
| 7 | In this study, a chain is comprised of a series of successive annual rates of return for a portfolio, whose range aligns with the life expectancy of the individual. Thus, for example, for a study period spanning from 1960 to 2022, in the case of a US woman with a life expectancy of 17 years, it is possible to construct 47 chains. |
| 8 | We define the “failure rate” as the proportion of chains that fail relative to the total number of chains considered. |
| 9 | The average number of years available among the chains that failed by default is calculated to obtain this result. |
| 10 | The result is derived from estimating the average number of potentially available years, assuming the excess capital accumulated by retirement is evenly distributed into the future, allocating the same amount each year as was determined in the final stipulated year. |
References
- Ang, Andrew, Joseph Chen, and Yuhang Xing. 2004. Downside Risk. Columbia Business School Working Paper. Available online: https://www0.gsb.columbia.edu/faculty/aang/papers/downside.pdf (accessed on 13 December 2023).
- Bengen, William P. 1994. Determining Withdrawal Rates Using Historical Data. Journal of Financial Planning 7: 171–80. [Google Scholar]
- Bengen, William P. 2001. Conserving Client Portfolios during Retirement Part IV. Journal of Financial Planning 14: 110–19. [Google Scholar]
- Betzuen, Amaia Jone, and Amancio Betzuen. 2023a. Metric That Represents an Advance in the Quality of the Choice of the Best Strategy for Decumulating a Portfolio. Paper presented at the XXX International Conference of AEDEM, Tangier, Morocco, September 3–5. [Google Scholar]
- Betzuen, Amaia Jone, and Amancio Betzuen. 2023b. The Problem of the Sustainability of the Capital Decumulation Rate and a Proposed Solution. Paper presented at the XXX International Conference of AEDEM, Tangier, Moroscco, September 3–5. [Google Scholar]
- Blanchett, David M. 2007. Dynamic Allocation Strategies for Distribution Portfolios: Determining the Optimal Distribution Glide Path. Journal of Financial Planning 20: 68–81. [Google Scholar]
- Blanchett, David M., Maciej Kowara, and Peng Chen. 2012. Optimal Withdrawal Strategy for Retirement-Income Portfolios. The Retirement Management Journal 2: 7–20. [Google Scholar]
- Blanchett, David M., Matthieu Buffenoir, David Kemp, and Stig Watt. 2016. Safe Withdrawal Rates for Retirees in the United Kingdom: Where Did the 4% Rule Come From and What Is the Impact of Today’s Low Bond Yields? Morningstar Research. Available online: https://www.sterlingfs.co.uk/wp-content/uploads/2020/08/Morningstar-Safe-Withdrawal-Rate.pdf (accessed on 7 January 2023).
- Clare, Andrew, James Seaton, Peter Smith, and Stephen Thomas. 2022. Measuring Success in Decumulation: The Minimum Acceptable Annual Withdrawal Rate (MAAW). SSRN. Available online: https://ssrn.com/abstract=4099452 (accessed on 30 December 2022).
- Dimson, Elroy, Paul Marsh, and Mike Staunton. 2002. Triumph of the Optimists: 101 Years of Investment Returns. Princeton: Princeton University Press. Available online: https://www.academia.edu/41012838/TRIUMPH_OF_THE_OPTIMISTS (accessed on 22 September 2023).
- Dimson, Elroy, Paul Marsh, and Mike Staunton. 2023. Credit Suisse Global Investment Returns Yearbook 2023 Summary Edition. Zurich: Credit Suisse Research Institute. [Google Scholar]
- Drew, Michael E., and Adam N. Walk. 2015. Just How Safe Are ‘Safe Withdrawal Rates’ in Retirement? Financial Planning Research Journal 1: 22–32. [Google Scholar] [CrossRef]
- Estrada, Javier. 2000. The Cost of Equity in Emerging Markets: A Downside Risk Approach. Paper presented at EFMA 2000 Athens, EFA 2000 London, and FMA 2000 Edinburgh, August; Available online: https://ssrn.com/abstract=170748 (accessed on 28 September 2023).
- Estrada, Javier. 2018a. From Failure to Success: Replacing the Failure Rate. The Journal of Wealth Management 20: 9–21. [Google Scholar] [CrossRef]
- Estrada, Javier. 2018b. Maximum Withdrawal Rates: An Empirical and Global Perspective. Journal of Retirement 5: 57–71. [Google Scholar] [CrossRef]
- Estrada, Javier. 2021. The Sustainability of (Global) Withdrawal Strategies. Journal of Financial Planning 34: 82–98. [Google Scholar] [CrossRef]
- Finke, Michael S., Wade D. Pfau, and David M. Blanchett. 2013. The 4% Rule is Not Safe in a Low-Yield World. Journal of Financial Planning 26: 46–55. [Google Scholar] [CrossRef]
- Fong, Joelle H., Benedict S. K. Koh, Olivia S. Mitchell, and Susann Rohwedder. 2021. Financial Literacy and Financial Decision-Making at Older Ages. Pacific-Basin Finance Journal 65: 101481. [Google Scholar] [CrossRef]
- Frank, Larry R., and David M. Blanchett. 2010. The Dynamic Implications of Sequence Risk On a Distribution Portfolio. Journal of Financial Planning 23: 52–61. [Google Scholar]
- Frank, Larry R., John B. Mitchell, and David M. Blanchett. 2011. Probability-of-Failure-Based Decision Rules to Manage Sequence Risk in Retirement. Journal of Financial Planning 24: 46–55. [Google Scholar]
- Guyton, Jonathan. 2004. Decision Rules and Portfolio Management for Retirees: Is the ‘Safe’ Initial Withdrawal Rate Too Safe? Journal of Financial Planning 17: 50–58. [Google Scholar]
- Guyton, Jonathan, and William Klinger. 2006. Decision Rules and Maximum Initial Withdrawal Rates. Journal of Financial Planning 19: 49–57. [Google Scholar]
- Ho, Kai, Moshe A. Milevsky, and Chris Robinson. 1994. Asset Allocation, Life Expectancy, and Shortfall. Financial Services Review 3: 109–26. [Google Scholar] [CrossRef]
- Human Mortality Database. n.d. Available online: www.mortality.org (accessed on 3 February 2024).
- Hyams, S. D., H. R. Davies, A. J. M. Findlater, A. Gilbert, K. Hollister, F. J. Kiely, T. J. Jablonski, C. M. Squirrell, and O. H. Warren. 2022. Pension Decumulation Pathways—A Proposed Approach. British Actuarial Journal 27: e16. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An Analysis of Decision under Risk. Econometrica 47: 263–91. [Google Scholar] [CrossRef]
- Kahneman, Daniel, Jack L. Knetsch, and Richard H. Thaler. 1991. Anomalies: The Endowment Effect, Loss Aversion, and Status Quo Bias. Journal of Economic Perspectives 5: 193–206. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- Pfau, Wade D. 2011. Can We Predict the Sustainable Withdrawal Rate for New Retirees? Journal of Financial Planning 24: 40–47. [Google Scholar]
- Pye, Gordon B. 2000. Sustainable Investment Withdrawals. Journal of Portfolio Management 26: 73–83. [Google Scholar] [CrossRef]
- Sharpe, William, Jason Scott, and John Watson. 2007. Efficient Retirement Financial Strategies. Pension Research Council Working Paper Series. Available online: https://ssrn.com/abstract=1005652 (accessed on 22 December 2022).
- Sortino, Frank, and Robert Van Der Meer. 1991. Downside Risk. Journal of Portfolio Management 17: 27–31. [Google Scholar] [CrossRef]
- Spitzer, John J., Jeffrey C. Strieter, and Sandeep Singh. 2008. Adaptive Withdrawals. Journal of Investing 67: 45–58. [Google Scholar] [CrossRef]
- Stout, Robert G., and John B. Mitchell. 2006. Dynamic Retirement Withdrawal Planning. Financial Services Review 15: 117–31. [Google Scholar]
- Suarez, E. Dante, Antonio Suarez, and Daniel T. Walz. 2015. The Perfect Withdrawal Amount: A Methodology for Creating Retirement Account Distribution Strategies. Financial Services Review 24: 331–57. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).