1. Introduction
Financial derivatives are synthetic instruments that are linked to underlying financial instruments or indicators, and through which specific financial risks can be transferred among various economic agents and entities. The options allow for the creation of a vast array of investment strategies for any volatility level of the market. The straddle option trading strategy is defined as buying or selling both call and put options at the same strike price and maturity date (
Hull 2014). This strategy is preferred when there is a huge uncertainty about and volatility of the price movement in the underlying asset. In a short position, the profit is limited to the option premium as long as the price of the underlying asset is between the breakeven legs; however, the loss is unlimited if the price of the underlying asset increases and decreases out of breakeven legs. It is a very risky strategy. In the long position, the profit is unlimited as long as the price of the underlying asset increases or decreases beyond breakeven legs; however, the maximum loss possible is the option premium. Thus, the expected return of an option straddle strategy depends on the implied volatility of the underlying asset.
Mayhew (
1995) summarizes various implied volatility calculation methods, including weighted average implied volatilities among others, and proposes the implied volatility to be calculated numerically.
Coval and Shumway (
2001) found that an at-the-money straddle option strategy generally yields negative returns because of the volatility risk premium.
Berestycki et al. (
2004) propose a new approach to determine the implied volatility for European call or put options in the framework of stochastic volatility models. They found the implied volatility by solving a quasi-linear parabolic partial differential equation.
Goltz and Lai (
2009) examine the return properties of straddle strategies within portfolios. They conclude that straddle strategies are not profitable investment strategies with neutral or negative returns.
Degiannakis et al. (
2018) compare the forecasting power of implied volatility and predict the implied volatility indexes for 1 day and 10 days ahead. They found that the forecasting ability of the non-parametric techniques is significant in shorter periods.
Liu et al. (
2021) recently applied the Artificial Bee Colony with Back Propagation (BP) neural network to predict implied volatility and found that this model outperforms other models in prediction exercises.
Suleymanov et al. (
2024) analyzed nine stocks from Nasdaq-100 and found that volatility clustering is continuous for the sample with a forecastable impact on variability.
Gao et al. (
2018) studied straddle option strategy returns around earnings announcements and found that the returns are positive and significant in these periods, whereas they are negative in normal periods. They also documented that smaller firms and firms with higher historical volatility, transaction costs, and with more volatile historical earnings surprises have higher positive straddle strategy returns around earning announcements. In exploring these results, we observed that the implied volatility of stocks surges before the earnings call. Thus, the implied volatility of the stock gets higher just before the straddle strategy. This means that a trader opens a position when the implied volatility of the stock increases, which leads to higher premiums and the released earnings announcement cannot create sufficient volatility. To mitigate the problem, we propose measuring the volatility of an underlying stock in the last predefined period and comparing it with historical volatility.
We extended these studies and built a model which gave us insights into the changing of volatility for upcoming days unrelated to any corporate events by analyzing assets’ volatility in currency. Exploring the volatility in currency with a given quantitative and statistical model within the selecting period, our model is designed to analyze stocks’ historical and actual volatility in currency. Visualized data give decision-makers a better prediction of the changing premium of the option. A higher actual volatility in currency indicates a higher value of the premium and vice versa. The estimation of such volatilities in currency can be used in building various multi-leg option strategies. We developed the AON software v2.0 and algorithm based on the empirical work experience of several years. The process is depicted in
Chart 1. The algorithm has proven its effectiveness many times, and allows us to predict the success of our trading strategies within a 95% confidence interval and see that these estimated price volatilities can be used in short and long straddles.
The primary objective of this study was to identify stocks suitable for implementing a straddle strategy based on volatility criteria. At the 95% confidence interval, we aimed to ascertain maximum volatility for selection at the highest percentile and minimum volatility for selection at the lowest percentile. A key limitation of this research was the assumption that stocks will either sustain or decrease volatility at these extreme percentiles over time.
In this paper, we describe the entire algorithm for making investment decisions and building typical trading strategies in the market as of 1 April 2021. Thus, instead of a standard description of the history of successful trading, we show which option positions we would analyze to make a profit with a pre-calculated probability of success.
This study demonstrates the algorithm for analyzing the current market and building a trading strategy by placing a potential order with execution for the future (until 21 May 2021, the regular expiration date for stock option trading on CBOE), and provides a unique opportunity to evaluate the success of this strategy in the near future. The rest of the paper is structured as follows.
Section 2 describes the data and methodology used in the study.
Section 3 discusses the empirical findings. Finally,
Section 4 presents a summary and the concluding remarks.
2. Data and Methodology
We use S&P500 index mid-cap stocks with the market capitalization of over USD 2 billion. The daily prices from 10 February 2020 to 1 April 2021 for selected stocks are studied. The SPX experienced a significant decline (−34.6%), reaching 2191.86 by 23 March 2020. Remarkably, the SPX took approximately 6 months to recover from this downturn, regaining its pre-crash levels by September 2020. This significant period of volatility and recovery is a key focus of our research. Applying the following criteria, we narrowed the selection.
Price: Less than USD 150. We are setting a maximum asset price of USD 150 to ensure accessibility among investors, fostering liquidity and making premiums more affordable when purchasing both call and put options.
Average intraday volume: Over 750,000 transactions to include those with strong liquidity and investment potential.
Ratio of the current and 3-month average intraday adjusted volume: Over 0.75 to reinforce the efficacy of the primary screening process.
Optionable and short able. Filtering the market with these criteria, we came up with a list of 130 more liquid stocks.
Appendix A presents the selected stocks.
Methodology
Our study starts from a defined expiry date; earnings call at least 25 trading days (in this study 35 trading days) before regular expiry date. The chosen expiry date is the optimal holding period (OHP) for this study. Once the OHP is defined, we applied our model to build bars using the same number of daily candles. This bar shows actual volatility in currency (
$) for the selected period. To measure the level of volatility in currency and perform statistical analysis, we set up new bars with simple moving average (SMA) using historical data (–in this study 250 trading days). After building all bars, we undertook statistical analysis to find the maximum and minimum volatilities in the currency, and then added values to see dispersion in the 95% confidence interval. As a result of these analyses, visualized data show maximum and minimum volatility in the currency for a selected number of bars. We can compare the actual volatility in currency with historical volatility in the currency. In analyzing assets by this model, we can open position when the volatility in currency is maximally near the historically low volatility in currency, because the volatility in currency can be changing during OHP. Our aim was to calculate the maximum and minimum price movements in one direction. We built Fintech software v2.0, which enables calculations, analysis, and data visualization automatically for added tickers. By applying the strategy algorithm, the software is willing to group tickers accordingly. A representative bar of a stock under study is shown in
Figure 1. To measure the highest price change in one direction, we used the closing price and the peak high and low prices.
The formulas below are applied in the calculation of the algorithm of the model. Using these formulas, we determined the maximum price movement in each period and maximum price movement in one direction. The first step is to choose the optimal holding period of 35 days for the study. The second step is to choose the necessary data length, herein 250 bars. Based on these inputs, we obtained the maximum and minimum historical volatility in USD, as well as the volatility of the last bar. To make Formulas (1) and (2) applicable, we first combined the bars. Calculating
in Formula (1), we found the range of the maximum and minimum prices of the stocks during the period.
where
κ denotes the closing price of the first day in the bar,
μ denotes the minimum of the low prices in the bar, and
η denotes the maximum of the high prices.
We combined bars based on the selected trading days; then, we compared the last bars with the remaining bars. The software calculates bars applying the simple moving average method.
where
k is the distance from close to close,
Μ denotes the minimum of the closing prices in the bar, and
H denotes the maximum of the closing prices. Using the formula, we calculated the range of the maximum and minimum price movements of the stock in one direction within the selected period. The system automatically combined bars based on the selected trading days; then, we compare the last bars with remaining bars.
We calculated daily volatility with the following:
where
is the volatility,
is previous day’s closing price,
is the minimum price on day
t, and
is the maximum price on day
t.
Estimating Equations (1)–(3) through the selected stock data, we obtain the implied volatility in USD. We converted these data to percentage and set up a 5% airbag–95% confidence interval level. We added them in percentile and visualized the data. By using these levels, we compared historical bars with the last bar and proceeded to make decisions on whether to open a position or not. It means that by evaluating the last bar, there is the possibility to identify either the long or short straddle strategy. The main limitation of this algorithm is that volatility can increase above 95% or decrease below 5%. For this reason, we set a 95% confidence interval and checked bars in the percentile histogram, which provides some opinion from past data. All charts are presented in the
Appendix A and
Appendix B of this paper.
3. Discussion
As a result of screening the market, we selected 130 stocks listed on the S&P500 Index. We obtained strategy prices from a broker as of 1 April 2021. All other calculations include 1-year historical data for 35 trading days up to 21 May 2021, the regular expiration day for options.
We screened stocks to get the best result, and as a first step, we started from the analysis of the bid/ask ratios. We eliminated stocks with a bid/ask ratio of 10% or more from our analysis. There is a high liquidity risk as we open the position with the indicated ask price, while the bid price is significantly low. To mitigate this type of risk, it is possible to set orders. In sorting for liquidity based on the bid–ask spread of 10%, we first eliminated 64 stocks which had a bid–ask spread higher than 10%. Then, the remaining 66 stocks were filtered against last bar’s rank in a percentile histogram to be less than 25%. A higher value of last bars means higher volatility of the stock and higher premium prices. The list of all stocks, with their bid–ask ratio and the last bar’s percentile and other information, is provided in
Appendix A.
We then checked the percentage level of the last bars, comparing them with historical data to locate the last bars in the percentile histogram. As a result, we eliminated 30 more stocks, leaving only 36 tickers in the pool. We further manually checked the histogram levels calculated by the algorithmic system to get the best results.
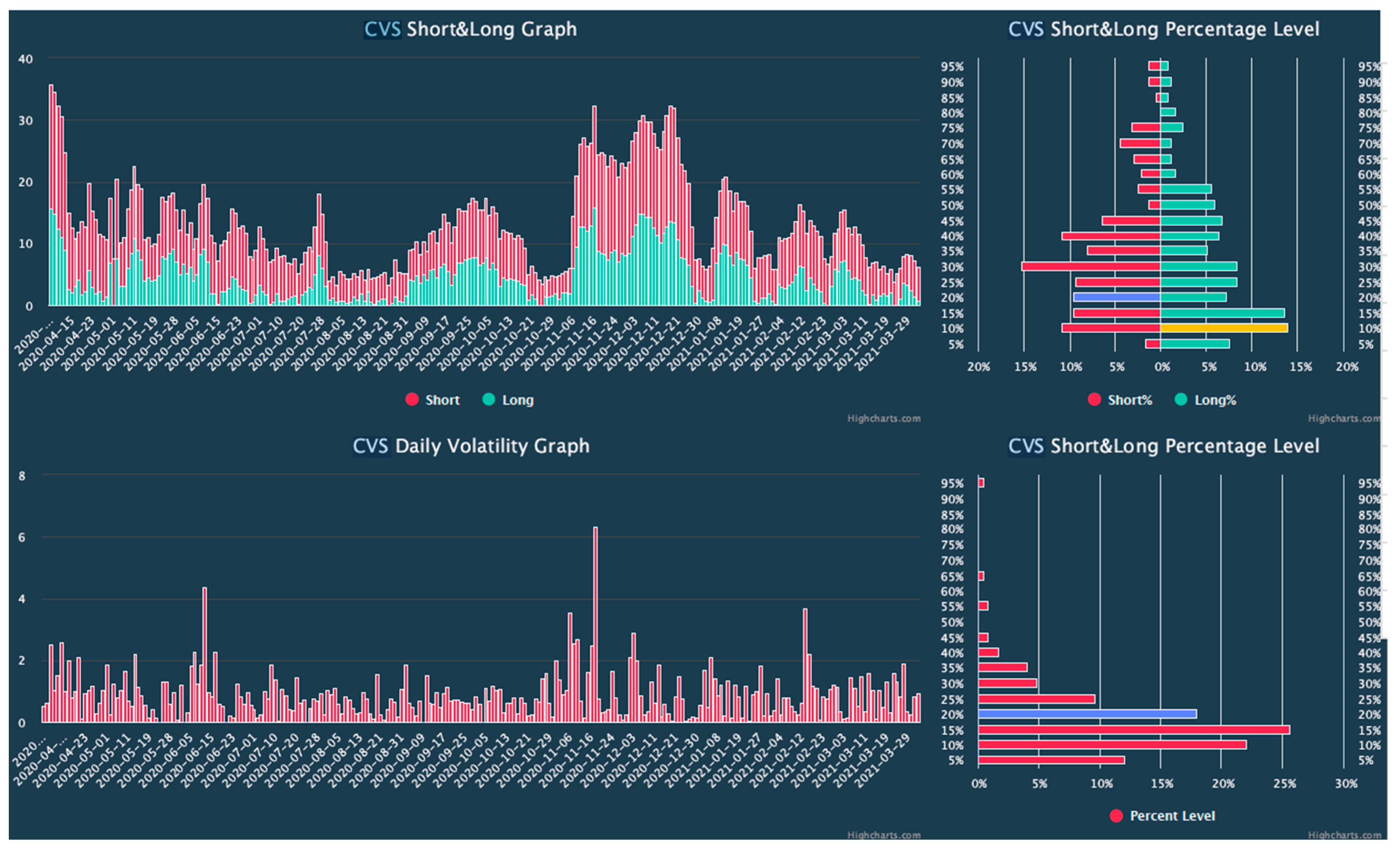
In the third stage, we proceeded to select the stocks with a volatility nearest to the minimum of the histogram and determined that the stocks CTSH, CVS, EIX, KO, NEM, VFC, and MKC are more suitable for building the straddle strategies.
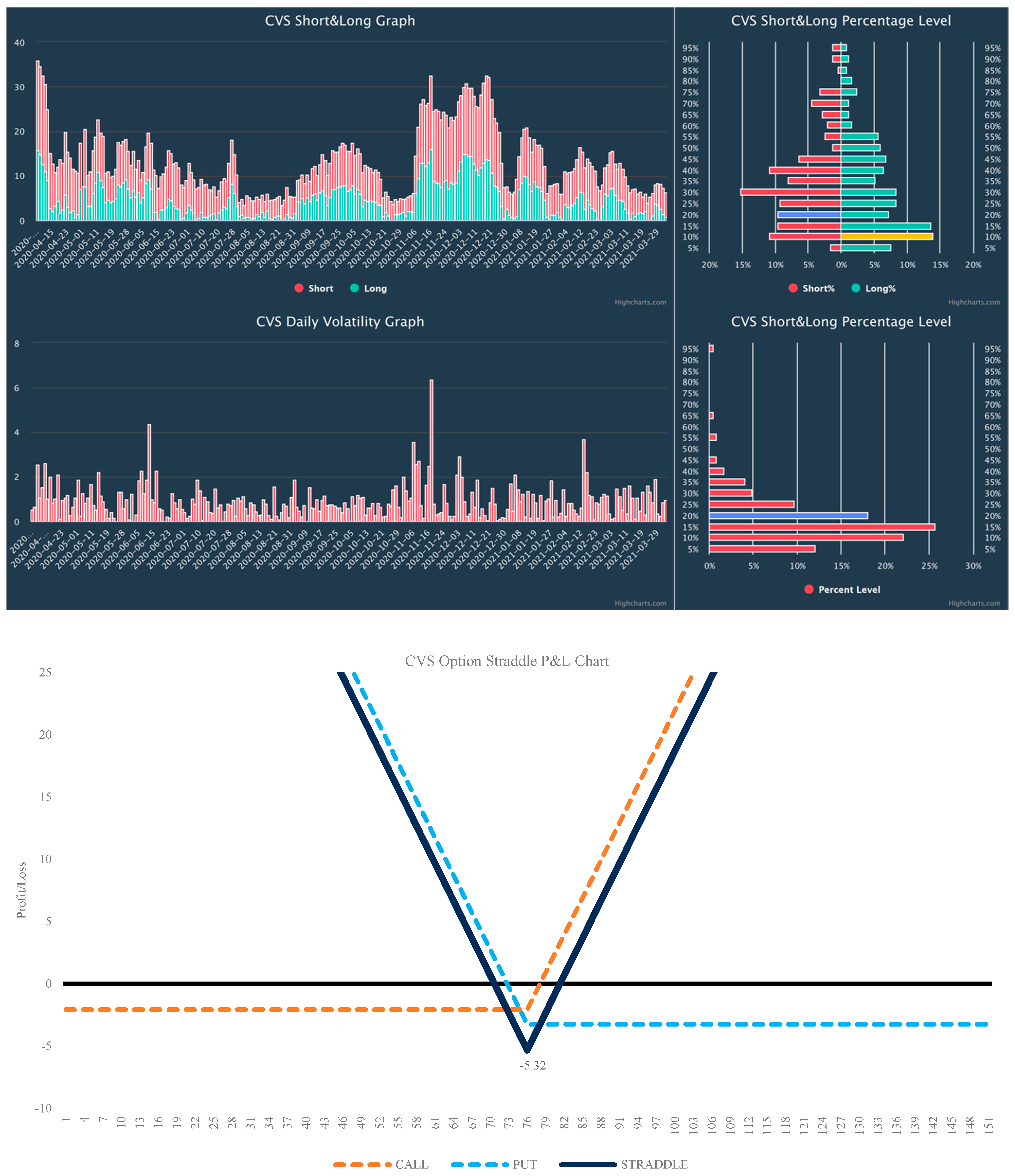
Figure 2 shows the characteristics of the selected CVS stock as a representative. Other finalist stocks’ bars are presented in
Appendix B.
At this point, we are in the position to estimate the call and put options’ premiums. According to the
Black and Scholes (
1973) model, it is clear that if a stock’s volatility increases, the premium of its option increases as well. As we calculate the volatility of the last bar for the predefined optimal holding period, we must compare it with the historical volatility. To implement this, we built bars with the same period by using historical data. Visualizing these bars, we constructed histograms and applied percentile ranking with a 95% confidence interval to see the level of the last recent bar’s volatility of the stock and compare it with its historical volatility. If the last bar’s volatility is low, it means that the stock’s volatility will most likely increase, and we expect that the premium will begin to increase and our option strategy will be beneficial. In other words, for a given chart, if the last bar’s level is low, we expect that the stock’s implied volatility will rise and the premium of this strategy will also rise.
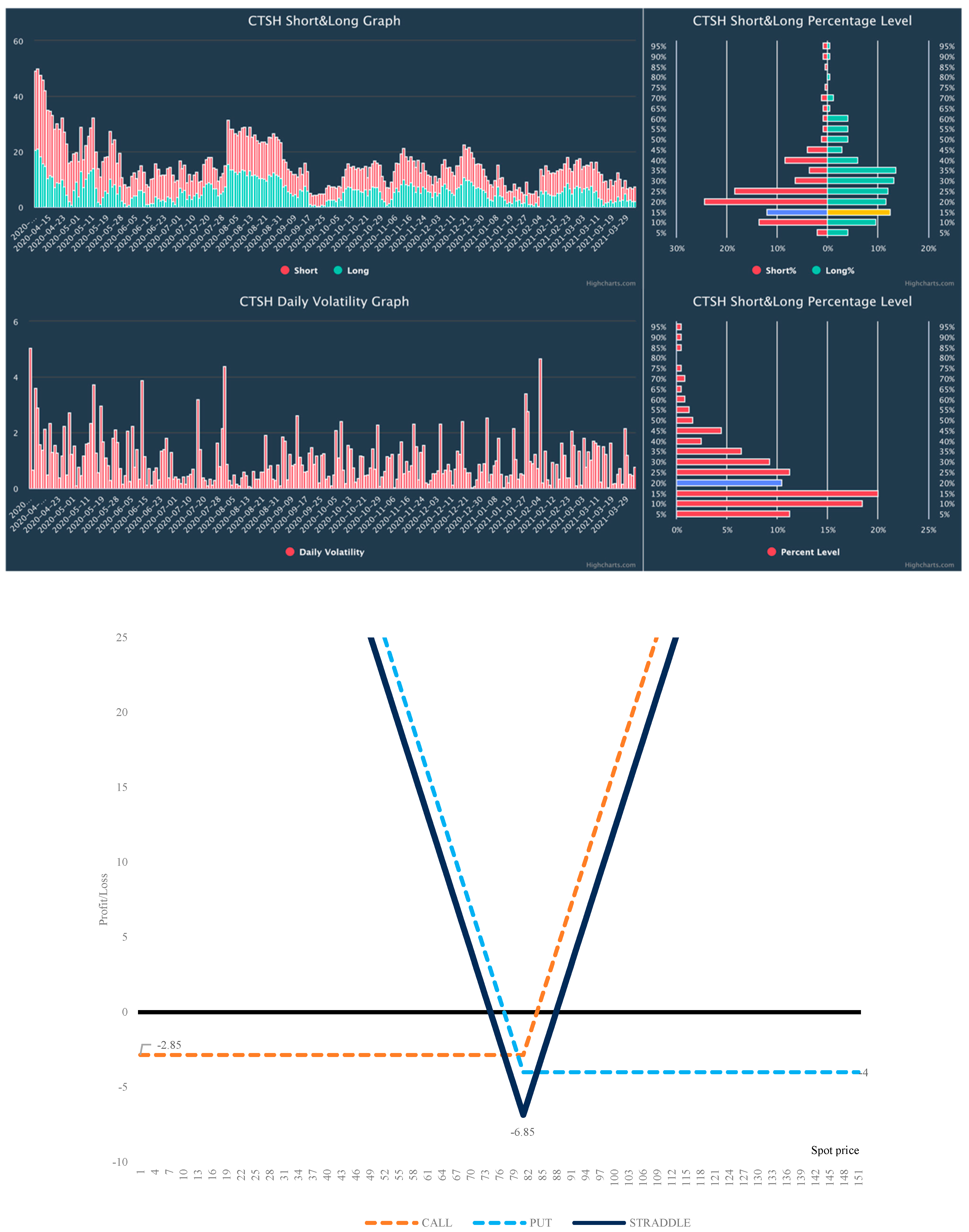
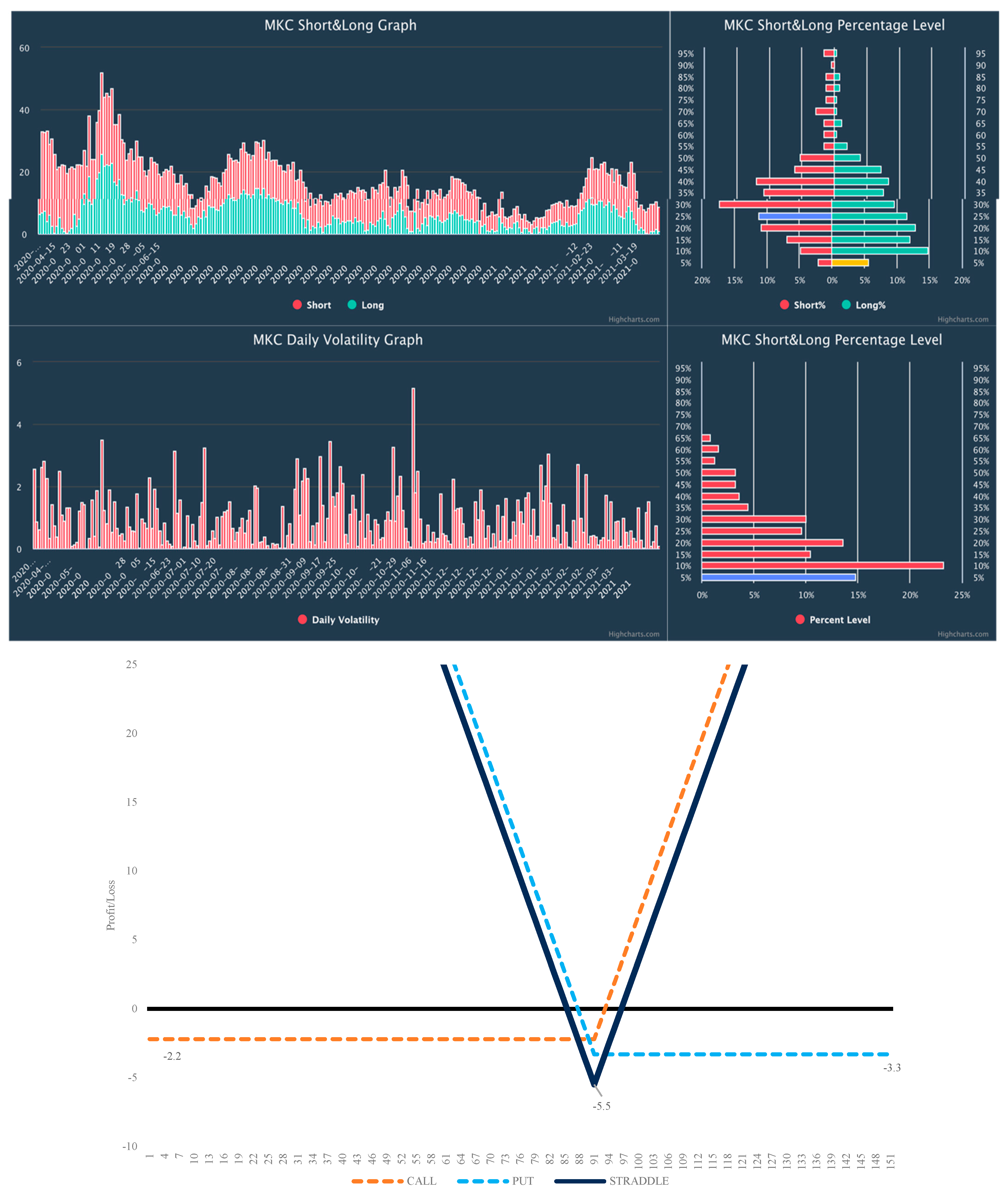
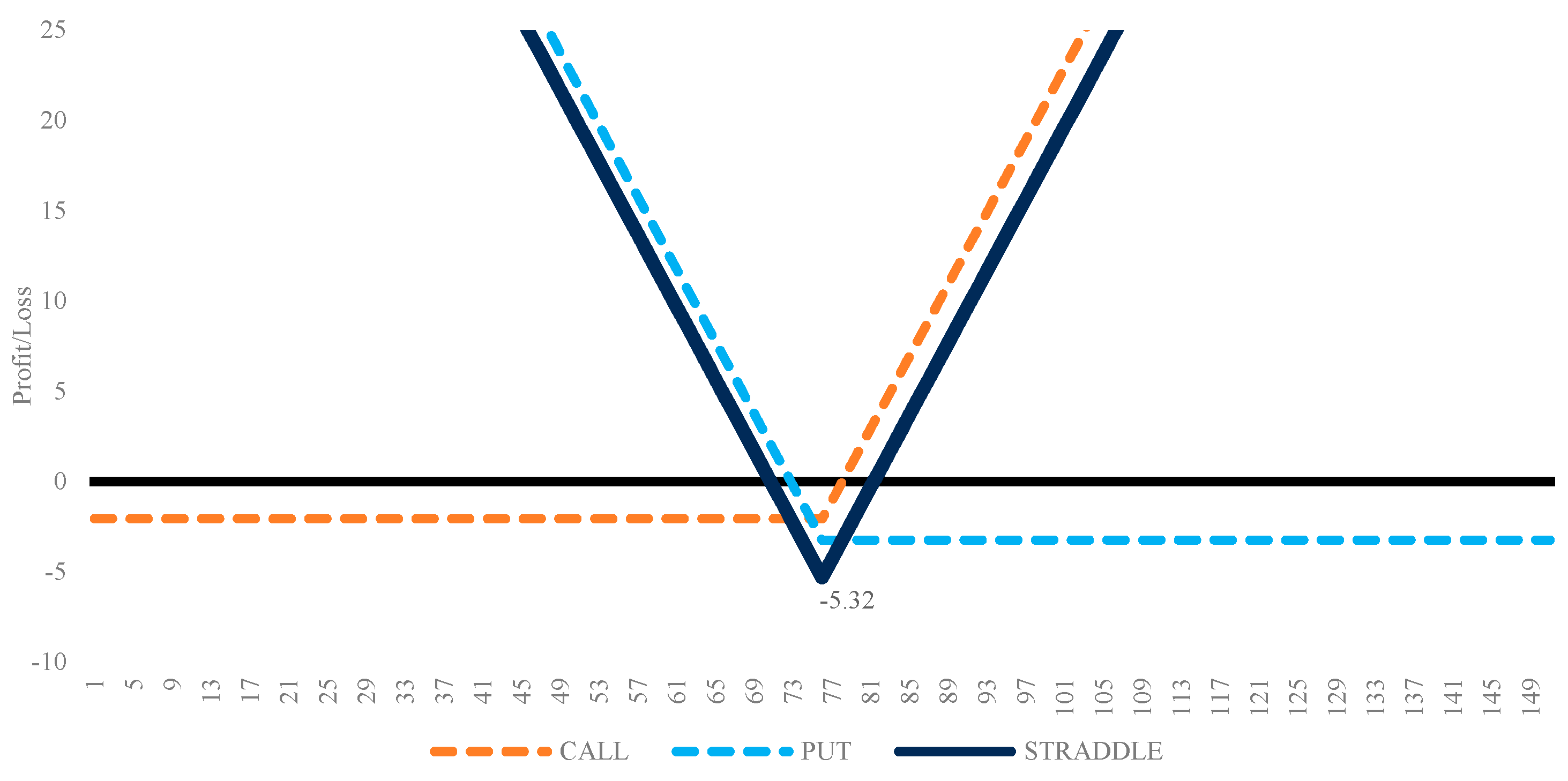
In
Figure 3 below, we observe that the total price of call and put options is USD 5.32. According to our system, we are confident that the volatility will increase, and the stock’s price will move more than the premium paid. Based on this outcome, we decided to open the long straddle strategy for the selected seven tickers. All other stocks’ charts are presented in
Appendix B.
4. Conclusions
It is well known that straddle is an option strategy of buying or selling both call and put options at the same strike price and the expiration date. The main expectation from the strategy is that the price of the underlying stock will rise or decline due to the changes in implied volatility. The main purpose of this study was to determine volatility, forecast the expected volatility based on historical volatility, and build a profitable straddle strategy.
We first ascertained an OHP of 35 days and the chance to hold the option until the expiration date. Thus, we need to have information about the volatility in the underlying stock’s price. To do this, we set up bars using the same number of historical daily candles. That means that we combined 35-days’ daily candles and obtained one bar. Then, we measured the volatility of the bar with Equations (1) and (2). The results show the maximum and minimum movements of volatility in one direction. Following this procedure and based on historical data, we set up 250 bars and calculated the volatility of each bar to be able to compare it with the most recent bar.
Based on the maximum and minimum movements of the bars, we put in max 95%–min 5% percentile ranking at the 95% confidence level and visualize the histograms. We were then able to see exactly when the stock was more volatile and the range of high movements. Using this, we examined the volatility of the recent bar and compared it with other bars and the whole histogram. If the volatility of the recent bar was near or on the minimum of the predefined interval, then the long straddle position was appropriate. On the other hand, if the volatility of the recent bar was near or on the maximum of the predefined interval, then the short straddle position was beneficial.
To automate and speed up the calculations, we developed a software named analytical option navigator (AON). We selected 130 stocks from S&P500 with the current price of less than USD 100, trading volume of less than 750,000, and other filters for the period of 1 April to 21 May 2021.
With these stocks, we set up 250 bars and applied elimination rules to arrive at seven stocks which were appropriate for the long straddle strategy. This technique and algorithm can be improved in the future via artificial intelligence to cover more historical data and speed up the strategy selection process. Our empirical exercise indicates that the stocks analyzed with the algorithm generate positive returns along a spectrum of changing volatilities of the underlying assets.
The scope of this study is not confined to equities alone; it encompasses a broad range of financial instruments, including exchange-traded funds (ETFs), individual stocks, indexes, and futures, provided that the data are meticulously curated. Future research endeavors may focus on integrating cryptocurrency and foreign exchange (ForEx) pairs, with the intention of applying these findings to leveraged products.
Author Contributions
Conceptualization, O.R. and F.A.; methodology, O.R. and R.A.; software, O.R.; validation, E.S. and F.A.; resources, E.S.; data curation, O.R. and R.A.; writing—original draft preparation, O.R. and F.A; writing—review and editing, R.A. and E.S.; visualization, O.R.; supervision, R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
| Ticker | Last Price | Max High Move * | Max Low Move * | Last Bar * | Last Bar in Percentile * | Min High Move ** | Min Low Move ** | Last Bar ** | Last Bar in Percentile ** | Strategy Ask | Strategy Bid | CALL BID | CALL ASK | PUT ASK | PUT BID | Bid/Ask Spread |
|---|
| ADM | 57.65 | 15.53 | 1.7 | 4.2 | 21.27 | 8.67 | 0.03 | 2.73 | 33.12 | 4.85 | 4.35 | 3.4 | 3.8 | 1.05 | 0.95 | 0.8969072 |
| AES | 27.07 | 12.92 | 1.33 | 3.17 | 19.29 | 7.68 | 0 | 0.93 | 15.9 | 2.65 | 2.45 | 1.2 | 1.3 | 1.35 | 1.25 | 0.9245283 |
| AMCR | 11.66 | 4.47 | 0.41 | 0.97 | 17.41 | 2.74 | 0.01 | 0.36 | 16.54 | 1.05 | 0.8 | 0.2 | 0.35 | 0.7 | 0.6 | 0.7619048 |
| AMD | 81.09 | 39.36 | 5.08 | 18.8 | 41.02 | 36.84 | 0.02 | 11.57 | 33.23 | 9.55 | 9.25 | 5.2 | 5.35 | 4.2 | 4.05 | 0.9685864 |
| AOS | 67.87 | 13.98 | 2.74 | 9.04 | 55.44 | 13.53 | 0 | 6.78 | 50.1 | 6.65 | 6.05 | 1.85 | 2.05 | 4.6 | 4.2 | 0.9097744 |
| APA | 18.85 | 24.78 | 1.93 | 6.87 | 24.46 | 22.24 | 0.01 | 1.87 | 12.53 | 3.99 | 3.45 | 1.22 | 1.39 | 2.6 | 2.23 | 0.8646617 |
| APH | 67.05 | 20.33 | 2.62 | 7.71 | 30.91 | 13.7 | 0.03 | 0.76 | 9.77 | 7.25 | 5.05 | 3.6 | 4.7 | 2.55 | 1.45 | 0.6965517 |
| ATVI | 95.54 | 23.1 | 3.95 | 14.18 | 53.08 | 21.09 | 0.04 | 7.7 | 37.75 | 9.1 | 8.8 | 4.5 | 4.65 | 4.45 | 4.3 | 0.967033 |
| BAC | 39.49 | 16.9 | 1.52 | 7.09 | 37.59 | 12.88 | 0.01 | 6.61 | 51.15 | 3.67 | 3.55 | 1.55 | 1.59 | 2.08 | 2 | 0.9673025 |
| BAX | 84.32 | 24.06 | 3.03 | 8.7 | 29.27 | 17.12 | 0.02 | 6.46 | 38.89 | 7.55 | 5.5 | 3.5 | 4.7 | 2.85 | 2 | 0.7284768 |
| BEN | 30.16 | 10.76 | 1.77 | 3.33 | 20.62 | 9.3 | 0 | 2.94 | 33.45 | 2.25 | 1.9 | 1.1 | 1.25 | 1 | 0.8 | 0.8444444 |
| BF-B | 69.65 | 26.87 | 3.59 | 8.71 | 24.79 | 20.31 | 0.01 | 6.8 | 35.1 | 7.55 | 1.9 | 0.4 | 4.7 | 2.85 | 1.5 | 0.2516556 |
| BKR | 21.73 | 11.79 | 1.69 | 3.11 | 17.65 | 9.16 | 0.05 | 0.8 | 12.41 | 2.85 | 2.5 | 1.05 | 1.2 | 1.65 | 1.45 | 0.877193 |
| BLL | 86.27 | 27.3 | 4.29 | 7.79 | 18.69 | 16.43 | 0.02 | 2.26 | 17.29 | 6.65 | 6.15 | 2.45 | 2.65 | 4 | 3.7 | 0.924812 |
| BMY | 62.93 | 20.31 | 2.69 | 4.43 | 13.89 | 16.26 | 0.02 | 2.94 | 21.18 | 4.08 | 3.94 | 2.24 | 2.31 | 1.77 | 1.7 | 0.9656863 |
| CFG | 44.94 | 24.66 | 2.12 | 7.19 | 25.24 | 19.88 | 0.01 | 4.57 | 25.65 | 5.25 | 4.6 | 2.1 | 2.5 | 2.75 | 2.5 | 0.8761905 |
| CHD | 86.53 | 28.63 | 2.53 | 6.1 | 17.31 | 22.18 | 0.08 | 3.29 | 18.07 | 6.7 | 6.1 | 3.7 | 4 | 2.7 | 2.4 | 0.9104478 |
| CHRW | 97.15 | 22.56 | 3.41 | 7.94 | 26.29 | 18.89 | 0.02 | 6.19 | 34.43 | 8.1 | 7.4 | 3.5 | 3.9 | 4.2 | 3.9 | 0.9135802 |
| CL | 78.55 | 18.2 | 1.49 | 4.97 | 23.74 | 9.79 | 0.03 | 0.56 | 9.89 | 4.65 | 4.25 | 2.45 | 2.7 | 1.95 | 1.8 | 0.9139785 |
| CMA | 71.74 | 39.15 | 4.02 | 10.69 | 22.09 | 33.77 | 0.01 | 8.7 | 28.17 | 8.4 | 7.5 | 3.5 | 3.8 | 4.6 | 4 | 0.8928571 |
| CMCSA | 54.75 | 14.44 | 2.24 | 5.84 | 31.56 | 9.86 | 0.01 | 2 | 23.18 | 4.18 | 3.62 | 1.52 | 1.73 | 2.45 | 2.1 | 0.8660287 |
| CNC | 63.25 | 29.15 | 3.37 | 5.26 | 11.6 | 21.2 | 0.08 | 2.19 | 13.99 | 6.85 | 5.84 | 3.2 | 3.9 | 2.95 | 2.64 | 0.8525547 |
| CPB | 49.97 | 13.14 | 1.37 | 5.26 | 34.75 | 11.09 | 0 | 3 | 29.35 | 3.35 | 2.95 | 1.3 | 1.55 | 1.8 | 1.65 | 0.880597 |
| CSCO | 51.98 | 14.45 | 1.59 | 5.36 | 31.38 | 9.92 | 0.04 | 4.4 | 44.72 | 3.91 | 3.77 | 1.46 | 1.5 | 2.41 | 2.31 | 0.9641944 |
| CTSH | 78.88 | 30.08 | 3.12 | 5.41 | 12.64 | 21.08 | 0.15 | 1.91 | 12.57 | 6.85 | 6.51 | 2.63 | 2.85 | 4 | 3.88 | 0.950365 |
| CTVA | 46.74 | 11.19 | 1.9 | 4.94 | 34.45 | 9 | 0.05 | 3.2 | 36.68 | 4.85 | 4.05 | 2.05 | 2.3 | 2.55 | 2 | 0.8350515 |
| CVS | 74.3 | 19.96 | 2.8 | 5.58 | 19.58 | 15.93 | 0.01 | 0.7 | 8.9 | 5.32 | 5.17 | 2.02 | 2.07 | 3.25 | 3.15 | 0.9718045 |
| DISCA | 43.31 | 38.06 | 1.83 | 32.59 | 81.41 | 35.85 | 0 | 2.24 | 10.62 | 8.6 | 8.4 | 4.5 | 4.9 | 3.7 | 3.9 | 0.9767442 |
| DOW | 64.6 | 26.81 | 3.26 | 9.6 | 29.23 | 17.2 | 0.06 | 6.93 | 41.07 | 6.5 | 5.78 | 2.73 | 3 | 3.5 | 3.05 | 0.8892308 |
| DRE | 42.86 | 13.64 | 1.77 | 4.22 | 23.58 | 7.64 | 0 | 0.9 | 15.6 | 3.8 | 2.9 | 0.35 | 0.7 | 3.1 | 2.55 | 0.7631579 |
| DUK | 96.28 | 40.3 | 3.53 | 7.5 | 14.72 | 21.31 | 0.01 | 5.86 | 29.72 | 5.6 | 5.15 | 1.65 | 1.8 | 3.8 | 3.5 | 0.9196429 |
| DVN | 23.5 | 18.02 | 1.15 | 6.83 | 35.3 | 14.01 | 0 | 4.2 | 31.98 | 4.02 | 3.55 | 1.59 | 1.68 | 2.34 | 1.96 | 0.8830846 |
| EIX | 58.29 | 33.94 | 2.47 | 4.42 | 10.58 | 23.95 | 0 | 0.05 | 5.19 | 4.2 | 3.89 | 2.39 | 2.5 | 1.7 | 1.5 | 0.9261905 |
| EMR | 90.41 | 34.34 | 3.6 | 8.22 | 18.53 | 22.05 | 0.01 | 5.25 | 26.4 | 7 | 6.3 | 3.2 | 3.5 | 3.5 | 3.1 | 0.9 |
| EOG | 75.34 | 50.28 | 4.72 | 17.51 | 30.27 | 35.95 | 0.14 | 15.7 | 44.11 | 12.25 | 10.15 | 4.95 | 6.25 | 6 | 5.2 | 0.8285714 |
| EW | 83.84 | 26.93 | 4.82 | 9.63 | 24.58 | 22.61 | 0 | 4.23 | 21.84 | 7.6 | 5.95 | 2.45 | 3.2 | 4.4 | 3.5 | 0.7828947 |
| EXC | 43.91 | 21.1 | 1.34 | 4.39 | 18.89 | 14.06 | 0.01 | 1.17 | 12.43 | 2.9 | 2.65 | 1.15 | 1.3 | 1.6 | 1.5 | 0.9137931 |
| FANG | 81.22 | 64.74 | 4.75 | 20.98 | 29.35 | 46.28 | 0.07 | 13.45 | 31.06 | 15.1 | 14.1 | 7.5 | 8 | 7.1 | 6.6 | 0.9337748 |
| FAST | 51.11 | 12.3 | 1.86 | 4.09 | 24.22 | 11.56 | 0 | 4.04 | 36.45 | 4.6 | 4.2 | 2.75 | 2.95 | 1.65 | 1.45 | 0.9130435 |
| FBHS | 97.15 | 39.09 | 4.37 | 10.02 | 19.65 | 31.99 | 0.02 | 6.73 | 23.89 | 9.2 | 8.3 | 4 | 4.4 | 4.8 | 4.3 | 0.9021739 |
| FE | 34.31 | 21.13 | 1.49 | 5.76 | 24.57 | 16.4 | 0.03 | 3.19 | 22.37 | 2.7 | 2.44 | 1.2 | 1.35 | 1.35 | 1.24 | 0.9037037 |
| FITB | 37.98 | 18.73 | 1.64 | 8.21 | 39.6 | 13.78 | 0.01 | 5.73 | 42.39 | 4.15 | 3.8 | 1.9 | 2.05 | 2.1 | 1.9 | 0.9156627 |
| FOX | 35 | 18.4 | 1.74 | 11.39 | 57.13 | 12.77 | 0 | 4.25 | 34.95 | 5.3 | 3.65 | 1.75 | 3 | 2.3 | 1.9 | 0.6886792 |
| FTV | 70.9 | 33.76 | 2.5 | 5.53 | 13.72 | 17.07 | 0.02 | 0.37 | 6.85 | 6.75 | 6.15 | 3.5 | 3.9 | 2.85 | 2.65 | 0.9111111 |
| GILD | 66.44 | 18.97 | 2.82 | 5.53 | 20.1 | 15.42 | 0.01 | 0.48 | 7.75 | 5.45 | 2.93 | 1.77 | 2.1 | 3.35 | 1.16 | 0.5376147 |
| GIS | 60.92 | 16.58 | 2.47 | 5.79 | 26.18 | 15.91 | 0.07 | 4.01 | 27.39 | 3.55 | 3.2 | 1.85 | 2.05 | 1.5 | 1.35 | 0.9014085 |
| GLW | 43.99 | 10.85 | 1.82 | 7.36 | 60.22 | 8.28 | 0.01 | 7.23 | 83.57 | 4.44 | 3.78 | 1.84 | 2.22 | 2.22 | 1.94 | 0.8513514 |
| GPS | 29.95 | 13.41 | 2.16 | 9.68 | 65.16 | 12.13 | 0.06 | 6.68 | 54.36 | 4.18 | 3.52 | 1.47 | 2 | 2.18 | 2.05 | 0.8421053 |
| HAS | 95.46 | 57.55 | 4.29 | 8.84 | 12.69 | 26.22 | 0.06 | 4.81 | 21.34 | 9.9 | 8.94 | 4.3 | 4.9 | 5 | 4.64 | 0.9030303 |
| HBI | 19.37 | 7.76 | 0.67 | 2.77 | 31.66 | 6.46 | 0.01 | 0.9 | 17.42 | 2.75 | 2.45 | 1.35 | 1.5 | 1.25 | 1.1 | 0.8909091 |
| HES | 74.48 | 38.66 | 5.16 | 18.32 | 40.36 | 28.43 | 0 | 16.56 | 57.42 | 9.6 | 9.1 | 4.3 | 4.6 | 5 | 4.8 | 0.9479167 |
| HFC | 38.02 | 24.55 | 2.67 | 11.08 | 39.59 | 16.85 | 0.05 | 6.71 | 40.68 | 6.5 | 5.15 | 2.45 | 3.4 | 3.1 | 2.7 | 0.7923077 |
| HIG | 68.28 | 39.49 | 2.98 | 19.24 | 45.08 | 24.58 | 0.04 | 17.92 | 70.57 | 8 | 6.65 | 2.55 | 3 | 5 | 4.1 | 0.83125 |
| HPE | 15.7 | 7.04 | 0.64 | 1.95 | 23.48 | 4.81 | 0 | 1.51 | 33.25 | 1.55 | 1.25 | 0.45 | 0.6 | 0.95 | 0.8 | 0.8064516 |
| HSIC | 68.67 | 31.86 | 4.62 | 8.92 | 19.21 | 25.85 | 0.02 | 0.95 | 8.24 | 6.55 | 6.45 | 2.25 | 2.85 | 3.7 | 4.2 | 0.9847328 |
| HWM | 31.82 | 22.69 | 1.52 | 4.21 | 16.44 | 21.96 | 0.05 | 3.07 | 17.41 | 4.35 | 4 | 1.9 | 2.1 | 2.25 | 2.1 | 0.9195402 |
| INCY | 83.01 | 41.63 | 5 | 9.47 | 15.98 | 36.15 | 0.04 | 1.98 | 9.84 | 12.8 | 4.05 | 2.2 | 7 | 5.8 | 1.85 | 0.3164063 |
| INFO | 99.5 | 36.3 | 3.74 | 6.56 | 12.79 | 22.14 | 0.02 | 6.32 | 30.63 | 8.1 | 5.55 | 2.25 | 2.7 | 5.4 | 3.3 | 0.6851852 |
| INTC | 64.55 | 23.48 | 3.11 | 6.78 | 21.21 | 15.8 | 0.05 | 3.89 | 26.94 | 6.36 | 6.1 | 2.7 | 2.81 | 3.55 | 3.4 | 0.9591195 |
| IP | 54.29 | 16.89 | 2.39 | 8.81 | 44.85 | 11.81 | 0.02 | 6.12 | 51.56 | 4.8 | 4.2 | 1.75 | 2.05 | 2.75 | 2.45 | 0.875 |
| IR | 49.61 | 21.64 | 2.02 | 7.58 | 30.5 | 12.95 | 0.01 | 5.58 | 43.74 | 4.95 | 4.5 | 2.05 | 2.3 | 2.65 | 2.45 | 0.9090909 |
| IVZ | 25.75 | 10.65 | 0.95 | 3.47 | 28.38 | 8.66 | 0.02 | 3.16 | 37.71 | 3.3 | 2.95 | 1.3 | 1.45 | 1.85 | 1.65 | 0.8939394 |
| K | 63.34 | 16.56 | 2.33 | 8.32 | 42.88 | 9.7 | 0.05 | 6.34 | 63.66 | 4.05 | 3.75 | 2.35 | 2.5 | 1.55 | 1.4 | 0.9259259 |
| KEY | 20.27 | 12.57 | 0.95 | 2.98 | 20.72 | 9.61 | 0 | 1.44 | 18.49 | 3.2 | 2.6 | 1.35 | 1.8 | 1.4 | 1.25 | 0.8125 |
| KIM | 19.2 | 11.62 | 1.19 | 1.86 | 10.78 | 10.41 | 0.05 | 1.25 | 15.42 | 2.2 | 1.97 | 0.57 | 0.65 | 1.55 | 1.4 | 0.8954545 |
| KMI | 16.84 | 12.82 | 0.75 | 2.18 | 15.66 | 8.02 | 0.01 | 2.15 | 29.04 | 1.46 | 1.36 | 0.47 | 0.52 | 0.94 | 0.89 | 0.9315068 |
| KO | 52.51 | 23.86 | 1.85 | 3.64 | 12.32 | 13.26 | 0 | 2.21 | 20 | 2.91 | 2.8 | 1.43 | 1.49 | 1.42 | 1.37 | 0.9621993 |
| LW | 78.08 | 56.81 | 3.62 | 9.15 | 14.36 | 44.05 | 0.02 | 0.82 | 6.64 | 8.4 | 6.8 | 2.1 | 3.4 | 5 | 4.7 | 0.8095238 |
| LYV | 88.07 | 54.38 | 5.19 | 13.59 | 20.37 | 39.62 | 0.01 | 7.03 | 20.95 | 11.6 | 11 | 5.8 | 6.1 | 5.5 | 5.2 | 0.9482759 |
| MAS | 60.99 | 18.51 | 2.82 | 6 | 23.24 | 14.01 | 0.02 | 5.98 | 43.34 | 4.9 | 4.55 | 2.65 | 2.85 | 2.05 | 1.9 | 0.9285714 |
| MDLZ | 58.44 | 18.47 | 1.38 | 4.55 | 21.69 | 8.86 | 0.01 | 2.76 | 32.97 | 3.55 | 3.3 | 2.15 | 2.3 | 1.25 | 1.15 | 0.9295775 |
| MGM | 39.7 | 26.44 | 1.66 | 6.74 | 23.45 | 19.11 | 0.07 | 4.4 | 25.47 | 5.65 | 5.4 | 2.53 | 2.65 | 3 | 2.87 | 0.9557522 |
| MKC | 89.24 | 26.42 | 2.57 | 7.85 | 24.92 | 25.51 | 0.08 | 0.64 | 6.98 | 5.5 | 5 | 2 | 2.2 | 3.3 | 3 | 0.9090909 |
| MNST | 91.36 | 20.34 | 3.98 | 6.98 | 21.5 | 16.31 | 0.15 | 1.42 | 12.07 | 8 | 6.8 | 4.2 | 4.5 | 3.5 | 2.6 | 0.85 |
| MO | 51 | 14.94 | 2.18 | 9.28 | 55.08 | 10.87 | 0 | 7.69 | 68.67 | 3.75 | 3.58 | 2.31 | 2.44 | 1.31 | 1.27 | 0.9546667 |
| MOS | 31.26 | 12.91 | 1.51 | 7.35 | 51.11 | 8.85 | 0.01 | 3.41 | 39.62 | 4.73 | 4.45 | 2.37 | 2.51 | 2.22 | 2.08 | 0.9408034 |
| MPC | 55.8 | 45 | 2.99 | 10.17 | 20.38 | 35.95 | 0.14 | 6.04 | 19.83 | 7.65 | 7.26 | 3.85 | 4 | 3.65 | 3.41 | 0.9490196 |
| MRO | 11.79 | 7.45 | 0.57 | 4.54 | 56.93 | 6.79 | 0 | 3.04 | 45.29 | 2.18 | 2.08 | 0.93 | 0.98 | 1.2 | 1.15 | 0.9541284 |
| MS | 78.22 | 29.11 | 3.01 | 12.92 | 39.17 | 19.37 | 0.03 | 4.5 | 25.8 | 7.54 | 7.24 | 2.59 | 2.74 | 4.8 | 4.65 | 0.9602122 |
| MU | 92.41 | 28.86 | 3.55 | 9.27 | 25.34 | 22.99 | 0.09 | 5.93 | 27.95 | 10.75 | 10.4 | 5.25 | 5.4 | 5.35 | 5.15 | 0.9674419 |
| MXIM | 95.45 | 21.27 | 2.95 | 10.12 | 40.22 | 16.82 | 0.03 | 0.51 | 7.57 | 10.4 | 8.2 | 4.3 | 5.4 | 5 | 3.9 | 0.7884615 |
| NEM | 61.81 | 25.5 | 4.27 | 5.25 | 9.15 | 23.99 | 0.1 | 3.43 | 17.55 | 5.71 | 5.4 | 3.63 | 3.85 | 1.86 | 1.77 | 0.9457093 |
| NTAP | 73.65 | 22.75 | 2.65 | 10.33 | 39.39 | 21.78 | 0.01 | 4.49 | 23.52 | 7.5 | 6.7 | 2.4 | 2.9 | 4.6 | 4.3 | 0.8933333 |
| NUE | 79.88 | 29.06 | 3.25 | 27.91 | 90.99 | 26.32 | 0.17 | 25.03 | 90.56 | 9.2 | 8.6 | 4.2 | 4.5 | 4.7 | 4.4 | 0.9347826 |
| NWS | 24 | 7.17 | 1.08 | 2.67 | 28.5 | 6.69 | 0.02 | 1.03 | 18.63 | 4 | 1.2 | 0.2 | 1.8 | 2.2 | 1 | 0.3 |
| O | 65.11 | 44.44 | 2.55 | 4.66 | 9.53 | 33.59 | 0.01 | 2.18 | 10.82 | 3.65 | 3.35 | 1.65 | 1.75 | 1.9 | 1.7 | 0.9178082 |
| OKE | 51.35 | 65.36 | 2.51 | 7.63 | 12.33 | 53.61 | 0.05 | 7.07 | 16.8 | 5.95 | 5.55 | 3.1 | 3.3 | 2.65 | 2.45 | 0.9327731 |
| OMC | 75.91 | 32.41 | 2.96 | 11.92 | 32.38 | 24.91 | 0.06 | 9.89 | 40.6 | 7.1 | 6.25 | 3.5 | 4.1 | 3 | 2.75 | 0.8802817 |
| ORCL | 71.81 | 15.8 | 2.11 | 10.92 | 62.92 | 13.17 | 0.02 | 9.11 | 67.21 | 4.56 | 4.4 | 1.74 | 1.8 | 2.76 | 2.66 | 0.9649123 |
| OXY | 27.38 | 33.97 | 1.83 | 7.54 | 20.99 | 28.67 | 0.15 | 2.4 | 12.1 | 5.04 | 4.75 | 2.55 | 2.72 | 2.32 | 2.2 | 0.9424603 |
| PAYX | 98.76 | 42.36 | 3.35 | 10.72 | 22 | 25.29 | 0.03 | 8.47 | 35.07 | 8.1 | 5.35 | 3.3 | 4.7 | 3.4 | 2.05 | 0.6604938 |
| PBCT | 18.1 | 6.98 | 0.74 | 4.35 | 57.07 | 6.26 | 0 | 3.05 | 48.85 | 2.3 | 1.65 | 0.75 | 1.05 | 1.25 | 0.9 | 0.7173913 |
| PCAR | 92.03 | 26.43 | 3.67 | 8.99 | 26.04 | 18.92 | 0.1 | 6.57 | 35.94 | 8.1 | 7.3 | 3.7 | 4 | 4.1 | 3.6 | 0.9012346 |
| PEAK | 32.71 | 18.7 | 1.3 | 2.34 | 10.38 | 14.21 | 0.04 | 1.51 | 14.34 | 2.65 | 2.17 | 0.75 | 1 | 1.65 | 1.42 | 0.8188679 |
| PEG | 59.67 | 25.21 | 2.4 | 4.8 | 14.47 | 12.17 | 0 | 1.1 | 13.13 | 3.75 | 3.25 | 1.45 | 1.8 | 1.95 | 1.8 | 0.8666667 |
| PGR | 95.55 | 21.22 | 5.21 | 10.61 | 35.36 | 15.4 | 0 | 9.18 | 58.65 | 6.8 | 6.1 | 3.3 | 3.6 | 3.2 | 2.8 | 0.8970588 |
| PHM | 53.48 | 29.55 | 2.83 | 7.2 | 19.72 | 24.95 | 0.01 | 3.97 | 19.29 | 6.1 | 5.7 | 2.1 | 2.3 | 3.8 | 3.6 | 0.9344262 |
| PM | 88.06 | 33.63 | 3.97 | 5.89 | 10.83 | 16.08 | 0 | 2.7 | 20.11 | 5.78 | 5.3 | 2.98 | 3.25 | 2.53 | 2.32 | 0.916955 |
| PNW | 81.81 | 43.55 | 3.05 | 6.77 | 13.27 | 27.94 | 0.01 | 5.15 | 21.56 | 7.6 | 5.05 | 3.3 | 4.5 | 3.1 | 1.75 | 0.6644737 |
| PPL | 28.77 | 17.79 | 0.91 | 2.06 | 11.13 | 11.99 | 0.02 | 0.83 | 11.09 | 1.75 | 1.5 | 0.6 | 0.75 | 1 | 0.9 | 0.8571429 |
| PSX | 83.16 | 50.15 | 5.14 | 13.35 | 21.42 | 34.58 | 0.5 | 5.92 | 19.31 | 9.9 | 9.2 | 4.6 | 5 | 4.9 | 4.6 | 0.9292929 |
| PWR | 89.17 | 20.24 | 2.98 | 13.21 | 58.34 | 16.61 | 0.08 | 12.16 | 70.77 | 9.4 | 8.8 | 4 | 4.2 | 5.2 | 4.8 | 0.9361702 |
| RF | 21.06 | 9.6 | 0.9 | 3.27 | 29.52 | 7.43 | 0.01 | 1.72 | 25.74 | 2.45 | 2.05 | 1.05 | 1.3 | 1.15 | 1 | 0.8367347 |
| RHI | 77.66 | 27.12 | 3.56 | 10.44 | 31.28 | 21.64 | 0.12 | 4.6 | 23.74 | 8.4 | 5.6 | 1.3 | 2.9 | 5.5 | 4.3 | 0.6666667 |
| RTX | 77.28 | 51.92 | 3.59 | 7.73 | 12.71 | 37.64 | 0.03 | 4.95 | 16.77 | 7.06 | 6.09 | 4.2 | 4.75 | 2.31 | 1.89 | 0.8626062 |
| SEE | 45.6 | 18.04 | 2.27 | 4.28 | 16.47 | 9.97 | 0 | 2.1 | 23.96 | 4.15 | 3.7 | 2.1 | 2.45 | 1.7 | 1.6 | 0.8915663 |
| SO | 62.33 | 27.85 | 1.86 | 4.6 | 14.49 | 14 | 0.02 | 1.04 | 11.57 | 3.65 | 3.25 | 1.3 | 1.45 | 2.2 | 1.95 | 0.890411 |
| STT | 84.95 | 36.66 | 3.31 | 14.97 | 36.47 | 22.63 | 0.01 | 12.03 | 52.82 | 8.2 | 7.6 | 3.8 | 4.1 | 4.1 | 3.8 | 0.9268293 |
| STX | 78.49 | 19.03 | 3.71 | 6.04 | 18.69 | 18.57 | 0.04 | 6.03 | 34.09 | 8.55 | 7.65 | 4.2 | 4.7 | 3.85 | 3.45 | 0.8947368 |
| SYF | 41.66 | 21.49 | 2.38 | 6.33 | 23.62 | 17.78 | 0.08 | 4.38 | 26.86 | 4.9 | 4.35 | 1.95 | 2.15 | 2.75 | 2.4 | 0.8877551 |
| SYY | 77.99 | 51.04 | 4.65 | 7.75 | 11.01 | 31.82 | 0.04 | 1.77 | 9.9 | 7.55 | 6.95 | 2.55 | 2.75 | 4.8 | 4.4 | 0.9205298 |
| TPR | 41.03 | 18.63 | 1.37 | 7.3 | 35.92 | 15.06 | 0.03 | 1.91 | 16.26 | 6.15 | 5.6 | 3.3 | 3.7 | 2.45 | 2.3 | 0.9105691 |
| TRMB | 80.74 | 26.12 | 2.78 | 8.05 | 25.32 | 18.02 | 0.04 | 7.7 | 43.34 | 10.55 | 9.2 | 2.5 | 2.95 | 7.6 | 6.7 | 0.8720379 |
| TSN | 74.87 | 37.58 | 2.77 | 12.8 | 30.93 | 23.7 | 0.04 | 9.53 | 41.1 | 6.15 | 5.36 | 2.78 | 3.05 | 3.1 | 2.58 | 0.8715447 |
| TXT | 57.03 | 27.38 | 2.7 | 6.59 | 19.19 | 20.61 | 0.17 | 6.39 | 32.39 | 7.6 | 5.45 | 3.7 | 4.5 | 3.1 | 1.75 | 0.7171053 |
| UAA | 21.97 | 9.34 | 1.24 | 2.27 | 16.44 | 7.74 | 0.01 | 1.02 | 16.76 | 4.06 | 3.14 | 1.21 | 1.61 | 2.45 | 1.93 | 0.773399 |
| UDR | 44.36 | 21.73 | 1.8 | 2.71 | 9.11 | 15.09 | 0.01 | 1.04 | 11.15 | 3.8 | 3.01 | 0.9 | 1.3 | 2.5 | 2.11 | 0.7921053 |
| UNM | 28.14 | 20.54 | 1.71 | 6.06 | 25.79 | 15.48 | 0 | 3.86 | 27.44 | 4.15 | 3.8 | 0.85 | 0.95 | 3.2 | 2.95 | 0.9156627 |
| VFC | 79.49 | 38.92 | 3.93 | 5.11 | 8.04 | 28 | 0 | 1 | 8.21 | 7.5 | 7.12 | 3.32 | 3.4 | 4.1 | 3.8 | 0.9493333 |
| VIAC | 44.64 | 54.26 | 2.2 | 44.77 | 78.59 | 49.36 | 0.04 | 12.56 | 27.85 | 9.6 | 9.1 | 4.4 | 4.6 | 5 | 4.7 | 0.9479167 |
| VLO | 75.3 | 53.17 | 4.74 | 19.84 | 33.06 | 36.42 | 0.21 | 10.75 | 31.2 | 9.75 | 9.25 | 4.45 | 4.75 | 5 | 4.8 | 0.9487179 |
| VTR | 54.4 | 49.7 | 3.1 | 7.35 | 13.21 | 33.65 | 0.02 | 3.65 | 14.71 | 5.05 | 4.45 | 1.85 | 2.3 | 2.75 | 2.6 | 0.8811881 |
| WAB | 78.99 | 44.94 | 5.65 | 9.99 | 14.94 | 30.92 | 0.02 | 2.05 | 10.91 | 8.6 | 7.4 | 3.1 | 4 | 4.6 | 4.3 | 0.8604651 |
| WBA | 54.75 | 16.22 | 2.22 | 6.66 | 33.54 | 11.61 | 0.02 | 4.63 | 40.8 | 5.31 | 4.04 | 1.94 | 2.34 | 2.97 | 2.1 | 0.7608286 |
| WDC | 71.37 | 42.16 | 3.28 | 9.02 | 18.29 | 26.7 | 0.1 | 7.41 | 29.73 | 10.85 | 10.4 | 4.65 | 4.85 | 6 | 5.75 | 0.9585253 |
| WELL | 73.25 | 65.57 | 3.29 | 9.57 | 14.08 | 47.33 | 0.13 | 6.82 | 17.76 | 7 | 6.53 | 2.1 | 2.4 | 4.6 | 4.43 | 0.9328571 |
| WRB | 76.49 | 36.43 | 2.56 | 8.81 | 21.61 | 25.66 | 0.04 | 7.93 | 32.72 | 6.65 | 3.95 | 2.7 | 4.1 | 2.55 | 1.25 | 0.593985 |
| WU | 25.15 | 9.11 | 1.11 | 2.17 | 16.93 | 6.57 | 0.01 | 1.59 | 26.68 | 2.1 | 1.85 | 1 | 1.1 | 1 | 0.85 | 0.8809524 |
| WY | 36.84 | 17.77 | 2.02 | 2.63 | 8.49 | 13.08 | 0.01 | 2.59 | 22.77 | 5.1 | 4.55 | 2.12 | 2.4 | 2.7 | 2.43 | 0.8921569 |
| XEL | 66.79 | 24.58 | 2.71 | 5.68 | 17.22 | 11.56 | 0.02 | 5.22 | 45.55 | 4.6 | 4.25 | 3 | 3.2 | 1.4 | 1.25 | 0.923913 |
Appendix B
Figure A1.
Volatility analysis CTSY and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A1.
Volatility analysis CTSY and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A2.
Volatility analysis CVS and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A2.
Volatility analysis CVS and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A3.
Volatility analysis EIX and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A3.
Volatility analysis EIX and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A4.
Volatility analysis KO and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A4.
Volatility analysis KO and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
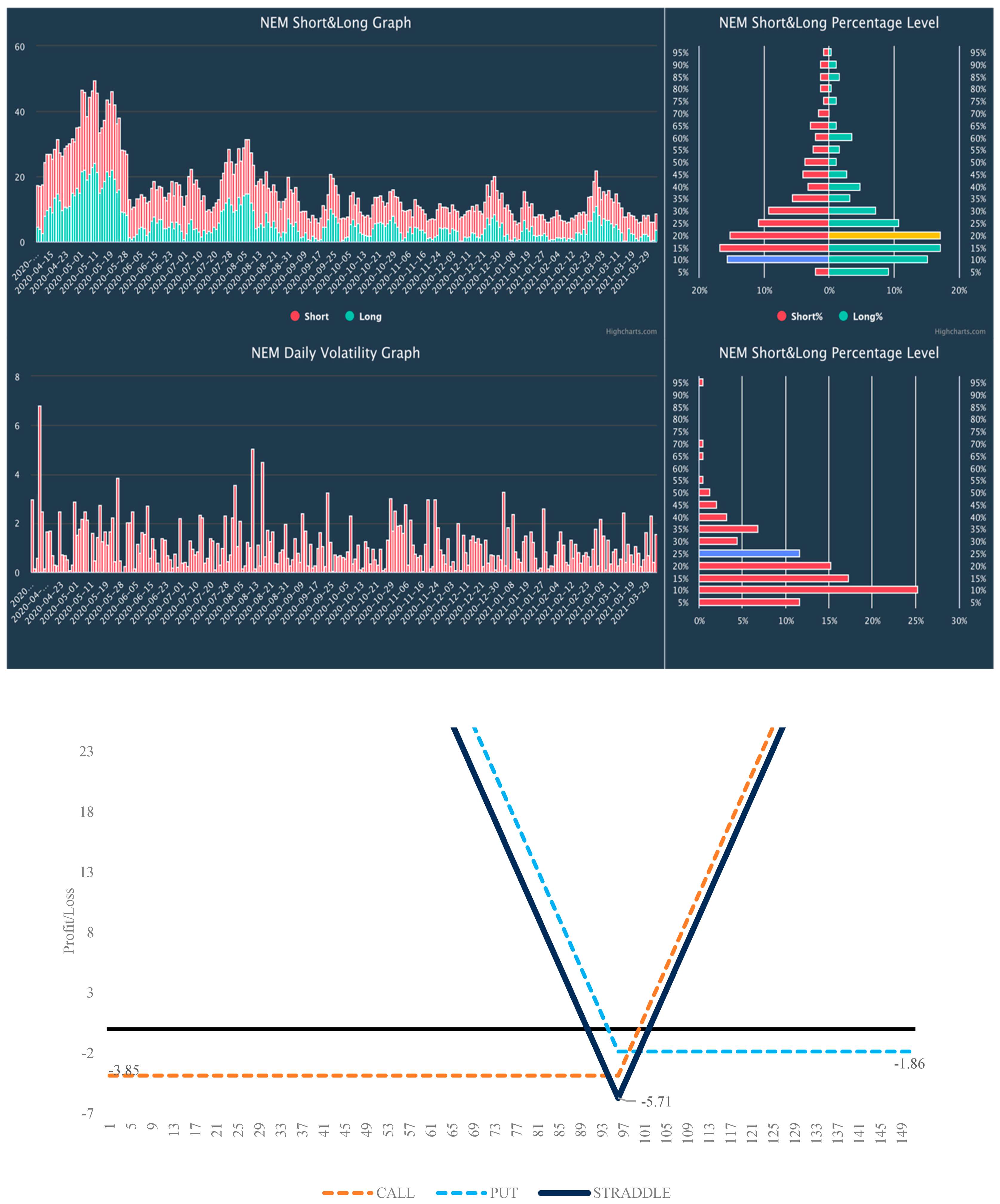
Figure A5.
Volatility analysis NEM and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A5.
Volatility analysis NEM and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
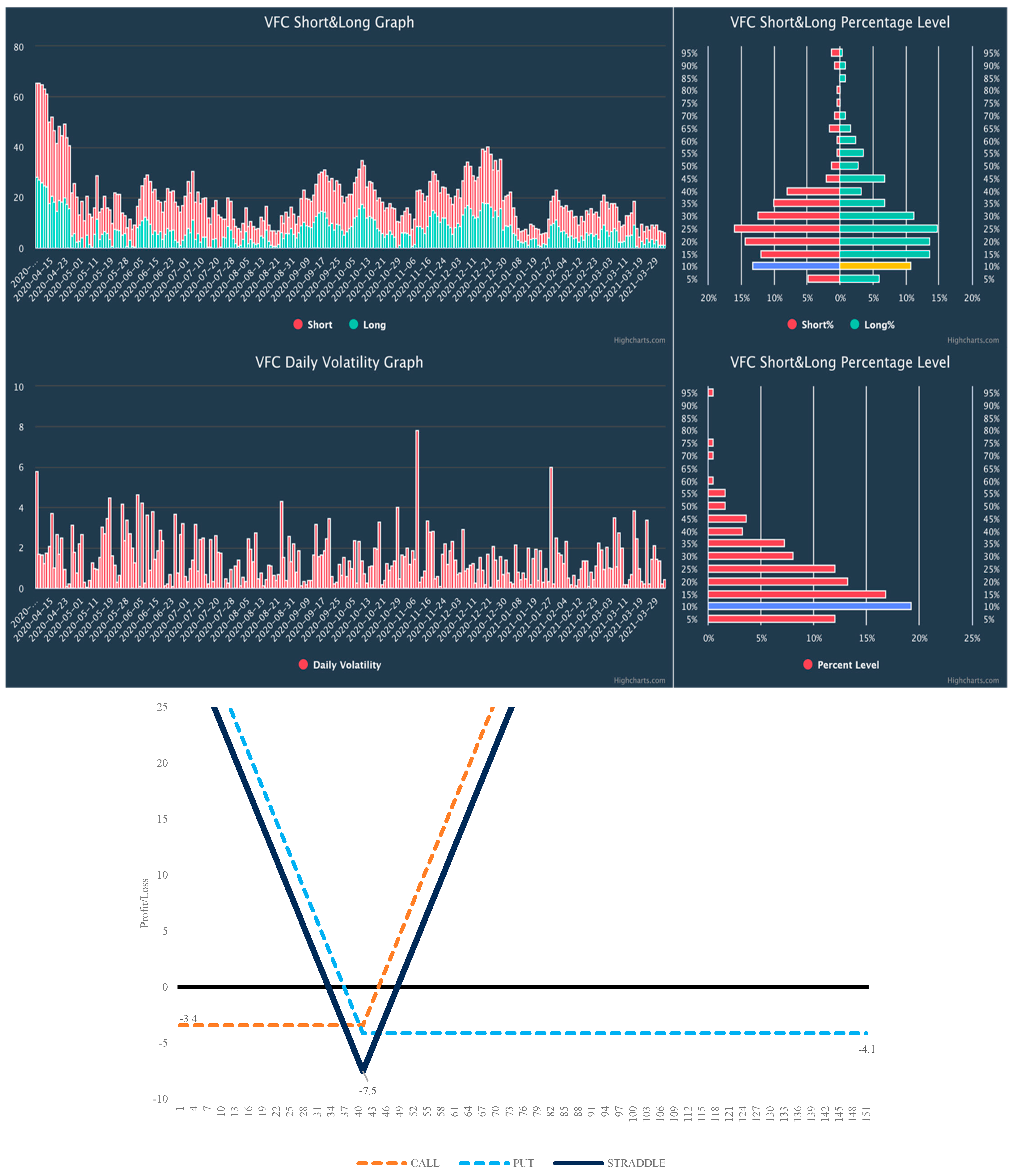
Figure A6.
Volatility analysis VFC and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A6.
Volatility analysis VFC and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A7.
Volatility analysis MKC and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
Figure A7.
Volatility analysis MKC and Straddle payoff chart. The red bars below mean the daily volatility calculated as a percentage change from the previous day’s high and low. Purple and yellow bars show current volatility levels. Source: Interactive Brokers.
References
- Berestycki, Henri, Jérôme Busca, and Igor Florent. 2004. Computing the implied volatility in stochastic volatility models. Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences 57: 1352–73. [Google Scholar] [CrossRef]
- Black, Fischer, and Myron Scholes. 1973. The Pricing of Options and Corporate Liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Coval, Joshua D., and Tyler Shumway. 2001. Expected Option Returns. The Journal of Finance 56: 983–1009. [Google Scholar] [CrossRef]
- Degiannakis, Stavros, George Filis, and Hossein Hassani. 2018. Forecasting global stock market implied volatility indices. Journal of Empirical Finance 46: 111–29. [Google Scholar] [CrossRef]
- Gao, Chao, Yuhang Xing, and Xiaoyan Zhang. 2018. Anticipating Uncertainty: Straddles around Earnings Announcements. Journal of Financial and Quantitative Analysis 53: 2587–617. [Google Scholar] [CrossRef]
- Goltz, Felix, and Wan Ni Lai. 2009. Empirical Properties of Straddle Returns. The Journal of Derivatives 17: 38–48. [Google Scholar] [CrossRef]
- Hull, John. 2014. Options, Futures and Other Derivatives, 9th ed. Upper Saddle River: Prentice Hall. [Google Scholar]
- Liu, Dehong, Yucong Liang, Lili Zhang, Peter Lung, and Rizwan Ullah. 2021. Implied volatility forecast and option trading strategy. International Review of Economics & Finance 71: 943–54. [Google Scholar] [CrossRef]
- Mayhew, Stewart. 1995. Implied Volatility. Financial Analysts Journal 51: 8–20. Available online: http://www.jstor.org/stable/4479853 (accessed on 31 July 2021). [CrossRef]
- Suleymanov, Elchin, Magsud Gubadli, and Ulvi Yagubov. 2024. Test of Volatile Behaviors with the Asymmetric Stochastic Volatility Model: An Implementation on Nasdaq-100. Risks 12: 76. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).