Some Results on Bivariate Squared Maximum Sharpe Ratio

Abstract

The Sharpe ratio is a widely used tool for assessing investment strategy performance. An essential part of investing involves creating an appropriate portfolio by determining the optimal weights for desired assets. Before constructing a portfolio, selecting a set of investment opportunities is crucial. In the absence of a risk-free asset, investment opportunities can be identified based on the Sharpe ratios of risky assets and their correlation. The maximum squared Sharpe ratio serves as a useful metric that summarizes the performance of an investment opportunity in a single value, considering the Sharpe ratios of assets and their correlation coefficients. However, the assumption of a normal distribution in asset returns, as implied by the Sharpe ratio and related metrics, may not always hold in practice. Non-normal returns with a non-linear dependence structure can result in an overestimation or underestimation of these metrics. Copula functions are commonly utilized to address non-normal dependence structures. This study examines the impact of asset dependence on the squared maximum Sharpe ratio using copulas and proposes a copula-based approach to tackle the estimation issue. The performance of the proposed estimator is illustrated through simulation and real-data analysis.

1. Introduction

In finance the trade-off between return and risk is a key consideration when choosing the best portfolio. Performance measures are important tools for assessing portfolio risk and return. The Sharpe ratio Sharpe (1966) is a popular performance measure for portfolio managers, evaluating the performance of a portfolio by calculating the mean and standard error. The portfolio with the maximum Sharpe ratio represents the highest return-to-risk trade-off. Therefore, the investment goal is to achieve the maximum Sharpe ratio. The portfolio that maximizes the Sharpe ratio lies on the mean-variance-efficient frontier. This portfolio corresponds to the point where the capital market line is tangent to the frontier, and, as such, it is known as the tangency portfolio Markowitz (1952). While the Sharpe ratio is commonly used in investment strategies, the squared Sharpe ratio is also used as a performance measure in the literature; see, e.g., Treynor and Black (1973) and Grinold and Kahn (1999), among many others. In this paper, we focus on the squared maximum Sharpe ratio (SMSR) widely used in testing arbitrage pricing theory. Chamberlain and Rothschild (1982) used SMSR to establish a bound for the sum of squared pricing errors in beta pricing equations. MacKinlay (1995) used SMSR to examine the multifactor model’s plausibility in explaining anomalies in the capital asset pricing model. Zhang (2009) developed test statistics based on the sample SMSR of factors extracted from individual stocks. Barillas et al. (2020) used SMSR in an asymptotic analysis under general distributional assumptions for model comparison. An important aspect of an investment is forming a suitable portfolio by estimating the optimal weights for the desired assets. Before forming a portfolio, selecting an investment opportunity set of assets is crucial. In the absence of a risk-free asset, the investment opportunities can be determined based on the Sharpe ratios of risky assets and their correlation. The maximum squared Sharpe ratio is a suitable index that summarizes the performance of an investment opportunity in a single value, based on the Sharpe ratios of assets and the correlation coefficients between them. The main assumption for the appropriateness of the Sharpe ratio and related measures is the normality of asset returns. When returns are non-normal with a non-linear dependence structure, these measures could be either overestimated or underestimated. Choy and Yang (2021) demonstrated that under the assumption of a multivariate normal distribution for excess returns, the sample SMSR has a significant upward bias, and they improved several estimators of SMSR. Dealing with non-normal returns in portfolio selection is an important consideration for investors, as it can significantly impact their portfolio’s performance. Investors can account for non-normal returns by adjusting expected returns, using alternative risk measures such as value at risk and conditional value at risk, and considering alternative asset classes. Another common approach to accounting for non-normal dependence structure is the use of copulas (see, Cherubini et al. 2004; Embrechts et al. 2002, 2003; Fantazzini 2008; He and Gong 2009), which are a powerful tool for modeling the dependence structure between different assets in a portfolio. By using copulas, investors can gain a more accurate understanding of how different assets move relative to each other, helping them build more efficient and diversified portfolios. Although the squared maximum Sharpe ratio was developed in recent years, little research has been done to address its compatibility as a measure of performance. As argued by Kourtis (2016), the expected squared Sharpe ratio rises with the number of assets and the maximum Sharpe ratio, while it falls with the length of the data. In this paper, we focus on the SMSR of a two-asset portfolio. This index summarizes the joint performance of a bivariate random vector of asset returns as a single value, which could help in selecting the components of a two-asset portfolio. A topic in statistical arbitrage technique, pairs trading, explores how to identify a suitable pair for trading Ramos-Requena et al. (2020). This paper makes two contributions toward the squared maximum Sharpe ratio. First, we study the effect of dependence on SMSR. Several theoretical properties of the bivariate Sharpe ratio, in terms of copulas, are given in Section 2. The copula-based bivariate Sharpe ratio is presented in Section 3. In Section 4, we provide an estimator for the proposed copula-based bivariate Sharpe ratio. A simulation study is performed in this section. A real-data analysis is provided in Section 5. Section 6 concludes the paper.

2. Bivariate Squared Maximum Sharpe Ratio

Consider two assets, A and B, with the returns $R_t^A$ and $R_t^B$ over a time interval t (e.g., $R_t^A$ and $R_t^B$ could be the daily returns, so $t=$ one day), respectively, defined on a common probability space $(\mathsf{\Omega },F,P)$, endowed with a filtration $F=\{F_t:T\ge t\ge 0\}$ representing the information available to the investor up to time T. Let b be a benchmark investment strategy, and let $R_b$ denote its return over a time interval t. The benchmark b may be riskless, hence $R_b$ may be a fixed constant. We only present the case that the processes from which the excess returns are sampled are stationary. That is, the means and the variances of returns and the covariance between them are fixed for any time interval t. The excess returns over the risk-free asset are random variables, which we denote by continuous random variables $X=R_t^A-R_b$ and $Y=R_t^B-R_b$. Let $P=wX+(1-w)Y$, be a two-asset portfolio with dependent components X and Y, where $0<w<1$ is the weight of X and $1-w$ is the weight of Y. Let ${\mu }_X=E\left(X\right)$ and ${\sigma }_X^2=\mathrm{var}\left(X\right)$ be the mean and variance of X and ${\mu }_Y=E\left(Y\right)$, ${\sigma }_X^2=\mathrm{var}\left(X\right)$ be the mean and variance of Y. We assume that variances exist and are non-zero. By definition, the Sharpe ratios (SRs) of X and Y are given by $S{R}_X=\frac{{\mu }_X}{{\sigma }_X}$ and $S{R}_Y=\frac{{\mu }_Y}{{\sigma }_Y}$, respectively. The Sharpe ratio of the portfolio P as a function of the weight w is given by

$${\mathrm{SR}}_P\left(w\right)={\displaystyle \frac{w{\mu }_X+(1-w){\mu }_Y}{\sqrt{w^2{\sigma }_X^2+{(1-w)}^2{\sigma }_Y^2+2w(1-w){\sigma }_{X,Y}}}},$$

(1)

where ${\sigma }_{X,Y}=\mathrm{cov}(X,Y)$. It is known that the maximum happens at

$$w^{*}=\frac{{\mu }_X{\sigma }_Y^2-{\mu }_Y{\sigma }_{X,Y}}{{\mu }_X{\sigma }_Y^2+{\mu }_Y{{\sigma }_X}_t^2-({\mu }_X+{\mu }_Y){\sigma }_{X,Y}};$$

that is ${max}_{w}S{R}_P\left(w\right)=S{R}_P\left(w^{*}\right)$.

Definition 1.

Let $\rho \in [-1,1]$ be the Pearson’s correlation of the excess returns X and Y with the Sharpe ratios $S{R}_X$ and $S{R}_X$, respectively. The bivariate squared maximum Sharpe ratio of a two-asset portfolio with the components X and Y (denoted by SMSR$(X,Y)$) is defined by

$$SMSR(X,Y)=\frac{S{R}_X^2+S{R}_Y^2-2\rho S{R}_{X}S{R}_Y}{1-{\rho }^2}.$$

(2)

For the case of uncorrelated assets, i.e., $\rho =0$, we have $SMSR(X,Y)=S{R}_X^2+S{R}_Y^2$. For the cases $\rho =-1$ or $\rho =1$, $SMSR(X,Y)=+\infty$.

Remark 1.

By considering the SMSR(X,Y) as a bivariate Sharpe ratio, which is a function of the marginal Sharpe ratios and the correlation coefficient of the asset’s returns as outlined in this paper, one can effectively choose the components of a portfolio. For instance, when forming a portfolio with two assets, such as between the options $(X_1,Y_1)$ and $(X_2,Y_2)$, the more suitable option is the one with a higher SMSR(X,Y) value. This approach can serve as a pre-selection of suitable assets for portfolio formation, followed by determining the optimal weights of these selected assets in the next step.

As noted in Dowd (2000), using the traditional Sharpe ratio may result in significant errors when determining whether the true correlation is non-zero. When forming a portfolio with two assets, let us consider two options: $(X_1,Y_1)$ and $(X_2,Y_2)$. In a given period, suppose that the Sharpe ratio of the returns for both options are equal, i.e., $S{R}_{X_1}=S{R}_{X_2}=1.5$ and $S{R}_{Y_1}=S{R}_{Y_2}=2$, but the correlation coefficient of $(X_1,Y_1)$ is equal to 0.4 and the correlation of $(X_2,Y_2)$ is equal to 0.8. Based on $SMSR(X,Y)$, which option is suitable for forming a portfolio? To provide a proper answer, we need to examine the impact of correlation on the bivariate squared maximum Sharpe ratio.

Proposition 1.

Let $S{R}_X>0$ and $S{R}_Y>0$ be the Sharpe ratios of X and Y and let $\kappa =min(\frac{S{R}_X}{S{R}_Y},\frac{S{R}_Y}{S{R}_X})$. For SMSR(X,Y) defined by (2), the following hold:

(i) 

SMSR(X,Y) is decreasing in ρ, for $\rho \in [-1,\kappa ]$;

(ii) 

SMSR(X,Y) is increasing in ρ, for $\rho \in [\kappa ,1]$;

(iii) 

SMSR$(X,Y)\ge max(S{R}_X^2,S{R}_Y^2)$, for each $\rho \in [-1,1]$, and the equality holds if, and only if, $\rho =min(\frac{S{R}_X}{S{R}_Y},\frac{S{R}_Y}{S{R}_X})$.

Proof. 

The derivative of SMSR(X,Y) with respect to $\rho$ is given by

$$\frac{d}{d\rho }SMSR(X,Y)=\frac{2S{R}_{X}S{R}_Y(t-\rho )(\rho -\frac{1}{t})}{{(1-{\rho }^2)}^2},$$

where $t=S{R}_X/S{R}_Y$. Note that $\kappa =min(t,\frac{1}{t})$. For $\rho =\kappa$, we have that $\frac{d}{d\rho }SMSR(X,Y)=0$. For $-1\le \rho \le \kappa \le 1$, we have that $t-\rho >0$ and $\rho -\frac{1}{t}<0$ and thus, $\frac{d}{d\rho }SMSR(X,Y)<0$. Similarly, for $0<\kappa \le \rho \le 1$, we have that $t-\rho >0$ and $\rho -\frac{1}{t}>0$ or $t-\rho <0$ and $\rho -\frac{1}{t}<0$, and thus $\frac{d}{d\rho }SMSR(X,Y)>0$, which completes the proof of parts (i) and (ii). For part (iii), let $SMSR(X,Y):=SMSR\left(\rho \right)$. From parts (i) and (ii), for $\rho \le \kappa$, we have that $SMSR\left(\rho \right)\ge SMSR\left(\kappa \right)$, and for $\rho \ge \kappa$, $SMSR\left(\rho \right)\ge SMSR\left(\kappa \right)$. Since $SMSR\left(\kappa \right)=max(S{R}_X^2,S{R}_Y^2)$, it follows that SMSR$(X,Y)\ge max(S{R}_X^2,S{R}_Y^2)$, for each $\rho \in [-1,1]$. To prove the last part, if $\rho =\kappa$, then $SMSR\left(\rho \right)=S{R}_Y^2$ for $S{R}_X<S{R}_Y$, and $SMSR\left(\rho \right)=S{R}_X^2$, for $S{R}_Y<S{R}_X$, that is $SMSR\left(\rho \right)=max(S{R}_X^2,S{R}_Y^2)$. Conversely, if $SMSR\left(\rho \right)=max(S{R}_X^2,S{R}_Y^2)$, then $\rho =S{R}_X/S{R}_Y$ for $S{R}_X<S{R}_Y$ and $\rho =S{R}_Y/S{R}_X$ for $S{R}_Y<S{R}_X$, that is $\rho =min(\frac{S{R}_X}{S{R}_Y},\frac{S{R}_Y}{S{R}_X})$.  □

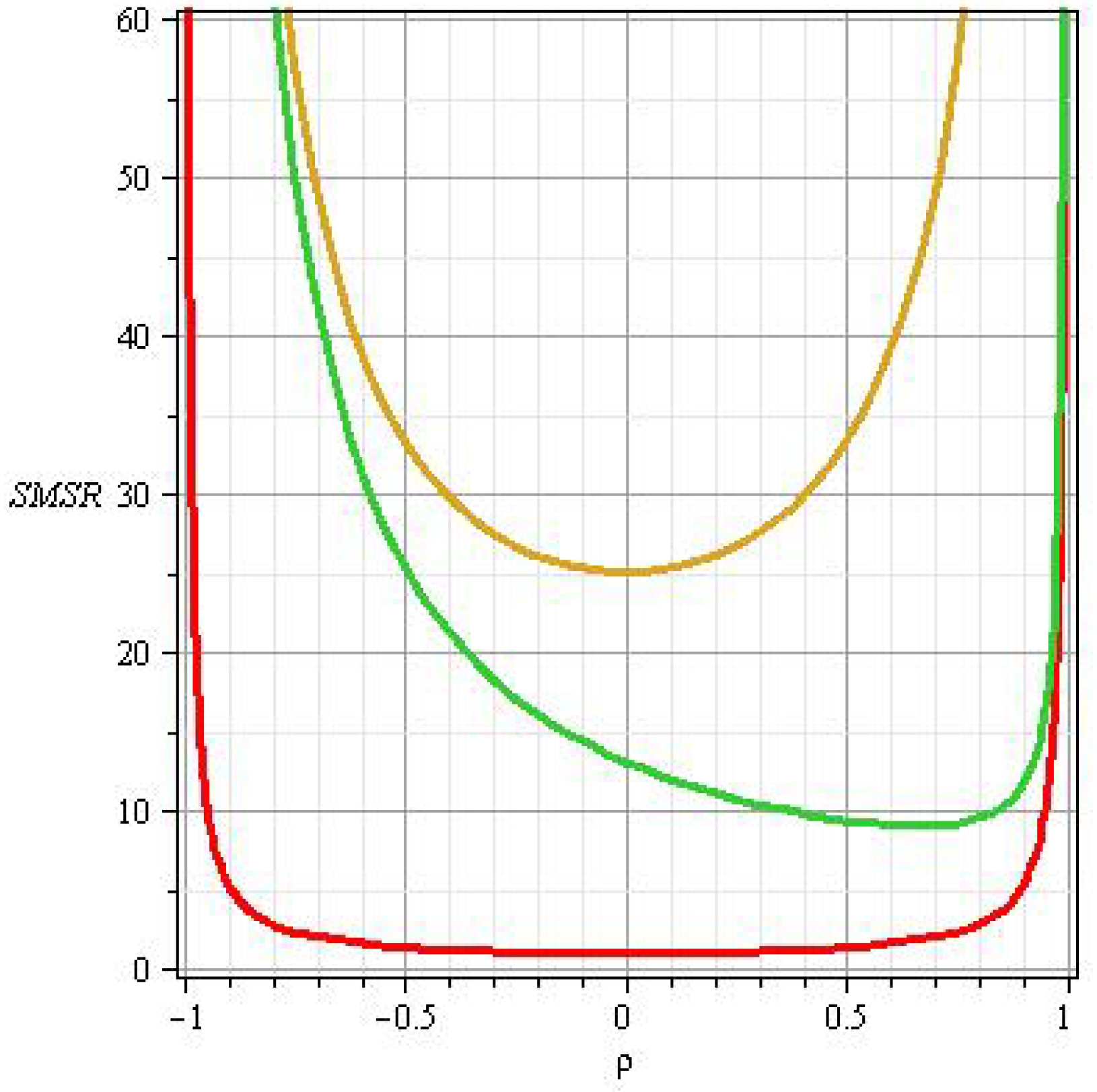
Figure 1 shows the plot of $SMSR(X,Y)$ as a function of $\rho$ for different values of $S{R}_X$ and $S{R}_Y$ to illustrate the results of Proposition 1.

Proposition 2.

For each $\rho \in [-1,1]$, $\frac{{(S{R}_X-S{R}_Y)}^2}{1-{\rho }^2}\le SMSR(X,Y)\le \frac{{(S{R}_X+S{R}_Y)}^2}{1-{\rho }^2}$.

Proof. 

The result from the inequalities $S{R}_X^2+S{R}_Y^2-2\rho S{R}_{X}S{R}_Y\ge {(S{R}_X-S{R}_Y)}^2$ and $S{R}_X^2+S{R}_Y^2-2\rho S{R}_{X}S{R}_Y\le {(S{R}_X+S{R}_Y)}^2$ that hold for each $\rho \in [-1,1]$ and $S{R}_X>0$ and $S{R}_Y>0$.  □

Figure 2 shows the upper and lower bound for $SMSR(X,Y)$ that is provided in Proposition 2. In the statistical literature, it is common to assume that log-returns are distributed as a normal distribution. The following example illustrates the effect of dependence on $SMSR(X,Y)$ of log-normal returns.

Example 1.

Let X and Y be log-normal random variables with the bivariate density function given by Mielke et al. (1977)

$$f(x,y)=\frac{1}{2\pi xy\alpha \beta \sqrt{1-r^2}}{e}^{-Q(x,y)},$$

where

$$Q(x,y)=\frac{1}{2(1-r^2)}\left\{{\left[\frac{log(x/A)}{\alpha }\right]}^2+{\left[\frac{log(y/B)}{\beta }\right]}^2-2r\left[\frac{log(x/A)}{\alpha }\right]\left[\frac{log(y/B)}{\beta }\right]\right\},$$

for $x>0$, $y>0$, $\alpha >0$, $\beta >0$, $A>0$, $B>0$ and $-1\le r\le 1$; where α and β are the marginal distribution shape parameters, A and B are the scale parameters, r is the dependence parameter. Clearly, X and Y have the univariate log-normal distribution with the means and the variances given by

$${\mu }_X=A{e}^{\frac{{\alpha }^2}{2}},{\sigma }_X^2=A^2{e}^{{\alpha }^2}(e^{{\alpha }^2}-1),$$

$${\mu }_Y=B{e}^{\frac{{\beta }^2}{2}},{\sigma }_Y^2=B^2{e}^{{\beta }^2}(e^{{\beta }^2}-1),$$

$$Cov(X,Y)=AB(e^{r\alpha \beta }-1)e^{\frac{({\alpha }^2+{\beta }^2)}{2}},$$

and

$${\rho }_{X,Y}=\frac{e^{r\alpha \beta }-1}{\sqrt{(e^{{\alpha }^2}-1)(e^{{\beta }^2}-1)}}.$$

Then,

$$S{R}_X=\frac{1}{\sqrt{e^{{\alpha }^2}-1}},S{R}_Y=\frac{1}{\sqrt{e^{{\beta }^2}-1}}.$$

Let $\kappa =min\left(\frac{S{R}_X}{S{R}_Y},\frac{S{R}_Y}{S{R}_X}\right)$. Then, it is easy to see that ${\rho }_{X,Y}\le \kappa$, if, and only if, $r\le min\left(\frac{\alpha }{\beta },\frac{\beta }{\alpha }\right)$.

The squared Sharpe ratio for the pair $(X,Y)$ is given by

$$SMSR(X,Y)=\frac{e^{{\alpha }^2}+e^{{\beta }^2}-2e^{r\alpha \beta }}{(e^{{\alpha }^2}-1)(e^{{\beta }^2}-1)-{(e^{r\alpha \beta }-1)}^2}.$$

Let $SMSR(X,Y):=SMSR\left(r\right)$. We note that

$$\frac{d}{dr}SMSR\left(r\right)=\frac{-2\alpha \beta e^{r\alpha \beta }(e^{{\beta }^2}-e^{r\alpha \beta })(e^{{\alpha }^2}-e^{r\alpha \beta })}{{\left(e^{{\alpha }^2+{\beta }^2}-e^{{\alpha }^2}-e^{{\beta }^2}+2e^{r\alpha \beta }-e^{2r\alpha \beta }\right)}^2}.$$

Thus, the function $SMSR\left(r\right)$ has a minimum at the point $r=min(\frac{\alpha }{\beta },\frac{\beta }{\alpha })$ and from Proposition 1, the following properties hold:

• If $r\le min(\frac{\alpha }{\beta },\frac{\beta }{\alpha })$, then $SMSR\left(r\right)$ is decreasing in r;
• If $r\ge min(\frac{\alpha }{\beta },\frac{\beta }{\alpha })$, then $SMSR\left(r\right)$ is increasing in r;
• For each $r\in [-1,1]$, $SMSR\left(r\right)\ge \frac{1}{e^{{(min(\alpha ,\beta ))}^2}-1}$, and the equality holds, if $r=min(\frac{\alpha }{\beta },\frac{\beta }{\alpha })$.

3. Copula-Based Squared Maximum Sharpe Ratio

Let X and Y be two continuous random variables with the univariate marginal cumulative distribution functions (CDF) $F\left(x\right)=P(X\le x)$ and $G\left(y\right)=P(Y\le y)$ for $x,y\in \mathbb{R}$ and the joint CDF $H(x,y)=P(X\le x,Y\le y)$. In Formula (2), $S{R}_X^2$ and $S{R}_Y^2$ are calculated from the marginal CDFs and $\rho$ is associated with the joint CDFs of X and Y. Following Sklar’s Theorem, see, Nelsen (2006), there exists a unique copula C such that

$$H(x,y)=C\left(F\right(x),G(y\left)\right),x,y\in \mathbb{R},$$

(3)

where $C(u,v)=P(U\le u,V\le v)$ is the joint CDF of the pair $(U,V)=\left(F\right(X),G(Y\left)\right)$ whose margins are uniform on [0, 1]. The copula C characterizes the dependence in the pair $(X,Y)$ Nelsen (2006). Let ${\sigma }_{X,Y}\left(C\right)$ denotes the covariance of random variables X and Y, whose associated copula is C. By using Hoeffding’s identity Hoeffding (1994) and transformations $u=F\left(x\right)$ and $v=G\left(y\right)$, from (3) we have

$$\begin{array}{ccc}\hfill {\sigma }_{X,Y}\left(C\right)& =& {\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }(H(x,y)-F\left(x\right)G\left(y\right))dxdy\hfill \\ & =& {\int }_0^1{\int }_0^1(C(u,v)-uv)d{F}^{-1}\left(u\right)d{G}^{-1}\left(v\right),\hfill \end{array}$$

(4)

or equivalently,

$$\begin{array}{ccc}\hfill {\sigma }_{X,Y}\left(C\right)& =& {\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }xydH(x,y)-{\mu }_X{\mu }_Y\hfill \\ & =& {\int }_0^1{\int }_0^1{F}^{-1}\left(u\right)G^{-1}\left(v\right)dC(u,v)-{\mu }_X{\mu }_Y.\hfill \end{array}$$

(5)

When the joint CDF of $(X,Y)$ is non-normal, we can model it by selecting suitable parametric forms for the marginal CDFs F, G, and the copula C in (3). For example, F might be the CDF of normal random variables with the parameters $\mu$ and ${\sigma }^2$ and G might the CDF of a gamma random variable with the parameters $\alpha$ and $\beta$ and the copula C might be taken from a parametric family of copulas. Popular choices of copulas are described in Joe (2014) and Nelsen (2006). The main advantage of this approach is that the distributions F, G, and C in (3) can be chosen independently of one another. The means ${\mu }_X$, ${\mu }_Y$ and the variances ${\sigma }_X^2$ and ${\sigma }_Y^2$ of X and Y are calculated from the marginal CDFs, and their Pearson’s correlation coefficient can be obtained by

$${\rho }_C=\frac{{\int }_0^1{\int }_0^1{F}^{-1}\left(u\right)G^{-1}\left(v\right)dC(u,v)-{\mu }_X{\mu }_Y}{{\sigma }_X{\sigma }_Y}.$$

(6)

In the following, we define the copula-based version of the squared maximum Sharpe ratio of a two-asset portfolio with the components X and Y and the associated copula C, denoted $SMS{R}_C(X,Y)$.

Definition 2.

Let $(X,Y)$ be a pair of continuous random variables with the marginal CDF F (of X) and G (of Y) and associated copula C. We define the copula-based squared maximum Sharpe ratio of a two-asset portfolio with the excess returns X and Y and the marginal, the Sharpe ratios $S{R}_X$ and $S{R}_X$, by

$$SMS{R}_C(X,Y)=\frac{S{R}_X^2+S{R}_Y^2-2{\rho }_{C}S{R}_{X}S{R}_Y}{1-{\rho }_C^2}.$$

(7)

A copula C is said to be positive quadrant dependent (PQD) if for all $(u,v)\in {[0,1]}^2$, $C(u,v)\ge \mathsf{\Pi }(u,v)$, and negative quadrant dependent (NQD) if $C(u,v)\le \mathsf{\Pi }(u,v)$, where $\mathsf{\Pi }(u,v)=uv$, is the copula of independent random variables Nelsen (2006). The following result compares the $SMS{R}_C(X,Y)$ of a pair of dependent returns under a copula C with the $SMS{R}_{\mathsf{\Pi }}(X,Y)$ of the independent copula $\mathsf{\Pi }$.

Proposition 3.

Let $(X,Y)$ be two excess returns with the Sharpe ratios $S{R}_X=a>0$ and $S{R}_Y=b>0$ and the associated copula C.

(i) 

If C is PQD, then $SMS{R}_C(X,Y)\le (\ge )SMS{R}_{\mathsf{\Pi }}(X,Y)$, if and only if, ${\rho }_C\le (\ge ){\kappa }_H$, where ${\kappa }_H=\frac{2ab}{a^2+b^2}$;

(ii) 

If C is NQD then, $SMS{R}_C(X,Y)\ge SMS{R}_{\mathsf{\Pi }}(X,Y)$.

Proof. 

Note that $SMS{R}_{\mathsf{\Pi }}(X,Y)=a^2+b^2$. Let

$$SMS{R}_C(X,Y):=SMS{R}_C\left({\rho }_C\right)=\frac{a^2+b^2-2ab{\rho }_C}{1-{\rho }_C^2}.$$

We note that $SMS{R}_C\left({\kappa }_H\right)=a^2+b^2=SMS{R}_{\mathsf{\Pi }}(X,Y)$. If C is PQD, then $C(u,v)\ge uv$. By using (5), we have that ${\rho }_C\ge 0$. For ${\rho }_C\ge 0$, it is easy to see that $SMS{R}_C\left({\rho }_C\right)\le (\ge )SMS{R}_C\left({\kappa }_H\right)$, if and only if, ${\rho }_C\le (\ge ){\kappa }_H$. If C is NQD, then ${\rho }_C\le 0$, and thus $\frac{a^2+b^2-2ab{\rho }_C}{1-{\rho }_C^2}\ge \frac{a^2+b^2}{1-{\rho }_C^2}\ge a^2+b^2$, which completes the proof.  □

Remark 2.

The above result shows that, when the returns are positively or negatively dependent, but considered independent, the SMSR(X,Y) is more or less estimated.

Example 2.

Let X and Y be two exponential random variables with means ${\displaystyle \frac{1}{{\lambda }_1}}$ and ${\displaystyle \frac{1}{{\lambda }_2}}$, respectively, and the associated FGM copula Nelsen (2006) given by

$$C_{\theta }(u,v)=uv[1+\theta (1-u)(1-v)],-1\le \theta \le 1.$$

(8)

So, ${\sigma }_C={\displaystyle \frac{\theta }{4{\lambda }_1{\lambda }_2}}$, ${\rho }_C={\displaystyle \frac{\theta }{4}}$, and $S{R}_X=S{R}_Y=1$. Therefore, $SMS{R}_{C_{\theta }}(X,Y)={\displaystyle \frac{8}{4+\theta }}\in [\frac{8}{5},\frac{8}{3}]$, which is decreasing with respect to the dependency parameter θ and does not depend on the marginal parameters ${\lambda }_1$ and ${\lambda }_2$. The value of the $SMS{R}_{C_{\theta }}(X,Y)$ decreases as the dependence between X and Y increases. For the case of independence, i.e., $\theta =0$, we have $SMS{R}_{C_0}(X,Y)=2$. Note that the copula $C_{\theta }$ is PQD (NQD) for $\theta \ge 0$ $(\theta \le 0)$.

The following example compares two investment opportunity sets $(X_1,Y_1)$ and $(X_2,Y_2)$ with the common marginal CDFs and different dependence structures.

Example 3.

Let X and Y be two beta random variables having the CDFs

$$F\left(x\right)=x^{\alpha },0<x<1,\mathrm{a}ndG\left(y\right)=y^{\beta },0<y<1,$$

with $\alpha >0$ and $\beta >0$, and the associated copula $C_{\theta }$ be the FGM copula given by (8). The joint CDF of $(X,Y)$ is given by

$$H(x,y)=x^{\alpha }{y}^{\beta }[1+\theta (1-x^{\alpha })(1-y^{\beta })],x,y\in [0,1],$$

with $-1\le \theta \le 1$. It is easy to see that

$$S{R}_X=\sqrt{\alpha (\alpha +2)},S{R}_Y=\sqrt{\beta (\beta +2)}.$$

We note that $\frac{S{R}_X}{S{R}_Y}\le 1$, if and only if, $\alpha \le \beta$. The Pearson’s correlation is given by

$${\rho }_C=\frac{\theta \sqrt{\alpha \beta (\alpha +2)(\beta +2)}}{(2\alpha +1)(2\beta +1)}.$$

The expression for $SMS{R}_{C_{\theta }}(X,Y)$ is given by

$$SMS{R}_{C_{\theta }}(X,Y)=\frac{\alpha (\alpha +2)+\beta (\beta +2)-2\theta \alpha \beta (\alpha +2)(\beta +2){\left[(2\alpha +1)(2\beta +1)\right]}^{-1}}{1-{\theta }^2\alpha \beta (\alpha +2)(\beta +2){\left[(2\alpha +1)(2\beta +1)\right]}^{-2}}.$$

Let $\kappa =min\left(\frac{S{R}_X}{S{R}_Y},\frac{S{R}_Y}{S{R}_X}\right)=min\left(\sqrt{\frac{\alpha (\alpha +2)}{\beta (\beta +2)}},\sqrt{\frac{\beta (\beta +2)}{\alpha (\alpha +2)}}\right)$. It follows that ${\rho }_C\le \kappa$ if and only if, $\theta \le {\kappa }^{\prime }$, where ${\kappa }^{\prime }=min\left(\frac{(2\alpha +1)(2\beta +1)}{\beta (\beta +2)},\frac{(2\alpha +1)(2\beta +1)}{\alpha (\alpha +2)}\right)$. From Proposition 1,

• If $\theta \le {\kappa }^{\prime }$, then $SMS{R}_{C_{\theta }}(X,Y)$ is decreasing in ${\rho }_C$;
• If $\theta \ge {\kappa }^{\prime }$, then $SMS{R}_{C_{\theta }}(X,Y)$ is increasing in ${\rho }_C$.

Since ρ is an increasing function of θ, then the following hold

• If $\theta \le {\kappa }^{\prime }$, then $SMS{R}_{C_{\theta }}(X,Y)$ is decreasing in θ;
• If $\theta \ge {\kappa }^{\prime }$, then $SMS{R}_{C_{\theta }}(X,Y)$ is increasing in θ.

For $i=1,2$, let $(X_i,Y_i)$ have the FGM copula $C_{{\theta }_i}$. Then, from Proposition 1, the following hold

• If ${\theta }_1\le {\theta }_2\le {\kappa }^{\prime }$, then $SMS{R}_{C_{{\theta }_1}}(X,Y)\ge SMS{R}_{C_{{\theta }_2}}(X,Y)$;
• If ${\kappa }^{\prime }\le {\theta }_1\le {\theta }_2$, then $SMS{R}_{C_{{\theta }_1}}(X,Y)\le SMS{R}_{C_{{\theta }_2}}(X,Y)$;
• If ${\theta }_1\le {\kappa }^{\prime }\le {\theta }_2$, then the value of $SMS{R}_{C_{{\theta }_1}}(X,Y)$ and $SMS{R}_{C_{{\theta }_2}}(X,Y)$ care not comparable.

Note that ${\rho }_C={\kappa }_H$, where ${\kappa }_H=\frac{2S{R}_{X}S{R}_Y}{S{R}_X^2+S{R}_Y^2}$, if and only if, $\theta ={\kappa }_H^{\prime }$, where ${\kappa }_H^{\prime }=\frac{2(2\alpha +1)(2\beta +1)}{\alpha (\alpha +2)+\beta (\beta +2)}$. Since for $\theta \ge 0$, the copula $C_{\theta }$ is PQD, then from Proposition 3, $SMS{R}_{C_{\theta }}(X,Y)\le (\ge )S{R}_X^2+S{R}_Y^2$, if $\theta \le {\kappa }_H^{\prime }(\theta \ge {\kappa }_H^{\prime })$. For $\theta \le 0$, $C_{\theta }$ is NQD, and then, $SMS{R}_{C_{\theta }}(X,Y)\ge S{R}_X^2+S{R}_Y^2$.

4. Estimators of Squared Maximum Sharpe Ratio

Let $(X_t,Y_t)$, $t=1,2,\dots ,n$, be a sample of size n from a pair $(X,Y)$. A natural estimator of $SMSR(X,Y)$ defined by (2) is its sample version given by

$$\widehat{SMSR}(X,Y)=\frac{{\widehat{SR}}_X^2+{\widehat{SR}}_Y^2-2r{\widehat{SR}}_X{\widehat{SR}}_Y}{1-r^2},$$

(9)

where $\overline{X}={\displaystyle \frac{1}{n}}{\sum }_{t=0}^n{X}_t$, $\overline{Y}={\displaystyle \frac{1}{n}}{\sum }_{t=0}^n{Y}_t$, ${\widehat{SR}}_X=\frac{\overline{X}}{S_X},{\widehat{SR}}_Y=\frac{\overline{Y}}{S_Y}$ and

$$r=\frac{{\sum }_{t=1}^n(X_t-\overline{X})(Y_t-\overline{Y})}{\sqrt{{\sum }_{t=1}^n{(X_t-\overline{X})}^2{\sum }_{t=1}^n{(Y_t-\overline{Y})}^2}},$$

(10)

is the sample Pearson’s correlation coefficient. We note that the expression (2) for $\widehat{SMSR}(X,Y)$ can be rewritten as

$$\widehat{SMSR}(X,Y)={\overline{\mathbf{Z}}}^T{\mathbf{S}}^{-1}\overline{\mathbf{Z}},$$

where

$$\overline{\mathbf{Z}}={(\overline{X},\overline{Y})}^T,\mathbf{S}=\left[\begin{array}{cc}{S}_X^2& S_{XY}\\ S_{XY}& S_Y^2\end{array}\right],$$

with

$$S_X^2=\frac{1}{n-1}\sum _{t=1}^n{(X_t-\overline{X})}^2,S_Y^2=\frac{1}{n-1}\sum _{t=1}^n{(Y_t-\overline{Y})}^2,S_{XY}=\frac{1}{n-1}\sum _{t=1}^n(X_t-\overline{X})(Y_t-\overline{Y}).$$

Under the explicit assumption that the returns are normally distributed, from the standard theory of normal quadratic form, see, e.g., Anderson et al. (1958), we have that

$$n-22\widehat{SMSR}(X,Y)\sim F(2,n-2,\delta ),$$

where $F(2,n-2,\delta )$ is the non-central F-distribution Anderson et al. (1958) with 2 and $n-2$ degree of freedom and non-centrality parameter $\delta =nSMSR(X,Y)$. Note that

$$E\left(\widehat{SMSR}(X,Y)\right)=\frac{nSMSR(X,Y)+2}{n-4}.$$

Thus, $\widehat{SMSR}(X,Y)$ is a biased estimator of $SMSR(X,Y)$.

An estimator for the copula-based $SMS{R}_C(X,Y)$ defined by (7) could be found as follows:

Step 1.

Based on a random sample $(X_1,Y_1),\dots ,(X_n,Y_n)$, find suitable models for the marginal distributions, namely $\widehat{F}$ and $\widehat{G}$, using the standard goodness-of-fit tests;

Step 2.

Compute the marginal Sharpe ratios ${\widehat{SR}}_X^{*}$ and ${\widehat{SR}}_Y^{*}$ from the estimated marginal distributions by ${\widehat{SR}}_X^{*}=\frac{{\widehat{\mu }}_X}{{\widehat{\sigma }}_X}$ and ${\widehat{SR}}_Y^{*}=\frac{{\widehat{\mu }}_Y}{{\widehat{\sigma }}_Y}$;

Step 3.

Choose a suitable copula model, namely $\widehat{C}$, using the copula goodness-of-fit testing Genest et al. (2009) for the dependence structure of data;

Step 4.

Compute the copula-based estimator of Pearson’s correlation coefficient ${\rho }_C$, denoted by $r_C$ using

$$r_C=\frac{{\int }_0^1{\int }_0^1{\widehat{F}}^{-1}\left(u\right){\widehat{G}}^{-1}\left(v\right)d\widehat{C}(u,v)-{\widehat{\mu }}_X{\widehat{\mu }}_Y}{{\widehat{\sigma }}_X{\widehat{\sigma }}_Y};$$

(11)

Step 5.

Compute the copula-based estimator of $SMS{R}_C(X,Y)$ by

$${\widehat{SMSR}}_C(X,Y)=\frac{{\widehat{S{R}^{*}}}_X^2+{\widehat{S{R}^{*}}}_Y^2-2r_C{\widehat{S{R}^{*}}}_X{\widehat{S{R}^{*}}}_Y}{1-r_C^2}.$$

(12)

When dealing with time-series data for underlying commodities, the initial step involves conducting standard tests, such as those proposed by Box and Pierce (1970) and Ljung and Box (1978), on the log-returns and their squared values to identify any presence of autocorrelation and heteroscedasticity within the series. If these tests yield insignificant results, the log-returns can be considered as a random sample from a distribution F, leading us to proceed with Step 1. In cases where strong autocorrelation and heteroscedasticity are observed, it is necessary to apply a time-series model initially to eliminate temporal dependence. Subsequently, the marginal parameters can be derived using the filtered residuals, and a copula can be fitted to these residuals, which are then transformed to uniform marginals. An estimator for the copula-based $SMS{R}_C(X,Y)$ as defined by (7) can be obtained as follows:

Step 1.

Fit appropriate models to the time-series data and obtain their standardized residuals;

Step 2.

Transform the marginal standardized residuals into uniformly distributed samples;

Step 3.

Estimate the dependence structure of two uniformly distributed residuals using copula modeling by maximum likelihood method;

Step 4.

Generate n random samples $(S_{1t},S_{2t})$, $t=1,\dots ,n$ with the estimated copula models. Apply probability integral transform to $(S_{1t},S_{2t})$, $t=1,\dots ,n$ and then, calculate the Pearson’s moment correlation $r_C$ and the marginal Sharpe ratios ${\widehat{SR}}_X^{*}$ and ${\widehat{SR}}_Y^{*}$ based on the means and variances of the estimated models;

Step 5.

Compute the copula-based estimator of $SMS{R}_C(X,Y)$ by (12).

In this section, we compare the values of the copula-based ($SMS{R}_C(X,Y)$) and empirical ($SMSR(X,Y)$) squared maximum Sharpe ratio by simulation. In the simulation, we consider the effect of sample size, marginal distributions, dependence structure, and the level of dependency. The simulation study was carried out according to a factorial design involving four factors that affect the estimation process:

(1)

Sample size: $n\in \{50,200,500\}$;

(2)

Type of marginal distributions: symmetric (normal distribution) and skewed (gamma distribution);

(3)

Dependence structure, represented by the copula C:

• Clayton (an asymmetric copula with the lower tail dependence)

  $$C_{\theta }(u,v)={\{max(u^{-\theta }+v^{-\theta }-1,0)\}}^{-\frac{1}{\theta }},\theta \in [-1,\infty )-\left\{0\right\};$$
• Frank (a symmetric copula)

  $$C_{\theta }(u,v)=-\frac{1}{\theta }ln\left(1+\frac{(e^{-\theta u}-1)(e^{-\theta v}-1)}{e^{-\theta }-1}\right),\theta \in (-\infty ,\infty )-\left\{0\right\};$$
• Gumbel (an asymmetric copula with the upper tail dependence)

  $$C_{\theta }(u,v)=exp\{-{[{(-ln\left(u\right))}^{\theta }+{(-ln\left(v\right))}^{\theta }]}^{\frac{1}{\theta }}\},\theta \in [1,\infty );$$

(4)

Degree of dependence in terms of Kendall’s tau

$$\tau =4{\int }_0^1{\int }_0^1{C}_{\theta }(u,v)d{C}_{\theta }(u,v)-1,$$

at $\tau \in \{-0.3,0.3,0.8\}$, which corresponds to $\theta \in \{-0.46,0.86,8\}$ for the Clayton copula and $\theta \in \{-2.93,2.93,18.20\}$ for the Frank copula. For the Gumbel copula we consuder $\tau \in \{0.3,0.8\}$ which corresponds to $\theta \in \{1.43,5\}$.

For each combination of factors, 1000 random samples were generated, and the values of $SMS{R}_C(X,Y)$ were computed. The results are shown in

Table 1. The exact values and simulation results for $SMS{R}_C(X,Y)$, when the marginal distributions are $X\sim N(1,2)$ and $Y\sim N(1,2)$, the copula $C\in \{Clayton,Frank,Gumbel\}$, and different level of dependency in terms of Kendall’s $\tau$ and sample size $n\in \{50,200,500\}$.

Exact ${\mathit{SMSR}}_{\mathit{C}}(\mathit{X},\mathit{Y})$	Copula	$\mathit{\tau }$	n	${\widehat{\mathit{SMSR}}}_{\mathit{C}}(\mathit{X},\mathit{Y})$		$\widehat{\mathit{SMSR}}(\mathit{X},\mathit{Y})$		RE	Negative Bias
				Bias	MSE	Bias	MSE		${\widehat{\mathit{SMSR}}}_{\mathit{C}}(\mathit{X},\mathit{Y})$	$\widehat{\mathit{SMSR}}(\mathit{X},\mathit{Y})$
0.5218	Clayton	0.8	50	0.0684	0.0757	0.0565	0.0720	0.9511	45.12	47.11
			200	0.0174	0.0150	0.0145	0.0148	0.9842	47.22	48.20
			500	0.0055	0.0058	0.0044	0.0058	0.9956	48.94	49.31
0.6869	Clayton	0.3	50	0.1077	0.1307	0.0909	0.1247	0.9551	42.80	44.78
			200	0.0239	0.0246	0.0201	0.0243	0.9891	46.54	47.78
			500	0.0103	0.0094	0.0089	0.0094	1.0045	47.02	47.61
1.7720	Clayton	−0.3	50	0.1373	0.1659	0.1250	0.1839	1.1086	39.50	41.75
			200	0.0353	0.0312	0.0339	0.0376	1.2043	44.18	44.79
			500	0.0132	0.0118	0.0119	0.0144	1.2256	46.18	46.53
0.5219	Frank	0.8	50	0.0978	0.0782	0.0866	0.0738	0.9436	39.80	41.45
			200	0.0239	0.0144	0.0210	0.0141	0.9791	44.90	45.94
			500	0.0095	0.0053	0.0084	0.0053	0.9897	46.64	47.34
0.7054	Frank	0.3	50	0.1001	0.1050	0.0827	0.0998	0.9502	42.36	44.55
			200	0.0245	0.0196	0.0205	0.0192	0.9791	45.62	46.70
			500	0.0085	0.0074	0.0069	0.0073	0.9931	47.87	48.65
1.7168	Frank	−0.3	50	0.2003	0.4053	0.1778	0.4026	0.9931	41.50	43.30
			200	0.0477	0.0740	0.0427	0.0776	1.0477	45.50	46.52
			500	0.0168	0.0275	0.0150	0.0294	1.0691	47.67	48.59
0.5139	Gumbel	0.8	50	0.1029	0.0830	0.0892	0.0789	0.9496	39.81	41.61
			200	0.0258	0.0141	0.0230	0.0138	0.9806	44.13	45.18
			500	0.0099	0.0053	0.0088	0.0052	0.9925	46.43	47.01
0.6866	Gumbel	0.3	50	0.1183	0.1027	0.1039	0.0977	0.9520	37.21	41.52
			200	0.0241	0.0182	0.0205	0.0180	0.9872	45.49	46.85
			500	0.0101	0.0067	0.0087	0.0067	0.9975	46.79	47.40

and

Table 2. Simulation results for $SMS{R}_C(X,Y)$, when the marginal distributions are $X\sim gamma(1,2)$ and $Y\sim gamma(1,2)$, the copula $C\in \{Clayton,Frank,Gumbel\}$, and different level of dependency in terms of Kendall’s $\tau$ and sample size $n\in \{50,200,500\}$.

Exact ${\mathit{SMSR}}_{\mathit{C}}(\mathit{X},\mathit{Y})$	Copula	$\mathit{\tau }$	n	${\widehat{\mathit{SMSR}}}_{\mathit{C}}(\mathit{X},\mathit{Y})$		$\widehat{\mathit{SMSR}}(\mathit{X},\mathit{Y})$		RE	Negative Bias
				Bias	MSE	Bias	MSE		${\widehat{\mathit{SMSR}}}_{\mathit{C}}(\mathit{X},\mathit{Y})$	$\widehat{\mathit{SMSR}}(\mathit{X},\mathit{Y})$
0.5980	Clayton	0.8	50	0.0260	0.0123	0.0870	0.0290	2.3532	44.73	32.16
			200	0.0073	0.0026	0.0242	0.0065	2.4773	46.66	38.78
			500	0.0022	0.0009	0.0094	0.0025	2.5781	48.56	43.42
0.8359	Clayton	0.3	50	0.0397	0.0239	0.1156	0.0601	2.5170	43.56	33.18
			200	0.0087	0.0050	0.0299	0.0129	2.5706	47.08	40.32
			500	0.0029	0.0019	0.0116	0.0051	2.6269	48.62	44.42
1.1921	Clayton	−0.3	50	0.0560	0.0234	0.2179	0.1780	7.5780	37.35	29.06
			200	0.0120	0.0043	0.0552	0.0340	7.7702	44.18	39.01
			500	0.0050	0.0017	0.0226	0.0136	7.9614	46.53	42.78
0.5588	Frank	0.8	50	0.0288	0.0094	0.0987	0.0284	3.0173	42.02	28.50
			200	0.0074	0.0019	0.0268	0.0062	3.2380	45.33	36.98
			500	0.0023	0.0007	0.0109	0.0023	3.2798	48.01	41.80
0.7737	Frank	0.3	50	0.0424	0.0179	0.1141	0.0582	3.2398	40.50	31.73
			200	0.0088	0.0034	0.0288	0.0112	3.2489	46.67	40.09
			500	0.0042	0.0012	0.0120	0.0043	3.3303	46.92	42.86
1.3151	Frank	−0.3	50	0.0652	0.0422	0.2436	0.2016	4.7797	39.46	28.75
			200	0.0152	0.0085	0.0696	0.0437	5.1292	45.02	37.54
			500	0.0071	0.0032	0.0285	0.0169	5.2931	45.57	41.88
0.5079	Gumbel	0.8	50	0.0410	0.0109	0.0930	0.0367	3.3562	36.85	30.67
			200	0.0087	0.0019	0.0241	0.0079	4.0439	44.88	40.12
			500	0.0027	0.0007	0.0093	0.0030	4.3266	46.68	43.81
0.6468	Gumbel	0.3	50	0.0453	0.0177	0.1284	0.0692	3.8939	40.00	29.80
			200	0.0107	0.0033	0.0372	0.0157	4.7633	44.69	38.87
			500	0.0046	0.0012	0.0150	0.0061	4.8852	46.01	42.88

. The tables provide the copula structure, dependency level (Kendall’s $\tau$), the exact values of $SMS{R}_C(X,Y)$, considered sample sizes (n), the simulated bias (Bias), and mean square error (MSE) for the empirical estimator $\widehat{SMSR}(X,Y)$ defined by (2) and the copula-based estimator ${\widehat{SMSR}}_C(X,Y)$ defined by (12), as well as the relative efficiency (RE) and negative bias of two estimators. The results show that the MSE and bias in all cases decrease with the sample size, as expected. As we see, the relative efficiency of the copula-based estimator compared to the empirical method increases significantly when the sample size and level of dependence increase. From Table 2, it can be seen that when the marginal distributions are skewed, the copula-based estimator will have a much better performance than the empirical method. In summary, when the assets are normally distributed, using the copula-based method or empirical method to estimate the $SMS{R}_C(X,Y)$ does not make much difference.

5. Empirical Analysis

In this section, we will compare the estimation of $SMS{R}_C(X,Y)$ using real data analysis. We will use the copula-based method under the assumption of normality and also under the independence of returns. The stock market considered is SP 500, and the daily asset returns of five stocks, namely, Amazon, Apple, Google, Tesla, and Microsoft, are used. The period is from the 1 January 2018 to the 31 December 2022. The data sets are selected from “finance.yahoo.com (accessed on 26 February 2023)”. As an application of $SMS{R}_C(X,Y)$ in selecting stocks for investment, we consider each stock pair as an investment opportunity to build a portfolio with two assets. Using these five stocks, we can form 10 two-asset portfolios with the investment opportunity pairs in the set {(Amazon, Microsoft), (Apple, Microsoft), (Google, Microsoft), (Microsoft, Tesla), (Amazon, Apple), (Apple, Tesla), (Apple, Google), (Google, Tesla), (Amazon, Google), and (Amazon, Tesla).} Looking at the summary statistics and histograms (not shown here), it seems that all returns are almost symmetric. The high positive values of kurtosis for all returns indicate that the underlying distributions of all returns are heavy-tailed.

As the stock returns follow a time-series pattern, we seek appropriate models to analyze them. Common approaches for modeling and predicting the volatility of financial time series include the Autoregressive Moving Average (ARMA) model, the Autoregressive Conditional Heteroscedasticity (ARCH) model, the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model, and hybrid ARMA-GARCH models. The fitted time-series models are detailed in

Table 3. Fitted ARMA-GARCH time-series models for each return.

Return	Time-Series Model	Fitted Model
Amazon	AR(1)-GARCH(1,1)	$x_t=0.0012+0.0106x_{t-1}+a_t$, $a_t={\sigma }_t{ϵ}_t$, ${\sigma }_t^2=0.000012+0.1404a_{t-1}^2+0.8484{\sigma }_{t-1}^2$, ${ϵ}_t\sim t\left(5.45\right)$
Apple	AR(1)-GARCH(1,1)	$x_t=0.0019-0.0290x_{t-1}+a_t$, $a_t={\sigma }_t{ϵ}_t$, ${\sigma }_t^2=0.000016+0.1324a_{t-1}^2+0.8392{\sigma }_{t-1}^2$, ${ϵ}_t\sim t\left(5.68\right)$
Google	AR(1)-GARCH(1,1)	$x_t=0.0014-0.0360x_{t-1}+a_t$, $a_t={\sigma }_t{ϵ}_t$, ${\sigma }_t^2=0.000010+0.1048a_{t-1}^2+0.8838{\sigma }_{t-1}^2$, ${ϵ}_t\sim t\left(5.68\right)$
Microsoft	AR(1)-GARCH(1,1)	$x_t=0.0018-0.0908x_{t-1}+a_t$, $a_t={\sigma }_t{ϵ}_t$, ${\sigma }_t^2=0.000010+0.1564a_{t-1}^2+0.8271{\sigma }_{t-1}^2$, ${ϵ}_t\sim t\left(6.40\right)$
Tesla	GARCH(1,1)	$x_t=0.0019+a_t$, $a_t={\sigma }_t{ϵ}_t$, ${\sigma }_t^2=0.000052+0.0909a_{t-1}^2+0.8946{\sigma }_{t-1}^2$, ${ϵ}_t\sim t\left(3.71\right)$

. Various models have been employed to model the volatility of Tesla’s returns, and overall, the GARCH(1,1) model outperformed others:

$$r_t={\mu }_0+{ϵ}_t,{\sigma }_t^2=\omega +\alpha {ϵ}_{t-1}^2+\beta {\sigma }_{t-1}^2,$$

where ${\sigma }_t^2$ represents the conditional variance, ${ϵ}_t$ denotes the residual returns defined as ${ϵ}_t={\sigma }_t{Z}_t$, with $Z_t$ being an i.i.d. process with zero mean and unit variance, and ${\mu }_0$, $\omega ,\alpha ,\beta >0$ are the estimated parameters detailed in Table 3. The volatility of the returns from Amazon, Apple, Google, and Microsoft has also been modeled using different approaches, and overall, the ARMA(1,0)-GARCH(1,1) model demonstrated a better fit:

$$r_t={\mu }_0+a_0{r}_{t-1}+{ϵ}_t,{\sigma }_t^2=\omega +\alpha {ϵ}_{t-1}^2+\beta {\sigma }_{t-1}^2,$$

with the estimated parameters provided in Table 3. We examined four symmetric distributions—Normal, Cauchy, Logistic, and Student-t Johnson et al. (1995)—for filtered conditional residuals.

Table 4. Fitted marginal distributions of for filtered residual of each return.

Return	Distribution	Paremeters	Loglikelihood	AIC	BIC	K.S Statistic	p-Value
Amazon	normal	$\mu =-0.0287$, $\sigma =0.6891$	−1316.62	2637.234	2647.51	0.0711	0.00
	Cauchy	location = 0.0028, scale = 0.3186	−1326.07	2656.15	2666.42	0.0516	0.00
	Logistic	location = −0.0184, scale = 0.3558	−1243.16	2490.31	2500.59	0.0391	0.04
	Student-t	df = 3.31	−1224.47	2454.95	2470.36	0.0213	0.61
Apple	normal	$\mu =-0.0391$, $\sigma =0.8885$	−1636.31	3276.61	3286.89	0.0712	0.00
	Cauchy	location = −0.0203, scale = 0.4199	−1654.49	3312.97	3323.25	0.0577	0.00
	Logistic	location = −0.0257, scale = 0.4581	−1558.08	3120.16	3130.44	0.0353	0.08
	Student-t	df = 3.64	−1540.42	3086.83	3102.25	0.0174	0.83
Google	normal	$\mu =-0.0323$, $\sigma =0.6679$	−1277.20	2558.40	2568.68	0.0801	0.00
	Cauchy	location = 0.0028, scale = 0.3053	−1280.69	2565.38	2575.65	0.0530	0.00
	Logistic	location = −0.0184, scale = 0.3442	−1202.82	2409.65	2419.93	0.0436	0.02
	Student-t	df = 3.22	−1182.44	2370.89	2386.30	0.0229	0.52
Microsoft	normal	$\mu =-0.0318$, $\sigma =0.7911$	−1490.27	2984.56	2994.83	0.0801	0.00
	Cauchy	location = −0.0025, scale = 0.3642	−1481.97	2967.94	2978.22	0.0530	0.00
	Logistic	location = −0.0183, scale = 0.4019	−1397.15	2798.30	2808.58	0.0436	0.02
	Student-t	df = 3.40	−1373.91	2753.83	2769.24	0.0229	0.52
Tesla	normal	$\mu =-0.0085$, $\sigma =0.6882$	−1314.97	2633.94	2644.22	0.0721	0.00
	Cauchy	location = −0.0058, scale = 0.3134	−1310.95	2625.90	2636.17	0.0475	0.00
	Logistic	location = −0.0067, scale = 0.3529	−1236.46	2476.93	2487.21	0.0421	0.02
	Student-t	df = 3.13	−1213.15	2432.29	2447.71	0.0218	0.59

displays the estimated parameters, Loglikelihood, Akaike’s Information Criterion (AIC), the Kolmogorov–Smirnov (K-S) statistic, and p-values of the fitted distributions. It is evident that the distribution of all filtered returns deviates significantly from normal, and the Student-t distribution emerges as a suitable choice. The density function of Student-t vs. the degree of freedom is given by:

$$f\left(x\right)=\frac{\Gamma \left(\frac{\nu +1}{2}\right)}{\sqrt{\nu \pi }\Gamma \left(\frac{\nu }{2}\right)}{\left(1+\frac{x^2}{\nu }\right)}^{-\frac{\nu +1}{2}},x\in R,\nu >0.$$

The marginal squared Sharpe ratios estimated under the fitted models and the normality assumption (empirical) are shown in

Table 5. Estimated marginal squared Sharpe ratios ($S{R}^2$) of returns.

Return	Distribution Based	Empirical
Amazon	0.0345	0.0371
Apple	0.0635	0.0778
Google	0.0508	0.0456
Microsoft	0.0691	0.0668
Tesla	0.0339	0.0317

. Next, we estimated the dependence parameters using the maximum likelihood method. Before modeling the dependence structure between margin-filtered returns, we transformed the standardized residuals into uniformly distributed data. To model the dependence of each pair of returns, we utilized the filtered residuals of the fitted time series models and identified a suitable copula for them. We considered some commonly used families of copulas in finance, including elliptical copulas (Gaussian, Student-t) and Archimedean copulas (Gumbel, Frank, and Clayton). Parameter estimation is based on the so-called inference for margins, which is a two-stage method, see, Joe (2014). The fitted copulas are presented in

Table 6. Fitted copulas for each pair of filtered residual of fitted models.

Pair of Returns	Copula	$\mathit{\theta }$	Loglikelihood	Sn	AIC	BIC
(Amazon, Microsoft)	Student-t	0.75, df = 3.61	537.00	0.0807	−1070.09	−1059.91
	Gumbel	2.08	460.00	0.2844	−917.99	−912.90
	Clayton	2.40	440.70	0.1338	−879.42	−874.32
	Frank	6.72	460.10	0.2076	−918.26	−913.17
	Normal	0.74	479.20	0.1009	−956.42	−951.34
(Apple, Microsoft)	Student-t	0.76, df = 3.06	582.10	0.0290	−1160.21	−1150.04
	Gumbel	2.19	513.30	0.1607	−1024.56	−1019.47
	Clayton	2.54	449.40	0.2377	−896.74	−891.65
	Frank	7.02	488.30	0.1439	−974.68	−969.59
	Normal	0.76	515.40	0.0435	−1028.86	−1023.77
(Google, Microsoft)	Student-t	0.81, df = 2.66	686.9	0.0386	−1369.85	−1359.67
	Gumbel	2.39	600.0	0.1834	−1197.94	−1192.85
	Clayton	2.94	549.9	0.2386	−1097.89	−1092.80
	Frank	7.85	565.7	0.1945	−1129.31	−1124.22
	Normal	0.79	599.3	0.0574	−1196.58	−1191.49
(Microsoft, Tesla)	Student-t	0.46, df = 6.32	166.50	0.0281	−329.07	−318.80
	Gumbel	1.40	137.60	0.1075	−273.23	−268.10
	Clayton	0.88	140.90	0.1352	−279.81	−274.67
	Frank	3.04	138.60	0.0840	−275.24	−270.10
	Normal	0.46	153.10	0.0400	−304.23	−299.09
	BB1	$\theta$ = 0.42, $\delta$ = 1.2	168.81	0.0243	−333.63	−323.36
(Amazon, Apple)	Student-t	0.69, df = 4.44	429.60	0.0656	−855.23	−844.96
	Gumbel	1.83	364.20	0.2502	−726.48	−721.35
	Clayton	1.92	341.30	0.1589	−680.50	−675.37
	Frank	5.62	377.80	0.1921	−753.66	−748.52
	Normal	0.68	385.00	0.0862	−768.00	−762.86
(Apple, Tesla)	Student-t	0.48, df = 6.46	173.10	0.0393	−342.10	−331.82
	Gumbel	1.40	138.00	0.1551	−274.04	−268.91
	Clayton	0.92	155.00	0.0903	−307.91	−302.77
	Frank	3.16	149.20	0.0909	−296.33	−291.19
	Normal	0.47	159.10	0.0487	−316.23	−311.10
	Survival BB1	$\theta$ = 0.09, $\delta$ = 1.4	178.41	0.0369	−352.83	−342.55
(Apple, Google)	Student-t	0.71, df = 3.67	467.30	0.0742	−930.65	−920.47
	Gumbel	1.93	392.80	0.2679	−783.55	−778.46
	Clayton	2.08	390.80	0.1326	−779.55	−774.46
	Frank	6.02	396.30	0.1928	−790.66	−785.57
	Normal	0.71	409.60	0.0938	−817.26	−812.17
(Google, Tesla)	Student-t	0.43, df = 7.43	135.70	0.0475	−267.35	−257.08
	Gumbel	1.34	108.40	0.1580	−214.70	−209.56
	Clayton	0.80	121.50	0.0725	−240.91	−235.77
	Frank	2.81	120.70	0.0943	−239.35	−234.21
	Normal	0.42	126.20	0.0574	−250.32	−245.18
	Survival BB1	$\theta$ = 0.07, $\delta$ = 1.35	139.80	0.0423	−275.61	−265.33
(Amazon, Google)	Student-t	0.74, df = 3.72	519.40	0.0658	−1011.14	−1000.96
	Gumbel	2.01	425.20	0.2529	−848.31	−843.22
	Clayton	2.30	405.80	0.1540	−809.60	−804.51
	Frank	6.51	441.30	0.1895	−880.50	−875.41
	Normal	0.72	433.30	0.0838	−864.66	−859.57
(Amazon, Tesla)	Student-t	0.46, df = 6.81	157.80	0.0408	−311.64	−301.36
	Gumbel	1.38	126.80	0.1607	−251.63	−246.49
	Clayton	0.88	132.90	0.0802	−263.78	−258.64
	Frank	3.05	138.90	0.1046	−275.72	−270.58
	Normal	0.45	145.80	0.0572	−289.53	−284.39
	Survival BB1	$\theta$ = 0.11, $\delta$ = 1.37	161.74	0.0388	−319.48	−309.21

. To select the most appropriate copulas, we employed the BiCopSelect function in the R package VineCopula Nagler et al. (2023). A review and comparison of copula goodness-of-fit test procedures can be found in Genest et al. (2009). The log-likelihood values, the Cramér–von Mises statistic $S_n$, the Akaike information criterion (AIC), and the Bayesian Information Criteria (BIC) of the fitted models are detailed in Table 6. The Gaussian copula and Student-t copula outperform the other three, based on a larger log-likelihood and smaller AIC and BIC values. The returns of portfolios (1), (2), (3), (5), (7), and (9) fit well with the Student-t copula, as follows:

$$C_{\rho ,\nu }(u,v)=T_{\rho ,\nu }(T_{\nu }^{-1}\left(u\right),T_{\nu }^{-1}\left(v\right)),$$

where $T_{\nu }(.)$ and $T_{\nu }^{-1}(.)$ are the CDF of the Student-t random variable with the degrees of freedom $v\in N-\left\{0\right\}$ and its inverse, and $T_{\rho ,\nu }(.,.)$ is the bivariate Student-t distribution with the correlation parameter $-1\le \rho \le 1$ and the degrees of freedom $\nu$ Joe (2014). The returns of the portfolio (4) fit well with the BB1 copula Joe (2014) given by

$$C(u,v)={\{1+{[{(u^{-\theta }-1)}^{\delta }+{(v^{-\theta }+1)}^{\delta }]}^{\frac{1}{\delta }}\}}^{\frac{1}{\theta }},\theta \ge 0,\delta \ge 1.$$

The returns of the portfolios (6), (8), and (10) fit with the survival of the BB1 copula, i.e., $C_S(u,v)=u+v-1+C(1-u,1-v)$. The estimated parameters $\theta$ and $\delta$ are given in Table 6. Finally,

Table 7. The estimated $SMS{R}_C(X,Y)$ for each pair of returns.

Pair of Returns	$\mathit{\tau }$	${\mathit{r}}_{\mathit{C}}$	r	Copula-Based	Under Independence	Empirical
(Amazon, Microsoft)	0.539	0.749	0.716	0.0054	0.0060	0.0047
(Apple, Microsoft)	0.552	0.759	0.775	0.0051	0.0088	0.0062
(Google, Microsoft)	0.600	0.809	0.811	0.0048	0.0073	0.0046
(Microsoft, Tesla)	0.307	0.480	0.469	0.0046	0.0059	0.0045
(Amazon, Apple)	0.487	0.688	0.653	0.0042	0.0052	0.0064
(Apple, Google)	0.504	0.707	0.704	0.0041	0.0066	0.0060
(Apple, Tesla)	0.317	0.484	0.474	0.0040	0.0051	0.0061
(Google, Tesla)	0.285	0.439	0.418	0.0027	0.0037	0.0023
(Amazon, Google)	0.532	0.739	0.685	0.0026	0.0038	0.0021
(Amazon, Tesla)	0.308	0.476	0.437	0.0016	0.0023	0.0017

shows the value of the copula-based $SMS{R}_C(X,Y)$ defined by (12), the value of the $SMS{R}_C(X,Y)$ under the independence assumption, and the empirical value of the $SMSR(X,Y)$ defined by (9). The value of the Pearson correlation coefficient of the returns for each portfolio is calculated with the copula-based method (11) and the ordinary empirical value is shown in Table 7. It can be seen that all five stocks have a high positive correlation with each other, and the correlation between Microsoft and the other four stocks is higher. According to the results of Table 5 and Table 7, the copula-based estimator is consistent with Part 3 of Proposition 1. The value of $SMS{R}_C(X,Y)$ for each pair of stocks is greater than the squared Sharpe ratio of the marginal stocks. The estimated values of $SMS{R}_C(X,Y)$ in Table 7 are consistent with the result of Proposition 3, that is, in the case that stocks have positive dependence, the value of the copula-based estimator of $SMS{R}_C(X,Y)$ is always smaller than the value of $SMSR(X,Y)$ under the assumption of independence. Therefore, if dependence is not considered in the estimation of $SMSR(X,Y)$, it gives misleading results. As an application of $SMSR(X,Y)$ in selecting stocks for investment, if we consider each stock pair as an investment opportunity set to build a portfolio with two assets, according to Table 7, the order of selecting options based on the three estimation methods is not the same. Therefore, incorrectly considering the assumption of independence will produce the wrong results. Based on the value of $SMS{R}_C(X,Y)$, the first three options are the (Microsoft, Amazon), (Microsoft, Apple), and (Microsoft, Tesla) pairs.

6. Conclusions

One of the key issues in investment is creating a suitable portfolio by estimating optimal weights for desired assets. Before forming a portfolio, selecting an investment opportunity set of assets is crucial. In the absence of a risk-free asset, the investment opportunities can be determined based on the Sharpe ratios of risky assets and their correlation. The maximum Sharpe ratio is a suitable index that summarizes the performance of an investment opportunity in a single value, which is a function of the Sharpe ratios of assets and their correlation coefficients. In this study, we examined the maximum square of the Sharpe ratio as the Sharpe ratio of a vector and obtained results about the dependence effect on this measure. We provided a copula-based estimator for it and investigated the performance of the proposed index by simulating and analyzing real data. The bivariate squared maximum Sharpe ratio was considered in this study, and future work could be developed for dimensions bigger than 2.