Trading Activity in the Corporate Bond Market: A SAD Tale of Macro-Announcements and Behavioral Seasonality?
Abstract
1. Introduction
2. Literature Review
2.1. Seasonal Affective Disorder
2.2. Macroeconomic Effects
2.3. Microstructural and Other Effects
2.4. Deterministic Seasonality, Other Effects, and Modeling Implications
3. Empirical Methodology
3.1. General-to-Specific Modeling and Autometrics
3.2. General Unrestricted Model
- is the dependent variable, representing returns and measures of trading activity.
- α (Alpha) is the constant term, representing the model’s intercept.
- ϕ (Phi) is the coefficient for the first-order autoregressive term Yt−1.
- γ (Gamma) is the coefficient for the time trend t, representing seasoning of corporate bonds—i.e., decrease in trading as bonds age.
- denotes behavioral SAD factors, with (Theta) coefficients.
- denotes the macroeconomic announcement variables, with i indicating the specific announcement and j representing the lag order (0 or 1). Announcements are unemployment claims, nonfarm payrolls, core CPI, and core PPI and are measured in both standardized surprises and absolute standardized surprises.13,14
- (Beta) are the coefficients for the macroeconomic announcement variables.
- represents other exogenous variables, with (Psi) as coefficients.
- SISs are the step indicator saturation variables, capturing level shifts or structural breaks, with τs (Tau) coefficients.
- IISl are the impulse indicator saturation variables, addressing outlier effects at specific points in time, with λl (Lambda) as coefficients.
- ϵt (Epsilon) is the error term, accounting for unobserved factors affecting Yt.
4. Description of Data
4.1. Dependent Variables: Return Data and Trading Activity
4.2. Independent Variables: Economic Survey, Ratings, and Seasonal Data
5. Empirical Results
5.1. Performance Regressions
5.2. Trading Activity Results—Total and Large-Volume Trades
5.3. Analysis of Trading Activity—Inter-Dealer Trades
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Day-of-Week and Time-of-Day Effects
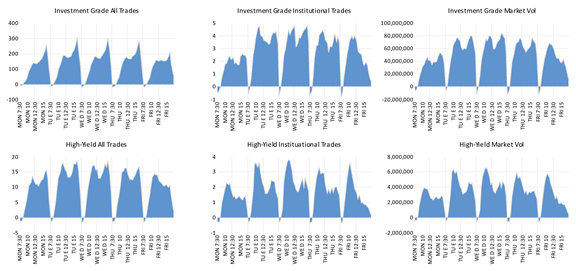
Appendix B. Unit Root Tests
| Grade | Unit Root Tests | ADF T-Stat | ADF Prob. |
| Investment Grade | Total Trades | −3.8509 | 0.0026 |
| Institutional Trades | −4.3574 | 0.0004 | |
| Intermediated Trades | −3.7879 | 0.0032 | |
| Intermediated Institutional Trades | −5.0374 | 0.0000 | |
| AAA | AAA Total Trades | −5.3356 | 0.0000 |
| AAA Institutional Trades | −19.7355 | 0.0000 | |
| AAA Financial Trades | −5.4464 | 0.0000 | |
| AAA Institutional Nonfinancial Trades | −20.8957 | 0.0000 | |
| High-Yield | Total Trades | −4.6561 | 0.0001 |
| Institutional Trades | −4.6287 | 0.0001 | |
| Intermediated Trades | −15.9030 | 0.0000 | |
| Intermediated Institutional Trades | −5.1554 | 0.0000 | |
| Note: This table contains results of augmented Dickey–Fuller unit root tests on the dependent variables in this study. Full sample period is used in all tests. | |||
Appendix C. Predictor Description for General Unrestricted Model
| Predictor | Lag Structure | Description |
| Macro-Announcement Surprises | Contemporaneous, Lag 1 | Standardized Surprises and Absolute Standardized Surprises for Nonfarm Payrolls, Initial Jobless Claims, Core CPI, Core PPI |
| Macroeconomic Announcement Day | Contemporaneous, Lead 1, Lag 1 | Dummy Variables for Surprises for Nonfarm Payrolls, Initial Jobless Claims, Core CPI, Core PPI |
| Credit Quality | Contemporaneous | Moody’s Ratings (Aggregate Net Credit Notches Up/Down) |
| Financial Market Returns | Contemporaneous, Lag 1 | S&P 500 Returns |
| Seasonal—Month of Year | Contemporaneous | December, January(January Effect) |
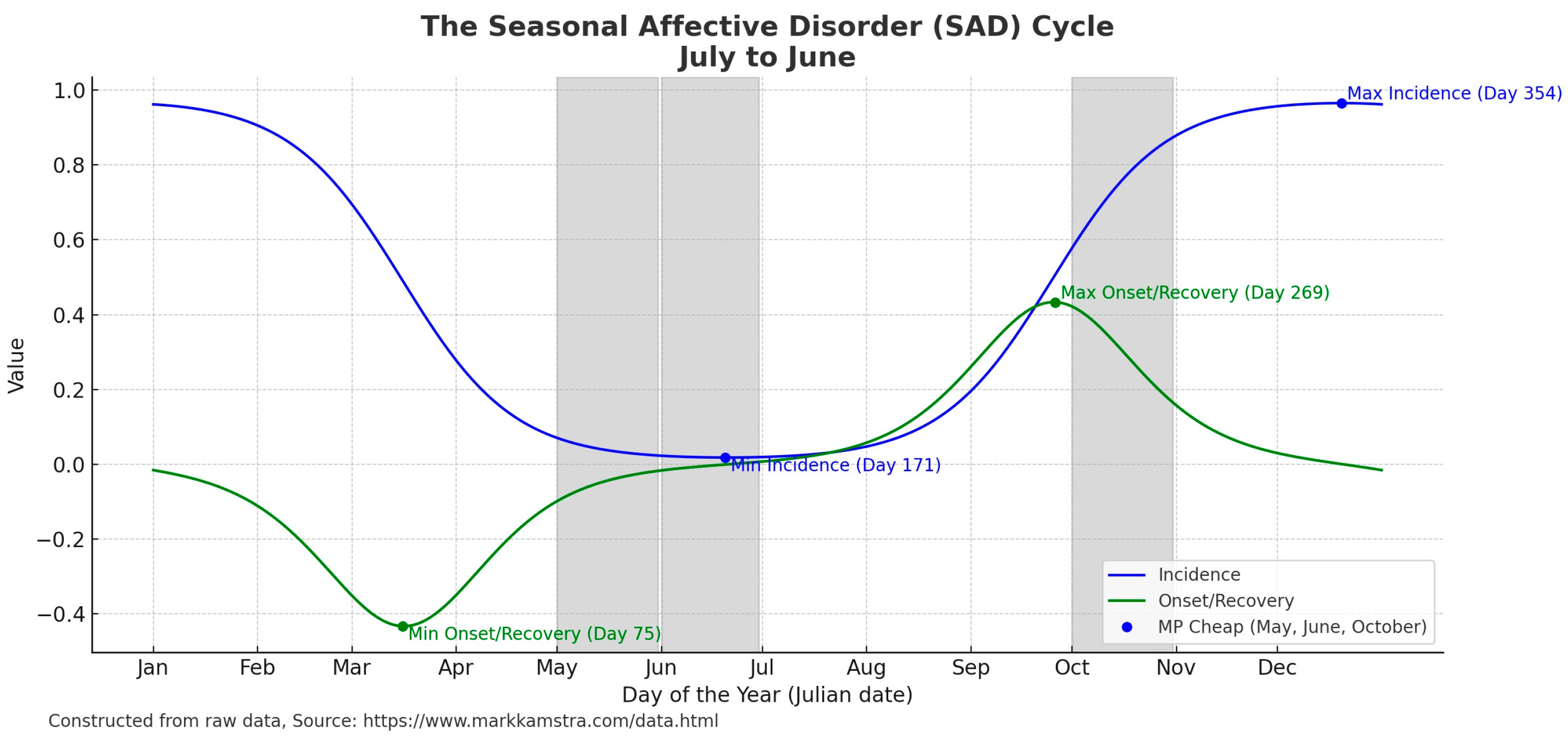
| Seasonal—Behavioral/Mood | Contemporaneous | Incidence and Onset of Seasonal Affective Disorder |
| Seasonal—Trend | Contemporaneous | Linear Time Trend |
| Seasonal—Pricing | Contemporaneous | Dummy Variable for Expensive and Cheap Loan Periods |
| Seasonal—Holiday | Contemporaneous, Lead 1, Lag 1 | Dummy Variable |
| Leads/Lags of Variables | Lead 1, Lag 1 | Anticipatory Behavior (Lead 1) are “Set-Up Effects”, Delayed Effects (Lag 1) |
Appendix D. AAA and AAA-Financial Trading Activity
| Investment Grade | Financial | |||
|---|---|---|---|---|
| Independent Variable | AAA Total Trades Coefficient | AAA Institutional Trades Coefficient | AAA Financial Total Trades Coefficient | AAA Financial Institutional Trades Coefficient |
| Trend | −0.54 **+ | |||
| S&P 500 Volume | 1.50 **+ | 21.77 **+ | 2.31 **+ | |
| S&P 500 Volume (−1) | −20.14 **+ | −1.53 **+ | ||
| Nonfarm Payrolls SS | 15.54 **+ | |||
| ABS Consumer Price Index SS | −2.11 **+ | −1.72 **+ | ||
| ABS Nonfarm Payrolls SS (+1) | −20.05 **+ | −15.77 **+ | ||
| Murfin Petersen Cheap | 332.71 **+ | 560.72 **+ | ||
| Monday | −13.04 **+ | −11.85 **+ | ||
| Tuesday | 14.75 **+ | 1.18 **+ | ||
| Wednesday | 1.70 **+ | 1.33 **+ | ||
| Friday | −42.71 **+ | −34.13 **+ | ||
| December | −25.36 ** | −1.90 **+ | ||
| NYSE Holiday | −255.93 **+ | −227.14 **+ | ||
| NYSE Holiday (+1) | −39.15 **+ | −39.56 **+ | ||
| NYSE Early Close | −182.78 **+ | −118.01 **+ | ||
| SAD Incidence | 2.17 **+ | |||
| SAD Onset | −71.86 **+ | |||
| Impulse Indicators | 19 | 6 | 20 | 10 |
| Step Indicators | 36 | 22 | 31 | 22 |
| AR 1-2 test | 0.93 [0.3933] | 0.25 [0.7809] | 0.66 [0.5161] | 0.84 [0.4317] |
| ARCH 1-1 test | 0.14 [0.7131] | 0.08 [0.7825] | 1.06 [0.3047] | 0.00 [0.9948] |
| Normality test | 3.61 [0.1643] | 39.97 [0.0000] ** | 0.10 [0.9496] | 9.10 [0.0106] * |
| Hetero test | 0.69 [0.9303] | 0.92 [0.5688] | 0.96 [0.5515] | 1.71 [0.0102] * |
| RESET23 test | 1.09 [0.3360] | 0.90 [0.4056] | 4.51 [0.0115] * | 0.93 [0.3937] |
| 1 | The Gets approach is also known as the “LSE Econometric Approach”, based on its origin at the London School of Economics during the 1970s under econometricians Denis Sargan and Sir David F. Hendry. |
| 2 | See also: with respect to volatility, Jones et al. (1998) and, with respect to US Treasury Auctions, Smales (2021), Amin and Tédongap (2023), and Forest and Mackey (2023). |
| 3 | See also: Holden et al. (2018) examine OTC corp bonds from a price discovery perspective. Also, Pasquariello and Sandulescu (2023) relate liquidity to speculation. |
| 4 | We found holiday effects on stock prices as far back in the literature as Fields (1934). Ariel (1990) studies higher stock returns ahead of holidays. Cadsby and Ratner (1992) extend this line of research internationally. Further extensions are found in Kim and Park (1994) and Meneu and Pardo (2004). |
| 5 | The rule involves selling previously purchased securities (that have since lost value) prior to the end of the calendar year to capture tax benefits and reacquiring them at the start of the subsequent year. |
| 6 | |
| 7 | See also: Hendry et al. (1984), Hendry (1988), Doornik and Hendry (2015), and Hendry and Mizon (2016). In particular, Hendry (2024) presents an review of the Gets methodology with recent advancements. |
| 8 | While the approach of Pesaran and Shin (1998), Pesaran et al. (2001), and Nica et al. (2023) bears similarity to the Gets approach, particularly with its emphasis on lag reduction and specification testing, Hendry’s automated Gets approach is preferable in terms of its ability to achieve parsimony in a financial context, where the long-run properties are of less interest, given the assumption of market efficiency. |
| 9 | Automated model selection procedures have also been examined by White (1990), Hoover and Perez (1999), Hendry and Krolzig (1999), Phillips (2005), McAleer (2005), Perez-Amaral et al. (2005), Groen and Kapetanios (2013), Bredahl Kock and Teräsvirta (2015), and Guerard et al. (2020). |
| 10 | Normality test is that of Doornik and Hansen (2008). |
| 11 | An open-source alternative to Autometrics can be found in R package, gets, in Pretis et al. (2018). The package can be customized to emulate the commercial implementation in OxMetrics via PcGive. |
| 12 | Forest (2018b) demonstrates the effectiveness of Gets in eliminating omitted variable bias in the Treasury market. See also: Pellini (2021), Khan et al. (2021), Muhammadullah et al. (2022), and Bonnier (2022). |
| 13 | We note the use of competing announcement measures. Consistent with the literature, our priors are that directional sensitivity to macroeconomic announcement surprises was seen in the retention of standardized surprise variables in performance regressions, while trading activity responsiveness would be found by retention of the absolute surprises. This is consistent with Brenner et al. (2009), who use an absolute measure in the return equation of their DCC model, while absolute announcement shocks are employed in the variance equation. Absolute surprises are commonly used as predictors that are inherently non-negative such as volatility. |
| 14 | The ability of Gets to handle competing variable definitions is described in Granger and Hendry (2005) (see question 5) and in Hendry and Doornik (2014). See also: Granger (2009). |
| 15 | Corporate bond market returns were calculated from the Bank of America Merrill Lynch US Corporate Master Total Return Index and the US High Yield Master II Total Return Index. Both series are downloadable from the Federal Reserve Bank of St. Louis FRED Database series, bamlcc0a0cmtriv and bamlhyh0a0hym2triv, respectively. |
| 16 | The data were retrieved from Yahoo! Finance. |
| 17 | Details can be found at http://www.finra.org/industry/trace (accessed on 27 January 2024). |
| 18 | Ronen and Zhou (2013) defined a top bond as an issue that attracts mostly institutional trades following the release of firm-specific information. These bonds help to facilitate the price discovery process. |
| 19 | |
| 20 | This allows us to evaluate the hypothesis that debt trades frequently as they age—this phenomenon is known as the “seasoning” effect. |
| 21 | “Core rates” exclude food and energy prices which tend to be volatile and can deviate from underlying price pressures. Market participants rely on the core rates to provide a better representation of the underlying pressures. |
| 22 | Heuson and Su (2003), exploring option-implied volatility behavior for US Treasuries, observed increased implied volatility the day prior to announcements that were later followed by a normalization. |
| 23 | Time-of-day effects are also visually discernable in Appendix A. |
| 24 | These include path dependency and repeated selection, among others. For more elaboration, see Hendry and Doornik (2014). |
| 25 | As we also found that the TRACE data exhibit an abundance of these “paired bond trades”, we employed the same 60-second filtering to the raw data to eliminate distortions arising from IDI trades. |
| 26 | The authors establish a link between trading activity, liquidity, and credit risk. See also: Ismailescu and Kazemi (2010). |
| 27 | Li and Galvani (2021), for instance, show differences in behavior on same-issuer bonds and show that informed trading applies asymmetrically between top and nontop bonds. In other words, just because a company has actively traded top bonds does not mean that we expect all their bonds to behave consistently. |
References
- Ai, Hengjie, and Ravi Bansal. 2018. Risk Preferences and the Macroeconomic Announcement Premium. Econometrica 86: 1383–430. [Google Scholar] [CrossRef]
- Amin, Shehryar, and Roméo Tédongap. 2023. The changing landscape of treasury auctions. Journal of Banking & Finance 148: 106714. [Google Scholar] [CrossRef]
- Ariel, R. A. 1990. High Stock Returns Before Holidays: Existence and Evidence on Possible Causes. Journal of Finance 45: 1611–26. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Arnaud Mehl. 2019. On the global financial market integration “swoosh” and the trilemma. Journal of International Money and Finance 94: 227–45. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Marie Hoerova. 2014. The VIX, the variance premium and stock market volatility. Journal of Econometrics 183: 181–92. [Google Scholar] [CrossRef]
- Bekaert, Geert, Robert J. Hodrick, and Xiaoyan Zhang. 2012. Aggregate Idiosyncratic Volatility. Journal of Financial and Quantitative Analysis 47: 1155–85. [Google Scholar] [CrossRef]
- Bhardwaj, Ravinder K., and Leroy D. Brooks. 1992. The January Anomaly: Effects of Low Share Price, Transaction Costs, and Bid-Ask Bias. The Journal of Finance 47: 553–75. [Google Scholar] [CrossRef]
- Biais, Bruno, and Richard C. Green. 2007. The Microstructure of the Bond Market in the 20th Century. Review of Economic Dynamics 33: 250–71. [Google Scholar] [CrossRef]
- Bonnier, Jean-Baptiste. 2022. Forecasting crude oil volatility with exogenous predictors: As good as it GETS? Energy Economics 111: 106059. [Google Scholar] [CrossRef]
- Branch, Ben. 1977. A Tax Loss Trading Rule. The Journal of Business 50: 198–207. [Google Scholar]
- Bredahl Kock, Anders, and Timo Teräsvirta. 2015. Forecasting Macroeconomic Variables Using Neural Network Models and Three Automated Model Selection Techniques. Econometric Reviews 35: 1753–79. [Google Scholar] [CrossRef]
- Brenner, Menachem, Paolo Pasquariello, and Marti Subrahmanyam. 2009. On the Volatility and Comovement of US Financial Markets around Macroeconomic News Announcements. Journal of Financial and Quantitative Analysis 44: 1265–89. [Google Scholar] [CrossRef]
- Cadsby, Charles Bram, and Mitchell Ratner. 1992. Turn-of-Month and Pre-Holiday Effects on Stock Returns: Some International Evidence. Journal of Banking & Finance 16: 497–509. [Google Scholar] [CrossRef]
- Cai, Fang, Song Han, Dan Li, and Yi Li. 2019. Institutional herding and its price impact: Evidence from the corporate bond market. Journal of Financial Economics 131: 139–67. [Google Scholar] [CrossRef]
- Castle, Jennifer L., and David F. Hendry. 2014. Model selection in under-specified equations facing breaks. Journal of Econometrics 178: 286. [Google Scholar] [CrossRef]
- Castle, Jennifer L., David F. Hendry, and Andrew B. Martinez. 2017. Evaluating Forecasts, Narratives and Policy Using a Test of Invariance. Econometrics 5: 39. [Google Scholar] [CrossRef]
- Chatrath, Arjun, Hong Miao, Sanjay Ramchander, and Sriram Villupuram. 2012. Corporate Bonds, Macroeconomic News, and Investor Flows. Journal of Fixed Income 22: 25–40. [Google Scholar] [CrossRef]
- Dewachter, Hans, Leonardo Iania, Wolfgang Lemke, and Marco Lyrio. 2019. A macro–financial analysis of the corporate bond market. Empirical Economics 57: 1911–33. [Google Scholar] [CrossRef]
- Dhrymes, Phoebus J. 1971. Distributed Lags: Problems of Estimation and Formulation. San Francisco: Holden-Day. [Google Scholar]
- Dolvin, Steven D., Mark K. Pyles, and Qun Wu. 2009. Analysts Get SAD Too: The Effect of Seasonal Affective Disorder on Stock Analysts’ Earnings Estimates. Journal of Behavioral Finance 10: 214–25. [Google Scholar] [CrossRef]
- Doornik, Jurgen A. 2009. Autometrics. Oxford: Oxford University Press. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., and David F. Hendry. 2015. Statistical model selection with “Big Data”. Cogent Economics & Finance 3: 1045216. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., and Henrik Hansen. 2008. An Omnibus Test for Univariate and Multivariate Normality. Oxford Bulletin of Economics and Statistics 70: 927–39. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., David F. Hendry, and Felix Pretis. 2015. Detecting Location Shifts during Model Selection by Step-Indicator Saturation. Econometrics 3: 240–64. [Google Scholar] [CrossRef]
- Elton, Edwin, Martin J. Gruber, Deepak Agrawal, and Christopher Mann. 2001. Explaining the Rate Spread on Corporate Bonds. Journal of Finance LVI: 247–77. [Google Scholar] [CrossRef]
- Ericsson, Neil R. 2016. Eliciting GDP forecasts from the FOMC’s minutes around the financial crisis. International Journal of Forecasting 32: 571–83. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1991. Efficient Capital Markets II. The Journal of Finance 46: 1575–617. [Google Scholar] [CrossRef]
- Fedenia, Mark, Tavy Ronen, and Seunghan Namc. 2021. Machine Learning in the Corporate Bond Market and Beyond: A New Classifier. Available online: https://ssrn.com/abstract=3848068 (accessed on 27 January 2024). [CrossRef]
- Fields, M. J. 1934. Security Prices and Stock Exchange Holidays in Relation to Short Selling. Journal of Business 7: 328–33. [Google Scholar] [CrossRef]
- Fisher, Adlai, Charles Martineau, Jinfei Sheng, and Stijn Van Nieuwerburgh. 2022. Macroeconomic Attention and Announcement Risk Premia. The Review of Financial Studies 35: 5057–93. [Google Scholar] [CrossRef]
- Fisher, Irving. 1925. Our Unstable Dollar and the So-called Business Cycle. Journal of the American Statistical Association 20: 179–202. [Google Scholar] [CrossRef]
- Fisher, Irving. 1937. Note on a Short-Cut Method for Calculating Distributed Lags. International Statistical Bulletin 29: 323–27. [Google Scholar]
- Forest, James J. 2018a. Essays in Financial Economics: Announcement Effects in Fixed Income Markets. Ph.D. dissertation, Department of Finance, Isenberg School of Management, University of Massachusetts—Amherst, Amherst, MA, USA; p. 164. [Google Scholar] [CrossRef]
- Forest, James J. 2018b. The Effect of Macroeconomic Announcements on Credit Markets: An Autometric General-to-Specific Analysis of the Greenspan Era. Working Paper. Amherst: University of Massachusetts. [Google Scholar] [CrossRef]
- Forest, James J., and Paul Turner. 2013. Alternative estimators of cointegrating parameters in models with nonstationary data: An application to US export demand. Applied Economics 45: 629–36. [Google Scholar] [CrossRef]
- Forest, James J., and Scott P Mackey. 2023. The Effect of Treasury Auctions on Returns: The 1990s Experience. Academy of Economics and Finance Journal 14: 1–10. [Google Scholar] [CrossRef]
- Frühwirth, Manfred, and Leopold Sögner. 2015. Weather and SAD related mood effects on the financial market. Quarterly Review of Economics and Finance 57: 11–31. [Google Scholar] [CrossRef]
- Frydman, Roman, and Joshua R. Stillwagon. 2018. Fundamental factors and extrapolation in stock-market expectations: The central role of structural change. Journal of Economic Behavior & Organization 148: 189–98. [Google Scholar] [CrossRef]
- Frydman, Roman, Nicholas Mangee, and Josh Stillwagon. 2020. How Market Sentiment Drives Forecasts of Stock Returns. Journal of Behavioral Finance 22: 351–67. [Google Scholar] [CrossRef]
- Garrett, Ian, Mark J. Kamstra, and Lisa A. Kramer. 2005. Winter blues and time variation in the price of risk. Journal of Empirical Finance 12: 291–316. [Google Scholar] [CrossRef]
- Granger, Clive W. J. 2009. In Praise of Pragmatics in Econometrics. In The Methodology and Practice of Econometrics: A Fetschrift in Honour of David F. Hendry. Edited by Jennifer L. Castle and Neil Sheppard. Oxford: Oxford University Press. [Google Scholar]
- Granger, Clive W. J., and David F. Hendry. 2005. A Dialogue Concerning a New Instrument for Econometric Modeling. Econometric Theory 21: 278–97. [Google Scholar] [CrossRef]
- Green, T. Clifton. 2004. Economic News and the Impact of Trading on Bond Prices. Journal of Finance 59: 1201–19. [Google Scholar] [CrossRef]
- Groen, Jan J. J., and George Kapetanios. 2013. Model Selection Criteria for Factor-Augmented Regressions. Oxford Bulletin of Economics and Statistics 75: 37–63. [Google Scholar] [CrossRef]
- Guerard, John, Dimitrios Thomakos, and Foteini Kyriazi. 2020. Automatic time series modeling and forecasting: A replication case study of forecasting real GDP, the unemployment rate and the impact of leading economic indicators. Cogent Economics & Finance 8: 1759483. [Google Scholar] [CrossRef]
- Hendry, David F. 1988. Encompassing. National Institute Economic Review 125: 88–103. [Google Scholar] [CrossRef]
- Hendry, David F. 1993. Econometrics: Alchemy of Science? Economica 47: 387–406. [Google Scholar] [CrossRef]
- Hendry, David F. 1995. Dynamic Econometrics. Oxford: Oxford University Press. [Google Scholar] [CrossRef]
- Hendry, David F. 2024. A Brief History of General-to-specific Modelling. Oxford Bulletin of Economics and Statistics 86: 1–20. [Google Scholar] [CrossRef]
- Hendry, David F., Adrian R. Pagan, and J. Denis Sargan. 1984. Dynamic Specification. In Handbook of Econometrics. Edited by Zvi Griliches and Michael D. Intriligator. Amsterdam: North Holland, pp. 1023–100. [Google Scholar] [CrossRef]
- Hendry, David F., and Felix Pretis. 2023. Quantifying the Uncertainty around Break Dates in Step-Indicator Saturation. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Hendry, David F., and Grayham E. Mizon. 2016. Improving the teaching of econometrics. Cogent Economics & Finance 4: 1170096. [Google Scholar] [CrossRef]
- Hendry, David F., and Hans-Martin Krolzig. 1999. Improving on ‘Data mining reconsidered’ by K.D. Hoover and S.J. Perez. The Econometrics Journal 2: 202–19. [Google Scholar] [CrossRef]
- Hendry, David F., and Jurgen A. Doornik. 2014. Empirical Model Discovery and Theory Evaluation: Automatic Selection Methods in Econometrics. Cambridge: MIT Press. [Google Scholar]
- Heuson, Andrea J., and Tie Su. 2003. Intra–day Behavior of Treasury Sector Index Option Implied Volatilities around Macroeconomic Announcements. Financial Review 38: 161–77. [Google Scholar] [CrossRef]
- Holden, Craig W., Yifei Mao, and Jayoung Nam. 2018. Price Discovery in the Stock, OTC Corporate Bond, and NYSE Corporate Bond Markets. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Hong, Harrison, and Jialin Yu. 2009. Gone fishin’: Seasonality in trading activity and asset prices. Journal of Financial Markets 12: 672–702. [Google Scholar] [CrossRef]
- Hoover, Kevin D., and Stephen Perez. 1999. Data mining reconsidered: Encompassing and the general-to-specific approach to specification search. Econometrics Journal 2: 167–91. [Google Scholar] [CrossRef]
- Ismailescu, Iuliana, and Hossien B. Kazemi. 2010. The Reaction of Emerging Market Credit Default Swap Spreads to Sovereign Credit Rating Changes. Journal of Banking and Finance 34: 2861–73. [Google Scholar] [CrossRef]
- Jacobsen, Ben, and Wessel Marquering. 2008. Is it the weather? Journal of Banking & Finance 32: 526–40. [Google Scholar] [CrossRef]
- Jiang, Hao, and Zheng Sun. 2015. News and Corporate Bond Liquidity. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Johansen, Søren, and Bent Nielsen. 2009. An Analysis of the Indicator Saturation Estimator as a Robust Regression Estimator. In The Methodology and Practice of Econometrics: Festschrift in Honour of David F. Hendry. Edited by J. L. Castle and N. Shephard. Oxford: Oxford University Press, pp. 1–36. [Google Scholar] [CrossRef]
- Jones, Charles M., Owen Lamont, and Robin L. Lumsdaine. 1998. Macroeconomic News and Bond Market Volatility. Journal of Financial Economics 47: 315–37. [Google Scholar] [CrossRef]
- Kamstra, Mark J., and Lisa A. Kramer. 2023. Seasonality in stock returns and government bond returns. In Handbook of Financial Decision Making. Edited by G. Hilary and D. McLean. Northampton: Edward Elgar Publishing, pp. 36–62. [Google Scholar]
- Kamstra, Mark J., Lisa A. Kramer, and Maurice D. Levi. 2003. Winter Blues: A SAD Stock Market Cycle. American Economic Review 93: 324–43. [Google Scholar] [CrossRef]
- Kamstra, Mark J., Lisa A. Kramer, and Maurice D. Levi. 2009. Is it the weather? Comment. Journal of Banking & Finance 33: 578–82. [Google Scholar] [CrossRef]
- Kamstra, Mark J., Lisa A. Kramer, and Maurice D. Levi. 2012. A careful re-examination of seasonality in international stock markets: Comment on sentiment and stock returns. Journal of Banking & Finance 36: 934–56. [Google Scholar] [CrossRef]
- Kamstra, Mark J., Lisa A. Kramer, Maurice D. Levi, and Russ Wermers. 2017. Seasonal Asset Allocation: Evidence from Mutual Fund Flows. Journal of Financial and Quantitative Analysis 52: 71–109. [Google Scholar] [CrossRef]
- Kamstra, Mark J., Lisa A. Kramer, Maurice D. Levi, and Tan Wang. 2014. Seasonally Varying Preferences: Theoretical Foundations for an Empirical Regularity. Review of Asset Pricing Studies 4: 39–77. [Google Scholar] [CrossRef]
- Keef, Stephen P., and Mohammed S. Khaled. 2011. A review of the seasonal affective disorder hypothesis. Journal of Socio-Economics 40: 959–67. [Google Scholar] [CrossRef]
- Kelly, Patrick J., and Felix Meschkle. 2010. Sentiment and Stock Returns: The SAD Anomaly Revisited. Journal of Banking & Finance 34: 1308–26. [Google Scholar] [CrossRef]
- Khan, Faridoon, Amena Urooj, Kalim Ullah, Badr Alnssyan, Zahra Almaspoor, and Paulo Jorge Silveira Ferreira. 2021. A Comparison of Autometrics and Penalization Techniques under Various Error Distributions: Evidence from Monte Carlo Simulation. Complexity 2021: 9223763. [Google Scholar] [CrossRef]
- Kim, Chan-Wung, and Jinwoo Park. 1994. Holiday Effects and Stock Returns: Further Evidence. Journal of Financial and Quantitative Analysis 29: 145–57. [Google Scholar] [CrossRef]
- Koyck, L M. 1954. Distributed Lags and Investment Analysis. Amsterdam: North-Holland. [Google Scholar] [CrossRef]
- Levi, Maurice D., Lisa A. Kramer, and Mark J. Kamstra. 2015. Seasonal Variation in Treasury Returns. Critical Finance Review 4: 45–115. [Google Scholar] [CrossRef]
- Li, Lifang, and Valentina Galvani. 2021. Informed Trading and Momentum in the Corporate Bond Market. Review of Finance 25: 1773–816. [Google Scholar] [CrossRef]
- Lin, Mei-Chen. 2015. Seasonal affective disorder and investors’ response to earnings news. International Review of Financial Analysis 42: 211–21. [Google Scholar] [CrossRef]
- Lindvall, John R. 1977. New Issue Corporate Bonds, Seasoned Market Efficiency and Yield Spreads. Journal of Finance 32: 1057–67. [Google Scholar] [CrossRef]
- Maxwell, William F. 1998. The January Effect in the Corporate Bond Market: A Systematic Examination. Financial Management 27: 18–30. [Google Scholar] [CrossRef]
- McAleer, Michael. 2005. Automated Inference and Learning in Modeling Financial Volatility. Econometric Theory 21: 232–61. [Google Scholar] [CrossRef]
- Meeker, J. Edward. 1922. The Work of the Stock Exchange. New York: Ronald Press Company. [Google Scholar]
- Meneu, Vicente, and Angel Pardo. 2004. Pre-Holiday Effect, Large Trades and Small Investor Behavior. Journal of Empirical Finance 11: 231–46. [Google Scholar] [CrossRef]
- Muhammadullah, Sara, Amena Urooj, Faridoon Khan, Mohammed N. Alshahrani, Mohammed Alqawba, Sanaa Al-Marzouki, and Peican Zhu. 2022. Comparison of Weighted Lag Adaptive LASSO with Autometrics for Covariate Selection and Forecasting Using Time-Series Data. Complexity 2022: 2649205. [Google Scholar] [CrossRef]
- Murfin, Justin, and Mitchell Petersen. 2016. Loans on sale: Credit market seasonality, borrower need, and lender rents. Journal of Financial Economics 121: 300–26. [Google Scholar] [CrossRef]
- Nica, Ionut, Irina Georgescu, Camelia Delacea, and Nora Chirita. 2023. Toward Sustainable Development: Assessing the Effects of Financial Contagion on Human Well-Being in Romania. Risks 11: 204. [Google Scholar] [CrossRef]
- Nippani, Srinivas, and Anita K. Pennathur. 2004. Day-of-the-week effects in commercial paper yield rates. The Quarterly Review of Economics and Finance 44: 508–20. [Google Scholar] [CrossRef]
- Pasquariello, Paolo, and Mirela Sandulescu. 2023. Speculation and Liquidity in Stock and Corporate Bond Markets. Ann Arbor: University of Michigan, p. 70. [Google Scholar] [CrossRef]
- Pellini, Elisabetta. 2021. Estimating income and price elasticities of residential electricity demand with Autometrics. Energy Economics 101: 105411. [Google Scholar] [CrossRef]
- Perez-Amaral, Teodosio, Giampiero M. Gallo, and Halbert White. 2005. A Comparison of Complementary Automatic Modeling Selection: RETINA and PcGets. Econometric Theory 21: 262–77. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Yongcheol Shin. 1998. An Autoregressive Distributed Lag Modelling Approach to Cointegration Analysis. In Econometric Society Monographs. Cambridge: Cambridge University Press, pp. 371–413. [Google Scholar]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Phillips, Peter C. B. 2005. Automated Discovery in Econometrics. Econometric Theory 21: 3–20. [Google Scholar] [CrossRef]
- Pretis, Felix, J. James Reade, and Genaro Sucarrat. 2018. Automated General-to-Specific (GETS) Regression Modeling and Indicator Saturation for Outliers and Structural Breaks. Journal of Statistical Software 86: 1–44. [Google Scholar] [CrossRef]
- Pretis, Felix, Lea Schneider, Jason E. Smerdon, and David F. Hendry. 2016. Detecting Volcanic Eruptions in Temperature Reconstructions by Designed Break-Indicator Saturation. Journal of Economic Surveys 30: 403–29. [Google Scholar] [CrossRef]
- Ronen, Tavy, and Xing Zhou. 2013. Trade and Information in the Corporate Bond Market. Journal of Financial Markets 16: 61–103. [Google Scholar] [CrossRef]
- Santos, Carlos. 2008. Impulse saturation break tests. Economics Letters 98: 136–43. [Google Scholar] [CrossRef]
- Santos, Carlos, David F. Hendry, and Soren Johansen. 2007. Automatic selection of indicators in a fully saturated regression. Computational Statistics 23: 317–35. [Google Scholar] [CrossRef]
- Savor, Pavel, and Mungo Wilson. 2013. How Much Do Investors Care About Macroeconomic Risk? Evidence from Scheduled Economic Announcements. Journal of Financial and Quantitative Analysis 48: 343–75. [Google Scholar] [CrossRef]
- Savor, Pavel, and Mungo Wilson. 2014. Asset pricing: A tale of two days. Journal of Financial Economics 113: 171–201. [Google Scholar] [CrossRef]
- Schneeweis, Thomas, and J. Randall Woolridge. 1979. Capital Market Seasonality: The Case of Bond Returns. Joural of Financial and Quantitative Analysis 14: 939–58. [Google Scholar] [CrossRef]
- Shultz, Birl. 1946. The Securities Market and How It Works. New York: Harper Bros Publishers. [Google Scholar]
- Smales, L. A. 2021. Macroeconomic news and treasury futures return volatility: Do treasury auctions matter? Global Finance Journal 48: 100537. [Google Scholar] [CrossRef]
- Sorensen, Eric H. 1982. On the Seasoning Process of New Bonds: Some Are More Seasoned Than Others. Journal of Financial and Quantitative Analysis XVII: 195–208. [Google Scholar] [CrossRef]
- Stillwagon, Josh R. 2016. Non-linear exchange rate relationships: An automated model selection approach with indicator saturation. The North American Journal of Economics and Finance 37: 84–109. [Google Scholar] [CrossRef]
- Stillwagon, Josh R. 2017. TIPS and the VIX: Spillovers from Financial Panic to Breakeven Inflation in an Automated, Nonlinear Modeling Framework. Oxford Bulletin of Economics and Statistics 80: 218–35. [Google Scholar] [CrossRef]
- Sucarrat, Genaro, and Alvaro Escribano. 2012. Automated Model Selection in Finance: General-to-Specific Modelling of the Mean and Volatility Specifications. Oxford Bulletin of Economics and Statistics 74: 716–35. [Google Scholar] [CrossRef]
- Thaler, Richard H. 1987. Anomalies: The January Effect. Economic Perspectives 1: 197–201. [Google Scholar] [CrossRef]
- Tolikas, Konstantinos. 2018. The lead-lag relation between the stock and the bond markets. The European Journal of Finance 24: 849–66. [Google Scholar] [CrossRef]
- van Dijk, Dick, Robin L. Lumsdaine, and Michel van der Wel. 2016. Market Set-up in Advance of Federal Reserve Policy Rate Decisions. The Economic Journal 126: 618–53. [Google Scholar] [CrossRef]
- Wachter, Jessica A, and Yicheng Zhu. 2021. A Model of Two Days: Discrete News and Asset Prices. The Review of Financial Studies 35: 2246–307. [Google Scholar] [CrossRef]
- Wang, Junbo, and Chunchi Wu. 2015. Liquidity, credit quality, and the relation between volatility and trading activity: Evidence from the corporate bond market. Journal of Banking & Finance 50: 183–203. [Google Scholar] [CrossRef]
- Wei, Jason. 2018. Behavioral biases in the corporate bond market. Journal of Empirical Finance 46: 34–55. [Google Scholar] [CrossRef]
- Wei, Jason, and Xing Zhou. 2016. Informed Trading in Corporate Bonds Prior to Earnings Announcements. Financial Management 45: 641–74. [Google Scholar] [CrossRef]
- White, Halbert. 1990. A Consistent Model Selection Procedure Based on M-Testing. In Modelling Economic Series. Edited by Clive W. J. Oxford: Granger. [Google Scholar]
- Wit, J. N. M. 1998. Irving Fisher: Pioneer on Distributed Lags. Amsterdam: Econometric Research and Special Studies Department. De Nederlandsche Bank, p. 8. [Google Scholar]
- Zitzewitz, Eric. 2011. Paired Bond Trades. Working Paper. Hanover: Dartmouth College. [Google Scholar] [CrossRef]

| Investment-Grade Bond Sample | High-Yield Bond Sample | |||||
|---|---|---|---|---|---|---|
| Filtered Sample | Financial | Nonfin. | Full Sample | Financial | Nonfin. | Full Sample |
| Number of Bonds | 262 | 179 | 441 | 6 | 32 | 38 |
| Days Traded | 506 | 506 | 506 | 422 | 422 | 422 |
| Total Trades | 984,362 | 555,245 | 1,539,606 | 9406 | 90,941 | 100,858 |
| Mean Trades Per Day | 1945 | 1097 | 3043 | 22 | 216 | 239 |
| Std. Dev. Trades per Day | 282 | 158 | 419 | 11 | 63 | 64 |
| Mean Par Vol. Per Day, USD | 754 | 106 | 395 | 571,481 | 79,757,235 | 80,328,716 |
| Std. Dev. Par Vol. Per Day, USD | 220 | 142 | 335 | 447,379 | 33,472,549 | 33,490,159 |
| Mean Par Vol. Per Trade, USD | 0.39 | 0.10 | 0.13 | 25,638 | 370,103 | 336,103 |
| Mean Trades Per Day Per Bond | 7.40 | 6.10 | 6.90 | 3.70 | 7.00 | 6.50 |
| Coeff. Of Var. Trades Per Day | 0.14 | 0.14 | 0.14 | 0.51 | 0.29 | 0.27 |
| Independent Variable | Return S&P 500 Coefficient | Return Inv. Grade Bonds Coefficient | Return High-Yield Bonds Coefficient |
|---|---|---|---|
| Constant | −0.19 a | 0.16 **+ | |
| Moody’s (−1) | 0.02 **+ | ||
| S&P 500 Volume | −0.04 ** | ||
| S&P 500 Return (−1) | 0.03 **+ | ||
| Core CPI SS | −0.05 ** | ||
| Nonfarm Payrolls SS | −0.11 **+ | ||
| Jobless Claims SS | 0.06 **+ | ||
| Core PPI SS | −0.13 ** | ||
| Impulse Indicators | 8 | 7 | 19 |
| Step Indicators | 12 | 22 | 46 |
| AR 1-2 test | 2.91 [0.0556] | 3.04 [0.0489] * | 4.55 [0.0110] * |
| ARCH 1-1 test | 0.32 [0.5707] | 0.00 [0.9967] | 0.00 [0.9556] |
| Normality test | 1.26 [0.5327] | 2.16 [0.3391] | 7.13 [0.0282] * |
| Hetero test | NR | 0.62 [0.9138] | 0.93 [0.6177] |
| RESET23 test | 0.00 [1.0000] | 0.25 [0.7752] | 1.10 [0.3353] |
| Log-likelihood | −487.69 | 98.34 | 674.80 |
| Parameters | 21 | 32 | 70 |
| Observations | 541 | 540 | 540 |
| Investment Grade | High Yield | |||
|---|---|---|---|---|
| Independent Variable | Total Trades Coefficient | Institutional Trades Coefficient | Total Trades Coefficient | Institutional Trades Coefficient |
| Trend | −2.30 ** | 0.19 ** | ||
| Moody’s (−1) | 1.78 ** | |||
| S&P 500 Volume | 9.14 **+ | 32.77 **+ | ||
| ABS Nonfarm Payrolls SS (−1) | −162.05 **+ | |||
| ABS Core CPI SS | 8.96 **+ | |||
| Monday | −224.11 **+ | −23.05 **+ | −8.61 **+ | |
| Tuesday | 95.11 **+ | 30.89 **+ | ||
| Wednesday | 19.83 ** | |||
| Friday | −443.70 **+ | −19.60 **+ | −38.87 **+ | −10.60 **+ |
| January | 25.42 ** | |||
| December | −163.40 **+ | −15.27 **+ | −34.44 **+ | −13.61 ** |
| NYSE Holiday | −2369.94 **+ | −28.90 **+ | −169.80 **+ | −29.29 **+ |
| NYSE Holiday (+1) | −413.48 **+ | |||
| NYSE Early Close | −1885.02 **+ | −31.59 **+ | −97.11 **+ | −32.42 ** |
| Murfin Petersen Cheap | 4348.37 ** | 33.97 **+ | 30.87 ** | |
| SAD Incidence | 67.09 **+ | |||
| SAD Onset/Recovery | −663.62 **+ | |||
| Impulse Indicators | 20 | 13 | 13 | 15 |
| Step Indicators | 47 | 25 | 27 | 25 |
| AR 1-2 test | 1.11 [0.3302] | 2.28 [0.1036] | 0.49 [0.6118] | 1.43 [0.2412] |
| ARCH 1-1 test | 0.02 [0.8759] | 1.62 [0.2040] | 2.17 [0.1416] | 0.90 [0.3420] |
| Normality test | 2.04 [0.3609] | 4.85 [0.0885] | 5.85 [0.0537] | 7.34 [0.0255] * |
| Hetero test | 0.99 [0.5037] | 0.92 [0.5978] | 0.85 [0.7226] | 1.43 [0.0646] |
| RESET23 test | 0.20 [0.8169] | 6.94 [0.0011] ** | 0.29 [0.7454] | 1.00 [0.3697] |
| Investment Grade | High Yield | |||
|---|---|---|---|---|
| Independent Variable | Intermediated Total Trades Coeff. | Intermediated Institutional Trades Coeff. | Intermediated Total Trades Coeff. | Intermediated Institutional Trades Coeff. |
| S&P 500 Volume | 53.386 **+ | 1.666 **+ | 11.815 **+ | 2.469 **+ |
| ABS Core PPI SS (−1) | 45.695 **+ | |||
| ABS Core PPI SS | −1.495 ** | |||
| Monday | −0.945 **+ | |||
| Tuesday | 31.088 **+ | 1.148 **+ | 4.892 **+ | |
| Wednesday | 1.244 **+ | |||
| Friday | −78.720 **+ | −1.073 **+ | −6.958 **+ | −1.243 ** |
| Murfin Petersen Cheap | 733.311 **+ | |||
| NYSE Holiday | −554.854 **+ | −3.669 **+ | −20.965 **+ | −3.626 **+ |
| NYSE Holiday (+1) | −119.735 **+ | −1.567 ** | ||
| NYSE Holiday (−1) | 227.439 **+ | |||
| NYSE Early Close | −321.619 **+ | |||
| NYSE Early Close (−1) | ||||
| December | −2.049 **+ | −4.658 **+ | −3.586 **+ | |
| SAD Incidence | −19.671 **+ | |||
| SAD Onset/Recovery | −126.954 **+ | |||
| Impulse Indicators | 7 | 25 | 18 | 18 |
| Step Indicators | 36 | 16 | 22 | 25 |
| AR 1-2 test | 0.57 [0.5670] | 3.58 [0.0287] * | 0.15 [0.8575] | 0.30 [0.7405] |
| ARCH 1-1 test | 0.13 [0.7144] | 1.05 [0.3069] | 0.19 [0.6608] | 6.06 [0.0142] * |
| Normality test | 1.88 [0.3902] | 5.45 [0.0656] | 8.84 [0.0121] * | 9.06 [0.0108] * |
| Hetero test | 0.70 [0.9131] | 1.59 [0.0509] | 1.06 [0.3840] | 1.62 [0.0255] * |
| RESET23 test | 0.99 [0.3724] | 0.30 [0.7390] | 0.99 [0.3742] | 1.45 [0.2352] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forest, J.J.; Branch, B.S.; Berry, B.T. Trading Activity in the Corporate Bond Market: A SAD Tale of Macro-Announcements and Behavioral Seasonality? Risks 2024, 12, 80. https://doi.org/10.3390/risks12050080
Forest JJ, Branch BS, Berry BT. Trading Activity in the Corporate Bond Market: A SAD Tale of Macro-Announcements and Behavioral Seasonality? Risks. 2024; 12(5):80. https://doi.org/10.3390/risks12050080
Chicago/Turabian StyleForest, James J., Ben S. Branch, and Brian T. Berry. 2024. "Trading Activity in the Corporate Bond Market: A SAD Tale of Macro-Announcements and Behavioral Seasonality?" Risks 12, no. 5: 80. https://doi.org/10.3390/risks12050080
APA StyleForest, J. J., Branch, B. S., & Berry, B. T. (2024). Trading Activity in the Corporate Bond Market: A SAD Tale of Macro-Announcements and Behavioral Seasonality? Risks, 12(5), 80. https://doi.org/10.3390/risks12050080







