Beneath the Surface: Disentangling the Dynamic Network of the U.S. and BRIC Stock Markets’ Interrelations Amidst Turmoil
Abstract
1. Introduction
2. Study Background and Literature Review
3. Data and Methodology
3.1. Data
3.2. Methodology
3.2.1. Dynamic Condition Correlation (DCC) GARCH
3.2.2. Time-Varying Parameter Vector Autoregression (TVP-VAR) Approach
4. Results
4.1. Summary Statistics
4.2. Dynamic Conditional Correlation Among Markets
4.3. Average Connectedness Among Markets
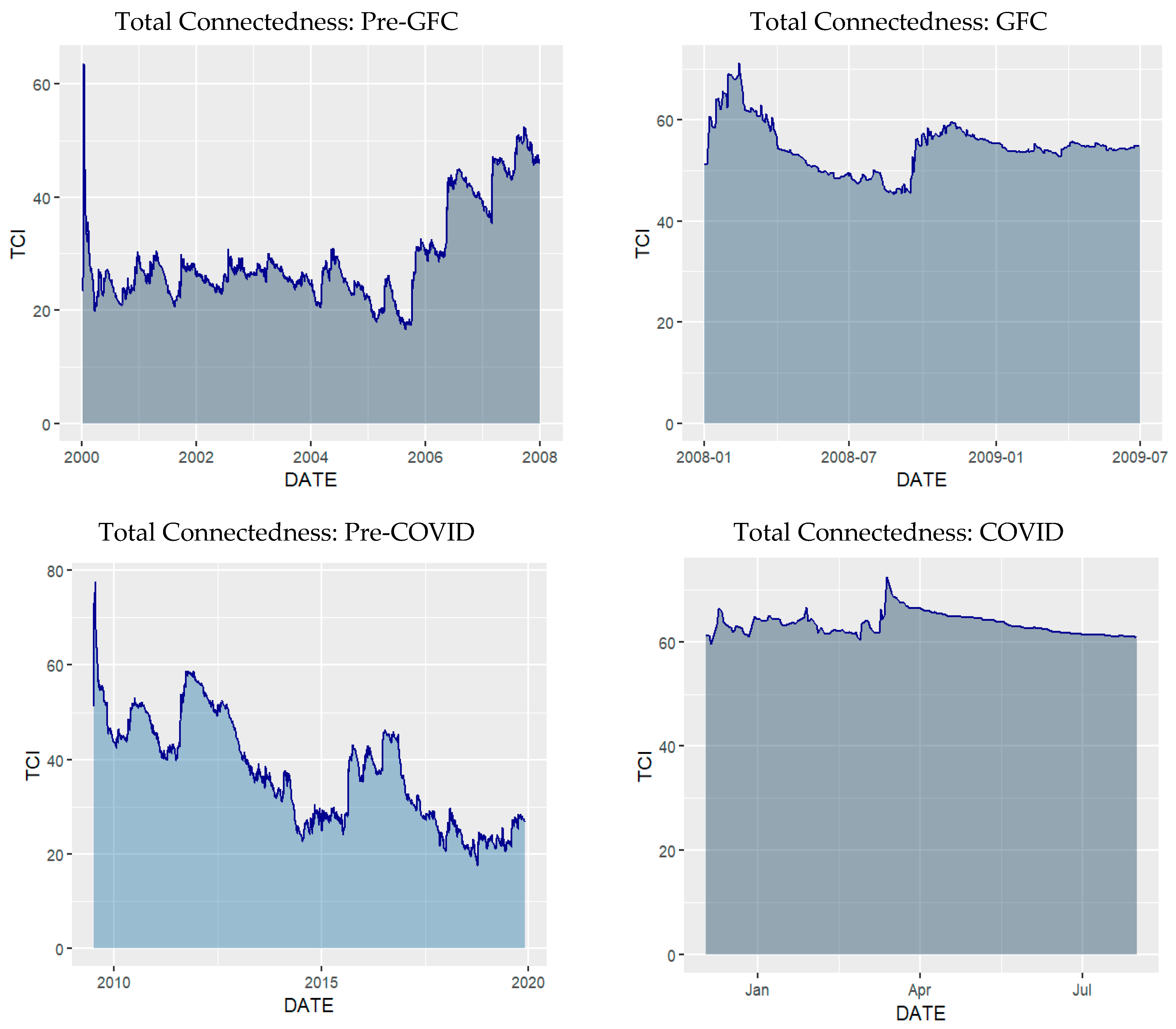
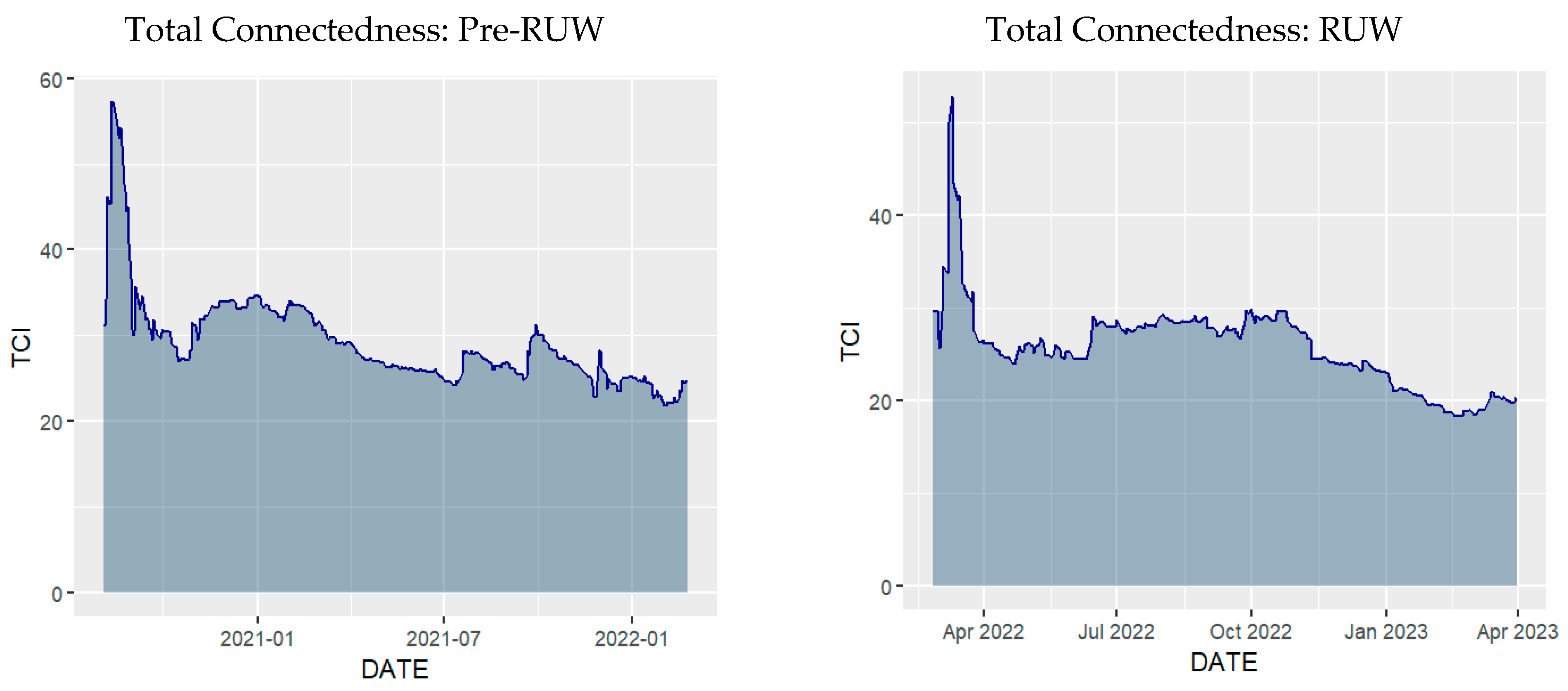
4.4. Total Dynamic Connectedness Among Markets
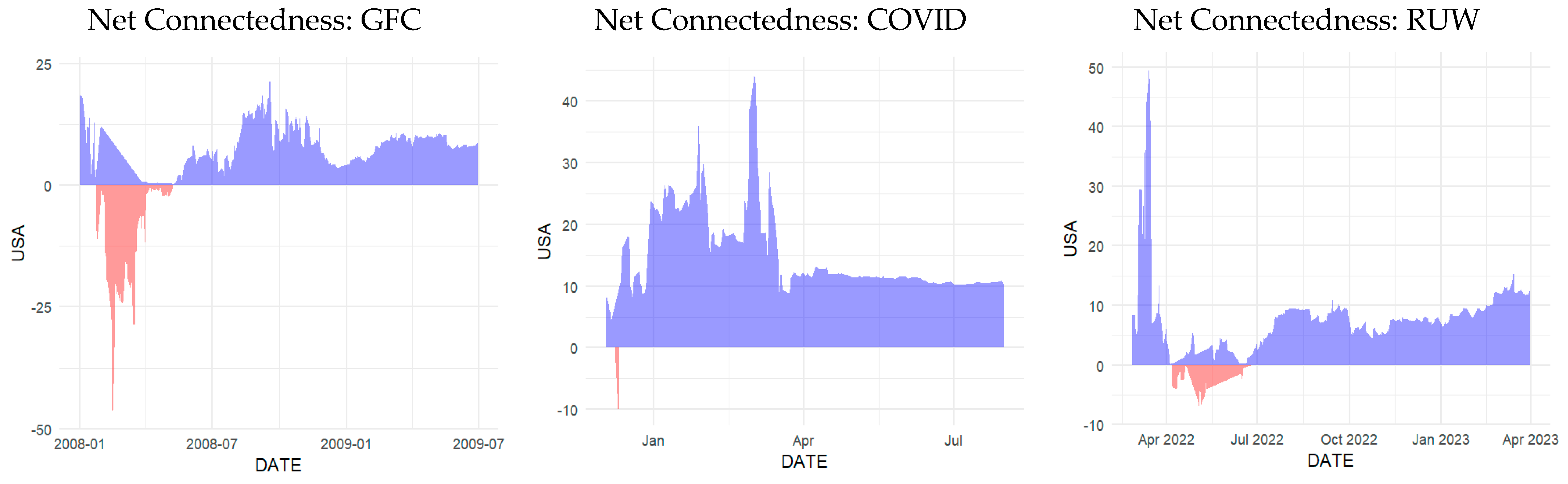
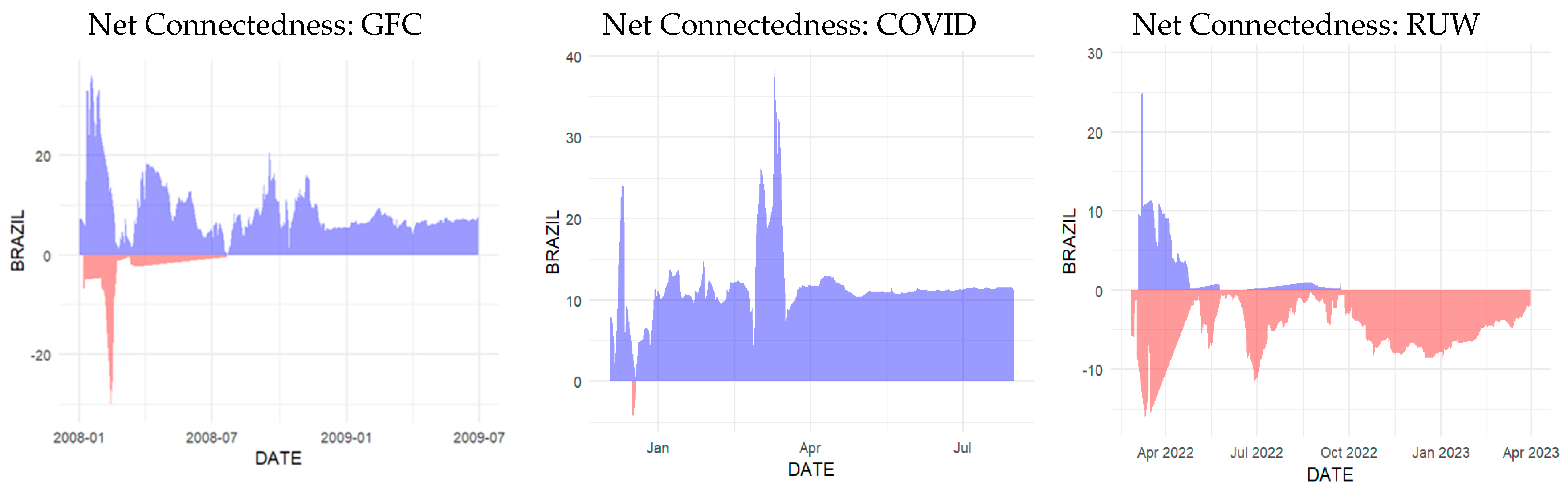
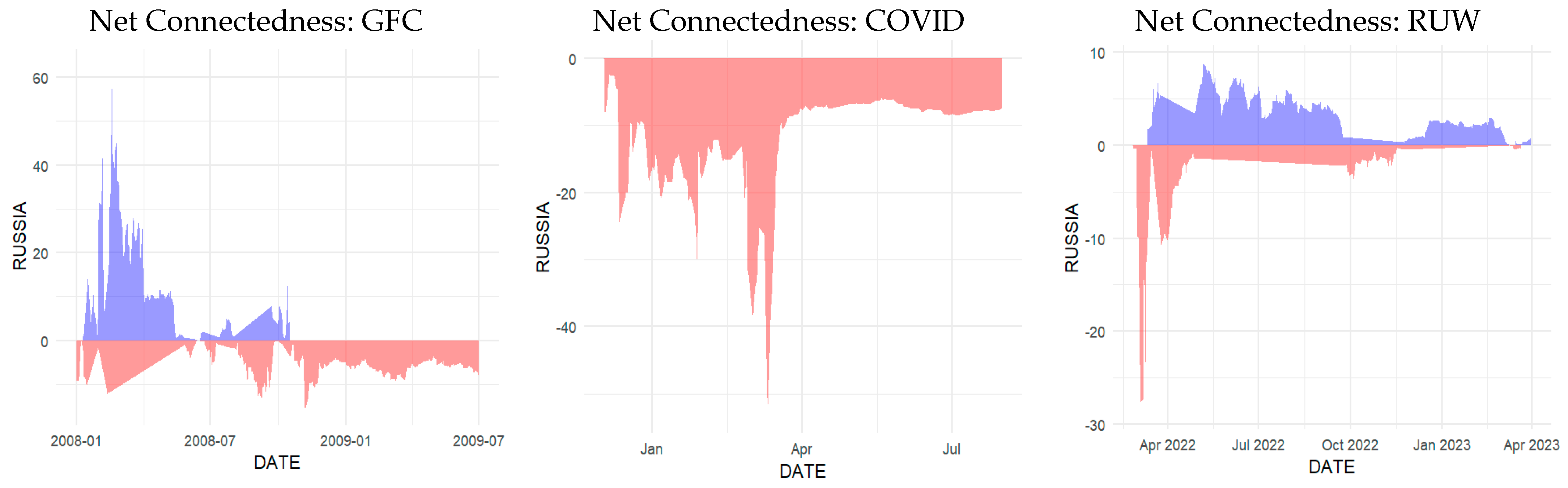
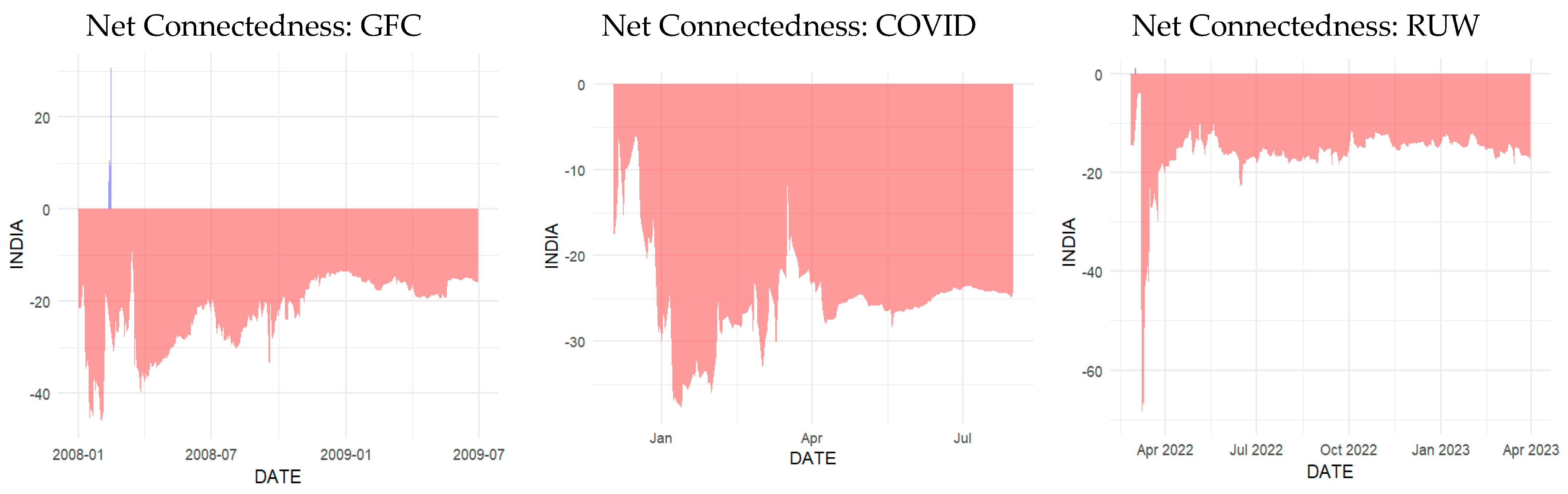
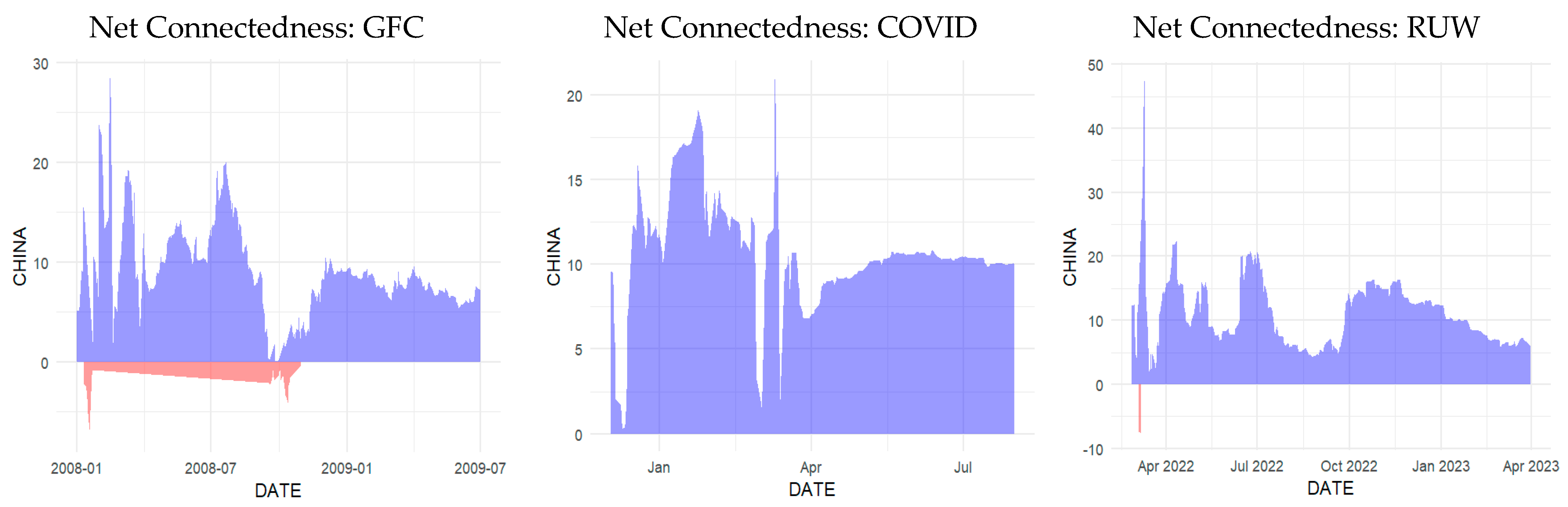
4.5. Dynamic Net Directional Connectedness Among Markets
4.6. Short and Long-Term Connectedness
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alfreedi, Ajab A. 2019. Shocks and Volatility Spillover Between Stock Markets of Developed Countries and GCC Stock Markets. Journal of Taibah University for Science 13: 112–20. [Google Scholar] [CrossRef]
- Aloui, Riadh, Mohamed Safouane Ben Aïssa, and Duc Khuong Nguyen. 2011. Global financial crisis, extreme interdependences, and contagion effects: The role of economic structure? Journal of Banking and Finance 35: 130–41. [Google Scholar] [CrossRef]
- Antonakakis, Nikolaos, Ioannis Chatziantoniou, and David Gabauer. 2020. Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. Journal of Risk and Financial Management 13: 84. [Google Scholar] [CrossRef]
- Anyikwa, Izunna, and Andrew Phiri. 2023. Quantile connectedness amongst BRICS equity markets during the COVID-19 pandemic and Russia–Ukraine war. Cogent Economics and Finance 11: 2251300. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Campbell R. Harvey. 2000. Foreign speculators and emerging equity markets. The Journal of Finance 55: 565–613. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Campbell R. Harvey. 2003. NBER Working Paper Series Market Integration and Contagion. Available online: http://www.nber.org/papers/w9510 (accessed on 25 July 2024).
- Bekaert, Geert, Michael Ehrmann, Marcel Fratzscher, and Arnaud Mehl. 2014. The Global Crisis and Equity Market Contagion. Journal of Finance 69: 2597–649. [Google Scholar] [CrossRef]
- Bekiros, Stelios D. 2014. Contagion, decoupling and the spillover effects of the US financial crisis: Evidence from the BRIC markets. International Review of Financial Analysis 33: 58–69. [Google Scholar] [CrossRef]
- Ben Amar, Amine, Fateh Bélaïd, Adel Ben Youssef, and Khaled Guesmi. 2021. Connectedness among regional financial markets in the context of the COVID-19. Applied Economics Letters 28: 1789–96. [Google Scholar] [CrossRef]
- Bhar, Ramaprasad, and Biljana Nikolova. 2007. Analysis of Mean and Volatility Spillovers Using BRIC Countries, Regional and World Equity Index Returns. Source: Journal of Economic Integration 22: 369–81. [Google Scholar] [CrossRef]
- Bhar, Ramaprasad, and Biljana Nikolova. 2009. Return, volatility spillovers and dynamic correlation in the BRIC equity markets: An analysis using a bivariate EGARCH framework. Global Finance Journal 19: 203–18. [Google Scholar] [CrossRef]
- Bhuyan, Rafiqul, Mohammad G. Robbani, Bakhtear Talukdar, and Ajeet Jain. 2016. Information transmission and dynamics of stock price movements: An empirical analysis of BRICS and US stock markets. International Review of Economics and Finance 46: 180–95. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bouri, Elie, Donald Lien, David Roubaud, and Syed Jawad Hussain Shahzad. 2018. Fear Linkages Between the US and BRICS Stock Markets: A Frequency-Domain Causality. International Journal of the Economics of Business 25: 441–54. [Google Scholar] [CrossRef]
- Bouzzine, Yassin Denis, and Rainer Lueg. 2020. The contagion effect of environmental violations: The case of Dieselgate in Germany. Business Strategy and the Environment 29: 3187–202. [Google Scholar] [CrossRef]
- Carrieri, Francesca, Vihang Errunza, and Ked Hogan. 2007. Characterizing World Market Integration through Time. Journal of Financial and Quantitative Analysis 42: 915–40. [Google Scholar] [CrossRef]
- Cepoi, Cosmin-Octavian. 2020. Asymmetric dependence between stock market returns and news during COVID-19 financial turmoil. Finance Research Letters 36: 101658. [Google Scholar] [CrossRef]
- Chakrabarti, Prasenjit, Mohammad Shameem Jawed, and Manish Sarkhel. 2021. COVID-19 pandemic and global financial market interlinkages: A dynamic temporal network analysis. Applied Economics 53: 2930–45. [Google Scholar] [CrossRef]
- Chen, Anthony W., Jim Chen, and V. Reddy Dondeti. 2020. The US-China trade war: Dominance of trade or technology? Applied Economics Letters 27: 904–9. [Google Scholar] [CrossRef]
- Christodoulakis, George A., and Stephen E. Satchell. 2002. Correlated ARCH (CorrARCH): Modelling the time-varying conditional correlation between financial asset returns. European Journal of Operational Research 139: 351–70. [Google Scholar] [CrossRef]
- Corbet, Shaen, Yang Hou, Yang Hu, and Les Oxley. 2022. Financial contagion among COVID-19 concept-related stocks in China. Applied Economics 54: 2439–52. [Google Scholar] [CrossRef]
- Dahir, Ahmed Mohamed, Fauziah Mahat, Bany-Ariffin Amin Noordin, and Nazrul Hisyam Ab Razak. 2020. Dynamic connectedness between Bitcoin and equity market information across BRICS countries: Evidence from TVP-VAR connectedness approach. International Journal of Managerial Finance 16: 357–71. [Google Scholar] [CrossRef]
- Dakhlaoui, Imen, and Chaker Aloui. 2016. The interactive relationship between the US economic policy uncertainty and BRIC stock markets. International Economics 146: 141–57. [Google Scholar] [CrossRef]
- Das, Sanjiv Ranjan, and Raman Uppal. 2004. Systemic risk and international portfolio choice. Journal of Finance 59: 2809–34. [Google Scholar] [CrossRef]
- Derbali, Abdelkader, Kamel Naoui, Mounir Ben Sassi, and Mohamed Marouen Amiri. 2022. Do COVID-19 Epidemic Explains the Dynamic Conditional Correlation between China’s Stock Market Index and International Stock Market Indices? Chinese Economy 55: 227–42. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2012. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting 28: 57–66. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2014. On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics 182: 119–34. [Google Scholar] [CrossRef]
- Dimitriou, Dimitrios, Dimitris Kenourgios, and Theodore Simos. 2013. Global financial crisis and emerging stock market contagion: A multivariate FIAPARCH-DCC approach. International Review of Financial Analysis 30: 46–56. [Google Scholar] [CrossRef]
- Dong, Jichang, Xiaoting Liu, Kangxian Ji, Xiuting Li, and Zhi Dong. 2023. Peer Effects in Financial Investment of Board-interlocked Firms: An Information Sharing Perspective. Economic Analysis and Policy 80: 1490–508. [Google Scholar] [CrossRef]
- Dungey, Mardi, George Milunovich, Susan Thorp, and Minxian Yang. 2015. Endogenous crisis dating and contagion using smooth transition structural GARCH. Journal of Banking and Finance 58: 71–79. [Google Scholar] [CrossRef]
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business and Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Engle, Robert. F., and Kevin Sheppard. 2001. NBER Working Paper Series Theoretical and Empirical Properties of Dynamic Conditional Correlation Multivariate GARCH. Available online: http://weber.ucsd.edu/~ksheppar/research/frames.htm (accessed on 15 August 2024).
- Forbes, Kristin J., and Roberto Rigobon. 2002. No contagion, only interdependence: Measuring stock market comovements. The Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Gębka, Bartosz, and Dobromił Serwa. 2007. Intra- and inter-regional spillovers between emerging capital markets around the world. Research in International Business and Finance 21: 203–21. [Google Scholar] [CrossRef]
- Gong, Chen, Pan Tang, and Yutong Wang. 2019. Measuring the network connectedness of global stock markets. Physica A: Statistical Mechanics and Its Applications 535: 122351. [Google Scholar] [CrossRef]
- Greenwood-Nimmo, Matthew, Viet Hoang Nguyen, and Yongcheol Shin. 2021. Measuring the Connectedness of the Global Economy. International Journal of Forecasting 37: 899–919. [Google Scholar] [CrossRef]
- Habiba, Umm E., Shen Peilong, Wenlong Zhang, and Kashif Hamid. 2020. International stock markets Integration and dynamics of volatility spillover between the USA and South Asian markets: Evidence from Global financial crisis. Journal of Asia Business Studies 14: 779–94. [Google Scholar] [CrossRef]
- Hammoudeh, Shawkat, Sang Hoon Kang, Walid Mensi, and Duc Khuong Nguyen. 2016. Dynamic Global Linkages of the BRICS Stock Markets with the United States and Europe Under External Crisis Shocks: Implications for Portfolio Risk Forecasting. World Economy 39: 1703–27. [Google Scholar] [CrossRef]
- Jondeau, Eric, and Michael Rockinger. 2006. The Copula-GARCH model of conditional dependencies: An international stock market application. Journal of International Money and Finance 25: 827–53. [Google Scholar] [CrossRef]
- Koop, Gary, M. Hashem Pesaran, and Simon M. Potter. 1996. Impulse response analysis in nonlinear multivariate models. Journal of Econometrics 74: 119–47. [Google Scholar] [CrossRef]
- Kumar, Rakesh, and Raj S. Dhankar. 2017. Financial instability, integration and volatility of emerging South Asian stock markets. South Asian Journal of Business Studies 6: 177–90. [Google Scholar] [CrossRef]
- Lakshmi, P., S. Visalakshmi, and Kavitha Shanmugam. 2015. Intensity of shock transmission amid US-BRICS markets. International Journal of Emerging Markets 10: 311–28. [Google Scholar] [CrossRef]
- Majdoub, Jihed, and Walid Mansour. 2014. Islamic equity market integration and volatility spillover between emerging and US stock markets. North American Journal of Economics and Finance 29: 452–70. [Google Scholar] [CrossRef]
- McIver, Ron P., and Sang Hoon Kang. 2020. Financial crises and the dynamics of the spillovers between the U.S. and BRICS stock markets. Research in International Business and Finance 54: 101276. [Google Scholar] [CrossRef]
- Mensi, Walid, Ferihane Zaraa Boubaker, Khamis Hamed Al-Yahyaee, and Sang Hoon Kang. 2018. Dynamic volatility spillovers and connectedness between global, regional, and GIPSI stock markets. Finance Research Letters 25: 230–38. [Google Scholar] [CrossRef]
- Mensi, Walid, Shawkat Hammoudeh, Duc Khuong Nguyen, and Sang Hoon Kang. 2016. Global financial crisis and spillover effects among the U.S. and BRICS stock markets. International Review of Economics and Finance 42: 257–76. [Google Scholar] [CrossRef]
- Mensi, Walid, Shawkat Hammoudeh, Juan Carlos Reboredo, and Duc Khuong Nguyen. 2014. Do global factors impact BRICS stock markets? A quantile regression approach. Emerging Markets Review 19: 1–17. [Google Scholar] [CrossRef]
- Miyakoshi, Tatsuyoshi. 2003. Spillovers of stock return volatility to Asian equity markets from Japan and the US. Journal of International Financial Markets, Institutions and Money 13: 383–99. [Google Scholar] [CrossRef]
- Mokni, Khaled, and Faysal Mansouri. 2017. Conditional dependence between international stock markets: A long memory GARCH-copula model approach. Journal of Multinational Financial Management 42–43: 116–31. [Google Scholar] [CrossRef]
- Morales, Lucia, and Bernadette Andreosso-O’Callaghan. 2012. The Current Global Financial Crisis: Do Asian Stock Markets Show Contagion or Interdependence Effects? Journal of Asian Economics 23: 616–26. [Google Scholar] [CrossRef]
- Mugerman, Yevgeny, Orly Sade, and Moses Shayo. 2014. Long term savings decisions: Financial reform, peer effects and ethnicity. Journal of Economic Behavior and Organization 106: 235–53. [Google Scholar] [CrossRef]
- Muguto, Lorraine, and Paul-Francois Muzindutsi. 2022. A Comparative Analysis of the Nature of Stock Return Volatility in BRICS and G7 Markets. Journal of Risk and Financial Management 15: 85. [Google Scholar] [CrossRef]
- Nath Mukherjee, Kedar, and Ram Kumar Mishra. 2010. Stock market integration and volatility spillover: India and its major Asian counterparts. Research in International Business and Finance 24: 235–51. [Google Scholar] [CrossRef]
- Panda, Pradiptarathi, Shobana Vasudevan, and Babita Panda. 2021. Dynamic connectedness among BRICS and major countries stock markets. Journal of Public Affairs 21: e2265. [Google Scholar] [CrossRef]
- Pesaran, H. Hashem, and Yongcheol Shin. 1998. Generalized impulse response analysis in linear multivariate models. Economics Letters 58: 17–29. [Google Scholar] [CrossRef]
- Rehman, Mobeen Ur, Nasir Ahmad, Syed Jawad Hussain Shahzad, and Xuan Vinh Vo. 2022. Dependence dynamics of stock markets during COVID-19. Emerging Markets Review 51: 100894. [Google Scholar] [CrossRef]
- Rejeb, Aymen Ben, and Adel Boughrara. 2015. Financial integration in emerging market economies: Effects on volatility transmission and contagion. Borsa Istanbul Review 15: 161–79. [Google Scholar] [CrossRef]
- Sahadudheen, I., and P. K. Kumar. 2023. On the Time-varying Correlations and Hedging Effectiveness: An Analysis of Crude Oil, Gold, and Stock Market. International Journal of Energy Economics and Policy 13: 353–63. [Google Scholar] [CrossRef]
- Sarwar, Ghulam, and Walayet Khan. 2017. The effect of US stock market uncertainty on emerging market returns. Emerging Markets Finance and Trade 53: 1796–811. [Google Scholar] [CrossRef]
- Singh, Amanjot, and Manjit Singh. 2017. A revisit to stock market contagion and portfolio hedging strategies: BRIC equity markets and financial crisis. International Journal of Law and Management 59: 618–35. [Google Scholar] [CrossRef]
- Syriopoulos, Theodore, Beljid Makram, and Adel Boubaker. 2015. Stock market volatility spillovers and portfolio hedging: BRICS and the financial crisis. International Review of Financial Analysis 39: 7–18. [Google Scholar] [CrossRef]
- Škrinjarić, Tihana, and Boško Šego. 2020. Risk connectedness of selected CESEE stock markets: A spillover index approach. China Finance Review International 10: 447–72. [Google Scholar] [CrossRef]
- Todea, Alexandru. 2016. Cross-correlations between volatility, volatility persistence and stock market integration: The case of emergent stock markets. Chaos, Solitons and Fractals 87: 208–15. [Google Scholar] [CrossRef]
- Tse, Yiu Kuen, and Albert K. C. Tsui. 2002. A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations. Journal of Business and Economic Statistics 20: 351–62. [Google Scholar] [CrossRef]
- Wang, Lihong. 2014. Who moves East Asian stock markets? The role of the 2007–2009 global financial crisis. Journal of International Financial Markets, Institutions and Money 28: 182–203. [Google Scholar] [CrossRef]
- Wang, Ping, and Peijie Wang. 2010. Price and volatility spillovers between the Greater China Markets and the developed markets of US and Japan. Global Finance Journal 21: 304–17. [Google Scholar] [CrossRef]
- Wen, Fenghua, Aojie Shui, Yuxiang Cheng, and Xu Gong. 2022. Monetary policy uncertainty and stock returns in G7 and BRICS countries: A quantile-on-quantile approach. International Review of Economics and Finance 78: 457–82. [Google Scholar] [CrossRef]
- Wen, Fenghua, Longhao Xu, Guangda Ouyang, and Gang Kou. 2019. Retail investor attention and stock price crash risk: Evidence from China. International Review of Financial Analysis 65: 101376. [Google Scholar] [CrossRef]
- Xu, Haifeng, and Shigeyuki Hamori. 2012. Dynamic linkages of stock prices between the BRICs and the United States: Effects of the 2008-09 financial crisis. Journal of Asian Economics 23: 344–52. [Google Scholar] [CrossRef]
- Yadav, Miklesh Prasad, Sudhi Sharma, and Indira Bhardwaj. 2023. Volatility Spillover Between Chinese Stock Market and Selected Emerging Economies: A Dynamic Conditional Correlation and Portfolio Optimization Perspective. Asia-Pacific Financial Markets 30: 427–44. [Google Scholar] [CrossRef]
- Yousaf, Imran, Ritesh Patel, and Larisa Yarovaya. 2022. The reaction of G20+ stock markets to the Russia–Ukraine conflict “black-swan” event: Evidence from event study approach. Journal of Behavioral and Experimental Finance 35: 100723. [Google Scholar] [CrossRef]
- Yu, Honghai, Wangyu Chu, Yu’ang Ding, and Xuezhou Zhao. 2021. Risk contagion of global stock markets under COVID-19: A network connectedness method. Accounting and Finance 61: 5745–82. [Google Scholar] [CrossRef]
- Yu, Xiaoling, Kaitian Xiao, and Junping Liu. 2022. Dynamic co-movements of COVID-19 pandemic anxieties and stock market returns. Finance Research Letters 46: 102219. [Google Scholar] [CrossRef]
- Zhang, Bing, Xindan Li, and Honghai Yu. 2013. Has recent financial crisis changed permanently the correlations between BRICS and developed stock markets? North American Journal of Economics and Finance 26: 725–38. [Google Scholar] [CrossRef]
- Zhang, Dayong, Min Hu, and Qiang Ji. 2020. Financial markets under the global pandemic of COVID-19. Finance Research Letters 36: 101528. [Google Scholar] [CrossRef] [PubMed]
| Unit Root Tests | USA | Brazil | Russia | India | China | |
|---|---|---|---|---|---|---|
| Whole period | ADF | −86.401 *** | −79.793 *** | −74.875 *** | −23.428 *** | −80.403 *** |
| PP | −86.743 *** | −79.855 *** | −74.853 *** | −74.069 *** | −80.387 *** | |
| GFC | ADF | −17.737 *** | −20.072 *** | −18.922 *** | −18.030 *** | −9.403 *** |
| PP | −23.312 *** | −20.266 *** | −18.906 *** | −17.964 *** | −19.997 *** | |
| COVID | ADF | −8.971 *** | −17.230 *** | −13.157 *** | −4.8211 *** | −7.581 *** |
| PP | −18.610 *** | −16.689 *** | −13.345 *** | −15.070 *** | −14.455 *** | |
| Russia–Ukraine war | ADF | −17.222 *** | −15.246 *** | −12.366 *** | −16.084 *** | −17.323 *** |
| PP | −17.231 *** | −15.182 *** | −13.663 *** | −16.082 *** | −17.310 *** |
| Whole Sample Period | |||||
|---|---|---|---|---|---|
| USA | Brazil | Russia | India | China | |
| Mean | 0.000167 | 0.000297 | 0.000461 | 0.000404 | −0.000075 |
| Maximum | 0.109572 | 0.136782 | 0.252261 | 0.15999 | 0.108742 |
| Minimum | −0.12765 | −0.15994 | −0.40467 | −0.14102 | −0.185411 |
| Std. Dev. | 0.012281 | 0.017296 | 0.019912 | 0.013971 | 0.015022 |
| Skewness | −0.37998 | −0.36564 | −1.50107 | −0.36382 | −0.591315 |
| Kurtosis | 13.61945 | 10.04371 | 46.20689 | 13.11404 | 12.07948 |
| Jarque–Bera | 28,644.56 | 12,672.96 | 474,042.4 | 25,984.29 | 21,185.96 |
| Observations | 6065 | 6065 | 6065 | 6065 | 6065 |
| GFC Period | |||||
| USA | Brazil | Russia | India | China | |
| Mean | −0.0012 | −0.00052 | −0.00168 | −0.00081 | −0.001787 |
| Maximum | 0.109572 | 0.136782 | 0.252261 | 0.159900 | 0.108742 |
| Minimum | −0.0947 | −0.12096 | −0.20657 | −0.11604 | −0.085991 |
| Std. Dev. | 0.024216 | 0.029523 | 0.041166 | 0.027091 | 0.023571 |
| Skewness | −0.03467 | 0.156046 | 0.134626 | 0.359640 | 0.198653 |
| Kurtosis | 6.356229 | 6.301127 | 11.06203 | 6.700210 | 6.075616 |
| Jarque–Bera | 183.1226 *** | 178.6662 *** | 1057.367 *** | 230.8949 *** | 156.2806 *** |
| Observations | 390 | 390 | 390 | 390 | 390 |
| COVID-19 Period | |||||
| USA | Brazil | Russia | India | China | |
| Mean | 0.000241 | −0.00021 | −7.7E−05 | −0.00045 | −0.000967 |
| Maximum | 0.089683 | 0.130228 | 0.074349 | 0.085947 | 0.085495 |
| Minimum | −0.12765 | −0.15994 | −0.08646 | −0.14102 | −0.185411 |
| Std. Dev. | 0.025084 | 0.032611 | 0.018199 | 0.023387 | 0.025413 |
| Skewness | −0.76243 | −1.3346 | −0.87346 | −1.47954 | −2.662569 |
| Kurtosis | 9.588661 | 11.09162 | 10.41566 | 12.55391 | 20.90228 |
| Jarque–Bera | 329.6777 *** | 523.3176 *** | 418.3986 *** | 721.0735 *** | 2514.619 *** |
| Observations | 173 | 173 | 173 | 173 | 173 |
| RUW Period | |||||
| USA | Brazil | Russia | India | China | |
| Mean | −0.0002 | −0.00026 | 0.000634 | 0.000214 | 0.000290 |
| Maximum | 0.053953 | 0.053934 | 0.182620 | 0.028646 | 0.067144 |
| Minimum | −0.0442 | −0.03407 | −0.09256 | −0.02783 | −0.064385 |
| Std. Dev. | 0.014406 | 0.013209 | 0.020815 | 0.009492 | 0.015064 |
| Skewness | −0.08249 | 0.001794 | 1.813561 | 0.034353 | −0.452916 |
| Kurtosis | 3.652415 | 3.345173 | 25.31709 | 3.546894 | 5.798817 |
| Jarque–Bera | 5.377739 *** | 1.414991 *** | 6070.602 *** | 3.607790 *** | 102.7651 *** |
| Observations | 285 | 285 | 285 | 285 | 285 |
| Markets | Parameters | Full Sample Period | Pre-GFC Period | GFC Period | Pre-COVID-19 Period | COVID-19 Period | Pre-RUW Period | RUW Period |
|---|---|---|---|---|---|---|---|---|
| USA | ||||||||
| Mean Equation | ∅ | 0.0005879 (6.498) *** | 0.000322 (2.166) ** | 0.000432 (2.321) ** | 0.000676 (8.787) *** | 0.001837 (3.500) *** | 0.000877 (3.737) *** | 0.000632 (2.087) * |
| Variance Equation | ω | 0.020422 (4.562) *** | 0.009340 (1.853) * | 0.057420 (2.635) * | 3.281429 (4.299) *** | 0.051629 (2.572) ** | 10.571124 (2.075) ** | 0.670556 (2.433) ** |
| α | 0.113992 (9.293) *** | 0.061329 (5.983) *** | 0.1068897 (4.854) *** | 0.158134 (6.715) *** | 0.498028 (2.890) ** | 0.198597 (2.450) ** | 0.047034 (2.927) ** | |
| β | 0.871696 (68.87) *** | 0.930407 (78.51) *** | 0.883479 (47.72) *** | 0.806534 (34.97) *** | 0.633315 (9.610) *** | 0.690326 (6.761) *** | 0.928259 (26.37) *** | |
| Brazil | ||||||||
| Mean Equation | ∅ | 0.000594 (3.327) *** | 0.001069 (2.831) ** | 0.000461 (2.447) ** | 0.000440 (1.842) * | 0.002805 (2.832) *** | 0.000234 (2.447) ** | 0.000872 (2.065) ** |
| Variance Equation | ω | 0.06372 (4.383) *** | 0.097427 (1.920) * | 0.194173 (3.980) ** | 0.086248 (2.881) ** | 0.617885 (3.919) *** | 0.088692 (2.476) ** | 0.054143 (1.780) * |
| α | 0.06965 (7.709) *** | 0.050696 (3.579) *** | 0.083052 (3.041) ** | 0.063634 (4.188) *** | 0.733887 (2.004) ** | 0.040674 (3.842) *** | 0.016067 (2.9940) ** | |
| β | 0.906499 (75.52) *** | 0.918045 (34.26) *** | 0.888660 (23.13) *** | 0.890693 (33.70) *** | 0.427400 (1.782) ** | 0.903952 (19.38) *** | 0.952687 (50.48) *** | |
| Russia | ||||||||
| Mean Equation | ∅ | 0.000879 (4.403) *** | 0.001760 (4.349) *** | 0.003521 (2.311) * | 0.000631 (2.921) ** | 0.001828 (1.990) ** | 0.000751 (2.608) ** | 0.000432 (1.998) * |
| Variance Equation | ω | 0.037590 (2.522) *** | 0.167927 (2.878) ** | 0.107360 (3.2406) *** | 0.034789 (2.978) ** | 0.034761 (2.221) ** | 0.0524335 (3.0422) *** | 0.063553 (2.115) ** |
| α | 0.095274 (4.889) *** | 0.102866 (5.027) *** | 0.138664 (4.617) *** | 0.063924 (3.995) *** | 0.285345 (1.799) * | 0.069171 (3.642) *** | 0.0953147 (2.806) ** | |
| β | 0.897911 (48.13) *** | 0.856273 (31.38) *** | 0.869230 (20.72) *** | 0.914625 (36.89) *** | 0.760668 (7.823) *** | 0.844911 (57.22) *** | 0.826081 (30.79) *** | |
| India | ||||||||
| Mean Equation | ∅ | 0.000820 (5.699) *** | 0.001368 (4.540) *** | 0.006422 (3.358) ** | 0.000614 (3.381) *** | 0.000970 (2.314) ** | 0.0001483 (2.986) ** | 0.000156 (2.097) ** |
| Variance Equation | ω | 0.021997 (3.892) *** | 0.093540 (2.418) ** | 0.493278 (2.166) ** | 1.403304 (2.270) ** | 0.109995 (2.519) ** | 0.046170 (2.242) ** | 0.332010 (2.124) ** |
| α | 0.098485 (7.976) *** | 0.138956 (4.183) *** | 0.111842 (2.442) ** | 0.057700 (4.372) *** | 0.297892 (2.819) ** | 0.075352 (2.039) ** | 0.072550 (3.753) *** | |
| β | 0.89159 (68.33) *** | 0.819878 (17.39) *** | 0.828468 (24.05) *** | 0.927276 (53.69) *** | 0.722456 (11.641) *** | 0.893663 (31.53) *** | 0.917331 (19.31) *** | |
| China | ||||||||
| Mean Equation | ∅ | 0.000423 (3.485) *** | 0.000401 (2.178) ** | 0.000532 (2.065) ** | 0.000461 (1.985) * | 0.001558 (2.454) ** | 0.000855 (3.115) *** | 0.001332 (1.689) * |
| Variance Equation | ω | 0.024070 (3.721) *** | 0.013246 (2.483) ** | 0.077611 (2.154) ** | 0.041020 (2.603) ** | 0.059569 (2.887) * | 0.164314 (2.145) ** | 0.328271 (2.310) ** |
| α | 0.099782 (7.331) *** | 0.083252 (4.738) *** | 0.115248 (2.376) ** | 0.084019 (4.687) *** | 0.415478 (2.023) ** | 0.099299 (2.701) ** | 0.234947 (2.294) ** | |
| β | 0.893009 (65.93) *** | 0.907074 (49.55) *** | 0.87482 (22.23) *** | 0.898721 (43.61) *** | 0.704481 (7.055) *** | 0.772168 (9.9175) *** | 0.619684 (5.643) *** | |
| DCC with Correlation Targeting | |||||||
|---|---|---|---|---|---|---|---|
| Full Sample Period | Pre-GFC Period | GFC Period | Pre-COVID-19 Period | COVID-19 Period | Pre-RUW Period | RUW Period | |
| 0.51596 [0.0259] (19.86) *** | 0.535842 [0.03078] (17.40) *** | 0.705684 [0.02985] (23.64) *** | 0.49906 [0.02405] (20.75) *** | 0.57780 [0.07720] (7.484) *** | 0.41570 [0.0454] (9.137) *** | 0.40977 [0.0938] (4.366) *** | |
| 0.23082 [0.0352] (6.554) *** | 0.168647 [0.03755] (4.490) *** | 0.372997 [0.04648] (8.024) *** | 0.30788 [0.03155] (9.757) *** | 0.38560 [0.06792] (5.677) *** | 0.31395 [0.0491] (6.389) *** | 0.0441 [0.06811] (0.6482) | |
| 0.18540 [0.0307] (6.032) *** | 0.111953 [0.03702] (3.024) *** | 0.314770 [0.03846] (8.184) *** | 0.22590 [0.03141] (7.191) *** | 0.29458 [0.07772] (3.790) *** | −0.06248 [0.0533] (−1.170) | 0.1909 [0.08170] (2.338) ** | |
| 0.49965 [0.0249] (20.01) *** | 0.459456 [0.0404] (11.36) *** | 0.608969 [0.03152] (19.32) *** | 0.53332 [0.02066] (25.80) *** | 0.63125 [0.04890] (12.91) *** | 0.46859 [0.0480] (9.762) *** | 0.5378 [0.05451] (9.864) *** | |
| 0.24056 [0.0330] (7.275) *** | 0.208511 [0.03720] (5.605) *** | 0.434715 [0.04352] (9.987) *** | 0.29501 [0.03453] (8.542) *** | 0.35407 [0.07237] (4.892) *** | 0.26689 [0.0504] (5.290) *** | 0.0321 [0.06381] (0.5040) | |
| 0.18792 [0.0290] (6.466) *** | 0.135223 [0.03643] (3.712) *** | 0.277899 [0.05031] (5.523) *** | 0.21806 [0.02548] (8.558) *** | 0.24336 [0.07348] (3.312) *** | −0.0162 [0.0604] (−0.2689) | 0.1513 [0.08541] (1.772) ** | |
| 0.34727 [0.0290] (11.95) *** | 0.338266 [0.03668] (9.221) *** | 0.542671 [0.03480] (15.59) *** | 0.35186 [0.02505] (14.04) *** | 0.47542 [0.08263] (5.753) *** | 0.28937 [0.0563] (5.135) *** | 0.2422 [0.07581] (3.195) *** | |
| 0.22407 [0.0371] (6.026) *** | 0.189175 [0.0374] (5.050) *** | 0.328020 [0.05189] (6.321) *** | 0.27010 [0.03456] (7.816) *** | 0.31707 [0.09379] (3.381) *** | −0.03736 [0.0549] (−0.6799) | 0.0605 [0.07205] (0.8398) | |
| 0.35447 [0.0403] (8.793) *** | 0.30632 [0.03600] (8.509) *** | 0.584128 [0.04131] (14.14) *** | 0.39285 [0.03467] (11.33) *** | 0.52788 [0.05624] (9.386) *** | 0.55056 [0.0410] (13.42) *** | 0.1252 [0.08515] (1.470) | |
| 0.27529 [0.0351] (7.821) *** | 0.219546 [0.03846] (5.708) *** | 0.456858 [0.04655] (9.813) *** | 0.29939 [0.02811] (10.65) *** | 0.45236 [0.06561] (6.894) *** | −0.0211 [0.0502] (−0.4200) | 0.3112 [0.07307] (4.260) *** | |
| Alpha | 0.00715 [0.00201] (3.554) *** | 0.00778 [0.00482] (1.613) | 0.05833 [0.02580](2.260) ** | 0.01419 [0.0119](1.192) | 0.08169 [0.9619](1.3375) *** | 0.02967 [0.0147](2.017) * | 0.01422 [0.0060](2.345) * |
| Beta | 0.98771 [0.00490] (201.3) *** | 0.98208 [0.01951] (50.32) *** | 0.148711 [0.22340](0.6657) | 0.95431 [0.0612](15.58) *** | 0.96431 [0.02454](39.29) | 0.77267 [0.1259](6.134) *** | 0.9523 [0.01467](64.88) *** |
| Full Sample Period: Long Run | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| USA | Brazil | Russia | India | China | From | ||||||||
| USA | 49.11 | 13.54 | 10.88 | 10.22 | 16.25 | 50.89 | |||||||
| Brazil | 15.93 | 47.88 | 13.56 | 10.15 | 12.48 | 52.12 | |||||||
| Russia | 12.68 | 15.83 | 46.07 | 11.42 | 14.01 | 53.93 | |||||||
| India | 14.08 | 13.1 | 13.66 | 46 | 13.17 | 54 | |||||||
| China | 11.75 | 13.91 | 12.53 | 9.16 | 52.65 | 47.35 | |||||||
| To | 54.43 | 56.38 | 50.62 | 40.94 | 55.9 | 258.28 | |||||||
| Inc.Own | 103.55 | 104.27 | 96.69 | 86.94 | 108.56 | TCI | |||||||
| NET | 3.55 | 4.27 | −3.31 | −13.06 | 8.56 | 51.65% | |||||||
| Pre-GFC Period | GFC Period | ||||||||||||
| USA | Brazil | Russia | India | China | From | USA | Brazil | Russia | India | China | From | ||
| USA | 66.24 | 11.29 | 4.25 | 4.12 | 14.1 | 53.76 | USA | 50.51 | 24.7 | 5.04 | 3.24 | 16.51 | 49.49 |
| Brazil | 11.26 | 44.22 | 17.86 | 11.06 | 15.6 | 55.78 | Brazil | 23.17 | 49.02 | 8.46 | 4.4 | 14.95 | 50.98 |
| Russia | 3.95 | 20.13 | 49.4 | 11.65 | 14.87 | 50.6 | Russia | 5.62 | 19.56 | 44.12 | 8.61 | 22.09 | 55.88 |
| India | 5.18 | 18.91 | 19.14 | 45 | 11.78 | 55 | India | 12.69 | 5.82 | 11.37 | 46.18 | 23.94 | 53.82 |
| China | 13.63 | 16.01 | 15.02 | 9.18 | 46.16 | 53.84 | China | 19.93 | 14.99 | 15.3 | 11.32 | 38.47 | 61.53 |
| To | 34.02 | 66.38 | 56.27 | 36.02 | 56.34 | 248.98 | To | 61.4 | 65.06 | 40.17 | 27.57 | 77.49 | 271.69 |
| Inc.Own | 100.26 | 110.56 | 105.67 | 81.01 | 102.5 | TCI | Inc.Own | 111.91 | 114.08 | 84.29 | 73.75 | 115.96 | TCI |
| NET | 0.26 | 10.56 | 5.67 | −18.99 | 2.5 | 49.79% | NET | 11.91 | 14.08 | −15.71 | −26.25 | 15.96 | 54.33% |
| Pre-COVID-19 Period | COVID-19 Period | ||||||||||||
| USA | Brazil | Russia | India | China | From | USA | Brazil | Russia | India | China | From | ||
| USA | 55.27 | 11.73 | 8.19 | 10.51 | 14.29 | 44.73 | USA | 23.24 | 15.2 | 29.15 | 2.95 | 29.46 | 76.76 |
| Brazil | 7.8 | 62.58 | 13.66 | 3.67 | 12.29 | 37.42 | Brazil | 15.64 | 25.85 | 21.02 | 4.73 | 32.77 | 74.15 |
| Russia | 12.23 | 14.57 | 57.2 | 7.96 | 8.04 | 42.8 | Russia | 15.6 | 9.67 | 41.31 | 1.6 | 31.81 | 58.69 |
| India | 11.36 | 13.69 | 8.99 | 51.78 | 14.18 | 48.22 | India | 16.38 | 19.16 | 22.62 | 12.63 | 29.21 | 87.37 |
| China | 12 | 19.11 | 12.13 | 5.13 | 51.62 | 48.38 | China | 15.9 | 16.3 | 24.25 | 3.26 | 40.29 | 59.71 |
| To | 43.39 | 59.11 | 42.98 | 27.28 | 48.8 | 221.55 | To | 63.52 | 60.33 | 97.03 | 12.55 | 123.25 | 356.68 |
| Inc.Own | 98.66 | 121.69 | 100.18 | 79.05 | 100.42 | TCI | Inc.Own | 86.76 | 86.18 | 138.35 | 25.17 | 163.54 | TCI |
| NET | −1.34 | 21.69 | 0.18 | −20.95 | 0.42 | 44.31% | NET | −13.24 | −13.82 | 38.35 | −74.83 | 63.54 | 71.33% |
| Pre-RUW Period | RUW Period | ||||||||||||
| USA | Brazil | Russia | India | China | From | USA | Brazil | Russia | India | China | From | ||
| USA | 33.09 | 9.71 | 26.71 | 1.89 | 28.6 | 66.91 | USA | 59.93 | 11.32 | 0.56 | 5.25 | 22.94 | 40.07 |
| Brazil | 1.77 | 93.67 | 1.34 | 1.52 | 1.7 | 6.33 | Brazil | 19.22 | 64.88 | 0.5 | 7.92 | 7.48 | 35.12 |
| Russia | 26.2 | 11.29 | 32.31 | 2.56 | 27.54 | 67.69 | Russia | 7.46 | 4.34 | 81.6 | 1.27 | 5.32 | 18.4 |
| India | 4.15 | 1.28 | 5.34 | 83.79 | 5.54 | 16.21 | India | 7.56 | 5.32 | 0.21 | 77.65 | 9.27 | 22.35 |
| China | 28.03 | 9.32 | 27.46 | 2.79 | 32.41 | 67.59 | China | 18.38 | 7.23 | 2.04 | 10.12 | 62.24 | 37.76 |
| To | 60.25 | 31.6 | 60.85 | 8.74 | 63.29 | 224.73 | To | 52.62 | 28.21 | 3.3 | 24.56 | 45.01 | 153.7 |
| Inc.Own | 93.34 | 125.26 | 93.16 | 92.53 | 95.7 | TCI | Inc.Own | 112.54 | 93.1 | 84 | 102.21 | 107.25 | TCI |
| NET | −6.66 | 25.26 | −6.64 | −7.47 | −4.3 | 44.94% | NET | 12.54 | −6.9 | −15.1 | 2.21 | 7.25 | 30.74% |
| Short-Term Spillover | ||||||
|---|---|---|---|---|---|---|
| USA | Brazil | Russia | India | China | FROM | |
| USA | 56.27 | 16.72 | 5.68 | 4.66 | 16.68 | 43.73 |
| Brazil | 17.76 | 60.83 | 6.47 | 4.41 | 10.53 | 39.17 |
| Russia | 9.58 | 9.05 | 64.86 | 5.39 | 11.11 | 35.14 |
| India | 9.81 | 7.78 | 6.14 | 67.18 | 9.09 | 32.82 |
| China | 18.37 | 10.26 | 9.21 | 6.17 | 55.98 | 44.02 |
| TO | 55.53 | 43.82 | 27.50 | 20.63 | 47.41 | 194.88 |
| Inc.Own | 111.79 | 104.65 | 92.36 | 87.81 | 103.39 | TCI |
| NET | 11.79 | 4.6 | −7.64 | −12.19 | 3.39 | 38.98 |
| Long-Term Spillover | ||||||
| USA | Brazil | Russia | India | China | FROM | |
| USA | 54.94 | 16.81 | 6.14 | 5.12 | 16.98 | 45.06 |
| Brazil | 17.92 | 59.23 | 6.92 | 4.97 | 10.96 | 40.77 |
| Russia | 10.42 | 9.49 | 62.76 | 5.92 | 11.41 | 37.24 |
| India | 10.42 | 8.44 | 6.68 | 64.85 | 9.61 | 35.15 |
| China | 18.56 | 10.60 | 9.66 | 6.57 | 54.61 | 45.39 |
| TO | 57.32 | 45.33 | 29.40 | 22.59 | 48.96 | 203.60 |
| Inc.Own | 112.26 | 104.57 | 92.16 | 87.44 | 103.57 | TCI |
| NET | 12.26 | 4.5 | −7.84 | −12.56 | 3.57 | 40.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalissery, N.; Nishad, T.M.; Naushad, J.A.; Tabash, M.I.; Al-Absy, M.S.M. Beneath the Surface: Disentangling the Dynamic Network of the U.S. and BRIC Stock Markets’ Interrelations Amidst Turmoil. Risks 2024, 12, 202. https://doi.org/10.3390/risks12120202
Chalissery N, Nishad TM, Naushad JA, Tabash MI, Al-Absy MSM. Beneath the Surface: Disentangling the Dynamic Network of the U.S. and BRIC Stock Markets’ Interrelations Amidst Turmoil. Risks. 2024; 12(12):202. https://doi.org/10.3390/risks12120202
Chicago/Turabian StyleChalissery, Neenu, T. Mohamed Nishad, J. A. Naushad, Mosab I. Tabash, and Mujeeb Saif Mohsen Al-Absy. 2024. "Beneath the Surface: Disentangling the Dynamic Network of the U.S. and BRIC Stock Markets’ Interrelations Amidst Turmoil" Risks 12, no. 12: 202. https://doi.org/10.3390/risks12120202
APA StyleChalissery, N., Nishad, T. M., Naushad, J. A., Tabash, M. I., & Al-Absy, M. S. M. (2024). Beneath the Surface: Disentangling the Dynamic Network of the U.S. and BRIC Stock Markets’ Interrelations Amidst Turmoil. Risks, 12(12), 202. https://doi.org/10.3390/risks12120202







