Quantum Computing Approach to Realistic ESG-Friendly Stock Portfolios
Abstract
1. Introduction
2. Results
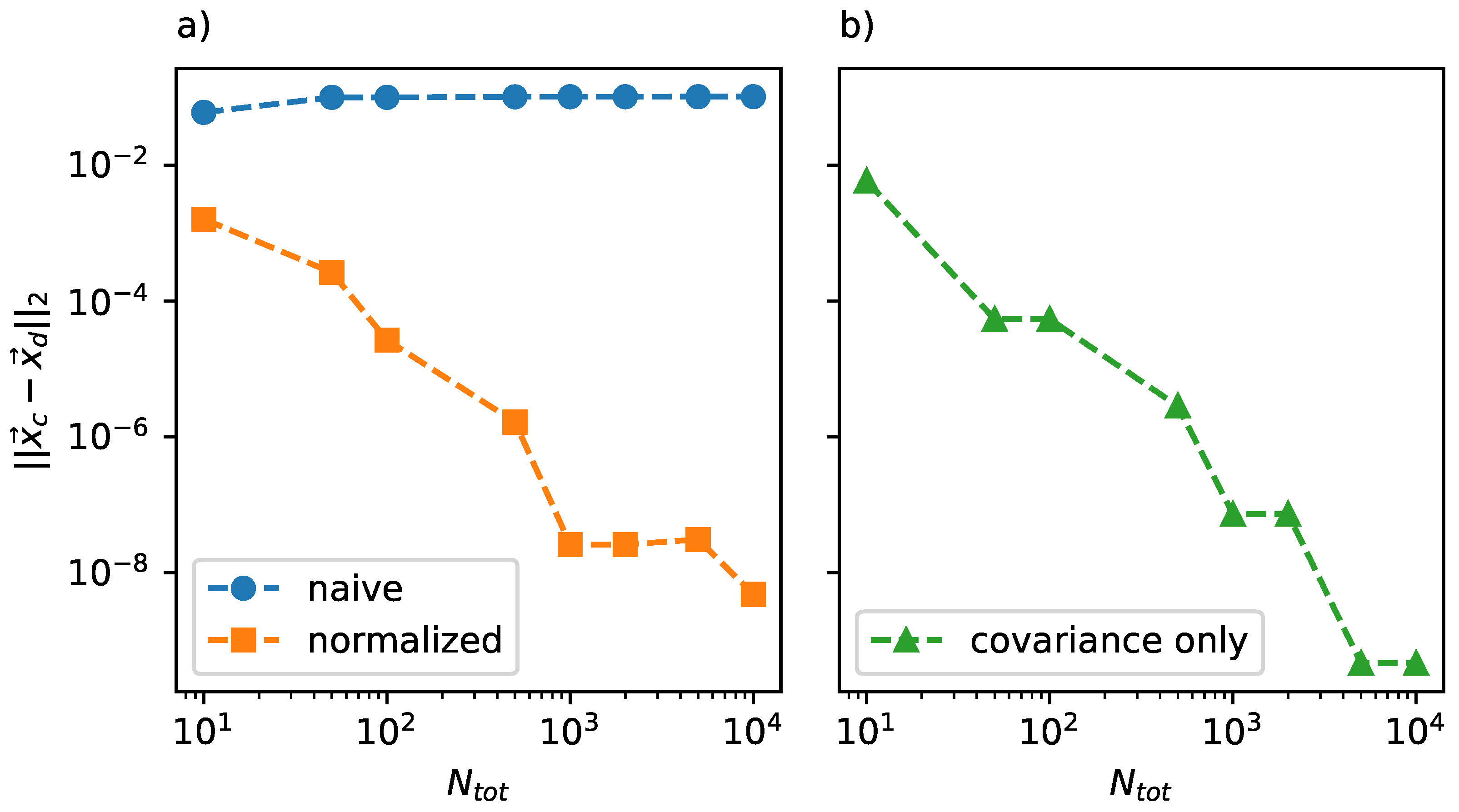
2.1. Discrete Markowitz Portfolio Theory and the Role of the Risk-Aversion Parameter
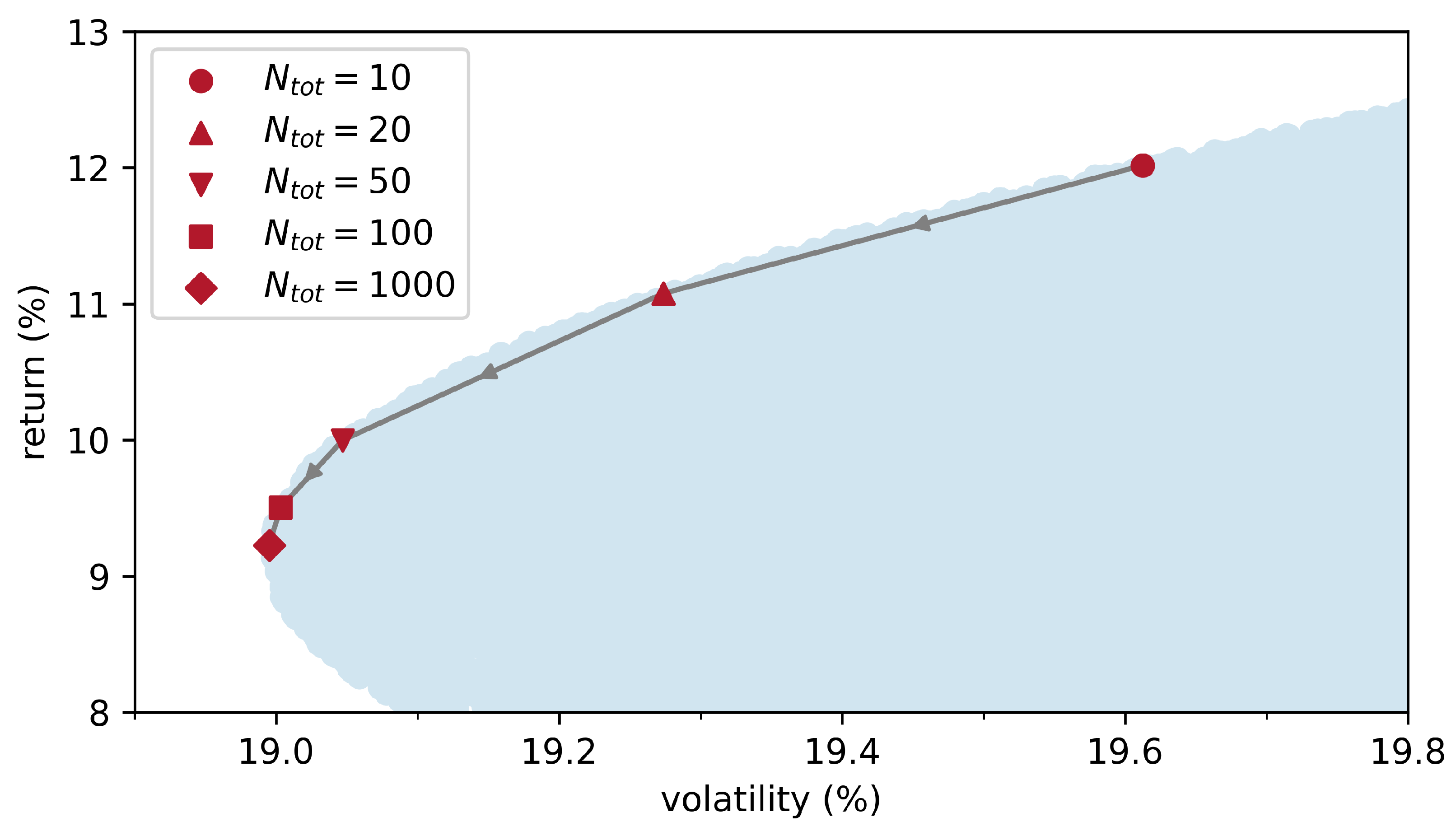
2.2. Discrete Markowitz Portfolio Theory with a Limited Investment Budget
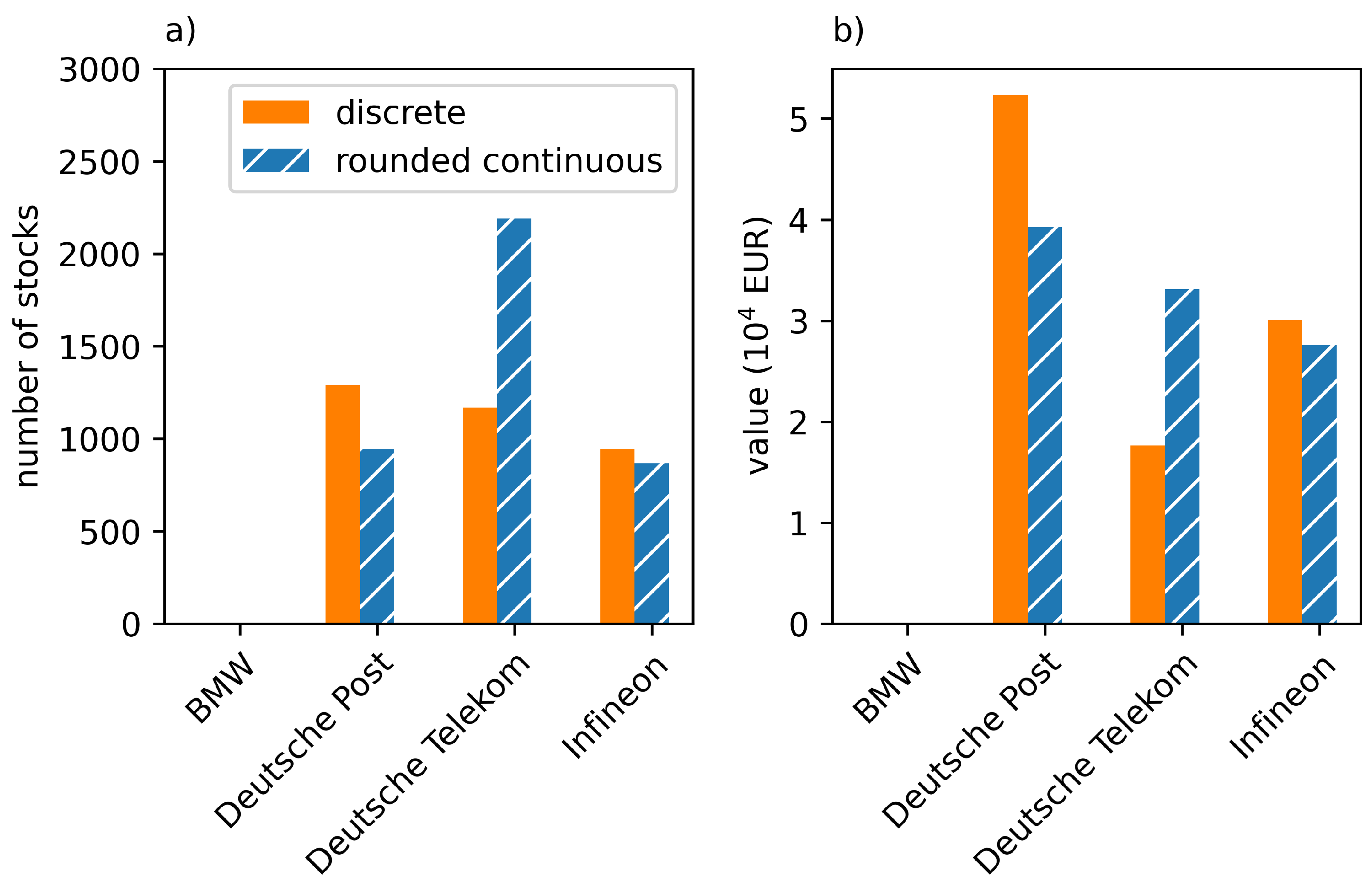
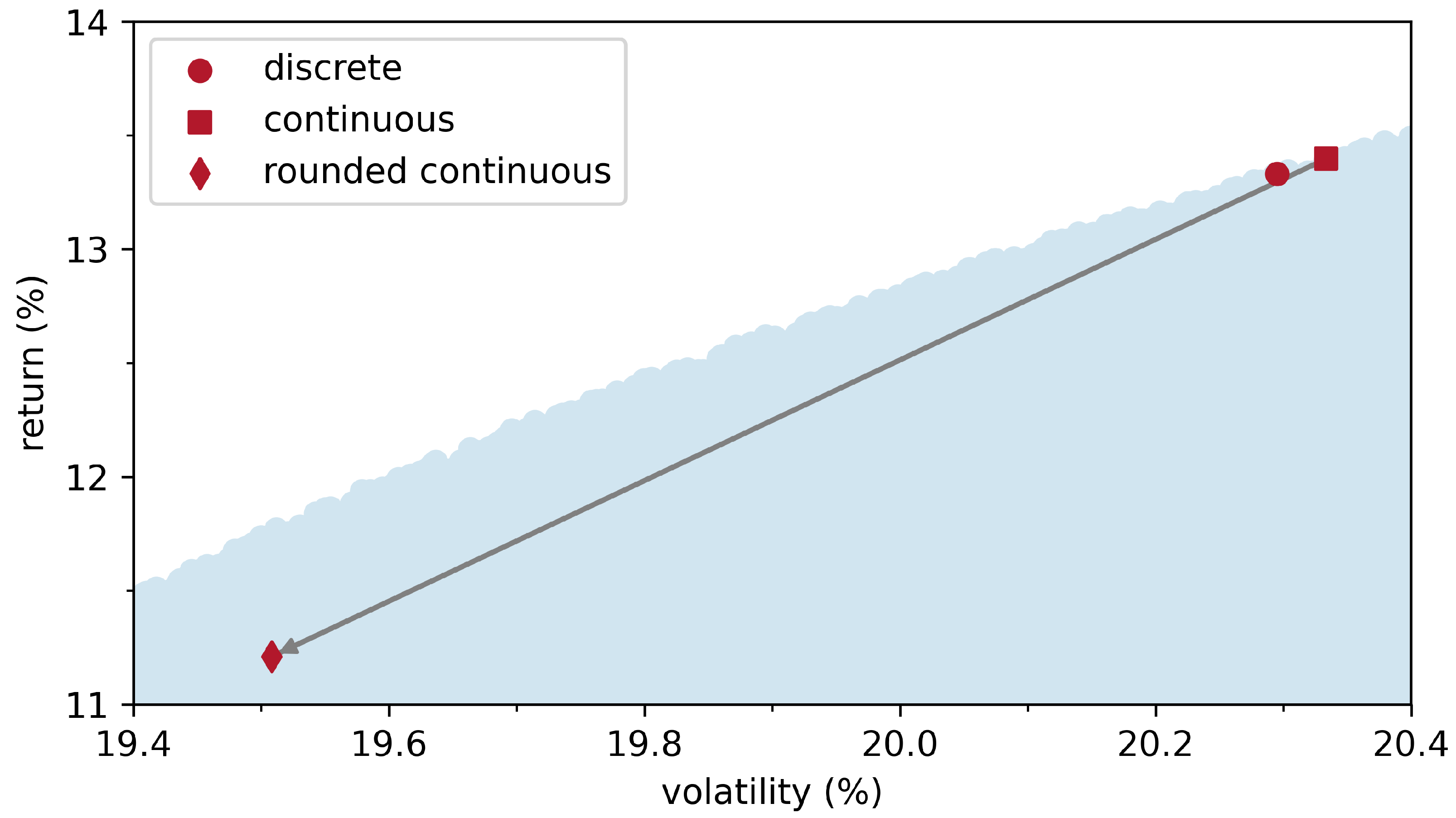
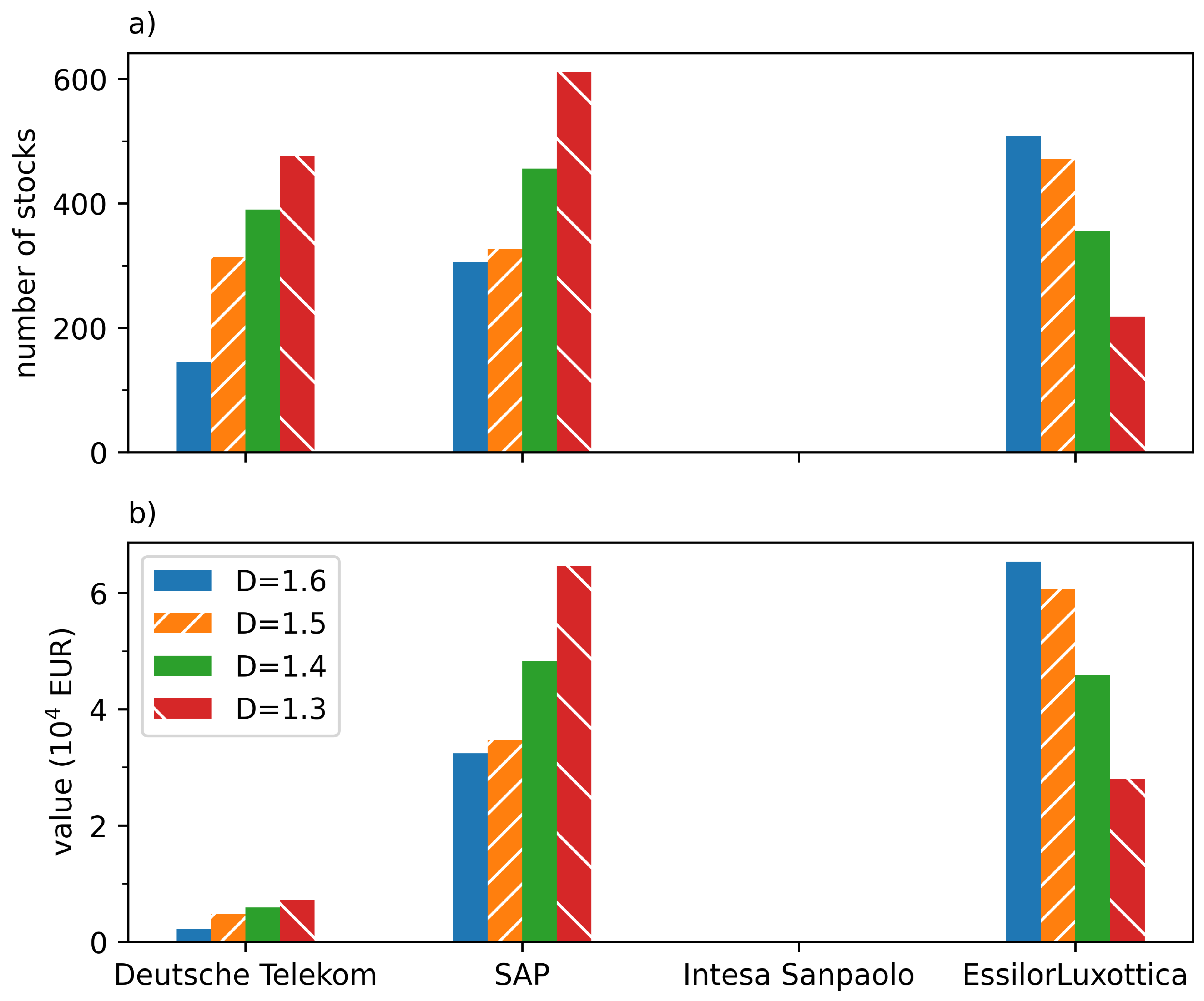
2.3. Incorporation of ESG Data into Markowitz Portfolio Theory
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MPT | Markowitz portfolio theory |
| DMPT | discrete Markowitz portfolio theory |
| NP | non-polynomial |
| QPU | quantum processing unit |
| qubit | quantum bit |
| ESG | environmental, social, governance |
| CRR | capital requirements regulation |
| CRD | capital requirements directive |
| DJIA | Dow Jones industrial average |
| 1 | https://ocean.dwavesys.com/ (accessed on 21 March 2024). |
References
- Abrams, Daniel S., and Seth Lloyd. 1998. Nonlinear quantum mechanics implies polynomial-time solution for np-complete and #p problems. Physical Review Letters 81: 3992–95. [Google Scholar] [CrossRef]
- Agrawal, Akshay, Robin Verschueren, Steven Diamond, and Stephen Boyd. 2018. A rewriting system for convex optimization problems. Journal of Control and Decision 5: 42–60. [Google Scholar] [CrossRef]
- Alessandrini, Fabio, and Eric Jondeau. 2021. Optimal strategies for esg portfolios. The Journal of Portfolio Management 47: 114–38. [Google Scholar] [CrossRef]
- Amon, Julian, Margarethe Rammerstorfer, and Karl Weinmayer. 2021. Passive esg portfolio management—The benchmark strategy for socially responsible investors. Sustainability 13: 9388. [Google Scholar] [CrossRef]
- Atz, Ulrich, Tracy Van Holt, Zongyuan Zoe Liu, and Christopher C. Bruno. 2023. Does sustainability generate better financial performance? review, meta-analysis, and propositions. Journal of Sustainable Finance & Investment 13: 802–25. [Google Scholar] [CrossRef]
- Auer, Benjamin R., and Frank Schuhmacher. 2016. Do socially (ir)responsible investments pay? new evidence from international esg data. The Quarterly Review of Economics and Finance 59: 51–62. [Google Scholar] [CrossRef]
- Bae, Kee-Hong, Sadok El Ghoul, Zhaoran Jason Gong, and Omrane Guedhami. 2021. Does csr matter in times of crisis? evidence from the COVID-19 pandemic. Journal of Corporate Finance 67: 101876. [Google Scholar] [CrossRef]
- Berg, Florian, Julian F. Kölbel, and Roberto Rigobon. 2022. Aggregate Confusion: The Divergence of ESG Ratings. Review of Finance 26: 1315–44. [Google Scholar] [CrossRef]
- Bonami, Pierre, and Miguel A. Lejeune. 2009. An exact solution approach for portfolio optimization problems under stochastic and integer constraints. Operations Research 57: 650–70. [Google Scholar] [CrossRef]
- Branda, Martin. 2015. Diversification-consistent data envelopment analysis based on directional-distance measures. Omega 52: 65–76. [Google Scholar] [CrossRef]
- Brandhofer, Sebastian, Daniel Braun, Vanessa Dehn, Gerhard Hellstern, Matthias Hüls, Yanjun Ji, Ilia Polian, Amandeep Singh Bhatia, and Thomas Wellens. 2022. Benchmarking the performance of portfolio optimization with qaoa. Quantum Information Processing 22: 25. [Google Scholar] [CrossRef]
- Breedt, André, Stefano Ciliberti, Stanislao Gualdi, and Philip Seager. 2018. Is ESG an Equity Factor or Just an Investment Guide? Available online: https://ssrn.com/abstract=3207372 (accessed on 21 March 2024). [CrossRef]
- Bruno, Michelangelo, and Valentina Lagasio. 2021. An overview of the european policies on esg in the banking sector. Sustainability 13: 12641. [Google Scholar] [CrossRef]
- Buonaiuto, Giuseppe, Francesco Gargiulo, Giuseppe De Pietro, Massimo Esposito, and Marco Pota. 2023. Best practices for portfolio optimization by quantum computing, experimented on real quantum devices. Scientific Reports 13: 19434. [Google Scholar] [CrossRef] [PubMed]
- Castro, Francisco, Jesús Gago, Isabel Hartillo, Justo Puerto, and Jose Maria Ucha. 2011. An algebraic approach to integer portfolio problems. European Journal of Operational Research 210: 647–59. [Google Scholar] [CrossRef]
- Cesarone, Francesco, Manuel Luis Martino, and Alessandra Carleo. 2022. Does esg impact really enhance portfolio profitability? Sustainability 14: 2050. [Google Scholar] [CrossRef]
- Chen, Bingren, Hanqing Wu, Haomu Yuan, Lei Wu, and Xin Li. 2023. Quantum portfolio optimization: Binary encoding of discrete variables for qaoa with hard constraint. arXiv arXiv:2304.06915. [Google Scholar] [CrossRef]
- Chen, Li, Lipei Zhang, Jun Huang, Helu Xiao, and Zhongbao Zhou. 2021. Social responsibility portfolio optimization incorporating esg criteria. Journal of Management Science and Engineering 6: 75–85. [Google Scholar] [CrossRef]
- Cohen, Jeffrey, Alex Khan, and Clark Alexander. 2020a. Portfolio optimization of 40 stocks using the dwave quantum annealer. arXiv arXiv:2007.01430. [Google Scholar] [CrossRef]
- Cohen, Jeffrey, Alex Khan, and Clark Alexander. 2020b. Portfolio optimization of 60 stocks using classical and quantum algorithms. arXiv arXiv:2008.08669. [Google Scholar] [CrossRef]
- Coleman, Thomas F., Yuying Li, and Jay Henniger. 2006. Minimizing tracking error while restricting the number of assets. Journal of Risk 8: 33. [Google Scholar] [CrossRef]
- Demers, Elizabeth, Jurian Hendrikse, Philip Joos, and Baruch Lev. 2021. Esg did not immunize stocks during the COVID-19 crisis, but investments in intangible assets did. Journal of Business Finance & Accounting 48: 433–62. [Google Scholar] [CrossRef]
- De Spiegeleer, Jan, Stephan Höcht, Daniel Jakubowski, Sofie Reyners, and Wim Schoutens. 2023. Esg: A new dimension in portfolio allocation. Journal of Sustainable Finance & Investment 13: 827–67. [Google Scholar] [CrossRef]
- Diamond, Steven, and Stephen Boyd. 2016. CVXPY: A Python-embedded modeling language for convex optimization. Journal of Machine Learning Research 17: 1–5. [Google Scholar]
- D-Wave Systems Inc. 2021. Hybrid Solver for Constrained Quadratic Models. Technical Report 14-1055A-A. Burnaby: D-Wave Systems Inc. [Google Scholar]
- Elsokkary, Nada, Faisal Shah Khan, Davide La Torre, Travis S. Humble, and Joel Gottlieb. 2017. Financial Portfolio Management Using d-Wave Quantum Optimizer: The Case of Abu Dhabi Securities Exchange. Technical Report. Oak Ridge: Oak Ridge National Lab. (ORNL). [Google Scholar]
- Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. 2014. A quantum approximate optimization algorithm. arXiv arXiv:1411.4028. [Google Scholar] [CrossRef]
- García, Fernando, Tsvetelina Gankova-Ivanova, Jairo González-Bueno, Javier Oliver, and Rima Tamošiūnienė. 2022. What is the cost of maximizing ESG performance in the portfolio selection strategy? The case of The Dow Jones Index average stocks. Entrepreneurship and Sustainability Issues 9: 178–92. [Google Scholar] [CrossRef] [PubMed]
- Grant, Erica, Travis S. Humble, and Benjamin Stump. 2021. Benchmarking quantum annealing controls with portfolio optimization. Physical Review Applied 15: 014012. [Google Scholar] [CrossRef]
- Herman, Dylan, Cody Googin, Xiaoyuan Liu, Yue Sun, Alexey Galda, Ilya Safro, Marco Pistoia, and Yuri Alexeev. 2023. Quantum computing for finance. Nature Reviews Physics 5: 450–65. [Google Scholar] [CrossRef]
- Hirschberger, Markus, Ralph E. Steuer, Sebastian Utz, Maximilian Wimmer, and Yue Qi. 2013. Computing the nondominated surface in tri-criterion portfolio selection. Operations Research 61: 169–83. [Google Scholar] [CrossRef]
- Jacquier, Antoine, Oleksiy Kondratyev, Alexander Lipton, and Marcos Lopez de Prado. 2022. Quantum Machine Learning and Optimisation in Finance: On the Road to Quantum Advantage. Birmingham: Packt Publishing. [Google Scholar]
- Jobst, Norbert J., Michael D. Horniman, Cormac A. Lucas, and Gautam Mitra. 2001. Computational aspects of alternative portfolio selection models in the presence of discrete asset choice constraints. Quantitative Finance 1: 489. [Google Scholar] [CrossRef]
- Kellerer, Hans, Renata Mansini, and M. Grazia Speranza. 2000. Selecting portfolios with fixed costs and minimum transaction lots. Annals of Operations Research 99: 287–304. [Google Scholar] [CrossRef]
- King, Andrew D., Jack Raymond, Trevor Lanting, Richard Harris, Alex Zucca, Fabio Altomare, Andrew J. Berkley, Kelly Boothby, Sara Ejtemaee, Colin Enderud, and et al. 2023. Quantum critical dynamics in a 5000-qubit programmable spin glass. Nature 617: 61–66. [Google Scholar] [CrossRef] [PubMed]
- Kolm, Petter N., Reha Tütüncü, and Frank J. Fabozzi. 2014. 60 years of portfolio optimization: Practical challenges and current trends. European Journal of Operational Research 234: 356–71. [Google Scholar] [CrossRef]
- Kolouri, Soheil, Se Rim Park, Matthew Thorpe, Dejan Slepcev, and Gustavo K. Rohde. 2017. Optimal mass transport: Signal processing and machine-learning applications. IEEE Signal Processing Magazine 34: 43–59. [Google Scholar] [CrossRef] [PubMed]
- Lang, Jonas, Sebastian Zielinski, and Sebastian Feld. 2022. Strategic portfolio optimization using simulated, digital, and quantum annealing. Applied Sciences 12: 12288. [Google Scholar] [CrossRef]
- Larcker, David F., Lukasz Pomorski, Brian Tayan, and Edward Watts. 2022. Esg Ratings: A Compass without Direction. Rock Center for Corporate Governance at Stanford University Working Paper Forthcoming. Available online: https://ssrn.com/abstract=4179647 (accessed on 21 March 2024).
- La Torre, Mario, Fabiomassimo Mango, Arturo Cafaro, and Sabrina Leo. 2020. Does the esg index affect stock return? evidence from the eurostoxx50. Sustainability 12: 6387. [Google Scholar] [CrossRef]
- Lauria, Davide, W. Brent Lindquist, Stefan Mittnik, and Svetlozar T. Rachev. 2022. Esg-valued portfolio optimization and dynamic asset pricing. arXiv arXiv:2206.02854. [Google Scholar] [CrossRef]
- Li, Han-Lin, and Jung-Fa Tsai. 2008. A distributed computation algorithm for solving portfolio problems with integer variables. European Journal of Operational Research 186: 882–91. [Google Scholar] [CrossRef]
- López Prol, Javier, and Kiwoong Kim. 2022. Risk-return performance of optimized esg equity portfolios in the nyse. Finance Research Letters 50: 103312. [Google Scholar] [CrossRef]
- Lucas, Andrew. 2014. Ising formulations of many np problems. Frontiers in Physics 2: 5. [Google Scholar] [CrossRef]
- Mansini, Renata, and Maria Grazia Speranza. 1999. Heuristic algorithms for the portfolio selection problem with minimum transaction lots. European Journal of Operational Research 114: 219–33. [Google Scholar] [CrossRef]
- Maree, Chari, and Christian W. Omlin. 2022. Balancing profit, risk, and sustainability for portfolio management. Presented at 2022 IEEE Symposium on Computational Intelligence for Financial Engineering and Economics (CIFEr), Helsinki, Finland, May 4–5; New York: IEEE, pp. 1–8. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio selection. The Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- Mugel, Samuel, Carlos Kuchkovsky, Escolástico Sánchez, Samuel Fernández-Lorenzo, Jorge Luis-Hita, Enrique Lizaso, and Román Orús. 2022. Dynamic portfolio optimization with real datasets using quantum processors and quantum-inspired tensor networks. Physical Review Research 4: 013006. [Google Scholar] [CrossRef]
- Mugel, Samuel, Mario Abad, Miguel Bermejo, Javier Sánchez, Enrique Lizaso, and Román Orús. 2021. Hybrid quantum investment optimization with minimal holding period. Scientific Reports 11: 19587. [Google Scholar] [CrossRef] [PubMed]
- Nofsinger, John, and Abhishek Varma. 2014. Socially responsible funds and market crises. Journal of Banking & Finance 48: 180–93. [Google Scholar] [CrossRef]
- Orús, Román, Samuel Mugel, and Enrique Lizaso. 2019. Quantum computing for finance: Overview and prospects. Reviews in Physics 4: 100028. [Google Scholar] [CrossRef]
- Palmer, Samuel, Konstantinos Karagiannis, Adam Florence, Asier Rodriguez, Roman Orus, Harish Naik, and Samuel Mugel. 2022. Financial index tracking via quantum computing with cardinality constraints. arXiv arXiv:2208.11380. [Google Scholar] [CrossRef]
- Pedersen, Lasse Heje, Shaun Fitzgibbons, and Lukasz Pomorski. 2021. Responsible investing: The esg-efficient frontier. Journal of Financial Economics 142: 572–97. [Google Scholar] [CrossRef]
- Peyré, Gabriel, and Marco Cuturi. 2019. Computational optimal transport: With applications to data science. Foundations and Trends® in Machine Learning 11: 355–607. [Google Scholar] [CrossRef]
- Phillipson, Frank, and Harshil Singh Bhatia. 2021. Portfolio optimisation using the d-wave quantum annealer. In International Conference on Computational Science. New York: Springer, pp. 45–59. [Google Scholar] [CrossRef]
- Romero, Sebastián V., Eneko Osaba, Esther Villar-Rodriguez, Izaskun Oregi, and Yue Ban. 2023. Hybrid approach for solving real-world bin packing problem instances using quantum annealers. Scientific Reports 13: 11777. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, Gili, Poya Haghnegahdar, Phil Goddard, Peter Carr, Kesheng Wu, and Marcos López de Prado. 2016. Solving the optimal trading trajectory problem using a quantum annealer. IEEE Journal of Selected Topics in Signal Processing 10: 1053–60. [Google Scholar] [CrossRef]
- Rubio-García, Álvaro, Juan José García-Ripoll, and Diego Porras. 2022. Portfolio optimization with discrete simulated annealing. arXiv arXiv:2210.00807. [Google Scholar] [CrossRef]
- Sakuler, Wolfgang, Johannes M. Oberreuter, Riccardo Aiolfi, Luca Asproni, Branislav Roman, and Jürgen Schiefer. 2023. A real world test of portfolio optimization with quantum annealing. arXiv arXiv:2303.12601. [Google Scholar] [CrossRef]
- Shunza, Justus, Mary Akinyemi, and Chika Yinka-Banjo. 2023. Application of quantum computing in discrete portfolio optimization. Journal of Management Science and Engineering 8: 453–64. [Google Scholar] [CrossRef]
- Shushi, Tomer. 2022. The optimal solution of esg portfolio selection models that are based on the average esg score. Operations Research Letters 50: 513–16. [Google Scholar] [CrossRef]
- Streichert, Felix, Holger Ulmer, and Andreas Zell. 2004. Evolutionary algorithms and the cardinality constrained portfolio optimization problem. In Operations Research Proceedings 2003: Selected Papers of the International Conference on Operations Research (OR 2003), Heidelberg, Germany, September 3–5. New York: Springer, pp. 253–60. [Google Scholar] [CrossRef]
- Utz, Sebastian, Maximilian Wimmer, Markus Hirschberger, and Ralph E. Steuer. 2014. Tri-criterion inverse portfolio optimization with application to socially responsible mutual funds. European Journal of Operational Research 234: 491–98. [Google Scholar] [CrossRef]
- Varmaz, Armin, Christian Fieberg, and Thorsten Poddig. 2022. Portfolio Optimization for Sustainable Investments. Available online: https://ssrn.com/abstract=3859616 (accessed on 21 March 2024).
- Venturelli, Davide, and Alexei Kondratyev. 2019. Reverse quantum annealing approach to portfolio optimization problems. Quantum Machine Intelligence 1: 17–30. [Google Scholar] [CrossRef]
- Vielma, Juan Pablo, Shabbir Ahmed, and George L. Nemhauser. 2008. A lifted linear programming branch-and-bound algorithm for mixed-integer conic quadratic programs. INFORMS Journal on Computing 20: 438–50. [Google Scholar] [CrossRef]
- Villani, Cedric. 2003. Topics in Optimal Transportation. Graduate Studies in Mathematics. Providence: American Mathematical Society. [Google Scholar]
- Young, Martin R. 1998. A minimax portfolio selection rule with linear programming solution. Management Science 44: 673–83. [Google Scholar] [CrossRef]
- Zheng, Chao. 2021. Universal quantum simulation of single-qubit nonunitary operators using duality quantum algorithm. Scientific Reports 11: 3960. [Google Scholar] [CrossRef] [PubMed]

| D | in EUR | |
|---|---|---|
| 1.6 | 960 | 99,999.56 |
| 1.5 | 1112 | 99,998.61 |
| 1.4 | 1202 | 99,994.84 |
| 1.3 | 1305 | 99,932.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Catalano, F.; Nasello, L.; Guterding, D. Quantum Computing Approach to Realistic ESG-Friendly Stock Portfolios. Risks 2024, 12, 66. https://doi.org/10.3390/risks12040066
Catalano F, Nasello L, Guterding D. Quantum Computing Approach to Realistic ESG-Friendly Stock Portfolios. Risks. 2024; 12(4):66. https://doi.org/10.3390/risks12040066
Chicago/Turabian StyleCatalano, Francesco, Laura Nasello, and Daniel Guterding. 2024. "Quantum Computing Approach to Realistic ESG-Friendly Stock Portfolios" Risks 12, no. 4: 66. https://doi.org/10.3390/risks12040066
APA StyleCatalano, F., Nasello, L., & Guterding, D. (2024). Quantum Computing Approach to Realistic ESG-Friendly Stock Portfolios. Risks, 12(4), 66. https://doi.org/10.3390/risks12040066






