L1 Regularization for High-Dimensional Multivariate GARCH Models
Abstract
1. Introduction
2. Literature Review
3. The MGARCH–BEKK Representations with Regularization
3.1. The MGARCH–BEKK Representation
- (i)
- is a continuous function of , and there exists , , where represents the determinant of a matrix;
- (ii)
- For any , and are continuous functions of ;
- (iii)
- For any , , i.e., the largest modulus of eigenvalues of is less than 1.
3.2. Likelihood Function
- (i)
- When , for a nonrandom positive-definite matrix H;
- (ii)
- For the Fisher information matrix , ;
- (iii)
- For , is bounded for all and .
- (i)
- For , , where is the ith element of ;
- (ii)
- For a sufficiently large T, is almost surely positive definite, and
- (iii)
- There exists a neighborhood of such that, for all and and some ,
3.3. Penalty Function and Penalized Quasi-Likelihood
- (i)
- for some , and large T. Here, means is bounded by a constant and means when ;
- (ii)
- for some and large T, where d is the half-minimum signal we defined before.
4. Properties of the PQML Estimator and Implementation
4.1. Sparsity of the PQML Estimator
- (i)
- (Sparsity) with probability approaching one;
- (ii)
- (Rate of convergence)
4.2. Implementation and Selection of
5. Simulation
6. Real Data Applications
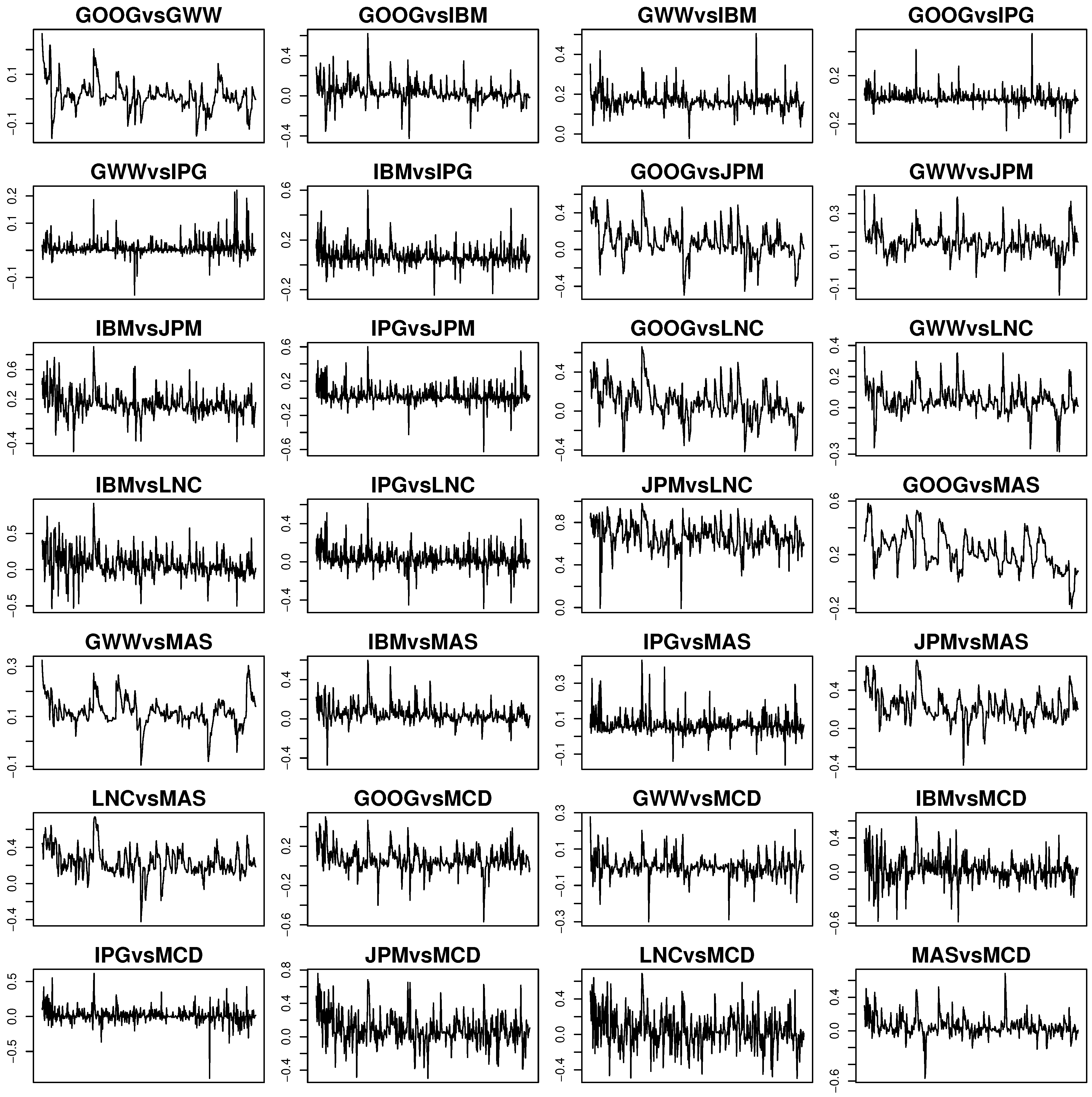
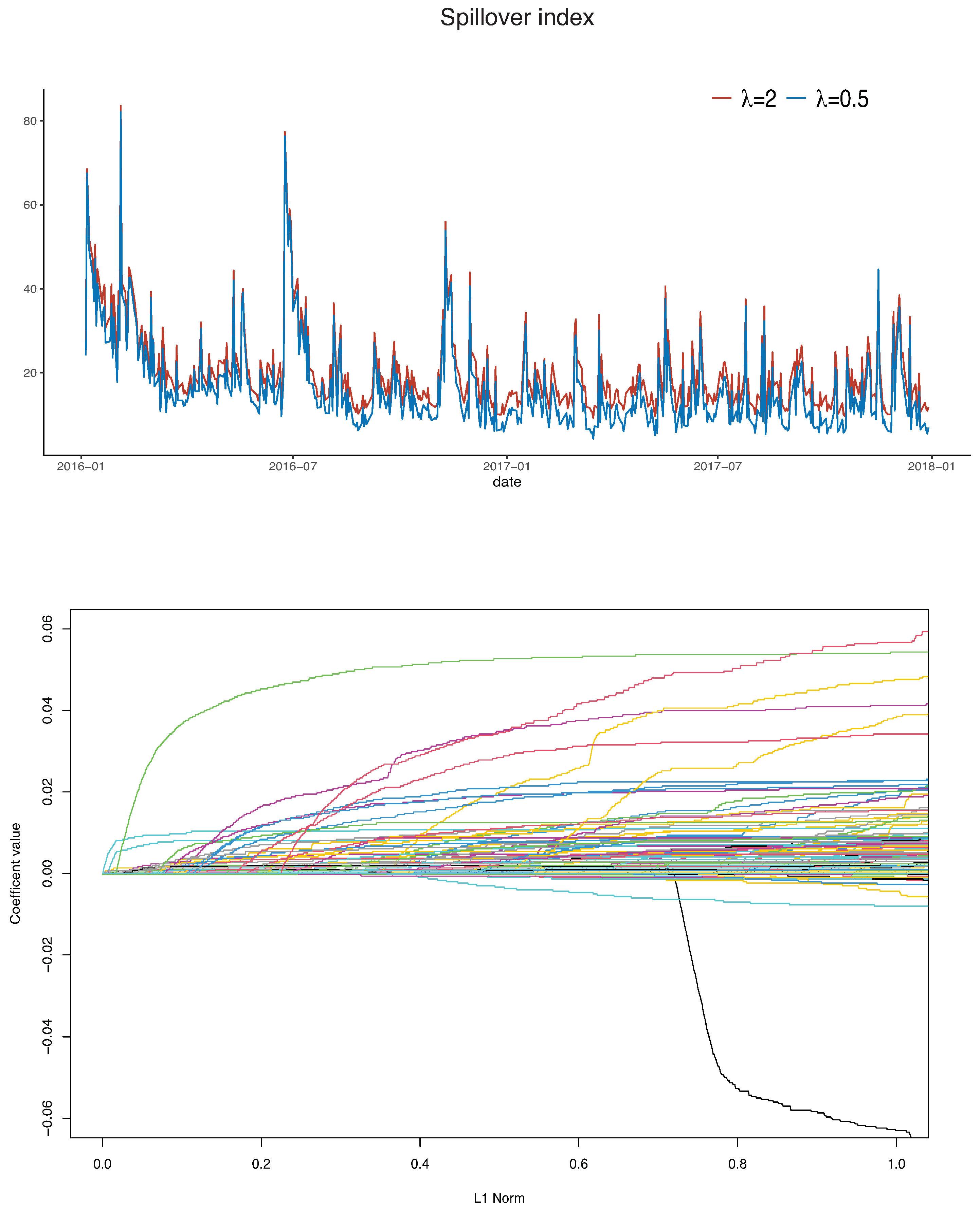
6.1. Volatility Spillovers
6.2. Portfolio Optimization
7. Discussion and Conclusive Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIC | Akaike information criterion |
| BEKK | Baba–Engle–Kraft–Kroner |
| BIC | Bayesian information criterion |
| CV | Cross-validation |
| DCC | Dynamic conditional correlation |
| GARCH | Generalized autoregressive conditionally heteroskedastic |
| GMV | Global minimum variance |
| IR | Information ratio |
| LARS | Least-angle regression |
| LASSO | Least absolute shrinkage and selection operator |
| MGARCH | Multivariate GARCH |
| PQL | Penalized quasi-likelihood |
| PQML | Penalized quasi-maximum likelihood |
| SCAD | Smoothly clipped absolute deviation |
| SD | Standard deviation |
Appendix A. Proofs of Propositions, Lemmas, and Theorems
Appendix A.1. Proof of Propostion 2
Appendix A.2. Proof of Proposition 4
Appendix A.3. Proof of Lemma 1
Appendix A.4. Proof of Lemma 2
Appendix A.5. Proof for Theorem 1
References
- Aielli, Gian Piero. 2013. Dynamic conditional correlation: On properties and estimation. Jouranl of Business and Economic Statistics 31: 282–99. [Google Scholar] [CrossRef]
- Alexander, Carol. 2000. Orthogonal methods for generating large positive semi-definite covariance matrices. In ICMA Centre Discussion Papers in Finance icma-dp2000-06. London: Henley Business School, Reading University. [Google Scholar]
- Ampountolas, Apostolos. 2022. Cryptocurrencies intraday high-frequency volatility spillover effects using univariate and multivariate GARCH models. International Journal of Financial Studies 10: 51. [Google Scholar] [CrossRef]
- Apergis, Nicholas, and Anthony Rezitis. 2001. Asymmetric cross-market volatility spillovers: Evidence from daily data on equity and foreign exchange markets. The Manchester School 69: 81–96. [Google Scholar] [CrossRef]
- Apergis, Nicholas, and Anthony Rezitis. 2003. An examination of okun’s law: Evidence from regional areas in greece. Applied Economics 35: 1147–51. [Google Scholar] [CrossRef]
- Baillie, Rechard T., and Tim Bollerslev. 1990. A multivariate generalized arch approach to modeling risk premia in forward foreign exchange rate markets. Journal of International Money and Finance 9: 309–24. [Google Scholar] [CrossRef]
- Basu, Sumanta, and George Michailidis. 2015. Regularized estimation in sparse high-dimensional time series model. The Annals of Statistics 43: 1535–67. [Google Scholar] [CrossRef]
- Bauwens, Luc, and Sébastien Laurent. 2005. A new class of multivariate skew densities, with application to generalized autoregressive conditional heteroscedasticity models. Journal of Business and Economic Statistics 23: 346–54. [Google Scholar] [CrossRef]
- Bickel, Peter J., and Elizaveta Levina. 2008. Covariance regularization by thresholding. The Annals of Statistics 36: 2577–604. [Google Scholar] [CrossRef] [PubMed]
- Billio, Monica, Massimiliano Caporin, Lorenzo Frattarolo, and Loriana Pelizzon. 2023. Networks in risk spillovers: A multivariate GARCH perspective. Econometrics and Statistics 28: 1–29. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1990. Comparing predictive accuracy modelling the coherence in short-run nominal exchange rates: A multivariate generalized arch model. The Review of Economics and Statistics 72: 498–05. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Robert Engle, and Jeffrey Wooldridge. 1988. A capital asset pricing model with time-varying covariances. Journal of Political Economy 96: 116–31. [Google Scholar] [CrossRef]
- Boudt, Kris, Jon Danielsson, and Sébastien Laurent. 2013. Robust forecasting of dynamic conditional correlation garch models. International Journal of Forecasting 29: 244–57. [Google Scholar] [CrossRef]
- Brodie, Joshua, Ingrid Daubechies, Christine De Mol, Domenico Giannone, and Ignace Loris. 2009. Sparse and stable markowitz portfolios. Proceedings of the National Academy of Sciences of the United States of America 106: 12267–72. [Google Scholar] [CrossRef]
- Cai, Tony, and Weidong Liu. 2011. Adaptive thresholding for sparse covariance matrix estimation. Journal of the American Statistical Association 106: 672–84. [Google Scholar] [CrossRef]
- Christiansen, Charlotte. 2007. Volatility-Spillover Effects in European Bond Markets. European Financial Management 13: 923–948. [Google Scholar] [CrossRef]
- Comte, Fabienne, and Offer Lieberman. 2003. Asymptotic theory for multivariate garch processes. Journal of Multivariate Analysis 84: 61–84. [Google Scholar] [CrossRef]
- DeMiguel, Victor, Lorenzo Garlappi, and Raman Uppal. 2007. Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? The Review of Financial Studies 22: 1915–53. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2009. Measuring financial asset return and volatitliy spillovers, with application to global equity markets. Economic Journal 199: 158–71. [Google Scholar] [CrossRef]
- Di Lorenzo, David, Giampalo Liuzzi, Francesco Rinaldi, Fabio Schoen, and Marco Sciandrone. 2012. A concave optimization-based approach for sparse portfolio selection. Optimization Methods and Software 27: 983–1000. [Google Scholar] [CrossRef]
- Efron, Bradley, Trevor Hastie, and Robert Tibshirani. 2004. Least angle regression. The Annals of Statistics 32: 407–99. [Google Scholar] [CrossRef]
- Engle, Rober. 1982. Autoregressive conditional heteroskedasticity with estimates of the variance of united kingdom inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert. 1990. Asset pricing with a factor-arch covariance structure: Empirical estimates for treasury bills. Journal of Econometrics 45: 213–37. [Google Scholar] [CrossRef]
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business and Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Engle, Robert, and Kenneth Kroner. 1995. Multivariate simultaneous generalized arch. Econometric Theory 11: 122–50. [Google Scholar] [CrossRef]
- Engle, Robert, and Riccardo Colacito. 2006. Testing and valuing dynamic correlations for asset allocation. Journal of Business and Economic Statistics 24: 238–53. [Google Scholar] [CrossRef]
- Engle, Robert, Olivier Ledoit, and Michael Wolf. 2019. Large dynamic covariance matrices. Journal of Business and Economic Statistics 37: 363–75. [Google Scholar] [CrossRef]
- Engle, Robert, Takatoshi Ito, and Wen-Ling Lin. 1990. Meteor showers or heat waves? Heteroskedastic intra-daily volatility in the foreign exchange market. Econometrica 58: 525–42. [Google Scholar] [CrossRef]
- Fan, Jianqing, and Jinchi Lv. 2011. Noncave penalized likelihood with np-dimensionality. IEEE Transactions on Information Theory 57: 5467–84. [Google Scholar] [CrossRef]
- Fan, Jianqing, and Runze Li. 2001. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association 96: 1348–60. [Google Scholar] [CrossRef]
- Fan, Yingying, and Cheng Yong Tang. 2013. Tuning parameter selection in high dimensional penalized likelihood. Journal of the Royal Statistical Society Series B: Statistical Methodology 75: 531–52. [Google Scholar] [CrossRef]
- Fastrich, Björn, Sandra Paterlini, and Peter Winker. 2015. Constructing optimal sparse portfolios using regularization methods. Computational Management Science 12: 417–34. [Google Scholar] [CrossRef]
- Francq, Christian, and Jean-Michel Zakoian. 2019. GARCH Models: Structure, Statistical Inference and Financial Applications. Hoboken: John Wiley & Sons. [Google Scholar]
- Friedman, Jerome, Trevor Hastie, Holger Höfling, and Robert Tibshirani. 2007. Pathwise coordinate optimization. The Annals of Applied Statistics 1: 302–32. [Google Scholar] [CrossRef]
- Giacometti, Rosella, Gabriele Torri, Kamonchai Rujirarangsan, and Michela Cameletti. 2023. Spatial Multivariate GARCH Models and Financial Spillovers. Journal of Risk and Financial Management 16: 397. [Google Scholar] [CrossRef]
- Hamao, Yasushi, Ronald W. Masulis, and Victor Ng. 1990. Correlations in price changes and volatility across international stock markets. The Review of Financial Studies 3: 281–307. [Google Scholar] [CrossRef]
- Hafner, Christian M., and Arie Preminger. 2009. Asymptotic theory for a factor GARCH model. Econometric Theory 25: 336–63. [Google Scholar] [CrossRef]
- Hafner, Christian M., Helmut Herwartz, and Simone Maxand. 2022. Identification of structural multivariate GARCH models. Journal of Econometrics 227: 212–27. [Google Scholar] [CrossRef]
- Hassan, Syed Aun, and Farooq Malik. 2007. Multivariate garch modeling of sector volatility transmission. The Quarterly Review of Economics and Finance 47: 470–80. [Google Scholar] [CrossRef]
- Hong, Junping, Yi Yan, Ercan Engin Kuruoglu, and Wai Kin Chan. 2023. Multivariate Time Series Forecasting With GARCH Models on Graphs. IEEE Transactions On Signal And Information Processing Over Networks 9: 557–68. [Google Scholar] [CrossRef]
- Kaltenhäuser, Bernd. 2002. Return and Volatility Spillovers to Industry Returns: Does EMU Play a Role? CFS Working Paper Series 2002/05. Frankfurt a. M.: Center for Financial Studies (CFS). [Google Scholar]
- Lam, Clifford, and Jianqing Fan. 2009. Sparsistency and rates of convergence in large covariance matrix estimation. The Annals of Statistics 37: 4254–78. [Google Scholar] [CrossRef] [PubMed]
- Lanne, Markku, and Pentti Saikkonen. 2007. A multivariate generalized orthogonal factor GARCH model. Journal of Business & Economic Statistics 25: 61–75. [Google Scholar]
- Ledoit, Olivier, and Michael Wolf. 2004. A well-conditioned estimator for large-dimensional covariance matrices. Journal of Multivariate Analysis 88: 365–411. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2012. Nonlinear shrinkage estimation of large-dimensional covariance matrices. The Annals of Statistics 40: 1024–60. [Google Scholar] [CrossRef]
- Ling, Shiqing, and Michael McAleer. 2003. Asymptotic theory for a vector arma-garch model. Econometric Theory 19: 280–310. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio selection. The Journal of Finance 7: 77–91. [Google Scholar]
- McAleer, Michael, Suhejia Hoti, and Felix Chan. 2009. Structure and asymptotic theory for multivariate asymmetric conditional volatility. Econometric Reviews 28: 422–40. [Google Scholar] [CrossRef]
- NASDAQ Stock Symbols. n.d. Stock Symbol. Available online: https://www.nasdaq.com/market-activity/stocks/ (accessed on 24 January 2024).
- Nicholson, William B., David S. Matteson, and Jacob Bien. 2017. VARX-L: Structured regularization for large vector autoregressions with exogenous variables. International Journal of Forecasting 33: 627–51. [Google Scholar] [CrossRef]
- Pan, Ming-Shiun, and L. Paul Hsueh. 1998. Transmission of stock returns and volatility between the U.S. and Japan: Evidence from the stock index futures markets. Asia-Pacific Financial Markets 5: 211–25. [Google Scholar] [CrossRef]
- Poignard, Benjamin. 2017. New Approaches for High-Dimensional Multivariate Garch Models. General Mathematics [math.GM]. Ph.D. thesis, Université Paris Sciences et Lettres, Paris, France. [Google Scholar]
- Ravikumar, Pradeep, Martin J. Wainwright, Garvesh Raskutti, and Bin Yu. 2011. High-dimensional covariance estimation by minimizing ℓ1-penalized log-determinant divergence. Electronic Journal of Statistics 5: 935–80. [Google Scholar] [CrossRef]
- Rio, Emmanuel. 2017. Asymptotic Theory of Weakly Dependent Random Processes. Berlin: Springer Nature. [Google Scholar]
- Sánchez García, Javier, and Salvador Cruz Rambaud. 2022. Machine Learning Regularization Methods in High-Dimensional Monetary and Financial VARs. Mathematics 10: 877. [Google Scholar] [CrossRef]
- Shiferaw, Yegnanew A. 2019. Time-varying correlation between agricultural commodity and energy price dynamics with Bayesian multivariate DCC-GARCH models. Physica A: Statistical Mechanics and Its Applications 526: 120807. [Google Scholar] [CrossRef]
- Siddiqui, Taufeeque Ahmad, and Mazia Fatima Khan. 2018. Analyzing spillovers in international stock markets: A multivariate GARCH approach. IMJ 10: 57–63. [Google Scholar]
- Sun, Wei, Junhui Wang, and Yixin Fang. 2013. Consistent selection of tuning parameters via variable selection stability. Journal of Machine Learning Research 14: 3419–40. [Google Scholar]
- Sun, Yan, and Xiaodong Lin. 2011. Regularization for stationary multivariate time series. Quantitative Finance 12: 573–86. [Google Scholar] [CrossRef]
- Theodossiou, Panayiotis, and Unro Lee. 1993. Mean and volatility spillovers across major national stock markets: Further empirical evidence. The Journal of Financial Research 16: 337–50. [Google Scholar] [CrossRef]
- Tibshirani, Robert. 1996. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 58: 267–88. [Google Scholar] [CrossRef]
- Tse, Yiu Kuen, and Albert K. C. Tsui. 2002. A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations. Journal of Business & Economic Statistics 20: 351–62. [Google Scholar]
- Uematsu, Yoshimasa. 2015. Penalized likelihood estimation in high-dimensional time series models and its application. arXiv arXiv:1504.06706. [Google Scholar]
- van der Weide, Roy. 2002. Go-garch: A multivariate generalized orthogonal garch model. Journal of Applied Econometrics 17: 549–64. [Google Scholar] [CrossRef]
- Vrontos, Ioannis, Petros Dellaportas, and Dimitris N. Politis. 2003. A full-factor multivariate garch model. The Econometrics Journal 6: 312–34. [Google Scholar] [CrossRef]
- Wang, Hansheng, Bo Li, and Chenlei Leng. 2009. Shrinkage tuning parameter selection with a diverging number of parameters. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 71: 671–83. [Google Scholar] [CrossRef]
- Worthington, Andrew, and Helen Higgs. 2004. Transmission of equity returns and volatility in asian developed and emerging markets: A multivariate garch analysis. International Journal of Finance & Economics 9: 71–80. [Google Scholar]
- Wu, Tong Tong, and Kenneth Lange. 2008. Coordinate descent algorithms for lasso penalized regression. Annals of Applied Statistics 2: 224–44. [Google Scholar] [CrossRef]
- Yuan, Ming, and Yi Lin. 2006. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 68: 49–67. [Google Scholar] [CrossRef]
- Zhang, Cun-Hui. 2010. Nearly unbiased variable selection under minimax concave penalty. Annals of Statistics 38: 894–942. [Google Scholar] [CrossRef]
- Zhang, Yongli, and Yuhong Yang. 2015. Cross-validation for selecting a model selection procedure. Journal of Econometrics 187: 95–112. [Google Scholar] [CrossRef]
- Zhao, Peng, and Bin Yu. 2006. On model selection consistency of lasso. Journal of Machine Learning Research 7: 2541–67. [Google Scholar]
- Zhao, Peng, and Bin Yu. 2007. Stagewise lasso. Journal of Machine Learning Research 8: 2701–26. [Google Scholar]
- Zou, Hui. 2006. The adaptive lasso and its oracle properties. Journal of the American Statistical Association 101: 1418–29. [Google Scholar] [CrossRef]
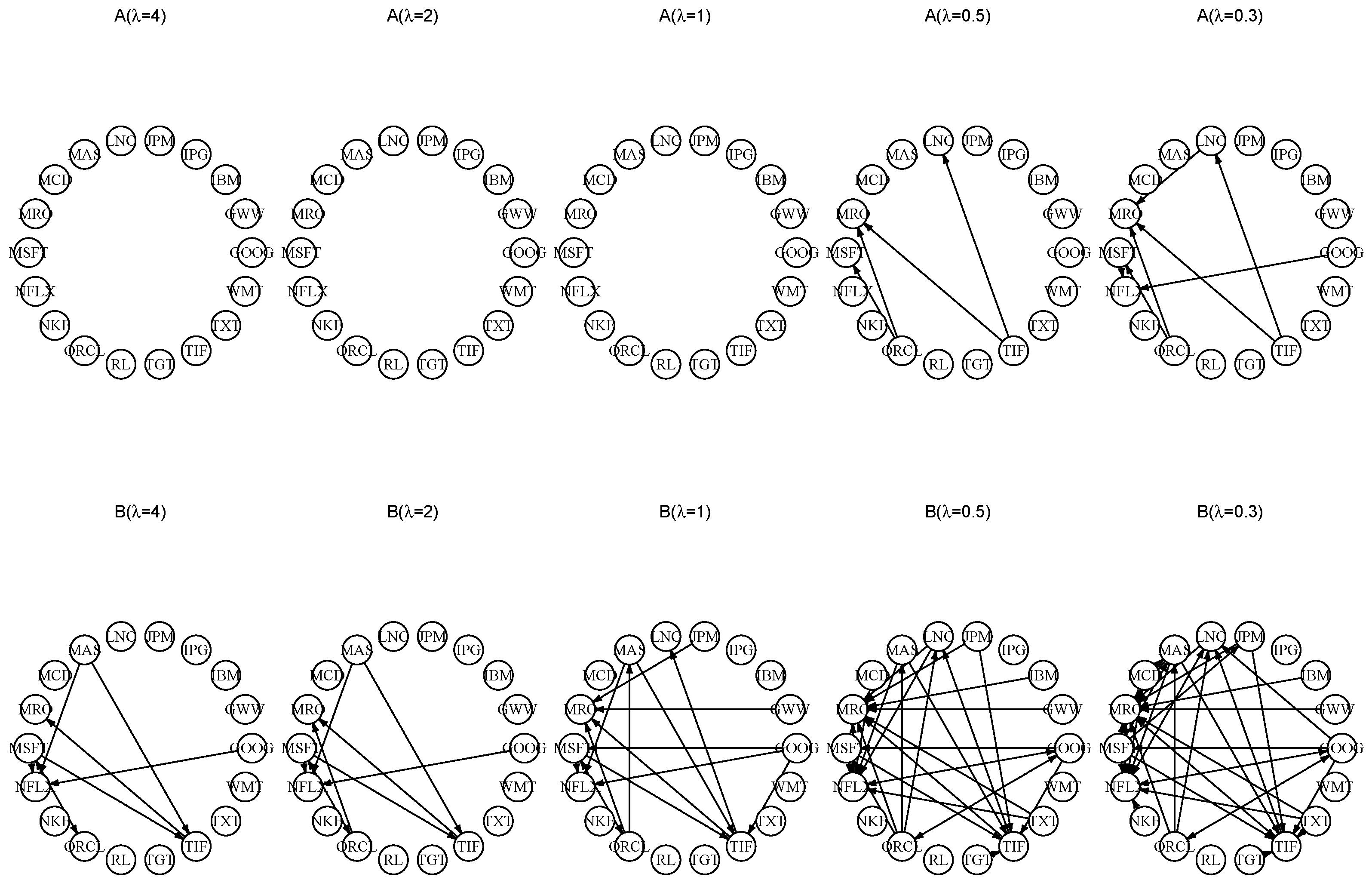
| Case 1 | Case 2 | |
|---|---|---|
| A | ||
| B | ||
| C |
| Case | 6 | 5 | 4 | 3 | 2 | 1 | 0.64 | 0.32 | 0.16 | 0.08 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.988 | 0.988 | 0.984 | 0.981 | 0.974 | 0.954 | 0.934 | 0.890 | 0.841 | 0.756 | ||
| (0.031) | (0.031) | (0.035) | (0.037) | (0.040) | (0.046) | (0.051) | (0.058) | (0.066) | (0.083) | ||
| 1 | 0.755 | 0.755 | 0.767 | 0.786 | 0.814 | 0.821 | 0.822 | 0.834 | 0.864 | 0.897 | |
| (0.028) | (0.033) | (0.035) | (0.036) | (0.024) | (0.014) | (0.013) | (0.026) | (0.034) | (0.038) | ||
| 0.151 | 0.151 | 0.150 | 0.147 | 0.142 | 0.133 | 0.132 | 0.131 | 0.128 | 0.125 | ||
| (0.029) | (0.029) | (0.029) | (0.029) | (0.030) | (0.032) | (0.032) | (0.031) | (0.030) | (0.029) | ||
| 3.104 | 3.533 | 2.370 | 1.611 | 0.735 | 0.461 | 0.359 | 0.325 | 0.289 | 0.282 | ||
| (6.463) | (7.124) | (5.471) | (4.158) | (1.051) | (0.460) | (0.356) | (0.294) | (0.242) | (0.257) | ||
| 0.985 | 0.985 | 0.983 | 0.977 | 0.960 | 0.918 | 0.889 | 0.841 | 0.805 | 0.767 | ||
| (0.030) | (0.030) | (0.034) | (0.034) | (0.043) | (0.048) | (0.052) | (0.052) | (0.054) | (0.065) | ||
| 2 | 0.740 | 0.742 | 0.745 | 0.752 | 0.759 | 0.766 | 0.765 | 0.767 | 0.768 | 0.782 | |
| (0.029) | (0.029) | (0.028) | (0.025) | (0.019) | (0.011) | (0.014) | (0.013) | (0.014) | (0.030) | ||
| 0.151 | 0.151 | 0.151 | 0.149 | 0.145 | 0.136 | 0.136 | 0.135 | 0.132 | 0.126 | ||
| (0.022) | (0.022) | (0.022) | (0.021) | (0.021) | (0.023) | (0.023) | (0.022) | (0.021) | (0.022) | ||
| 2.004 | 2.040 | 1.818 | 0.330 | 0.323 | 0.369 | 0.402 | 0.278 | 0.275 | 0.209 | ||
| (8.525) | (9.024) | (7.710) | (1.381) | (1.936) | (1.829) | (2.388) | (0.163) | (0.163) | (0.180) |
| Ticker | Company | Ticker | Company |
|---|---|---|---|
| GOOG | Alphabet Inc., Mountain View, CA, USA | GWW | W.W. Grainger, Inc., Lake Forest, FL, USA |
| IBM | International Business Machines Corporation, Armonk, NY, USA | JPM | JPMorgan Chase & Co., New York, NY, USA |
| MSFT | Microsoft Corporation, Redmond, WA, USA | NKE | Nike Inc., Beaverton, OR, USA |
| ORCL | Oracle Corporation, Austin, TX, USA | TIF | Tiffany & Co., New York, NY, USA |
| IPG | The Interpublic Group of Companies, New York, NY, USA | MAS | Masco Corporation, Livonia, MI, USA |
| MCD | Mcdonald’s Corp., Chicago, IL, USA | NFLX | Netflix, Inc., Los Gatos, CA, USA |
| RL | Ralph Lauren Corporation, New York, NY, USA | TXT | Textron Inc., Providence, RI, USA |
| LNC | Lincoln National Corporation, Radnor, PA, USA | MRO | Marathon Oil Corporation, Houston, TX, USA |
| TGT | Target Corporation, Minneapolis, MN, USA | WMT | Walmart Inc., Bentonville, AR, USA |
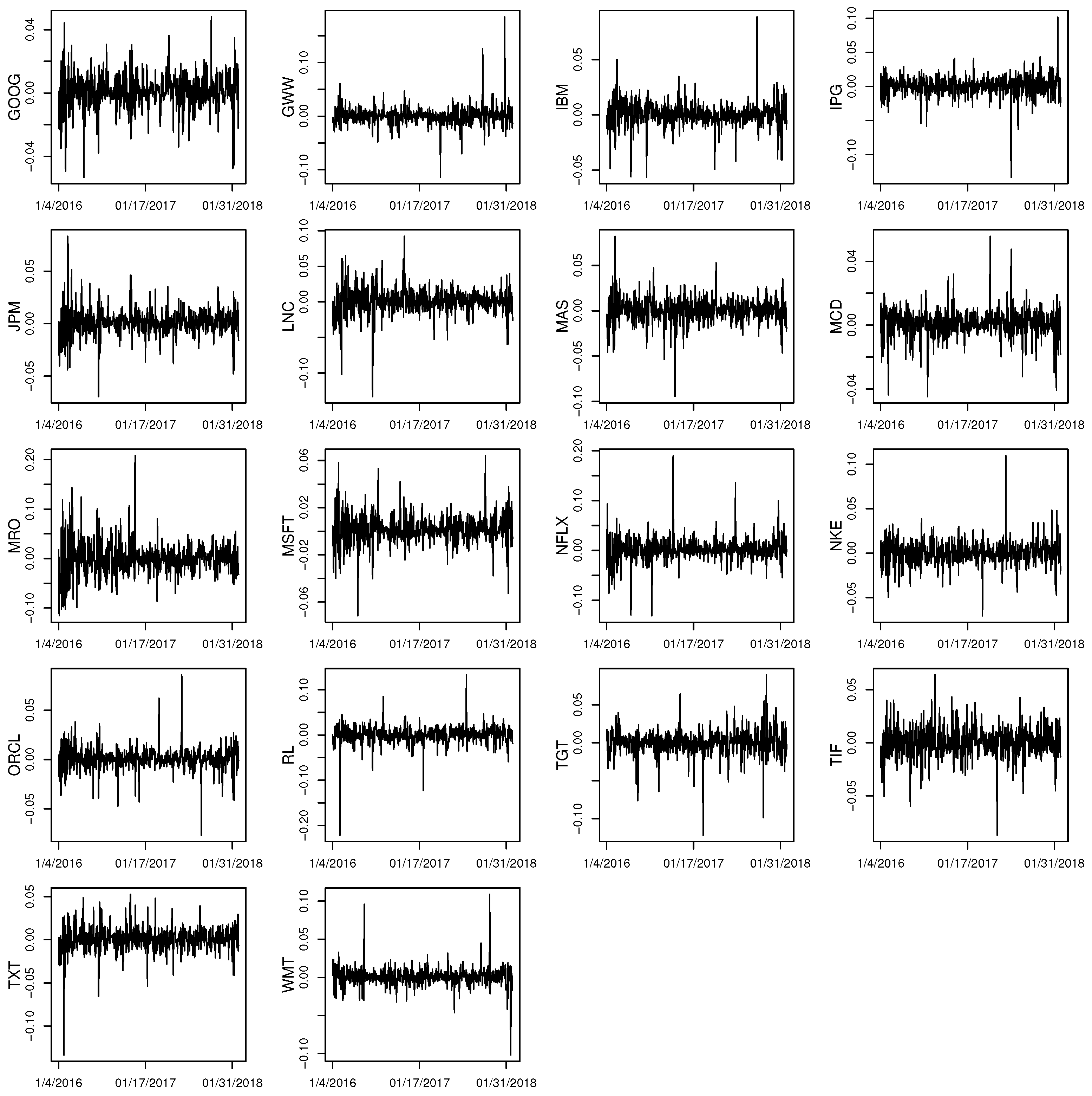
| GOOG | GWW | IBM | JPM | MSFT | NKE | ORCL | TIF | IPG | MAS | MCD | NFLX | RL | TXT | LNC | MRO | TGT | WMT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 7.037 × | 5.164 × | 4.297 × | 1.150 × | 1.033 × | 1.420 × | 6.439 × | 8.143 × | −7.648 × | 1.029 × | 8.891 × | 1.304 × | 1.610 × | 7.103 × | 1.148 × | 1.217 × | 5.523 × | 1.116 × |
| Std. Dev. | 0.013 | 0.016 | 0.011 | 0.013 | 0.012 | 0.014 | 0.012 | 0.015 | 0.015 | 0.014 | 0.009 | 0.023 | 0.021 | 0.015 | 0.019 | 0.034 | 0.017 | 0.012 |
| Skewness | −0.440 | 0.124 | 0.291 | 0.348 | 0.040 | 0.509 | 0.097 | −0.391 | −1.779 | −0.456 | 0.005 | 0.635 | −2.332 | −1.438 | −0.779 | 0.640 | −1.108 | 2.291 |
| Kurtosis | 6.120 | 16.399 | 14.446 | 8.907 | 8.926 | 11.683 | 15.022 | 6.274 | 16.842 | 9.409 | 9.640 | 17.196 | 33.455 | 17.970 | 10.830 | 7.383 | 13.600 | 24.910 |
| GOOG | 0.04 | 0.24 | 0.26 | 0.67 | 0.28 | 0.36 | 0.22 | 0.28 | 0.33 | 0.29 | 0.44 | 0.15 | 0.23 | 0.27 | 0.11 | 0.06 | 0.13 | |
| GWW | 0.38 | 0.34 | 0.13 | 0.17 | 0.16 | 0.24 | 0.29 | 0.27 | 0.03 | 0.06 | 0.09 | 0.34 | 0.28 | 0.21 | 0.16 | 0.09 | ||
| IBM | 0.38 | 0.30 | 0.15 | 0.42 | 0.27 | 0.30 | 0.31 | 0.12 | 0.13 | 0.15 | 0.39 | 0.37 | 0.19 | 0.15 | 0.14 | |||
| JPM | 0.37 | 0.23 | 0.38 | 0.41 | 0.31 | 0.44 | 0.23 | 0.19 | 0.28 | 0.52 | 0.78 | 0.36 | 0.16 | 0.09 | ||||
| MSFT | 0.26 | 0.45 | 0.29 | 0.29 | 0.38 | 0.35 | 0.36 | 0.19 | 0.32 | 0.33 | 0.20 | 0.08 | 0.12 | |||||
| NKE | 0.20 | 0.23 | 0.30 | 0.30 | 0.18 | 0.18 | 0.33 | 0.23 | 0.30 | 0.12 | 0.27 | 0.16 | ||||||
| ORCL | 0.34 | 0.26 | 0.36 | 0.26 | 0.26 | 0.15 | 0.30 | 0.35 | 0.19 | 0.09 | 0.12 | |||||||
| TIF | 0.23 | 0.33 | 0.14 | 0.18 | 0.25 | 0.33 | 0.42 | 0.26 | 0.27 | 0.11 | ||||||||
| IPG | 0.38 | 0.09 | 0.12 | 0.21 | 0.26 | 0.32 | 0.15 | 0.21 | 0.10 | |||||||||
| MAS | 0.28 | 0.23 | 0.26 | 0.36 | 0.46 | 0.20 | 0.24 | 0.12 | ||||||||||
| MCD | 0.14 | 0.13 | 0.12 | 0.16 | 0.07 | 0.09 | 0.16 | |||||||||||
| NFLX | 0.10 | 0.22 | 0.19 | 0.07 | 0.02 | 0.09 | ||||||||||||
| RL | 0.22 | 0.35 | 0.16 | 0.31 | 0.09 | |||||||||||||
| TXT | 0.53 | 0.26 | 0.17 | 0.09 | ||||||||||||||
| LNC | 0.39 | 0.19 | 0.05 | |||||||||||||||
| MRO | 0.08 | 0.04 | ||||||||||||||||
| TGT | 0.36 |
| Model | Mean (%) | SD. (%) | IR | Mean (%) | SD. (%) | IR |
|---|---|---|---|---|---|---|
| Equally weighted | 0.430 | 0.761 | 0.565 | |||
| GMV | ||||||
| Regularized BEKK | 0.390 | 0.650 | 0.601 | 0.352 | 0.652 | 0.540 |
| Factor GARCH | 0.326 | 0.885 | 0.368 | 0.223 | 1.200 | 0.186 |
| DCC–GARCH | 0.244 | 0.665 | 0.367 | 0.302 | 0.677 | 0.446 |
| Constant covariance | 0.261 | 0.658 | 0.397 | 0.165 | 0.777 | 0.212 |
| Regularized BEKK | 0.382 | 0.585 | 0.654 | 0.416 | 0.633 | 0.657 |
| Factor GARCH | 0.210 | 1.169 | 0.180 | 0.221 | 1.321 | 0.167 |
| DCC–GARCH | 0.286 | 0.631 | 0.452 | 0.316 | 0.660 | 0.479 |
| Constant covariance | 0.219 | 0.669 | 0.327 | 0.273 | 0.668 | 0.409 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Zou, H.; Xing, H. L1 Regularization for High-Dimensional Multivariate GARCH Models. Risks 2024, 12, 34. https://doi.org/10.3390/risks12020034
Yao S, Zou H, Xing H. L1 Regularization for High-Dimensional Multivariate GARCH Models. Risks. 2024; 12(2):34. https://doi.org/10.3390/risks12020034
Chicago/Turabian StyleYao, Sijie, Hui Zou, and Haipeng Xing. 2024. "L1 Regularization for High-Dimensional Multivariate GARCH Models" Risks 12, no. 2: 34. https://doi.org/10.3390/risks12020034
APA StyleYao, S., Zou, H., & Xing, H. (2024). L1 Regularization for High-Dimensional Multivariate GARCH Models. Risks, 12(2), 34. https://doi.org/10.3390/risks12020034






