Quantum Majorization in Market Crash Prediction
Abstract
1. Introduction
2. Methods
2.1. Alarm Systems
2.2. Quantum Majorization and the Measure
2.3. Reinforced Urn Processes
3. The Quantum Alarm System
4. Data and Calculations
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aït-Sahalia, Yacine, Julio Cacho-Diaz, and Roger J. A. Laeven. 2015. Modeling financial contagion using mutually exciting jump processes. Journal of Financial Economics 117: 585–606. [Google Scholar] [CrossRef]
- Alberti, Peter M., and Armin Uhlmann. 1982. Stochasticity and Partial Order. Berlin: Deutscher Verlag der Wissenschaften. [Google Scholar]
- Alessi, Lucia, and Carsten Detken. 2011. Quasi real time early warning indicators for costly asset price boom/bust cycles: A role for global liquidity. European Journal of Political Economy 27: 520–33. [Google Scholar] [CrossRef]
- Ang, Andrew, and Geert Bekaert. 2002. Short rate nonlinearities and regime switches. Journal of Economic Dynamics and Control 26: 1243–74. [Google Scholar] [CrossRef]
- Antunes, Marilia, Maria Antonia Amaral Turkman, and Kamil F. Turkman. 2003. A bayesian approach to event prediction. Journal of Time Series Analysis 24: 631–46. [Google Scholar] [CrossRef]
- Arnold, Barry C., and José María Sarabia. 2018. Majorization and the Lorenz Order with Applications in Applied Mathematics and Economics. Berlin and Heidelberg: Springer. [Google Scholar]
- Berg, Andrew, and Catherine Pattillo. 1999. Predicting currency crises: The indicators approach and an alternative. Journal of International Money and Finance 18: 561–86. [Google Scholar] [CrossRef]
- Bloomberg. 2024. Financial Crises Are a Us Feature Not a Bug. Available online: https://www.bloomberg.com/opinion/articles/2024-03-08/financial-crises-are-a-us-feature-not-a-bug (accessed on 21 October 2024).
- Bollerslev, Tim. 1987. A conditionally heteroskedastic time series model for speculative prices and rates of return. The Review of Economics and Statistics 69: 542–47. [Google Scholar] [CrossRef]
- Bouri, Elie, Peter Molnár, Georges Azzi, David Roubaud, and Lars Ivar Hagfors. 2017. On the hedge and safe haven properties of bitcoin: Is it really more than a diversifier? Finance Research Letters 20: 192–98. [Google Scholar] [CrossRef]
- Brigo, Damiano, and Fabio Mercurio. 2013. Interest Rate Models Theory and Practice. Springer Finance. Berlin and Heidelberg: Springer. [Google Scholar]
- Chavez-Demoulin, Valerie, Anthony C. Davison, and Alexander J. McNeil. 2005. Estimating value-at-risk: A point process approach. Quantitative Finance 5: 227–34. [Google Scholar] [CrossRef]
- Chen, Wei, Huilin Xu, Zhensong Chen, and Manrui Jiang. 2021. A novel method for time series prediction based on error decomposition and nonlinear combination of forecasters. Neurocomputing 426: 85–103. [Google Scholar] [CrossRef]
- Cheng, Dan, and Pasquale Cirillo. 2018. A Reinforced Urn Process Modeling of Recovery Rates and Recovery Times. Journal of Banking & Finance 96: 1–17. [Google Scholar]
- Cirillo, Pasquale, Jürg Hüsler, and Pietro Muliere. 2013. Alarm systems and catastrophes from a diverse point of view. Methodology and Computing in Applied Probability 15: 821–39. [Google Scholar] [CrossRef]
- Claessens, Mr Stijn, and Mr Ayhan Kose. 2013. Financial crises explanations, types, and implications. In IMF Staff Papers. Washington, DC: International Monetary Fund, vol. 28, pp. 1–65. [Google Scholar]
- de Finetti, Bruno. 2017. Theory of Probability: A Critical Introductory Treatment. Wiley Series in Probability and Statistics. Hoboken: Wiley. [Google Scholar]
- De Maré, Jacques. 1980. Optimal prediction of catastrophes with applications to gaussian processes. Annals of Probability 8: 841–50. [Google Scholar] [CrossRef]
- DeMiguel, Victor, Lorenzo Garlappi, and Raman Uppal. 2007. Optimal versus naive diversification: How inefficient is the 1/n portfolio strategy? The Review of Financial Studies 22: 1915–53. [Google Scholar] [CrossRef]
- Demirguc-Kunt, Ash, and Enrica Detragiache. 1999. Monitoring banking sector fragility: A multivariate logit approach. In IMF Staff Papers. Washington, DC: International Monetary Fund, vol. 147, pp. 1–27. [Google Scholar]
- Diaconis, Persi, and David A. Freedman. 1980. de finetti’s theorem for markov chains. Annals of Probability 8: 115–30. [Google Scholar] [CrossRef]
- Drehmann, Mathias, and Mikael Juselius. 2014. Evaluating early warning indicators of banking crises: Satisfying policy requirements. International Journal of Forecasting 30: 759–80. [Google Scholar] [CrossRef]
- Duchin, Ran, and Haim Levy. 2009. Markowitz versus the talmudic portfolio diversification strategies. The Journal of Portfolio Management 35: 71–74. [Google Scholar] [CrossRef]
- Embrechts, Paul, Claudia Klüppelberg, and Thomas Mikosch. 2003. Modelling Extremal Events: For Insurance and Finance. Berlin and Heidelberg: Springer Science & Business Media, vol. 33. [Google Scholar]
- Engle, Robert. 2004. Risk and volatility: Econometric models and financial practice. American Economic Review 94: 405–20. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. Econometrica: Journal of the Econometric Society 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert F., and Jeffrey R. Russell. 1997. Forecasting the frequency of changes in quoted foreign exchange prices with the autoregressive conditional duration model. Journal of Empirical Finance 4: 187–212. [Google Scholar] [CrossRef]
- Engle, Robert F., and Jeffrey R. Russell. 1998. Autoregressive conditional duration: A new model for irregularly spaced transaction data. Econometrica 66: 1127–62. [Google Scholar] [CrossRef]
- Filippopoulou, Chryssanthi, Emilios Galariotis, and Spyros Spyrou. 2020. An early warning system for predicting systemic banking crises in the eurozone: A logit regression approach. Journal of Economic Behavior & Organization 172: 344–63. [Google Scholar] [CrossRef]
- Fontanari, Andrea, Iddo Eliazar, Pasquale Cirillo, and Cornelis W. Oosterlee. 2020. Portfolio risk and the quantum majorization of correlation matrices. IMA Journal of Management Mathematics 32: 257–82. [Google Scholar] [CrossRef]
- Fortini, Sandra, and Sonia Petrone. 2012. Hierarchical Reinforced Urn Processes. Statistics & Probability Letters 82: 1521–29. [Google Scholar]
- Gospodinov, Nikolay. 2005. Testing for threshold nonlinearity in short-term interest rates. Journal of Financial Econometrics 3: 344–71. [Google Scholar] [CrossRef]
- Grage, Halfdan, Jan Holst, Georg Lindgren, and Mietek Saklak. 2010. Level crossing prediction with neural networks. Methodology and Computing in Applied Probability 12: 623–45. [Google Scholar] [CrossRef]
- Gresnigt, Francine, Erik Kole, and Philip Hans Franses. 2015. Interpreting financial market crashes as earthquakes: A new early warning system for medium term crashes. Journal of Banking & Finance 56: 123–39. [Google Scholar]
- Haas, Markus, Stefan Mittnik, and Marc S. Paolella. 2004. A new approach to markov-switching garch models. Journal of Financial Econometrics 2: 493–530. [Google Scholar] [CrossRef]
- Hamilton, James D. 1988. Rational-expectations econometric analysis of changes in regime: An investigation of the term structure of interest rates. Journal of Economic Dynamics and Control 12: 385–423. [Google Scholar] [CrossRef]
- Hardy, Godfrey Harold, John Edensor Littlewood, and George Pólya. 1952. Inequalities. Cambridge: Cambridge University Press. [Google Scholar]
- Hawkes, Alan G. 2022. Hawkes jump-diffusions and finance: A brief history and review. The European Journal of Finance 28: 627–41. [Google Scholar] [CrossRef]
- Holopainen, Markus, and Peter Sarlin. 2017. Toward robust early-warning models: A horse race, ensembles and model uncertainty. Quantitative Finance 17: 1933–63. [Google Scholar] [CrossRef]
- Homer, Sidney, and Richard Eugene Sylla. 1996. A History of Interest Rates. New Brunswick: Rutgers University Press. [Google Scholar]
- Hull, John C. 2023. Risk Management and Financial Institutions, 6th ed. New York: Wiley. [Google Scholar]
- Hüsler, Juerg, and Michael Schmidt. 1996. A note on the point processes of rare events. Journal of Applied Probability 33: 654–63. [Google Scholar] [CrossRef]
- International Banker. 2024. Anatomy of Financial Crises. Available online: https://internationalbanker.com/finance/anatomy-of-financial-crises (accessed on 21 October 2024).
- Kaminsky, Graciela, Saul Lizondo, and Carmen M Reinhart. 1998. Leading indicators of currency crises. In IMF Staff Papers. Washington, DC: International Monetary Fund, vol. 45, pp. 1–48. [Google Scholar]
- Keys, Benjamin J., Tanmoy Mukherjee, Amit Seru, and Vikrant Vig. 2009. Financial regulation and securitization: Evidence from subprime loans. Journal of Monetary Economics 56: 700–20. [Google Scholar] [CrossRef]
- Knight, Will. 2017. The Dark Secret at the Heart of AI. Technology Review 120: 54–63. [Google Scholar]
- Laloux, Laurent, Pierre Cizeau, Jean-Philippe Bouchaud, and Marc Potters. 1999. Noise dressing of financial correlation matrices. Physical Review Letters 83: 1467. [Google Scholar] [CrossRef]
- Laloux, Laurent, Pierre Cizeau, Marc Potters, and Jean-Philippe Bouchaud. 2000. Random matrix theory and financial correlations. International Journal of Theoretical and Applied Finance 3: 391–97. [Google Scholar] [CrossRef]
- Lanfranchi, Mirko. 2022. Portfoliorisiko mit Quantum Majorization messen. Bachelor thesis, ZHAW School of Management and Law, Winterthur, Switzerland. [Google Scholar]
- le Bris, David. 2018. What is a market crash? The Economic History Review 71: 480–505. [Google Scholar] [CrossRef]
- Lindgren, Georg. 1975. Prediction from a Random Time Point. The Annals of Probability 3: 412–23. [Google Scholar] [CrossRef]
- Lindgren, Georg. 1980. Model processes in nonlinear prediction with application to detection and alarm. The Annals of Probability 8: 775–92. [Google Scholar] [CrossRef]
- Lo Duca, Marco, and Tuomas A. Peltonen. 2013. Assessing systemic risks and predicting systemic events. Journal of Banking & Finance 37: 2183–95. [Google Scholar] [CrossRef]
- Mahmoud, Hosam M. 2009. Polya Urn Models. New York: CRC Press. [Google Scholar]
- Makridakis, Spyros, Evangelos Spiliotis, and Vassilios Assimakopoulos. 2018. Statistical and machine learning forecasting methods: Concerns and ways forward. PLoS ONE 13: e0194889. [Google Scholar] [CrossRef] [PubMed]
- Malevergne, Yannick, and Didier Sornette. 2006. Extreme Financial Risks: From Dependence to Risk Management. Berlin and Heidelberg: Springer. [Google Scholar]
- McNeil, Alexander J., Ruediger Frey, and Paul Embrechts. 2015. Quantitative Risk Management. Princeton: Princeton University Press. [Google Scholar]
- Montana, J Rhet. 2021. Predicting Stock Market Crashes Using Urns and the Quantum Lorenz Ordering of Correlation Matrices. Master’s thesis, Delft University of Technology, Delft, The Netherlands. Available online: http://resolver.tudelft.nl/uuid:ccdb64e3-1b01-4c31-b72c-0dfbcbffa8b0 (accessed on 16 December 2024).
- Monteiro, Magda, Isabel Pereira, and Manuel G. Scotto. 2008. Optimal alarm systems for count processes. Communications in Statistics-Theory and Methods 37: 3054–76. [Google Scholar] [CrossRef]
- Muliere, Pietro, Piercesare Secchi, and Stephen G. Walker. 2000. Urn Schemes and Reinforced Random Walks. Stochastic Processes and Their Applications 88: 59–78. [Google Scholar] [CrossRef]
- Muliere, Pietro, Piercesare Secchi, and Stephen G. Walker. 2003. Reinforced Random Processes in Continuous Time. Stochastic Processes and Their Applications 104: 117–30. [Google Scholar] [CrossRef]
- Nelsen, Roger B. 1997. Dependence and order in families of archimedean copulas. Journal of Multivariate Analysis 60: 111–22. [Google Scholar] [CrossRef]
- Nelsen, Roger B. 2006. An Introduction to Copulas. New York: Springer. [Google Scholar]
- Olkin, Ingram, and Albert W. Marshall. 2016. Inequalities: Theory of Majorization and Its Applications. Cambridge: Academic Press, vol. 143. [Google Scholar]
- Oosterlee, Cornelis W., and Lech A. Grzelak. 2019. Mathematical Modeling and Computation in Finance: With Exercises and Python and Matlab Computer Codes. Singapore: World Scientific Publishing Europe Limited. [Google Scholar]
- Park, Andreas, and Hamid Sabourian. 2011. Herding and contrarian behavior in financial markets. Econometrica 79: 973–1026. [Google Scholar] [CrossRef][Green Version]
- Peluso, Stefano, Antonietta Mira, and Pietro Muliere. 2015. Reinforced urn processes for credit risk models. Journal of Econometrics 184: 1–12. [Google Scholar] [CrossRef]
- Petropoulos, Fotios, Daniele Apiletti, Vassilios Assimakopoulos, Mohamed Zied Babai, Devon K. Barrow, Souhaib Ben Taieb, Christoph Bergmeir, Ricardo J. Bessa, Jakub Bijak, John E. Boylan, and et al. 2022. Forecasting: Theory and practice. International Journal of Forecasting 38: 705–871. [Google Scholar] [CrossRef]
- Pfann, Gerard A., Peter C. Schotman, and Rolf Tschernig. 1996. Nonlinear interest rate dynamics and implications for the term structure. Journal of Econometrics 74: 149–76. [Google Scholar] [CrossRef]
- Qin, Yao, Dongjin Song, Haifeng Chen, Wei Cheng, Guofei Jiang, and Garrison Cottrell. 2017. A dual-stage attention-based recurrent neural network for time series prediction. arXiv arXiv:1704.02971. [Google Scholar]
- Rapach, David E., Jack K. Strauss, and Guofu Zhou. 2010. Out-of-sample equity premium prediction: Combination forecasts and links to the real economy. The Review of Financial Studies 23: 821–62. [Google Scholar] [CrossRef]
- Sarlin, Peter, and Tuomas A. Peltonen. 2013. Mapping the state of financial stability. Journal of International Financial Markets, Institutions and Money 26: 46–76. [Google Scholar] [CrossRef]
- Sornette, Didier. 2003. Critical market crashes. Physics Reports 378: 1–98. [Google Scholar] [CrossRef]
- Sornette, Didier. 2017. Why Stock Markets Crash: Critical Events in Complex Financial Systems. Princeton: Princeton Science Library, Princeton University Press. [Google Scholar]
- Sornette, Didier, and Andres Johansen. 2006. Endogenous versus exogenous crashes in financial markets. Brussels Economic Review 53: 201–53. [Google Scholar]
- Souto Arias, Luis A., and Pasquale Cirillo. 2021. Joint and survivor annuity valuation with a bivariate reinforced urn process. Insurance: Mathematics and Economics 99: 174–89. [Google Scholar] [CrossRef]
- Souto Arias, Luis A., Pasquale Cirillo, and Cornelis W. Oosterlee. 2025. The Heston-Queue-Hawkes process: A new self-exciting jump-diffusion model for options pricing, and an extension of the COS method for discrete distributions. Journal of Computational and Applied Mathematics 454: 116177. [Google Scholar] [CrossRef]
- Svensson, Anders, Jan Holst, R. Lindquist, and Georg Lindgren. 1996. Optimal prediction of catastrophes in autoregressive moving-average processes. Journal of Time Series Analysis 17: 511–31. [Google Scholar] [CrossRef]
- Taleb, Nassim Nicholas, Yaneer Bar-Yam, and Pasquale Cirillo. 2020. On single point forecasts for fat-tailed variables. International Journal of Forecasting 38: 413–22. [Google Scholar] [CrossRef]
- Tanaka, Katsuyuki, Takuji Kinkyo, and Shigeyuki Hamori. 2016. Random forests-based early warning system for bank failures. Economics Letters 148: 118–21. [Google Scholar] [CrossRef]
- Taylor, Stephen J. 2008. Modelling Financial Time Series. Singapore: World Scientific. [Google Scholar]
- Turkman, Maria Antonia Amaral, and Kamil F. Turkman. 1990. Optimal alarm systems for autoregressive processes: A bayesian approach. Computational Statistics & Data Analysis 10: 307–14. [Google Scholar] [CrossRef]
- Tölö, Eero. 2020. Predicting systemic financial crises with recurrent neural networks. Journal of Financial Stability 49: 100746. [Google Scholar] [CrossRef]
- World Economic Forum. 2020. This Is the Impact of the Coronavirus on Business. Available online: https://www.weforum.org/agenda/2020/02/why-is-coronavirus-a-global-business-risk/ (accessed on 5 October 2021).
- Zheng, Haitao, Ishwar V. Basawa, and Somnath Datta. 2006. Inference for pth-order random coefficient integer-valued autoregressive processes. Journal of Time Series Analysis 27: 411–40. [Google Scholar] [CrossRef]
- Zumbach, Gilles. 2011. Empirical properties of large covariance matrices. Quantitative Finance 11: 1091–102. [Google Scholar] [CrossRef]

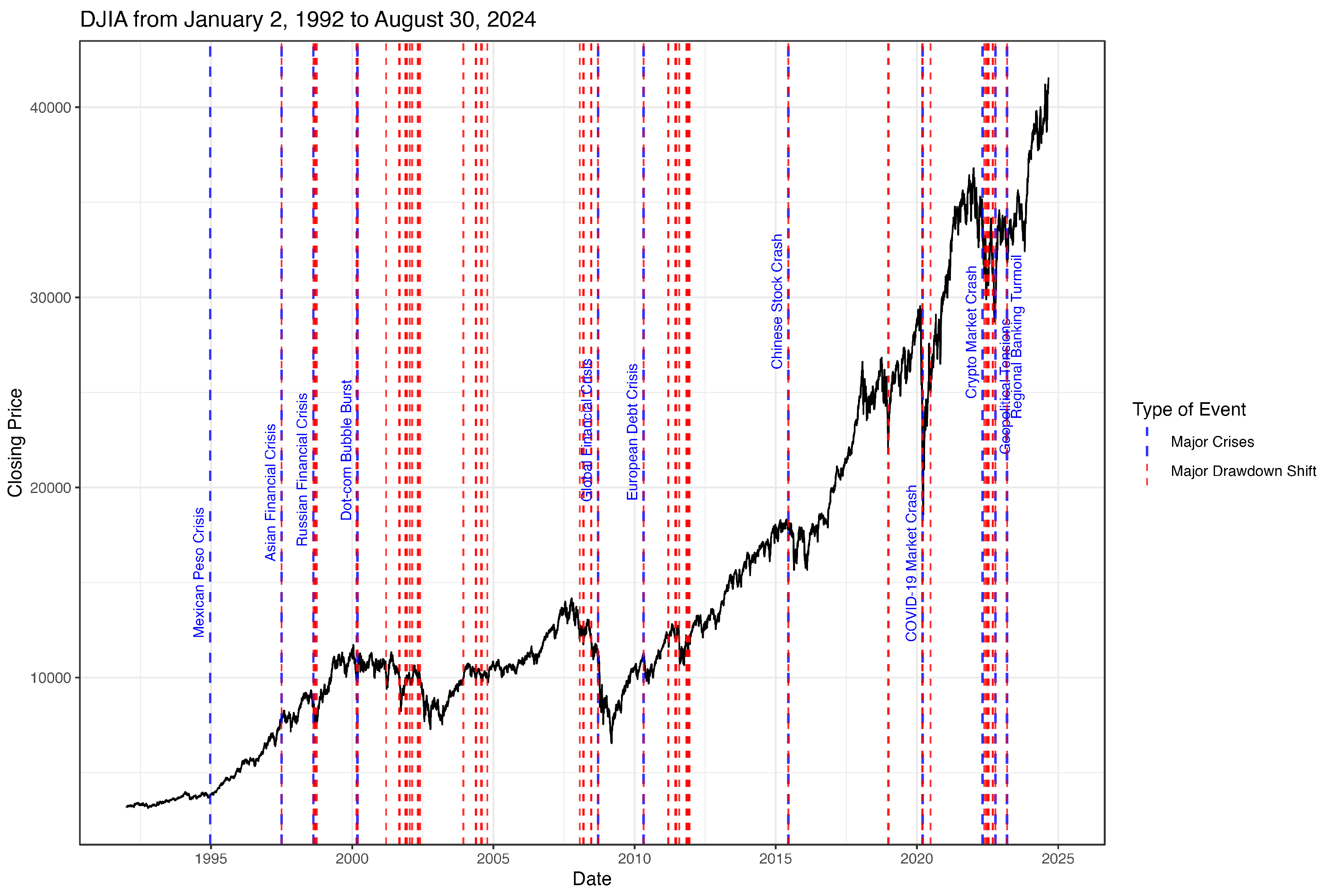
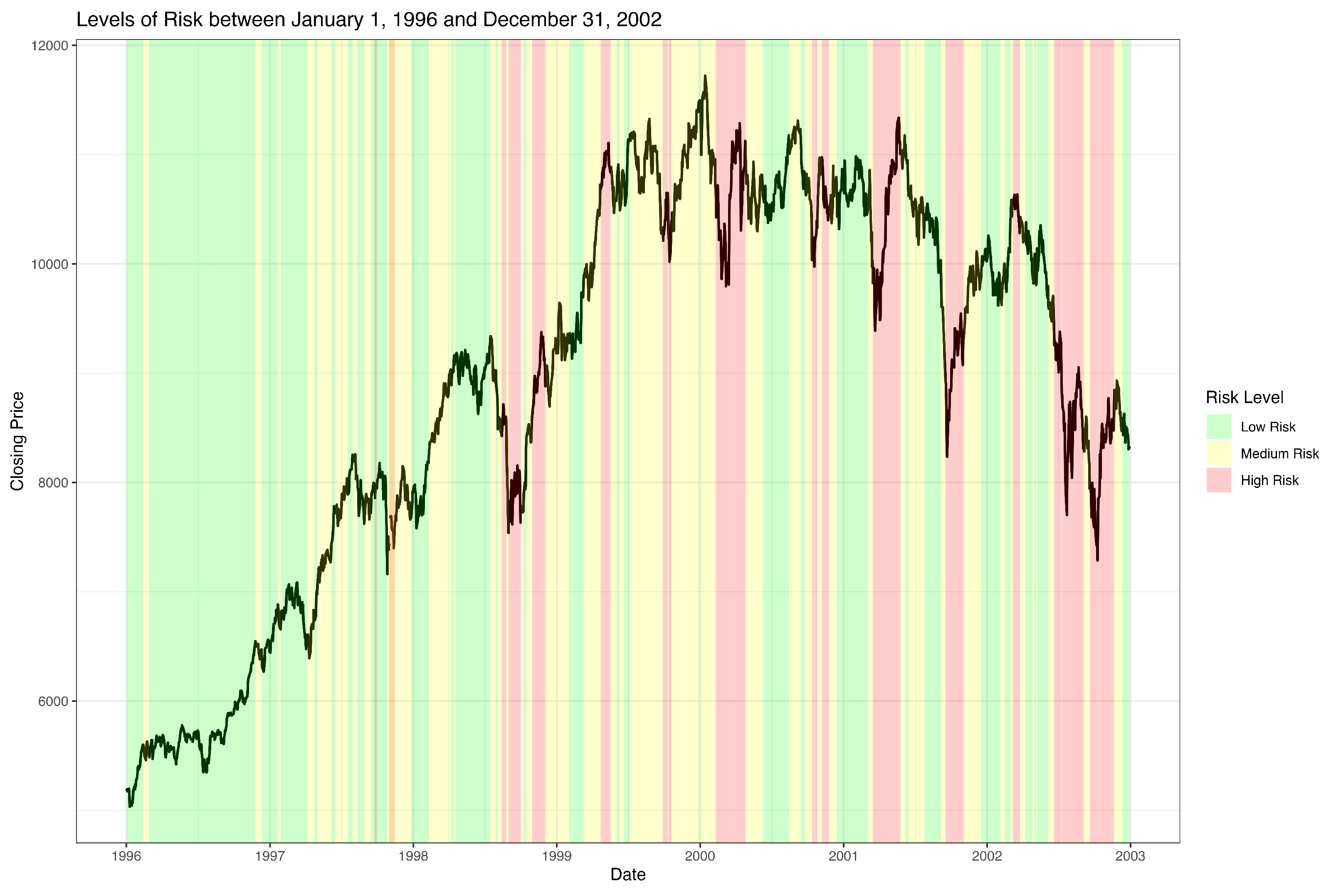
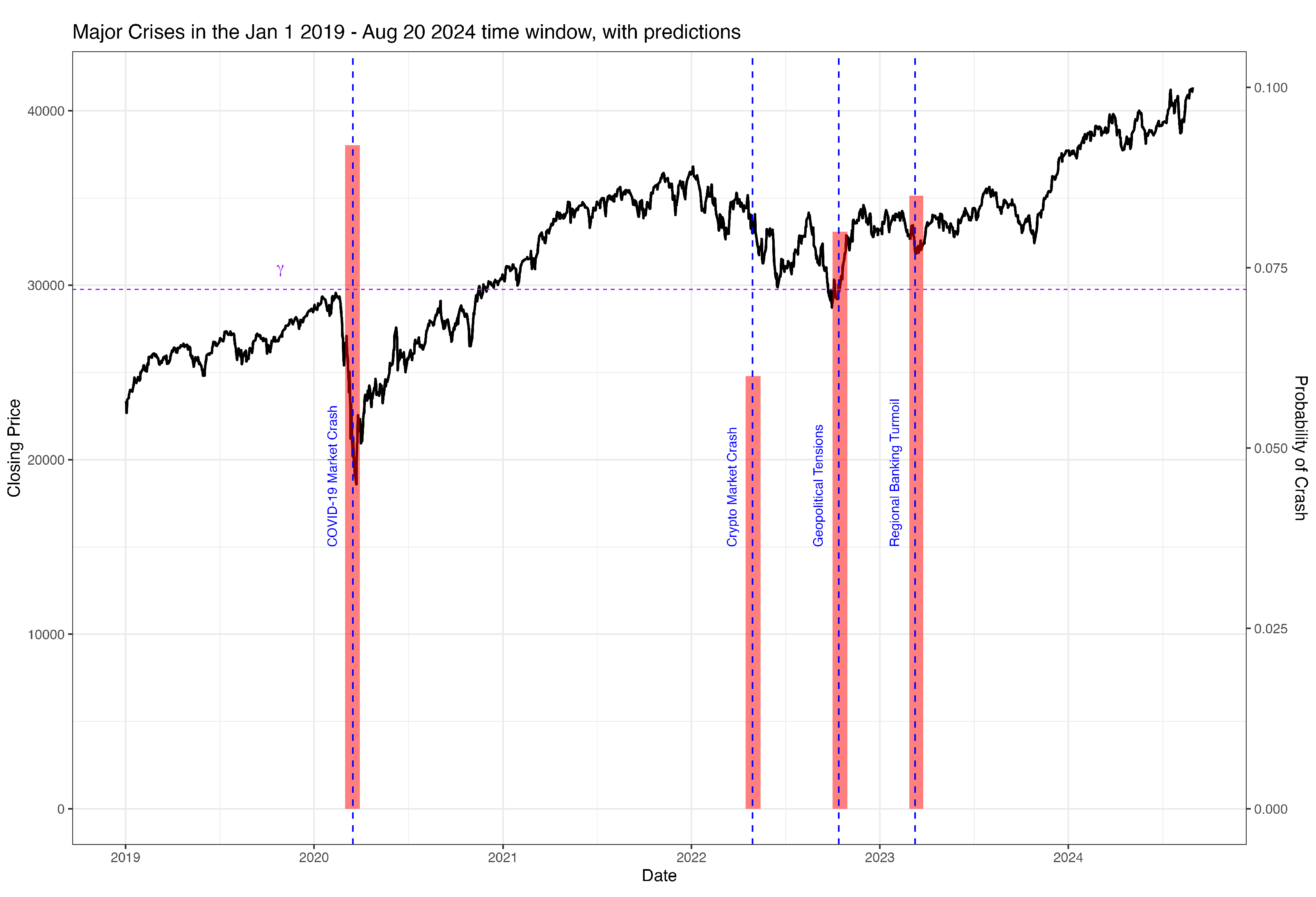
| Parameter | 4-Month () | 8-Month () | 12-Month () |
|---|---|---|---|
| 7 | 8 | 2 | |
| w | 0 | 0 | 2 |
| Operating Characteristic | 4-Month () | 8-Month () | 12-Month () |
|---|---|---|---|
| Number of correct non-alarms | 13 | 17 | 20 |
| Number of correct alarms | 5 | 8 | 8 |
| Number of false alarms | 9 | 5 | 2 |
| Number of undetected crashes | 6 | 3 | 3 |
| Model | Correct Alarms (%) | False Alarms (%) |
|---|---|---|
| Quantum Alarm System () | 72.7 [72.7–72.7] | 9.1 [9.1–13.6] |
| Time-Series Models (ARIMA(2,1,1)) | 45.4 (40–60) | 45.4 (30–50) |
| Threshold-Based Early Warning Systems | 54.5 (45–65) | 50.0 (30–50) |
| Logit/Probit Early Warning Systems | (55–75) | (20–40) |
| Advanced ML/Ensemble Methods | (70–85) | (15–25) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montana, J.R.; Souto Arias, L.A.; Cirillo, P.; Oosterlee, C.W. Quantum Majorization in Market Crash Prediction. Risks 2024, 12, 204. https://doi.org/10.3390/risks12120204
Montana JR, Souto Arias LA, Cirillo P, Oosterlee CW. Quantum Majorization in Market Crash Prediction. Risks. 2024; 12(12):204. https://doi.org/10.3390/risks12120204
Chicago/Turabian StyleMontana, J Rhet, Luis A. Souto Arias, Pasquale Cirillo, and Cornelis W. Oosterlee. 2024. "Quantum Majorization in Market Crash Prediction" Risks 12, no. 12: 204. https://doi.org/10.3390/risks12120204
APA StyleMontana, J. R., Souto Arias, L. A., Cirillo, P., & Oosterlee, C. W. (2024). Quantum Majorization in Market Crash Prediction. Risks, 12(12), 204. https://doi.org/10.3390/risks12120204









