Nonparametric Testing for Information Asymmetry in the Mortgage Servicing Market
Abstract
1. Introduction
2. Overview of the Mortgage Servicing Activity
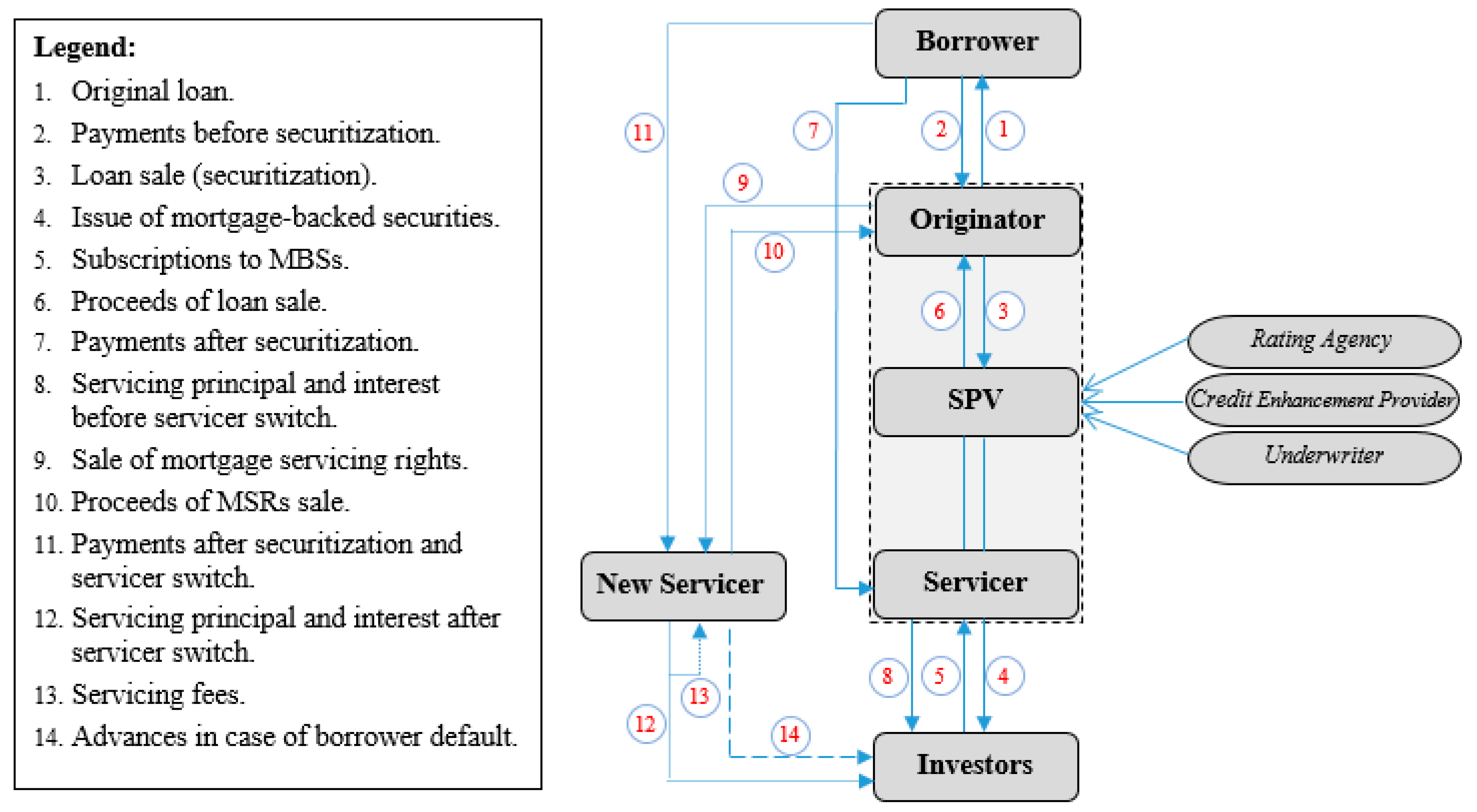
2.1. Representation of Mortgage Servicing Process
2.2. Cash Flows and Risks of the Servicer 1
3. The Nonparametric Estimation Framework
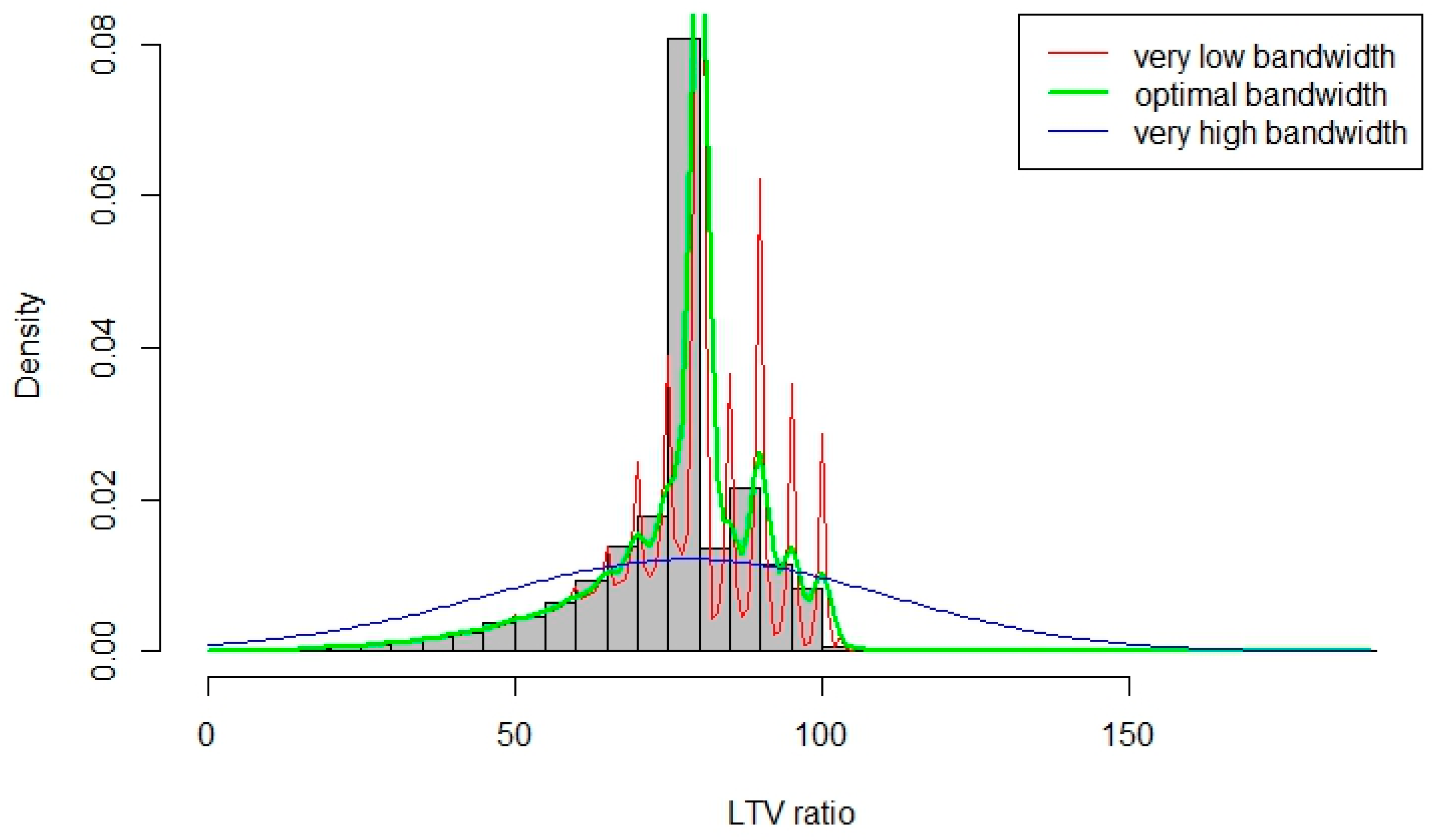
3.1. Motivation for Nonparametric Methods
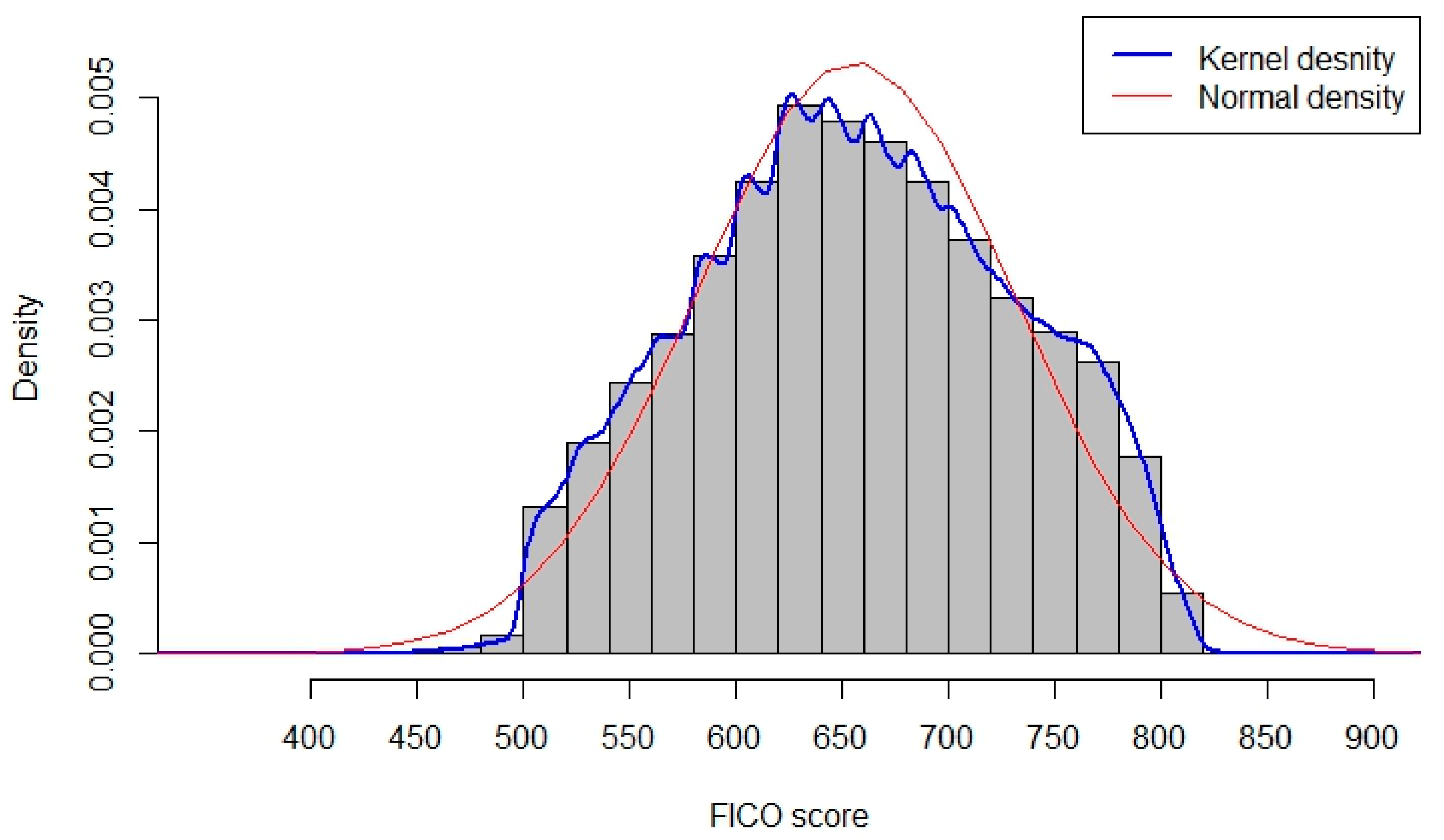
3.2. Multivariate Kernel Density Estimation with Mixed Data Types
3.3. Conditional Kernel Density Estimation for Information Asymmetry Test
4. Nonparametric Information Asymmetry Test
5. Data, Variables, and Summary Statistics
5.1. Data Source and Sample Construction
5.2. Variables and Hypotheses
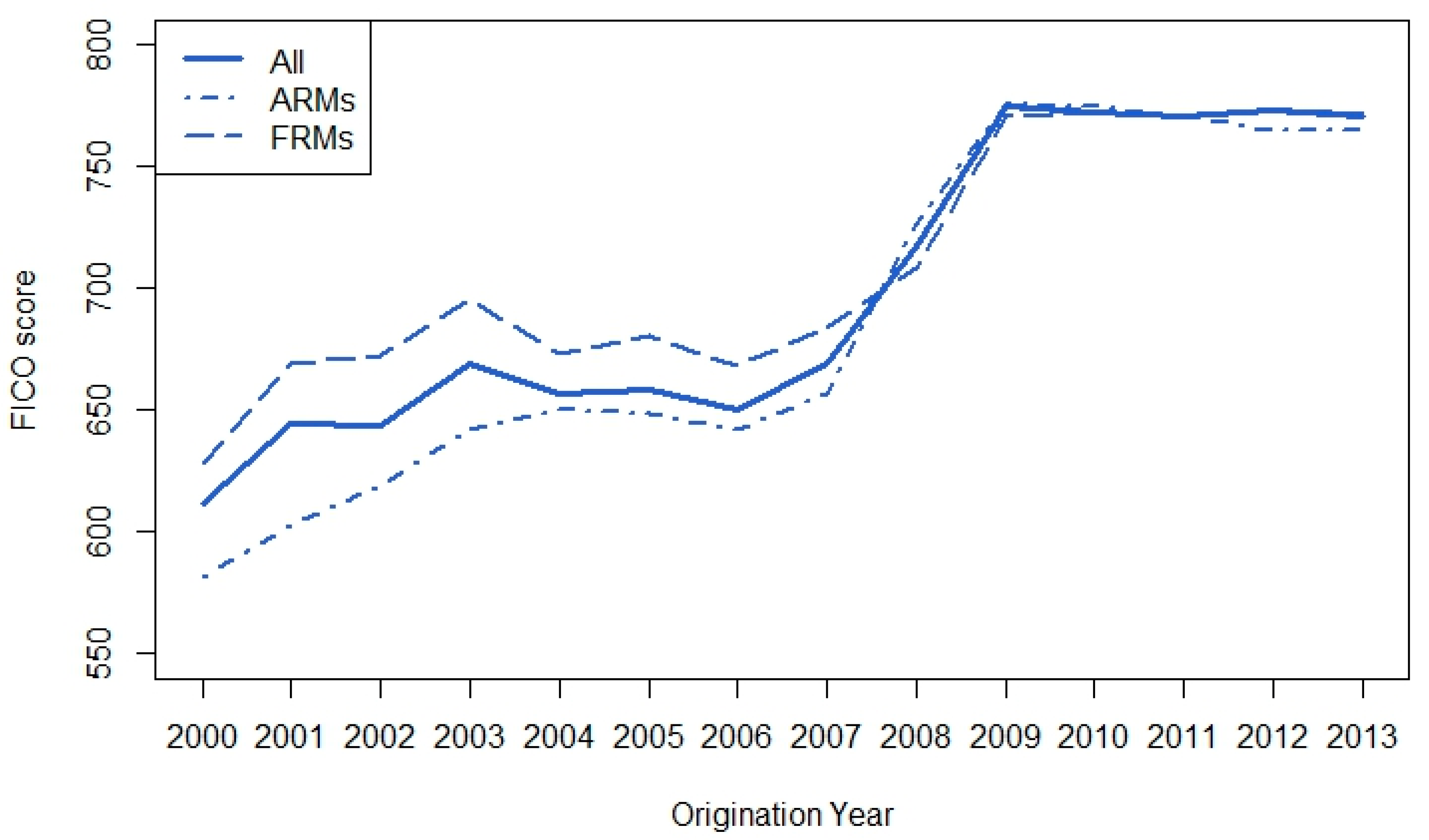
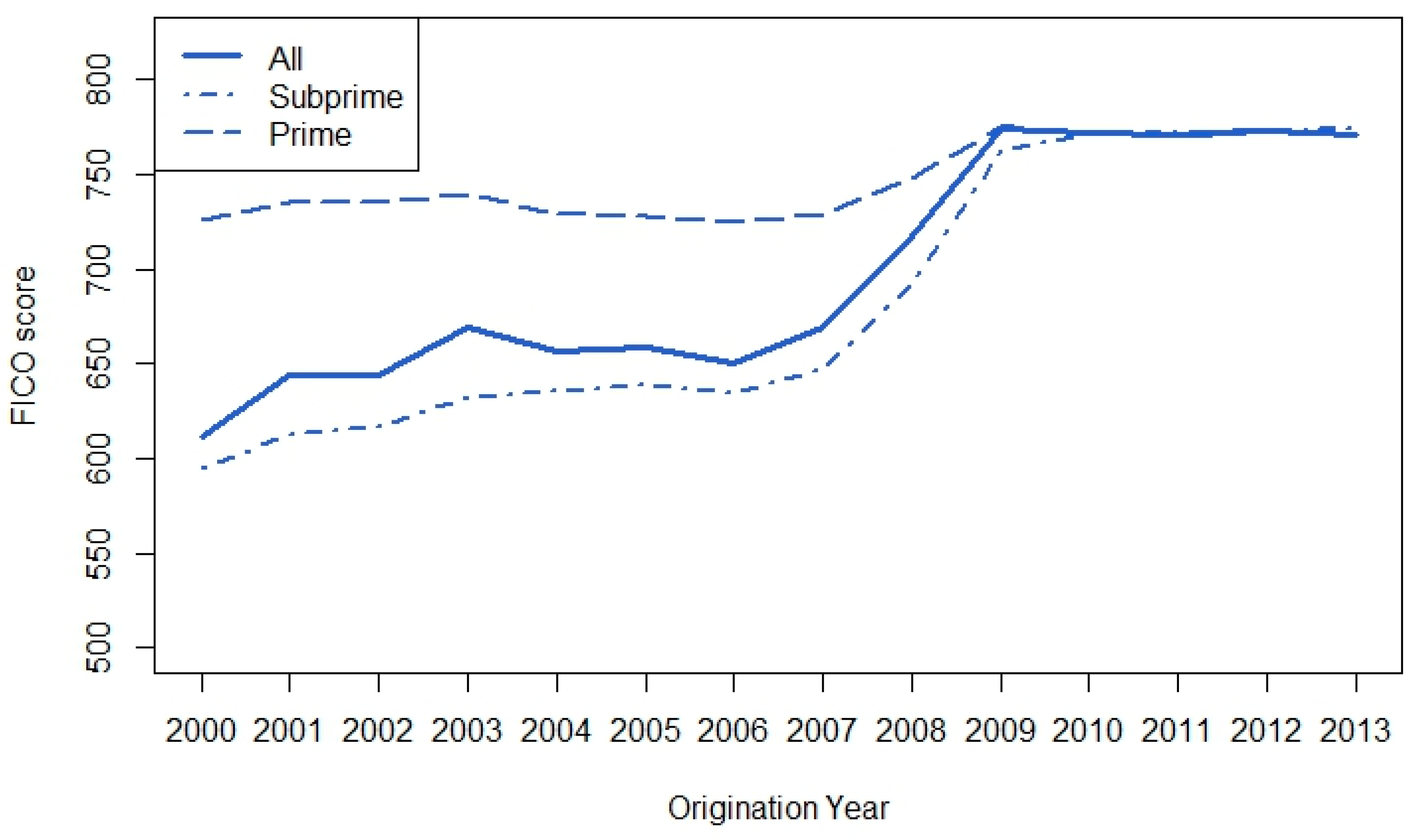
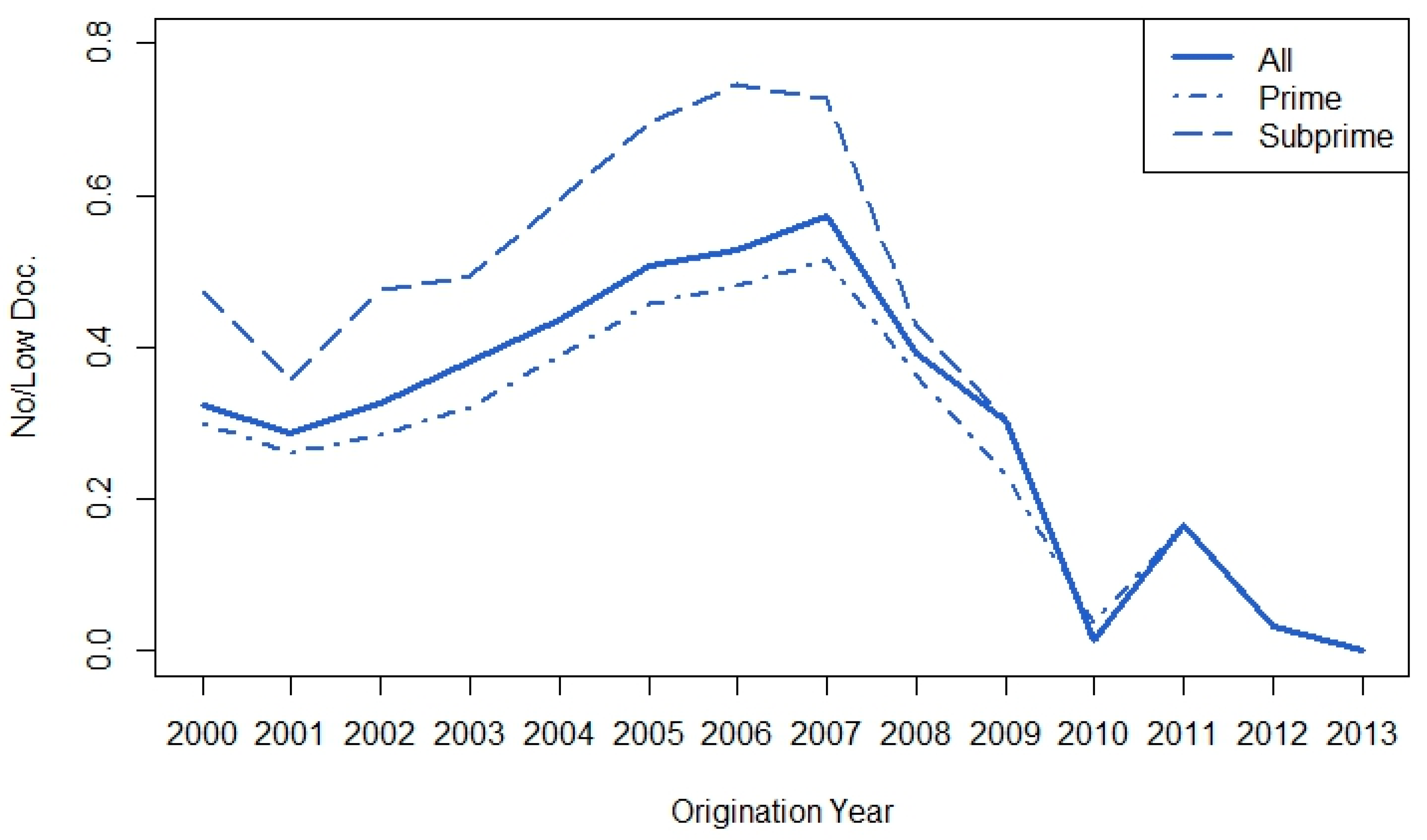
5.3. Descriptive Statistics
6. Empirical Results
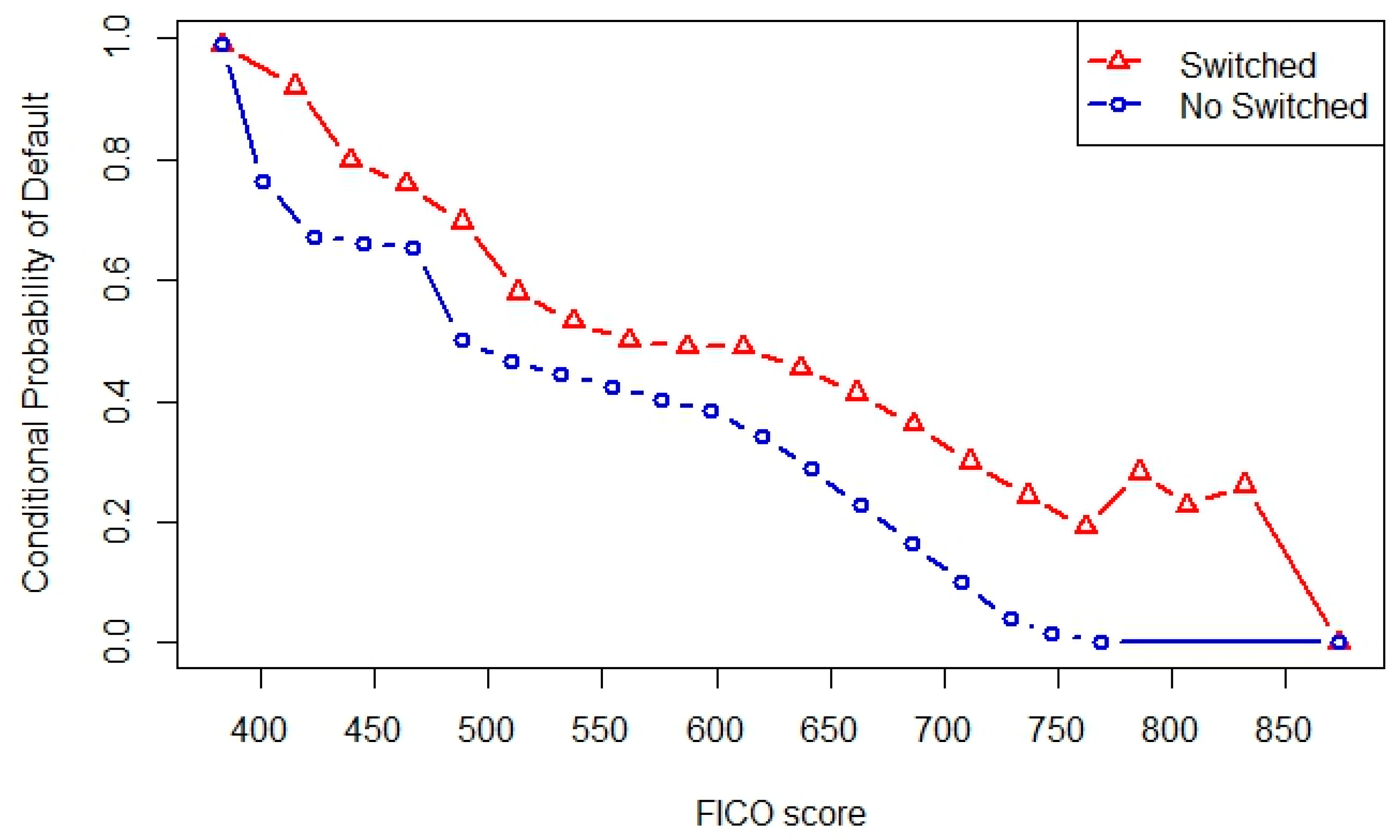
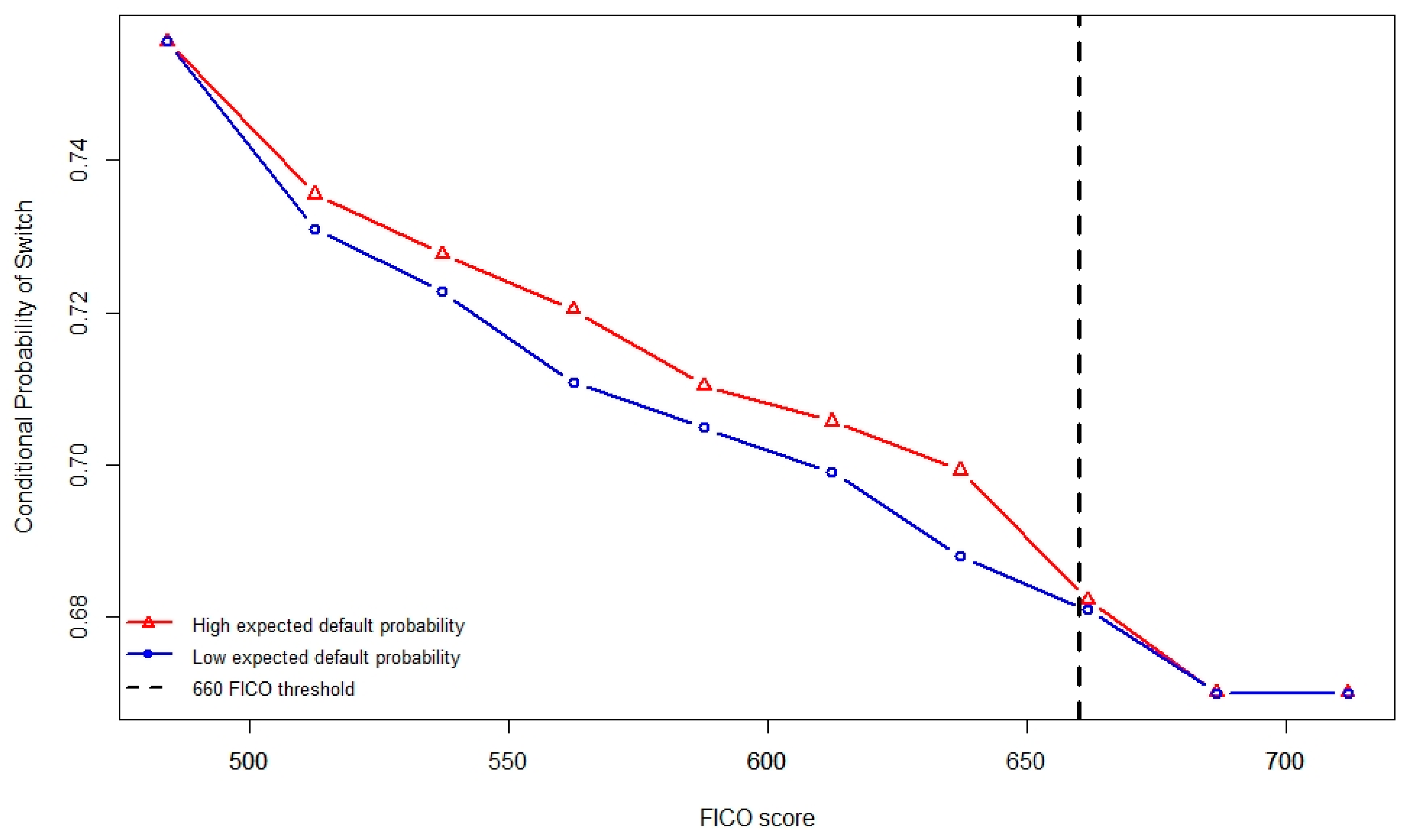
6.1. Nonparametric Methods
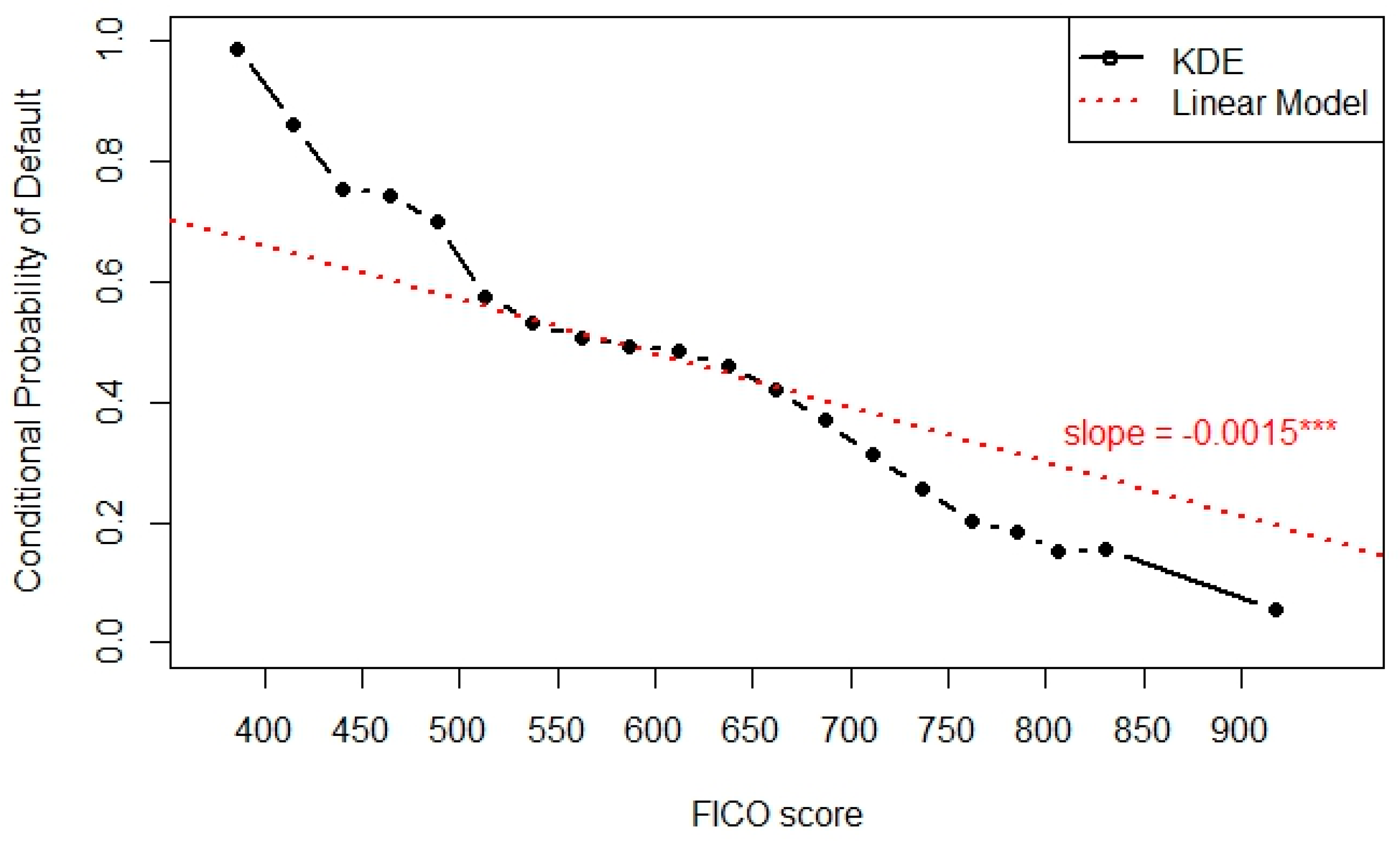
6.1.1. The Chiappori and Salanié (2000) Method
6.1.2. The Su and Spindler (2013) Method
6.2. Robustness Checks: Results of the Parametric Methods
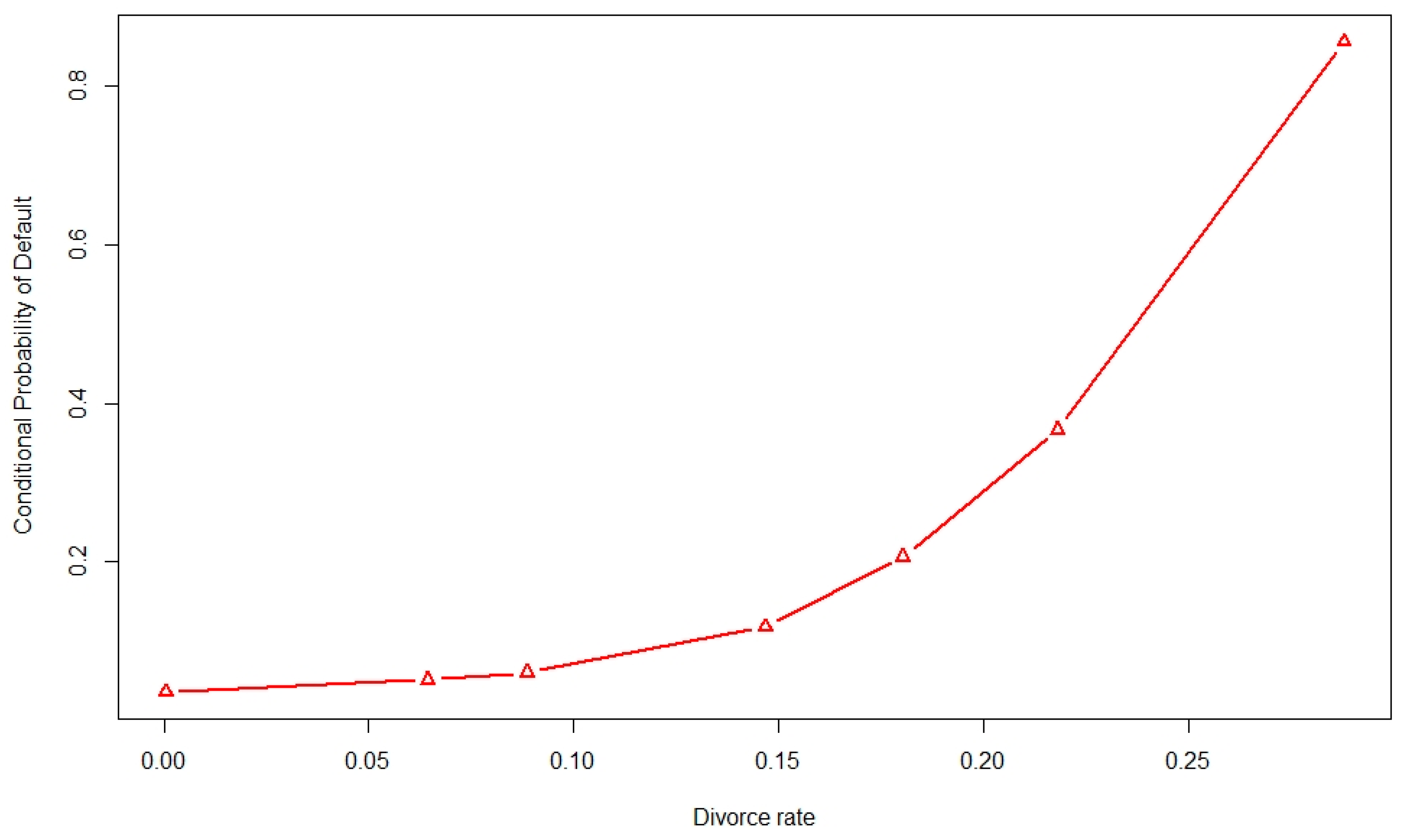
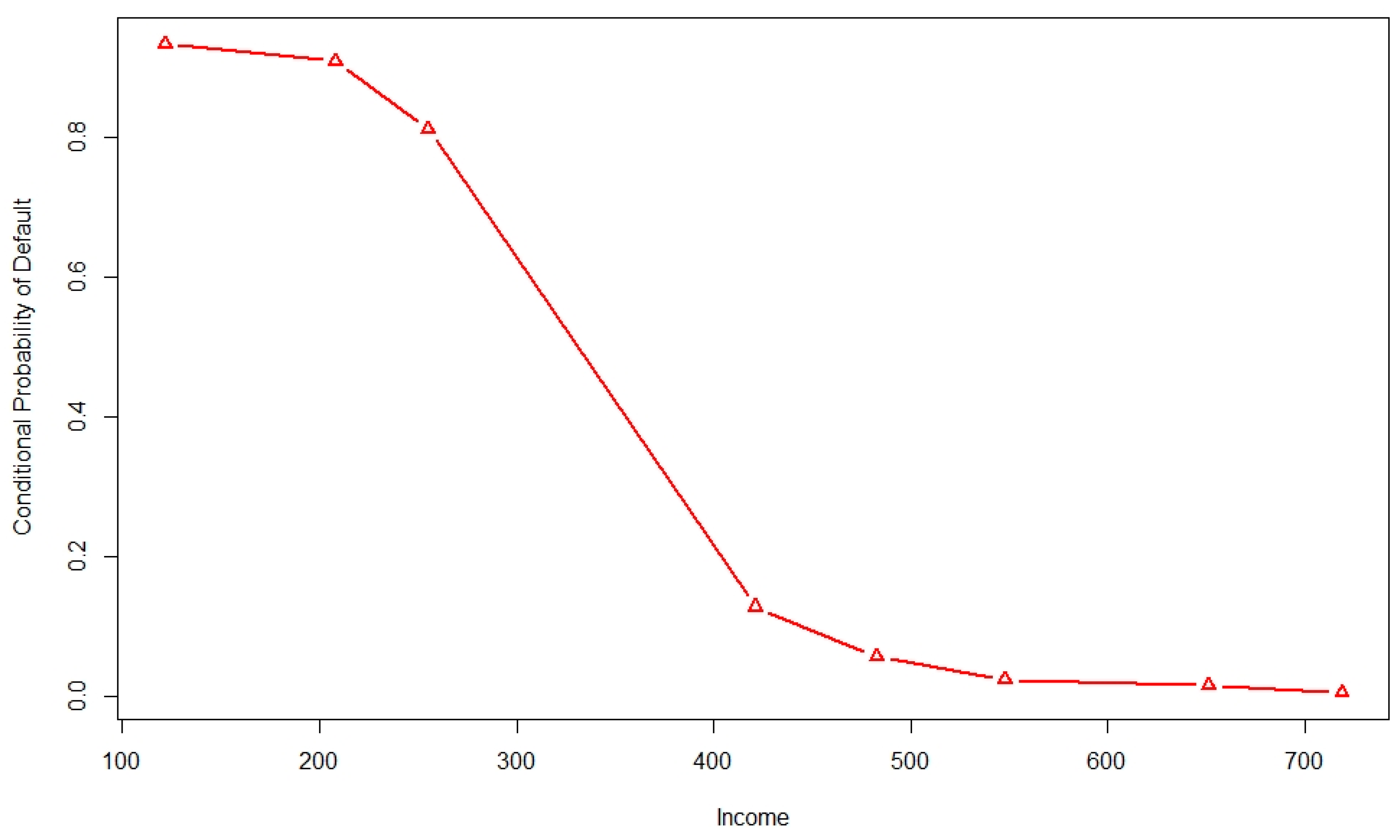
6.3. Causality: Results of the Two-Stage Nonparametric Framework
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Name | Type | Description | Source |
|---|---|---|---|
| Switch Servicer | Binary | Denotes the decision of the originating lender to sell or to retain the mortgage servicing right of a given loan. Takes the value of 1 if the originator decides to sell the underlying MSR and 0 if he retains the MSR and continues servicing the loan. | MBSData |
| Default | Binary | Denotes mortgage default. Takes the value of 1 if the borrower of a given mortgage misses three or more consecutive monthly payments (i.e., when the mortgage status is first labeled as 90+ days delinquent). | MBSData |
| FICO score | Continuous | The borrower’s FICO score created and calculated by the Fair Isaac Corporation. It measures the credit quality of borrowers by taking into account an individual’s payment history, length of credit history, current level of indebtedness, and types of credit used by the borrower. | MBSData |
| FICO660 | Binary | Takes the value of 1 if the borrower’s FICO score is above 660 and 0 otherwise. In general, a FICO score above 660 indicates that the individual has a good credit history. | MBSData |
| LTV | Continuous | The loan-to-value ratio calculated as the percentage of the first-lien mortgage to the total value of the property. It is one of the key risk factors used by U.S. lenders when qualifying borrowers for a mortgage. A high LTV ratio mirrors a loan with a low down payment for which the borrower has little equity stake in the property. | MBSData |
| LTV80 | Binary | Takes the value of 1 if the LTV ratio is equal to or higher than 80%. | MBSData |
| DTI | Continuous | The debt-to-income ratio calculated as the fraction of monthly mortgage payments to the borrower’s monthly income. DTI measures the borrower’s ability to honor periodic debt payments as it compares debt payments to the borrower’s income. | MBSData |
| No/Low doc. | Binary | Takes the value of 1 if the documentation level is labelled “missing” or “low”, and 0 otherwise. No- or low documentation mortgages designate loans for which the lender did not gather a sufficient level of information on the borrower’s reliability and credit worthiness. | MBSData |
| ln Amount | Continuous | The natural logarithm of the initial balance of the mortgage. Does not include either interest, taxes, or fees. | MBSData |
| Interest | Continuous | The interest rate was initially applied at the time of original underwriting. Higher interest rates usually reflect loans granted to borrowers with inferior credit quality, which increase their monthly debt payments. | MBSData |
| ARM | Binary | Takes the value of 1 if the loan type is an adjustable-rate mortgage and 0 if fixed-rate mortgage. ARM indicates whether the interest rate of a given mortgage is fluctuating over time based on a benchmark index plus an additional spread, called an ARM margin. | MBSData |
| ARM margin | Continuous | A fixed component added to the interest rate for ARM mortgages. The margin is constant throughout the lifetime of the mortgage, while the benchmark index fluctuates over time according to general market conditions. | MBSData |
| Balloon | Binary | Takes the value of 1 if the mortgage has a balloon payment structure, 0 otherwise. Balloon mortgagors make only interest payments during the lifetime of the loan. At the term end, the borrower repays the entire principal at once. | MBSData |
| GSE conforming | Binary | Takes the value of 1 if the lender follows the GSEs’ lending guidelines and 0 otherwise. Following the GSEs’ recommendations, we classify a mortgage as conforming if the borrower’s FICO score is above 660 and the loan amount is below the conforming loan limit in place at the time of origination and the LTV is either less than 80% or the loan has private mortgage insurance in the case that the LTV ratio is above 80%. Since conforming loans meet the GSE lending standards, the conforming dummy variable indicates whether the mortgage was eligible to be sold to the GSEs at origination. | MBSData |
| Subprime | Binary | Denotes subprime mortgages. A mortgage is labelled “Subprime” at origination if the borrower’s FICO score is lower than 580 or the LTV ratio is higher than 90%. | MBSData |
| Prime | Binary | Denotes prime mortgages. A mortgage is considered as “Prime” if the borrower’s FICO score is higher than 660 and the LTV ratio is lower than 80%. | MBSData |
| Prep. Penalty | Binary | Equals to 1 if the mortgage contract includes a prepayment penalty clause and 0 otherwise. Accordingly, the borrower will pay a penalty if he chooses to pre-pay the loan within a certain time period. The penalty is based on the remaining mortgage balance and the number of months worth of interest. | MBSData |
| Purchase | Binary | Takes the value of 1 if the loan purpose is labeled “Purchase” a property and 0 otherwise. | MBSData |
| Refin. cash-out | Binary | Equals to 1 if the loan is granted for the purpose of refinancing an existing loan with “cash-out”. A cash-out refinance mortgage is a new loan in which the amount is greater than the existing mortgage amount, which will be refinanced. Since the borrower refinances for more than the amount owed, he/she takes the difference in cash. | MBSData |
| Refin. no cash-out | Binary | Equals to 1 if the loan is granted for the purpose of refinancing an existing loan with “no-cash-out”. A no-cash-out refinance mortgage is a new loan in which the amount is equal to or lower than the existing mortgage amount. The main purpose of such loans is usually to lower the interest rate charge on the loan. | MBSData |
| Service fee | Continuous | The servicing fee that the servicer of the deal charges as compensation for costs he bears. It is expressed as a fixed percentage of the declining balance of the mortgage. | MBSData |
| Age at default | Continuous | The age-at-default is measured as the total number of months since origination when the default is first recorded. | MBSData |
| Default N | Binary | Denoting the fraction of mortgages that default within N months since origination. | MBSData |
| Income | Continuous | The annual growth rate of personal income, which is defined as an individual’s total earnings from wages, investment interest, and other sources. The seasonally unadjusted U.S. real disposable (after deducting tax) personal income data is retrieved from the US. Bureau of Economic Analysis’ web site. | bea.gov |
| Divorce | Continuous | The annual divorce rate calculated as the ratio of the number of marriages contracted and ended in divorce to the number of all marriages contracted in the same year. The divorce rate is commonly used as an indicator of social stress in the society. The seasonally unadjusted divorce rate is retrieved from the U.S. Census Bureau’s web site. | census.gov |
| GDP growth | Continuous | The annual growth rate of the U.S. Real Gross Domestic Product. The real GDP is collected from the Federal Reserve Bank of St. Louis’ web site. | stlouisfed.org |
| HPI growth | Continuous | The annual growth rate of the House Price Index for the U.S. We use the seasonally unadjusted purchase-only HPI index retrieved from the Federal Reserve Bank of St. Louis’ web site. | stlouisfed.org |
| σ interest | Continuous | The interest rate volatility calculated as the volatility on the 1-Year Treasury Constant Maturity Rate over the 24 months before origination. The monthly seasonally unadjusted treasury rate is collected from the Federal Reserve Bank of St. Louis’ web site. | stlouisfed.org |
| Credit spread | Continuous | The yield spread between AAA and Baa bond indexes. It is calculated as the interest rate difference between Moody’s Aaa and Baa Corporate Bond Yields. Both variables are seasonally unadjusted, recorded on a monthly basis, and retrieved from the Federal Reserve Bank of St. Louis’ web site. | stlouisfed.org |
| Judicial | Binary | Takes the value of 1 if the state laws require judicial procedures to foreclose on a mortgage and 0 if not. The variable is compiled based on information from the National Center for State Courts’ web site. | ncsc.org |
| SRR | Binary | Stands for Statutory Right of Redemption and takes the value of 1 if the state has statutory redemption laws. The variable is compiled based on information from the National Center for State Courts’ web site. | ncsc.org |
| Origination Year | Volume (in %) | Volume (in $B) | FICO Score | FICO. 660 | LTV Ratio | LTV. 80 | DTI | No/Low Doc. | Interest Rate | Balloon | ARM | ARM Margin | GSE Conf. | Prep. Penalty |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All period | 100.0 | 1509.1 | 657.12 | 0.48 | 76.93 | 0.60 | 38.65 | 0.47 | 6.97 | 0.06 | 0.63 | 5.00 | 0.17 | 0.49 |
| 2000 | 1.05 | 8.87 | 615.49 | 0.31 | 78.20 | 0.62 | 38.65 | 0.34 | 10.08 | 0.07 | 0.34 | 6.13 | 0.17 | 0.41 |
| 2001 | 2.47 | 32.07 | 648.33 | 0.47 | 76.87 | 0.56 | 37.74 | 0.29 | 8.56 | 0.03 | 0.36 | 6.09 | 0.23 | 0.33 |
| 2002 | 5.74 | 69.08 | 644.97 | 0.42 | 77.47 | 0.58 | 37.84 | 0.33 | 7.92 | 0.02 | 0.54 | 5.92 | 0.21 | 0.38 |
| 2003 | 11.46 | 170.89 | 670.12 | 0.56 | 75.14 | 0.51 | 36.95 | 0.38 | 6.60 | 0.01 | 0.49 | 5.18 | 0.25 | 0.31 |
| 2004 | 16.93 | 232.68 | 657.75 | 0.49 | 77.60 | 0.60 | 36.81 | 0.44 | 6.30 | 0.00 | 0.70 | 4.75 | 0.19 | 0.52 |
| 2005 | 27.28 | 411.36 | 658.81 | 0.49 | 76.97 | 0.62 | 38.33 | 0.51 | 6.51 | 0.02 | 0.69 | 4.91 | 0.16 | 0.53 |
| 2006 | 27.11 | 422.92 | 650.45 | 0.44 | 77.44 | 0.63 | 39.90 | 0.52 | 7.44 | 0.15 | 0.66 | 5.07 | 0.12 | 0.57 |
| 2007 | 7.79 | 153.39 | 668.92 | 0.56 | 75.92 | 0.56 | 39.17 | 0.57 | 7.32 | 0.12 | 0.52 | 4.50 | 0.15 | 0.47 |
| 2008 | 0.02 | 0.60 | 717.06 | 0.80 | 73.25 | 0.44 | 36.59 | 0.40 | 7.16 | 0.03 | 0.48 | 3.13 | 0.03 | 0.17 |
| 2009 | 0.00 | 0.21 | 774.60 | 1.00 | 53.11 | 0.06 | 36.00 | 0.30 | 4.79 | 0.00 | 0.83 | 2.04 | 0.03 | 0.00 |
| 2010 | 0.01 | 0.43 | 772.33 | 1.00 | 61.78 | 0.17 | 32.48 | 0.02 | 4.93 | 0.00 | 0.08 | 1.64 | 0.01 | 0.21 |
| 2011 | 0.02 | 1.17 | 770.62 | 1.00 | 66.60 | 0.23 | 32.98 | 0.17 | 4.72 | 0.00 | 0.06 | 1.83 | 0.01 | 0.16 |
| 2012 | 0.06 | 2.79 | 773.08 | 1.00 | 66.42 | 0.20 | 34.00 | 0.03 | 4.06 | 0.00 | 0.02 | 2.25 | 0.00 | 0.13 |
| 2013 | 0.06 | 2.67 | 771.14 | 1.00 | 66.24 | 0.19 | 30.80 | 0.00 | 3.91 | 0.00 | 0.01 | 2.53 | 0.00 | 0.01 |
| All | Payment Type | Loan Type | Financial Crisis | Default | Switch Servicer | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| FRM | ARM | Prime | Subprime | Before | After | No | Yes | No | Yes | ||
| FICO score | 657.12 | 678.00 | 644.84 | 730.93 | 634.87 | 655.92 | 671.02 | 669.62 | 635.77 | 660.62 | 654.23 |
| FICO.660 | 0.48 | 0.61 | 0.41 | 1.00 | 0.33 | 0.48 | 0.57 | 0.55 | 0.37 | 0.51 | 0.46 |
| LTV | 76.93 | 73.89 | 78.73 | 63.48 | 80.99 | 77.04 | 75.72 | 74.86 | 80.48 | 76.49 | 77.30 |
| LTV.80 | 0.60 | 0.48 | 0.67 | 0.00 | 0.78 | 0.60 | 0.55 | 0.53 | 0.72 | 0.58 | 0.61 |
| DTI | 38.65 | 37.64 | 39.08 | 35.71 | 39.10 | 38.60 | 39.09 | 37.63 | 39.91 | 38.02 | 38.95 |
| No/Low doc. | 0.47 | 0.46 | 0.48 | 0.63 | 0.43 | 0.46 | 0.55 | 0.45 | 0.50 | 0.49 | 0.45 |
| Interest rate | 6.97 | 7.10 | 6.89 | 5.57 | 7.39 | 6.94 | 7.26 | 6.71 | 7.41 | 6.86 | 7.05 |
| Balloon | 0.06 | 0.04 | 0.08 | 0.01 | 0.08 | 0.06 | 0.12 | 0.03 | 0.11 | 0.04 | 0.08 |
| ARM | 0.63 | 0.00 | 1.00 | 0.45 | 0.68 | 0.64 | 0.52 | 0.59 | 0.70 | 0.59 | 0.66 |
| ARM margin | 5.00 | . | 5.00 | 2.86 | 5.42 | 5.03 | 4.50 | 4.80 | 5.27 | 4.93 | 5.04 |
| Subprime | 0.77 | 0.66 | 0.83 | 0.00 | 1.00 | 0.77 | 0.72 | 0.70 | 0.89 | 0.75 | 0.78 |
| Prime | 0.23 | 0.34 | 0.17 | 1.00 | 0.00 | 0.23 | 0.28 | 0.30 | 0.11 | 0.25 | 0.22 |
| GSE Conf. | 0.17 | 0.25 | 0.12 | 0.56 | 0.05 | 0.17 | 0.15 | 0.21 | 0.10 | 0.19 | 0.15 |
| Prep. Penalty | 0.49 | 0.34 | 0.58 | 0.24 | 0.57 | 0.50 | 0.46 | 0.42 | 0.63 | 0.49 | 0.50 |
| Purchase | 0.37 | 0.30 | 0.42 | 0.22 | 0.42 | 0.38 | 0.30 | 0.36 | 0.40 | 0.36 | 0.39 |
| Refin. cash-out | 0.47 | 0.49 | 0.45 | 0.46 | 0.47 | 0.46 | 0.51 | 0.46 | 0.47 | 0.49 | 0.45 |
| Refin. no cash-out | 0.16 | 0.21 | 0.13 | 0.31 | 0.11 | 0.15 | 0.19 | 0.18 | 0.12 | 0.15 | 0.16 |
| Service fee | 0.44 | 0.38 | 0.47 | 0.33 | 0.47 | 0.44 | 0.39 | 0.42 | 0.46 | 0.41 | 0.46 |
| Switch servicer | 0.55 | 0.50 | 0.58 | 0.52 | 0.56 | 0.56 | 0.44 | 0.18 | 0.50 | 0.00 | 1.00 |
| Default | 0.37 | 0.30 | 0.41 | 0.18 | 0.43 | 0.35 | 0.54 | 0.00 | 1.00 | 0.26 | 0.62 |
| Age at default | 36.64 | 45.25 | 32.98 | 47.72 | 35.21 | 37.41 | 30.81 | . | 36.64 | 38.07 | 35.47 |
| Default 12 | 0.11 | 0.06 | 0.12 | 0.03 | 0.12 | 0.10 | 0.12 | . | 0.11 | 0.09 | 0.12 |
| Default 18 | 0.23 | 0.15 | 0.26 | 0.08 | 0.24 | 0.22 | 0.26 | . | 0.23 | 0.20 | 0.24 |
| Default 24 | 0.35 | 0.24 | 0.40 | 0.15 | 0.38 | 0.34 | 0.44 | . | 0.35 | 0.32 | 0.37 |
| Configuration | I | II | III | IV | V | VI | VII | IIX | IX |
|---|---|---|---|---|---|---|---|---|---|
| A. Fundamental loan and borrower characteristics | |||||||||
| FICO score | −0.0034 *** | −0.0034 *** | −0.0034 *** | −0.0034 *** | −0.0034 *** | −0.0034 *** | −0.0034 *** | −0.0034 *** | −0.0034 *** |
| LTV ratio | 0.0169 *** | 0.0172 *** | 0.0170 *** | 0.0171 *** | 0.0169 *** | 0.0175 *** | 0.0170 *** | 0.0172 *** | 0.0179 *** |
| ARM | 0.0980 *** | 0.1324 *** | 0.1290 *** | 0.1064 *** | 0.0866 *** | 0.0755 *** | 0.0940 *** | 0.0911 *** | 0.1206 *** |
| Balloon | 0.6336 *** | 0.5681 *** | 0.5770 *** | 0.5887 *** | 0.6384 *** | 0.6373 *** | 0.6344 *** | 0.6264 *** | 0.4146 *** |
| No/Low doc. | 0.3726 *** | 0.3742 *** | 0.3741 *** | 0.3707 *** | 0.3673 *** | 0.3602 *** | 0.3721 *** | 0.3690 *** | 0.3396 *** |
| GSE Conf. | −0.1939 *** | −0.1914 *** | −0.1895 *** | −0.1920 *** | −0.1905 *** | −0.1959 *** | −0.1918 *** | −0.1910 *** | −0.1567 *** |
| B. Economic general conditions | |||||||||
| GDP growth | −14.808 *** | −1.9725 *** | |||||||
| C. Housing market conditions | |||||||||
| HPI growth | −3.4660 *** | −7.6275 *** | |||||||
| D. Bond market conditions | |||||||||
| σ interest | 0.4669 *** | 1.0679 *** | |||||||
| Credit spread | 0.3561 *** | 1.8900 *** | |||||||
| E. State legal structure | |||||||||
| State FE | Yes | ||||||||
| Judicial | −0.0464 *** | −0.0421 *** | |||||||
| SRR | −0.0868 *** | −0.0853 *** | |||||||
| Intercept | 0.2878 *** | 0.6870 *** | 0.5697 *** | −0.1014 *** | 0.6244 *** | −0.1253 *** | 0.3277 *** | 0.3385 *** | 1.9433 *** |
| Pseudo R2 | 8.40 | 9.10 | 8.82 | 9.04 | 8.53 | 9.39 | 8.43 | 8.46 | 11.60 |
| Log-likelihood | −3.37 × 106 | −3.35 × 106 | −3.36 × 106 | −3.35 × 106 | −3.37 × 106 | −3.34 × 106 | −3.37 × 106 | −3.37 × 106 | −3.25 × 106 |
| Wald p-value | 0.00 | ||||||||
| LR p-value | 0.00 | ||||||||
| Configuration | I | II | III | IV | V | VI | VII | IIX | IX |
|---|---|---|---|---|---|---|---|---|---|
| A. Fundamental loan and borrower characteristics | |||||||||
| FICO score | −0.0036 *** | −0.0036 *** | −0.0036 *** | −0.0035 *** | −0.0036 *** | −0.0036 *** | −0.0036 *** | −0.0036 *** | −0.0037 *** |
| LTV ratio | 0.0164 *** | 0.0166 *** | 0.0165 *** | 0.0165 *** | 0.0164 *** | 0.0168 *** | 0.0165 *** | 0.0166 *** | 0.0173 *** |
| ARM | 0.0773 *** | 0.1117 *** | 0.1087 *** | 0.0858 *** | 0.0660 *** | 0.0587 *** | 0.0735 *** | 0.0713 *** | 0.1010 *** |
| Balloon | 0.6303 *** | 0.5647 *** | 0.5731 *** | 0.5852 *** | 0.6350 *** | 0.6368 *** | 0.6310 *** | 0.6240 *** | 0.4114 *** |
| No/Low doc. | 0.3740 *** | 0.3758 *** | 0.3758 *** | 0.3721 *** | 0.3687 *** | 0.3631 *** | 0.3736 *** | 0.3709 *** | 0.3417 *** |
| GSE Conf. | −0.1844 *** | −0.1817 *** | −0.1798 *** | −0.1825 *** | −0.1810 *** | −0.1871 *** | −0.1823 *** | −0.1819 *** | −0.1475 *** |
| B. Economic general conditions | |||||||||
| GDP growth | −14.788 *** | −1.8866 *** | |||||||
| C. Housing market conditions | |||||||||
| HPI growth | −3.5125 *** | −7.6803 *** | |||||||
| D. Bond market conditions | |||||||||
| σ interest | 0.4624 *** | 1.0581 *** | |||||||
| Credit spread | 0.3491 *** | 1.8732 *** | |||||||
| E. State legal structure | |||||||||
| State FE | Yes | ||||||||
| Judicial | −0.0447 *** | −0.0412 *** | |||||||
| SRR | −0.0752 *** | −0.0737 *** | |||||||
| Intercept | 0.5435 *** | 0.9450 *** | 0.8307 *** | 0.1598 *** | 0.8735 *** | 0.1316 *** | 0.5821 *** | 0.5876 *** | 2.1942 *** |
| Pseudo R2 | 8.50 | 9.19 | 8.92 | 9.12 | 8.62 | 9.43 | 8.52 | 8.54 | 11.60 |
| Log-likelihood | −3.41 × 106 | −3.39 × 106 | −3.40 × 106 | −3.39 × 106 | −3.41 × 106 | −3.38 × 106 | −3.42 × 106 | −3.42 × 106 | −3.30 × 106 |
| Wald p-value | 0.00 | ||||||||
| LR p-value | 0.00 | ||||||||
| Configuration | I | II | III | IV | V | VI | VII | IIX | IX |
|---|---|---|---|---|---|---|---|---|---|
| A. Fundamental loan and borrower characteristics | |||||||||
| FICO score | −0.0034 *** | −0.0033 *** | −0.0034 *** | −0.0033 *** | −0.0034 *** | −0.0034 *** | −0.0034 *** | −0.0034 *** | −0.0035 *** |
| LTV ratio | 0.0169 *** | 0.0169 *** | 0.0168 *** | 0.0172 *** | 0.0169 *** | 0.0170 *** | 0.0170 *** | 0.0170 *** | 0.0178 *** |
| ARM | 0.0978 *** | 0.1157 *** | 0.1028 *** | 0.1191 *** | 0.0820 *** | 0.0824 *** | 0.0942 *** | 0.0930 *** | 0.0885 *** |
| Balloon | 0.6464 *** | 0.6156 *** | 0.6361 *** | 0.5640 *** | 0.6522 *** | 0.6571 *** | 0.6469 *** | 0.6412 *** | 0.4378 *** |
| No/Low doc. | 0.3444 *** | 0.3476 *** | 0.3455 *** | 0.3398 *** | 0.3375 *** | 0.3379 *** | 0.3440 *** | 0.3417 *** | 0.3064 *** |
| GSE Conf. | −0.1921 *** | −0.1946 *** | −0.1928 *** | −0.1834 *** | −0.1869 *** | −0.1979 *** | −0.1902 *** | −0.1901 *** | −0.1474 *** |
| B. Economic general conditions | |||||||||
| GDP growth | −8.4588 *** | 11.941 *** | |||||||
| C. Housing market conditions | |||||||||
| HPI growth | −0.7645 *** | −6.5539 *** | |||||||
| D. Bond market conditions | |||||||||
| σ interest | 0.6250 *** | 1.4068 *** | |||||||
| Credit spread | 0.4258 *** | 1.8676 *** | |||||||
| E. State legal structure | |||||||||
| State FE | Yes | ||||||||
| Judicial | −0.0413 *** | −0.0402 *** | |||||||
| SRR | −0.0621 *** | −0.0545 *** | |||||||
| Intercept | 0.2735 *** | 0.4876 *** | 0.3351 *** | −0.2557 *** | 0.6864 *** | −0.1608 *** | 0.3083 *** | 0.3090 *** | 1.1864 *** |
| Pseudo R2 | 8.22 | 8.41 | 8.24 | 9.37 | 8.42 | 9.21 | 8.24 | 8.25 | 11.50 |
| Log-likelihood | −3.03 × 106 | −3.03 × 106 | −3.03 × 106 | −2.99 × 106 | −3.03 × 106 | −3.00 × 106 | −3.03 × 106 | −3.03 × 106 | −2.92 × 106 |
| Wald p-value | 0.00 | ||||||||
| LR p-value | 0.00 | ||||||||
| Configuration | I | II | III | IV | V | VI | VII | IIX | IX |
|---|---|---|---|---|---|---|---|---|---|
| A. Fundamental loan and borrower characteristics | |||||||||
| FICO score | −0.0036 *** | −0.0036 *** | −0.0036 *** | −0.0035 *** | −0.0036 *** | −0.0036 *** | −0.0036 *** | −0.0036 *** | −0.0037 *** |
| LTV ratio | 0.0163 *** | 0.0164 *** | 0.0163 *** | 0.0166 *** | 0.0163 *** | 0.0163 *** | 0.0164 *** | 0.0165 *** | 0.0172 *** |
| ARM | 0.0775 *** | 0.0954 *** | 0.0826 *** | 0.0986 *** | 0.0619 *** | 0.0660 *** | 0.0740 *** | 0.0735 *** | 0.0694 *** |
| Balloon | 0.6409 *** | 0.6099 *** | 0.6303 *** | 0.5582 *** | 0.6465 *** | 0.6543 *** | 0.6414 *** | 0.6367 *** | 0.4336 *** |
| No/Low doc. | 0.3452 *** | 0.3486 *** | 0.3465 *** | 0.3407 *** | 0.3383 *** | 0.3402 *** | 0.3448 *** | 0.3431 *** | 0.3080 *** |
| GSE Conf. | −0.1820 *** | −0.1845 *** | −0.1827 *** | −0.1733 *** | −0.1769 *** | −0.1885 *** | −0.1803 *** | −0.1803 *** | −0.1382 *** |
| B. Economic general conditions | |||||||||
| GDP growth | −8.4972 *** | 11.542 *** | |||||||
| C. Housing market conditions | |||||||||
| HPI growth | −0.7942 *** | −6.5161 *** | |||||||
| D. Bond market conditions | |||||||||
| σ interest | 0.6198 *** | 1.3822 *** | |||||||
| Credit spread | 0.4142 *** | 1.8360 *** | |||||||
| E. State legal structure | |||||||||
| State FE | Yes | ||||||||
| Judicial | −0.0391 *** | −0.0388 *** | |||||||
| SRR | −0.0502 *** | −0.0428 *** | |||||||
| Intercept | 0.5317 *** | 0.7481 *** | 0.5958 *** | 0.0110 | 0.9336 *** | 0.1011 *** | 0.5649 *** | 0.5605 *** | 1.4420 *** |
| Pseudo R2 | 8.31 | 8.49 | 8.32 | 9.43 | 8.49 | 9.25 | 8.32 | 8.33 | 11.51 |
| Log-likelihood | −3.08 × 106 | −3.07 × 106 | −3.08 × 106 | −3.04 × 106 | −3.07 × 106 | −3.04 × 106 | −3.08 × 106 | −3.08 × 106 | −2.97 × 106 |
| Wald p-value | 0.00 | ||||||||
| LR p-value | 0.00 | ||||||||
| Model | Two-Stage IV Probit | DLB Linear Model | Bivariate Probit | ||||
|---|---|---|---|---|---|---|---|
| 1st Stage | 2nd Stage | 1st Stage | 2nd Stage | 2nd Stage | Default | Switch Serv. | |
| Dependent Var. | Default | Switch Serv. | Default | Switch Serv. | Switch Serv. | ||
| Instruments | |||||||
| Income | −0.0006 *** | −0.0002 *** | |||||
| Divorce | 0.3028 *** | 0.2069 *** | |||||
| Pr(Default = 1) | 0.5197 *** | ||||||
| Ê(Default) | 0.4443 *** | 0.1183 *** | |||||
| Default | 0.3260 *** | ||||||
| FICO score | −0.0037 *** | −0.0012 *** | −0.0037 *** | −0.0001 *** | |||
| LTV ratio | 0.0174 *** | 0.0030 *** | 0.0051 *** | 0.0007 *** | 0.0007 *** | 0.0174 *** | 0.0030 *** |
| ARM | 0.1018 *** | −0.1840 *** | 0.0371 *** | −0.0749 *** | −0.0749 *** | 0.1005 *** | −0.1712 *** |
| Balloon | 0.4097 *** | −0.0194 *** | 0.1557 *** | −0.0435 *** | −0.0435 *** | 0.4053 *** | 0.0582 *** |
| No/Low doc. | 0.3416 *** | 0.1590 *** | 0.1087 *** | 0.0472 *** | 0.0472 *** | 0.3431 *** | 0.1696 *** |
| GSE Conf. | −0.1446 *** | 0.0785 *** | −0.0426 *** | 0.0676 *** | 0.0676 *** | −0.1434 *** | 0.0015 |
| GDP growth | −4.7726 *** | 4.3899 *** | −1.8273 *** | 3.5229 *** | 3.5229 *** | −1.8682 *** | −0.5094 *** |
| HPI growth | −7.6137 *** | −5.8278 *** | −2.5897 *** | −0.9331 *** | −0.9331 *** | −7.6081 *** | −7.7881 *** |
| σ interest | 0.9214 *** | 0.6408 *** | 0.2792 *** | 0.1016 *** | 0.1016 *** | 1.0572 *** | 0.8377 *** |
| Credit spread | 1.9721 *** | 1.1882 *** | 0.6366 *** | 0.0236 *** | 0.0236 *** | 1.8768 *** | 1.9701 *** |
| Judicial | −0.0416 *** | 0.0122 *** | −0.0130 *** | 0.0062 *** | 0.0062 *** | −0.0410 *** | 0.0019 |
| SRR | −0.0729 *** | 0.0294 *** | −0.0233 *** | 0.0118 *** | 0.0118 *** | −0.0743 *** | 0.0326 *** |
| R2 | 11.7 | 38.0 | 14.1 | 31.2 | 38.6 | ||
| ρ | 0.6190 *** | ||||||
| Model | Two-Stage IV Probit | DLB Linear Model | Bivariate Probit | ||||
|---|---|---|---|---|---|---|---|
| 1st Stage | 2nd Stage | 1st Stage | 2nd Stage | 2nd Stage | Default | Switch Serv. | |
| Dependent Var. | Default | Switch Serv. | Default | Switch Serv. | Switch Serv. | ||
| Instruments | |||||||
| Income | −0.0012 *** | −0.0004 *** | |||||
| Divorce | 3.8303 *** | 1.3157 *** | |||||
| Pr(Default=1) | 0.6350 *** | ||||||
| Ê(Default) | 0.3639 *** | 0.0550 *** | |||||
| Default | 0.3089 *** | ||||||
| FICO score | −0.0035 *** | −0.0011 *** | −0.0035 *** | −0.0001 *** | |||
| LTV ratio | 0.0181 *** | 0.0004 *** | 0.0050 *** | 0.0002 *** | 0.0002 *** | 0.0179 *** | 0.0031 *** |
| ARM | 0.0926 *** | −0.2652 *** | 0.0328 *** | −0.0912 *** | −0.0912 *** | 0.0866 *** | −0.2397 *** |
| Balloon | 0.4051 *** | −0.0681 *** | 0.1604 *** | −0.0403 *** | −0.0403 *** | 0.4340 *** | 0.0663 *** |
| No/Low doc. | 0.2985 *** | 0.0895 *** | 0.0904 *** | 0.0296 *** | 0.0296 *** | 0.3079 *** | 0.1282 *** |
| GSE Conf. | −0.1384 *** | 0.0823 *** | −0.0376 *** | 0.0550 *** | 0.0550 *** | −0.1427 *** | 0.0196 *** |
| GDP growth | 7.5664 *** | 16.7512 *** | 1.8333 *** | 7.3254 *** | 7.3254 *** | 11.7905 *** | 18.9797 *** |
| HPI growth | −3.3490 *** | −5.6139 *** | −1.1534 *** | −0.8432 *** | −0.8432 *** | −6.4116 *** | −6.9225 *** |
| σ interest | 0.5626 *** | 1.0320 *** | 0.1439 *** | 0.2578 *** | 0.2578 *** | 1.3962 *** | 1.3139 *** |
| Credit spread | 1.7920 *** | 1.6191 *** | 0.5576 *** | 0.1905 *** | 0.1905 *** | 1.8542 *** | 1.9820 *** |
| Judicial | −0.0420 *** | 0.0109 *** | −0.0127 *** | 0.0062 *** | 0.0062 *** | −0.0410 *** | 0.0088 *** |
| SRR | −0.0525 *** | 0.0467 *** | −0.0162 *** | 0.0161 *** | 0.0161 *** | −0.0545 *** | 0.0553 *** |
| R2 | 12.1 | 38.0 | 14.0 | 30.4 | 37.3 | ||
| ρ | 0.6004 *** | ||||||
| Model | Two-Stage IV Probit | DLB Linear Model | Bivariate Probit | ||||
|---|---|---|---|---|---|---|---|
| 1st Stage | 2nd Stage | 1st Stage | 2nd Stage | 2nd Stage | Default | Switch Serv. | |
| Dependent Var. | Default | Switch Serv. | Default | Switch Serv. | Switch Serv. | ||
| Instruments | |||||||
| Income | −0.0012 *** | −0.0004 *** | |||||
| Divorce | 3.7299 *** | 1.3072 *** | |||||
| Pr(Default = 1) | 0.5789 *** | ||||||
| Ê(Default) | 0.3292 *** | 0.0136 *** | |||||
| Default | 0.3156 *** | ||||||
| FICO score | −0.0038 *** | −0.0012 *** | −0.0037 *** | −0.0001 *** | |||
| LTV ratio | 0.0174 *** | 0.0001 ** | 0.0049 *** | 0.0004 *** | 0.0004 *** | 0.0172 *** | 0.0031 *** |
| ARM | 0.0734 *** | −0.2599 *** | 0.0269 *** | −0.0881 *** | −0.0881 *** | 0.0690 *** | −0.2402 *** |
| Balloon | 0.4015 *** | −0.0562 *** | 0.1566 *** | −0.0329 *** | −0.0329 *** | 0.4295 *** | 0.0663 *** |
| No/Low doc. | 0.3003 *** | 0.0931 *** | 0.0929 *** | 0.0319 *** | 0.0319 *** | 0.3090 *** | 0.1280 *** |
| GSE Conf. | −0.1294 *** | 0.0791 *** | −0.0370 *** | 0.0531 *** | 0.0531 *** | −0.1337 *** | 0.0191 *** |
| GDP growth | 7.3051 *** | 16.9002 *** | 1.8576 *** | 7.4274 *** | 7.4274 *** | 11.4314 *** | 18.9506 *** |
| HPI growth | −3.4066 *** | −5.7247 *** | −1.1831 *** | −0.9145 *** | −0.9145 *** | −6.4057 *** | −6.9189 *** |
| σ interest | 0.5607 *** | 1.0537 *** | 0.1501 *** | 0.2713 *** | 0.2713 *** | 1.3720 *** | 1.3126 *** |
| Credit spread | 1.7675 *** | 1.6508 *** | 0.5631 *** | 0.2088 *** | 0.2088 *** | 1.8242 *** | 1.9798 *** |
| Judicial | −0.0406 *** | 0.0102 *** | −0.0125 *** | 0.0058 *** | 0.0058 *** | −0.0388 *** | 0.0089 *** |
| SRR | −0.0409 *** | 0.0438 *** | −0.0125 *** | 0.0144 *** | 0.0144 *** | −0.0435 *** | 0.0558 *** |
| R2 | 12.0 | 38.0 | 14.2 | 30.4 | 37.7 | ||
| ρ | 0.6230 *** | ||||||

| 1 | The contents of this section are based on the report of the Mortgage Bankers Association and PricewaterhouseCoopers (2015), and the report to Congress by the Board of Governors of the Federal Reserve System (2016). |
References
- Agarwal, Sumit, and Itzhak Ben-David. 2018. Loan prospecting and the loss of soft information. Journal of Financial Economics 129: 608–28. [Google Scholar] [CrossRef]
- Agarwal, Sumit, and Robert Hauswald. 2010. Distance and private information in lending. The Review of Financial Studies 23: 2757–88. [Google Scholar] [CrossRef]
- Agarwal, Sumit, Yan Chang, and Abdullah Yavas. 2012. Adverse selection in mortgage securitization. Journal of Financial Economics 105: 640–60. [Google Scholar] [CrossRef]
- Albertazzi, Ugo, Ginette Eramo, Leonardo Gambacorta, and Carmelo Salleo. 2015. Asymmetric information in securitization: An empirical assessment. Journal of Monetary Economics 71: 33–49. [Google Scholar] [CrossRef]
- Ambrose, Brent W., Michael LaCour-Little, and Anthony B. Sanders. 2005. Does regulatory capital arbitrage, reputation, or asymmetric information drive securitization? Journal of Financial Services Research 28: 113–33. [Google Scholar] [CrossRef]
- Ashcraft, Adam B., Kunal Gooriah, and Amir Kermani. 2019. Does skin-in-the-game affect security performance? Evidence from the conduit CMBS market. Journal of Financial Economics 134: 333–54. [Google Scholar] [CrossRef]
- Begley, Taylor A., and Amiyatosh Purnanandam. 2017. Design of financial securities: Empirical evidence from private-label RMBS deals. Review of Financial Studies 30: 120–61. [Google Scholar] [CrossRef]
- Board of Governors of the Federal Reserve System. 2016. Report to the Congress on the Effect of Capital Rules on Mortgage Servicing Assets. Available online: https://www.federalreserve.gov/publications/other-reports/files/effect-capital-rules-mortgage-servicing-assets-201606.pdf (accessed on 25 September 2024).
- Bubb, Ryan, and Alex Kaufman. 2014. Securitization and moral hazard: Evidence from credit score cutoff rules. Journal of Monetary Economics 63: 1–18. [Google Scholar] [CrossRef]
- Centorrino, Samuele, and Jean-Pierre Florens. 2021. Nonparametric instrumental variable estimation of binary response models with continuous endogenous regressors. Econometrics and Statistics 17: 35–63. [Google Scholar]
- Chiappori, Pierre-André, and Bernard Salanié. 2000. Testing for asymmetric information in insurance markets. Journal of Political Economy 108: 56–78. [Google Scholar] [CrossRef]
- Das, Mitali. 2005. Instrumental variables estimators of nonparametric models with discrete endogenous regressors. Journal of Econometrics 124: 335–61. [Google Scholar] [CrossRef]
- Dionne, Georges, Christian Gouriéroux, and Charles Vanasse. 2001. Testing for evidence of adverse selection in the automobile insurance market: A comment. Journal of Political Economy 109: 444–53. [Google Scholar] [CrossRef]
- Dionne, Georges, Christian Gouriéroux, and Charles Vanasse. 2006. Informational Content of Household Decisions with Applications to Insurance under Asymmetric Information. In Competitive Failures in Insurance Markets: Theory and Policy Implications. Edited by P. A. Chiappori and C. Gollier. Cambridge, MA: MIT Press, pp. 159–84. [Google Scholar]
- Dionne, Georges, Mélissa La Haye, and Anne-Sophie Bergerès. 2015. Does asymmetric information affect the premium in mergers and acquisitions? Canadian Journal of Economics/Revue Canadienne D’économique 48: 819–52. [Google Scholar] [CrossRef]
- Dionne, Georges, Pascal St-Amour, and Désiré Vencatachellum. 2009. Asymmetric information and adverse selection in mauritian slave auctions. The Review of Economic Studies 76: 1269–95. [Google Scholar] [CrossRef]
- Dionne, Georges, Pierre-Carl Michaud, and Maki Dahchour. 2013. Separating moral hazard from adverse selection and learning in automobile insurance: Longitudinal evidence from France. Journal of the European Economic Association 11: 897–917. [Google Scholar] [CrossRef]
- Elul, Ronel. 2016. Securitization and mortgage default. Journal of Financial Services Research 49: 281–309. [Google Scholar] [CrossRef]
- Filomeni, Stefano. 2024. Securitization and risk appetite: Empirical evidence from US banks. Review of Quantitative Finance and Accounting 63: 433–68. [Google Scholar] [CrossRef]
- Fisher, Nicholas I., and Peter Hall. 1990. On bootstrap hypothesis testing. Australian Journal of Statistics 32: 177–90. [Google Scholar] [CrossRef]
- Gete, Pedro, and Michael Reher. 2021. Mortgage securitization and shadow bank lending. The Review of Financial Studies 34: 2236–74. [Google Scholar] [CrossRef]
- Gorton, Gary, and Andrew Metrick. 2012. Securitization. NBER, Working Paper 18611. Available online: https://www.nber.org/papers/w18611 (accessed on 25 September 2024).
- Horowitz, Joel L. 2011. Applied nonparametric instrumental variables estimation. Econometrica 79: 347–94. [Google Scholar]
- Keys, Benjamin J., Amit Seru, and Vikrant Vig. 2012. Lender screening and the role of securitization: Evidence from prime and subprime mortgage markets. The Review of Financial Studies 25: 2071–108. [Google Scholar] [CrossRef]
- Keys, Benjamin J., Tanmoy Mukherjee, Amit Seru, and Vikrant Vig. 2010. Did securitization lead to lax screening? Evidence from subprime loans. The Quarterly Journal of Economics 125: 307–62. [Google Scholar] [CrossRef]
- Krainer, John, and Elizabeth Laderman. 2014. Mortgage loan securitization and relative loan performance. Journal of Financial Services Research 45: 39–66. [Google Scholar] [CrossRef]
- Li, Qi, and Jeffrey Scott Racine. 2007. Nonparametric Econometrics: Theory and Practice. Princeton: Princeton University Press. [Google Scholar]
- Liberti, José María, and Mitchell A. Petersen. 2018. Information: Hard and soft. Review of Corporate Finance Studies 8: 1–41. [Google Scholar] [CrossRef]
- MacKinnon, James G. 2009. Bootstrap hypothesis testing. Handbook of Computational Econometrics 183: 213. [Google Scholar]
- Malekan, Sara, and Georges Dionne. 2014. Securitization and optimal retention under moral hazard. Journal of Mathematical Economics 55: 74–85. [Google Scholar] [CrossRef]
- Maliar, Serguei, and Bernard Salanié. 2023. Testing for Asymmetric Information in Insurance with Deep Learning. Working Paper. New York: Columbia University. 32p. [Google Scholar]
- Morgan, Lewis. 2018. Guide to the Credit Risk Retention Rules for Securitization. Available online: https://www.morganlewis.com/pubs/2024/07/a-guide-to-the-credit-risk-retention-rules (accessed on 25 September 2024).
- Mortgage Bankers Association (MBA), and PwC US (PricewaterhouseCoopers). 2015. The Changing Dynamics of the Mortgage Servicing Landscape. Available online: https://www.housingwire.com/wp-content/uploads/media/images/15217_MBA_PWC_White_Paper.pdf (accessed on 25 September 2024).
- Parzen, Emanuel. 1962. On estimation of a probability density function and mode. The Annals of Mathematical Statistics 33: 1065–76. [Google Scholar] [CrossRef]
- Passmore, Wayne, and Roger Sparks. 2024. Government-Sponsored Mortgage Securitization and Financial Crises. Washington, DC: Finance and Economics Discussion Series Federal Reserve Board. [Google Scholar]
- Racine, Jeffrey S. 2008. Nonparametric econometrics: A primer. Foundations and Trends in Econometrics 3: 1–88. [Google Scholar] [CrossRef]
- Rosenblatt, Murray. 1956. Remarks on some nonparametric estimates of a density function. In The Annals of Mathematical Statistics. Berlin and Heidelberg: Springer, pp. 832–37. [Google Scholar]
- Su, Liangjun, and Martin Spindler. 2013. Nonparametric testing for asymmetric information. Journal of Business & Economic Statistics 31: 208–25. [Google Scholar]

| Configuration | I | II | III | IV | V | VI | VII | IIX | IX | X | XI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FICO.660 | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| LTV.80 | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| ARM | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| No/Low doc. | - | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Balloon | - | - | Yes | - | - | - | Yes | Yes | Yes | Yes | Yes |
| GSE Conf. | - | - | - | Yes | - | - | Yes | - | - | Yes | - |
| Subprime | - | - | - | - | Yes | - | - | Yes | - | - | Yes |
| Prep. penalty | - | - | - | - | - | Yes | - | - | Yes | Yes | Yes |
| # variables | 3 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 |
| # cells (M) | 8 | 16 | 32 | 32 | 32 | 32 | 64 | 64 | 64 | 128 | 128 |
| Method 1: | |||||||||||
| KS p-value | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Method 2: | |||||||||||
| χ2(1) crit. value | 3.84 | 3.84 | 3.84 | 3.84 | 3.84 | 3.84 | 3.84 | 3.84 | 3.84 | 3.84 | 3.84 |
| Rejection rate | 0.75 | 1.00 | 0.81 | 0.92 | 1.00 | 0.91 | 0.75 | 0.81 | 0.83 | 0.73 | 0.83 |
| Method 3: | |||||||||||
| χ2(M) crit. value | 15.51 | 26.30 | 46.19 | 46.19 | 46.19 | 46.19 | 84.82 | 84.82 | 84.82 | 124.34 | 124.34 |
| S value | 6388.6 | 4491.4 | 6840.3 | 5577.2 | 4491.4 | 9638.9 | 7628.9 | 6840.3 | 11,089.8 | 11,230.5 | 11,089.8 |
| Model | Two-Stage IV Probit | DLB Linear Model | Bivariate Probit | ||||
|---|---|---|---|---|---|---|---|
| 1st Stage | 2nd Stage | 1st Stage | 2nd Stage | 2nd Stage | Default | Switch Serv. | |
| Dependent Var. | Default | Switch Serv. | Default | Switch Serv. | Switch Serv. | ||
| Instruments | |||||||
| Income | −0.0007 *** | −0.0002 *** | |||||
| Divorce | 0.2896 *** | 0.2104 *** | |||||
| Pr(Default = 1) | 0.5334 *** | ||||||
| Ê(Default) | 0.4871 *** | 0.1683 *** | |||||
| Default | 0.3188 *** | ||||||
| FICO score | −0.0035 *** | −0.0011 *** | −0.0035 *** | −0.0001 *** | |||
| LTV ratio | 0.0180 *** | 0.0029 *** | 0.0051 *** | 0.0004 *** | 0.0004 *** | 0.0180 *** | 0.0030 *** |
| ARM | 0.1212 *** | −0.1867 *** | 0.0430 *** | −0.0795 *** | −0.0795 *** | 0.1184 *** | −0.1707 *** |
| Balloon | 0.4129 *** | −0.0225 *** | 0.1596 *** | −0.0525 *** | −0.0525 *** | 0.4085 *** | 0.0582 *** |
| No/Low doc. | 0.3395 *** | 0.1579 *** | 0.1062 *** | 0.0437 *** | 0.0437 *** | 0.3416 *** | 0.1699 *** |
| GSE Conf. | −0.1537 *** | 0.0777 *** | −0.0432 *** | 0.0699 *** | 0.0699 *** | −0.1524 *** | 0.0020 |
| GDP growth | −4.9640 *** | 4.4784 *** | −1.8759 *** | 3.5329 *** | 3.5329 *** | −1.9603 *** | −0.5005 *** |
| HPI growth | −7.5731 *** | −5.8147 *** | −2.5375 *** | −0.8476 *** | −0.8476 *** | −7.5398 *** | −7.7918 *** |
| σ interest | 0.9305 *** | 0.6387 *** | 0.2736 *** | 0.0887 *** | 0.0887 *** | 1.0688 *** | 0.8380 *** |
| Credit spread | 1.9934 *** | 1.1789 *** | 0.6298 *** | 0.0044 *** | 0.0044 *** | 1.8957 *** | 1.9713 *** |
| Judicial | −0.0425 *** | 0.0129 *** | −0.0129 *** | 0.0066 *** | 0.0066 *** | −0.0426 *** | 0.0018 |
| SRR | −0.0844 *** | 0.0321 *** | −0.0267 *** | 0.0145 *** | 0.0145 *** | −0.0851 *** | 0.0321 *** |
| R2 | 11.7 | 38.0 | 13.8 | 31.2 | 38.2 | ||
| ρ | 0.5965 *** | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jedidi, H.; Dionne, G. Nonparametric Testing for Information Asymmetry in the Mortgage Servicing Market. Risks 2024, 12, 192. https://doi.org/10.3390/risks12120192
Jedidi H, Dionne G. Nonparametric Testing for Information Asymmetry in the Mortgage Servicing Market. Risks. 2024; 12(12):192. https://doi.org/10.3390/risks12120192
Chicago/Turabian StyleJedidi, Helmi, and Georges Dionne. 2024. "Nonparametric Testing for Information Asymmetry in the Mortgage Servicing Market" Risks 12, no. 12: 192. https://doi.org/10.3390/risks12120192
APA StyleJedidi, H., & Dionne, G. (2024). Nonparametric Testing for Information Asymmetry in the Mortgage Servicing Market. Risks, 12(12), 192. https://doi.org/10.3390/risks12120192







