Investment Portfolio Allocation and Insurance Solvency: New Evidence from Insurance Groups in the Era of Solvency II

Abstract

This study examines the effect of the investment portfolio structure on insurers’ solvency, as measured by the Solvency Capital Requirement ratio. An empirical sample of 88 EU-based insurance groups was analyzed to provide robust evidence of the portfolio’s impact on the Solvency Capital Requirement ratio from 2016 to 2022. Linear regression and supervised machine learning models, particularly extra trees regression, were used to predict the solvency ratios, with the latter outperforming the former. The investigation was supplemented with panel data analysis. Firm-specific factors, including, unit-linked and index-linked liabilities, firm size, investments in property, collective undertakings, bonds and equities, and the ratio of government bonds to corporate bonds and country-specific factors, such as life and non-life market concentration, domestic bond market development, private debt development, household spending, banking concentration, non-performing loans, and CO₂ emissions, were found to have an important effect on insurers’ solvency ratios. The novelty of this research lies in the investigation of the connection of solvency ratios with variables that prior studies have not yet explored, such as portfolio asset allocation, the life and non-life insurance market concentration, and unit-linked and index-linked products, via the employment of a battery of traditional and machine enhanced methods. Furthermore, it identifies the relation of solvency ratios with bond market development and investments in collective undertakings. Finally, it addresses the substantial solvency risks posed by the high banking sector concentration to insurers under Solvency II.

1. Introduction

The insurance industry has undergone various regulatory changes over the years, particularly with the implementation of the Solvency II (SII) framework for European insurers on 1 January 2016. This new framework has garnered both support and criticism from industry stakeholders, with insurers being among the critics. Critics argue that the regulations may not fully account for the insurance industry’s ability to hold certain types of assets (Insurance Europe and Oliver Wyman 2013). With the introduction of the Solvency II Directive, the regulatory capital regime for insurers in the European Union has shifted from a volume-based measure to a risk-based approach.

The aim of this approach is to establish a more standardized and comprehensive regulatory framework for the European insurance industry that better reflects an insurer’s underlying risk profile. This new framework emphasizes the importance of governance systems, risk management functions, and actuarial functions. Under the SII regime companies are required to conduct an Own Risk and Solvency Assessment (ORSA) to identify their risks and the capital required to manage them. The goal of the ORSA process is to provide a holistic view of the risks to which an insurance company is exposed by analyzing its current financial position and strategy.

Asset allocation is a crucial aspect of the insurance industry, involving the strategic selection between different major asset classes, such as bonds and equities, with the aim of optimizing the risk/return trade-off in the portfolio (Sharpe 1992; Bodie et al. 2011). It is essential for insurers to meet their ongoing obligations, and insurers typically invest a material portion of their capital in fixed-income securities, including both government and corporate bonds (Berends et al. 2013). This is because fixed-income securities, such as government bonds, which usually exhibit high credit ratings, are generally perceived as more secure investments (Bodie et al. 2011). Asset allocation practices and ORSA (EIOPA 2015a, 2015b) are both essential components of an insurer’s risk management strategy. Insurers must adhere to regulatory requirements for asset allocation and ORSA implementation to ensure compliance and financial stability.

The connection between new regulatory requirements and investment decisions has not been comprehensively explored, particularly regarding the potential influence on solvency ratios. As a result, the following research questions arise: What are the factors, relevant to the investment portfolio structure, that influence the solvency ratio of an insurance company? Are there any additional country-/market-, or firm-/product-specific factors that affect the solvency ratio?

The purpose of this study is to address these research questions by unveiling (primarily) the investment portfolio-related parameters that are important for the solvency of an insurer, as measured by the Solvency Capital Requirement (SCR) ratio. At the same time, it aims to identify additional firm-specific and country-specific factors, most of which are relevant to the investment and insurance markets or to investment-linked insurance products, that affect solvency. More specifically, it considers novel factors that may influence the solvency ratio, including the concentration levels in life and non-life insurance markets and the impact of specific insurance products, such as unit-linked and index-linked products. Furthermore, it explores previously unexamined relationships, including the connection between bond market development and solvency ratio, as well as the effect of investments in collective undertakings on the solvency ratio. Finally, it emphasizes the potential risks associated with a highly concentrated banking sector posed to insurance companies operating under the Solvency II regulatory framework. To reach these findings, it employs multiple analytical (traditional and machine-enhanced) methodologies.

Consequently, this research contributes—via the aforementioned novelties—to the understanding of the determinants that impact an insurer’s solvency, focusing initially on the investment-related ones, which offers a fresh approach compared to the existing literature. At the same time, it uncovers potential risks within the insurance industry—in terms of their effect on an insurer’s solvency ratio, which can assist in improving the assessment and management of risks under the Solvency II framework.

2. Literature Review

The European insurance industry, in particular, has a considerable influence beyond providing economic protection to policyholders. In Q2 2023, the total investments of European Economic Area insurers amounted to EUR 8.6 trillion, with life insurers holding EUR 3.5 trillion, non-life insurers EUR 1.1 trillion, composite insurers EUR 3.3 trillion, and re-insurers EUR 0.7 trillion. Unit-linked assets amounted to EUR 2.1 trillion and non-unit-linked assets to EUR 6.5 trillion (EIOPA 2023b).

European insurers under Solvency II must maintain sufficient capital to cover potential losses, and this framework affects asset allocation by setting varying capital requirements for different asset classes, thereby influencing portfolio risk and return profiles (Heinrich and Wurstbauer 2014, 2018). Insurers must balance achieving target returns with Solvency II constraints, often resulting in shifting investments towards assets with lower capital charges (Heinrich and Wurstbauer 2018; Kouwenberg 2018). Solvency II aims to ensure financial stability but may unintentionally prompt insurers to reallocate investments inefficiently and increase portfolio risk (Heinrich and Wurstbauer 2014). The impact of Solvency II varies among insurers, with well-capitalized ones potentially achieving high returns and efficient portfolios, while undercapitalized ones may struggle (Heinrich and Wurstbauer 2018).

Evidence suggests that Solvency II may not significantly constrain market risk, implying limited changes to investment strategies (Höring 2013). While designed to protect policyholders, Solvency II can alter investment behavior, influencing capital market dynamics and product offerings (Douglas et al. 2017; Heinrich and Wurstbauer 2014). The impact of Solvency II on investment allocation and solvency varies among insurers based on their capitalization and asset classes (Heinrich and Wurstbauer 2018; Höring 2013)

Asset allocation strategies play a crucial role in ensuring the financial stability of insurance companies. Research studies have primarily focused on the impact of insurers’ investments on the likelihood of default (e.g., Chen and Wong 2004; Sharpe and Stadnik 2007; Moreno et al. 2020), examining the effects of investment returns (e.g., Chen and Wong 2004; Eling and Jia 2018) and specific investments on insurers’ default probabilities (Sharpe and Stadnik 2007).

However, other factors that affect default probabilities, such as profitability, liquidity, leverage, product mix, and investment performance, have not been adequately addressed in these studies. Furthermore, macroeconomic conditions, particularly in developed countries, can significantly impact the probability of insurer failure. Factors like wholesale prices, loans from financial institutions, inflation, unemployment, and stock market performance can all contribute to economic distress and insurer failure (Caporale et al. 2017; Zhang and Nielson 2015; Chen and Wong 2004; BarNiv and Hershbarger 1990). Insurer failures can have severe consequences, affecting not only confidence in the industry but also the stability of the financial system and ultimately economic conditions (e.g., Shim 2017).

Previous research has underscored the importance of both macroeconomic indicators and company-specific factors in forecasting insolvency. Browne and Hoyt (1995) posit that macroeconomic factors can predict the insolvency of property and casualty insurers. Zhang and Nielson (2015), Cheng and Weiss (2012), and Pasiouras and Gaganis (2013) stress the significance of both macroeconomic and company-specific factors, with macroeconomic indicators playing a particularly crucial role. Doumpos et al. (2017) find that incorporating both country-level macroeconomic data and sector-level data enhances forecasting performance.

This study contributes to the existing literature by covering the gaps emerging from this review. More specifically, it captures the importance of certain asset classes on the solvency ratio, which is fresh evidence compared to the effect of insurers’ investments on the likelihood of default, as well as the effect of investment returns and specific investments on insurers’ default probabilities that the extant literature has researched. It further examines the relationship of solvency ratios with life and non-life insurance market concentration, unit-linked and index-linked products, which has not been addressed at all. It establishes the connection of solvency ratios with domestic bond market development and investments in collective undertakings, which has remained unexplored. Finally, it unveils the material solvency risks posed to insurers under Solvency II from the high banking sector concentration, whose importance has not been realized.

3. Data and Methodology

3.1. Data

The data preparation and processing phase proved to be challenging in this work. The database contained a large number of missing values for several variables related to the asset mix of insurance groups. In order to address this issue, we reduced the number of insurance groups from 300 to 88, focusing on those operating in the EU over a seven-year period (2016–2022). This decision was made due to the lack of data required for our research.

The group data are represented by seven numerical values of a real data type, each value representing a firm-specific factor in the form of a ratio, with the exception of group size, which is measured as the natural logarithm of total assets. In addition, 13 country-specific factors are included in our model in the form of a ratio.

The target variable is the SCR ratio, which is also a real number. The solvency task can thus be formulated as a regression problem with 20 input characteristics and one output (i.e., the SCR ratio). The independent variables, or features, comprise firm-specific factors (of which the investment-related ones are of primary interest) such as unit-linked and index-linked liabilities, firm size, investments in property, collective undertakings, bonds and equities, and the ratio of government bonds to corporate bonds and country-specific factors, such life and non-life concentration, bond market development (as a percentage of GDP), private debt (as a percentage of GDP), real GDP growth, long-term interest rates, household spending (as a percentage of GDP), inflation change, government expenditure, banking concentration, regulatory capital, non-performing loans, and CO₂ emissions.

The data for the SCR ratios and variables related to insurance groups, such as the size of the group, the proportion of investments in real estate, bonds, shares, and collective investment schemes, the ratio of investments in government bonds to corporate bonds, and unit-linked and index-linked liabilities as a percentage of liabilities, were collected and constructed from the annual Solvency Financial Condition Reports (SFCRs) based on data from the Insurance Risk Data database for each group (Insurance Risk Data 2023).

The market share data for the top three life and non-life insurance providers in terms of national gross written premiums, as a measure of life and non-life market concertation, were obtained from the European Insurance Overviews for the years 2018 to 2023, which were published annually by the European Insurance and Occupational Pensions Authority (EIOPA 2018, 2019, 2020, 2021, 2022b, 2023a).

To obtain a comprehensive understanding of the domestic bond market’s development, we utilized the percentage of total domestic public debt securities (amount outstanding) issued on domestic markets, as a proportion of GDP, which was obtained from the European Central Bank’s Data Portal (European Central Bank—ECB Data Portal 2023).

The data for private debt as a percentage of GDP and real GDP growth were obtained from the International Monetary Fund (IMF) database (International Monetary Fund 2023b). Meanwhile, the long-term interest rates were sourced from the Organization for Economic Co-operation and Development (OECD) database (OECD 2023).

The data on household expenditure as a percentage of GDP and annual percentage change in inflation were obtained from the World Bank Open Data database (World Bank Open Data 2023). The Financial Soundness Indicators (FSIs) provided by the International Monetary Fund (International Monetary Fund 2023a) were the source for the information on banking concentration (the percentage of banking assets held by the three largest banks), the ratio of regulatory capital to risk-weighted assets, and the ratio of non-performing loans to total gross loans. The Global Carbon Atlas (Global Carbon Atlas 2023) was the source for the CO₂ emissions per person data.

The proxy used for solvency was the SCR ratio, which is the sum of eligible own funds divided by the SCR, calculated on a consolidated basis. The SCR is the amount of assets that insurance and reinsurance companies are required to hold in order to have a 99.5% confidence that they will be able to meet policyholders’ claims under extreme expected losses. The SCR takes into account life, health, market, credit, operational, and counterparty risks and must be recalculated at least annually. Eligible capital is the portion of actual capital that is eligible to cover the SCR and the Minimum Capital Requirement (MCR), which is the minimum safety net of capital adequacy over one year. Eligibility is determined by the supervisor and includes limits on the amount of each tier that an insurer can use to cover its SCR and MCR and must be greater than 100% (EIOPA 2020).

At this point, we highlight the consideration of the totally new (compared to the literature) variables, namely, life and non-life insurance market concentration and unit-linked and index-linked products. We elaborate on their definitions, their relevance to the insurance activity, and their association with the solvency ratio.

Life insurance (non-life insurance) concentration is the market share of the top 3 life (non-life) insurers, as measured by the ratio (in percent) of the sum of their life (non-life) gross written premia over the total life (non-life) gross written premia produced by all life (non-life) insurers in a country. Market share serves as a common concentration measure. Witkowska (2023) asserts that “the more insurers sell insurance in a country, the lower the concentration ratio”, indicating an inverse relationship between the number of insurers and market concentration. In 2022, Germany and France exhibited the largest shares of the global business insurance market among EU countries, reflecting high concentration (Witkowska 2023). While market share and the number of insurers constitute standard concentration measures, it is imperative to account for sector-specific differences and inefficiencies related to high concentration.

Life (non-life) insurance concentration indicates the portion of insurance that is underwritten by the top life (non-life) insurers in terms of market share. High concentration is indicative of increased insurance (and potentially investment, credit, and operational) risk exposure by these providers, which affects the solvency capital required to provide a cushion for these risks. Consequently, it is associated with the Solvency Capital Requirement ratio of the (especially high market share) insurers.

Unit-linked and index-linked products are life insurance products that package insurance protection with investments—realized via an underlying investment portfolio. There are several variants, some of which are rather innovative, depending on the way the life protection is offered and the funds that support it are constructed. The policyholders pay periodic or lump-sum premia, part of which is directed to pay for the life insurance and part of which is invested (although there are other alternatives to this) in one or more (mutual or internal) funds. Unit-linked insurance policies have become popular as they enable policyholders to invest premiums in various funds, with the investment risk borne by the policyholder (Hsu and Yan 2007; Vojvodić et al. 2023).

At the maturity of the policy the insured receive the value of the underlying investment portfolio. In case of death, the insured receives the value of the underlying portfolio and the sum assured (or the maximum of the two). Thus, benefits are directly correlated to the value of units in UCITS or assets in an internal fund owned by the insurer (Cristina and Diana-Maria 2015).

Index-linked products are a special type of such products whose investment component is linked to a stock (or other) index that serves as a benchmark for the underlying investment portfolio (Cristina and Diana-Maria 2015).

These products offer enhanced return potential but also increased risks for policyholders, effectively transferring investment risk from the insurer to the policyholder (Dimitrov 2022). This transfer raises concerns regarding the adequacy of consumer information and the balance between price and benefits (Dimitrov 2022). In conclusion, unit-linked and index-linked products signify a significant shift in the life insurance market by integrating insurance with investment opportunities. However, their increasing prevalence necessitates transparent consumer information and robust regulatory oversight to ensure policyholders’ protection (Cristina and Diana-Maria 2015; Dimitrov 2022).

Unit-linked and index-linked products transfer the investment risk from the insurer to the insured, whereas in traditional endowment (or pure endowment products), the risk is borne by the insurance companies, as they offer a guaranteed (technical) interest rate/return. As a result, the insurer does not carry the risk of life insurance options and guarantees, which affects the insurers’ exposure to insurance and investment risks. It thus influences the solvency capital required to cover these risks and, as a consequence, the Solvency Capital Requirement ratio of the insurer.

The variables are presented in

Table 1. Brief definition and role of the model variables.

Variables	Description	Role	Source
Target variable
SCR ratio	Solvency Capital Requirement ratio.	Solvency of the insurer	Insurance Risk Data (2023)
Features (Explanatory Variables)
Size	Total assets (natural logarithm).	Size of the insurance group	Insurance Risk Data (2023)
Property	Property as percent of investments.	Investment portfolio diversification	Insurance Risk Data (2023)
Government bonds to corporate bonds	Ratio of investments in government bonds to investments in corporate bonds.	Diversification of the insurance group’s bond investment portfolio	Insurance Risk Data (2023)
Collective	Collective investment undertakings as percent of investments.	Investment portfolio diversification	Insurance Risk Data (2023)
Unit_linked	Unit_linked and Index_linked as percent of liabilities.	Risk transfer from insurer to policyholder	Insurance Risk Data (2023)
Equities	Equities as percent of total investments.	Investment portfolio diversification	Insurance Risk Data (2023)
Bonds	Bonds as percent of total investments.	Investment portfolio diversification	Insurance Risk Data (2023)
Life concentration	Market share of the 3 biggest life premium writers of the national gross written premium.	Competition in the life insurance sector	EIOPA (2018, 2019, 2020, 2021, 2022b, 2023a)
Non-life concentration	Market share of the 3 biggest non-life premium writers of the national gross written premium.	Competition in the non-life insurance sector	EIOPA (2018, 2019, 2020, 2021, 2022b, 2023a)
Bond market	It covers long-term bonds and notes, treasury bills, commercial paper, and other short-term notes issued on domestic markets.	Domestic bond market development	European Central Bank—ECB Data Portal (2023)
Private debt	Total stock of loans and debt securities issued by households and nonfinancial corporations as a share of GDP.	Domestic private dept development	International Monetary Fund (2023b)
Real GDP growth	The real economic growth rate, or real GDP growth rate, measures economic growth, as expressed by the gross domestic product (GDP), from one period to another, adjusted for inflation or deflation.	Economic growth	World Economic Outlook (October 2023), International Monetary Fund (2023a)
Interest	Long-term interest rates are determined by the lender’s price, the borrower’s risk, and the decline in the capital value of government bonds maturing in ten years.	Low interest rates encourage investment in new equipment, while high interest rates discourage it, contributing to economic growth	OECD (2023)
Household spending	Household consumption expenditure is the final consumption expenditure made by residents to meet their daily needs, including housing, water, electricity, gas, and other fuels.	Household living costs	World Bank Open Data (2023)
Inflation change	Inflation rate, average consumer prices (annual percent change).	The rise in the cost of living in a country	World Bank Open Data (2023)
Government expenditure	General government expenditure indicates the size of government in each country as share of GDP, its approaches to public goods and services provision, and social protection measures.	Government spending in relation to GDP refers to public goods and services and social protection	International Monetary Fund (2023a)
Banking concentration	Banking concentration: percent of bank assets held by the top three banks.	Controlling for alternative choices in the cash deposits of insurance groups	International Monetary Fund (2023a)
Regulatory capital	Regulatory capital to risk-weighted assets. The capital adequacy of deposit-taking institutions.	The degree of robustness of financial institutions	International Monetary Fund (2023b)
Non-performing loans	The ratio of non-performing loans to total gross loans, as instability can disrupt economic activity and impose costs. A high ratio indicates loan portfolio deterioration.	Financial system strength	International Monetary Fund (2023b)
CO2 emissions	CO2 emissions per person are measured as the total CO2 produced by a country as a result of human activities divided by the population of that country. Carbon dioxide emissions are the main cause of global climate change, but the allocation of responsibility among regions, countries, and individuals remains a contentious issue in international discussions.	Climate change	Global Carbon Atlas (2023)

.

3.2. Summary Statistics—Correlation Analysis

The summary statistics of the key variables at the company level (

Table 2. Summary statistics and frequencies of the model variables for 2016–2022.

	Mean	Standard Deviation	Min	Max	5th Percentile	10th Percentile	25th Percentile	75th Percentile	90th Percentile	95th Percentile
Size	17.198	1.651	3.807	20.566	14.973	15.273	16.143	18.309	19.279	19.964
Property	0.047	0.048	0.000	0.275	0.000	0.001	0.009	0.066	0.109	0.152
Government bonds to corporate bonds	2.022	5.402	0.000	82.399	0.096	0.254	0.468	1.733	3.261	5.927
Collective	0.172	0.152	0.000	0.757	0.010	0.019	0.048	0.253	0.402	0.462
Unit_linked	0.201	0.236	−0.552	2.865	0.003	0.008	0.037	0.289	0.512	0.677
Equities	0.040	0.061	0.000	0.466	0.000	0.001	0.008	0.051	0.085	0.121
Bonds	0.653	0.173	0.141	0.993	0.322	0.395	0.547	0.787	0.852	0.896
Life concentration	0.380	0.133	0.240	0.781	0.242	0.243	0.270	0.450	0.600	0.640
Non-life concentration	0.362	0.145	0.140	0.700	0.140	0.149	0.260	0.466	0.58	0.6
Bond market	0.682	0.291	0.111	1.411	0.246	0.338	0.470	0.916	1.105	1.187
Private debt	1.664	0.554	0.670	4.068	1.103	1.175	1.222	2.116	2.419	2.497
Real GDP growth	0.015	0.035	−0.112	0.131	−0.065	−0.038	0.011	0.029	0.048	0.064
Interest	0.006	0.009	−0.005	0.061	−0.004	−0.004	0.000	0.011	0.017	0.022
Household spending	0.524	0.056	0.302	0.650	0.437	0.449	0.503	0.540	0.601	0.629
Inflation change	0.023	0.024	−0.011	0.144	0.001	0.002	0.008	0.025	0.069	0.082
Government expenditure	0.217	0.022	0.157	0.264	0.186	0.189	0.198	0.236	0.246	0.255
Banking concentration	0.696	0.121	0.332	0.959	0.450	0.579	0.634	0.791	0.876	0.905
Regulatory capital	0.195	0.021	0.138	0.269	0.167	0.177	0.180	0.206	0.224	0.233
Non-performing loans	0.028	0.023	0.003	0.171	0.009	0.010	0.020	0.029	0.035	0.060
CO2 emissions	14.214	3.158	6.870	29.701	9.311	10.010	11.748	16.179	17.816	18.660
SCR ratio	2.547	1.135	1.000	8.560	1.437	1.564	1.890	2.885	3.836	4.692

Source: Authors’ estimates using Python and Stata. N = 616.

) displayed negative values for the percentage of unit-linked and index-linked liabilities. Negative values for unit-linked and index-linked liabilities in SFCRs may arise from a combination of market-consistent valuation adjustments, the nature of the products, and the financial strategies employed by insurance companies. These values should be interpreted within the broader context of the insurer’s overall solvency and financial condition, as well as the regulatory environment in which they operate (Cristina and Diana-Maria 2015; Gatzert and Heidinger 2019; Jaśkiewicz 2020; Wünsch 2019; Zariņa et al. 2018).

Furthermore, some companies had no investments in property, government bonds, or shares. Excluding unit-linked and index-linked investments, the exposure to collective investment undertakings ranged from 17.2% to 75.7%, bonds from 65.3% to 99.3%, and shares from 4% to 46.6%.

The summary statistics at the market level also exhibited wide variations: Concentration in the life insurance market ranged from 24% to 78.1%, and in the non-life insurance market, it ranged from 14% to 70%. As a share of GDP, domestic public debt ranged from 11.1% to 141.1%, private debt from 67% to 406.8%, household expenditure from 30.2% to 65%, and government expenditure from 15.7% to 26.4%. Real GDP growth ranged from −11.2% to 13.1%, and long government bond yields from −0.5% to 6.05%. The annual inflation rate ranged from −1.1% to 14.4%. Bank concentration ranged from 33.17% to 95.88%, regulatory capital from 13.8% to 26.9%, and non-performing loans from 0.3% to 17.1%. CO₂ emissions ranged from 6.87 to 29.70 tonnes per habitat. In terms of solvency, the SCR ratio ranged from 100% (the safety threshold) to 856%.

Table 3. Correlation matrix of the model explanatory variables for 2016–2022.

	Size	Property	Government Bonds to Corporate Bonds	COLLECTIVE	Unit_Linked	Equities	Bonds	Life Concentration	Non-Life Concentration	Bond Market	Private Debt	Real GDP Growth	Interest	Household Spending	Inflation Change	Government Expenditure	Banking Concentration	Regulatory Capital	Non-Performing Loans	Co2 Emissions	SCR Ratio
Size	1
Property	−0.2656	1
Gov_bonds to corp_bonds	−0.1766	−0.0187	1
Collective	−0.0898	−0.0198	−0.1782	1
Unit_linked	0.1524	−0.0225	−0.1204	−0.2197	1
Equities	−0.0240	0.3316	−0.0407	−0.2205	0.1240	1
Bonds	0.0171	−0.2520	0.1353	−0.6131	−0.1202	−0.2227	1
Life concentration	−0.2024	0.3905	0.0968	−0.2269	0.2527	0.1672	−0.0074	1
Non-life concentration	−0.2246	0.2248	0.1654	−0.2123	0.4620	0.1770	−0.1342	0.6441	1
Bond market	0.1544	−0.0580	0.0818	−0.2633	−0.1090	0.0210	0.2827	−0.0513	−0.1562	1
Private debt	0.2082	0.1188	−0.1420	−0.2272	0.4434	0.3480	−0.0336	0.2632	0.0564	−0.1247	1
Real GDP growth	−0.0552	0.0380	0.0329	−0.0558	0.0702	0.0601	−0.0266	0.0783	0.0817	−0.1349	−0.0161	1
Interest	−0.0704	0.0753	0.3206	−0.2458	0.0933	0.0279	0.1216	0.2280	0.3178	0.2868	−0.1140	0.2503	1
Household spending	0.0375	−0.1116	0.1873	−0.1452	−0.1945	−0.0274	0.1433	−0.1052	−0.0482	0.7600	−0.5178	−0.0323	0.3803	1
Inflation change	−0.0029	0.0644	−0.0501	0.0823	0.1238	−0.0100	−0.1565	0.0600	0.1130	−0.0215	−0.0288	0.3517	0.5364	−0.0553	1
Government expenditure	0.2115	0.0899	−0.1260	−0.0185	0.2124	0.2529	−0.1757	0.1501	−0.0558	−0.1593	0.6323	−0.1128	−0.2808	−0.4391	0.0477	1
Banking concentration	−0.0171	0.0984	−0.1337	0.2553	0.0276	0.0112	−0.2701	0.0954	0.0835	−0.6425	0.1575	−0.0121	−0.3059	−0.5954	0.0057	0.5535	1
Regulatory capital	0.0901	0.1293	−0.0454	−0.0387	0.5594	0.2967	−0.3436	0.3175	0.5174	−0.3411	0.5561	0.0138	−0.0716	−0.4682	0.1596	0.4875	0.2887	1
Non-performing loans	−0.1269	−0.0598	0.4967	−0.1484	−0.2996	−0.1706	0.3111	−0.0856	−0.0196	0.2737	−0.3423	−0.0099	0.2903	0.3387	−0.2339	−0.3467	−0.1686	−0.5344	1
CO2 emissions	−0.2168	−0.1164	0.1510	0.1329	−0.3995	−0.2956	0.0593	−0.0390	−0.0447	−0.2413	−0.5299	0.0856	−0.0013	0.0284	−0.0481	−0.4550	−0.0094	−0.3459	0.1845	1
SCR ratio	−0.0264	−0.0152	−0.0871	0.2752	−0.2983	−0.1557	−0.1170	−0.4238	−0.2723	−0.2832	−0.2968	0.0000	−0.2338	−0.1305	−0.0124	−0.1564	0.1325	−0.1771	−0.0062	0.2742	1

presents the pairwise correlation of the independent variables utilized in the analysis. This information reveals the correlation between the various characteristics or factors, which can be useful in identifying the most significant financial factors that impact solvency ratios. According to Table 3, the Solvency Capital Requirement (SCR) ratio is most strongly correlated with the life concentration, with a correlation coefficient of −0.424. The next two correlated characteristics are unit-linked and index-linked liabilities, as well as bond market development, with correlation scores of −0.30 and −0.28, respectively.

3.3. Methodology

The field of statistics employs fixed functional forms for dependent and independent variables, frequently based on economic theories. Traditional econometric models can be used to investigate the relation among these variables. Ordinary least squares (OLS) is the most widely used approach, which aims to minimize the sum of squares of residuals.

Recently, though, machine learning approaches have been introduced to address similar problems. Machine learning is an effective tool that learns from past data and operates automatically. It discovers patterns in data (Bzdok 2017; Bzdok et al. 2017) and is applicable to a broad range of problems (Berry and Linoff 2009; Kudyba and Kudyba 2014; Sarker 2021), demonstrating high efficiency and accuracy in prediction and classification. Machine learning is widely utilized in various sectors, including finance (Heaton et al. 2017) and insurance (Lin et al. 2017) in private industries and healthcare (Topol 2019) and education (Peters 2018) in public services.

To forecast insolvency and bankruptcy, statistical and AI approaches are commonly integrated into empirical models (Kumar and Ravi 2007). Statistical methods such as multivariate discriminant analysis (Meyer and Pifer 1970; Trieschmann and Pinches 1973; Sinkey 1975; Ambrose and Carroll 1994) and logistic regression (Martin 1977; Chen and Wong 2004; Campbell et al. 2008; Cheng and Weiss 2012; Zhang and Nielson 2015; Rauch and Wende 2015) have been employed in the financial literature, while hazard models (Tian et al. 2015; Eling and Jia 2018) and partial least squares (Mselmi et al. 2017) have also been utilized. However, these models rely on specific data distribution assumptions that, if violated, can impact accuracy (Kumar and Ravi 2007; Wang et al. 2014). Conversely, AI methods, particularly machine learning, have increasingly been embraced for predicting insolvency and failure.

AI techniques for foreseeing insurance company insolvency involve neural networks (NN), XGBoost, random forest (RF), and support vector machines (SVMs) (Tam and Kiang 1992; Brockett et al. 1994, 1997, 2006; Geng et al. 2015; Climent et al. 2019; Carmona et al. 2019; Tanaka et al. 2016; du Jardin 2021; Eling and Jia 2018). Lee and Urrutia (1996) reported that hazard and logit models exhibit comparable predictive accuracy.

According to Brockett et al. (2006), it was found that neural network methods surpass statistical approaches in predicting the financial distress of life insurers. Moreover, Carmona et al. (2019) discovered that XGBoost outperforms logistic and random forest methods. Additionally, Barboza et al. (2017) revealed that random forest outperforms several benchmark approaches, including logistic regression and neural networks, for predicting corporate insolvency.

In the domain of financial insolvency in property and casualty insurance, machine learning models and artificial intelligence (AI) methods are commonly employed. For instance, Chiet et al. (2009) conducted studies using AI methods, while Brockett et al. (1994, 1997, 2006) utilized neural networks, Rustam and Saragih (2021) applied random forest, Rustam and Yaurita (2018) used support vector machines (SVMs), and Vargas et al. (2003) employed rough set theory.

ML techniques differ from traditional econometric methods, which are typically assessed using metrics derived from in-sample tests (e.g., R², p-values) and out-of-sample tests (e.g., bias, accuracy). These methods divide the data into training and test data (in-sample and out-of-sample) and employ cross-validation to train a model. According to the “no free lunch” theorem, there is no single machine learning model that can be considered the best for a given dataset. Therefore, it is advisable for economists to utilize a range of methods and to draw upon both statistical and algorithmic traditions (Wolpert 1996; Athey and Imbens 2019).

In the realm of supervised learning, algorithms are trained on labeled datasets that have already been identified as providing answers to a particular question. This approach enables machines to learn from past experiences and make well-informed decisions. Supervised learning refers to the process by which machines are taught to map input data to output data based on a set of labeled examples. This is achieved by training algorithms on a labeled dataset, which consists of a selection of training examples.

The input dataset is divided into training and testing datasets. The training dataset contains an output variable that needs to be predicted or classified. All algorithms learn some type of pattern from the training dataset and apply it to the testing dataset for prediction or classification. They begin with a training set of n data pairs (x_i, y_i), i = 1, …, n. The vector x denotes a point in p-dimensional space, x_i = (x_i1, …, x_ip), with the coordinate x_ij corresponding to the ith value of the feature x_j. The samples are assumed to be independently and identically distributed (i.i.d.) instances of a fixed but unknown joint distribution P (X, Y).

The objective of supervised learning is to infer a function f: X→Y that maps x vectors to y outcomes. The performance of the model is evaluated using a loss function, which quantifies the error of the model on an independent test set sampled from the same distribution.

To implement the models in this study, we utilized Python 3.9, along with several machine learning and data analysis libraries and frameworks, including NumPy, Pandas, Scikit-learn, and Matplotlib. Our research was based on pooled OLS (the basic linear regression model) and supervised ML models, such as random forest, extra trees, gradient boosting, and eXtreme gradient boosting (XGBoost). Additionally, we implemented SVM (support vector machine) regression and MLP (Multi-Level Perceptron) regression; however, the results of the latter were superior to the other supervised ML models mentioned above.

Decision trees are a simple and easy-to-interpret model for classification and regression tasks. Random forests and extra trees are two ensemble methods that enhance the performance of individual trees by reducing variance and increasing predictive accuracy. These approaches typically exhibit better predictive performance and are less susceptible to overfitting than single decision trees, as demonstrated by Denuit et al. (2020) and Zhang et al. (2014). Furthermore, extra trees are more efficient since they randomize cut points and attribute selection, thereby reducing computational complexity, as emphasized by Zhang et al. (2014).

A decision tree is a non-parametric supervised learning algorithm used for classification and regression tasks. It comprises a hierarchical tree structure with a root node, branches, internal nodes, and leaf nodes. The root node, devoid of incoming branches, connects to internal or decision nodes through outgoing branches. These nodes evaluate features to create homogeneous subsets, known as leaf or terminal nodes, representing all possible outcomes in the dataset (Abellán and Masegosa 2009). The leaf nodes represent all possible outcomes within the dataset (Figure 1).

The random forest methodology constructs numerous decision trees by employing distinct data subsets and features, subsequently aggregating their results through averaging or voting. This technique enhances model performance and decreases the likelihood of overfitting. Unlike conventional approaches that select the optimal feature to split a node, random forests choose the best feature from a random subset. The algorithm necessitates only two hyperparameters to be tuned: the maximum number of features in a tree and the maximum tree depth (Denuit et al. 2020) (Figure 2).

Extreme Random Trees, or extra trees, employ a stochastic method by randomly selecting thresholds rather than seeking the optimal one (Geurts et al. 2006). This technique examines random splits across a subset of features, unlike random forests, which assess all possible splits within a subset (Figure 3). Extra trees provide two primary advantages: they diminish bias by sampling the entire dataset during tree construction, thereby preventing biases from various data subsets, and they reduce variance by randomizing node splits in decision trees, diminishing the algorithm’s susceptibility to specific features or patterns in the dataset (Papadopoulos et al. 2017).

All variables in our dataset were normalized to a zero mean and unit variance to ensure comparability and consistent ranges among features. This process, known as feature normalization, is crucial because feature magnitude affects numerous machine learning techniques. Features with larger scales can dominate the learning process, potentially skewing results. Scaling features ensure equal contribution to learning, thereby improving performance and convergence speed for algorithms such as gradient boosting, k-nearest neighbors, and support vector machines. Furthermore, scaling prevents numerical instability due to large-scale disparities, which is essential for distance calculations or matrix operations. By scaling, each feature is given equal consideration, eliminating bias from larger-scale features. This practice, which is uncommon in traditional economics, prevents models from merely memorizing values for prediction (Müller and Guido 2017, pp. 17–18).

Our dataset, consisting of 616 observations, was tested using k-fold cross-validation (Chen 2021) to prevent overfitting. In this method, the training data are divided into k subsets, and training and testing are performed k times. In each iteration, a different subset is used to test the model, while the remaining k − 1 subsets are used to train the model. The overall performance of each model is calculated as the average performance over all iterated k subsets.

Reserving 25 percent of the data for testing is standard practice according to the literature, which ensures that the supervised learning method generalizes to unobserved data (Müller and Guido 2017, pp. 17–18).

Following this approach, we split the data in each model into 75% training and 25% testing and used the R² metric and the root mean square error (RMSE) to compare and estimate the accuracy of the models. The RMSE is a measure of the differences between the observed and predicted values, so lower RMSE values are expected from regression models. On the other hand, R² indicates how well the regression model fits the observed values of the dependent variable, so higher R² values are desirable.

We also conducted a separate analysis of the feature importance for each model, as it is essential to understand the factors affecting the SCR ratio. Feature importance values are the average weights of nodes in decision trees or forests, representing the number of training samples associated with each node (Chen 2021), they provide a ranking of variables according to their contribution to the model and their significance in generating a forecast. Feature importance identifies and ranks the most influential features contributing to the model’s predictive power, while feature selection chooses a subset of relevant features for model construction (Chemmakha et al. 2022).

They are similar to standardized regression coefficients (beta coefficients) in conventional statistics (Newman and Browner 1991) but differ in one critical aspect. Beta coefficients can be positive, negative, or zero, but the importance of the characteristic is always non-negative. Consequently, they provide no information about the positive or negative correlation between a predictor and the target variable.

4. Empirical Results

Our research analyzes the impact of insurers’ investment portfolios on insurers’ solvency ratios (SCR ratios). According to our analysis, which employed linear regression as the base model and supervised machine learning models, the performance of supervised ML was superior to traditional linear regression in random forest, extra trees, gradient boosting, eXtreme gradient boosting (XGBoost), Support Vector Regression (SVR), and Multi-Layer Perceptron (MLP), achieving better results in extra trees regression. Traditional linear regression attained an R² of 38.64 (as shown in

Table 4. The basic linear regression model (based on a train/test split of standardized data).

	R2	RMSE
Training set score:	0.386375	0.783342
Test set score:	0.338236	0.745446
Variables	Coefficients	p-values
Size	0.02969	0.66016
Property	0.136532 **	0.00495
Government bonds to corporate bonds	−0.03930	0.45367
Collective	−0.04763	0.45970
Unit_linked	−0.227071 ***	0.00021
Equities	−0.08617	0.08162
Bonds	−0.07999	0.22194
Life concentration	−0.414205 ***	0.00000
Non-life concentration	0.10211	0.24075
Bond market	−0.303901 ***	0.00083
Private debt	−0.06004	0.52401
Real GDP growth	0.00570	0.89916
Interest	−0.158275 *	0.03175
Household spending	0.00830	0.94519
Inflation change	0.07852	0.22976
Government expenditure	−0.04218	0.59264
Banking concentration	−0.06013	0.41616
Regulatory capital	−0.02360	0.79039
Non-performing loans	−0.00628	0.92353
CO2 emissions	0.06236	0.27160
Intercept	0.000000	1.00000

Statistical significance—p < 0.001: ***; 0.01: **; 0.05: *. Source: Authors’ estimates using Python. N = 616.

).

4.1. Linear Regression

According to the results of the basic linear regression presented in Table 4, it is evident that investments in property, unit-linked and index-linked liabilities, life market concentration, domestic bond market development, and long-term interest rates have a statistically significant influence on the solvency ratios of insurance firms.

The results of linear regression indicate that property exerts a positive statistically significant impact on the SCR ratio, whereas unit-linked, life concentration, bond market, and interest rate post a negative statistically significant effect on the SCR ratio. The remaining variables have no statistical significance.

4.2. Machine-Enhanced Methods

The findings of the tree-based models are displayed in

Table 5. Outcome of all regression models for our dataset, linear regression and supervised learning models, random forest, extra trees, gradient boosting, XGBoost, SVR, and MLP, for the period 2016–2022.

	R2		RMSE
	Train	Test	Train	Test
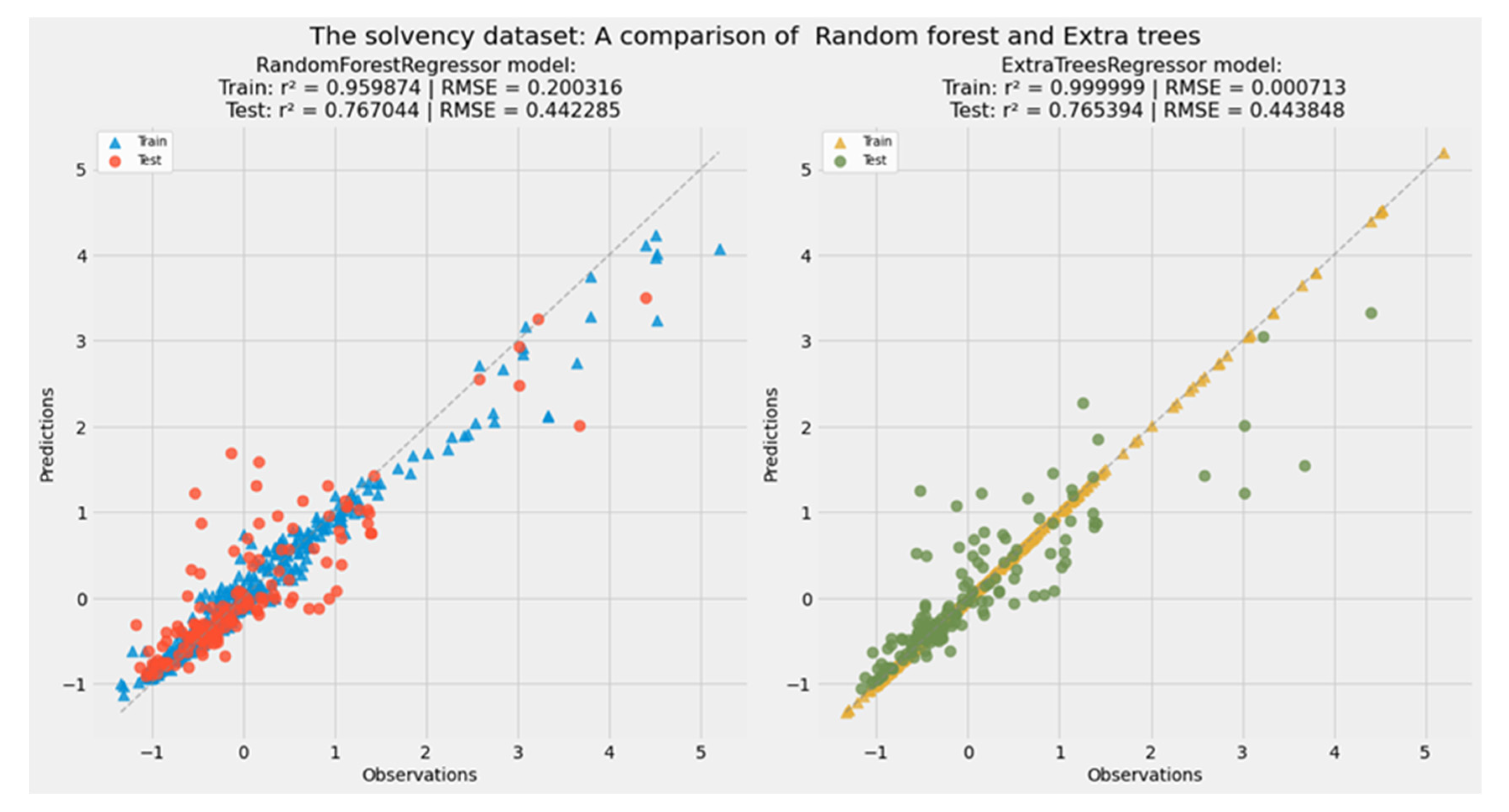
Linear regression	0.386375	0.338101	0.783342	0.745522
Random forest regression	0.959874	0.767044	0.200316	0.442285
Extra trees regression	0.999999	0.765394	0.000713	0.443848
Gradient boosting regression	0.799700	0.628627	0.447549	0.558431
XGBoost (extreme gradient boosting regression)	0.917349	0.655580	0.287491	0.537785
SVM (support vector machine)	0.628154	0.496709	0.609792	0.650091
MLP Regression (Multi-Level Perceptron regression)	0.838898	0.570523	0.400128	0.600530
No of Observations	462	154	462	154

Source: Authors’ estimates using Python. N = 616.

, where it becomes apparent that the random forest and extra trees models yield impressive accuracy, with R² values reaching or even surpassing 0.96.

The random forest model is less accurate than the extra trees model. The RMSE value for extra trees was 0.000713, indicating that the model had a low average percentage error. The root mean square error (RMSE) is a metric used to measure the average difference between the predicted and actual values generated by a statistical model. It is calculated as the square root of the average of the squared residuals, and its unit is the same as the dependent variable. A value of 0 indicates perfect accuracy, while low values indicate good fit and accuracy. High values suggest poor fit and lower accuracy. The RMSE is a widely used measure of prediction error and is commonly used in regression and other statistical models.

The visual representation of the estimated and observed values can be found in Figure 4. After careful consideration of the available data, the extra trees model was chosen to perform additional analysis.

Based on the results of the extra tree regression (

Table 6. Extra trees regression.

	R2	RMSE
Train	0.999999	0.000713
Test	0.765394	0.443848
Dependent Variable: SCR ratio
Variable:	Importance:	Variable:	Importance:
Property	0.21	Bonds	0.03
Life concentration	0.18	Household spending	0.01
Unit_linked	0.16	Banking concentration	0.01
Size	0.1	Non-performing loans	0.01
Bond market	0.07	CO2 emissions	0.01
Non-Life concentration	0.06	Real GDP growth	0
Government bonds to corporate bonds	0.05	Interest	0
Private debt	0.04	Inflation change	0
Collective	0.03	Government expenditure	0
Equities	0.03	Regulatory capital	0
	Train	Test
No. of Observations	462	154

Source: Authors’ estimates using Python. N = 616.

), it can be concluded that investment behavior, as well as various firm-specific characteristics, including investments in property, unit-linked and index-linked liabilities, firm size, the government-to-corporate bond investment ratio, and investments in collective undertakings, equities, and bonds, and country-specific factors, such as life and non-life market concentration, domestic bond market development, private debt development, household spending, banking concentration, non-performing loans, and CO₂ emissions, can predict the solvency of insurance companies (as they exhibit positive/non-zero importance).

4.3. Panel Data Analysis

In addition to pooled OLS and ML-based techniques, we performed additional analysis using panel data, so as to provide additional support to the evidence that the previously employed methods revealed (following the recommendation of the anonymous reviewer). Panel data analysis offers several advantages such as incorporating time-series and cross-sectional dimensions, addressing individual heterogeneity, reducing multicollinearity, and increasing degrees of freedom. Our panel data exhibit autocorrelation, cross-sectional dependence, and heteroscedasticity, posing significant econometric challenges.

This study uses the time-series cross-sectional Prais–Winsten (PW) regression with the panel-corrected standard error (PCSE) model as a baseline estimate, allowing for heteroskedastic and contemporaneously correlated disturbances across the panel. The PCSE correction mitigates statistical overconfidence often associated with the feasible generalized least-square estimator when total periods are smaller than total sample entities (countries, companies, etc.) (Beck and Katz 1995; Bailey and Katz 2011; Moundigbaye et al. 2018; Hoechle 2007).

The general empirical model that examines the factors affecting SCR ratio is:

$${SCRratio}_{i,t}=a+\beta {Firm}_{i,t}+\gamma {Country}_{i,t} + {\epsilon }_{\iota ,\tau }$$

(1)

The dependent variable is the SCR ratio, as mentioned above. Firm and country represent firm-specific and country specific variables, as described earlier in the text. Two tests were used for panel level heteroscedasticity: the Modified Wald test and the LR test. The Wooldridge test is used to test for autocorrelation in panel data. The results of heteroscedasticity and autocorrelation indicate that heteroscedasticity and autocorrelation exist in our panel data. In this context, we adopted the PCSE model following the panel data estimation as shown in the basic equation, following Bailey and Katz (2011) and Jönsson (2005), to address the heteroscedasticity, cross-sectional dependence, and autocorrelation in the variables in a small dataset with short period (T) and large cross-sectionals (N). The results are displayed in

Table 7. Prais–Winsten regression, correlated panel-corrected standard errors (PCSEs).

Dependent Variable: SCR Ratio
Variable	Coef.	St. Err.	t-Value	p-Value	95% Confidence	Interval
Size	−0.026	0.032	−0.81	0.419	−0.089	0.037
Property	2.353 **	0.921	2.56	0.011	0.548	4.157
Government bonds to corporate bonds	−0.007 **	0.003	−2.26	0.024	−0.013	−0.001
Collective	0.452	0.363	1.25	0.212	−0.258	1.163
Unit_linked	−0.372	0.345	−1.08	0.282	−1.049	0.305
Equities	−0.519	0.767	−0.68	0.499	−2.023	0.986
Bonds	−0.296	0.275	−1.08	0.282	−0.834	0.243
Life concentration	−2.972 **	0.546	−5.44	0	−4.043	−1.901
Non-Life concentration	−0.039	0.606	−0.06	0.948	−1.227	1.148
Bond market	−0.854 **	0.256	−3.33	0.001	−1.356	−0.352
Private debt	−0.415 **	0.113	−3.69	0	−0.636	−0.194
Real GDP growth	0.139	0.422	0.33	0.741	−0.687	0.966
Interest	−4.573	6.166	−0.74	0.458	−16.659	7.513
Household spending	−2.56 *	1.005	−2.55	0.011	−4.531	−0.59
Inflation change	0.849	1.682	0.5	0.614	−2.449	4.146
Government expenditure	2.931	2.956	0.99	0.321	−2.862	8.724
Banking concentration	−0.871	0.585	−1.49	0.137	−2.018	0.276
Regulatory capital	−1.913	2.37	−0.81	0.419	−6.558	2.731
Non-performing loans	−0.514	1.538	−0.33	0.738	−3.528	2.5
CO2 emissions	0.039 *	0.018	2.13	0.034	0.003	0.075
Constant	6.681 **	0.918	7.28	0	4.882	8.481
Mean dependent var		2.547		Standard dependent var		1.135
R-squared		0.454		No. of observations		616
Chi-square		433.169		Prob > chi2		0

Statistical significance: 0.01: **; 0.05: *. Source: Authors’ estimates using Stata. N = 616.

.

The results of the panel data analysis complement the results of pooled OLS. More specifically, when it comes to property, we realize that it has a positive statistically significant impact on the SCR ratio, whereas unit-linked, life concentration, and bond market show a negative statistically significant effect on the SCR ratio. Furthermore, the ratio of government to corporate bonds, private debt, and household spending exert a negative, whereas CO₂ emissions post a positive, statistically significant influence on the SCR ratio. The rest of the variables are not statistically significant.

5. Discussion

Summing up, this research examines the effect of insurance groups’ investment portfolios on their solvency ratios from 2016 to 2022, using data from 88 European Union insurance groups. Employing linear regression and various supervised machine learning models, this study finds that extra trees regression outperforms traditional linear regression in predicting solvency ratios. The extra trees regression results, considering the values of feature importance, indicate that investment behavior, firm-specific characteristics (such as investments in property, unit-linked and index-linked liabilities, firm size, government-to-corporate bond investment ratio, and investments in collective undertakings, equities, and bonds), and country-specific factors (including life and non-life market concentration, domestic bond market development, private debt development, household spending, banking concentration, non-performing loans, and CO₂ emissions) are important for insurance companies’ solvency.

We hereby attempt to explain the importance exhibited by these variables, as evidenced by the extra trees approach, supplemented by the findings of the traditional econometric models (where appropriate). The elaboration takes place following the importance as displayed in Table 6. Linear regression coefficients and significance come from Table 4; the respective coefficients and significance for the panel data analysis come from Table 7.

5.1. Property

Starting with property investing, we observe that the results from the SCR ratio panel data analysis show that the coefficient of property investments is positive and significant, providing support to the findings of the linear regression and machine-enhanced methods. More specifically, a one percent increase in the property allocation leads to a 2.3% increase in the SCR ratio. This is in line with the linear regression output, which indicates a 0.14% increase. Apparently, as the value of property holdings soars, the value of total assets gets higher, and this leads to an increase in the SCR ratio.

Investing in commercial or residential property involves varying levels of risk, which are influenced by factors such as location, market conditions, and property type. Residential property typically has lower risk due to the consistent demand for housing. However, real estate market volatility can impact property values, which, in turn, can affect balance sheets and solvency ratios. Unlike stocks and bonds, real estate is relatively illiquid, and market downturns can hinder quick sales, straining liquidity, and solvency. Property may provide rental income, enhancing cash flows and supporting liabilities, but maintenance costs, taxes, and management fees can offset rental income, impacting profitability and solvency. Diversifying investments across property types and locations can help mitigate risks and stabilize returns, positively influencing solvency ratios. On the other hand, overexposure to a single property type or market increases risk and can harm solvency ratios if markets decline. Economic cycles and downturns can reduce property values and rental income, negatively affecting financial health and solvency ratios. Additionally, interest rate changes impact property investment returns; rising interest rates increase borrowing costs and reduce property values, affecting solvency ratios. Therefore, insurers’ property investments influence solvency ratios in a complex manner, shaped by market conditions, regulatory frameworks, and investment strategies. Solvency II regulation may not significantly restrict the impact of property investments on solvency ratios; market dynamics and insurers’ risk appetites are critical in determining these investments’ effects on financial stability (Aldukhova et al. 2020; Guidara and Lai 2015; Höring 2013; Krausch 2016; Leinonen 2005; Wolski and Zaleczna 2010, 2011). While some insurers reap the benefits of these investments (Chou and Chang 2011), others do not find them advantageous (Wolski and Zaleczna 2010). Regulatory frameworks significantly impact insurers’ decisions regarding property investments (Krausch 2016), and insurers must carefully align their property investment strategies with solvency management (Abdelzaher and Born 2022; Guidara and Lai 2015; Siopi et al. 2023).

5.2. Concentration in the Life and Non-Life Insurance Markets

Monitoring the level of concentration in the life and non-life insurance markets and its implications for insurer solvency is an issue of great importance to regulatory bodies, policyholders, and insurers. The coefficient of concentration in the life insurance market (as estimated by the panel data analysis) demonstrates a negative and statistically significant relationship. A one percent increase in the life insurance concentration results in an almost 3% drop in the SCR ratio. This is consistent with the linear regression coefficient that indicates a 0.4% drop in the SCR ratio. This emanates from the fact that market leaders may be inclined to launch riskier products (capitalizing on economies of scale and stronger balance sheets) and the other players follow them (so as to remain competitive). Consequently, the assumed risk is higher compared to the assets held, which reduces the SCR ratio.

A high concentration of firms in the market may lead to reduced diversification, as dominant players may become overconfident and pose systemic risks to the industry if they encounter financial difficulties. Dominant firms may also exert significant market power, potentially leading to complacency in maintaining adequate capital buffers and taking on riskier investments due to a perceived “too big to fail” status. Failure of a dominant firm can have significant consequences for the market, including amplifying shocks across interconnected firms. While consumer confidence may rise if dominant firms are perceived as stable, their failure or distress can have a severe impact on trust in the industry. The existing literature does not directly address market concentration in relation to solvency ratios but provide insights into factors affecting solvency and financial stability. Mathur and Paul (2014) examined the efficiency of non-life insurers in India, identifying financial ratios as key to technical efficiency, which could indirectly influence solvency. Zariņa et al. (2018) report on the solvency ratios of Baltic non-life insurers under Solvency II, noting strong capitalization but not linking it to market concentration. Joo (2013) assessed the solvency of Indian non-life insurers post-liberalization, suggesting that the claim ratio and firm size affect solvency, implying a possible indirect relationship between market concentration and solvency. The relevant research does not explicitly investigate the impact of market concentration on solvency ratios; it instead provides information on factors such as efficiency, capitalization, and regulatory frameworks, which are essential for understanding how market concentration might affect insurers’ solvency. It is thus realized that further research specifically addressing this relationship is necessary to draw definitive conclusions (Joo 2013; Mathur and Paul 2014; Zariņa et al. 2018).

5.3. Unit-Linked and Index-Linked Products

Unit-linked and index-linked products have a direct impact on the solvency ratios of insurance companies by integrating insurance coverage with investment components that are tied to underlying assets or indices. The linear regression coefficient shows that a 1% increase in the unit-linked portfolio would lead to a 0.2% drop in the SCR ratio. The negative effect is justified by the fact that they assume the protection risk (hence, the denominator increases), whereas the assets are allocated to investments not held by the insurer (which leaves the numerator almost the same). In any case, the impact of UL products needs to be further researched due to their complex structure.

Although the available literature does not directly address the impact of these products on solvency ratios, it does provide valuable insights. Kaur and Bansal (2016) conducted a study on the performance of unit-linked insurance plans (ULIPs) in India, focusing on risk and return, which can indirectly affect solvency ratios. Gupta (2012) discussed regulatory changes to ULIPs in India, which aimed to increase the insurance component over the investment component, potentially influencing the risk profile of these products and, consequently, solvency ratios. Therefore, although the relevant research does not explicitly analyze the impact of unit-linked and index-linked products on solvency ratios, it emphasizes the complexity of these products associated with the regulatory environment. The performance of these products, which is influenced by market conditions and regulations, affects the risk profile and capital adequacy of insurance firms, which are crucial components of solvency assessments (Kaur and Bansal 2016; Gupta 2012).

5.4. Size

Size proved to be an important variable for the SCR ratio. This may be attributed to the fact that large insurance companies enhance their solvency by diversifying their operations across products and regions, leveraging economies of scale, and maintaining access to capital. These strategies help reduce costs in administration, claims processing, and investment management while also increasing their negotiating power and capital reserves. In addition, they invest in advanced risk management tools and attract top talent. However, large insurers can create systemic risks, and managing their diversified operations may lead to inefficiencies and complex interdependencies. In contrast, small insurance companies typically focus on niche markets and offer customized products and services. They adapt quickly to market changes and foster strong customer relationships, improving service, loyalty, and local market understanding. While the failure of small insurers may not significantly impact the broader financial system, their limited diversification increases exposure to specific risks. These companies often struggle to access capital markets and have smaller reserves and capital buffers, making them more vulnerable to financial shocks. They also experience higher per-unit costs and have limited resources for advanced risk management. As a result, large insurers generally have higher solvency ratios compared to small insurers that specialize in specific markets or products. The relationship between company size and solvency in the insurance industry is multifaceted, with studies indicating both positive and negative correlations. Abduh and Isma (2016) identifies a negative relationship between company size and solvency in the context of life insurance and family takaful in Malaysia, suggesting that larger companies may face greater solvency challenges (Abduh and Isma 2016). Conversely, Sutanto et al. (2023) find that company size has a significant influence on the solvency of the insurance industry, although it does not specify the direction of this relationship (Sutanto et al. 2023). Interestingly, Lee (2018) and Kartini (2023) present contrasting findings. Lee (2018) reports that firm size has a significant positive influence on an insurer’s solvency in the property-liability insurance industry in Taiwan (Lee 2018), while Kartini (2023) indicates that company size, along with other factors, has a significant impact on financial performance, which could be indirectly related to solvency (Kartini 2023).

5.5. Bond Markets

To understand the importance of bond markets, we realize that a well-established domestic bond market provides essential, diversified investment options for financial health and fulfilling long-term commitments. The negative and significant coefficient of bond market development in both the panel data analysis and linear regression on insurance solvency leads to several important conclusions. The increase in the bond market by 1% would lead to a decrease in the SCR ratio by approximately 0.9% (0.3%) as per the evidence of the panel data analysis (linear regression). This results from the fact that when the bond market increases, the value of the required assets increases (the denominator) as bonds constitute the primary investment of insurers (especially life insurers) for the portfolio earmarked to provide cushion for the assumed risks. However, as total assets contain other asset classes (the numerator), their value may not increase the same, thus leading to a drop in the SCR ratio. Bond market development appears to have an adverse effect on insurance solvency, contrary to some expectations. This finding aligns with (Drenovak et al. 2020), which suggests that regulatory efficient portfolios under Solvency II are dominated by short-term and BBB-rated bonds, indicating a potential weakness in the regulation that may lead to overexposure to higher credit risk (Drenovak et al. 2020). The negative relationship could be attributed to the inefficiency of the over-the-counter (OTC) secondary corporate bond market and the lack of trade transparency, as highlighted in (Berrich et al. 2022). Interestingly, this result contradicts some other findings in the literature. For instance, (Nneka et al. 2022) and (Ugbam et al. 2023) report positive effects of government bond capitalization on economic growth, which could indirectly benefit insurance solvency. However, these papers also note the negative effects of corporate bond capitalization on economic growth in developing countries (Nneka et al. 2022; Ugbam et al. 2023). This discrepancy underscores the complex relationship between bond markets and financial stability. In conclusion, the negative coefficient suggests that policymakers and insurance companies should carefully consider their exposure to bond markets. As (Shiu 2005) indicates, solvency determinants can change over time, emphasizing the need for dynamic risk management strategies. Furthermore, the findings highlight the importance of diversification in investment portfolios and the potential risks associated with over-reliance on bond markets for maintaining solvency in the insurance sector (Drenovak et al. 2020; Shiu 2005).

Offering a variety of securities enables insurers (and all investors) to achieve risk diversification and effectively manage interest rate, credit, and duration risks. The regular interest payments from bonds aid in cash flow management and obligation fulfillment, while high-quality bonds safeguard capital and minimize default risk, contributing to financial stability. Furthermore, developed markets offer greater liquidity, facilitating efficient trading necessary for short-term liability management and liquidity ratio maintenance. This liquidity and market transparency enable effective security pricing, allowing for informed investment choices and precise portfolio assessments. The Solvency II framework mandates that insurers hold high-quality, liquid assets, favoring government and investment-grade corporate bonds due to their lower risk weights, thus boosting solvency ratios. A robust bond market typically reflects a stable, expanding economy, reducing default risk and enhancing issuers’ creditworthiness, which benefits insurers’ portfolios and supports a stable interest rate environment for improved interest rate risk management. In contrast, underdeveloped bond markets limit investment choices, resulting in increased risk concentration, reduced liquidity, greater volatility, and potential solvency challenges.

The literature on factors affecting insurers’ solvency has been thoroughly examined, but it fails to make a direct connection between the development of domestic bond markets and solvency ratios. For instance, Siopi et al. (2023) identify key determinants such as reinvestment rates and long-term investments that impact EU insurers’ solvency, but they do not address domestic bond markets. Similarly, Düll et al. (2017) discuss sovereign risk transmission and the impact of sovereign bond portfolios on insurer risk, but they omit the role of domestic bond markets (Düll et al. 2017). Ziemele and Voronova (2013) and Kramarić et al. (2019) explore the Solvency II framework and insurers’ soundness determinants but do not connect domestic bond market development to solvency ratios (Kramarić et al. 2019; Ziemele and Voronova 2013). Siddik et al. (2022) and Tsvetkova (2023) contribute to understanding insurers’ financial stability but do not establish a direct link with domestic bond market development (Siddik et al. 2022; Tsvetkova 2023). In summary, while the literature covers a range of factors influencing insurers’ solvency, including investment strategies, regulatory frameworks, and macroeconomic conditions, there is a gap in the direct examination of the relationship between the development of domestic bond markets and insurers’ solvency ratios.

5.6. Government to Corporate Bonds

The appropriate ratio of government to corporate bonds in insurance investment portfolios is critical for maintaining solvency, given the varying risk levels and capital requirements of different asset classes. The panel data analysis shows that a 1% increase in the government-to-corporate bond ratio produces a less than 0.1% drop in the solvency ratio. The explanation for this effect is similar to the one provided in the previous paragraph for the bond market development, as the investment portfolios of insurance companies, especially the fixed income one, invest more in government than in corporate bonds. As a matter of fact, the government bond market materially exceeds the corporate one.

Heinrich and Wurstbauer (2014) note that the low-interest rate environment has led insurers to diversify from low-yield government bonds to alternative assets, such as real estate and infrastructure. This shift aims to fulfill obligations from existing life insurance contracts, but it may conflict with the Solvency II Directive, which imposes higher capital requirements and could lead to inefficient capital allocation if optimization diverges from traditional asset allocation (Heinrich and Wurstbauer 2014). Höring (2013) suggests that Solvency II might not significantly constrain market risk, as it demands less capital than Standard and Poor’s for the same risks, potentially leaving investment strategies unchanged (Höring 2013). Conversely, Graham et al. (2014) find that increased government debt issuance is negatively correlated with corporate debt and investment but positively correlated with corporate liquidity, influencing asset pricing and investor portfolio allocations (Graham et al. 2014). The balance between government and corporate bonds in insurance portfolios is influenced by regulatory frameworks such as Solvency II, which ensures solvency through appropriate capital requirements. Although the shift to alternative assets may be a response to low yields on government bonds, it is crucial to consider the potential for increased portfolio risk and broader capital market implications (Heinrich and Wurstbauer 2014). The actual impact of Solvency II on investment strategies remains uncertain, as it may be less restrictive than other models (Höring 2013). The interplay between government debt issuance and corporate financial policies further complicates this relationship, affecting investment and liquidity strategies (Graham et al. 2014). Therefore, insurance companies must carefully navigate these factors to maintain solvency while optimizing investment returns.

5.7. Private Debt

The expansion of the domestic private debt market presents both challenges and opportunities for insurance companies as investors. The significant negative coefficient of domestic private debt on insurance solvency (as per the panel data analysis) indicates that a one percent increase in the domestic private debt market implies a 0.4 decline in the SCR ratio. A potential interpretation is that when the debt of individuals/households and enterprises increases, then the share of the wallet left for insurance decreases. This leads to reduced assets for the insurers as, on the one hand, they receive less premia, but, on the other hand, they may still have to assume the risks but at lower rates so as to remain affordable (allowing for a lower margin). This reduces the numerator but increases the denominator (or leaves it the same), which yields a lower SCR ratio. This suggests that elevated private sector debt levels may compromise the financial stability of insurance firms. The negative correlation between domestic private debt and insurance solvency underscores the financial system’s interconnectedness. It highlights the necessity of monitoring private sector debt levels and their potential effects on the insurance industry’s financial health.

A developed private debt market extends the range of investment options available to insurers, enabling them to diversify their portfolios beyond traditional public debt. By investing in various types of private debt, insurance companies can reduce the risks associated with specific borrowers or sectors. Life insurers, who hold a significant amount of private debt, must continuously assess borrower credit quality and manage risk (Pottier 2007). Regulatory constraints and financial market development affect investment decisions and portfolio optimization, potentially limiting investment opportunities and affecting the risk–return trade-off (Kočović et al. 2015). Despite market growth, issues such as lengthy issuance processes, substantial issuer requirements, and inadequate trading platforms and information systems persist, affecting liquidity and price formation (OECD 2012). Furthermore, insurance companies exhibit procyclical investment behavior during market shocks, which can destabilize the macroeconomic environment (Duijm and Bisschop 2018). This contrasts with countercyclical strategies that could enhance financial stability. Thus, while the expanding domestic private debt market allows for portfolio diversification and higher returns, it also brings regulatory, developmental, and risk management challenges. Additionally, procyclical tendencies during downturns may exacerbate financial instability, necessitating a nuanced understanding of investment behavior within market dynamics (Duijm and Bisschop 2018). Consequently, insurance companies must navigate these complexities to capitalize on the growing private debt market.

5.8. Collective Undertakings

Previous studies do not specifically address the relationship between insurance companies’ investments in collective undertakings and their solvency ratios. However, certain research does touch on investment activities and their solvency implications. Siopi et al. (2023) identify key determinants of solvency, such as reinvestment rates and long-term investments, which may include collective undertakings. Szaniewski (2021) discusses legal restrictions on insurers’ investments under Solvency II, which may indirectly impact these investments. Despite these findings, there are contradictions regarding the relationship between investment activities and solvency. Szaniewski (2021) notes that Solvency II has introduced stricter regulations, potentially impacting investments in collective undertakings. Although these studies do not explicitly analyze the impact of investments in collective undertakings on solvency ratios, they provide insights into the broader relationship between investment decisions and solvency. The predictive role of investment-related variables, the influence of capital requirements on risk-taking, and the regulatory environment under Solvency II could indirectly affect how investments in collective undertakings impact solvency ratios. Further research is necessary to establish a direct causal link between these investments and solvency outcomes.

5.9. Bonds and Equities

Insurers’ solvency ratios are significantly impacted by their investment choices, particularly their allocations to bonds and equities. According to Fung et al. (2018), the implementation of the China Risk-Oriented Solvency System (C-ROSS) has prompted life insurers to alter their asset allocations, focusing on asset–liability duration matching and the risks associated with equity investments. This shift is critical for managing interest rate risk, given the scarcity of long-term bonds in China, which can affect solvency (Fung et al. 2018). Chen et al. (2020) support the idea that insurers with higher operating risks tend to adopt conservative investment strategies, favoring lower credit risk exposure, thereby potentially enhancing their solvency ratios. Conversely, Niedrig and Gründl (2015) argue that contingent convertible (CoCo) bonds could improve life insurers’ solvency through lower capital requirements and higher coupon rates, despite the risks of converting these bonds into bank shares. This suggests that CoCo bonds can affect solvency ratios based on their design and regulatory context (Niedrig and Gründl 2015). Therefore, investment in bonds and equities significantly influences insurers’ solvency ratios. Conservative strategies may improve solvency by reducing financial risk (Chen et al. 2020), while innovative instruments like CoCo bonds present both opportunities and challenges, depending on regulatory conditions and bond specifics (Niedrig and Gründl 2015). The overall solvency effect hinges on balancing these factors and managing associated risks effectively.

5.10. Household Disposable Income

Household disposable income, as an indicator of economic well-being, has a material impact on the demand for insurance, which in turn affects the financial health of insurance companies. The coefficient of the household spending variable in the panel data analysis showcases that a 1% increase in household spending produces a 2.6% reduction in the SCR ratio. Although the existing literature does not directly link household expenditure to insurer solvency ratios, this may be due to the fact that when household spending increases, the share of wallet directed to insurance decreases; this leads to lower premia underwritten and thus lower assets (disproportional to increased claims/loses).

The finding suggests that various financial and operational factors, possibly influenced by household spending, affect insurer solvency. Siopi et al. (2023), Safari et al. (2015), and Ritho (2023) discuss factors such as the reinvestment rate, financial ratios, and the loss ratio, which could be impacted by changes in household expenditure patterns, affecting insurance claims and premium payments. Research indicates that household expenditure, especially catastrophic health expenditure (CHE), can negatively affect solvency ratios (Jung et al. 2022). The decline in financial health is attributed to financial balance and liquid asset loss rather than wealth or income size (Jung et al. 2022). The relationship between household debt and spending patterns is complex, with competing hypotheses suggesting different effects of pre-crisis debt on spending during crises (Svensson 2021). While household expenditure can impact solvency ratios, the relationship is intricate and involves multiple factors, requiring further research to establish a direct link between household expenditure and insurer solvency ratios.

When disposable income is high, households have the capacity to purchase more insurance, which can lead to increased profitability for insurers (OECD 2011). Conversely, low disposable income can reduce insurance demand, negatively impacting insurers’ financial stability. However, disposable income is not the sole determinant; other macroeconomic factors, such as inflation and interest rates, also play crucial roles. For example, inflation can adversely affect insurance company profits, as seen in Kenya (Muteru and Omagwa 2024). Additionally, the financial stability of insurance firms is influenced by firm-specific factors, such as size, investment performance, and liquidity ratio, as well as broader economic conditions (Chen and Wong 2004). Therefore, while household disposable income indirectly affects insurance companies’ financial health, it must be considered in conjunction with other macroeconomic and firm-specific factors that collectively influence profitability and stability (Chen and Wong 2004; Muteru and Omagwa 2024; OECD 2011).

5.11. Banking Concentration

High levels of concentration in the banking sector pose significant solvency risks to insurers. The financial difficulties of dominant banks can cause widespread instability, affecting insurers’ investments, particularly those heavily invested in the banking industry. Increased concentration also heightens counterparty risk in financial transactions and derivatives. When a few large banks fail, systemic risks arise, impacting insurers’ assets and liabilities. In response to banking crises, regulatory and monetary measures, such as lower interest rates, can reduce insurers’ investment income. Financial stress can lead to liquidity shortages and reduced lending, potentially affecting policyholders’ financial health and increasing claims. This connection is not explicitly addressed in the provided literature. The studies offer insights into the broader impacts of Solvency II on insurers’ financial stability and investment behavior. Douglas et al. (2017) indicate that Solvency II might prompt UK life insurers to de-risk their portfolios in response to changes in risk-free interest rates, influenced by the framework’s risk margin design (Douglas et al. 2017). Niedrig and Gründl (2015) discuss the potential for life insurers to hold contingent convertible (CoCo) bonds, possibly affected by banking sector stability, given insurers’ significant holdings of European bank bonds (Niedrig and Gründl 2015). Conversely, Höring (2013) finds that Solvency II may not significantly alter insurers’ investment strategies, as it does not serve as a binding capital constraint for market risk compared to other models like Standard and Poor’s (Höring 2013). Siddik et al. (2022) emphasize the negative impact of financial insolvency on profitability in the non-life insurance sector, suggesting that banking sector concentration and financial stability could affect insurers’ solvency and profitability (Siddik et al. 2022). It can be inferred from the examined literature that Solvency II’s effects on insurers are intricate, but further investigation is needed to determine the direct impact of banking sector concentration on solvency risks under this regulatory framework beyond the scope of the cited studies.

5.12. Non-Performing Loans

Non-performing loans (NPLs) signal higher loan default risk, affecting banks’ stability and, consequently, insurers connected through investments or reinsurance. The relationship between loan performance and financial stability is complex and influenced by various factors, as demonstrated by Hada et al. (2020), Nadalizadeh et al. (2019), and Wang (2017). Intriguingly, while NPLs can pose risks for banks, external factors such as foreign direct investment (FDI) may mitigate NPLs during economic crises, as indicated by Ozili et al. (2020). Additionally, the stability of the insurance sector is influenced by its capital adequacy and the use of reinsurance as a risk management tool, although excessive reliance on reinsurance may signal financial difficulties within insurance companies, as pointed out by Chen et al. (2001) and Harrington (2005). In conclusion, NPLs are a key indicator of financial health within the banking sector, with potential implications for insurers through investment and reinsurance linkages. The stability of both banks and insurers is crucial for maintaining the overall health of the financial system, and understanding the factors that affect NPLs is essential for managing risk and ensuring financial stability, as emphasized by Dissanayake and Samarathunga (2019), Hao et al. (2023), and Park and Xie (2014).

5.13. CO₂ Emissions

The panel data analysis indicates that a one percent increase in carbon dioxide emissions leads to a less than 0.1% increase in the SCR ratio. This is potentially a result of the fact that overall higher CO₂ emissions lead to increased risk for which insurers safeguard additional capital, as this risk has been escalated by the regulatory authorities.

Carbon dioxide emissions are the main cause of global climate change (Solomon et al. 2009). The European regulator recently upscaled the importance of climate change as a risk that needs to be separately monitored—also in ORSA—by insurers (EIOPA 2022a). Consequently, understanding the importance of CO₂ emissions for an insurer’s solvency is key. The relationship between climate change, natural disasters, and insurance solvency is complex. Yang (2023) indicates that a third of insurers may not sufficiently consider climate change impacts, while Sheehan et al. (2023) suggest the development of resilience and mitigation strategies in collaboration with disaster risk management communities. This reflects the industry’s recognition of the need to adapt to climate-related risks. Furthermore, Krauss (2024) highlights the insurance industry’s critical role in managing emerging risks and contributing to climate resilience discussions. Climate change poses significant risks to insurers by potentially increasing loss ratios due to more frequent and severe natural disasters (Benali and Feki 2017; Born and Viscusi 2006). This could challenge the solvency of insurance companies, underscoring the importance of regulatory frameworks like “Solvency II” to maintain financial stability (Siopi et al. 2023; Ziemele and Voronova 2013). However, the industry is also seen as a key player in developing strategies to manage and mitigate these risks (Krauss 2024; Sheehan et al. 2023). Therefore, while climate change presents challenges to insurers, it also offers opportunities for the industry to innovate and strengthen its role in promoting resilience against natural disasters.

5.14. Interest Rates

Finally, the level of interest rates negatively affects the SCR ratio as per the linear regression outcomes, although it posts no importance according to the machine-enhanced methods and no statistical significance as per the panel data findings. As a matter of fact, a one percent increase in interest rates leads to a 0.2% decrease in the SCR ratio. To understand this, we recall that an increase in long-term interest rates reduces the values of both assets and liabilities; thus, both the numerator and the denominator. The exact impact on the SCR ratio depends on the duration gap of the two, which explains why the effect is close to zero. However, the small negative influence may be due to the fact that as interest rates increase, investors tend to move from the equity market to fixed-income markets, hence leading to an additional drop in the value of total assets, i.e., the numerator. In addition, interest rates soared from low (even zero or negative in some countries) to higher (positive) levels in the period under examination. Thus, justifies the finding, which may need to be further researched.

The aforementioned findings clearly influence the investment portfolio allocation of the insurance companies (which, in turn, affects the SCR ratio) as the SCR ratio is derived as the ratio of the available assets over the assets earmarked/funds required to support the risks assumed by the insurer. The findings indicate that property is the most important asset class (as per the extra trees approach) and, at the same time, it exerts a positive statistically significant impact (as per the traditional linear regression and panel data models). Investments in bonds, equities, and collective undertakings are also important in portfolio construction (as the extra trees method indicates). In the compilation of the investment portfolio, the asset mix in terms of government to corporate bonds is also important. Further to that, the bond market itself is important. As a matter of fact, interest rates proved to be significant (as per the linear regression method), which reflects the material shift from low (even zero or negative in some cases) interest rates to higher (positive) interest rates in the period under examination.

Besides the clear influence of property, supported by all methods employed, the exact indication of whether to increase or decrease equity and/or bond holdings and, within this, what mix of government to corporate bonds to choose, depends on the period under investigation and the risk appetite as well as the risk tolerance of each insurer. The approach is not uniquely defined, and considering risk tolerance and risk appetite, insurers tend to balance the market, credit/counterparty, liquidity, concentration, insurance, and operational risks they are exposed to. The effect of diversification is also accounted for. At the same time, within the Solvency II framework, certain limitations apply in terms of the permissible investment allocation.

Consequently, when it comes to investment portfolio allocation, insurers (through their investment and risk management teams) need to consider the desired market, credit, liquidity, concentration, and diversification risks so as to construct the optimal portfolio in terms of their risk target. This determines the asset allocation, which, as evidenced by the outcome of the models employed, confirms the focus on the main asset classes, namely, property, bonds (government and corporate), equity, and collective undertakings. This allocation is dynamic and not static. Investment managers choose a blend of active and passive management to deliver this goal. Rebalancing may be required as the performance of the various asset classes changes or as the markets move.

The other variables that are not necessarily investment-related that were found to be important influence the portfolio allocation implicitly, as they affect one or more of the other risk categories mentioned (such as insurance and/or operational risk). The shift in these risks caused by the other factors (e.g., by the unit-linked share in the products sold, the life and non-life concentration, CO₂ emissions, etc.) may require a portfolio rebalancing so as to ensure the optimal blend of risks.

6. Conclusions and Further Research

This study contributes to the existing literature in three primary ways. First, it investigates the effect of the investment portfolio structure on insurers’ solvency ratios via the consideration of investment portfolio-related parameters (among an array of parameters) that are important for the solvency of an insurer. Firm-specific characteristics such as investments in property, unit-linked and index-linked liabilities, firm size, government-to-corporate bond investment ratio, and investments in collective undertakings, equities, and bonds, as well as country-specific factors like market concentration, domestic bond market development, private debt development, household spending, banking concentration, non-performing loans, and CO₂ emissions, can predict insurance companies’ solvency, as measured by the SCR ratio. Second, it employs a series of methodologies—linear regression, Prais–Winsten regression, correlated panel-corrected standard errors (PCSEs), and several supervised machine learning models—to conclude, based on machine learning, that the extra trees regression outperforms traditional linear regression, Prais–Winsten regression, and correlated panel-corrected standard errors (PCSEs) in predicting solvency ratios. Third, it elucidates the importance of variables that have not been previously considered in relation to the solvency of insurers, although they are relevant (directly or indirectly) to the determination of their investment portfolio structure. These include the life and non-life insurance market concentration, the unit-linked and index-linked products, the bond market development, and the investments in collective undertakings, as well as the banking sector concentration.

Insurance companies may potentially derive significant benefits from diversifying their investment portfolios through the incorporation of real estate (property) and collective investment undertakings, as well as by transitioning from government to corporate bonds. At the same time, they need to decide on the mix of bond and equity assets. Real estate investments have a complex impact on solvency ratios. Despite potentially higher returns in certain interest rate environments, they attract higher capital charges under Solvency II. Optimal asset allocation depends on the insurer’s capitalization, profitability, and competitive landscape as well as the desired risk appetite and ensured risk tolerance. Adjusting the asset mix in property investments, along with bonds and equity to reach solvency ratio targets requires careful evaluation of market conditions and insurer-specific factors. Insurers must consider the potential for higher returns against increased capital charges. Real estate investments yield stable, long-term income through rentals, offer capital appreciation, and hedge against inflation. They enhance portfolio diversification and provide tangible assets with intrinsic value. Additionally, they offer tax benefits through depreciation/amortization, allow leverage via mortgage financing, and opportunities for value-added improvements.

When rebalancing the asset mix in collective investments, insurers should adopt a comprehensive approach that aligns regulatory requirements with traditional portfolio optimization while remaining adaptable to market conditions. This involves analyzing each investment’s marginal SCR contribution and utilizing a core–satellite framework with strategic and tactical asset management mandates. Additionally, integrating asset–liability management into risk limit systems is crucial due to the interplay between core insurance business and investments. Collective investment undertakings offer access to diversified asset portfolios and professional management. They provide economies of scale, reduce overall costs, and enable efficient liquidity management. These undertakings expose investors to various asset classes and markets, offer regulatory oversight and protection, and facilitate easy entry and exit of investments, potentially yielding higher returns through active management.

Shifting from government to corporate bonds can potentially enhance solvency ratios by increasing net yield on capital. However, this shift entails greater risk. While corporate bonds may offer higher yields, they also require higher capital reserves, potentially negating solvency ratio benefits. Optimal asset allocation should maximize expected returns on the insurer’s own funds while adhering to SCR limits for market risk.

The product mix is also important. Unit-linked and index-linked insurance products present distinct challenges in managing solvency ratios, as they tie policyholder benefits to specific assets or indices. Insurers should implement robust hedging strategies, focus on asset–liability matching, and consider unhedgeable risks. Unit-linked products enable policyholders to share in market gains, offer flexible investment choices, and ensure fund performance transparency. These products often have lower fees than traditional insurance products and can be customized based on individual risk profiles. They ease portfolio rebalancing, offer potentially higher returns compared to guaranteed products, and clearly separate insurance from investment components.

Index-linked products yield returns tied to specific market indices, potentially offering higher returns than traditional fixed-income investments. They provide some protection against market downturns with principal guarantees and simplify investment decisions for policyholders. These products reduce active management costs, provide broad market exposure, and allow for easy performance benchmarking.

This study’s limitations stem from the constrained scope and depth of available SFCR data, attributable to restrictions in firm quantity, geographical focus, and publicly accessible information, potentially impacting the generalizability of findings and underscoring the necessity for expanded data access to enhance research on insurance firm solvency.

The specific role of collective investment undertakings remains underexplored. Future research should investigate how they might alter insurers’ risk profiles and solvency, considering the transmission effects from sovereign risk to insurers.