Dynamic Programming for Designing and Valuing Two-Dimensional Financial Derivatives

Abstract

We use dynamic programming, finite elements, and parallel computing to design and evaluate two-dimensional financial derivatives. Our dynamic program is flexible, as it divides the evaluation process into two components: one related to the dynamics of the underlying process and the other to the characteristics of the financial derivative. It is efficient as it uses local polynomials at each step of the backward recursion to approximate the option value function, while it assumes only a numerical (but not a statistical) error and a state (but not a time) discretization. Parallel computing is used to speed up the model resolution and enhance its overall efficiency. To support our construction, we evaluate American options, which are subject to market risk, and exchangeable bonds, which are subject to default risk.

1. Introduction

This paper aims to design a flexible dynamic program (DP) and efficiently evaluate two-dimensional financial derivatives. This methodology is highly flexible because it relies on known transition parameters of the underlying process and known payoff functions of financial derivatives. Moreover, it is efficient because it uses local polynomials to approximate the value functions at each step of the backward recursion. Our model assumes only a numerical (but not a statistical) error and a state (but not a time) discretization. As an illustration, we evaluate American options and exchangeable bonds.

DP and finite elements (local approximations) have been efficiently used for valuing one-dimensional financial derivatives. See Ben-Ameur et al. (2016) and Ayadi et al. (2016) for methods in valuing American-style options and corporate securities. Since this approach is not feasible in high-dimensional state spaces, DP is usually combined with the Monte Carlo simulation and spectral analysis (global approximations) to approximate the value functions at each step of the backward recursion. In this case, the numerical error is amplified by a statistical error underlying the Monte Carlo approach, which can be seen as an extra cost to overcome the curse of dimensionality.

The modeling process assumes a constant search for the best compromise between accuracy and computing time. Local approximations are much more accurate than global approximations, but they are more time-consuming. Parallel computing is used to speed up the model resolution at each step of the backward recursion and to enhance the overall efficiency of the numerical procedure. This paper supports the idea that DP combined with finite elements remains effective for valuing low-dimensional financial derivatives. Methods for model-dimensional reduction can help to reach this objective (Reisinger and Wittum 2007).

American-style financial derivatives cannot be valued in closed form and must be approximated in some way. The literature reports three main backward pricing methodologies, namely, the lattice approach, finite differences, and dynamic programming. They all compete for valuing low-dimensional financial derivatives, but DP is the main methodology used in high-dimensional state spaces since it naturally combines with the Monte Carlo simulation.

The lattice approach assumes a discrete model that usually converges to a continuous counterpart when the time and space increments tend to zero. It runs in two steps. The first step builds the lattice forward, while the second step evaluates financial derivatives backward in time (Boyle 1988; Boyle et al. 1989; Kamrad and Ritchken 1991). The discrete approach and the continuous approach can be combined to improve the efficiency of the lattice construction (Bayer et al. 2022; Bungartz et al. 2012; Kargin 2005; Tanaka 2014).

Finite differences assume state and time discretizations of continuous models and numerically solve partial differential equations that characterize the (holding) value function of an option contract at each evaluation node (Hartley 2000). Berridge and Schumacher (2008) and Dockendorf and Paxson (2015) considered European exotic options, specifically focusing on the construction of the evaluation grid nodes. Pettersson et al. (2008) and Milovanović and Von Sydow (2018) used spectral analysis, while Wang et al. (2023) and Glau and Wunderlich (2022) used neural networks for value-function approximations at each step of their numerical procedures. Multiple methods have been used to address the weakness of the differential operator near the option exercise frontier (Attipoe and Tambue 2022; Heo et al. 2019; Kim et al. 2016). Methods for model dimension reduction are used to overcome the curse of dimensionality (Caldana et al. 2016; Hanbali and Linders 2019).

The main challenge in valuing high-dimensional American options in continuous models, which combines dynamic programming and Monte Carlo simulation, is twofold. On the one hand, if the sole evaluation node is at inception, forward DP considers sub-optimal stopping policies, given that the true option exercise strategy is unknown (Andersen and Broadie 2004; Boyle et al. 1997; Broadie and Detemple 1997; Del Moral et al. 2012; Ibáñez and Zapatero 2004; Liu and Hong 2009). On the other hand, if the evaluation process is achieved along the random sample paths of the underlying asset vector, backward DP solves the model recursively from the option maturity down to the origin. At each step of the backward recursion and each evaluation node, a poor Monte Carlo simulation of size one is used to estimate the option (holding) value since the underlying trajectories never intersect. The literature reports several remedies. The bundling-based approach assumes that sample paths in the same neighborhood have the same evaluation root (Barraquand and Martineau 1995; Raymar and Zwecher 1997; Bally and Pages 2003a, 2003b; Bally and Printems 2005; Jin et al. 2007, 2013). This approach goes back to Tilley (1993) and Raymar and Zwecher (1997) for valuing one-dimensional American options. The least squares-based approach adjusts the poor Monte Carlo estimates of size one at each step of the backward recursion via global approximations, such as linear, local, and robust regressions (Carrière 1996; Longstaff and Schwartz 2001; Tompaidis and Yang 2014; Tsitsiklis and Van Roy 1999) and neural networks (Chen and Wan 2021; Kohler et al. 2010). The simulated tree-based approach augments the number of simulated paths at each evaluation node (Broadie and Glasserman 1997). Forward and backward DP create a dual approach for valuing multivariate American options (Broadie and Glasserman 1997; Haugh and Kogan 2004; Rogers 2002). These methodologies inherit statistical errors from the generation of random paths and numerical errors from multiple approximations. Variance reduction techniques can be employed to enhance the overall efficiency of the numerical experiment (Dang et al. 2015; Giles 2015).

We propose a two-dimensional backward DP approach, which assumes only numerical (but not statistical) errors and state (but not time) discretization. Accurate local polynomials are employed to approximate the option value function at each step of the backward recursion, with parallel computing utilized to enhance the overall efficiency of the procedure.

The rest of this paper is organized as follows. Section 2 presents our model for valuing two-dimensional American options, Section 3 focuses on exchangeable bonds, and Section 4 concludes the paper.

2. Designing and Valuing American Options

We consider a frictionless market in which two stocks, $S^1$ and $S^2$, are traded continuously and move according to a bivariate lognormal process. The risk-free rate, $r_f$, is assumed to be constant. This market is known to be arbitrage-free and complete. Thus, there exists a unique risk-neutral probability measure $\mathbb{Q}$ under which the state process $(S^1,S^2)$ moves according to the following stochastic differential equation:

$${\displaystyle \frac{d{S}_t^i}{S_t^i}}=(r_f-d_i)dt+{\sigma }_{i}d{W}_t^i,\mathrm{for}i=1,2,$$

(1)

where $d_i$ denotes the continuous dividend rate of stock i, ${\sigma }_i$ denotes its log-return volatility, and $(W^1$, $W^2)$ denotes a bivariate correlated Brownian motion with the following:

$$\mathrm{Cor}(W_t^1,W_t^2)=\rho ,\mathrm{for}\mathrm{all}t>0.$$

The analytical solution of (1) is as follows:

$$S_u^i=S_t^{i}exp\left[\left(r_f-d_i-{\displaystyle \frac{{\sigma }_i^2}{2}}\right)\left(u-t\right)+{\sigma }_i\left(W_u^i-W_t^i\right)\right],\mathrm{for}0\le t\le u.$$

(2)

An American option on $(S^1,S^2)$ with maturity T is defined by its cash-flow process, $\kappa (t,x,y)\ge 0$, where $x=S_t^1$ and $y=S_t^2$ denote the levels of the underlying stocks at time $t\in [0,T]$. This is the option exercise value $v_t^e(x,y)=\kappa (t,x,y)$. Examples include the exchange option, as follows:

$$\kappa (t,x,y)=max(x-y,0),$$

the call-on-max option, as follows:

$$\kappa (t,x,y)=max(max(x,y)-K,0),$$

and the put-on-min option, as follows:

$$\kappa (t,x,y)=max(K-min(x,y),0),$$

where K denotes the option strike price. The exchange option gives the option holder the right to exchange $S^2$ for $S^1$; the call-on-max option gives its holder the right to purchase the higher-priced asset at the strike price K; and the put-on-min gives the right to sell the lower-priced asset at the strike K. Stulz (1982) and Johnson (1987) derived closed-form solutions for their European counterparts, characterized by the following:

$$\kappa (t,x,y)=0,\mathrm{for}0\le t<T.$$

We herein consider Bermudan options with $N+1$ regular exercise opportunities, that is, $t_0=0,t_1,\dots ,t_N=T$, where $t_{n+1}-t_n=\mathsf{\Delta }t$. No-arbitrage pricing gives the following:

$$v_{t_n}^h(x,y)={\mathbb{E}}^{\mathbb{Q}}\left[e^{-r_f\mathsf{\Delta }t}{v}_{t_{n+1}}(S_{t_{n+1}}^1,S_{t_{n+1}}^2)\mid (S_{t_n}^1,S_{t_n}^2)=(x,y)\right],$$

(3)

where $v_{t_n}^h(x,y)$ and $v_{t_n}(x,y)=max(v_{t_n}^h(x,y),v_{t_n}^e(x,y))$ denote the option holding value and overall option value functions at $(t_n,x,y)$. We set $v_{t_N}^h(x,y)=0$ for all $x>0$ and $y>0$.

The expectation in Equation (3) cannot be computed in closed form and has to be approximated in some way. Valuing American options can be interpreted as an optimal Markov decision process (stochastic dynamic program) since the option value function is forward-looking and known at maturity.

Let $\mathcal{G}$ be a set of grid points $\{(a_1,b_1),(a_1,b_2),\dots ,(a_p,b_q)\}$ such that $max(\mathsf{\Delta }{a}_k,\mathsf{\Delta }{b}_l)\to 0$ and $\mathbb{Q}[(S_t^1,S_t^2)\in [a_p,\infty )\times {\mathbb{R}}_{+}^{*}\cup {\mathbb{R}}_{+}^{*}\times [b_q,\infty )]\to 0$, when p and $q\to \infty$. We set $a_0=b_0=0$ and $a_{p+1}=b_{q+1}=\infty$. The rectangle $[a_i,a_{i+1})\times [b_j,b_{j+1})$ is designated by $R_{ij}$.

Define the transition tables $T^{00},T^{10},T^{01}$, and $T^{11}$ as follows:

$$T_{klij}^{\nu \mu }={\mathbb{E}}^{\mathbb{Q}}\left[{\left(S_{t_{n+1}}^1\right)}^{\nu }{\left(S_{t_{n+1}}^2\right)}^{\mu }\mathbb{I}\left((S_{t_{n+1}}^1,S_{t_{n+1}}^2)\in R_{ij}\right)\mid (S_{t_n}^1,S_{t_n}^2)=(a_k,b_l)\right],\mathrm{for}\nu \mathrm{and}\mu \in \{0,1\}.$$

(4)

For example, $T_{klij}^{00}$ represents the transition probability that the Markov process $(S^1,S^2)$ moves from $(a_k,b_l)$ at $t_n$ and visits the rectangle $R_{ij}$ at $t_{n+1}$. The rest of the transition tables represent truncated first-order direct and cross-moments of the state process $(S^1,S^2)$ at $t_{n+1}$ given the current position $(a_k,b_l)$ at $t_n$. The computation of these transition parameters, which are at the heart of our DP approach, can be treated as a fixed cost, provided that the Markov state process is homogeneous, $t_{n+1}-t_n$ is a positive constant, and the grid points, $\mathcal{G}$, are fixed over time. We derive them in closed form in Appendix A.

Assume that an approximation of the option value function is available at a future decision date $t_{n+1}$ on $\mathcal{G}$, as indicated by ${\tilde{v}}_{t_{n+1}}(a_k,b_l)$, for $k=1,\dots ,p$ and $l=1,\dots ,q$. This is not really a strong assumption since the option value function is known at maturity in closed form, that is, ${\tilde{v}}_{t_N}=v_{t_N}=v_{t_N}^e$. DP acts as follows:

• Use a bilinear piecewise polynomial and interpolate the option value function ${\tilde{v}}_{t_{n+1}}$ at $t_{n+1}$ from $\mathcal{G}$ to the overall state space ${[0,\infty )}^2$ by setting the following:

  $${\widehat{v}}_{t_{n+1}}(x,y)=\sum _{i=0}^p\sum _{j=0}^q\left({\alpha }_{ij}^{n+1}+{\beta }_{ij}^{n+1}x+{\gamma }_{ij}^{n+1}y+{\delta }_{ij}^{n+1}xy\right)\times \mathbb{I}\left((x,y)\in R_{ij}\right),$$

  (5)

  where the local coefficients ${\alpha }_{ij}^{n+1}$, ${\beta }_{ij}^{n+1}$, ${\gamma }_{ij}^{n+1}$, and ${\delta }_{ij}^{n+1}$ for $i=1,\dots ,p-1$ and $j=1,\dots ,q-1$ are derived in closed form by solving a system of linear equations:

  $$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\widehat{v}}_{t_{n+1}}(a_i,b_j)={\tilde{v}}_{t_{n+1}}(a_i,b_j)\hfill \\ & {\widehat{v}}_{t_{n+1}}(a_{i+1},b_j)={\tilde{v}}_{t_{n+1}}(a_{i+1},b_j)\hfill \\ & {\widehat{v}}_{t_{n+1}}(a_i,b_{j+1})={\tilde{v}}_{t_{n+1}}(a_i,b_{j+1})\hfill \\ & {\widehat{v}}_{t_{n+1}}(a_{i+1},b_{j+1})={\tilde{v}}_{t_{n+1}}(a_{i+1},b_{j+1})\hfill \end{array}\right.\end{array}$$

  (6)

  and the rest are set to their adjacent counterparts;
• Use no-arbitrage pricing and approximate the option holding value function at $t_n$ on $\mathcal{G}$:

  $$\begin{array}{ccc}\hfill {\tilde{v}}_{t_n}^h(a_k,b_l)& =& {\mathbb{E}}^{\mathbb{Q}}\left[e^{-r_f\mathsf{\Delta }t}{\widehat{v}}_{t_{n+1}}(S_{t_{n+1}}^1,S_{t_{n+1}}^2)\mid (S_{t_n}^1,S_{t_n}^2)=(a_k,b_l)\right]\hfill \\ & =& e^{-r\mathsf{\Delta }t}\sum _{i,j}\left({\alpha }_{ij}^{n+1}{T}_{klij}^{00}+{\beta }_{ij}^{n+1}{T}_{klij}^{10}+{\gamma }_{ij}^{n+1}{T}_{klij}^{01}+{\delta }_{ij}^{n+1}{T}_{klij}^{11}\right);\hfill \end{array}$$

  (7)
• Approximate the option value function at $t_n$ on $\mathcal{G}$:

  $$\begin{array}{ccc}\hfill {\tilde{v}}_{t_n}(a_k,b_l)& =& max(v_{t_n}^e(a_k,b_l),{\tilde{v}}_{t_n}^h(a_k,b_l));\hfill \end{array}$$

  (8)
• Go to step 1 and repeat until $t_n=0$.

Equation (7) splits the option holding value into two parts: The local coefficients are related to the option contract and the transition parameters to the dynamics of the state process. Overall, the option holding value is calculated by summing local future value components, each multiplied by their associated transition parameters, and then discounted back at the risk-free rate. The same equation shows that DP assumes a space discretization, but not time discretization, and does respect the true dynamics of the state process. Note that the time increment $\mathsf{\Delta }t$ does not need to be small as it is required by the lattice approach and by finite differences. Our numerical procedure can be designed to stop and evaluate option contracts only at decision dates since the transition parameters are derived in closed form for any positive time increment $\mathsf{\Delta }t$. For a European option, set $\mathsf{\Delta }t$ at the option maturity and run DP in one step; for a Bermudan option, set $\mathsf{\Delta }t$ at the time interval between two decision dates and run DP in multiple steps. For example, we can fix $\mathsf{\Delta }t$ at the time interval between two coupon dates for options embedded in bonds that can be exercised only at payment dates. Finally, Equation (5) shows that DP ends up with an interpolation ${\widehat{v}}_{t_n}(x,y)$ of $v_{t_n}\left(x,y\right)$, for all $t_n,x>0$ and $y>0$. Thus, the first and second derivatives of $v_{t_n}\left(x,y\right)$ become available at all $(t_n,x,y)$, among other sensitivity coefficients. For example, the approximated deltas at $(t_0,x_0,y_0)$ are as follows:

$${\displaystyle \frac{\partial {\widehat{v}}_{t_0}(x_0,y_0)}{\partial x}}={\beta }_{ij}^0+{\delta }_{ij}^0{y}_0\mathrm{and}{\displaystyle \frac{\partial {\widehat{v}}_{t_0}(x_0,y_0)}{\partial y}}={\gamma }_{ij}^0+{\delta }_{ij}^0{x}_0,$$

given that $(x_0,y_0)\in R_{ij}$. Higher-order local approximations are more accurate but more time-consuming.

At each step $t_n$ of the backward recursion, the computational effort underlying Equation (7) can be conducted simultaneously for $k=1,\dots ,p$ and $l=1,\dots ,q$. We used parallel computing to improve the overall efficiency of our DP procedure. The code lines are written in C and compiled with GCC. Parallel computing was performed using the MPI library. We used the supercomputer Briarée managed by Calcul Québec and Compute Canada.1 Briarée has 8064 CPUs (cores), each running at the speed of 2.667 GHz. See Appendix B for further details.

Our numerical experiment focuses on the put-on-min option contract.

Table 1. European put-on-min options—DP vs. Boyle (1988).

	DP with a Grid Size $\mathit{pq}$
	${72}^2$	${144}^2$	${300}^2$	Boyle	Closed form
$K=35$	1.411	1.392	1.388	1.425	1.387
40	3.837	3.805	3.800	3.778	3.798
45	7.543	7.508	7.501	7.475	7.500
Number of cores	576	1728	1800
Total CPU time	(0.93)	(5.40)	(34.48)
Linear CPU time	(0.65)	(4.11)	(11.99)	10 time steps
$K=35$	1.504	1.410	1.391	1.392	1.387
40	3.970	3.832	3.805	3.795	3.798
45	7.694	7.537	7.507	7.499	7.500
Number of cores	576	1728	1800
Total CPU time	(2.14)	(10.29)	(67.01)
Linear CPU time	(1.83)	(8.85)	(46.91)	50 time steps

and

Table 2. American put-on-min option—DP vs. Boyle (1988).

	DP with a Grid Size $\mathit{pq}$
	${72}^2$	${144}^2$	${300}^2$	Boyle
$K=35$	1.436	1.416	1.413	1.450
40	3.918	3.887	3.881	3.870
45	7.713	7.678	7.671	7.645
Number of cores	576	1728	1800
Total CPU time	(1.01)	(5.79)	(36.63)
Linear CPU time	(0.67)	(4.51)	(13.75)	10 time steps
$K=35$	1.535	1.440	1.422	1.423
40	4.064	3.926	3.899	3.892
45	7.880	7.727	7.697	7.689
Number of cores	576	1728	1800
Total CPU time	(1.96)	(9.94)	(66.45)
Linear CPU time	(1.71)	(8.46)	(46.43)	50 time steps

compare DP to Boyle (1988), which uses a two-dimensional binomial tree for valuing European vs. American put-on-min options. The closed-form solution for the European contract is given in Stulz (1982). We set $S_0^1=S_0^2=40$, $d_1=d_2=0$, ${\sigma }_1=0.2$, ${\sigma }_2=0.3$, $\rho =0.5$, $r_f=5\%$ (effective) $\equiv 0.04879$ (continuously compounded), and $T=7$ months $\equiv 0.58333$ years.

As explained above, DP does not need time discretization. For comparison purposes, we run DP with the same number of time steps as Boyle (1988). When the number of time steps is low, DP performs almost perfectly, while the binomial tree method is less accurate. As expected, with a higher number of time steps, the binomial tree converges and achieves accuracy comparable to that of DP. Boyle (1988) does not report computing times. Each DP’s CPU time (in seconds) can be split into a fixed cost, associated with the transition parameters, and a linear cost, associated with the backward recursion. The fixed cost accounts for a sizable portion of the total CPU time. The relevant DP’s computing time is the linear CPU time since the transition parameters can be computed only once or twice a day, following the model estimation step.

Table 3. American put-on-min options—DP vs. Rogers (2002); Jin et al. (2007), and Hartley (2000).

	DP with a Grid Size $\mathit{pq}$
$(S_0^1$, $S_0^2)$	${72}^2$	${144}^2$	${300}^2$	Rogers	Jin et al.	Hartley
(80, 80)	37.94	37.42	37.31	[37.35, 37.65]	[37.10, 37.40]	37.30
(80, 100)	32.78	32.20	32.09	[32.12, 32.26]	[31.84, 32.14]	32.08
(80, 120)	29.83	29.26	29.15	[29.18, 29.32]	[28.89, 29.24]	29.14
(100, 100)	25.89	25.20	25.07	[24.93, 25.23]	[24.83, 25.16]	25.06
(100, 120)	21.78	21.07	20.92	[20.89, 21.09]	[20.68, 20.99]	20.91
(120,120)	16.86	16.10	15.94	[15.99, 16.19]	[15.67, 16.00]	15.92
Number of cores	576	1728	1800
Total CPU time	(1.66)	(8.70)	(46.72)	(180)	(24)
Linear CPU time	(1.60)	(8.41)	(43.58)	51 time steps

compares DP to alternative methodologies based on the Monte Carlo simulation in the context of the dual approach of Rogers (2002) and the bundling approach by Jin et al. (2007). Their random samples are of sizes $10,000$ and $60,000$, respectively. We report their respective $95\%$ confidence intervals. Hartley (2000) used finite differences. The parameters are $K=100$, $d_1=d_2=0$, $\rho =0$, ${\sigma }_1={\sigma }_2=0.6$, $r=0.06$, and $T=0.5$. DP values, obtained with $p=q=300$, almost always belong to their associated $95\%$ confidence intervals and compare extremely well with Hartley’s (2000) values, which were described by Rogers (2002) as extremely accurate. 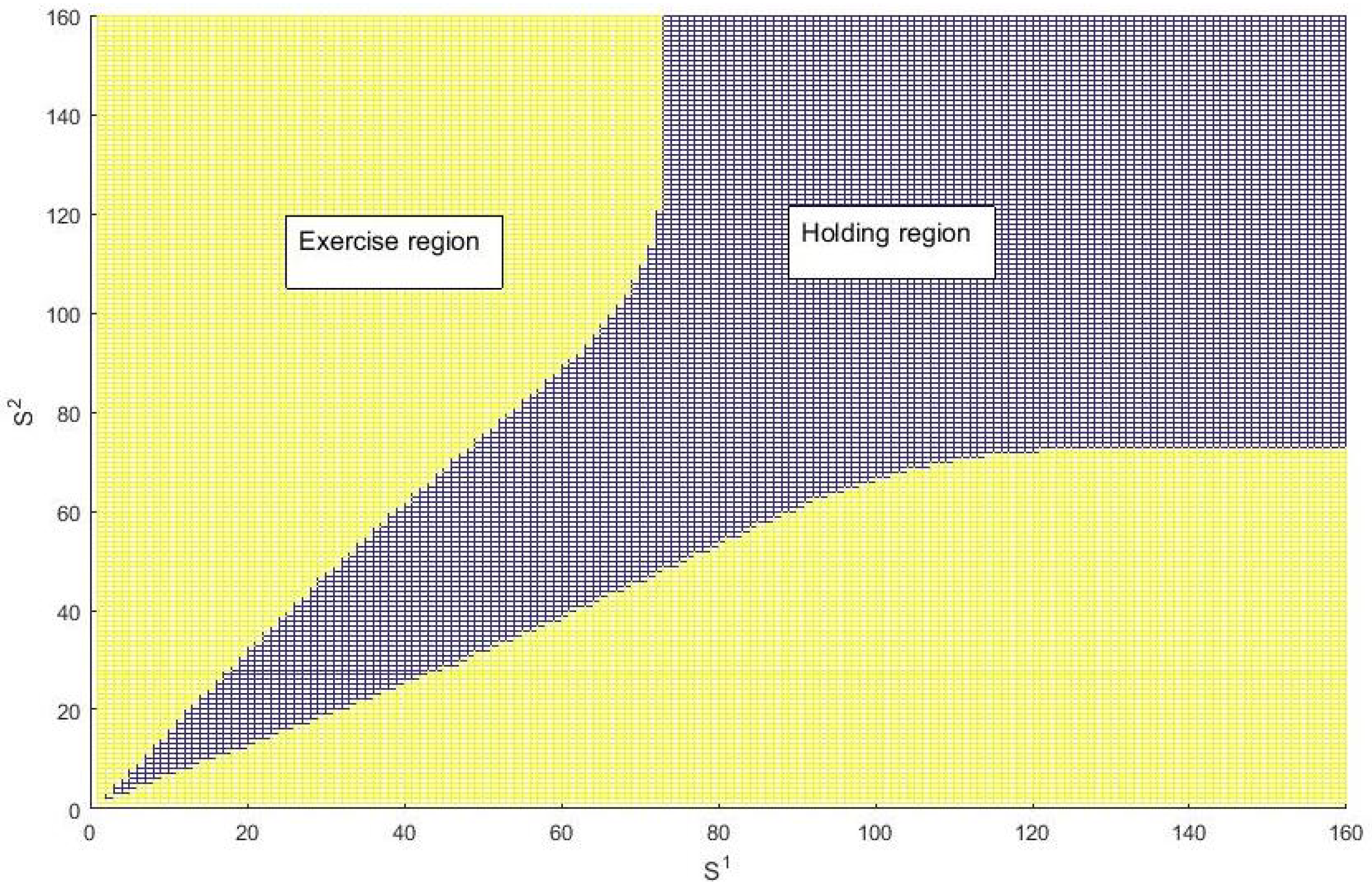Figure 1 plots the exercise region of a put-on-min option at the fourth of ten decision dates, where $K=100$. For example, it is optimal to hold the option when $(S_{t_4}^1,S_{t_4}^2)=(60,60)$, even though exercising the option has value.

3. Designing and Valuing Exchangeable Bonds

An exchangeable bond allows bondholders the discretion to convert their holdings into shares of a company other than the issuer. This instrument is subject to both the credit risk of the issuing company and the market risk of the underlying stock.

Exchangeable bonds have been offered since the early 1970s. About 14% of convertible bonds were exchangeable in the US, according to Grimwood and Hodges (2002). The issuance of exchangeable bonds is mainly motivated in the literature as a tax-saving strategy (Jones and Mason 1986) and/or a divesting policy (Barber 1993).

We consider a public company with a debt portfolio made of a senior straight bond and a junior exchangeable bond. This (issuing) firm is assumed to hold the shares underlying the exchangeable bond, which are pledged to junior bondholders who have priority on the pledged shares under default.

The balance-sheet equality (BSE) of the issuing firm depends on whether the exchange option was already exercised or not, which results in the following:

$$a+s\times \mathbb{I}(f_{t_{n-1}}=0)+{\mathrm{TB}}_{t_n}(a,s,f)-{\mathrm{BC}}_{t_n}(a,s,f)=D_{t_n}^s(a,s,f)+D_{t_n}^j(a,s,f)+{\mathcal{E}}_{t_n}(a,s,f),$$

(9)

where $s=S_{t_n}$ denotes the value of the shares underlying the exchangeable bond, $a+s=A_{t_n}+S_{t_n}$ denotes the value of the issuing firm’s assets; $f_{t_{n-1}}=1$ if the exchange option was exercised before or at $t_{n-1}$, and 0 otherwise (held until $t_{n-1}$), with $f=f_{t_{n-1}}$. We assume that the evaluation date $t_n$ belongs to the coupon/capital payment dates $\mathcal{P}=\{t_0,t_1,\dots ,t_N\}$. The couple $(A,S)$ is modeled as a lognormal process, as described in Equation (1). This two-dimensional structural setting builds on the work of Ayadi et al. (2016), who considered junior and senior debt portfolios without embedded options.

The value functions ${\mathrm{TB}}_{t_n}(a,s,f),{\mathrm{BC}}_{t_n}(a,s,f),D_{t_n}^s(a,s,f),D_{t_n}^j(a,s,f),$ and ${\mathcal{E}}_{t_n}(a,s,f)$ represent the (net present) values of tax benefits, bankruptcy costs, the senior straight bond, the junior exchangeable bond, and equity of the issuing firm at $(t_n,a,s,f)$, respectively. In particular, $D_{t_n}^j(a,s,1)=0$, for all $a>0$ and $s>0$. Each value function is characterized by two components, namely, its current cash flows and future potentialities, as shown in

Table 4. Value functions at $(t_N,a,s,1)$.

	Survival	Default
BSE	$\mathit{a}\mathbf{>}{\mathit{d}}_{\mathit{N}}^{\mathit{s}}\mathbf{-}$${\mathbf{tb}}_{\mathit{N}}^{\mathit{s}}$	$\mathit{a}\mathbf{\le }{\mathit{d}}_{\mathit{N}}^{\mathit{s}}\mathbf{-}$${\mathbf{tb}}_{\mathit{N}}^{\mathit{s}}$
$+a$	a	a
+TB	${\mathrm{tb}}_N^s$	0
−BC	0	$-wa$
=	=	=
$+D^s$	$d_N^s$	$(1-w)a$
$+\mathcal{E}$	$a-(d_N^s-$${\mathrm{tb}}_N^s)$	0

,

Table 5. Value functions at $(t_N,a,s,0)$.

	Solvent company: $a+s>d_N-$ ${\mathrm{tb}}_N$
	Holding	Exercising
	$s\le P_N^j$	$s>P_N^j$
	(1) Survival	(2) Survival	(3) Default
BSE		$a>d_N^s+C_N^j-$${\mathrm{tb}}_N$	$a\le d_N^s+C_N^j-$${\mathrm{tb}}_N$
$+a$	a	a	a
$+s$	s	s	s
+TB	${\mathrm{tb}}_N$	${\mathrm{tb}}_N$	0
−BC	0	0	$-wa$
=	=	=	=
$+D^s$	$d_N^s$	$d_N^s$	$min(d_N^s,(1-w)a)$
$+D^j$	$d_N^j$	$s+C_N^j$	$s+max((1-w)a-d_N^s,0)$
$+\mathcal{E}$	$a+s-(d_N-$${\mathrm{tb}}_N)$	$a-(d_N^s+C_N^j-$${\mathrm{tb}}_N)$	0
	Stressed company: $a+s\le d_N-$ ${\mathrm{tb}}_N$
	Holding	Exercising
	$(1-w)a\ge d_N^s$	$(1-w)a<d_N^s$
	(4) Default	(5) Survival	(6) Default
BSE		$a>d_N^s+C_N^j-$${\mathrm{tb}}_N$	$a\le d_N^s+C_N^j-$${\mathrm{tb}}_N$
$+a$	a	a	a
$+s$	s	s	s
+TB	0	${\mathrm{tb}}_N$	0
−BC	$-wa$	0	$-wa$
=	=	=	=
$+D^s$	$d_N^s$	$d_N^s$	$(1-w)a$
$+D^j$	$s+(1-w)a-d_N^s$	$s+C_N^j$	s
$+\mathcal{E}$	0	$a-(d_N^s+C_N^j-$${\mathrm{tb}}_N)$	0

,

Table 6. Value functions at $(t_n,a,s,1)$.

	Survival	Default
BSE	$\overline{\mathcal{E}}>{\mathit{d}}_{\mathit{n}}^{\mathit{s}}\mathbf{-}$${\mathbf{tb}}_{\mathit{n}}^{\mathit{s}}$	$\overline{\mathcal{E}}\mathbf{\le }{\mathit{d}}_{\mathit{n}}^{\mathit{s}}\mathbf{-}$${\mathbf{tb}}_{\mathit{n}}^{\mathit{s}}$
$+a$	a	a
+TB	$\overline{\mathrm{TB}}+$${\mathrm{tb}}_n^s$	0
−BC	$-\overline{\mathrm{BC}}$	$-wa$
=	=	=
$+D^s$	${\overline{D}}^s+d_n^s$	$(1-w)a$
$+\mathcal{E}$	$\overline{\mathcal{E}}-(d_n^s-$${\mathrm{tb}}_n^s)$	0

and

Table 7. Value functions at $(t_n,a,s,0)$.

	Solvent company: $\overline{\overline{\mathcal{E}}}>d_n-$ ${\mathrm{tb}}_n$
	Holding	Exercising
	$s\le {\overline{\overline{D}}}^j+P_n^j$	$s>{\overline{\overline{D}}}^j+P_n^j$
	Survival	Survival	Default
BSE		$\overline{\mathcal{E}}>d_n^s+C_n^j-$${\mathrm{tb}}_n$	$\overline{\mathcal{E}}\le d_n^s+C_n^j-$${\mathrm{tb}}_n$
$+a$	a	a	a
$+s$	s	s	s
+TB	$\overline{\overline{\mathrm{TB}}}+$${\mathrm{tb}}_n$	$\overline{\mathrm{TB}}+$${\mathrm{tb}}_n$	0
−BC	$-\overline{\overline{\mathrm{BC}}}$	$-\overline{\mathrm{BC}}$	$-wa$
=	=	=	=
$+D^s$	${\overline{\overline{D}}}^s+d_n^s$	${\overline{D}}^s+d_n^s$	$min({\overline{D}}^s+d_n^s,(1-w)a)$
$+D^j$	${\overline{\overline{D}}}^j+d_n^j$	$s+C_n^j$	$s+max((1-w)a-{\overline{D}}^s-d_n^s,0)$
$+\mathcal{E}$	$\overline{\overline{\mathcal{E}}}-(d_n-$${\mathrm{tb}}_n)$	$\overline{\mathcal{E}}-(d_n^s+C_n^j-$${\mathrm{tb}}_n)$	0
	Stressed company $\overline{\overline{\mathcal{E}}}\le d_n-$ ${\mathrm{tb}}_n$
	Holding	Exercising
	$(1-w)a\ge {\overline{\overline{D}}}^s+d_n^s$	$(1-w)a<{\overline{\overline{D}}}^s+d_n^s$
	Default	Survival	Default
BSE		$a>{\overline{D}}^s+d_n^s+C_n^j-$${\mathrm{tb}}_n$	$a\le {\overline{D}}^s+d_n^s+C_n^j-$${\mathrm{tb}}_n$
$+a$	a	a	a
$+s$	s	s	s
+TB	0	$\overline{\mathrm{TB}}+$${\mathrm{tb}}_n$	0
−BC	$-wa$	$-\overline{\mathrm{BC}}$	$-wa$
=	=	=	=
$+D^s$	${\overline{\overline{D}}}^s+d_n^s$	${\overline{D}}^s+d_n^s$	$(1-w)a$
$+D^j$	$s+(1-w)a-{\overline{\overline{D}}}^s-d_n^s$	$s+C_n^j$	s
$+\mathcal{E}$	0	$\overline{\mathcal{E}}-(d_n^s+C_n^j-$${\mathrm{tb}}_n)$	0

.

The firm is committed to paying $d_n=d_n^s+d_n^j$ at $t_n$ to its creditors, where $d_n^s=C_n^s+P_n^s$ and $d_n^j=C_n^j+P_n^j$ denote the regular interest and principal payments to senior and junior bondholders, respectively. The current cash flow of ${\mathrm{TB}}_{t_n}$ is ${\mathrm{tb}}_n=r_c(C_n^s+C_n^j)=r_c{C}_n$ under survival at $t_n$, where $r_c$ denotes the corporate tax rate. The current cash flow of ${\mathrm{BC}}_{t_n}$ is proportional to the remaining firm’s asset value $wa=w{A}_{t_n}$, under default at $t_n$, where w denotes the bankruptcy cost parameter.

DP starts the resolution at maturity, where the value functions of the corporate securities in Equation (9) are known. Table 4 presents these value functions under the condition of exercise before $t_N$ ($f_{t_{N-1}}=1$), which is consistent with Ayadi et al. (2016). The junior debt and pledged shares vanish from the BSE at $t_N$. Table 5 reports six events under the assumption that the exchange option was held until $t_{N-1}$ ($f_{t_{N-1}}=0$), three of which happen under solvency, and the rest under financial stress. For example, event (3) reports the case of a solvent firm, where the junior bond is exchanged against the pledged shares, resulting in a default. The junior bondholders are paid $s+(1-w)a-d_N^s$ or s, depending on whether the senior bondholders are fully or partially paid. It could happen that $s+max((1-w)a-d_N^s,0)<d_N^j$, in which case junior bondholders are better off holding. For simplicity, we ignore this unlikely event. Event (5) reports the case of a stressed firm, where the exchange option is exercised, resulting in survival. Exercising the embedded option can lead a solvent company to default or a stressed company to survive.

Assuming the model has been solved backward in time from $t_N$ to $t_{n+1}$, the potential future values of a generic value function $v_{t_n}(a,s,f)$ for corporate security are given by the following equations:

$${\overline{v}}_{t_n}(a,s,1)={\mathbb{E}}^{\mathbb{Q}}\left[{\rho }_n{v}_{t_{n+1}}(A_{t_{n+1}},S_{t_{n+1}},1)\right|(A_{t_n},S_{t_n},f_{t_{n-1}})=(a,s,1)],$$

under the condition of exercising before $t_n$ and, therefore, exercising before $t_{n+1}$,

$$\begin{array}{cc}\hfill {\overline{v}}_{t_n}(a,s,0)& ={\mathbb{E}}^{\mathbb{Q}}\left[{\rho }_n{v}_{t_{n+1}}(A_{t_{n+1}},S_{t_{n+1}},1)\right|(A_{t_n},S_{t_n},f_{t_{n-1}})=(a,s,0)],\hfill \end{array}$$

when holding until $t_{n-1}$ and exercising at $t_n$, and

$$\begin{array}{cc}\hfill {\overline{\overline{v}}}_{t_n}(a,s,0)& ={\mathbb{E}}^{\mathbb{Q}}\left[{\rho }_n{v}_{t_{n+1}}(A_{t_{n+1}},S_{t_{n+1}},0)\right|(A_{t_n},S_{t_n},f_{t_{n-1}})=(a,s,0)],\hfill \end{array}$$

when holding until $t_n$, where ${\rho }_n=e^{-r_f(t_{n+1}-t_n)}$ denotes the risk-free discount factor over $[t_n,t_{n+1}]$. Thus, $\overline{v}$ is inferred from Table 6 at $t_{n+1}$, while $\overline{\overline{v}}$ is inferred from Table 7 at $t_{n+1}$. It is important to note that ${\overline{v}}_{t_n}(a,s,1)$ is a function of $(t_n,a)$ only (Ayadi et al. 2016). As explained in Section 2, DP alternates between an interpolation step and an integration step to solve the model at time $t_n$. Table 6 and Table 7 exhibit the value functions of corporate securities at $(t_n,a,s,f)$. The rest comes by backward induction. It is important to note that Table 4 and Table 5 are consistent with Table 6 and Table 7, given that the future potentialities of ${\mathrm{TB}}_{t_N}$, ${\mathrm{BC}}_{t_N}$, $D_{t_N}^s$, and $D_{t_N}^j$ are null, while ${\overline{\mathcal{E}}}_{t_N}=a$ and ${\overline{\overline{\mathcal{E}}}}_{t_N}=a+s$. Section 3 shows that DP is a flexible alternative for designing and evaluating complex financial derivatives.

4. Conclusions

We propose a dynamic programming approach for designing and valuing two-dimensional financial derivatives. Examples include American options and exchangeable bonds. Our dynamic program splits the evaluation process into two components related to the dynamics of the underlying process and the option contract. This results in high flexibility in the model-design step and efficiency in the model-resolution step. We use local polynomials and parallel computing to enhance the efficiency of the overall numerical procedure.

Future research avenues include the extension of our construction to alternative underlying processes and/or higher-dimensional state spaces, possibly by combining dynamic programming with methodologies for model-dimensional reduction. It is worth noting that the computing time of our numerical procedure drastically increases with the dimension of the state space. However, as briefly explained in the introduction, this paper is a step forward in designing and solving dynamic programs in intermediate dimensional state spaces, say one, two, and three. For higher dimensional state spaces, our strategy involves using principal component analysis and reducing the nominal dimension of the state space to a lower effective dimension. This is often relevant in finance, as explained by Wang and Sloan (2005). Thus, option contracts can be valued assuming only a numerical error but not a statistical (sampling) error. The relative efficiency of our dynamic program with respect to traditional multivariate pricing algorithms, such as the LSMC procedure, must be analyzed further.