1. Introduction
As (
Boland 2007, p. IX) has pointed out, when a practitioner wants to model losses, there is usually considerable concern about the chances and sizes of large claims. More precisely, the study of the right tail of the distribution results is very important in order to not underestimate the size of large losses. The term long tail is useful here and is applied to rank-size distributions or rank-frequency distributions, which often form power laws. In this sense, the Pareto distribution and generalisations of this simple distribution, such as the Stoppa distribution (see
Stoppa 1990;
Kleiber and Kotz 2003), have been considered in this case. Other alternatives to the Pareto distribution have been proposed recently in the statistical and applied statistical literature. Some of them are provided by
Sarabia and Prieto (
2009),
Gómez-Déniz and Calderín-Ojeda (
2014,
2015) and
Ghitany et al. (
2018), among others.
One of the main advantages obtained when the Stoppa distribution is considered is the fact that this is a max-stable (maximum of a number of random variables) distribution, which is also related to extreme value theory. This extreme property can, in turn, be highlighted by making a mixture (compound) of it, gaining an even heavier tail.
In this paper, we study properties and applications related to the mixture of the class of probability distributions built by Lehmann’s alternative (also known as max-stable or exponentiated distributions). The reader is recommended to see
Lehmann (
1953) and
Sarabia and Castillo (
2005), among other references. A positive random variable
X is said to be built by the Lehmann’s alternative method if its cumulative distribution function (cdf) can be represented as:
where
is a continuous cdf. This class of distributions is also known in the statistical literature as Lehmann’s alternative and exponentiated distribution. In practise, if
X represents, for instance, the loss of a given risk in a portfolio of insurances, a population of such policy-holders may be a ubiquitous variation in
-values because of small fluctuations in the mean of losses, so that a policy-holder selected at random can be regarded as having a random value of
, call it
. Here,
takes values in
. The distribution of
across the positive real numbers is referred to in the statistical literature as the mixing distribution (or density). These mixtures are useful in economics, financial, and actuarial fields, where extreme and long tails appear in the empirical data.
Although in the statistical literature, mixtures of discrete distributions for providing thick tails (for example, the well-known Poisson–Gamma distribution) are much more frequent, mixtures of continuous distributions have also been the subject of research in the field of applied statistics and, in particular, in actuarial statistics. One example of this is the exponential-inverse Gaussian model provided by
Frangos and Karlis (
2004). Other examples of continuous mixture distributions were studied by
Fung and Seneta (
2007) and
Gómez-Déniz et al. (
2013). Also, some mixtures of continuous distributions have recently been considered in the actuarial literature in
Tzougas and Karlis (
2020) and
Tzougas and Jeong (
2021).
The special case in which (
1) corresponds to the Stoppa cdf (see for example,
Stoppa 1990;
Kleiber and Kotz 2003)—which is a good description of the random behaviour of large losses—is studied in some detail. The Stoppa distribution is a generalisation of the classical Pareto distribution and is a max-stable distribution with a nice and simple cdf. We provide properties of this mixture, mainly related to the analysis of the tail of the distribution that makes it a candidate for fitting actuarial data with extreme observations. Inference procedures are discussed and applications to two well-known datasets are shown. Furthermore, two regression models for this mixture are derived to fit bodily injury claims data.
The remainder of the paper is organised as follows. The mixture representation of a max-stable distribution is provided in
Section 2. Here, the representation of the Stoppa distribution is also considered and some basic properties are derived.
Section 3 discusses properties related to the right tail of this mixture distribution. Some special cases of the mixing distribution are considered in
Section 4. In particular, special attention is paid to the generalised inverse Gaussian distribution, which includes as special cases the inverse Gaussian, Gamma, and exponential distributions, among other models. Next, the stochastic ordering of the resulting mixture models is examined. Finally, two regression models for this mixture of distributions are given. Then, three numerical applications are shown in
Section 5 and conclusions are provided in the last section.
2. Lehmann’s Alternative
The distribution function built by Lehmann’s alternative method,
, assumed that
, can be interpreted in different ways (see for instance
Sarabia and Castillo 2005); for example, it is the distribution of the last (maximum) order statistics in a random sample of size
n. That is, consider the sample
of
n independent and identically distributed random variables with common cdf
and define the ordered sample
. If the interest of the practitioner is the asymptotic distribution of the maxima
as
, the distribution of
results in
. On the other hand, exponentiated distributions of the form
also appear by applying the probability integral transformation or the quantile function of
G to a Beta distribution with parameters
and 1.
We now consider extensions of the distributions built by the Lehmann’s alternative method of the form
assuming that the parameter
is not constant and varies according to some known probability distribution, say
, depending on a vector of parameters
. This has the following stochastic representation,
Thus, we study the mixture of the form,
where
is a genuine mixing probability density function of
, the parametric space in which the parameter
moves, depending on a vector of parameters
. Another possibility, which will not be studied here, is to consider that the parameter
takes integer values
and allows
to follow a discrete distribution such as the geometric discrete distribution. This is the family of geometric max-stable distribution considered by
Marshall and Olkin (
1997).
Observe that (
2) can be written as
in which
denotes the moment-generating function. Thus, attending to (
3), any probability density function (pdf) with a closed-form for its moment generating function, such as the Gamma, the inverse Gaussian, and the generalised inverse Gaussian distributions, should be good candidates to introduce here.
The pdf, obtained from (
2), is given by
where
, and the hazard rate function results in
The Lehmann’s Alternative Stoppa Distribution
The natural generalisation of the Pareto distribution proposed by
Stoppa (
1990) (see also
Kleiber and Kotz 2003) has a nice and simple cumulative distribution function (hereafter cdf) representation given by
where
,
, and
is a shape parameter that allows for unimodality when
; furthermore, the mode is located at zero when
. Observe that
is the cdf of the classical Pareto distribution with scale parameter
and shape parameter
(see for instance
Arnold 1983) with pdf
and survival function
Note that (
4) obeys the cdf of a Lehmann’s alternative (max-stable) distribution, such as the one given in (
1). Thus, this cdf is simply a power transformation of the classical Pareto cdf obtained as a special case of (
4) for
. Some additional properties, such as moments, Lorenz curves, the Gini index, and estimation of this distribution can be found in (
Kleiber and Kotz 2003, chp. 3), where other generalisations of the classical Pareto distribution can also be viewed.
Henceforward, we will write
to denote that a continuous random variable with support in
follows the distribution given in (
4).
To see how the Stoppa model works as compared to the classical Pareto distribution, we will consider data taken from (
Hogg and Klugman 1984, p. 64) (see also
Boyd 1988), which concern 40 losses recorded in 1977 related to wind catastrophes. This set of empirical data was recorded to the nearest USD 1,000,000, although the data include only losses of USD 2,000,000. Maximum likelihood estimates were computed for the classical Pareto distribution and the Stoppa distribution, assuming
, and the results appear in
Table 1. As we can see, the Stoppa distribution provides a better fit than the one obtained with the classical Pareto distribution.
3. Extremal Properties
As was mentioned before, a random variable with non-negative support, such as the classical Pareto distribution, is commonly used in insurance and other financial scenarios to model the amount of claims (losses). In this sense, the size of the distribution tail is fundamental if it is desired that the chosen model allows us to capture amounts sufficiently far from the start of the distribution support, that is, extreme values. Due to this, the use of heavy right-tailed distributions such as the Pareto, lognormal, and Weibull (with shape parameter smaller than 1) distributions, among others, have been employed to model losses in motor third-party liability insurance, fire insurance, or catastrophe insurance, among others. In order to make the paper self-contained, in the following, we provide the formal definition of a heavy-tailed (heavy right-tailed) distribution (see
Rolski et al. 1999).
Definition 1. Any probability distribution that is specified through its cdf on the real line, is heavy right-tailed if .
Observe that is the hazard function of a random variable with cdf .
An important issue in extreme value theory is the regular variation (see
Bingham et al. 1989;
Konstantinides 2017); that is, a flexible description of the variation of some function according to the polynomial form of the type
,
. This concept is formalised in the following definition.
Definition 2. A distribution function (measurable function) is called regular varying at infinity with index if it holds thatwhere and the parameter is called the tail index. The next proposition establishes that the survival function of the distribution given in (
2) is a regular variation Lebesgue measure.
Proposition 1. The survival function of any mixture with cdf as the one given in (2) when is given in (5) is a survival function with regularly varying tails. Proof. This is straightforwardly verified by taking into account that
Now, taking into account that , the statement of the result follows immediately. □
Therefore, as a regular varying at infinity class is a long-tailed distribution, and the latter distribution is also heavy right-tailed, then any mixture of the Stoppa distribution is heavy right-tailed.
Corollary 1. If is a sequence of iid random variables with a survival function provided by and , thenwhere the symbol ∼
means it is asymptotically equivalent in probability. As a consequence of this result, if , then This result is important because, for large x, the event is due to the event . Thus, exceedances of high thresholds by the sum are explained by the exceedance of this cut-off by the largest value in the sample.
4. Some Candidates of Mixing Distributions
Consider the pdf of the generalised inverse Gaussian distribution given by
where
and
gives the modified Bessel function of the third kind and with index
given by
being the confluent hypergeometric function (
Johnson et al. 2005) in which integral representation,
A distribution with a pdf as the one given in (
6) will be denoted as
.
Its moment-generating function is given by
This distribution includes a lot of basic distributions such as the Gamma distribution ( and ); the reciprocal Gamma distribution ( and ); the inverse Gaussian distribution (); the hyperbolic distribution (); and others such as the exponential, chi-squared, half-normal, etc.
Now, by using (
3) together with (
7), we get the mixture of the Stoppa distributions with the generalised inverse Gaussian distribution (SGIG). In order to simplify the notation, we introduce the expression
. Then, its cdf results in
One special case obtained from the last is the mixture of the Stoppa distribution with the Gamma distribution (SG) with cdf,
Observe that, in this case, the mixture distribution is again a max-stable distribution. Another interesting sub-model obtained from the generalised inverse Gaussian distribution is the inverse Gaussian distribution, which is reached when
. In this case, (
3) can be written as
which corresponds to the mixture of the Stoppa model with the inverse Gaussian distribution (SIG).
Now, the pdf obtained from (
8) can be written as
From (
9), the pdf results in
It is known that
. Then, the pdf of the SIG distribution can be written as
In
Figure 1, some graphs of the pdf (
10) are shown for special cases of the parameters. As can be noted, all the cases shown in the graph include a large tail.
In financial economics and risk theory, the accurate calculation of risk capital is an issue of crucial interest to researchers, regulators of financial institutions, and commercial vendors of financial products and services. In this sense, the Value-at-Risk (VaR), which is defined as the amount of capital required to ensure that the insurer does not become insolvent with a high degree of certainty, is an important risk measure. For a random variable
X that follows the Stoppa and the different mixtures proposed here, i.e., the
q-quantile,
are given by
4.1. Stochastic Ordering
It is our goal now to investigate the stochastic order of the distribution in (
4) and its mixture. The analysis of stochastic ordering has been widely studied in many different areas such as economics, operations research, reliability, and statistics (e.g., survival analysis) among other fields. Also, comparing random variables is vital in risk theory. Numerous ordering concepts have been used in the statistical literature, e.g., the usual stochastic order, hazard rate order, reversed hazard rate order, and the likelihood ratio order among others. For a comprehensive understanding of stochastic ordering, the reader is encouraged to read
Shaned and Shanthikumar (
2007) and
Yu (
2009), among others. In this work, we use the stochastic dominance concept provided in
Dhaene et al. (
2006). We recall here the definition given in that book.
Definition 3. Let and be continuous random variables with cdf and , respectively. Then, is said to be smaller than in the stochastic dominance sense (written as ) if for all .
In the following result, it is shown that the stochastic dominance can be expressed in terms of the Value-at-Risk.
Proposition 2. Let and be continuous random variables with cdf and , respectively. We have that is smaller than in the stochastic dominance sense if and only if their respective quantiles are ordered: Proposition 3. Let and . Then, if , and , then .
Proof. If
,
and
, we have that
and therefore by using the previous theorem we have that
. □
Proposition 4. Let and . Then, if , , , and , then .
Proof. If
,
,
, and
, we have that
and therefore by using the previous theorem, we have that
. □
It is easy to see that, if and with , then . Furthermore, if and with , then . Now, we have the following result.
Theorem 1. Let and be two mixture random variables with cdfs and obtained from (3). If , then . More effort will be necessary to get this quantity for the SGIG distribution.
4.2. Estimation
In this section, we show how to estimate the parameters of the mixture distributions via maximum likelihood estimation. For that reason, let us assume that
is a random sample selected from the distribution of interest (
10) and also assume that
,
. The log-likelihood function, obtained from (
10), is proportional to
where
is the vector of parameters to be estimated.
Although in practice, the modified Bessel function of the third kind is implemented in most statistical packages (note that this is not the case of the econometric software
WinRats), it is convenient to express this function in terms of the modified Bessel function of the first kind,
. The relationship between both functions (see
Johnson et al. 2005, p. 19) is given by
where
is the modified Bessel function of the first kind. The advantage of this function is that it is written as a series representation that facilitates (by truncation) the estimation procedure of the parameters of the model. More details about the maximum likelihood estimation are given in the
Appendix A.
Conjugate Distribution
In this subsection, we will see that the GIG distribution is a conjugate distribution with respect to the Stoppa distribution.
Theorem 2. Let and suppose that, given , . Then we have that the posterior distribution of λ, given n years of individual independent experience, is again a , where the updated parameters are given by, Proof. The pdf of the Stoppa distribution, obtained from (
4), is given by
Thus, given the sample information
, the likelihood, taken from (
13), is proportional to
Therefore, by applying Bayes’ theorem, we have that the posterior is proportional to
which is a GIG distribution with parameters (
11) and (12). □
Observe that, if
and
follow a Gamma distribution with parameters
and
, then using the previous result, we have that the posterior mean of the parameter
given the sample information
results in
Consequently, this Bayesian expression takes the form
where
and
Since it is not verified that
, then it is not guaranteed that the mean of the predictive distribution coincides with the posterior mean, i.e.,
. Therefore, although the expression (
14) resembles the credibility formula widely introduced in actuarial statistics with credibility factor
, this is not a credibility premium since the purpose of that expression is to predict the expected aggregate claims size in the next period of time.
4.3. Novel Heavy-Tail Regression Models
The mean of the Stoppa distribution is given by the expression:
where
is the complete beta function defined as
with
and
. Therefore, the mean of the mixture Stoppa distribution can be obtained by compounding using the expression,
Then, given a sample
, the new heavy-tailed regression models can be derived by writing the scale parameter of each model as
Here, is a vector of explanatory variables and is a vector of regressors to be estimated. Note that, in the latter expression, does not depend on the subscript i. In the practical implementation, this parameter was chosen by using a grid search for manually specified values of this parameter in the interval .
4.3.1. SG Case
In this model, the log-likelihood function is given by
where
.
The maximum likelihood estimates of the SG distribution are obtained by solving the system of equations given by
where
and
.
From these equations, the entries of the observed information matrix can be derived after tedious algebra (not reproduced here) by differentiating these equations with respect to the
parameters. The function (
15) can be simply maximised by considering several values as seed points. Of course, the global maximum is not guaranteed by the difficulty to show that the log-likelihood function is concave. We have used different maximum search methods that are available in the
MAXIMIZE in-built function in the
WinRATS software package by using the BFGS algorithms.
4.3.2. SIG Case
When the mixing distribution is the inverse Gaussian, the log-likelihood function is given by
where
.
The normal equations are given, in this case, by
where
and
.
The standard errors of the estimates can be computed by following the same approach as above.
5. Numerical Experiments
In this section, the performance of the distributions introduced in this work is verified by employing three different sets of data. The first one is the
danishuni, which can be downloaded from the
R package
CASdatasets and also from
Extreme Value Statistics in S-plus libraries, collected at Copenhagen Reinsurance, comprising 2157 fire losses, adjusted for inflation to reflect 1985 values, over DKK 1,000,000 during the period 1980 to 1990, adjusted for inflation to reflect 1985. A detailed statistical analysis of this dataset can be found in
McNeil (
1988), in
Albrecher et al. (
2017), and also in
Embrechts et al. (
1997). The second dataset is
norfire, which is also available in the
R package
CASdatasets, and includes 9181 fire losses over the period 1972 to 1992 from an unknown Norwegian insurer. A priority of NKR 500,000 (if this amount is exceeded, the reinsurer becomes liable to pay) was applied to derive this set of data.
The estimates of the parameters and their corresponding
p-values (given in brackets), the negative of the maximum of the log likelihood function, and the AIC for the two aforementioned sets of data are shown in
Table 2 for the Stoppa distribution and for the three mixture models previously considered, i.e., SG, SIG, and SGIG. For all the models and the two datasets, the parameter
was chosen by using a grid search for manually specified values of this parameter in the interval
. The validation of the models is carried out using the following information criteria: the negative log likelihood (NLL), computed by taking the negative of the value of the log-likelihood evaluated at the maximum likelihood estimates, and the Akaike’s information criterion (AIC), computed as twice the NLL, evaluated at the ML estimates plus twice the number of estimated parameters. Moreover, we also incorporate the Kolmogorov–Smirnov test (KS) and the Anderson–Darling test (AD) to show the fit of the model to the empirical data in terms of the cdf. For these test statistics, smaller values of these tests indicate a better fit of the model to the empirical data. Note that they do not only provide a way to measure the fit in terms of the cdfs, but also allow us to perform hypothesis testing for model validation purposes. An extremely small
p-value might lead to a confident rejection of the null hypothesis that the data come from the given model. It can be seen that the SG distribution provides the best fit for the Danish dataset, whereas the SGIG returns the lowest values for NLL and AIC for the Norwegian set of data. For the former dataset, and using KS and AD tests, none of the models are rejected; however, it is noted that, for both tests, the Stoppa distribution is rejected for the Norwegian dataset.
For comparison reasons, we have also fitted shifted versions of lognormal, Weibull, and Burr distributions for the Danish and Norwegian datasets with the following densities:
respectively. For all these distributions, the parameter
was estimated by using the method explained above. A comparison of these models with the other heavy-tailed distributions used to model the Danish and the Norwegian datasets can be found in
Gómez-Déniz et al. (
2022) and
Gómez-Déniz and Calderín-Ojeda (
2015), respectively. This catalogue of heavy-tailed distributions includes shifted versions of the lognormal, inverse Gaussian, and generalised Gamma, and also inverse Gamma, log Gamma, and Fréchet and Pareto ArcTan, among other models.
The estimation of the parameters for all the distributions used in this work has been completed using the method of maximum likelihood by using
Mathematica® v.12.0 and has also been verified via
WinRATS v.7.0. The codes are available from the authors upon request. Standard errors of the estimates were obtained by finite differentiation. The
WinRATS v.7.0 software package also gives the option to directly calculate the maximum of the log-likelihood returning the entries of the Fisher information matrix. The parameters can also be estimated via an EM algorithm as shown in the
Appendix A.
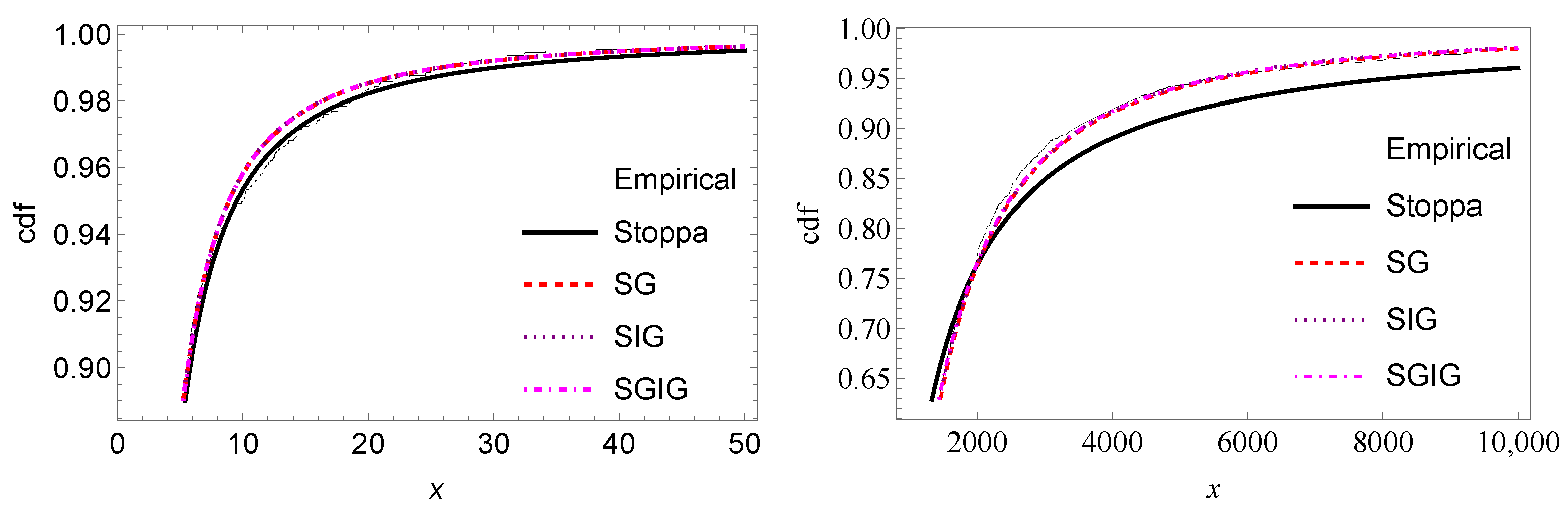
These results are confirmed by
Figure 2. In this figure, the graphs of the histogram of both datasets (Danish left, Norwegian right) are shown. We have also superimposed the fitted densities. Also in
Figure 3, we have plotted the smooth cdf of the empirical data, and the fitted cdf of all the distributions previously considered have been superimposed. It is observable that the SG (dashed line) and SGIG (dotted-dashed line) distributions adhere closely to Danish and Norwegian datasets, respectively.
Now, we select a distribution that yields a feasible characterisation of the loss process for both sets of data, we should check that the theoretical limited expected values, calculated numerically by
adhere closely to the empirical ones. As is already known, (
16) is the expected quantity per claim retained by the insured on a policy with a fixed amount deductible of
x. Here, the empirical limited expected value function was computed based on the expression
. Obviously, when
x tends to infinity,
and
converge to
and the sample mean, respectively.
Table 3 and
Table 4 display the limited expected value for several values of the policy limit
x considered for the Danish and Norwegian datasets, respectively. It is observed that that the values obtained from the mixing distributions adhere closely to the observed empirical limited expected values obtained, as compared to the Stoppa distribution for both datasets.
The absolute errors between the empirical values and the fitted values shown in
Table 3 and
Table 4 are shown in the graphs that appear in
Figure 4. As can be seen, at least for the Danish data, the fit is improved to the extent that the value of the deductible increases. The pattern for the Norwegian data is challenging to observe.
The third dataset deals with automobile bodily injury claims using data from the Insurance Research Council (IRC), a division of the American Institute for Chartered Property Casualty Underwriters and the Insurance Institute of America. The data, collected in 2002, include demographic information about the claimants, attorney involvement, and economic losses (in thousands of USD), among other variables. As several of these covariates include missing observations, we will only use a sample of 1091 losses. This dataset can also be downloaded from the
R package
CASdatasets, see also
Frees (
2010). We consider as a response variable the claimant’s total economic loss. The empirical distribution of this variable combines losses of small, moderate, and large sizes, which makes it suitable for fitting heavy-tailed distributions. Other remarkable features of this set of data are unimodality, skewness, and a long right tail, showing a high likelihood of extremely expensive losses. Below, in
Figure 5, we have plotted the histogram of this dataset. We have also superimposed the densities of the S, SG, and SIG distributions. The SIG distribution adheres closely to empirical data.
This dataset also includes the following covariates:
ATTORNEY takes the value 1 if the claimant is represented by an attorney and 0 otherwise;
CLMSEX takes the value 1 if the claimant is male and 0 otherwise;
MARRIED takes the value 1 if the claimant is married and 0 otherwise;
SINGLE takes the value 1 if the claimant is single and 0 otherwise;
WIDOWED takes the value 1 if the claimant is widowed and 0 otherwise;
CLMINSUR, whether or not the claimant’s vehicle was uninsured (=1 if yes and 0 otherwise);
SEATBELT, whether or not the claimant was wearing the seatbelt/child restraint (=1 if yes and 0 otherwise);
CLMAGE, claimant’s age.
Now, by using these covariates, we will explain the total losses in terms of the set of explanatory variables by using the Stoppa and SG and SIG regression models. From left to right, in
Table 5, the parameter estimates, standard errors (S.E.), and the corresponding
p-values calculated based on the
t-Wald statistics for the three regression models are illustrated. Furthermore, NLL and AIC values for each model are provided in the last two rows of the table. For the
ith policyholder, the total amount
follows the specified model whose scale parameter
depends on the above set of covariates through the aforementioned link function. In view of its relatively low
p-value, the estimates associated with the explanatory variables
INTERCEPT,
ATTORNEY,
SEATBELT, and
CLMAGE are statistically significant at the 5% significance levels for the three models considered. In addition, the shape parameter
is also statistically significant at the same nominal level for all the models discussed here. It is noted that the parameters of the mixing distribution are also significant at this nominal level. Finally, the SIG provides the best fit to this dataset in terms of the two measures of the model selection considered.
As the estimates of the parameter
significantly differ in these models, we now estimate the value of the tail index, i.e.,
estimated by the commonly used Hill’s estimator. For this, we consider the set of observations representing the
n losses
and let
be reordered (reversed order statistics) in such a way that
is the highest value in the sample. Then, we construct the sets of numbers
and
for
. The set
is defined by
and
. Then,
is an estimate of
when
k is increased until it seems inappropriate to proceed. Below,
Figure 6 presents the values of
when the value of
k takes values in
. Note that the values of the estimator stabilise in the neighbourhood of 1.1. These values can be compared with the estimate of the tail indexes
for each one of the thee models given in
Table 5. It would be interesting to study how the parameters’ estimates of these three models vary if we fix the the estimate of the tail index based on the Hill’s estimator and then estimate the other parameters via maximum likelihood estimation.