Abstract
We consider a two-dimensional risk model with simultaneous Poisson arrivals of claims. Each claim of the first input process is at least as large as the corresponding claim of the second input process. In addition, the two net cumulative claim processes share a common Brownian motion component. For this model we determine the Gerber–Shiu metrics, covering the probability of ruin of each of the two reserve processes before an exponentially distributed time along with the ruin times and the undershoots and overshoots at ruin.
1. Introduction
The existing ruin theory literature has a strong focus on the univariate setting featuring a single reserve process. In practice, however, the position of an insurance firm is often described by multiple, typically correlated, reserve processes. Multivariate ruin presents a challenging topic that can be dealt with explicitly only when imposing additional assumptions. Most notably, a certain ordering between the individual net cumulative claim processes, say for some , needs to be imposed. The ambition of this paper is to, in this multivariate context, not only assess the likelihood of ruin, but to also provide insight into ‘the way ruin occurs’. Indeed, through the so-called Gerber–Shiu metrics Gerber and Shiu (1998) we probabilistically describe the corresponding ruin times, undershoots, and overshoots. Throughout this paper we consider the case , but all results can be extended to higher dimensions, albeit at the price of the underlying analysis increasing in complexity.
Model—In this paper we analyze two net cumulative claim processes, say and , in which claims arrive simultaneously, according to a Poisson process with rate . These claims are 2-dimensional, componentwise non-negative independent and identically distributed random vectors that are distributed as the generic random vector .
We throughout assume the entries of this vector to be ordered in the sense that
where is a generic claim size corresponding to the net cumulative claim process , for . Above we mentioned that claims of both components arrive simultaneously, but by the ordering condition (1) those of the process can be void: observe that at any claim arrival in the process there is a claim arrival in the process, but not vice versa. The ordering condition for instance applies when the process corresponds to the losses for the whole portfolio, and the process to the losses ceded to the firm.
A specific feature of this paper is that we consider a perturbed risk model, in the sense that both processes and in addition contain a Brownian component. This component is common to both processes, and takes the form , where can be interpreted as the premium rate (which we assume is the same for both processes), and is a standard Brownian motion that is independent of the claim arrival process. The i-th net cumulative claim process thus becomes
for , with denoting a Poisson process with rate . It requires an elementary computation to verify that the corresponding bivariate Laplace exponent is given by
with
denoting the bivariate Laplace–Stieltjes transform (LST) of the random vector We let be the reserve level process pertaining to the i-th net cumulative claim process, with denoting the corresponding initial surpluses. Observe that the construction is such that the two individual net cumulative claim processes are ordered: for any , almost surely; the reserve level processes and are not necessarily ordered.
Seen from an economic perspective, the compound Poisson component can be seen to represent the ‘large’ claims, whereas the Brownian component corresponds to an aggregate of ‘small’ claims. Our model in which the net cumulative claim process is represented by such a superposition of a compound Poisson process and a Brownian motion is particularly relevant in light of the findings of Asmussen and Rosiński (2001). These imply that, under mild conditions, one can arbitrarily closely approximate any spectrally positive Lévy process (i.e., Lévy process without any negative jumps) by such a superposition.
Quantities of interest—The Gerber–Shiu metrics provide insight into the two individual reserve level processes at ruin. Concretely, with and , the focus lies on capturing a probabilistic description of the joint distribution of the random vectors
here is the ruin time corresponding to the net cumulative claim process , being defined as the smallest positive t such that , for . Our analysis enables us to probabilistically analyze these ruin times, jointly with the values of the reserve process immediately before ruin , typically referred to as the undershoot, and the values of the reserve process at ruin , representing the corresponding overshoot, for .
We characterize the underlying sextuple law (for the two ruin times, two undershoots, and two overshoots) by identifying its corresponding transform. Concretely, our aim is to identify, for and , (where for ), the object
Here is an exponentially distributed time with parameter sampled independently from everything else; by we mean that both ruin times and should be smaller than the random variable . As and are non-negative whereas is non-positive, we let and . We thus consider the classical Gerber–Shiu metrics, with penalty function .
In the sequel, we frequently suppress the parameters , as these are held constant throughout the analysis. Our work succeeds in finding in terms of its transform, for and ,
Related literature—We proceed by a (non-exhaustive) literature review, covering papers on multivariate risk for models of Cramér–Lundberg type, papers that focus on adding a Brownian perturbation, papers on the identification of corresponding Gerber–Shiu metrics, and additional related papers from the queueing literature.
Early papers on two-dimensional risk processes with some form of ordering of claim sizes are Avram et al. (2008a, 2008b). These works consider the joint ruin problem in the case of an insurer that splits claims and premia according to fixed proportions (which is a special case of our ‘ordered claim assumption’ (1)). A key observation is that the resulting two-dimensional ruin problem can be viewed as a one-dimensional crossing problem over a piece-wise linear barrier. Badescu et al. (2011) extended the model of Avram et al. (2008a, 2008b) by allowing additional claim arrivals at the first insurer. Gong et al. (2012) considered a discounted penalty function, adding Gerber–Shiu metrics (in that they include the surplus at ruin), and provide recursive integral formulas for that penalty function.
The present paper was inspired by the work Badila et al. (2014). Therein, under the ‘ordered claim assumption’ (1), the two-dimensional risk model with simultaneous Poisson arrivals is treated in detail. Compared to our objectives, two aspects are lacking: in the first place the focus lies on ruin probabilities only, meaning that the evaluation of the Gerber–Shiu metrics was not included, and in the second place there is no Brownian perturbation. Importantly, Badila et al. (2014) in addition establishes a bivariate duality result, which links the bivariate ruin model to a queueing model with two parallel queues and simultaneous Poisson arrivals at both queues—Assumption (1) translates into requiring that the service times at the first queue are always at least as large as the corresponding ones at the second queue. In particular, the infinite-horizon survival probabilities of the risk model are identified with the steady-state two-dimensional workload distribution in the queueing model. It is also shown in Badila et al. (2014) how this analysis can be extended to a setting with more than two insurers/queues. Another contribution of Badila et al. (2014) is that it highlights that the stationary distribution of the two-dimensional workload process in the queueing model without ordering of the service requirements can be found by using a boundary value technique. For this particular queueing model that was shown, in increasing level of generality, in Baccelli (1985); Cohen (1992); de Klein (1988). The implication of the duality is that one can thus also handle the two-dimensional risk model without the ordering constraint being in place—at least, in case one is interested in the transform of the ruin probabilities only (i.e., not covering Gerber–Shiu metrics).
In Gerber (1970), the classical one-dimensional Cramér–Lundberg model has been generalized by adding an independent Brownian motion component to the net cumulative claim process. For this perturbed model, Dufresne and Gerber (1991) analyzes the probability of ruin, as well as the separate probabilities of ruin caused by a claim or by the Brownian component. Wang (2001) has derived explicit expressions for the latter two probabilities in the case of exponentially distributed claim sizes. Tsai and Willmot (2002) has added the Gerber–Shiu metrics to the model of Dufresne and Gerber (1991) and Gerber (1970). Generalizing a result of Gerber and Landry (1998), they derive a defective renewal equation for the surplus process (expected discounted penalty function, involving both the deficit at ruin and the surplus immediately before ruin). This equation is then used to study the asymptotic behavior of the ruin probability when the initial capital tends to infinity. Li et al. (2019) studies the finite-time expected discounted penalty function (Gerber–Shiu) for the Cramér–Lundberg model with perturbations by solving a second-order partial integro-differential equation with boundary conditions. For the same model, Liu et al. (2017) considers the joint distribution of the time to ruin and the number of claims until ruin. In Su et al. (2019), approximations are developed using a Laguerre series expansion; see also Su and Wang (2021).
Briefly returning to the dual two-dimensional queueing model that is being studied in Badila et al. (2014), it is worthwhile to mention that this queueing model is there shown to be equivalent to a particular tandem fluid queue, viz., two queues in series in which the outflow of the first queue is a fluid, and with simultaneous Poisson arrivals with generic service time at the first queue and in the second queue. In turn, tandem fluid queues are equivalent to particular priority queues with preemptive resume priorities, as discussed in, e.g., Kella (1993); Mandjes and van Uitert (2005).
Main contributions—This paper generalizes the results in Badila et al. (2014) for a two-dimensional risk model with ordered claim sizes in three ways: we consider the probability of ruin before a finite time-horizon (rather than the all-time ruin probability), we add a Brownian component, and we consider the discounted penalty function with the Gerber–Shiu metrics. Our main results are Theorem 2 for the unperturbed case, and Theorem 3 for the case with a Brownian component. These theorems uniquely characterize, in terms of the transform , the probability of ruin before an exponential time, along with the distributions of the ruin times, the undershoots at ruin, and the overshoots at ruin. The two-dimensional case without the Brownian component was briefly considered in (Mandjes and Boxma 2023, §7.5). Importantly, as it turns out, the unperturbed model has to be treated rather differently than the perturbed model, in the sense that one cannot simply let the ‘diffusion parameter’ go to 0 in the perturbed model.
Organization—In Section 2, we provide a concise discussion of the univariate case, thus introducing some of the main tools that are used for the bivariate case. Section 3 provides some general results for the bivariate case, applied both to the unperturbed and perturbed risk models. Section 4 is devoted to the bivariate unperturbed risk model, while the bivariate perturbed risk model is analyzed in Section 5.
2. Univariate Case
In this section, we present a compact analysis of the univariate case. These univariate results will play a role in the bivariate case, but, as we will see, some are interesting in their own right, in particular the results for the case of the perturbed risk model, i.e., the model with
In this univariate setting, we can use a somewhat simpler notation than the one used throughout the remainder of the paper. We let be a compound Poisson process with drift (characterized by the arrival rate , the LST of the claim-size distribution ), and the premium rate ) perturbed by a Brownian motion. Concretely, the net cumulative claim process is defined by
where , with a standard Brownian motion (or: Wiener process), denoting a Poisson process with rate , and a non-negative parameter. With the firm’s initial capital being u, the evolution of the reserve level is given by It is readily checked that, for ,
Denote by and the running maximum process and running minimum process, respectively, corresponding to :
Recalling that is an exponentially distributed random variable, sampled independently of everything else, it is a well-known result that and have exponential distributions with parameters
respectively, where ; see, e.g., (Mandjes and Boxma 2023, Exercise 1.5.(ii)). By a time-reversibility argument, it follows that and are identically distributed, while it is an implication of the Wiener–Hopf decomposition that and are independent. Observe that .
Define the ruin time by
so that the finite-horizon ruin probability is given by . In this section, we study the transform of this finite-time ruin probability, jointly with the corresponding Gerber–Shiu metrics (i.e., the time of ruin , the value of the reserve process immediately before ruin , and the value of the reserve process at ruin ). This concretely means that in this univariate setting we analyze, with , the object
as and are non-negative whereas is non-positive, we let and . The objective of this section is to compute the transform with respect to u and t: with an exponentially distributed time with parameter sampled independently from everything else, we wish to find a closed-form expression for
The random variable is often referred to as an exponential clock; cf. Asmussen (1995). For conciseness, in the remainder of this section we write and Observe that the level u can be first exceeded either at a claim arrival, thus leading to positive undershoot and overshoot, or between claim arrivals (i.e., due to the Brownian component), thus leading to the undershoot and overshoot both being equal to zero. We refer to Figure 1 for a pictorial illustration of both cases. In the remainder of this section, we denote the Laplace exponent of the process by
and let be its right-inverse. In the unperturbed model, i.e., the model in which , various known methods can be used to identify . As can be found in, e.g., (Mandjes and Boxma 2023, Exercise 1.2) and, for a more general model, Boxma and Mandjes (2021),
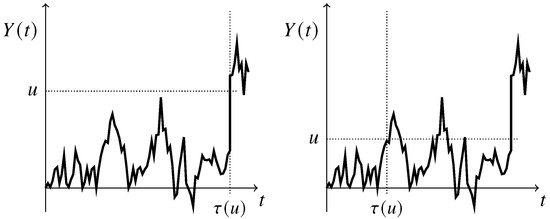
Figure 1.
Net cumulative claim process . Left panel: level u is exceeded due to a jump of the compound Poisson component. Right panel: level u is exceeded due to the Brownian component, i.e., with zero undershoot and overshoot.
A ‘density version’ of this result is given in (Kyprianou 2013, Theorem 5.5): there the so-called Gerber–Shiu measure is expressed in terms of scale functions pertaining to the underlying compound Poisson process.
We proceed by an analysis of the univariate perturbed model. As will become clear in the analysis, the fact that we assume to be positive is a crucial element in the derivation. It is noted that this univariate model has already been studied by Li et al. (2019), but it seems difficult to extend their approach to the bivariate case. In view of this, and also because the univariate model is very natural and important in its own right, we present two methods via which it can be analyzed in detail: a method that is based on conditioning on the first event (Section 2.1 and Appendix A), and a method based on Kolmogorov-type equations that seems particularly suitable for the bivariate model (Section 2.2). In Section 3, Section 4 and Section 5 we extensively build upon the ideas and results of the present section.
2.1. Solution by Conditioning on the First Event
Define as the counterpart of , but with a claim arriving at time 0. By conditioning on the maximum of the Brownian component until the first claim arrival, we obtain that, with denoting the ruin time corresponding to the Brownian motion ,
This decomposition can be understood as follows. The first term in the right-hand side of the previous display corresponds to the scenario that before the first event (i.e., either expiration of the ‘exponential clock’ or a claim arrival) the level u has already been exceeded, such that the undershoot and overshoot are both equal to zero. The second term corresponds to the scenario that has remained below level u until the first event (where it is observed that the densities of and factorize by the Wiener–Hopf decomposition, noting that the expression is weighted by an exponential density). Relying on a similar argumentation, we also observe that
From these relations for and , the transform can be identified in a relatively straightforward manner, as pointed out in Appendix A. Define
Theorem 1.
For any ,
This theorem has nice ramifications. If , (i.e., ruin eventually happens), the stationary overshoot can then be analyzed by considering with and letting To this end, we first verify that, for and ,
Observe that has an atom in zero, due to the fact that ruin can possibly be reached ‘due to the Brownian component’ (i.e., between two subsequent claims). By letting , we readily obtain
Considering this expression as , by an application of L’Hôpital’s rule, we have proven the following result.
Corollary 1.
If , then
The expression in the right-hand side of (5) is indeed between 0 and 1, as can be seen as follows. Because ,
Observing that is positive and that , we have the right-hand side of (5) being equal, at most, to 1.
2.2. Solution Using Kolmogorov-Type Equations
In this subsection, we detail an alternative approach that will be relied upon later in the paper. In this approach, we compare the object of interest at two points in time (located ‘close to’ each other). Indeed, as , owing to the memoryless property of the killing time , the following Kolmogorov-type identity holds: up to -terms,
cf. the line of reasoning in Boxma and Mandjes (2021) and references therein. The first term between the brackets on the right-hand side of (6) corresponds to the scenario with an arrival of a claim of size smaller than u, the second to the scenario with an arrival of a claim larger than u (so that the overshoot and undershoot can be assigned a value), and the third to the scenario of neither a claim arrival nor killing. Performing the substitution , we obtain, up to -terms,
The next step is to convert this equation into an integro-differential equation. With we obtain after dividing the entire equation by that
We now multiply the entire equation by and integrate over u. To this end, it can be verified that integration by parts yields
Due to the local behavior of Brownian motion, (for any ), so that
Solving from this relation, recognizing the Laplace exponent , we find
The unknown can be found using that any non-negative root of the denominator is a root of the denominator as well. This root being , we obtain
Inserting this , we recover Theorem 1.
3. Bivariate Risk Model: General Results
So as to treat the bivariate case, in principle both methods that were demonstrated in the previous section can be used. As it turns out, in this bivariate setting the Kolmogorov-type approach introduced in Section 2.2 works particularly conveniently: we derive an integral equation for in the bivariate case using this technique. In Section 4 and Section 5, we successively solve this integral equation for the unperturbed () and perturbed () cases. As the two cases have to be treated intrinsically differently, this division into two sections is natural.
Define, for , the univariate counterparts of :
describing the ruin times, undershoots and overshoots of the individual processes. In Section 2, we found the transform of , in both the unperturbed and the perturbed case, which in the sequel we denote by , for and . As , following the Kolmogorov-type reasoning, we find that the bivariate counterpart of (6) is, for any and with denoting , up to terms of order ,
in the case that ; if , the last term between brackets on the right-hand side has to be replaced by
Using the same procedure as in the univariate case, we find that (7) leads to the following integro-differential equation: for ,
From this point on, we have to distinguish between the cases , which will be handled in Section 4, and , which will be handled in Section 5.
We conclude this section with a useful auxiliary result, that is of crucial importance in Section 4 and Section 5. Importantly, it applies irrespective of whether is positive or zero. Observe that, for a given , we can rewrite the equation as
Fixing with and , due to the lemma below we can identify a unique such that in the right part of the complex plane; we denote this by .
Lemma 1.
For every with and , there exists a unique with that satisfies Equation (9). For any , the function is analytic in .
Proof.
We prove this by applying Rouché’s theorem. To this end, consider the contour consisting of (i) the line segment
with , and (ii) to its right the semicircle
For all such that we have that
recalling that we have assumed in (1) that almost surely. To prove (10) it therefore suffices to show that . This is done as follows.
- ∘
- Observe that on the line segment we have thatThis implies that on .
- ∘
- Observe that on the semicircle we have thatAs a consequence, for R large enough we have that on .
Now that we know that on , it follows by Rouché’s theorem that the equation has, for a given with and , a unique solution with . We use here that the quadratic function has a unique zero inside , which can be seen as follows. With the equation becomes which has precisely one positive root.
The first claim of the lemma now follows by sending R to ∞, and observing that , as given by (11), and are analytic on and inside . The fact that is analytic in follows by using the implicit function theorem; cf. (Evgrafov 1978, p. 101). □
4. Bivariate Unperturbed Risk Model
This section treats the unperturbed case (i.e., ); we shall see in Section 5 that having will force us to make a few significant changes in the ensuing analysis. With the integro-differential Equation (8) at our disposal, we proceed by performing the (double) transform with respect to : we multiply the full equation by (with ) and integrate over the non-negative and . After some elementary calculus it is found that the sum of the five terms on the right-hand side equals
where
The left-hand side can be evaluated using integration by parts, so as to obtain
where
Recalling that , this leads to the following result.
Proposition 1.
For any , , , ,
We have, however, not yet identified the functions . The key idea is that the almost sure ordering (1), which enforces , can be used to evaluate , where a crucial role is played by the fact that for all . Then, by Lemma 1 with (which we emphasize by writing rather than just ),
We proceed by determining in two steps: we first express in terms of an auxiliary function, and then we evaluate that function.
In our analysis, an important role is played by
where denotes the size of the claim in the net cumulative claim process at the ruin time corresponding to the net cumulative claim process . A key object is the transform of the ruin time, undershoot and overshoot related to the process , jointly with this random vector :
with . The ‘master equation’ is then given by
To parse this decomposition, first note that the first term on the right-hand side corresponds to the scenario that exceeds u for the first time at (i.e., ), and the second term to the scenario that u is not yet exceeded by at time (i.e., ). In this reasoning we use that for all , implying that cannot occur. We refer to Figure 2 for an illustration of both possible scenarios. Then the right-hand side of (14) follows by the following observations:
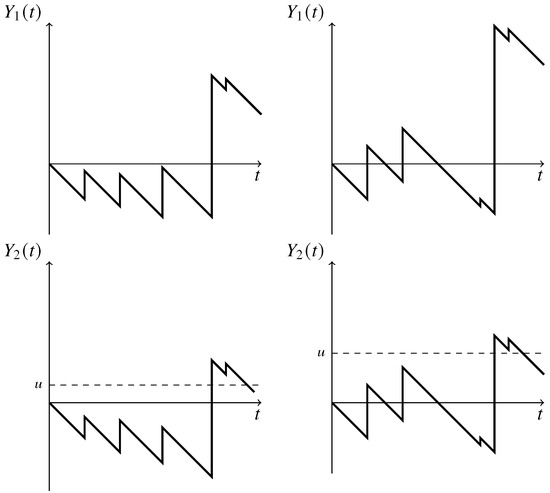
Figure 2.
Net cumulative claim processes and such that for all . The left panels display a scenario of in which , whereas the right panels display a scenario of in which .
- ∘
- In case , the undershoot isand the corresponding overshoot is
- ∘
By appealing to (14), it is immediate that the object of our interest equals
The main idea of the rest of our analysis is that we uniquely characterize by identifying the transform of . To this end, we define, for ,
It can be concluded that if we are able to compute for , we have (albeit implicitly) identified , which enables us to compute by (15); recall that we know , also appearing in (15) (via its transform).
To evaluate , we first study a more general object, from which later can be found:
note that . Again relying on a Kolmogorov-type derivation, we can determine the transform of . Indeed, as ,
up to -terms. The first double integral in (16) is the contribution due to the scenario that there is a claim arrival but that, despite this claim, remains below u; the second double integral represents the contribution due to the scenario that there is a claim arrival by which exceeds u. Subtracting from both sides of (16), dividing by , and letting , we obtain an integro-differential equation. Multiplying this equation by and integrating over u, using the same steps as in Section 3, we eventually find that
equals
Now (17) can be used to determine , as follows. Recall that for any (with non-negative real part, that is) for which , the term between brackets in (17) should vanish as well. Writing , with denoting the right-inverse of , we conclude
We have now found all ingredients that allow the evaluation of .
Proposition 2.
5. Bivariate Perturbed Risk Model
In this section, we consider the perturbed case, i.e., from now on we have that . Like in the unperturbed case, the starting point is the integro-differential Equation (8). Because of the Brownian term, we have that in this case both and attain positive values before , with a probability of 1. In particular, we now have , and hence , and . In the previous section, we needed to determine the ‘boundary transforms’ and ; in the current case, however, and are known.
Defining
a lengthy but elementary computation reveals that,
with the (known) function
Define, for , as our bivariate Laplace exponent. As an intermediate result, we have obtained the following proposition.
Proposition 3.
For any , , , ,
Observe that, reassuringly, Proposition 3 reduces to Proposition 1 when taking (despite that we could not follow the same argumentation). By Lemma 1, and using that any root of the denominator is a root of the numerator as well, we obtain that
cf. (13). We are thus left with identifying , which can be done relying on our ordering, mimicking the procedure followed in Section 4.
Denote, with as defined in Section 4,
(which, in this perturbed case, does not have any irregular behavior at ). The new master equation becomes
so that
The object of our interest, , is the transform of (21) with respect to . It therefore suffices to identify , which we do via its transform; bear in mind that we found the transform of in Section 2. Similar to what we have done before, we define now by
Let be as in Section 4, so that . As before, we find by first identifying the transform of . In our perturbed system, we have the following Kolmogorov-type equation: as ,
up to -terms. From this we obtain, as usual, an integro-differential equation: by the substitution and working out the Taylor expansions of the various functions involved, we find, with ,
here and are the first- and second-order derivatives of with respect to u, and we have used that
Now transform with respect to u, so as to obtain the transform . Multiplying by and integrating over u, and using that (bearing in mind that in this perturbed case), after considerable calculus we obtain that is given by
with Writing , with denoting the right-inverse of , this implies that is given by
Upon combining the above, we have identified .
We have thus found the Gerber–Shiu metrics in the coupled perturbed risk system, providing the joint distribution of the ruin times, undershoots and overshoots pertaining to and .
Author Contributions
Methodology, O.B., F.H. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research of Onno Boxma and Michel Mandjes has been funded by the NWO Gravitation project Networks, grant number 024.002.003.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proof of Theorem 1
Define analogously to , but with replaced by By a few standard computations, it follows from (3) that
with as given in (4). It is immediate that, with ,
so that, with as defined above,
Also,
Upon combining the above, we obtain after some straightforward calculus, recalling that is exponentially distributed with parameter ,
where the last equality is due to (A1). Now can be solved:
The last step is to determine the constant . Using the well-known principle that any root (in the right-half of the complex plane, that is) of the denominator should be a root of the numerator as well, we conclude that, with denoting the right inverse of ,
from which can be found. We have thus established Theorem 1.
References
- Asmussen, Søren. 1995. Stationary distributions for fluid flow models with or without Brownian noise. Stochastic Models 11: 21–49. [Google Scholar] [CrossRef]
- Asmussen, Søren, and Jan Rosiński. 2001. Approximations of small jumps of Lévy processes with a view towards simulation. Journal of Applied Probability 38: 482–93. [Google Scholar] [CrossRef]
- Avram, Florin, Zbigniew Palmowski, and Martijn Pistorius. 2008a. A two-dimensional ruin problem on the positive quadrant. Insurance: Mathematics and Economics 42: 227–34. [Google Scholar] [CrossRef]
- Avram, Florin, Zbigniew Palmowski, and Martijn Pistorius. 2008b. Exit problem of a two-dimensional risk process from the quadrant: Exact and asymptotic results. Annals of Applied Probability 18: 2421–49. [Google Scholar] [CrossRef]
- Baccelli, François. 1985. Two Parallel Queues Created by Arrivals with Two Demands: The M/G/2 Symmetrical Case. Research Report 426. Rocquencourt: INRIA. [Google Scholar]
- Badescu, Andrei L., Eric C. K. Cheung, and Landy Rabehasaina. 2011. A two-dimensional risk model with proportional reinsurance. Journal of Applied Probability 48: 749–65. [Google Scholar] [CrossRef][Green Version]
- Badila, E. S., O. J. Boxma, J. A. C. Resing, and E. M. M. Winands. 2014. Queues and risk models with simultaneous arrivals. Advances in Applied Probability 46: 812–31. [Google Scholar] [CrossRef]
- Boxma, Onno, and Michel Mandjes. 2021. Affine storage and insurance risk models. Mathematics of Operations Research 46: 1282–302. [Google Scholar] [CrossRef]
- Cohen, Jacob Willem. 1992. Analysis of Random Walks. Amsterdam: IOS Press. [Google Scholar]
- de Klein, Stephanus Johannes. 1988. Fredholm Integral Equations in Queueing Analysis. Ph.D. thesis, University of Utrecht, Utrecht, The Netherlands. [Google Scholar]
- Dufresne, Francois, and Hans U. Gerber. 1991. Risk theory for the compound Poisson process that is perturbed by diffusion. Insurance: Mathematics and Economics 10: 51–59. [Google Scholar] [CrossRef]
- Evgrafov, Marat Andreevich. 1978. Analytic Functions. New York: Dover Publications. [Google Scholar]
- Gerber, Hans U. 1970. An extension of the renewal equation and its application in the collective theory of risk. Skandinavisk Aktuarietidskrift 1970: 205–10. [Google Scholar] [CrossRef]
- Gerber, Hans U., and Bruno Landry. 1998. On the discounted penalty at ruin in a jump-diffusion and the perpetual put option. Insurance: Mathematics and Economics 22: 263–76. [Google Scholar] [CrossRef]
- Gerber, Hans U., and Elias SW Shiu. 1998. On the time value of ruin. North American Actuarial Journal 2: 48–72. [Google Scholar] [CrossRef]
- Gong, Lan, Andrei L. Badescu, and Eric CK Cheung. 2012. Recursive methods for a multi-dimensional risk process with common shocks. Insurance: Mathematics and Economics 50: 109–20. [Google Scholar] [CrossRef][Green Version]
- Kella, Offer. 1993. Parallel and tandem fluid networks with dependent Lévy inputs. Annals of Applied Probability 3: 682–95. [Google Scholar] [CrossRef]
- Kyprianou, Andreas E. 2013. Gerber–Shiu Risk Theory. New York: Springer. [Google Scholar]
- Li, Shuanming, Yi Lu, and Kristina P. Sendova. 2019. The expected discounted penalty function: From infinite time to finite time. Scandinavian Actuarial Journal 2019: 336–54. [Google Scholar] [CrossRef]
- Liu, Peng, Chunsheng Zhang, and Lanpeng Ji. 2017. A note on ruin problems in perturbed classical risk models. Statistics and Probability Letters 120: 28–33. [Google Scholar] [CrossRef]
- Mandjes, Michel, and Miranda van Uitert. 2005. Sample-path large deviations for tandem and priority queues with Gaussian inputs. Annals of Applied Probability 15: 1193–226. [Google Scholar] [CrossRef][Green Version]
- Mandjes, Michel, and Onno Boxma. 2023. The Cramér-Lundberg Model and Its Variants: A Queueing Perspective. New York: Springer. [Google Scholar][Green Version]
- Su, Wen, and Yunyun Wang. 2021. Estimating the Gerber-Shiu Function in Lévy insurance risk model by Fourier-cosine series expansion. Mathematics 9: 1402. [Google Scholar] [CrossRef]
- Su, Wen, Yaodi Yong, and Zhimin Zhang. 2019. Estimating the Gerber–Shiu function in the perturbed compound Poisson model by Laguerre series expansion. Journal of Mathematical Analysis and Applications 469: 705–29. [Google Scholar] [CrossRef]
- Tsai, Cary Chi-Liang, and Gordon E. Willmot. 2002. A generalized defective renewal equation for the surplus process perturbed by diffusion. Insurance: Mathematics and Economics 30: 51–66. [Google Scholar] [CrossRef]
- Wang, Guojing. 2001. A decomposition of the ruin probability for the risk process perturbed by diffusion. Insurance: Mathematics and Economics 28: 49–59. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).