1. Introduction
The desire of a consumer to compare multiple offers is widely recognised as a characteristic of rational consumption. However, this practice may become challenging when it comes to obtaining consumer loans. To compare loan offers from various lenders, the customer must complete loan applications with each lender and obtain each respective offer for comparison. Meanwhile, the borrower’s credit risk assessment is a process that requires the borrower’s data, consent to the processing of personal data, and time to perform the risk assessment and submit the loan offer. As is known, creditors apply different sets of rules for decision-making and credit scoring in their activities (
Špicas 2017), and so they may reject the credit application or provide the loan offer for a lower loan amount or a different period rather than what has been asked. Therefore, it can be said that the process of obtaining a loan offer is often associated with consumer stress, haste, and uncertainty. It is understandable that in such circumstances, consumers are not inclined to search for a loan for a long time on their own, and usually choose from one or two lenders (
Agarwal and Bos 2019). Additionally, the study conducted by
Agarwal and Bos (
2019) found that consumers who can qualify for a traditional consumer loan from their bank often make irrational decisions to take the loan from a more expensive alternative lending company.
This practical problem faced by consumers, together with the technological development of the lending market, created the prerequisites for the emergence of online loan comparison and brokerage platforms. This new business sector is growing rapidly, and in the first quarter of 2023, at least 200 OLCB platforms have been operating in the countries of the European Union. It can be said that the development of OLCB platforms shifted the lending market from being a seller’s (i.e., creditor’s) market to a buyer’s (i.e., borrower’s) market.
In order for an OLCB platform to be attractive to borrowers, it must ensure as much as possible that the borrower, after completing the application, will receive the loan offer that best suits his needs and capabilities. In order to accomplish this, the OLCB platform needs to gather loan offers for borrowers, i.e., customers of the OLCB platform, from as many creditors as possible; however, partnering with a large number of creditors presents challenges in their business domain. There are two distinct problems in this area.
First, including each additional creditor in the tenders will increase competition within the OLCB platform and reduce the economic utility of creditors already participating in tenders. Accordingly, the economic utility of each subsequent creditor’s participation in the OLCB platform will decrease. As competition between participating creditors increases, each creditor’s chance of winning the tender (the acceptance rate) decreases. In order to improve the acceptance rate, creditors tend to reduce loan prices and otherwise improve crediting conditions. As the number of creditors continues to increase or the ambitions of existing creditors grow, the OLCB platform’s operating model will potentially face a sustainability challenge.
Second, presenting a large number of offers makes it difficult for the customer to compare and choose, and may trigger the rejection effect (
Hajaj et al. 2017;
Iyengar and Lepper 2000).
Agarwal et al. (
2015) stated that even when choosing from a small number of offers, customers often choose a loan offer that is unfavourable in terms of price.
Given that creditors are an important and integral part of the business model of OLCB platforms, ensuring supply, it can be assumed that the (in)ability to involve and retain a large number of creditors is one of the main problems facing the further development of this business model. We assume that an OLCB platform’s ability to automatically evaluate the conversion probability of a set of loan offers presented to the borrower will allow the regulation of competition within the OLCB platform without reducing the value created for the borrower and without encouraging internal competition to overheat. Moreover, a model for the prediction of the acceptance probability will provide an opportunity to present loan offers to borrowers intelligently, eliminating low-valued offers and thus creating a more convenient environment for borrowers to make proper choices.
Many factors can influence a consumer’s behaviour and decision when choosing a loan offer: offered loan amount, repayment term, loan price and pricing structure, payment amount, expected time to money, the validity period of the offer, method of signing the contract, creditor’s brand, and many other factors (
Timmons et al. 2019;
Wonder et al. 2008). Accordingly, OLCB platforms face challenges in predicting customer needs and deciding how many and which creditors to include in the competition, what offers to make to the borrower, and when and in what form it is better to make an offer.
Thomas et al. (
2006) predicted that “acceptance probability models will become increasingly important as the consumer lending market matures and it becomes a buyers rather than a sellers market.” In the further study of
Seow and Thomas (
2007) it was stated that the acceptance probability problem would increase even more with the development of online brokering pages.
The comparison shopping website (CSW) as a separate business model is not new, and has been analysed in the scientific literature for over 20 years. The scientific research on this business sector can be divided according to the analysed areas. Consumer behaviour on comparison shopping websites was analysed by
White and Liao (
2021),
Marianov et al. (
2020),
Kwarteng et al. (
2020),
Hajaj et al. (
2017),
Gorodnichenko and Talavera (
2017),
Hajaj et al. (
2013),
Park and Gretzel (
2010),
Chatterjee and Wang (
2012), and
Robertshaw (
2011). The impact of comparison-shopping websites on the prices of goods and services and the cost of search was analysed by
Lindgren et al. (
2022),
Choe (
2021),
Lindgren (
2021),
Lindgren et al. (
2021a,
2021b),
Ronayne (
2021),
Kim et al. (
2020),
McDonald and Wren (
2017),
Nishida and Remer (
2018),
Bodur et al. (
2015) and
Chung (
2013). The impact of comparison-shopping sites on the market was analysed by
Antal (
2020),
Meuer et al. (
2019),
Holland et al. (
2016),
Jung et al. (
2014),
Tan et al. (
2010),
Broeckelmann and Groeppel-Klein (
2008),
Chevalier and Goolsbee (
2003) and
Tan (
2003). The development history and business models of CSWs were analysed by
Alam et al. (
2020),
Hillen (
2019),
Gupta et al. (
2017),
Broniarczyk and Griffin (
2014),
Passyn et al. (
2013),
Laffey (
2010),
Laffey and Gandy (
2009),
Wan et al. (
2007), and
Brown and Goolsbee (
2002). Technological issues facing CSWs were analysed by
Ambre et al. (
2017).
Most recently, the area of electronic goods comparison websites has been extensively analysed in scientific studies (
Lindgren et al. 2021b;
Lindgren 2021;
Böheim et al. 2021;
Alam et al. 2020;
Falkenberg and Buchwitz 2020;
Hackl and Winter-Ebmer 2020;
Thompson and Haynes 2017;
Hajaj et al. 2013,
2017;
Gorodnichenko and Talavera 2017;
Bodur et al. 2015;
Passyn et al. 2013;
Drechsler and Natter 2011;
Akimoto and Takeda 2009;
Broeckelmann and Groeppel-Klein 2008;
Su 2007;
Lee et al. 2004;
Baye et al. 2004;
Tan 2003;
Doorenbos et al. 1997). In comparison, fewer researchers have focused on the activities of service comparison websites.
McDonald and Wren (
2017) analysed insurance comparison websites, followed by
Robertshaw (
2011),
Laffey and Gandy (
2009),
Mayer et al. (
2005) and
Brown and Goolsbee (
2002). Electricity price comparison websites were analysed by
Uddin et al. (
2021),
Ronayne (
2021),
Antal (
2020),
Meuer et al. (
2019),
Nishida and Remer (
2018),
Natter et al. (
2015) and
Laffey (
2010). Financial product comparison websites have been analysed in publications by
Alfawzan and Alturki (
2018),
Laffey (
2010) and
Laffey and Gandy (
2009).
To analyse the raised problem from the perspective of a methodological approach, the questions of predicting the conversion probability have also been covered by researchers. The study of consumer loan acceptance probabilities was done by
Thomas et al. (
2006). In their study, logistic regression was applied to estimate the probability of the consumer loan offer acceptance. Moreover, the authors used linear programming techniques to optimise loan offer characteristics to maximise the acceptance probability. The authors had no available real live dataset, so an artificial dataset was created in the study by using a fantasy student’s current account. Moreover,
Lee et al. (
2017) applied dynamic programming techniques for the estimation of the acceptance probability of a credit card offer when choosing an optimal pricing model.
While the analysis of comparison-shopping websites and conversion prediction questions has been thoroughly explored in scientific studies from various angles, there is a lack of studies examining consumer behaviour in the context of online loan comparison and brokerage (OLCB) platforms. The analysis of scientific literature reveals a strong focus by researchers on predicting conversions through the examination of clickstream data from consumer browsing behaviour. The strength of this methodology is its wide applicability across diverse e-commerce systems. However, in the context of OLCB platforms, the models used for analysis may not produce accurate results for several reasons. Firstly, OLCB platforms handle a substantial amount of data that must be taken into account when building models. This includes information such as the customer’s demographics, finances, credit history, features and quantity of loan offers presented, and other data that could greatly enhance the accuracy of conversion probability models. Secondly, the issue of conversion prediction modelling in the context of OLCB platforms has not been thoroughly researched. The behaviour and decision-making of consumers when choosing a loan are likely to differ from those of consumers choosing non-financial products due to the inherent credit relationship and risk involved for both parties in the former situation. Thirdly, OLCB platforms have a unique characteristic in the customer journey: to receive binding loan offers, the customer must complete an application and provide other required personal information. This characteristic differs from the customer journey in other e-commerce websites, which have been the focus of most previous research. As a result, existing models based on browsing data may not perform optimally for OLCB platforms due to the distinctiveness of the customer journey in the latter.
The aim of this research is the development of statistical acceptance prediction models of loan offers in online loan comparison and brokerage (OLCB) platforms.
The most important contribution of this research is the application of machine learning techniques in the area of customers’ economical behaviours when choosing risk-related financial products from different providers online. To the best of our knowledge no conversion prediction models for OLCBs were provided in scientific literature to date.
The rest of the paper is structured as follows. The subsequent section describes the theoretical foundations of binary model development and evaluation. It is followed by a section describing the methodology of the research. The next section provides the empirical results and discussion. In the last section, the concluding remarks are presented.
2. Requirements for a Statistical Acceptance Prediction Model
From the perspective of e-commerce websites, the statistical conversion probability model is a technical tool that enhances understanding of customer behaviour, optimises the efficiency of e-commerce websites and marketing, and improves real-time customer path selection (
Fabra et al. 2020;
Koehn et al. 2020) and the pricing of goods and services (
Thomas et al. 2006;
Lee et al. 2017). This study estimates conversion probability (more accurately, acceptance probability) and develops a binary acceptance prediction model, classifying customers into two groups: those who will take advantage of the loan offers presented to them, referred to as “good” customers, and those who will not, who are referred to as “bad” customers. The creation of a statistical acceptance prediction model can be broken down into six steps: (1) needs and opportunities analysis, (2) formation of the data sample, (3) determination of the dependent variable, (4) independent variable selection, (5) model creation, and (6) evaluation of the model’s quantitative and qualitative characteristics (
Špicas 2017).
As was stated by
Banerjee et al. (
2017), OLCB platforms are operating in the environment of buyers, i.e., borrowers, and sellers, i.e., creditors, being horizontally differentiated, each having heterogeneous valuations and preferences for agents on the other side of the market. In those circumstances, the acceptance prediction model would serve as a technical tool for the optimisation of discovery mechanisms in a platform while seeking to maximise the acceptance rate, control the competition of the creditors and the economic benefit they gain from participation in contests, and minimise the risks of mismatching and misleading the customer. The main OLCB-platform operational features, such as the cross-knowledge of the public types of agents in the context of risk-related services, determine the need to include possible credit risk data in the set of dependent variables. An OLCB platform’s dependency on the network externality effect (
Banerjee et al. 2017;
Evans et al. 2011) determines the need to include dependent variables that describe the number and qualities of creditors participating in a contest. As transaction prices are determined by agents, and the setting of unfavourable prices for a customer is one of the main risks in OLCB platform operations, variables describing the pricing aspects of provided loan offers should also be included in the model’s dependent variables.
2.1. Related Work on Conversion Prediction Issue
With the increasing shift of businesses towards electronic sales channels, the importance of conversion prediction is growing rapidly. According to
Sheil et al. (
2018) research shows that e-commerce businesses can improve profits by 2 to 11% by using advanced conversion prediction tools. The increasing importance of the issue has sparked extensive attention from the scientific community for its analysis.
Usually, clickstream data is heavily utilised addressing the online behaviour prediction problem (
Koehn et al. 2020;
Requena et al. 2020). Clickstream data can be defined as a record of the sequence of clicks made by a user on a website, application, or digital product. It captures the path that a user takes as they navigate through the digital product, including the pages or screens visited, the links clicked, and the time spent on each page. A variety of features can be generated from clickstream data for the purpose of purchase prediction, including product viewing history, search history, customer behaviour patterns, session duration, bounce rates, click rates, and others (
Esmeli et al. 2021).
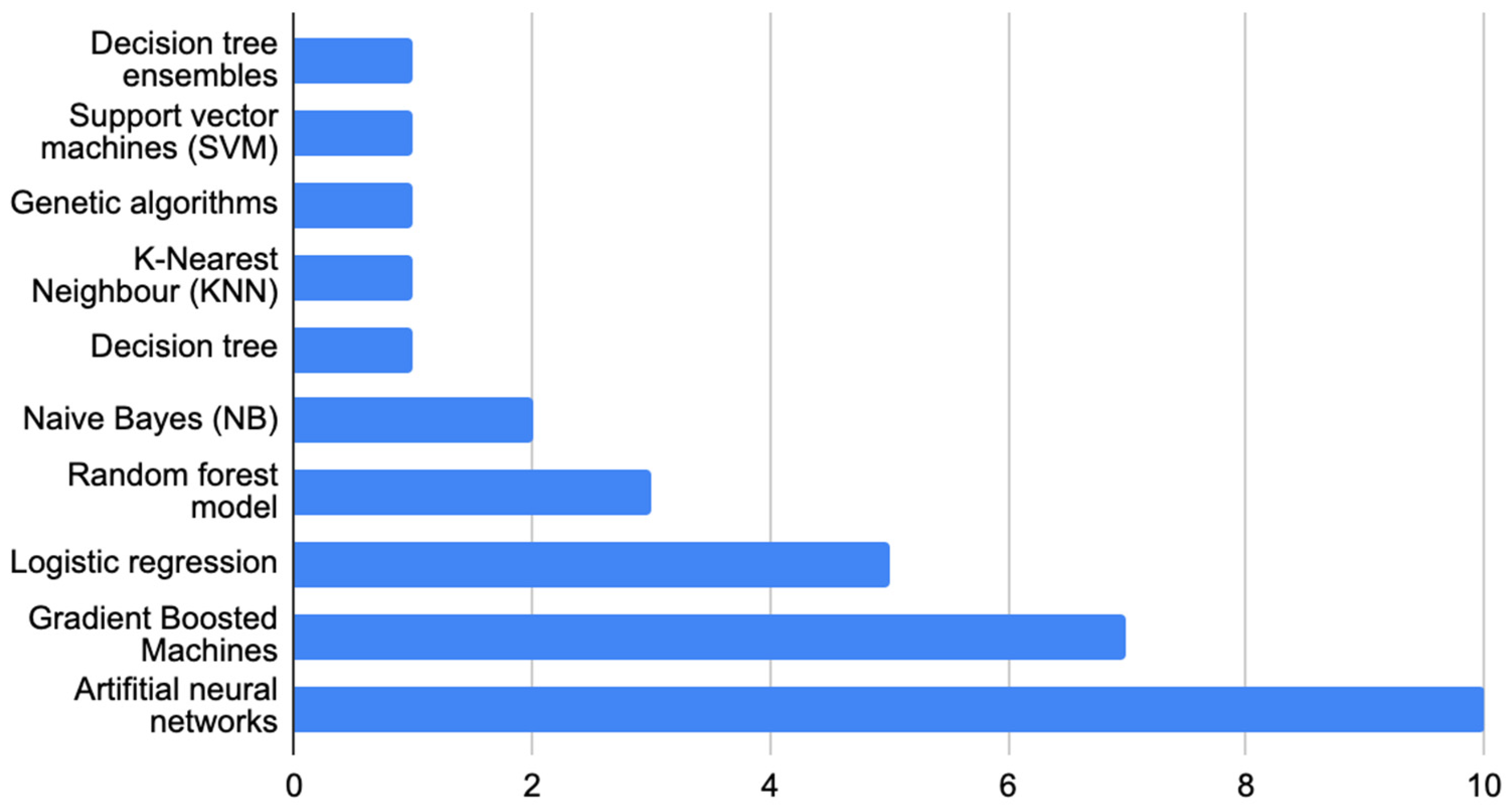
In recent studies, different classification methods have been employed to predict customer behaviour (see
Figure 1). A significant portion of the recent literature has utilised neural network-based models.
Fabra et al. (
2020) developed a neural network-based model to predict the user profiles of anonymous session data.
Koehn et al. (
2020) proposed a recurrent neural network (RNN)-based model to predict conversion rates from clickstream data.
Requena et al. (
2020) developed two types of conversion prediction models based on gradient-boosting machines (XGboost) and neural network frameworks. In
Requena et al.’s (
2020) study, different types of clickstream sequences were compared and two modelling approaches were proposed: first, analysing full sequences of clickstream data, and second, early-stage conversion probability prediction while analysing only part of each sequence.
Guo et al. (
2019) proposed the Deep Intent Prediction Model (DIPM) based on an attention-based neural network framework.
Cui et al. (
2018) modelled customer online behaviour, including semantic customer data from search engines and the authors’ applied recurrent neural network (RNN) together with a convolutional neural network (CNN) for behaviour modelling and Monte Carlo simulation to predict conversion in future sessions. Earlier applications of neural network frameworks can also be found in the literature (
Sheil et al. 2018;
Toth et al. 2017;
Hidasi et al. 2015;
Wu et al. 2015).
A review of related studies reveals that there is still a lack of coverage in the scientific literature regarding personalised conversion prediction models that can customise predictions for individual customers based on demographic, economic, or financial data. Additionally, the analysis of conversion prediction models for the lending industry has only briefly been covered; however, as lending products are tightly connected to counterparty risk, user behaviour when purchasing these products may differ significantly from that when purchasing other e-commerce products. Moreover, researchers have not yet investigated the conversion prediction issue for OLCB platforms. Given the limitations of the current state of research, we aim to advance the state of the art by proposing the conversion, i.e., acceptance, prediction models for the online loan comparison and brokerage (OLCB) platforms that incorporate relevant personal data. For this reason, it is appropriate to discuss the theoretical background for evaluating binary classification models.
2.2. Theoretical Foundations for the Evaluation of Binary Models
According to the content of analytical information, the methods for evaluating the discriminatory power of a binary model can be divided into two types: (1) methods that show the discriminatory properties of the model at a selected cut-off point, and (2) methods that show the overall discriminatory properties of the model regardless of the selected cut-off point. Below, these two types of evaluation methods are analysed separately.
2.2.1. Evaluation of a Model’s Discriminatory Power at a Selected Cut-Off Point
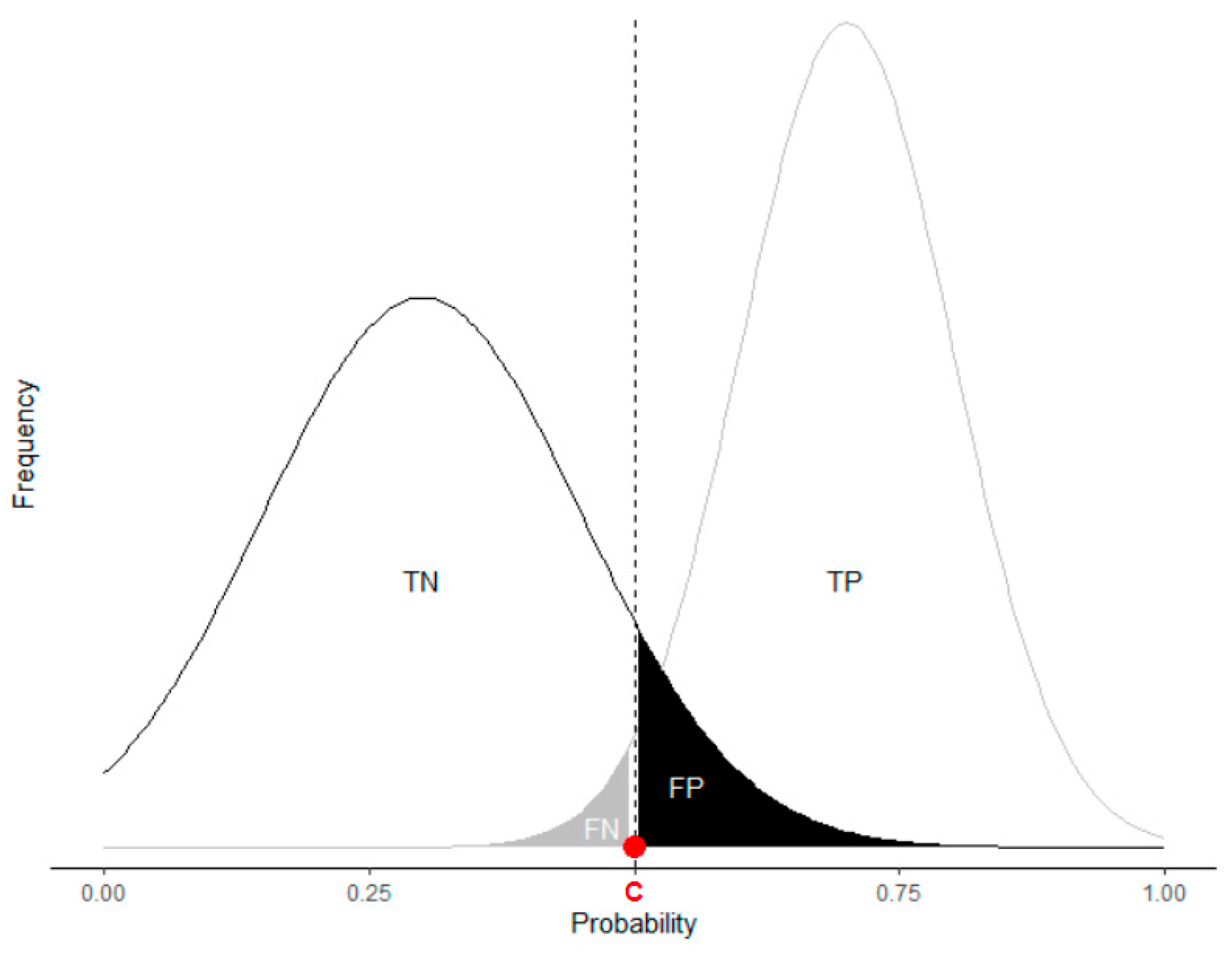
Let us say that OLCB platform clients are evaluated by a conversion prediction model. The model assigns each potential customer a rating R, and it is assumed that the higher the rating is, the greater is the probability that the customer will take advantage of loan offers. In binary classification, in order to divide customers into “good” and “bad” categories, a cut-off point C is established. It is assumed that clients with R ≤ C are unlikely to take advantage of offers, and conversely, customers with R > C are likely to take advantage of loan offers. Ideally, the model will assign R ≤ C to all customers who do not take advantage of offers, and conversely, R > C to customers who seek to take advantage of loan offers. However, in practice, ideal models are rare, and so the model will assign some “good” clients to the “bad” category and vice versa. In other words, when the model is applied and the cut-off point C is chosen, there can be four types of responses:
Customers to whom the model assigned R ≤ C and who did not take advantage of loan offers are considered correctly classified as “bad” customers (true negatives, TN);
Customers to whom the model assigned R > C and who did take advantage of loan offers are referred to as correctly classified “good” customers (true positives, TP);
Customers who were classified as “bad,” with R < C, but who took advantage of the offered loans are considered wrongly assigned to “bad” (false negatives, FN). This model error is also called a type I error;
Customers for whom the model assigned R > C, but who did not take advantage of loan offers, are referred to as wrongly positively classified clients (false positives, FP). This model error is called a type II error.
In
Figure 2, two hypothetical customer distributions, “bad” and “good,” are shown, starting from the left. The X-axis represents the scale of the rating assigned by the model, and the Y-axis represents the frequency of customer distribution. By choosing the cut-off point to be point C at 0.5, the parts of the distribution representing correctly and incorrectly classified customers are visible. From
Figure 2, it is clear that by changing the value of point C, we can reduce the proportion of FP or FN errors, but this would usually be done at the expense of the opposite error; i.e., by setting a more conservative point C value, such as 0.4, the proportion of incorrectly classified “bad” customers would decrease, but a larger portion of “good” customers would be lost (
Sobehart and Keenan 2001).
Further, in analysing the properties of the model, for simplicity,
Figure 2 can be transformed into confusion matrix form (
Table 1), which is widely applied in the scientific literature when analysing binary classification problems.
The columns of
Table 1 correspond to the predicted number of “good” and “bad” customers by the model, while the rows represent the actual customer conditions. Accordingly, the intersections of the rows and columns show the discriminative power of the model that has been discussed, i.e., TP, TN, FP, FN. The contents of the classification matrix enable the calculation of indicators that show the discriminative properties of the model at the selected cut-off point.
2.2.2. Model Discriminatory Power Assessment without Considering the Cut-Off Point
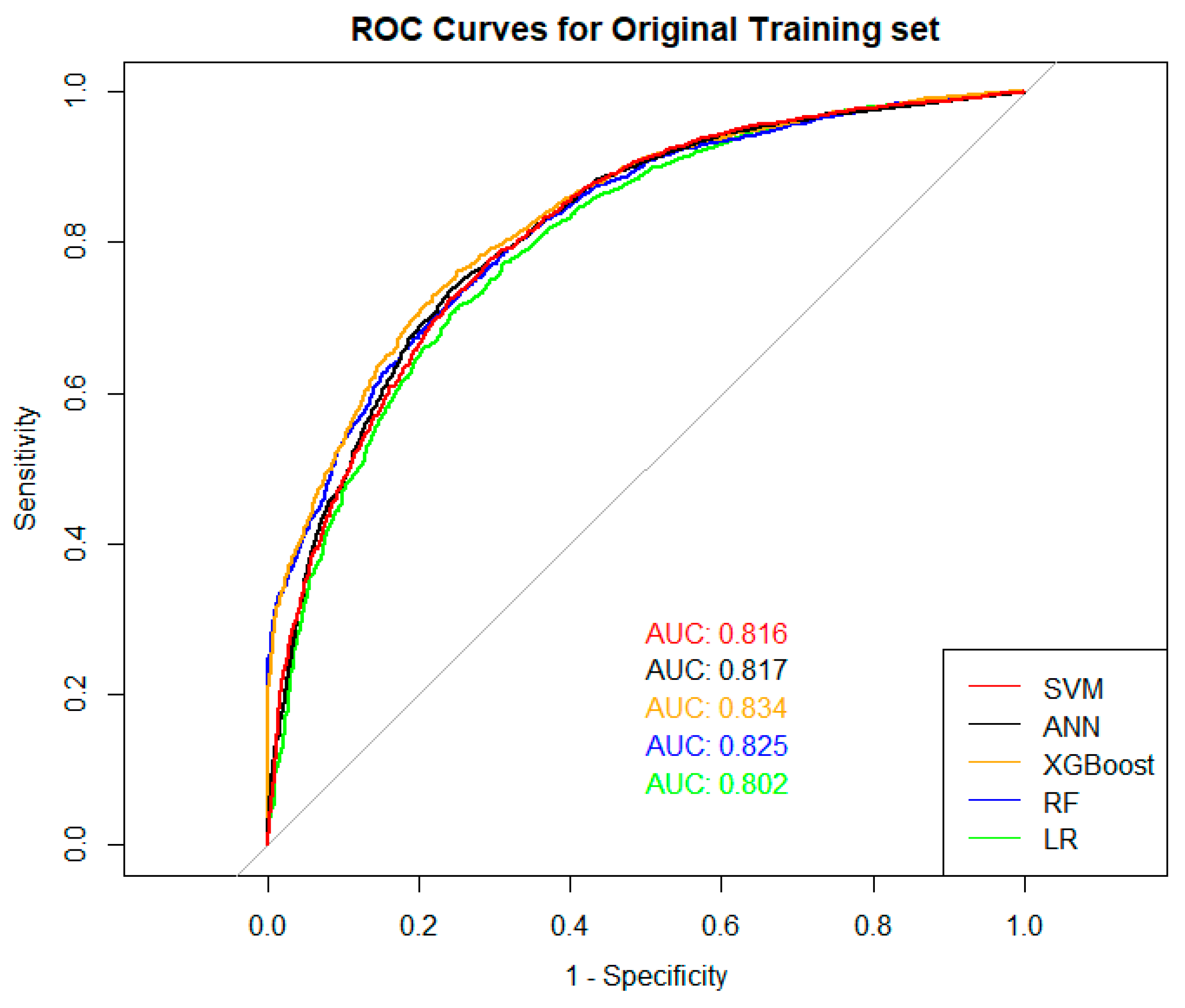
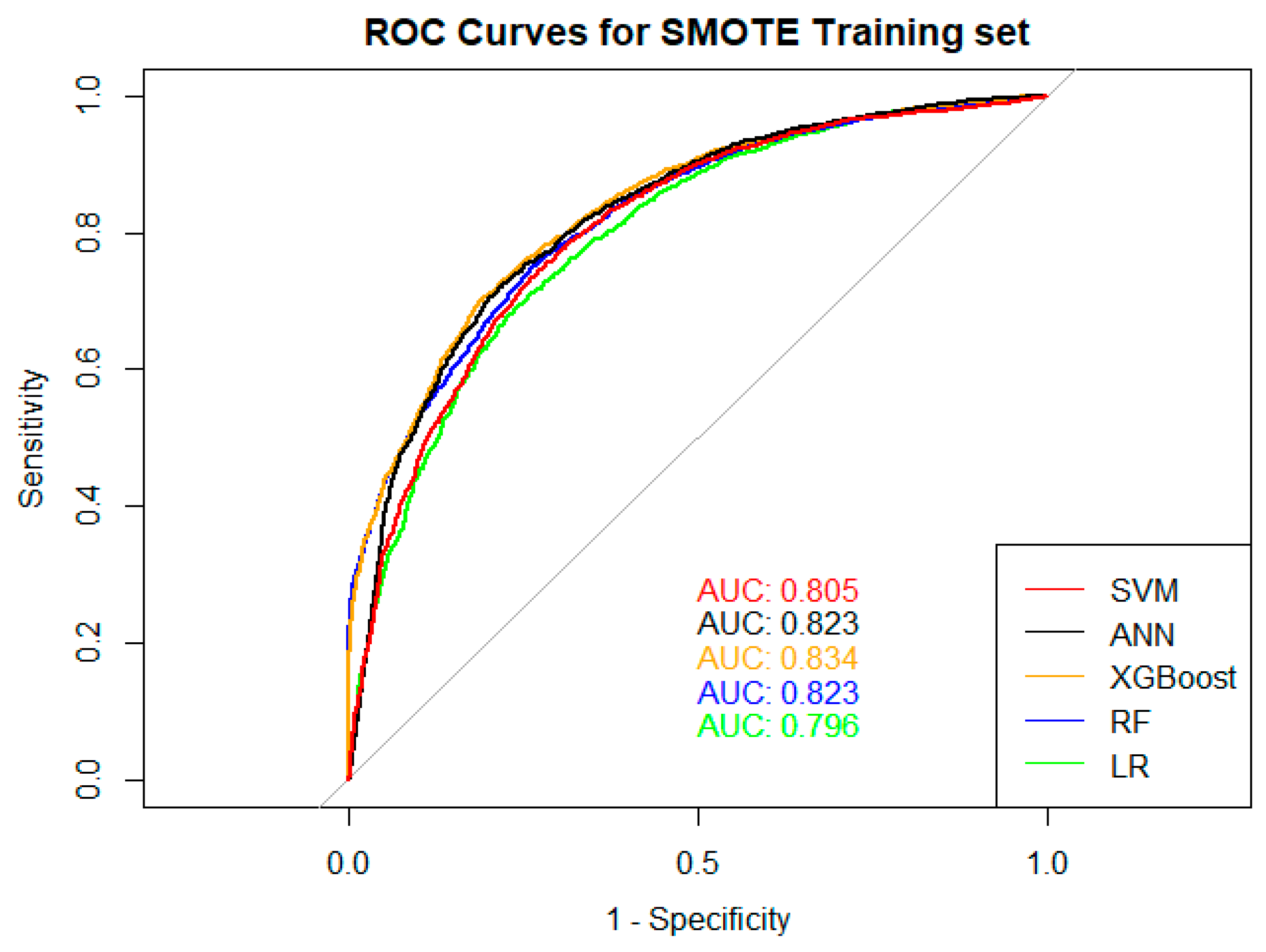
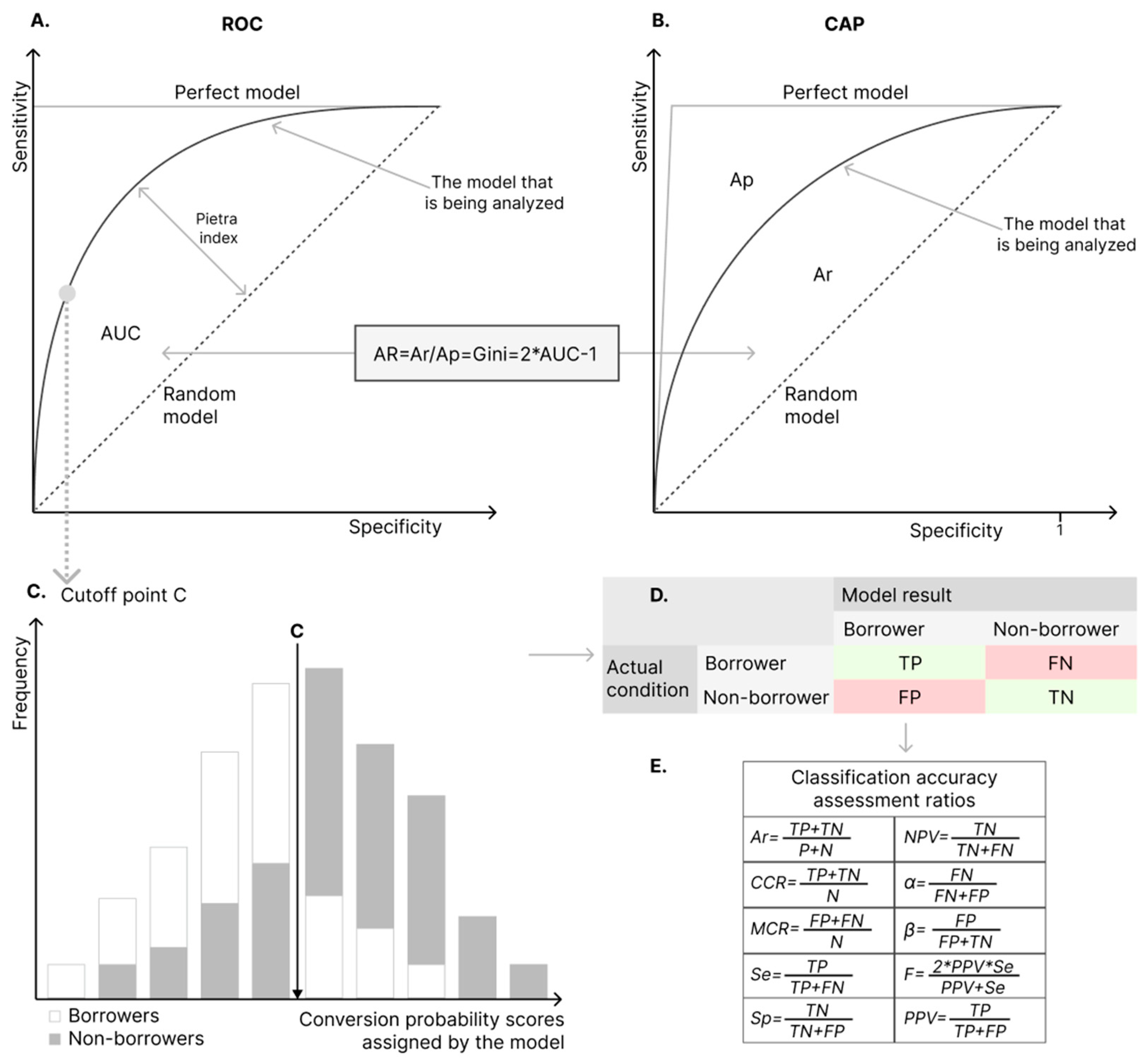
The receiver operating characteristic (ROC) curve is created for each possible cut-off point C, determining (1) the portion of “good” customers correctly classified by the model, i.e., the specificity of the model, which is characterised by the size of the X-axis, and (2) the portion of “bad” clients correctly identified by the model, i.e., the sensitivity of the model, which is indicated on the Y-axis of the graph. In this way, the graph shows a summary of the model’s discriminatory abilities in terms of first and type II errors for each possible cut-off point C (see
Figure 3A).
The closer the ROC curve is to the upper left corner, the more the model is considered to be of higher quality, and conversely, the closer the curve is to the line of the graph’s diagonal (see
Figure 3A, dotted line), the less discriminatory power the model has. A model whose ROC curve is close to the diagonal line is considered to be naive (random or coincidental).
The area under the ROC curve (AUC) summarises the discriminatory abilities of the model quantitatively. The AUC varies from 0 to 1, and the closer the model’s AUC is to 1, the more reliable it is considered. In other words, if the model’s AUC is 1, the model classifies “good” and “bad” customers with 100% accuracy. As mentioned, such models are impossible in practice.
The cumulative accuracy profile (CAP) curve, also known as the Gini curve, Lorenz curve, or power curve, is also used to assess the discriminatory abilities of the model. When creating the CAP curve, customers are first ranked according to the rating assigned by the model, from the riskiest to the least risky. The cut-off point is considered to be the rating assigned by the model. The Y-axis of the graph shows the sensitivity (Se) of the model, and the X-axis shows the cumulative share of customers (
Špicas 2017;
Irwin and Irwin 2012;
Dzidzevičiūtė 2013) (
Figure 3B).
It can be stated that the methods for evaluating the discriminatory power of a model— ROC and CAP curves, AUC, AR metrics, the Pietra index, and accuracy metrics—are all related by a linear relationship. This relationship is illustrated in
Figure 3.
In Part A of
Figure 3, the ROC curve is depicted, with the area under the curve being the AUC and the distance from the diagonal representing the naive model to the evaluated model’s ROC curve being the Pietra index.
In Part B of
Figure 3, the CAP curve is shown, with the area under the curve being the
, the area under the perfect model curve being the
, and the naive model’s CAP curve being represented by a dotted line.
A formula is provided between the ROC and CAP curves (
Figure 3A,B) demonstrating the linear relationship between the two methods.
In the ROC curve (
Figure 3A), a hypothetical cut-off point C is shown, with its “bad” and “good” customer classification divisions (
Figure 3C), the portions of customers correctly and incorrectly classified—which can be transformed into a classification matrix (
Figure 3D)—and accuracy metrics can be calculated from the matrix (
Figure 3E).
In scientific literature, the methods of evaluating a model are usually applied in two stages: first, a preliminary evaluation of the model is carried out, and second, backtesting of the model is conducted. The same methods discussed in this section are used for evaluation. The difference is that in the preliminary evaluation of the model, the cut-off point is determined expertly (usually by setting it at 0.5), and the model’s features are evaluated on a test sample formed from the initial sample available. In backtesting, the model is tested in a “production environment,” i.e., it is applied under real conditions (e.g., by simulating the model’s application on a platform for which it has been created), using available data and quantifying the cut-off point.