A Guaranteed-Return Structured Product as an Investment Risk-Hedging Instrument in Pension Savings Plans
Abstract
1. Introduction
2. The Structured Product
2.1. The SP Model
2.2. Numerical Example
3. Methodology
3.1. Creating the Database through Simulations
3.2. Analysis of Simulation Outcomes
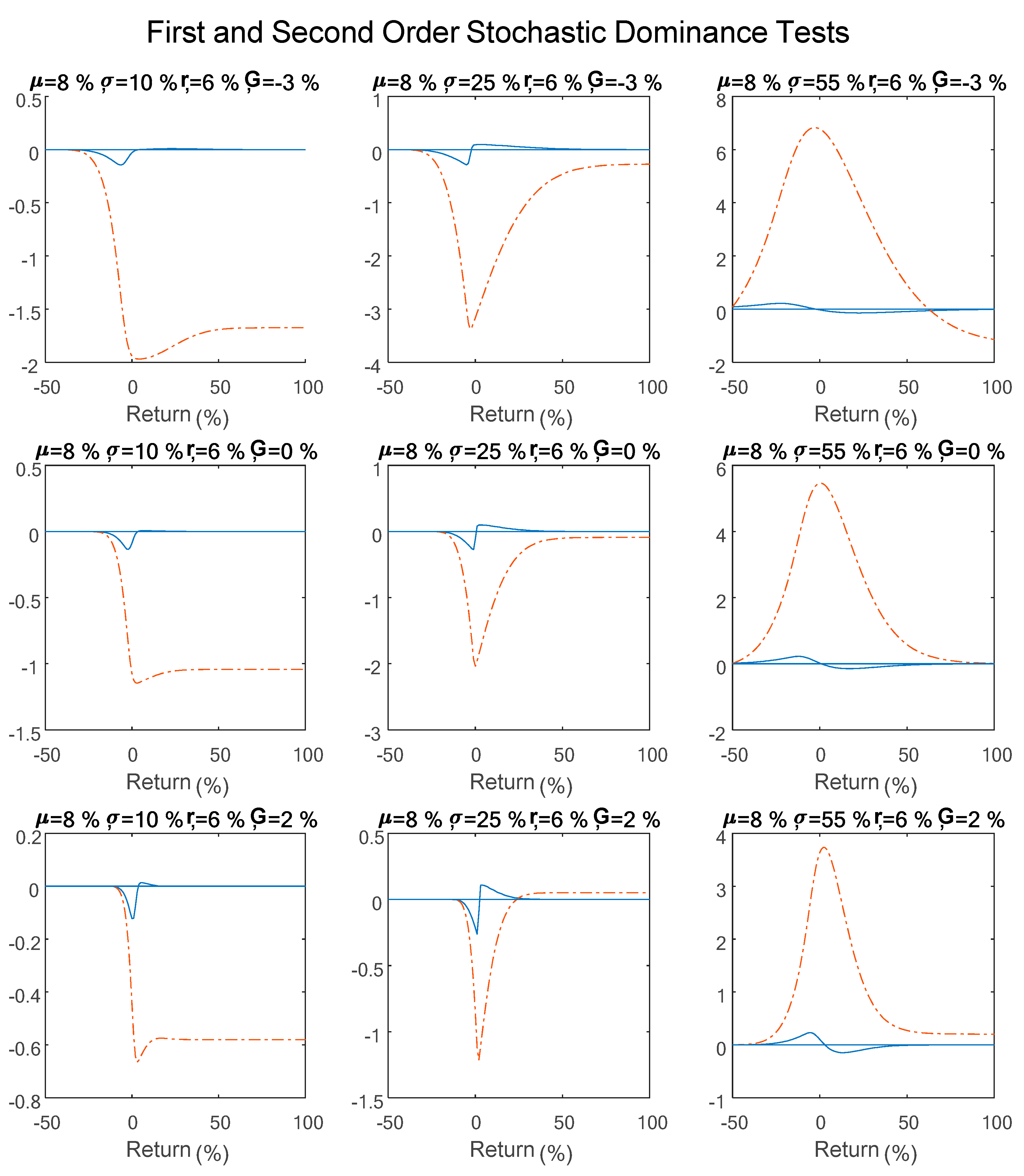
Return versus Risk Analysis
4. Results
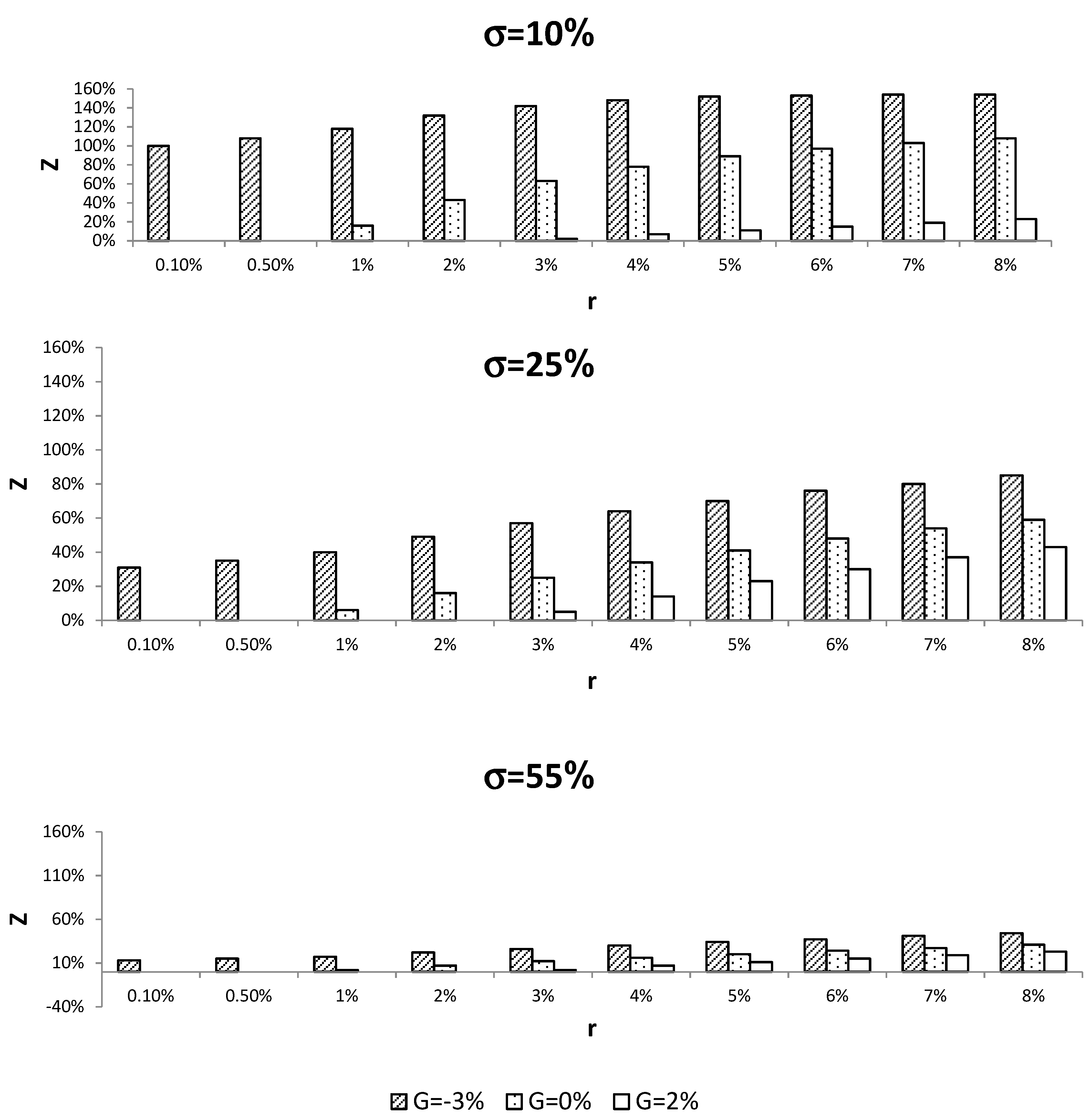
4.1. Sensitivity of Structured Product Characteristics to Market Conditions
4.2. Simulation Results
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Guaranteed Return (G) | Risk-Free Interest (r) | |||||||||
| 0.10% | 0.50% | 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | |
| −5% | 5.10% | 5.50% | 6.01% | 7.02% | 8.05% | 9.08% | 10.13% | 11.18% | 12.25% | 13.33% |
| −4% | 4.10% | 4.50% | 5.01% | 6.02% | 7.05% | 8.08% | 9.13% | 10.18% | 11.25% | 12.33% |
| −3% | 3.10% | 3.50% | 4.01% | 5.02% | 6.05% | 7.08% | 8.13% | 9.18% | 10.25% | 11.33% |
| −2% | 2.10% | 2.50% | 3.01% | 4.02% | 5.05% | 6.08% | 7.13% | 8.18% | 9.25% | 10.33% |
| −1% | 1.10% | 1.50% | 2.01% | 3.02% | 4.05% | 5.08% | 6.13% | 7.18% | 8.25% | 9.33% |
| 0% | 0.10% | 0.50% | 1.01% | 2.02% | 3.05% | 4.08% | 5.13% | 6.18% | 7.25% | 8.33% |
| 1% | 0.01% | 1.02% | 2.05% | 3.08% | 4.13% | 5.18% | 6.25% | 7.33% | ||
| 2% | 0.02% | 1.05% | 2.08% | 3.13% | 4.18% | 5.25% | 6.33% | |||
| 3% | - | 0.05% | 1.08% | 2.13% | 3.18% | 4.25% | 5.33% | |||
| 4% | - | - | 0.08% | 1.13% | 2.18% | 3.25% | 4.33% | |||
| 5% | - | - | - | 0.13% | 1.18% | 2.25% | 3.33% | |||
| 6% | - | - | - | - | 0.18% | 1.25% | 2.33% | |||
| 7% | - | - | - | - | - | 0.25% | 1.33% | |||
| 8% | - | - | - | - | - | - | 0.33% | |||
| 1 | In a DB pension scheme, the employee is assured of getting a constant future pension benefit from the point of retirement (the benefits usually depend on the employee’s length of employment and wage), paid for by the employer, who bears the longevity and investment risks. In a DC plan, the employee’s savings accumulated by periodic withholding of a given share of wage (usually with matching contributions by the employer) to a separate pension fund that manages the money, and the pension annuity is contingent on accrued deposits and investment returns. Hence, the individual pension saver bears the risks in pure DC pension schemes. |
| 2 | The literature offers several reasons for the shift from DB to DC pensions, including: (1) the industrial globalization trend and mobility of workers (Broadbent et al. 2006; Thomas et al. 2014; Fang 2016); (2) an increase in financial pressure on private firms that pay DB pensions (Bodie and Crane 1999; Whitehouse 2007); and (3) regulatory changes (e.g., in taxation and legislation) that favored the move to DC plans. |
| 3 | The option acquired by the pension institution is adjusted so as to be quoted at the exercise price commensurate with the current value of the benchmark index at the time the SP is sold for the customer (an in-the-money option) and on an expiration date that corresponds to the expiration date specified in the SP. Thus, insofar as the option cannot be exercised at the point of expiration (i.e., if the price of the benchmark index at the time of expiration is below the exercise price), the pension institution loses the premium that it paid for acquiring the option. |
| 4 | Alternatively, the pension member will have to pay higher fees for maintaining the percent portion to the benchmark index return. |
| 5 | In a DB pension scheme, the employee is assured of getting a constant future pension benefit from point of retirement (the benefits usually depend on the employee’s length of employment and wage), paid for by the employer, who bears the longevity and investment risks. In a DC plan, the employee’s savings accumulated by periodic withholding of a given share of wage (usually with matching contributions by the employer) to a separate pension fund that manages the money, and the pension annuity is contingent on accrued deposits and investment returns. Hence, the individual pension saver bears the risks in pure DC pension schemes. |
| 6 | Over long periods of time, the pension fund would probably prefer a strategy of buying call options to a term to maturity shorter than T (doing so several times until the contract ends) in order to lower the cost of buying the option. This strategy exposes the institutional entity to a risk originating in an increase in market volatility (which, if realized, would make the option much costlier); accordingly, the institution may demand a higher premium from the investors. However, due to market competition and its interest in attracting customers, the institutional entity would probably have to assume some of this risk itself. |
| 7 | The calculations relate to the net index value after dividend payments (and not to an index that includes dividend reinvestment). |
| 8 | We also carried out a sensitivity analysis of Z as a function of the issuer’s fee and operating expenses; the outcomes of the analysis were not substantially different. We chose to exemplify the analysis by setting M = 0.5%, which is the highest cumulative fee that can be charged against members of a DC-type pension fund in Israel (under the Supervision of Financial Services [Management Fees] Regulations, 5772–2012). |
| 9 | in Equation (9) describes a gross return of the index at the end of time T. |
| 10 | To demonstrate a large or small standard deviation, we calculated the annual standard deviation of the S&P 500 Index for the daily return during 2005–2015 by using an exponentially weighted time series with a lambda coefficient of 0.94, as in Hull (2012). The results showed that under normal market conditions (such as those before and after the crisis), the annual SD ranges from 7% to 12%; during the subprime crisis (September 2008–March 2009), in contrast, it was roughly 55%. |
| 11 | The SP is defined to a term of one year ahead (T = 1) under the assumption that the dividend return of the index is q = 3%, the issuer’s fee is M = 0.5% of the value of the investment, and the issuer’s operating expenses are J = 1% of total hedging cost. |
| 12 | We assume that in a competitive market in which several institutional players offer their customers a SP, the contracts will converge toward the maximum Z values that can be paid to the customer. |
| 13 | Based on daily average short-term (three-month) yields on government paper: https://data.oecd.org/interest/short-term-interest-rates.htm#indicator-chart (accessed on 18 March 2023). |
| 14 | This is based on an estimate of expected short-term interest for 2024–2025 in the OECD member states: https://data.oecd.org/interest/short-term-interest-rates-forecast.htm#indicator-chart (accessed on 20 March 2023). |
References
- Acerbi, Carlo, and Dirk Tasche. 2002. On the coherence of expected shortfall. Journal of Banking and Finance 26: 1487–503. [Google Scholar] [CrossRef]
- Antolín, Pablo, Stéphanie Payet, Edward Whitehouse, and Juan Yermo. 2011. The Role of Guarantees in Defined Contribution Pensions, OECD Working Papers on Finance, Insurance and Private Pensions, No. 11. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- Bateman, Hazel, Christine Eckert, Fedor Iskhakov, Jordan Louviere, Stephen Satchell, and Susan Thorp. 2018. Individual capability and effort in retirement benefit choice. Journal of Risk and Insurance 85: 483–512. [Google Scholar] [CrossRef]
- Benartzi, Shlomo, and Richard Thaler. 2001. Naive diversification strategies in defined contribution saving plans. American Economic Review 91: 79–98. [Google Scholar] [CrossRef]
- Black, Fisher, and Miron Scholes. 1973. The pricing of options and corporate liabilities. The Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Bodie, Zvi, and Dwight Crane. 1999. The design and production of new retirement savings products. Journal of Portfolio Management 25: 77–82. [Google Scholar] [CrossRef]
- Broadbent, John, Michael Palumbo, and Elizabeth Woodman. 2006. The Shift from Defined Benefit to Defined Contribution Pension Plans–Implications for Asset Allocation and Risk Management. Sydeny: Reserve Bank of Australia, Board of Governors of the Federal Reserve System and Bank of Canada. [Google Scholar]
- Célérier, Clair, and Boris Vallée. 2017. Catering to investors through security design: Headline rate and complexity. The Quarterly Journal of Economics 132: 1469–508. [Google Scholar] [CrossRef]
- Clark, Gordon, and Tessa Hebb. 2004. Pension fund corporate engagement: The fifth stage of capitalism. Relations Industrielles/Industrial Relations 59: 142–71. [Google Scholar] [CrossRef]
- Dichtl, Hubert, and Wolfgang Drobetz. 2011. Portfolio insurance and prospect theory investors: Popularity and optimal design of capital protected financial products. Journal of Banking and Finance 35: 1683–97. [Google Scholar] [CrossRef]
- Dimitrov, Stanislav, and Elroi Hadad. 2022. Pension tracking system application: A new supervision challenge in the EU. International Journal of Economic Sciences XI: 48–57. [Google Scholar] [CrossRef]
- European Commission. 2021. The 2021 Pension Adequacy Report. Luxembourg: Publications Office of the European Union, vol. 2. [Google Scholar]
- Fang, Hanming. 2016. Insurance markets for the elderly. Handbook of the Economics of Population Aging 1: 237–309. [Google Scholar]
- Gustman, Alan, and Thomas Steinmeier. 1992. The stampede toward defined contribution pension plans: Fact or fiction? Industrial Relations: A Journal of Economy and Society 31: 361–69. [Google Scholar] [CrossRef]
- Hadad, Elroi, Stanislav Dimitrov, and Jivka Stoilova-Nikolova. 2022. Development of capital pension funds in the Czech Republic and Bulgaria and readiness to implement PEPP. European Journal of Social Security 24: 342–60. [Google Scholar] [CrossRef]
- Hadar, Josef, and William Russell. 1969. Rules for ordering uncertain prospects. The American Economic Review 59: 25–34. [Google Scholar]
- Hens, Thorsten, and Marc Oliver Rieger. 2014. Can utility optimization explain the demand for structured investment products? Quantitative Finance 14: 673–81. [Google Scholar] [CrossRef]
- Hull, John. 2012. Options, Futures, and Other Derivatives, 8th ed. Chennai: Pearson Education India. [Google Scholar]
- Ibragimov, Rustam, and Johan Walden. 2007. The limits of diversification when losses may be large. Journal of Banking and Finance 31: 2551–69. [Google Scholar] [CrossRef]
- Jorion, Philippe. 2001. Value at Risk: The New Benchmark for Controlling Market Risk. New York: McGraw-Hill. [Google Scholar]
- Knoller, Christian. 2016. Multiple Reference Points and the Demand for Principal-Protected Life Annuities: An Experimental Analysis. Journal of Risk and Insurance 83: 163–79. [Google Scholar] [CrossRef]
- Lachance, Marie-Eve, Olivia Mitchell, and Kent Smetters. 2003. Guaranteeing defined contribution pensions: The option to buy back a defined benefit promise. Journal of Risk and Insurance 70: 1–16. [Google Scholar] [CrossRef]
- Longstaff, Francis. 2004. The flight-to-liquidity premium in U.S. Treasury bond prices. Journal of Business 77: 511–26. [Google Scholar] [CrossRef]
- Mohammadi, Arezoo, Mehrzad Minnoei, Zadollah Fathi, Mohamamd Ali Keramati, and Hossein Baktiari. 2022. Optimal allocation of bank resources and risk reduction through portfolio decentralization. International Journal of Economic Sciences 11: 92–143. [Google Scholar] [CrossRef]
- Næs, Randi, Johannes Skjeltorp, and Bent Arne Ødegaard. 2011. Stock market liquidity and the business cycle. The Journal of Finance 66: 139–76. [Google Scholar] [CrossRef]
- OECD. 2016. OECD Pensions Outlook 2016. Paris: OECD Publishing. [Google Scholar]
- OECD. 2020. OECD Pensions Markets in Focus. 2020. Paris: OECD Publishing. [Google Scholar]
- OECD. 2021. Short-Term Interest Rates (Indicator). Available online: https://www.oecd-ilibrary.org/finance-and-investment/short-term-interest-rates/indicator/english_2cc37d77-en (accessed on 26 October 2022).
- Quirk, James, and Rubin Saposnik. 1962. Admissibility and measurable utility functions. The Review of Economic Studies 29: 140–46. [Google Scholar] [CrossRef]
- Randle, Tony, and Heinz Rudolph. 2014. Pension Risk and Risk-Based Supervision in Defined Contribution Pension Funds. World Bank Policy Research Working Paper 6813. Washington: The World Bank. [Google Scholar]
- Rockafellar, Tyrrel, and Stanislav Uryasev. 2002. Conditional value-at-risk for general loss distributions. Journal of Banking and Finance 26: 1443–71. [Google Scholar] [CrossRef]
- Sortino, Frank, and Lee Price. 1994. Performance measurement in a downside risk framework. Journal of Investing 3: 50–8. [Google Scholar] [CrossRef]
- Thomas, Ashok, Luka Spataro, and Nanditha Mathew. 2014. Pension funds and stock market volatility: An empirical analysis of OECD countries. Journal of Financial Stability 11: 92–103. [Google Scholar] [CrossRef]
- Whitehouse, Edward. 2007. Life-Expectancy Risk And Pensions: Who Bears The Burden? Paris: Organisation for Economic Cooperation and Development (OECD). Available online: https://www.proquest.com/docview/189843487?accountid=27473&forcedol=true (accessed on 26 October 2022).
- Yosef, Rami. 2006. Floor Options on Structured Products and Life Insurance Contracts. Investment Management and Financial Innovations 3: 160–70. [Google Scholar]
| Guaranteed Return | Index | σ = 55% | σ = 25% | σ = 10% | |||
|---|---|---|---|---|---|---|---|
| Portfolio | SP | Portfolio | SP | Portfolio | SP | ||
| G = −3% | Avg. | 0.052 | 0.0474 | 0.0669 | 0.0621 | 0.1035 | 0.1067 |
| S.D. | 0.192 | 0.1486 | 0.1741 | 0.1289 | 0.1593 | 0.1308 | |
| Sharpe | 0.0623 | 0.050 | 0.1543 | 0.1713 | 0.3984 | 0.5098 | |
| Sortino | 9.8795 | 22.029 | 17.9197 | 62.642 | 40.124 | 157.78 | |
| VaR | 0.1588 | 0.03 | 0.1784 | 0.03 | 0.1446 | 0.03 | |
| CVaR | 0.1796 | 0.03 | 0.219 | 0.03 | 0.1967 | 0.03 | |
| G = 0% | Avg. | 0.0463 | 0.042 | 0.0541 | 0.05 | 0.0734 | 0.0742 |
| S.D. | 0.1011 | 0.0806 | 0.0917 | 0.07 | 0.0839 | 0.071 | |
| Sharpe | 0.0623 | 0.0251 | 0.1543 | 0.1426 | 0.3984 | 0.4814 | |
| Sortino | 12.998 | 3.5551 | 22.2919 | 18.5435 | 48.755 | 61.221 | |
| VaR | 0.0647 | 0 | 0.075 | 0 | 0.0572 | 0 | |
| CVaR | 0.0756 | 0 | 0.964 | 0 | 0.0846 | 0 | |
| G = 2% | Avg. | 0.0427 | 0.0384 | 0.0461 | 0.0419 | 0.0544 | 0.0525 |
| S.D. | 0.0434 | 0.0353 | 0.0394 | 0.0307 | 0.036 | 0.0311 | |
| Sharpe | 0.0623 | −0.045 | 0.1543 | 0.0621 | 0.3984 | 0.4021 | |
| Sortino | 9.801 | −5.915 | 18.678 | 6.3166 | 35.117 | 31.81 | |
| VaR | 0.005 | −0.02 | 0.0094 | −0.02 | 0.0018 | −0.02 | |
| CVaR | 0.0097 | −0.02 | 0.0186 | −0.02 | 0.0136 | −0.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afik, Z.; Hadad, E.; Yosef, R. A Guaranteed-Return Structured Product as an Investment Risk-Hedging Instrument in Pension Savings Plans. Risks 2023, 11, 107. https://doi.org/10.3390/risks11060107
Afik Z, Hadad E, Yosef R. A Guaranteed-Return Structured Product as an Investment Risk-Hedging Instrument in Pension Savings Plans. Risks. 2023; 11(6):107. https://doi.org/10.3390/risks11060107
Chicago/Turabian StyleAfik, Zvika, Elroi Hadad, and Rami Yosef. 2023. "A Guaranteed-Return Structured Product as an Investment Risk-Hedging Instrument in Pension Savings Plans" Risks 11, no. 6: 107. https://doi.org/10.3390/risks11060107
APA StyleAfik, Z., Hadad, E., & Yosef, R. (2023). A Guaranteed-Return Structured Product as an Investment Risk-Hedging Instrument in Pension Savings Plans. Risks, 11(6), 107. https://doi.org/10.3390/risks11060107






