Constant or Variable? A Performance Analysis among Portfolio Insurance Strategies
Abstract
1. Introduction
2. Portfolio Insurance Strategies: Definitions and Features
2.1. Constant Proportion Portfolio Insurance Strategy
- The choice of a floor, which represents the minimum value of the portfolio which is acceptable for an investor at any instant of time during the management period Its initial value, capitalized at the non-risky rate, must be equal to a predetermined percentage of the initial capital deposit;
- The choice of a dynamic investment rule on the risky asset defined as follows: the total amount (the exposure) invested into the underlying asset is equal to a fixed proportion m (the multiplier) of the difference between the portfolio value and the floor . Such a difference is called the cushion and is denoted by . Since the strategy results to be self-financing, the remaining amount, , is invested into the riskless asset , such as a money market account or a government bond, with log-return for each period
2.2. Time Invariant Portfolio Protection Strategy
2.3. Exponential Proportion Portfolio Insurance Strategy
2.4. Practical Issues for the Implementation of Portfolio Insurance Strategies
3. Simulation Setup
3.1. Data and Design of Empirical Analysis
- We randomly draw a market index (S&P500, Hang Seng, Nikkei 225 or FTSE 100) with replacement;
- We draw with replacement a starting date;
- Starting from the initial date obtained in Step 2, we analyze the one-year performance of CPPI, TIPP, and EPPI strategies for the drawn market, i.e., the 252 days following the starting date are used to evaluate the different portfolio insurance strategies;
- The procedure (Step 1–Step 3) is repeated 20,000 times.
3.2. Performance Measures and Statistical Tests
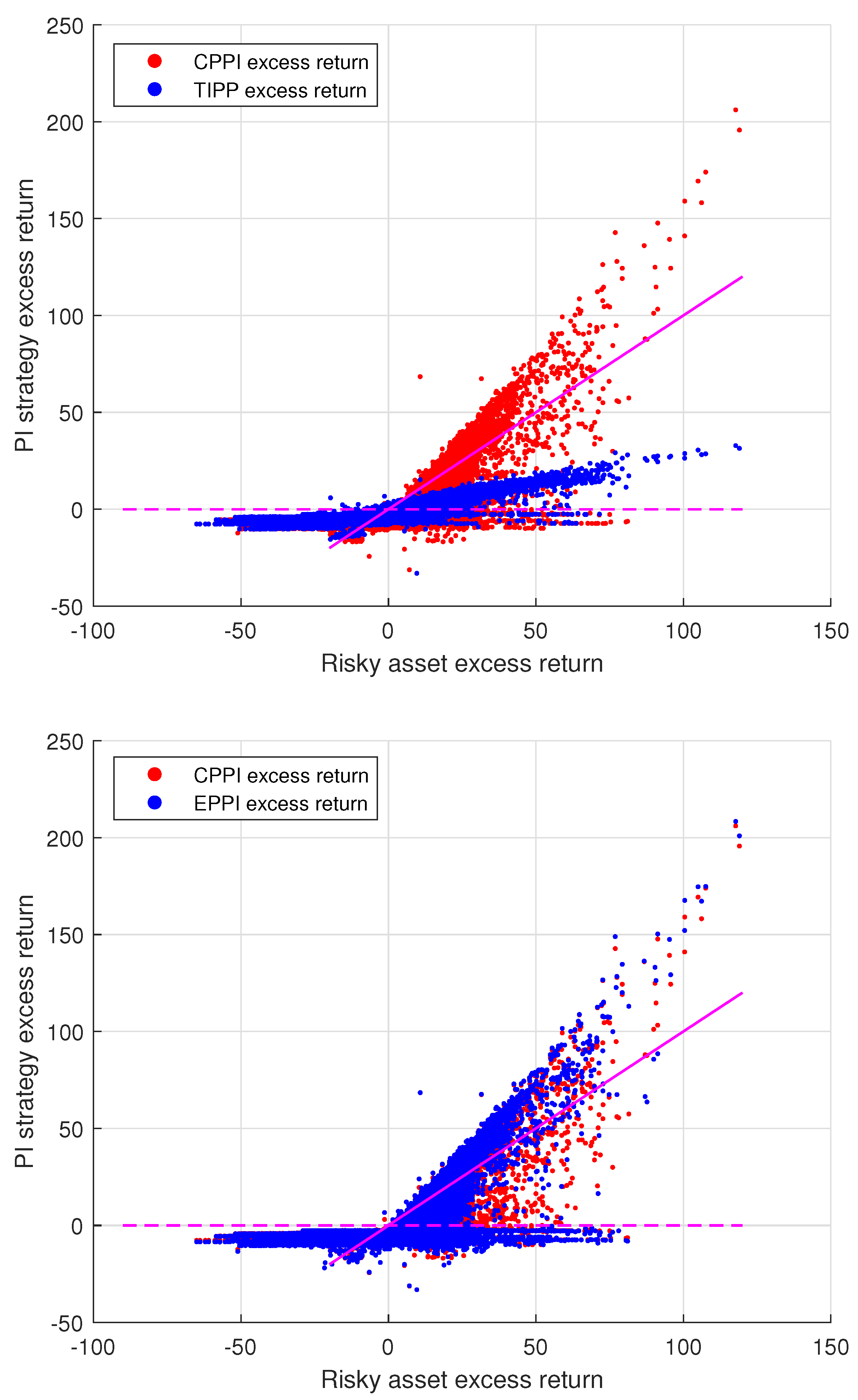
4. Performance Measurement Results
4.1. Constant Proportion Portfolio Insurance vs. Its Generalizations
4.2. Changing the Protection Level
4.3. Changing the Rebalancing Frequency
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Acerbi, Carlo, and Dirk Tasche. 2002. On the coherence of expected shortfall. Journal of Banking and Finance 26: 1487–503. [Google Scholar] [CrossRef]
- Annaert, Jan, Sofieke Van Osselaer, and Bert Verstraete. 2009. Performance evaluation of portfolio insurance strategies using stochastic dominance criteria. Journal of Banking and Finance 33: 272–80. [Google Scholar] [CrossRef]
- Ardia, David, Kris Boudt, and Marjan Wauters. 2016. Smart beta and cppi performance. Finance 37: 31–65. [Google Scholar] [CrossRef]
- Balder, Sven, Michael Brandl, and Antje Mahayni. 2009. Effectiveness of CPPI strategies under discrete-time trading. Journal of Economic Dynamics and Control 33: 204–20. [Google Scholar] [CrossRef]
- Benninga, Simon, and Marshall Blume. 1985. On the optimality of Portfolio Insurance. The Journal of Finance 40: 1341–52. [Google Scholar] [CrossRef]
- Black, Fischer, and Robert Jones. 1987. Simplifying portfolio insurance. Journal of Portfolio Management 14: 48–51. [Google Scholar] [CrossRef]
- Black, Fischer, and Robert Jones. 1988. Simplifying portfolio insurance for corporate pension plans. Journal of Portfolio Management 14: 33–37. [Google Scholar] [CrossRef]
- Brooks, Robert, and Haim Levy. 1993. Portfolio insurance: Does it pay? In Advances in Futures and Options Research. San Jose: JAI Press. [Google Scholar]
- Cesari, Riccardo, and David Cremonini. 2003. Benchmarking, portfolio insurance and technical analysis: A Monte Carlo comparison of dynamic strategies of asset allocation. Journal of Economic Dynamics and Control 27: 987–1011. [Google Scholar] [CrossRef]
- Chen, Ze, Bingzheng Chen, Yi Hu, and Hai Zhang. 2022. Hedge inflation risk of specific purpose guarantee funds. European Financial Management 28: 1104–36. [Google Scholar] [CrossRef]
- Christoffersen, Peter. 2003. Elements of Financial Risk Management. Cambridge: Academic Press. [Google Scholar]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Dichtl, Hubert, and Wolfgang Drobetz. 2011. Portfolio insurance and prospect theory investors: Popularity and optimal design of capital protected financial products. Journal of Banking and Finance 35: 1683–97. [Google Scholar] [CrossRef]
- Dichtl, Hubert, Wolfgang Drobetz, and Martin Wambach. 2017. A bootstrap-based comparison of portfolio insurance strategies. The European Journal of Finance 23: 31–59. [Google Scholar] [CrossRef]
- Dierkes, Maik, Carsten Erner, and Stefan Zeisberger. 2010. Investment horizon and the attractiveness of investment strategies: A behavioral approach. Journal of Banking and Finance 34: 1032–46. [Google Scholar] [CrossRef]
- Estep, Tony, and Mark Kritzman. 1988. TIPP: Insurance without complexity. Journal of Portfolio Management 14: 38. [Google Scholar] [CrossRef]
- Hamidi, Benjamin, Bertrand Maillet, and Jean-Luc Prigent. 2014. A dynamic autoregressive expectile for time-invariant portfolio protection strategies. Journal of Economic Dynamics and Control 46: 1–29. [Google Scholar] [CrossRef]
- Harvey, Campbell R., and Akhtar Siddique. 2000. Conditional skewness in asset pricing tests. The Journal of Finance 55: 1263–95. [Google Scholar] [CrossRef]
- Ho, Lan-chih, John Cadle, and Michael Theobald. 2010. Portfolio Insurance Strategies: Review of Theory and Empirical Studies. Boston: Springer, pp. 319–32. [Google Scholar]
- Ibragimov, Rustam, and Johan Walden. 2007. The limits of diversification when losses may be large. Journal of Banking & Finance 31: 2551–69. [Google Scholar]
- Jobson, J. Dave, and Bob M. Korkie. 1981. Performance hypothesis testing with the Sharpe and Treynor measures. Journal of Finance 36: 889–908. [Google Scholar] [CrossRef]
- Keating, Con, and William F. Shadwick. 2002. A universal performance measure. Journal of Performance Measurement 6: 59–84. [Google Scholar]
- Lee, Huai-I., Min-Hsien Chiang, and Hsinan Hsu. 2008. A new choice of dynamic asset management: The variable proportion portfolio insurance. Applied Economics 40: 2135–46. [Google Scholar] [CrossRef]
- Leland, Hayne E., and Mark Rubinstein. 1988. The evolution of portfolio insurance. In Portfolio Insurance: A Guide to Dynamic Hedging. New York: John Wiley & Sons. [Google Scholar]
- Levene, Howard. 1960. Robust tests for equality of variances. In Contributions to Probability and Statistics. Edited by Ingram Olkin. Palo Alto: Stanford University Press. [Google Scholar]
- Post, Thierry, Pim Van Vliet, and Haim Levy. 2008. Risk aversion and skewness preference. Journal of Banking and Finance 32: 1178–87. [Google Scholar] [CrossRef]
- Sanfilippo, Gilles. 2003. Stocks, bonds and the investment horizon: A test of time diversification on the French market. Quantitative Finance 3: 345–51. [Google Scholar] [CrossRef]
- Sharpe, William F. 1966. Mutual fund performance. The Journal of Business 39: 119–38. [Google Scholar] [CrossRef]
- Zieling, Daniel, Antje Mahayni, and Sven Balder. 2014. Performance evaluation of optimized portfolio insurance strategies. Journal of Banking and Finance 43: 212–25. [Google Scholar] [CrossRef]
| Reference | Dynamic PI Strategies | Static PI | Methodology | ||
|---|---|---|---|---|---|
| CPPI | TIPP | EPPI | Strategies | (Model-Free) | |
| Cesari and Cremonini (2003) | ✔ | ✔ | |||
| Lee et al. (2008) | ✔ | ✔ | |||
| Annaert et al. (2009) | ✔ | ✔ | ✔ | ||
| Dichtl and Drobetz (2011) | ✔ | ✔ | ✔ | ||
| Hamidi et al. (2014) | ✔ | ||||
| Zieling et al. (2014) | ✔ | ||||
| Ardia et al. (2016) | ✔ | ✔ | ✔ | ||
| Dichtl et al. (2017) | ✔ | ✔ | ✔ | ||
| Chen et al. (2022) | ✔ | ✔ | |||
| Our work | ✔ | ✔ | ✔ | ✔ | |
| Series | Average Return (%) | Standard Deviation () (%) | Skewness | Kurtosis | p-Value Autocorrelation (Ljung-Box Test) | p-Value Heteroscedasticity (Engle’s ARCH Test) |
|---|---|---|---|---|---|---|
| UKX | ||||||
| HSI | ||||||
| NKY | ||||||
| SPX |
| Portfolio Insurance Strategy | CPPI | TIPP | EPPI | EPPI | EPPI |
|---|---|---|---|---|---|
| (a = 5) | (a = 10) | (a = 20) | |||
| Rebalancing discipline | Daily | Daily | Daily | Daily | Daily |
| Protection level (%) | |||||
| Multiplier | 14 | 14 | - | - | - |
| - | - | 14 | 14 | 14 | |
| Initial equity allocation (%) | |||||
| Average excess return | *** | ||||
| Standard deviation | *** | *** | *** | ||
| Sharpe ratio | *** | ||||
| % | *** | ** | *** | *** | |
| Average negative excess return | *** | *** | |||
| VaR 5% | *** | * | *** | *** | |
| ES 5% | *** | *** | *** | *** | |
| Skewness | |||||
| Omega measure |
| Volatility Subgroup Rebalancing Discipline | Low Volatility Regime Daily | Medium Volatility Regime Daily | High Volatility Regime Daily | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Portfolio insurance strategy | CPPI | TIPP | EPPI | CPPI | TIPP | EPPI | CPPI | TIPP | EPPI |
| Protection level (%) | |||||||||
| Multiplier | 14 | 14 | - | 14 | 14 | - | 14 | 14 | - |
| - | - | 14 | - | - | 14 | - | - | 14 | |
| a | - | - | 20 | - | - | 20 | - | - | 20 |
| Initial equity allocation (%) | |||||||||
| Average excess return | *** | *** | *** | ||||||
| Standard deviation | *** | *** | *** | *** | *** | *** | |||
| Sharpe ratio | *** | *** | *** | *** | |||||
| % | *** | *** | *** | *** | *** | ||||
| Average negative excess return | *** | *** | *** | *** | *** | *** | |||
| VaR 5% | *** | *** | *** | *** | *** | *** | |||
| ES 5% | *** | *** | *** | *** | *** | *** | |||
| Skewness | |||||||||
| Omega measure | |||||||||
| Portfolio Insurance Strategy | CPPI | TIPP | EPPI | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rebalancing discipline | Daily | Daily | Daily | ||||||
| Protection level (%) | 90 | 95 | 90 | 95 | 90 | 95 | |||
| Multiplier | 14 | 14 | - | 14 | 14 | - | 14 | 14 | - |
| - | - | 14 | - | - | 14 | - | - | 14 | |
| a | - | - | 20 | - | - | 20 | - | - | 20 |
| Initial equity allocation (%) | |||||||||
| Average excess return | *** | *** | *** | *** | *** | *** | |||
| Standard deviation | *** | *** | *** | *** | *** | *** | |||
| Sharpe ratio | *** | *** | *** | *** | *** | *** | |||
| % | *** | *** | *** | *** | *** | *** | |||
| Average negative excess return | *** | *** | *** | *** | *** | *** | |||
| VaR 5% | *** | *** | *** | *** | *** | *** | |||
| ES 5% | *** | *** | *** | *** | *** | *** | |||
| Skewness | *** | *** | |||||||
| Omega measure | |||||||||
| Portfolio Insurance Strategy | CPPI | TIPP | EPPI | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rebalancing discipline | Daily | Weekly | Monthly | Daily | Weekly | Monthly | Daily | Weekly | Monthly |
| Protection level (%) | |||||||||
| Multiplier | 14 | 14 | - | 14 | 14 | - | 14 | 14 | - |
| - | - | 14 | - | - | 14 | - | - | 14 | |
| a | - | - | 20 | - | - | 20 | - | - | 20 |
| Initial equity allocation (%) | |||||||||
| Average excess return | *** | *** | *** | *** | *** | *** | |||
| Standard deviation | *** | *** | *** | *** | *** | *** | |||
| Sharpe ratio | *** | *** | *** | *** | *** | *** | |||
| % | *** | *** | *** | *** | *** | *** | *** | *** | |
| Average negative excess return | *** | *** | *** | *** | *** | *** | |||
| VaR 5% | *** | *** | *** | *** | *** | *** | |||
| ES 5% | *** | *** | *** | *** | *** | *** | |||
| Skewness | |||||||||
| Omega measure | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mancinelli, D.; Oliva, I. Constant or Variable? A Performance Analysis among Portfolio Insurance Strategies. Risks 2023, 11, 105. https://doi.org/10.3390/risks11060105
Mancinelli D, Oliva I. Constant or Variable? A Performance Analysis among Portfolio Insurance Strategies. Risks. 2023; 11(6):105. https://doi.org/10.3390/risks11060105
Chicago/Turabian StyleMancinelli, Daniele, and Immacolata Oliva. 2023. "Constant or Variable? A Performance Analysis among Portfolio Insurance Strategies" Risks 11, no. 6: 105. https://doi.org/10.3390/risks11060105
APA StyleMancinelli, D., & Oliva, I. (2023). Constant or Variable? A Performance Analysis among Portfolio Insurance Strategies. Risks, 11(6), 105. https://doi.org/10.3390/risks11060105






