BeVIXed: Trading Fear in the Volatility Complex

Abstract

We explain the evolution of the volatility market and present the infamous day of ‘Volmageddon’ as an insightful case study. Our survey focuses on the pricing and trading of volatility-linked assets, highlighting the impact of mechanical hedging in markets for futures and higher-order derivatives. We supplement the vast statistical analysis of volatility derivatives with a financial economist’s perspective.

1. Introduction

Financial market volatility continues to reign supreme. In this paper, we outline volatility’s progression from a theoretical risk measure to a tradable asset class, and describe the cataclysmic impact of mechanical hedging by major volatilty market participants.

The Chicago Board Options Exchange’s (CBOE) Volatility Index (VIX) is a widely followed index that calculates the implied volatility of the U.S. stock market for the next 30 days. Colloquially referred to as the ‘Fear Gauge’, the VIX is updated every 15 s during a trading day. The VIX lies at the heart of the Volatility Complex, as illustrated in Figure 1, which influences how traders price the sprawl of volatility-linked assets.

This paper is composed of two self-contained chapters. The first chapter builds the Volatility Complex from the ground up, beginning with the academic definition of volatility and ending with the construction of a volatility-linked exchanged traded product. Along the way, we cover the appropriate mathematical and financial prerequisites to understand the VIX calculation methodology. One goal is to demystify the inner workings of the derivative and volatility markets. The second chapter delineates the growth in shorting, or betting against, volatility and the reason behind such a trading strategy’s risk of backfiring. The carnage in financial products designed to short volatility on 5 February 2018 was later dubbed as ‘Volmageddon’.

The prevalent explanation of Volmageddon, which we expound upon, posits that higher order volatility-linked derivatives sparked a negative feedback loop in tandem with underlying assets further down the volatility ladder because of the price-insensitive hedging carried out by major market participants. We postulate that a similar ‘tail-wagging-the-dog’ effect occurred in the SPX options market on 20 March 2020, again due to a mechanical hedging strategy.

The post-crisis regulation gave birth to the ongoing, protracted boom in volatility-sensitive investing. However, this came with an unintended consequence, the volatility is now more volatile. In particular, drawdowns in volatility-linked assets have increased in both frequency and intensity Peterseil and Kawa (2019). Many have valiantly tried (and failed) to hedge against such drawdowns using assets in the complex. Mistakes are inevitable if investors do not fully understand what they are actually trading. In light of this truism, we hope the paper will serve as a valuable guide to help the reader navigate through—and skilfully manage—fear in the Volatility Complex. As Mark Twain supposedly opined, “It ain’t what you don’t know that gets you into trouble. It’s what you know for sure that just ain’t so”. This paper may be of use to regulators, academics, and, of course, investors.

2. The Volatility Complex

Simply put, volatility is financial uncertainty. If volatility can be quantified, then so can an investment’s risk profile. In 1952, Harry Markowitz explained volatility in statistical terms that allowed investors to better understand an investment portfolio’s return as a function of risk. About 20 years later, in 1973, Black and Scholes’ seminal paper ‘The Pricing of Options and Corporate Liabilities’ introduced a model to calculate implied, i.e., future, volatility from market prices of option contracts. Another 20 years later, in 1993, the CBOE launched the first version of the VIX, which computed the implied volatility of a basket of U.S. stocks with the help of the Black–Scholes–Merton model. In 2003, the CBOE changed the VIX’s calculation methodology to make it ‘model-free’. A couple of years later, derivatives on the VIX were rolled out and quickly picked up in popularity. Although the volatility market is relatively young (about 20 years), its rapid expansion provides an insight into how and why volatility derivatives became so popular with investors, ranging from retail to institutional.

2.1. Volatility as Risk

Any investment decision is based on two variables, risk and expected return. Risk is disliked (the less the better), and expected return is welcomed (the more the better). In practice, however, the investor is forced to make a trade-off between the two because an investment with higher expected return is usually accompanied with higher risk. So how is risk understood with respect to an expected return?

One way to measure risk is by the volatility of a financial asset’s return. Indeed, when the return is normally distributed, return and volatility fully describe this return profile. In less simple scenarios, the frequency of extreme events (thick tails), asymmetry (skewness), time-dependence (e.g., caused by the business cycle or crises), the unthinkable (non-anticipated changes, such as the occurrence of a ‘black swan’), and other dimensions, can also matter to the investor. 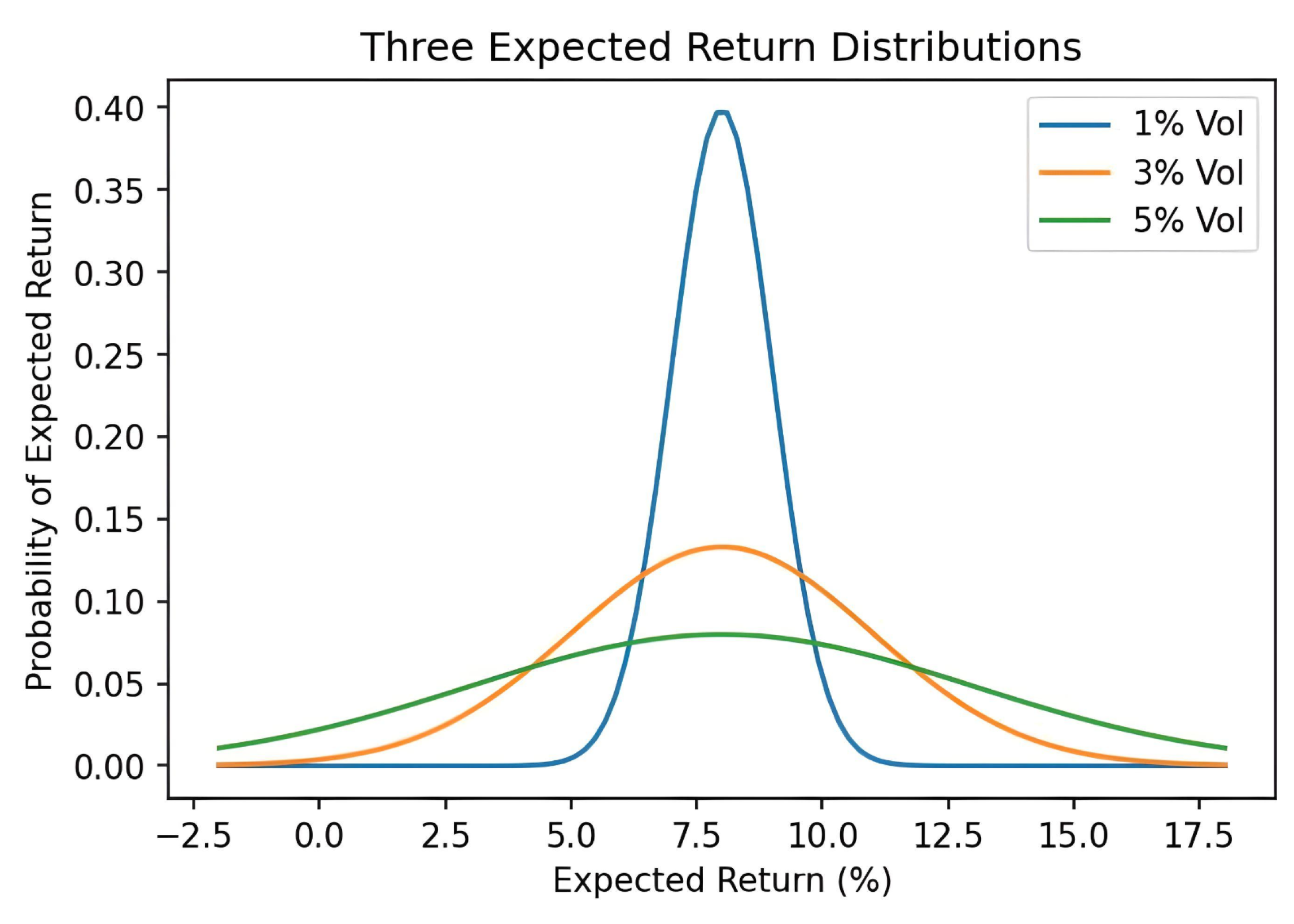Figure 2 illustrates how volatility corresponds to the degree of dispersion of an asset’s return. In this example with a normal distribution, the expected return is 8% for each asset. The distribution of (future) returns is symmetric about this expected return which means, for example, a future return of 12% is as likely as a return 4%.

The bell-shaped curve posits that future returns closer to the expected return are more likely than those further toward the tail ends. As volatility $\sigma$ increases, however, future returns away from the 8% mark increase in likelihood. Thus, the asset with 5% volatility is the riskiest of the three. In reality, however, one will find that the expected return increases with volatility.

There are subtleties in the semantics. An expected return is one you predict to see on average; a realized return is one you will observe in the future. There is a range of possible returns ex ante, but there will only be one return ex post. Risk, like expected return, is an ex ante concept because it is a feature of not-yet-realized returns. For example, consider an asset that promises you one of two returns, $20\%$ or $10\%$, with equal likelihood. The expected return is $15\%$, but it will never be physically realized.1

One of the biggest challenges in quantitative finance is to come up with a fairly tenable distribution of an asset’s future return. Are you able to provide a detailed account of the possible returns and their respective likelihoods of, say, Apple’s stock price in one year’s time? A more informed alternative to daft speculation is the projection of historical data into the future. Nevertheless, how likely is Apple’s past performance a ‘guarantee of its future results’? It is difficult to say, but the use of historical data to quantify a future return is a widely used rule-of-thumb by financial practitioners.

The S&P 500 index (SPX), which captures roughly 80% of the total U.S. stock market capitalization, is a measure of the near-term outlook of the United States’ economy. It might be more intuitive to think about the SPX as a financial barometer that indicates the expected weather of the general U.S. economy in the coming months.

Therefore, an investment in the index is an investment in the broad U.S. economy. The SPX is merely a tracker and not directly investable; its index ‘level’ is a number calculated from all 500 stocks and their respective market capitalizations. So one can invest in other instruments that either proxy the SPX or that expose you to risks associated with it. That sounds more complicated than it actually is.

One standard investment vehicle that tracks, and delivers, the returns of an underlying index is called the exchange-traded fund (ETF). In the case of the SPX, an issuer of the ETF pools together millions or billions of dollars to buy shares of businesses comprising the index in the right proportions. The issuer will then passively manage this ‘copy-of-SPX’ portfolio on behalf of the investor in exchange for a management fee. 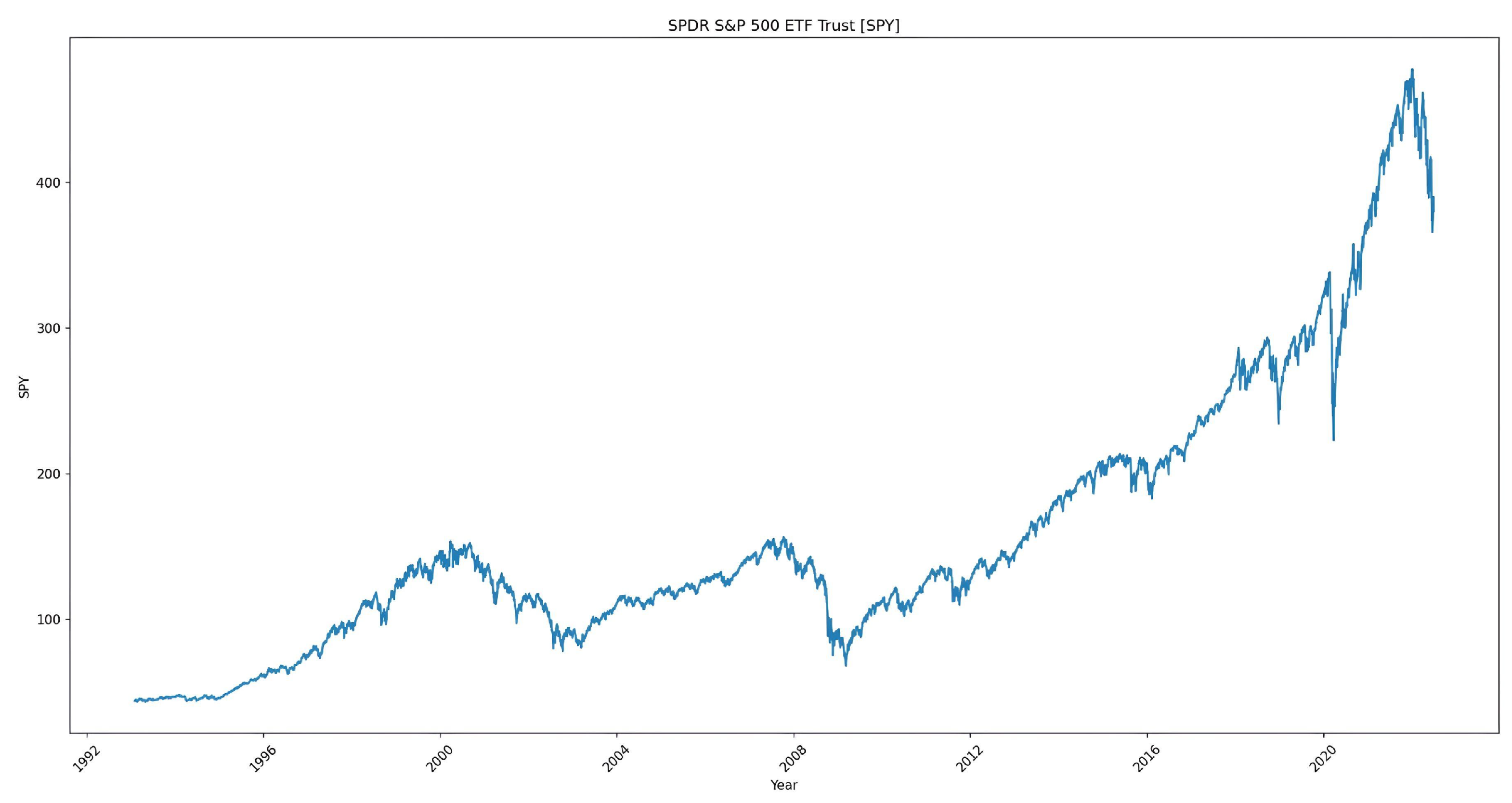Figure 3 depicts the past performance of the SPDR S&P 500 ETF Trust (SPY), a popular ETF on the S&P 500 index.

Two popular alternative investments are options and futures on the underlying SPX. Each one is a derivative contract with specifications on when to trade the underlying and for how much. A futures contract specifies a future date when the buyer purchases the underlying asset from the seller at the predetermined ‘future price’. Given the logistical challenges of delivering all 500 stocks associated with an SPX futures contract on the future date, the contract is instead settled on a cash basis. For example, if the SPX is higher than the predetermined future price on the future date, the buyer of the SPX futures receives the difference—in cash—from the seller.

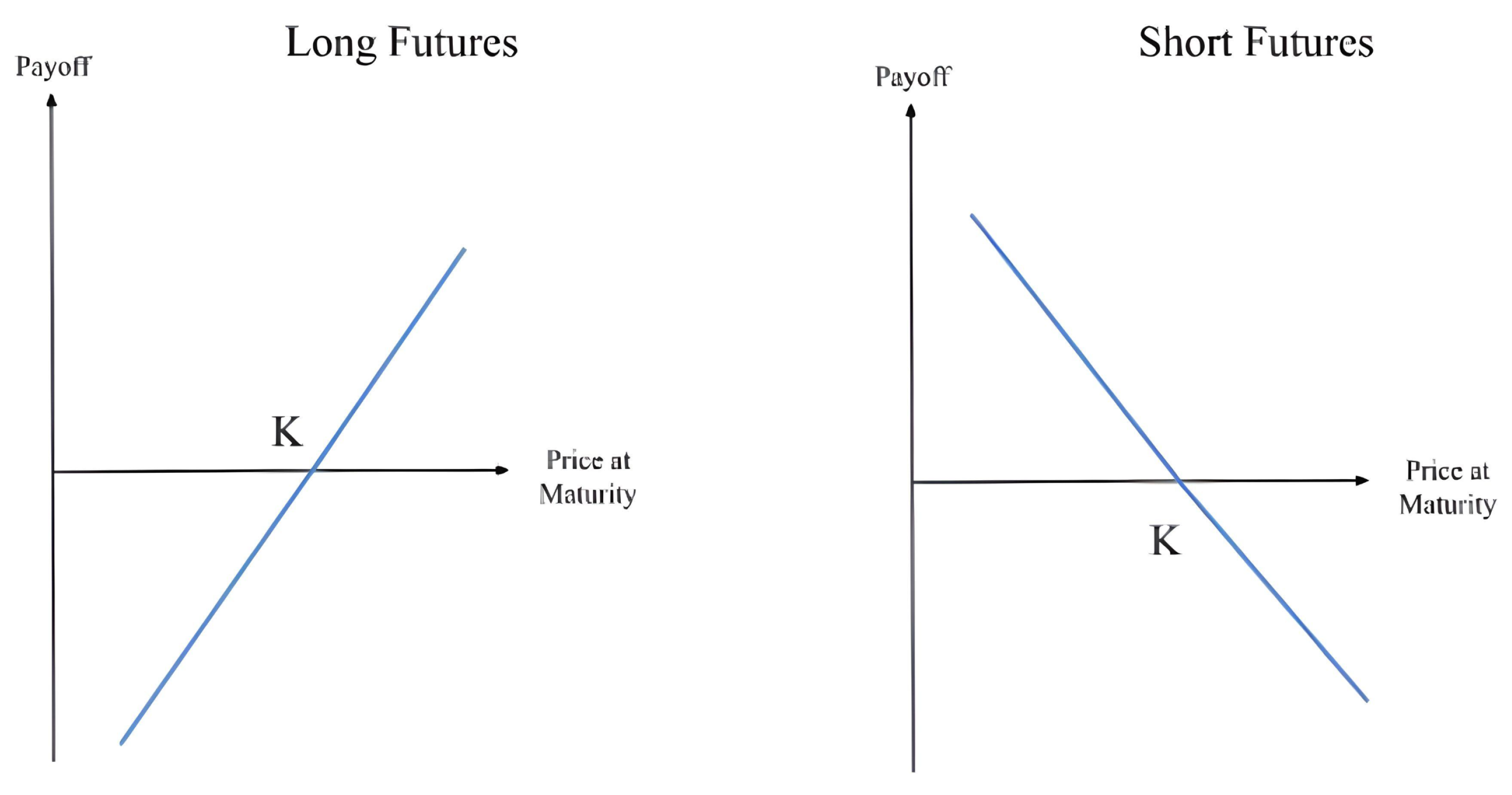
A futures contract, unlike other derivatives, requires no payment upfront from the buyer to the seller.2 Hence, the future price can be understood as the market’s expectation of where the SPX is going to be on the predetermined future date. Figure 4 depicts a futures contract’s payoff, from the point of view of the buyer and the seller. When a futures contract is agreed upon by both parties, the directional risk (i.e., whether the SPX will move up or down on the way to the future date) is taken up equally by both sides because the transaction is obligated to take place on the future date.

An option contract differs in this regard by requiring an upfront payment in exchange for the option or choice to conduct the transaction on the future date.3 An option contract’s specifications are those of the futures’, a future price and a future date. However, market players refer to an option’s future price as its strike price and its future date as its expiration date. The option to transact from the buyer’s point of view, i.e., the right to buy on expiration date, is a call option. Likewise, the right to sell is a put option.

The buyer of a call option, therefore, gains if the SPX’s level is higher than the strike price on the expiration date. The seller of the option will have to pay to the buyer the difference between the SPX and the strike price, i.e., cash settlement on expiration. However, if the SPX’s level is below the strike price, no payment is made as the rational choice for the buyer would be to not exercise her right to purchase the SPX for a higher price. In options-speak, this call option expires out-of-the-money.

With put options, the payment on the expiration date is different. Since the buyer has the right to sell, the option is only exercised if the SPX is below the strike price. In that case, the put option seller pays the buyer the difference between the strike and the SPX. If the SPX is above the strike at the expiry date, the option is out-of-the-money and not exercised. To avoid confusion between the price of an option with the price of, say, the SPX, market players refer to the option price (aka the upfront payment) as option premium or simply premium.

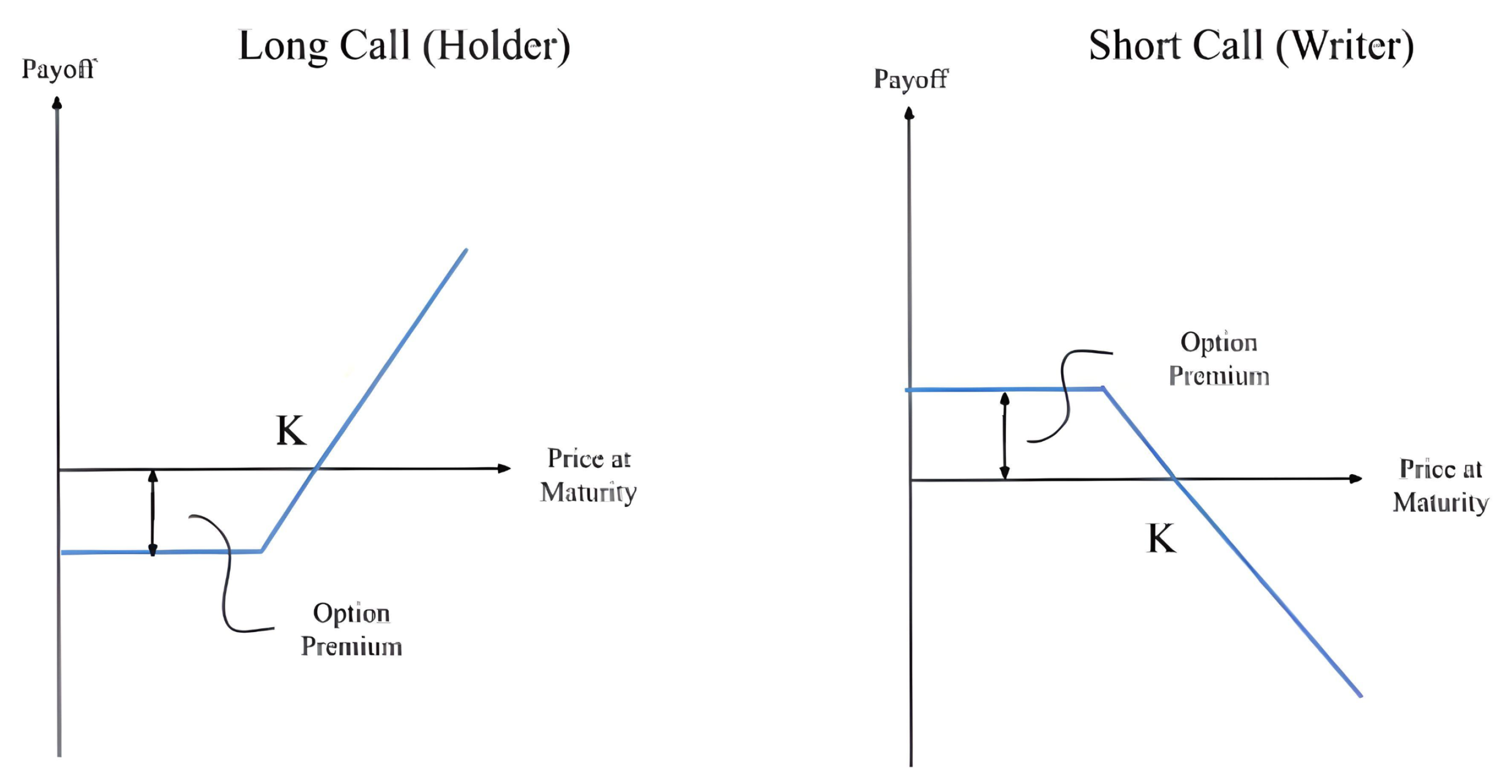
A profit and loss (PL for short) is the price to hold the derivative starting now less the payoff at maturity. A long call’s payoff, as shown in Figure 5, is only a neat approximation. In reality, its payoff is a convex function—i.e., a tilted smile of a curve above the approximation. For this reason, option contracts are a non-linear (i.e., convex) security. Likewise, futures contracts are a time-dependent linear derivative.

Pricing an options contract is no mean feat. For example, as a seller of a call option, how do you determine the fair value of your premium?4 Too high and there will be no buyers; too low and you will lose your shirt. Just right, and you would have received a Nobel prize. In 1997, Robert C. Merton and Myron S. Scholes were awarded the ‘Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel’ for the Black–Merton–Scholes (BSM5) option pricing formula.

The method is derived from an active trading strategy that is designed to perfectly replicate the payoff of an options contract using the underlying. The amount of cash required to mimic this payoff is simply the price of the option, i.e., the option premium, which is calculated for you by the formula. In technical terms, by dynamically trading with an amount equal to the option premium, one can fully hedge the option’s payoff.

The trading strategy is simple as it only depends on the sensitivity of the premium with respect to the change in the price of the underlying. For example, if the option premium went up (down) by USD 0.75 and the price of the underlying went up (down) by USD 1, then the trading strategy advises the investor to hold exactly 0.75 units of the underlying. In technical terms, the $\mathsf{\Delta }$ of an option provides the investor with an exact hedge. When a call option is hedged, the position in the underlying is positive (or, in finance terms, long) and money needs to be borrowed. When a put option is hedged, the position in the underlying is negative (short) and money is deposited.

In practical terms, the hedge makes the seller of an options contract ‘market-neutral’, i.e., it removes the directional risk associated with selling an option. The bet from the seller’s point of view is that the market goes down (up) and the call (put) option expires worthless.

Since hedging is of extreme importance to market participants, they have coined terms that express the underlying’s current price relative to the option’s strike price. An option is said to be ‘out of the money’ (OTM) if an expiration today will yield the contract worthless. Furthermore, an option is ‘in the money’ (ITM) if an expiration today will yield a positive payoff. Finally, an option is ‘at the money’ (ATM) if its strike price is the same as the current price of the underlying. 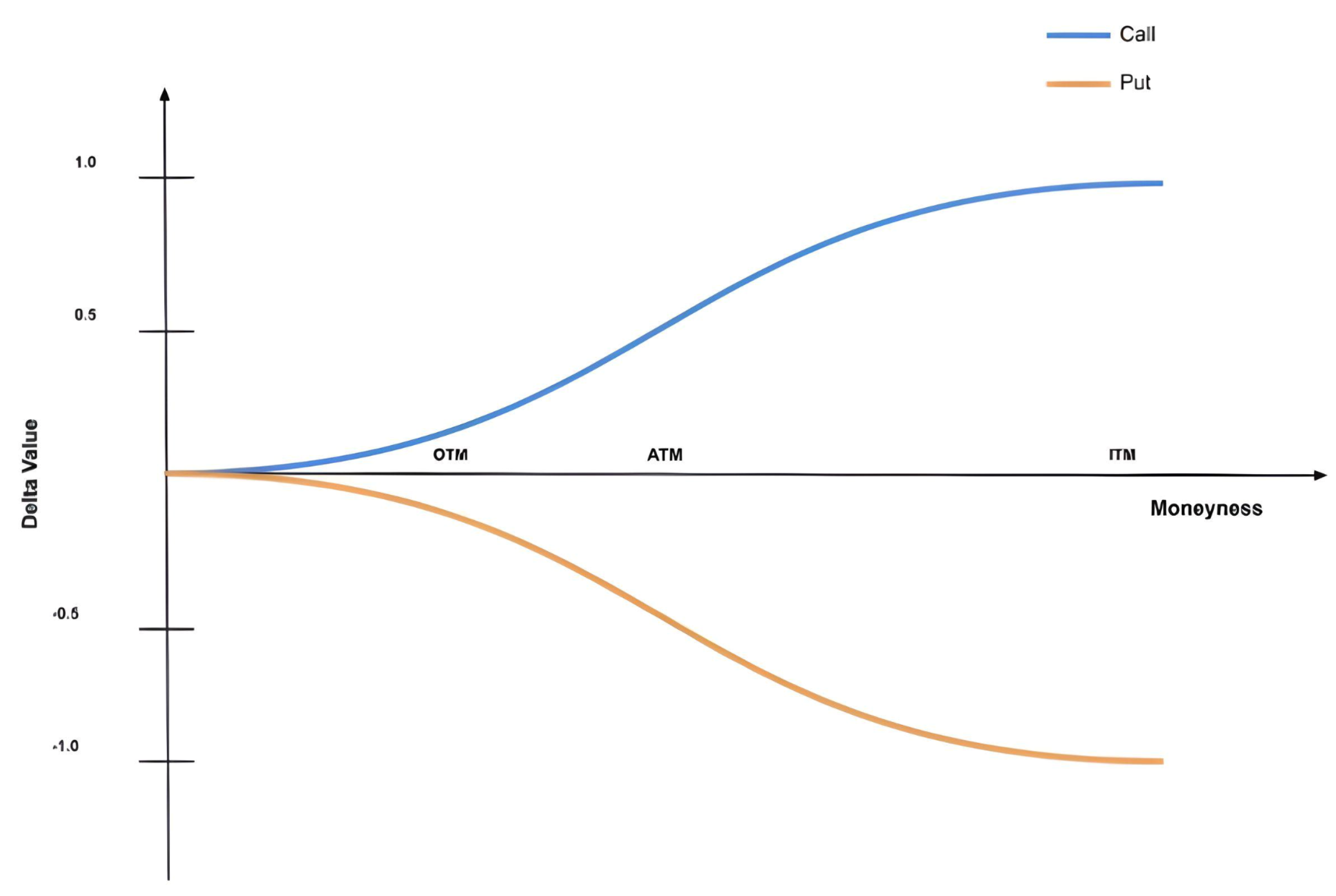Figure 6 presents how the delta value ($\mathsf{\Delta }$) of a call or a put varies with the moneyness of an option with respect to its strike. All most all options are issued with a strike close to the current price of the underlying.

So who trades options and for what reasons? Well, there are a few market players whose intentions are clear. Retail investors would buy a call (put) if they are more (less) optimistic than the average investor about the future development of the underlying. They are classified as ‘speculators’, along with hedge funds, etc., because they make directional bets in the market. You will also find several investment banks who sell, or underwrite, options. Their aim is to collect the option premia and then hedge much less than what the BSM model prescribes. In fact, managing a large book of derivatives implies that many idiosyncratic risks offset each other, and so the investment bank only needs to manage the residual risk, i.e., what is leftover. Needless to say, computing this residual risk is not a walk in the park!

On the other hand, futures are often used by asset managers who want to hedge their investment. Suppose you manage a portfolio worth USD 100 billion in assets and whose risk-return profile closely resembles the S&P 500 index. If you are concerned about tomorrow’s release of U.S. labour market data (i.e., the non-farm payroll), you can completely hedge your portfolio with an appropriate short futures position on the SPX. No matter what the markets tell you tomorrow, any change in the value of the S&P 500 will be matched (or closed out) by an opposite change in the value of the futures. You are, once again, market-neutral.

2.2. The CBOE Volatility Index

In 1993, the first volatility index was introduced by the CBOE to measure the 30-day implied volatility of the S&P 100 index. The old VIX, now called the VXO, took the average of the BSM implied volatilities6 from eight near-the-money (≈ATM) S&P 100 index options with the two nearest expirations. In 2003, the calculation methodology was changed to provide a ‘model-free’ measure of S&P 500 index’s 30-day expected volatility, Carr and Wu (2006). The methodology is in use to this day, and we aim to provide a sufficiently detailed discussion of it.

The VIX is quoted in volatility percentage points, when the VIX is at 15, it means that the (annualised) 30-day expected volatility of the S&P 500 is $15\%$. Rather counter-intuitively, it will make more sense to first understand how the VIX-squared works. The ${\mathrm{VIX}}^2$ is modelled after a variance swap, which is a forward contract on annualised variance expressed in variance percentage points, see Diamond (2012). A buyer and a seller of a variance swap agree on the variance swap rate $\tilde{V}$ when exchanging contracts. On expiration day T, the buyer pays the variance swap rate $\tilde{V}$ and receives the realized variance $V_T$. The buyer makes a profit when the realized variance is higher than the swap rate, and a loss otherwise. In other words, the buyer locks in on the swap rate—which can be interpreted as the expected value of the variance.

Formally, the CBOE defines the VIX as

$${\mathrm{VIX}}^2\equiv \tilde{V}$$

(1)

Here, the ${\mathrm{VIX}}^2$ is the variance swap rate of a variance swap on the S&P 500. The variance swap rate $\tilde{V}$ in a variance swap is analogous to the predetermined future price in a futures contract; i.e., the variance swap rate $\tilde{V}$ is the expectation of total realized variance $V_T$ on expiration. Mathematically, this is written as

$$\tilde{V}=\mathbb{E}\left[V_T\right]=\mathbb{E}\left[\frac{1}{T}{\int }_0^T{\sigma }_t^{2}dt\right]$$

(2)

Rather remarkably, the fair value of $\tilde{V}$ can be calculated directly from out-of-the-money put and call options on the S&P 500 index, see Demeterfi et al. (1999). This is formally expressed as

$${\mathrm{VIX}}^2\equiv \mathbb{E}\left[\frac{1}{T}{\int }_0^T{\sigma }_t^{2}dt\right]=\frac{2e^{rT}}{T}\left[{\int }_0^{F_0}\frac{{\mathrm{put}}_K}{K^2}dK+{\int }_{F_0}^{\infty }\frac{{\mathrm{call}}_K}{K^2}dK\right].$$

(3)

Here, $F_0$ is the forward price of the S&P 500 index at T days in the future, i.e., the market’s best guess where the S&P 500 will be at that time. The VIX uses all put options at strikes lower than $F_0$ and all call options at strikes higher than $F_0$. All of these options are currently, at the present $F_0$, out-of-the-money. The price of each option, whether a put or a call, is divided by its strike price squared, $K^2$.

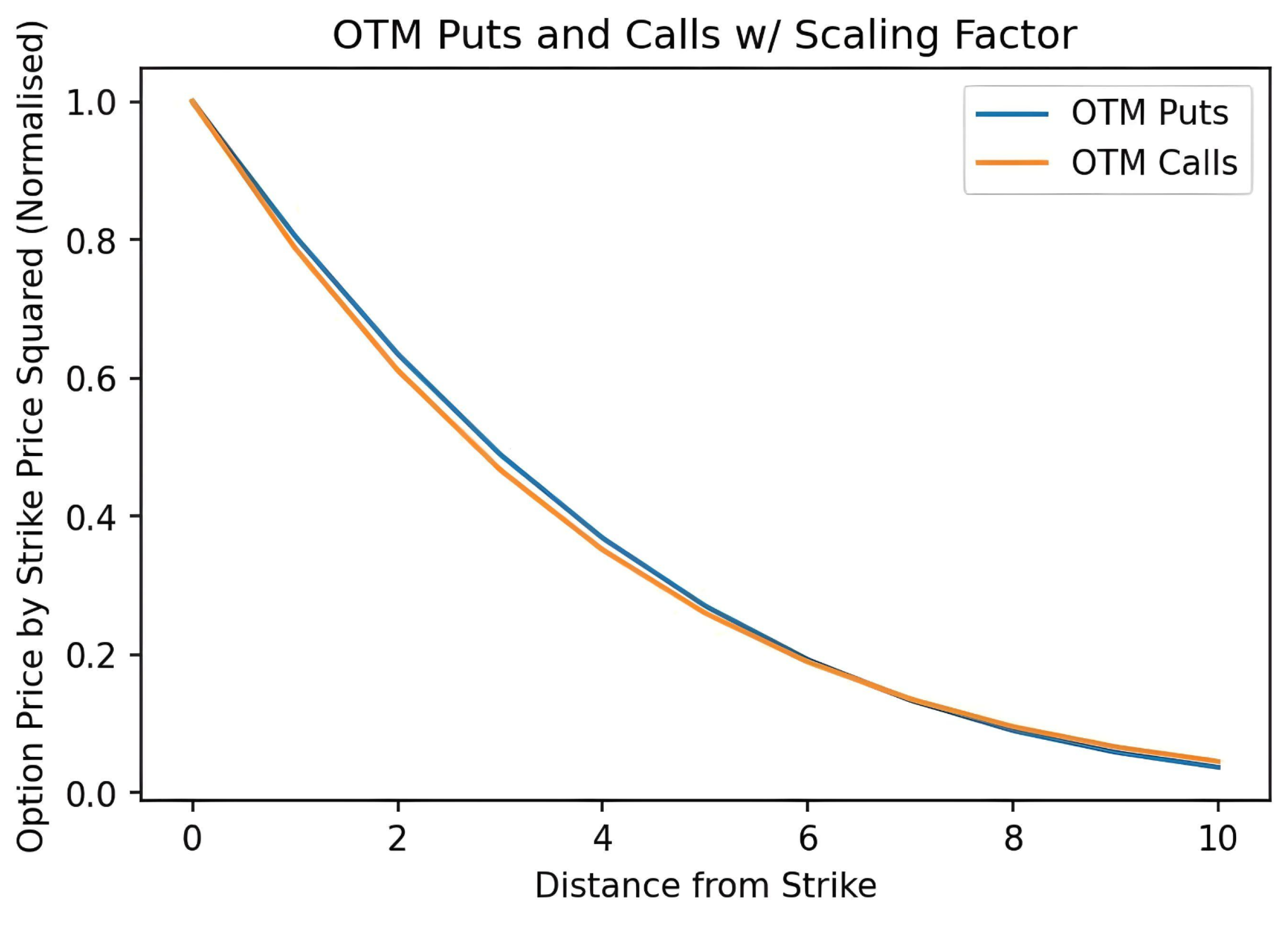
As the strike K becomes further out-of-the-money for both options, the scaling factor $1/K^2$ dampens the effect that these puts and calls have on the index’s final calculation (see Figure 7). Likewise, as the prices of puts and calls clustered near the strike increase, the index weighs them approximately at their face value. It is important to note that it is extremely rare to have the VIX jump because of an increase in purchases of SPX calls near the strike Wang (2021). Instead, the VIX spikes when market players bid up the prices of SPX puts in anticipation that the underlying index will precipitously decline in value in the near future. It is for this reason that the Volatility Index is given the moniker ‘fear gauge’.

Since there are not infinitely many SPX options, the CBOE applies the following discrete approximation:7

$${\mathrm{VIX}}^2=\left[\frac{2e^{rT}}{T}\sum _i\frac{Q\left(K_i\right)}{K_i^2}\mathsf{\Delta }{K}_i-\frac{1}{T}{\left(\frac{F_0}{K_0}-1\right)}^2\right].$$

(4)

Let us develop a qualitative feel for CBOE’s approximation. The integral over a continuum of options with strike prices K changes into a sum of currently traded options with their respective strike price $K_i$. The sum adds up prices of all available out-of-the-money puts and calls. The price is the midpoint of its bid-ask spread—expressed as the function $Q\left(K_i\right)$. The $\mathsf{\Delta }{K}_i$, a discrete modification to $dK$, is the sum of half the spread between its closest, neighbouring strike prices. There is, however, one catch: at $K_0$, the first strike below the forward price $F_0$ of the S&P 500 index, the call option is in-the-money. Indeed, the last term in (4) represents the correction needed to convert this in-the-money call into an out-of-the-money put.8

Remember that the new Volatility Index is defined as the square-root of a one-month variance swap rate on the SPX; however, the CBOE only makes use of SPX options with Friday expirations in their calculation. Here, SPX options with more than 23 days and less than 37 days to the Friday SPX expiration are weighted to yield a constant, 30-day measure of the expected volatility of the S&P 500 index.

Since the VIX cannot be traded or replicated (in contrast to stocks and stock market indices which can be either traded or replicated), the standard futures pricing relationship based on ‘cash-and-carry’ arbitrage9 does not hold. Hence, any fair-value calculation of a futures contract on the VIX will always be model-dependent.

However, there are upper and lower price bounds on VIX futures. The VIX is defined as the square-root of a one-month variance swap rate, i.e., the variance swap rate expressed in volatility units, on the SPX; it is not the one-month volatility swap rate on the SPX. The difference between the two is given by Jensen’s Inequality:

$$\mathrm{VIX}=\sqrt{\mathbb{E}\left[V_T\right]}\ge \mathbb{E}\left[\sqrt{V_T}\right]=\mathrm{Volatility}\mathrm{Swap}\mathrm{Rate}$$

(5)

A futures contract on the VIX, at time t with expiration $T^{\prime }$, is the expectation of square-root of expected total realized variance as shown below (Carr and Wu 2006).

$$\mathrm{VIX}\mathrm{futures}={\mathbb{E}}_t\left[\mathrm{VIX}\mathrm{at}\mathrm{time}{T}^{\prime }\right]={\mathbb{E}}_t\left[\sqrt{{\mathbb{E}}_{T^{\prime }}\left[\frac{1}{T}{\int }_{T^{\prime }}^{T^{\prime }+T}{\sigma }_t^{2}dt\right]}\right]$$

(6)

The mathematics here serves a symbolic purpose as it keeps the timeline in check. A typical volatility swap allows one to trade between realized and expected volatility. A forward volatility swap allows one to trade between future volatility percentages. While one fixes a volatility swap rate at the inception of a typical volatility swap, the fixing of a volatility swap rate on a forward volatility swap is set at some future time and the settlement day is on some time $T^{\prime }$ further in the future. A VIX futures contract is not your typical, over-the-counter volatility swap because it looks beyond the VIX, which itself is a forward-looking measure as it constantly gauges the expected square-root of variance of the SPX over the next 30 days. So then what is a VIX future?

By Jensen’s inequality, the price of a VIX futures is bounded below by a forward volatility swap rate. Likewise, the price of a VIX futures is bounded above by a forward variance swap rate, expressed in volatility percentage points. In practice, however, the VIX future price is set approximately to a forward volatility swap rate on the VIX. In volatility parlance, a VIX futures is simply referred to as a forward volatility swap.10 For cases where this is violated, see Van Tassel (2020).

2.3. Volatility as an Asset Class

The quantification of volatility via an index allowed investors to track expected volatility of the broad U.S. stock market. Soon, it led investors to crave for directional exposure on the VIX—but this is the equivalent of trading the market’s expectation of future volatility. The initial VIX futures contracts were introduced in 2004, and VIX options followed after in 2006. Both volatility derivatives are settled in cash.

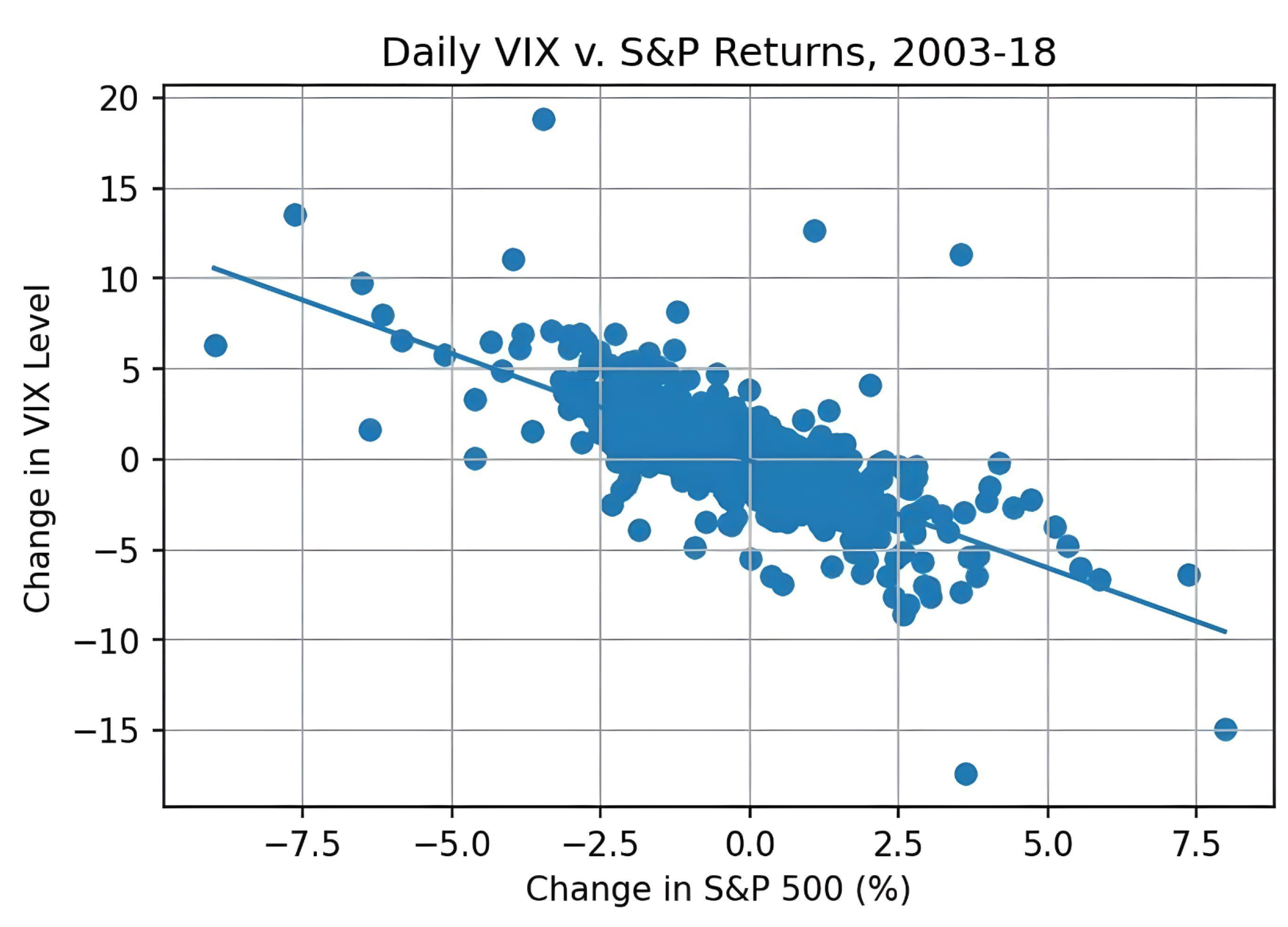
Historically, the correlation between daily returns of the S&P 500 index and daily changes in the VIX is around $-0.8$, see Macroption (2022). Figure 8 illustrates the negative relationship, leading up to and including Volmageddon.

Such a correlation exists for a valid reason. A VIX future, in terms of contract specifications, is just like any other futures contract. Namely, the buyer of a VIX future profits if the VIX at some date at or before expiry exceeds the future price, i.e., if the market’s expectation of volatility has increased since the buyer entered the contract. Sudden market drawdowns tend to increase the market’s expectation of volatility in the coming 30 days or so, therefore the price of near-term VIX futures shoots up. Likewise, the seller of a VIX futures profits if the market expects lower volatility in the short-term, which is usually associated with a rising market. Hence, the existence of the negative correlation between the VIX and SPX.

Of course correlation is not causality and there are several days where VIX and SPX move in opposite directions (all observations in the lower-left and upper-right quadrant in Figure 8). We also observe several outliers; the most extreme are a VIX movement of +19 resp. −17 while the SPX moved by less than $\pm 4\%$. The former will be discussed in detail in the next section on Volmageddon.

A VIX option contract’s specifications adhere to those of any regular option on an underlying. Purchasing a call (put) means to speculate on an increase (decrease) in short-term volatility. Again, wanting limited downside risk as a buyer of an option would naturally entail the issuer demanding an upfront premium in return.

One drawback of entering a longer dated futures contract is that the exposure to changes in future volatility declines as the expiration date approaches. Implementing a futures trading strategy that maintains a defined exposure to the VIX can be challenging for the retail investor. For instance, it may be difficult to manage a portfolio of VIX futures that is supposed to provide a constant 30-day forward-looking exposure to the VIX. This sounds like a job for an index!

The index’s aim is clear: track a time-varying basket of VIX futures that maintains an average of 30 days to expiration. This is obtained by continuously adjusting the relative proportion of VIX futures; each day, the index adds exposure to the second month futures contract and reduces exposure to the first (or front) month futures contract, thus maintaining 30 days to maturity. The so-called S&P 500 VIX Short-Term Futures Index (VIX Futures Index) does just that and is maintained by the S&P Dow Jones Indices LLC11. Like the S&P 500 index, this index cannot be directly invested in. Instead, VIX exchange-traded product (ETP) promises to track, and deliver, the returns of the VIX Futures Index.

Retail investors can buy ETPs from (and later sell them back to) their issuers, gaining access to an instrument that mimics changes in the 30-day VIX futures return. From the issuer’s point of view, keeping the index as an underlying allows the issuer to hedge by taking the opposite side of the trade. It would ensure that the issuer avoided all directional exposure to volatility, but it is not that simple.

The recipe to construct a VIX ETP involves choosing the type of product, and the direction and magnitude of the volatility trade. The two options permitted in each case are, respectively, an exchange-traded note (ETN) or exchange-traded fund (ETF); long or ‘inverse’; and leveraged or unleveraged.

For example, a 2X long leveraged VIX ETP with USD 100 million in assets would double the daily gains or losses for its investors by using a margin account to construct a USD 200 million notional position in VIX futures. Similarly, an unleveraged inverse VIX ETP would take short positions in VIX futures without any leverage.

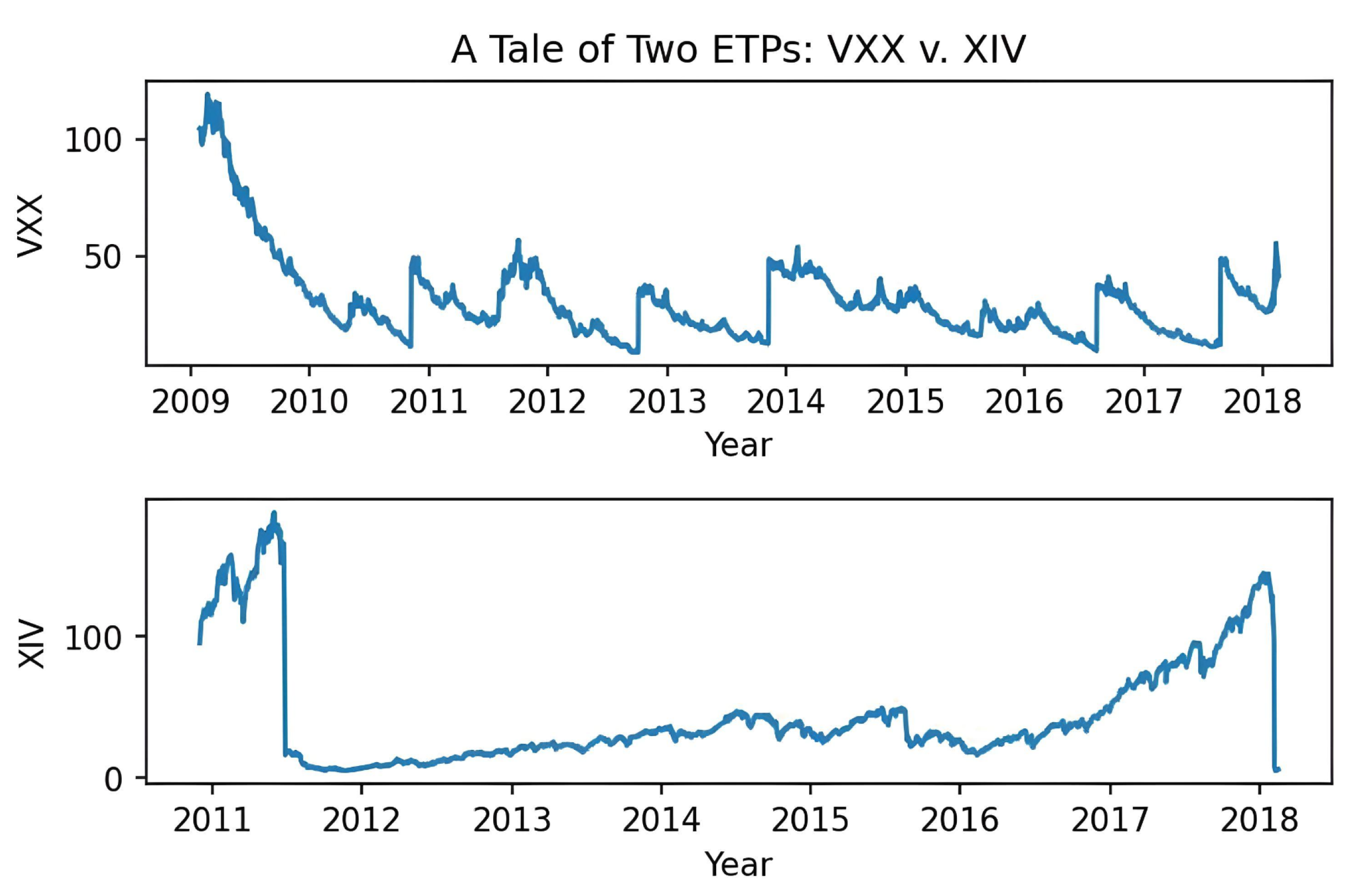
On 29 January 2009, Barclays LLC (Barclays) launched the first VIX ETP—the iPath S&P 500 VIX Short-Term Futures ETN (VXX)—that started trading on 30 January 2009. By 2016, the VXX ETP would be the fifth-most actively traded security in the US stock markets (Wigglesworth 2017). An ETN is simply an unsecured debt obligation. The issuer promises to pay a 30-day VIX future price at a pre-specified maturity date. At the same time, Barclays also launched another ETN which gives exposure to a weighted average VIX futures maturity of 5 months (VXZ). Such ETNs are still actively traded at the time of this writing. On 19 January 2018, Barclays relaunched the iPath Series B S&P 500 VIX Short-Term Futures ETN (VXX) after the previous series hit its maturity the same year. VXX’s new maturity is 23 January 2048 and has an annual management fee of 0.89%.

An ETN is different from an ETF. An ETF is secured by assets, e.g., an equity ETF, such as SPX, is backed by some proportion of the 500 stocks. When you own an ETF, you own a portfolio; when you own an ETN, you own a promise because an issuer can (in theory) invest the investors’ money in any asset. For the VXX, the investor is therefore exposed to credit risk, i.e., Barclays’ ability to keep its promise. However, there are two main reasons to own an ETN, a favourable tax treatment and—at least in theory—no tracking error, i.e., the value of the ETN follows the underlying index when traded in the secondary market due to arbitrageurs correcting mispricing. ETN issuers tend to also hedge some of the risk they are exposed to (Damato 2009).

In 2011, inverse VIX ETPs, which provided investors with the opportunity to short volatility, followed suit. The most popular inverse VIX ETP at the time was issued by Credit Suisse Group AG (Credit Suisse) and was called the Velocity Shares Daily Inverse VIX Short-Term Futures ETN (XIV). A directional counterpart to the VXX, XIV promised to replicate the inverse one-day return of the VIX Futures Index. For example, if the VIX Futures Index dropped by $10\%$, XIV would post an end-of-the-day return of $+10\%$ to its investors (see Figure 9). The XIV offered to harvest the ‘volatility risk premium’ by betting that near-term future, or expected, volatility will be lower than realized volatility. In practice, the XIV carried out its mandate by mechanically selling the same basket of near-term VIX futures that the VIX Futures Index tracks.

3. Volmageddon

On Monday, 5 February 2018, a day with unremarkable weather in Chicago and New York, the S&P 500 index dropped 4%. Such an event is rare and happens about twice per year on average. Given the historical correlation of −0.8 between the VIX and the SPX, the VIX should have responded with a rise of about 3.2 points. Instead, the VIX spiked by about 20 points, from 17 at open to 37 at close, which marked the largest ever recorded increase in the index in a single day. The VIX’s sudden skip, along with its tragic aftermath, would later aptly be dubbed ‘Volmageddon’.

3.1. The Big Volatility Short

After the Global Financial Crisis in 2007/2008, investors became painfully aware of the need to hedge against ‘tail risk’. This risk refers to the highly unlikely probability of extreme movements in asset prices.12 If one is exposed to such risk (as most equity investors are), one can suffer drastic losses in a short time period.

Given the historically negative correlation between the VIX and the S&P 500 index, many market participants conjectured that VIX futures—if properly traded—could protect them against tail risk. A corollary is that longing the S&P 500 index is equivalent to (implicitly) shorting volatility. Therefore, a long VIX futures position can hedge away potential volatility shocks in a portfolio resembling the S&P 500 Index.

This hedging tactic gained traction after the the launch of the first long VIX exchange-traded product (VXX) in 2009. While VIX futures were introduced a full five years earlier, it required a financial crisis and a complex financial instrument to track them to make their presence known to risk managers. The previous strategy of manually ‘rolling’ VIX futures contracts, i.e., paying monthly insurance premiums to tame the tail risk, was seen as a messy way of trading them.

After a couple of years of low volatility in 2009–2011 (see Figure 10), insuring against an event that did not occur started to lose its appeal. Investors began to ask: why not switch sides? Shorting VIX futures contracts mean they would collect, as opposed to pay, periodic insurance premiums. The introduction of the first inverse VIX ETP (XIV), in 2011, made this trade available to the general public. Around this time, however, the European debt crisis led to considerable economic uncertainty, and the VIX reached a two-year high of 48. After this spike, the VIX would stay low for the next seven years until 2018.13

The start of the new volatility regime quickly conjured up a self-reinforcing prophecy: shorting the VIX—via options and futures—drives down the index and, thus, benefits those who are short, making betting against rising volatility even more attractive.

Conceptually, trading volatility with these products is similar to buying or selling a volatility swap; an investor who is looking to short volatility sells implied volatility and receives realized volatility at expiration. The volatility risk premium, i.e., expected volatility less realized volatility, is what the short seller seeks to capture or ‘harvest’. Sellers of volatility collect periodic premiums, from buyers of volatility, in exchange for warehousing tail-risk. Unique to volatility markets, shorts make long-term bets while longs make short-term bets. However, the spread between implied and realized volatility narrows when selling insurance becomes a crowded trade.

Realistically, the dynamics of holding a short position against an index using futures contracts is different. Suppose you short 600 futures contracts, each with a notional value of USD 100, at a futures price of USD 10. If the futures index price goes up by 33%, your net asset value (NAV) drops from USD 60,000 to USD 40,000. However, the notional value of your position has become $-600\times$ USD $100\times 1.33=$ −USD $\mathrm{80,000}$. To restore the short position to your new NAV of USD 40,000, you have to buy futures at notional USD 40,000, i.e., USD 40,000/USD 100 = 400 contracts. If you are short, an adverse market move requires you to buy futures. If, instead, the market moves in your favour (falls), then you will have to sell more futures. In summary, an inverse VIX ETP (i.e., leverage -1) would sell (buy) if the price of futures goes down (up). A leveraged long VIX ETP (i.e., leverage > 1), rather surprisingly, works the exact same way! If the market moves up, the issuer has to go further long and buy futures contracts. If the market goes down, the issuer has to sell futures to reduce the notional amount of the position. Therefore, whether the exchange-traded product is inverse or leveraged long, both trade in the same direction in the futures market, buying when broad market goes up and selling when it goes down. For this reason, both inverse and leveraged long are simply referred to as leveraged VIX ETPs (Augustin et al. 2021). It does not take a genius to realize that this strategy can create a feedback loop if the issuers of leveraged ETPs are large enough and all trade in the same direction.

At the time, it was slowly becoming clear to certain market players that issuers of leveraged VIX ETPs were, themselves, the largest traders of VIX futures. Since issuers also generate revenue from management fees, and not from directional bets on volatility, they are incentivised to issue big or go home. Market players also knew when and how often issuers of VIX ETPs would bid up or down the prices of VIX futures contracts: two minutes before the close at 4:00 pm ET, every trading day!

It was a smart trading strategy for those who knew what to do, given that leveraged VIX ETPs had to buy VIX futures in the event of a VIX spike, simply buy those VIX futures earlier for cheap and sell them to their issuers later for more.

The scene was set for the seven-year volatility regime to come to an abrupt end. All the VIX needed to do now was vault higher than the market expected to set off a catastrophic feedback loop. On Friday, 2 February 2018, U.S. stocks sold off as investors worried that the Federal Reserve might raise interest rates faster than needed (Kawa 2019). The VIX began to rise.

3.2. The Volatility Storm

On Monday, 5 February 2018, US stock prices fell sharply as the S&P 500 declined by more than 4%. Amidst the stock market volatility, the VIX experienced its largest ever daily jump, rising 115% from 17 to 37. Credit Suisse’s XIV opened at USD 110 on that day, and closed around 10% lower at 4:00 pm ET. During after-hours, however, the price of XIV precipitously declined and had lost another 90% by around 6:30 pm ET (Franck 2018). So what happened? The XIV ETN became a victim of its own success.

We will use approximate numbers for a simpler illustration of what happened during market hours. For a more detailed account of that trading day, see Augustin et al. (2021). Recall that XIV was an exchange-traded note, with Credit Suisse as its issuer, that promised to track the inverse of the VIX short-term futures index. The prevalent theory is that XIV carried out the mechanical rebalancing strategy—as explained previously—at the end of the trading day (Augustin et al. 2021). As of Monday morning, the VIX stood at 15 and XIV had 15 million shares outstanding at a value of approximately USD 100 per share, or USD $1.5$ billion in net asset value. Credit Suisse’s XIV, tracking the inverse of the Index, maintained an appropriate short VIX futures position worth USD $1.5$ billion. So, for instance, if VIX futures jumps from 15 to 20 (a $33\%$ increase), XIV’s net asset value drops by $33\%$ to USD 1 billion. Post-jump, however, Credit Suisse’s short position now has a ‘notional’ value of USD 2 billion. In short, there is a mismatch between XIV’s NAV (which adjusts real-time as investors reprice the ETN’s shares accordingly) and Credit Suisse’s hedge (which needs to line up with NAV by the end of the trading day). In this specific VIX jump, Credit Suisse has to cut its volatility exposure in half by buying USD 1 billion VIX futures.

Towards the end of market’s close, market players—aiming to take advantage of the end-of-day hedging by issuers—started to bid up the price of VIX futures at 3:30 pm ET. The snowball effect then began after the large mechanical nature of the rebalancing. By 4:15 pm, near the close of the futures market in Chicago, the prices of the VIX futures had spiked.

Drastic market movements are, by their very nature, extremely rare. A sharp downward spiral can sometimes have a computer protocol kick in and temporarily halt trading in order to prevent an all-out market panic. The VIX Futures Index, as per its provider S&P Dow Jones Indices LLC (SEC v.S&P Dow Jones Indices LLC 2021), used a software that paused real-time updates in the event that the index moves by more than a pre-specified amount. The reasoning behind such a mechanism is obvious: if an index moves more than deemed ‘normal’, a human will need to intervene to ensure the price swing is not a computational mistake. It can be understood as a quality-control measure. On the day of 5 February 2018, prices of the underlying VIX futures fluctuated, and the index with it. Throughout the trading day there was no halting measure imposed by the index as there was no freakish market move. After market hours, however, between 4:00 pm and 5:08 pm, the VIX Futures Index told a different story (Levine 2018).

At 4:08 pm, in the span of one minute, 115,862 VIX futures contracts (or about 25% of the entire market) were transacted (Sushko and Turner 2018). A minute later, at 4:09 pm ET, the computer system stopped updating the S&P 500 VIX Short-Term Futures Index. For the next three minutes, the last reported value of 86 continued to be disseminated. At 4:12 pm ET, the index was updated in real time but froze again at 87 from 4:13–4:35 pm.

In this 22-minute interval, XIV’s published intraday indicative value14 was fixed at approximately USD 25 per share. This was not its true indicative value because the underlying index failed to update real-time changes in the VIX futures market. Investors were fooled into believing that the XIV had weathered the volatility storm on that day. From 4:35–5:08 pm ET, the XIV was sporadically updated with values between USD 24 and USD 27 per share. At 5:09 pm, XIV’s closing indicative value was finally published. It was a meagre USD $4.22$ per share, marking a 95% decline from its open on the day. Between 4:09 pm and 5:09 pm, USD 700 million in XIV shares were traded on the secondary market in the after-hours session. Buyers overpaid dramatically during this hour (Levine 2021). While VIX futures doubled and wiped out the value of XIV, investors of the note were completely oblivious.

The story of XIV’s issuer during Volmageddon was not as tragic. After the VIX’s unprecedented increase during the day, XIV’s issuer scrambled to align their hedged positions with their ETP’s net asset value by buying VIX futures at the day’s close. Naturally, this inadvertently pushed up the price of futures, further decreasing their net asset values and forcing them to buy even more futures. In the most extreme case, the issuer would have mechanically rebalanced their hedge until their wealth hits zero. Fortunately, there is some legal leeway buried in their prospectus where it is stated that they can redeem shares (essentially returning capital to the investors and exiting the market) in the event that the underlying short-term VIX futures index moves by more than 80% in a single day (XIV Prospectus 2018). On 21 February 2018, Credit Suisse announced the termination event and redeemed notes at USD 5.99 each (Stempel 2021). Since they earn fees from managing the product on behalf of investors, issuers did not have much to complain about: they simply promised to track the underlying index, be it broken or not.

This misinformation about XIV’s indicative value was an unintended consequence of the so-called ‘Auto Hold’ feature embedded in the S&P 500 Short-Term VIX Futures Index. The irregular pauses in the dissemination of real-time information caused substantial damage. Unfortunately, the index provider failed to disclose the existence of such a feature when it licensed the index to issuers. In May 2021, three years later, S&P Dow Jones Indices LLC agreed on a USD 9 million settlement with the U.S. Securities and Exchange Commission, see SEC v.S&P Dow Jones Indices LLC (2021).

What is clear is that trading VIX futures for hedging purposes can break the VIX Futures Index and ultimately affect the VIX note, which relies on the index to calculate its fair value. Additionally, hedging via VIX futures will always go against the performance of these notes. It is no surprise that investors who lost their shirts in February 2018 went on to accuse Credit Suisse of market manipulation. Although the initial class action lawsuit was dismissed, the appeal against that decision was successful (Stempel 2021). According to the case brought to the U.S. Court of Appeals for the Second Circuit (Chahal v. Credit Suisse Group AG 2021), the claimants say they lost USD 1.8 billion while the issuer made a profit of USD 475 million.

3.3. Vol ‘Til You Bawl

Three years after the delisting of XIV, in October 2021, Dynamic Shares Trust was given permission by the SEC to list the Dynamic Short Short-Term Volatility Futures ETF (WEIX). Its promise is the exact same as that of the demised XIV, to provide investors with the inverse daily returns of the S&P 500 VIX Short-Term Futures Index. However, Dynamic Shares Trust assured investors that this product is actively managed to “provide better risk management than passively managed short VIX short-term futures ETFs” (WEIX Prospectus 2022). In particular, WEIX will calculate its closing indicative value by using a time-weighted average price of 15 min to 4:00 pm ET rather than the futures settlement price, which is determined 2 min to close. This broader rebalancing period is a safety measure applied to prevent a spike (once again) in the VIX futures prices near closing (Peterseil and Greifeld 2021).

It is difficult to say with certainty whether the new rebalancing method will prove to be an effective solution. Most forms of rebalancing, i.e., periodically rolling over contracts, are inherently price-insensitive, the buying and selling is carried out without any heed to the asset’s price. If these mechanical trades are large enough, they will rapidly tear apart the very fabric of the underlying market, such as on 5 February 2018 and 19 October 1987.

We invite the reader to also look at the events during the week that ended on Friday, 20 March 2020, when the U.S. stock market found its floor. We postulate that a similar mechanical hedge rebalancing, this time performed by SPX options dealers, could have been the reason for the stock market drop. The so-called ‘Gamma Hedging’ is claimed to sway the S&P 500 index even to this day (Wang 2022). In options-speak, gamma measures how the delta of an option changes as the price of the underlying changes; in theory, a gamma hedge protects the investor from all of the underlying’s price changes. An SPX options dealer, as a market maker, avoids directional exposure associated with the trade by hedging with respect to an option’s gamma. This sounds awfully price-insensitive.

Table 1. Mechanical Hedge Rebalancing—VIX ETP Issuers and SPX Options Dealers.

	VIX ETP Issuers	SPX Options Dealers
Price-Insensitive Hedge	✓	✓
Buy into Rise, Sell into Decline	✓	✓ (Short Gamma)
Rebalancing Period	End of Trading Day	Third Friday of the Month
Day of Major Event	5 February 2018	20 March 2020

illustrates all of the similar hedging strategies deployed by VIX ETP issuers and SPX options dealers.

Roughly USD 3.2 trillion options, of which USD 1.7 trillion were SPX options, expired on the third Friday of September 2022. The monthly options expiration (OpEx) forces holders to either mechanically roll over existing positions or open new ones. In recent years, OpEx has become an important market phenomenon for market players (of all sizes) to try and trade around (Wang 2022). It is unclear if the tail will wag the underlying dog, again; nevertheless, it is clear that the more things change in the financial markets, the more things seem to stay the same.

4. Conclusions

This survey paper threw light on the Volatility Complex and presented the ill-famed Volmageddon as an instructive case study for investors. We described the calculation methodology of the CBOE VIX and the pricing techniques applied to the index’s higher order derivatives. We explained the reasoning behind the post-2008 strategy of harvesting the volatility risk premium via VIX futures and ETPs.

Our analysis sought to reveal the pernicious impact that price-insensitive hedge rebalancing by major market participants can have on the market microstructure. We posited that systematic gamma hedging by options dealers may have created a similar negative feedback loop that resulted in the market bottom on the third Friday of March 2020. We hope our intuitive analysis of the SPX options market promotes future research in this area.