Abstract
In recent multi-population stochastic mortality models, one critical scientific issue is the vague distinction between trend risk and population basis risk. In particular, the cross- and auto-correlations between the innovations of the latent factors representing the common trend and the population-specific trends are often assumed to be non-existent, although they are possibly statistically significant. While it is theoretically possible to capture such correlations by treating the latent factors as a vector time series, the resulting model would contain a large number of parameters, which may in turn lead to robustness problems. In this paper, we address these issues by the use of the product–ratio model. Contrary to the prevalent assumption of non-existent correlations, the latent factors under the product–ratio model are approximately uncorrelated. This permits us to disentangle trend risk and population basis risk, thereby sparing us from the need to use a heavily parameterized vector time-series process. Compared to the augmented common factor model, our approach demonstrates improved robustness in terms of correlation structures and hedging performance, offering a new perspective on treating cross- and auto-correlations between latent factors in mortality modeling.
1. Introduction
Recent advancements in public health and medical systems have significantly improved human mortality rates. For instance, the life expectancy at birth in the U.S. has increased dramatically from 60.91 in 1935 to 78.70 in 2010, a 30% increase over 75 years1. This pattern is also observed in other developed countries such as Canada. However, this remarkable progress in longevity is sometimes viewed as a social or economic burden. This is because the increased life expectancy substantially extends the duration of pension payments, posing a financial risk to insurance companies and pension plan providers. In actuarial studies, this is referred to as mortality risk (or longevity risk), which is the risk that insurance companies face financial strain due to policyholders living longer than expected.
Mortality risk is generally categorized into two types: trend risk and idiosyncratic risk. Idiosyncratic risk refers to the uncertainty associated with the realized death probability. This risk can be mitigated effectively by increasing the population base, thanks to the law of large numbers. Trend risk, however, is associated with the uncertainty in the increasing trends of life expectancy. It is a systematic risk that affects everyone and cannot be reduced simply by expanding the population base.
In longevity research, various stochastic mortality models have been developed to address mortality trend risk. The Lee–Carter model (), for example, decomposes log-central death rates into an age-period structure. The period effects, which reflect the dynamics of mortality over time, are modeled as a time series (typically random walk) to forecast future mortality, capturing trend risk. The CBD model () focuses on modeling death probability, with its decomposition including two period effects modeled as a bi-variate random walk, thus addressing mortality trend risk. Some researchers have extended these models to include cohort effects, assuming that mortality trend risk also exists along the year-of-birth direction. Notable models in this category include the Renshaw–Haberman model (), models M6/M7/M8 (), and the Plat model (). More recently, the Heat-Wave model () was proposed, differentiating short-term and long-term mortality improvements in its assessment of trend risk.
To manage emerging mortality risks, many pension providers use insurance-based solutions like buy-ins/buy-outs and longevity swaps. However, as some studies suggest (e.g., () and ()), the insurance industry can only absorb a limited portion of longevity risk, highlighting the need to find additional participants, such as capital market investors. In standardized index-based mortality derivatives, the payouts are linked to standardized mortality indexes. These financial products appeal to a broader range of participants because of their cost efficiency, high liquidity, and the way they mitigate concerns about information asymmetry. However, the use of standardized index-based mortality derivatives introduces population basis risk, stemming from the mismatch between the population tied to the liability and the one linked to the hedging instrument. Traditional mortality models, which typically focus on single populations, do not account for this risk.
To address population basis risk, various multi-population extensions to traditional mortality models have been proposed. For example, based on the Lee–Carter modeling framework, () proposed the augmented common factor model (ACF model), which assumes the existence of a common factor governing the mortality co-movement of all the underlying populations. Any deviations from the common trend are then absorbed by the population-specific factors. The ACF structure is then applied by () to model cause-of-death mortality data. () considered a three-way Lee-Carter model which incorporates the population effects in addition to the age and period effects in the original Lee-Carter model. This modeling approach is later generalized by () via the use of Tucker decomposition. Based on the CBD framework, () proposed a mortality model designed for two populations of similar size. (), on the other hand, developed a gravity model for populations with imbalance size. Notably, under the gravity model, the population with a bigger size is the main driving force while the population with a smaller size is orbiting the other population, similar to being attracted by gravity. (, ) considered a multi-population model where the underlying period effects from different populations are assumed to follow the vector auto-regressive (VAR) model and the vector error correction (VECM) model. Furthermore, () used a factor copula approach to capture mortality dependence among different populations. () combined Bühlmann credibility with a multi-population mortality model and proposed a new modeling method called the multi-dimensional Bühlmann credibility approach.
In most existing multi-population models, the distinction between trend risk and population basis risk is vague. In particular, the cross- and auto-correlations between the innovations of the latent factors representing the common trend and the population specific trends are often assumed to be non-existent, although they are possibly statistically significant. While it is theoretically possible to capture such correlations by treating the latent factors as a vector time series, the resulting model would contain a large number of parameters, which may in turn lead to robustness problems.
In this paper, we address the issue by the use of the product–ratio model (PR model) developed by (). The PR model includes a product model that uses the geometric mean of sub-populations to capture the overall mortality trend, and a ratio model that specifically models deviations between sub-populations. Our paper contributes to the literature in the following aspects. First, we specifically target the cross- and/or auto-correlation of latent factors, which is assumed to be non-existent and not studied extensively in the previous literature. Second, we utilize the property of the PR model that the latent factors are approximately uncorrelated and provides a new perspective on the disentangling of trend risk and population basis risk. Third, via the numerical comparison between the ACF model and the PR model, we found that the approach we consider yields term structures of correlations and hedging performances that are more robust with respect to how cross- and auto-correlations between the latent factors are treated.
The remainder of the paper is organized as follows. Section 2 describes the multi-population mortality models considered in this paper. Specifically, we consider the augmented common factor model and the product–ratio model. Section 3 provides the estimation results of the models and conducts the numerical analysis on various time series structures for the assumed models. Section 4 studies the hedge performance of the assumed models. And finally, Section 5 concludes the paper.
2. Mortality Models for Multiple Populations
2.1. Augmented Common Factor Model
We first present the augmented common factor model (the ACF model) developed by (), which can be used to model mortality rates for multiple populations. The ACF model extends the Lee–Carter model () to include a common factor that describes the mortality trend shared by all populations, and a population-specific factor which accommodate any population-specific deviation from the common trend. The ACF model with two populations is defined as follow:
where represents the central death rate for individuals at age x in year t from population i. Parameters , , and , are the age-specific parameters, with representing the level of (log-)mortality at age x from population i, and capturing the sensitivity of mortality rate to changes in the common trend and population-specific deviation. Parameter represents the co-movement of mortality shared by all populations and would generally be modeled by a random walk. Parameters and are population-specific deviations from the common trend, which would be modeled by some mean-reverting processes.
We assume the error terms in Equation (1) are normally distributed, that is, . The parameter estimation of the ACF model is then achieved through maximum likelihood estimation (MLE). We assume and to ensure the uniqueness of parameter estimation ().
After obtaining the MLE estimates, the sequences of , , and would be fitted to some time-series for the purpose of mortality forecast. Based on the same MLE estimates, we consider three time-series structures, denoted by the ACF0 model, ACF1 model, and ACF2 model, respectively. The definition of these three variants are summarized below:
- ACF0 Model:In the ACF0 model, we assume the three mortality indices , , and are independent. Under this assumption, , , and can be modeled by the following expression:whereThere are eight parameters in this model, which include , and .
- ACF1 Model:The ACF1 model extends the ACF0 model to incorporate the correlations between different sequences. As a result, the Q matrix is no longer diagonal and we haveComparing to the ACF0 model, the number of unknown parameters increase from eight to eleven due to the addition of off-diagonal covariance parameters , , and .
- ACF2 Model:In the ACF2 model, we consider a more complicated autoregressive structure, the vector autoregressive (VAR) structure, for , , and sequences. We consider the simplest lag-1 vector autoregression model, the VAR(1) model, which can be expressed as follow:whereIn this model, a fully vectorized autoregressive structure is used. Even in the simplest case, the VAR(1) structure, the number of unknown parameters increase to eighteen. For a more complicated autoregressive VAR(p) () structure, the number of unknown parameters would be .
2.2. Product–Ratio Model
In the traditional modeling approach, the number of unknown parameters increases dramatically when we additionally consider cross- and auto-correlations between the innovations of the common trend and the population specific trends. To overcome this over-parameterization problem, we consider the product–ratio model (the PR model) by (), under which the innovations are uncorrelated by construction. The PR model includes two parts, the product model and the ratio model, which are defined as follow:
- The product model is defined bywhere is the square root of the product of and , is the average level at age x for the product model, m is the number of components being considered, is the error.In the product model, the quantity log() captures the average of (log-) mortality rates under different populations. The product of and is then used to reflect the evolution of (average) mortality at age x.
- The ratio model is defined bywhere is the square root of the ratio of and , is the average level at age x for the ratio model, n is the number of components being considered, is the error.In the ratio model, the quantity log() captures the deviation between the two populations. The product of and is then used to reflect the evolution of such deviation at age x.
The parameter estimation of the PR model is achieved through the demography package () in R. We specify and such that the PR model is comparable to the ACF model defined in the previous section. The notation of and in the product model can be simplified to and , respectively.
The PR model does not directly model the log-central death rate. Instead, using Equations (2) and (3), the expression of the (log-) central death rates under the PR model can be computed via:
Similar to the ACF model, the sequences of , , and would be fitted to some time-series for the purpose of forecasting future mortality rates. We consider three variants of the PR model that are the same as those described in Section 2.1.
3. Numerical Analysis
3.1. Data
For illustration purpose, we consider U.S. males and Canadian males with age range between 20 and 100, and a sample period from 1950 to 20192. We obtain the mortality data for these two populations from the Human Mortality Database (HMD). The observations from the most recent years (i.e., year 2020 and year 2021) are excluded from this study to avoid the impact of COVID-19, so that we can be more focused on trend risk and basis risk.
3.2. Parameter Estimation
We fit the ACF model and the PR model to the U.S. and Canadian male populations. The parameter estimates for the ACF model and the PR model are shown in Figure 1 and Figure 2, respectively. The following observations can be made:
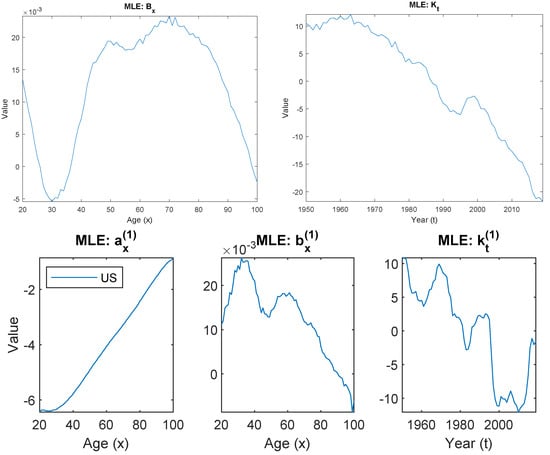
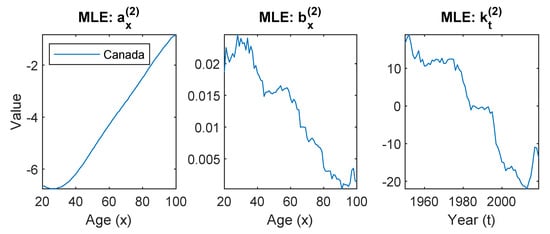
Figure 1.
Parameter estimates of the Augmented Common Factor model fitted to the U.S. and Canadian males with ages from 20 to 100 and years from 1950 to 2019.
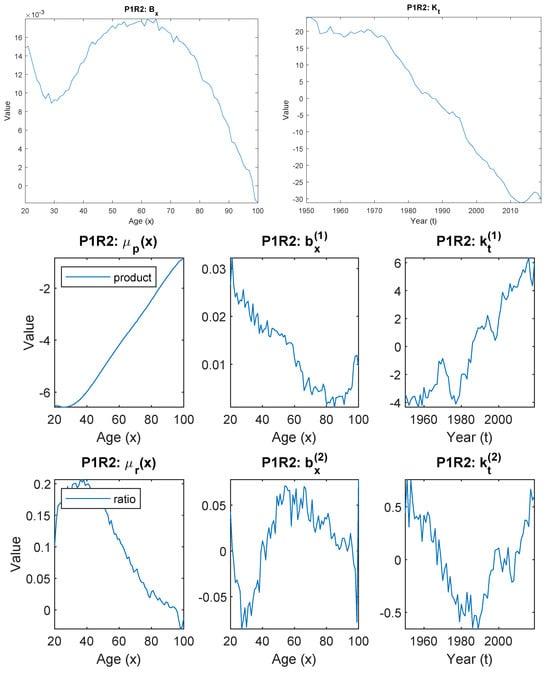
Figure 2.
Parameter estimates of the product–ratio model fitted to the U.S. and Canadian males with ages from 20 to 100 and years from 1950 to 2019.
- The ACF ModelThe ACF model uses the common factor to capture the general mortality trend shared by all populations, and the population-specific factor to capture any deviation from the common trend. The estimated values of are therefore representing the co-movement of the mortality dynamic shared by the two countries, and representing the common age sensitivity to such co-movement.For the U.S. and Canada, although they are not identical, these two countries do share a great amount of similarities in economy, culture, living style, and healthcare system. As a result, the estimated levels as well as the population-specific factors and from the two countries are quite similar to each other, causing a vague distinction between trend risk and basis risk.
- The PR ModelThe PR model, on the other hand, decomposes trend risk and population basis risk by construction, meaning that these two risks are separated in the first place when the product model and ratio model are defined. As a result, the product model would be solely focusing on trend risk while the ratio model is solely focusing on basis risk, respectively, leading to a clear distinction between the two.
- –
- In the product model, the estimated represents the mean level of the general trend. It carries very similar shape to both of and in the ACF model. The estimated carries similar downward pattern as that in the ACF model, representing general mortality improvement overtime. For the estimated , it presents similar peak (around age 70) and trough (around age 30) to those shown in the ACF model, with different magnitudes.
- –
- In the ratio model, the estimated describes the difference in the mean level between the two populations. It can be easily observed in the pattern of that the biggest difference between the two populations lies in the working age males (from 25 to 65). The gap closes out quickly toward older ages.Besides the difference in the mean level, the ratio model further decomposes the difference between the U.S. and Canada into two components, and . The upward pattern of suggests that the differences between the two countries are getting bigger over time, and the pattern of shows such a gap is more significant in young adults around age 20. The remaining residuals not explained through the first component are then captured by the second component .
3.3. The Time-Series Process
Once we obtain the estimates of , , and , we will fit these sequences to the VAR time series models as described in Section 2. In this subsection, we first explore the sample cross-correlation matrix (SCCM) of the time series sequences. We then present the model selection result for the three time series structures described in Section 2. Finally, we analyze the term structure of the death probability under different time series structures.
3.3.1. Sample Cross-Correlation Matrix
The sample cross-correlation matrix (SCCM) is typically used to measure the strength of linear dependence between time series. Considering the multivariate sequence () obtained in ACF model and PR model, we present the values of SCCM in Table 1. For the reader’s convenience, we also include the simplified SCCM in this table.

Table 1.
Sample cross-correlation matrix of the estimated sequence of () under the ACF model and the PR model. The symbol “.” means insignificance (at significance level), “+” means positive significance.
By comparing the results between the ACF model and the PR model, the following observations can be made. First, for the ACF model, some off-diagonal components are statistically significant. This finding highlights the existence of cross-correlations between different latent states in the ACF model.
On the other hand, for the PR model, all the off-diagonal components from lag 0 to lag 5 are insignificant. These insignificant values serve as the advantageous outcome of the PR model, since it is more capable of removing the cross-correlation among different latent states. With this advantage, a time series model with simpler structure could be used under the PR model.
The differing cross-correlations observed in the two models primarily stem from the different response variables they use. In the ACF model, the response variables are set to be the log mortality rates from sub-populations, which are highly correlated. On the other hand, the PR model operates differently: its product model uses the square root of the geometric mean to capture the joint movement of multiple populations, while its ratio model employs the square root of the ratio between two populations to capture their divergence. () demonstrated that these response variables in the PR model are largely uncorrelated, particularly when the variances among the sub-populations are relatively similar.
A final observation lies in the significant SCCM in the diagonal components of from lag 1 to 5. It suggests that , are serially correlated with their previous values, and, as such an auto-regressive structure is needed for each of and .
3.3.2. AICs and Likelihood Ratio Test
In this section, we compare the fitting performance of the time series models within each of the ACF modeling framework and the PR modeling framework. Since the two sets of model variants, (ACF0, ACF1, and ACF2) and (PR0, PR1, and PR2), are both nested models, we use the Akaike information criterion (AIC) to compare the fitting of different model variants. The value of AIC is computed as follow:
where is the maximized log-likelihood and is the number of unknown parameters in the model. The term can be viewed as a penalty term penalizing for the complexity of the model. Therefore, AIC can be viewed as a trade-off between the fitting performance and the model complexity. According to its definition, a model with a smaller value of AIC is preferred. In the following, we use restricted model to refer to a model with simpler model structure, and unrestricted model to a model with more complex structure within the nested models.
Table 2 shows the values of AIC for different time series models within the ACF framework (left panel) and within the PR framework (right panel). Let us first consider the results within the ACF framework. By comparing the pairs of “ACF0 vs. ACF1”, “ACF0 vs. ACF2”, “ACF1 vs. ACF2”, we can find that a more complicated model is always resulting in a greater value of , the maximized log-likelihood. This result is expected since these are all nested models where the restricted model is always a special case of an unrestricted model. More importantly, if we compare the AIC values, the unrestricted models are always preferred since they have smaller AIC values. It suggests that, under the ACF model framework, the restricted model does not provide adequate fit to the data, partly due to the significant cross-correlation among different latent states as presented in previous section.

Table 2.
The log-likelihood and AIC for different model variants.
Next we focus on the results for the PR framework. The same observation can be made regarding the value of when we compare the three pairs of “PR0 vs. PR1”, “PR0 vs. PR2”, “PR1 vs. PR2”. However, regarding the value of AIC, a conclusion opposite to that for the ACF framework will be drawn, since the restricted models are always having smaller AIC values. It matches the result represented in previous section where the cross-correlation coefficients are insignificant for the PR framework. It can be viewed as the main advantage of the PR model under which by construction separates the co-movement from the deviation of the two populations, and therefore disentangling trend risk and basis risk. Finally, it should be noted that the results between the two modeling framework are not directly comparable, since they are based on different estimated values of ().
Besides the comparison of the AIC values, we have also considered likelihood ratio (LR) tests to compare the goodness-of-fit of these nested models. The null hypothesis and alternative hypothesis of a LR test is summarized as follow:
The result of the LR test is summarized in Table 3. If p-value is less than 5%, it means the null is rejected and the unrestricted model is preferred, and vice versa. The same conclusion can be drawn; that is, among the ACF framework, the unrestricted model is preferred, due to the fact that the restricted model fails to adequately capture the cross-correlation among different latent states. On the other hand, among the PR model, the restricted model is preferred since the PR model by construction has separated common-factor from the population-specific deviation.

Table 3.
Likelihood ratio test result for the three variants of the ACF model and the PR model.
3.3.3. Term Structure of Correlation
Finally, we present the term structure of correlation between and , the death probabilities calculated for the two populations. Following (), the term structure of correlation is defined to be , for . For illustration, we select , and provide the term structure of correlation between and over the period of 2020 to 2069 (that is, a 50-year forecast window) in Figure 3. We assume constant force of mortality, so and is linked through the following equation:
The key findings are summarized into four aspects.
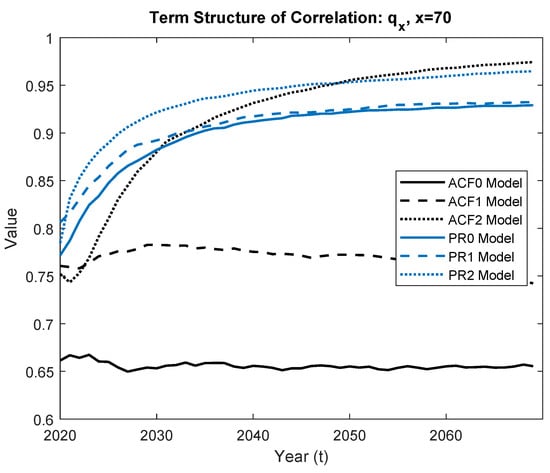
Figure 3.
The term structure of correlation between and , .
- ACF0 vs. ACF1Let us first focus on ACF0 model and ACF1 model. For these models, the only difference is the specification of Q matrix. To be more specific, In ACF0, the off-diagonal elements of Q matrix are zeros, while in ACF1, those elements are all non-zeros. The term structures of correlation under ACF0 and ACF1 have similar shape. However, a 10% increase is observed when the model does incorporate the off-diagonal covariance elements.
- ACF2 vs. ACF1 or ACF0The mortality indices in the ACF2 model follows a VAR(1) model where additional parameters are used to capture the cross-correlation among different period effects. Comparing to ACF1 and ACF0, a dramatic change of shape (the black dotted line) is observed for the ACF2, reflecting those additional interactions.
- PR0 vs. PR1 vs. PR2Within the PR framework, the resulting term structures of correlation from the three models carry two features. The first feature is related to the magnitudes of the lines, with the values being greater for more complex models. The second feature is related to the shape of the lines, where all three lines yield very similar patterns. This finding is consistent with the observations we made in Section 3.3.1 and Section 3.3.2. It also justifies the argument made by () that the latent factors are uncorrelated in the PR model.
- PR vs. ACFSince the two models have different model specification, the shape of the curve may not be the same. For the PR model, the three variants yield similar term structure of correlations, while for the ACF model, the ACF0 variant and ACF1 variant have omitted the cross-correlation between different latent states, and thereby not adequately fitting the data and leading to the worst term structure of correlations. When the full VAR structure is used in the ACF2 variant, its term structure of correlation would be similar to those in the PR framework.
4. Hedge Performance
In this section, we apply the ACF models and the PR models to longevity hedges and study their hedge performances.
4.1. Basic Set Up
We first describe the set up of the hedge. Suppose it is now time (the end of year ). We assume the hedger has a longevity liability that is a life annuity that pays USD 1at the end of each year, provided that the annuitant is alive. Let denotes the value of a life annuity sold to individuals aged x at time t. We consider a deferred life annuity that sold to age in years. The liability being hedged is , which can be expressed as
where w is the maximum age, r is the interest rate and is the underlying population of the liability.
The hedging instrument is a q-forward, which is a zero-coupon swap with the fix leg attached to the forward mortality rate determined at the beginning of the contract, and the floating leg being the realized mortality rate at maturity. We use to represent the value of a q-forward which is linked to reference age x and maturity time t. For simplicity, we assume only one q-forward is used in the hedge. The q-forward being used is denoted by , which has a reference age and maturity years from now. The value of can be expressed as
We assume the hedger’s goal is to minimize volatility of their longevity exposure over the long run. The hedging target is set to be
where N is the notional amount or the hedge ratio of the portfolio, and are the values of the liability and the q-forward at time . We obtain both and through simulation with detailed procedure provided in Appendix B. The hedge ratio N is obtained by matching the sensitivity of and with respect to , i.e., . The procedure for calculating and is provided in Appendix A. The effectiveness of the hedge is measured by , which is computed via the following equation
4.2. Illustration of Hedge Performance
To illustrate the hedge result, we consider the following set up for the liability and the q-forward.
- The liability is a life annuity sold to individuals aged 70 () 20 years from now (). The liability is linked to population 1, the U.S. males. The maximum age is set to be .
- The q-forward has a reference age of 65 () and will matures 20 years from now (). The q-forward is linked to population 2, the Canadian males.
- The interest rate is assumed to be 1% per annum.
To assess the impact of different VAR structures, we allow the simulation model (that is, the model used to generate the future mortality sample paths) to be different from the model used for hedge calibration. The values of hedge effectiveness and the associated notional amounts of the hedging instrument are provided in Table 4 and Table 5, respectively. In these two tables, each column corresponds to a particular simulation model and each row corresponds to a particular calibration model. For example, for the column of ACF0 and the row of ACF1, we use ACF0 to simulate and . We use ACF1 to derive the hedge ratio N. The values in the cell are the corresponding and N.

Table 4.
The value of hedging effectiveness (HE) in the longevity hedge under the ACF framework (left panel) and the PR framework (right panel), using different combinations of simulation model and hedge calibration model.

Table 5.
The notional amounts of q-forward in the longevity hedge under the ACF framework (left panel) and the PR framework (right panel), using different combinations of simulation model and hedge calibration model.
For the ACF framework, the hedge effectiveness is highly dependent on the model used for simulating the underlying mortality experience. The resulting HE ranges from 47.1669% to 77.8786%, with a maximum difference being as large as 30%. This reveals the model risk embedded in the ACF framework. When the time series model is not specified properly, the outcome of the hedge would also suffer. However, in practice, the hedger is always subject to model uncertainty, since the true underlying mortality model is unknown.
The PR framework, on the other hand, yields more robust result in hedging. Considering different combinations of simulation model and calibration model, very little change is observed in the resulting HE, where its value ranges from 68.1193% and 73.0943% with maximum difference of 4.9750% which is way smaller than that in the ACF framework.
5. Conclusions
In this paper, we apply the PR model developed by () to the U.S. male population and Canadian male population, with a goal of studying its performance in disentangling mortality trend risk and population basis risk. Under the PR model, the trend risk and basis risk are separated by construction when the product model and the ratio model are specified. Based on the U.S. and Canada’s data, we found that the cross-correlations of different latent states under the PR model are insignificant and the resulting time series structure is more parsimonious. This finding is in great contrast to the result obtained under the ACF framework, where cross-correlations are presented and the associated time series structure is heavily parameterized. We then apply both models to a longevity hedge. The hedge performance as well as the notional amounts of the hedging instruments under the PR framework are more robust.
In this paper, we only consider two populations. For future research, we may extend the PR model to more than two populations. The extension is not trivial. Based on the current structure, the ratio model which focus on capturing deviations among different populations need to be extended to accommodate any pair-wise combinations. If we have a large population size, say 10 populations, the equations required in the ratio model would be increase significantly to , which is way more than the number of equations required in the traditional ACF model. As a final item of note, when applying the PR model, we should always consider populations similar mortality experience. As pointed out by (), the geometric mean and the ratio of the two populations are roughly uncorrelated when they share a similar mortality experience, which advocates the use of the PR model in this case. Extra caution should be taken when dealing with populations that have significantly different mortality experiences.
Author Contributions
Conceptualization, J.S.-H.L.; Methodology, Y.L. and J.S.-H.L.; Validation, Y.L.; Formal analysis, Y.L. and J.S.-H.L.; Investigation, Y.L.; Writing—original draft, Y.L. and J.S.-H.L.; Writing—review & editing, J.S.-H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.mortality.org accessed on 1 September 2023.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Partial Derivatives of Liability and Hedging Instrument
Appendix A.1. The ACF Model:
Liability:
At time , we project the life table and we have
The partial derivatives w.r.t. and can then be computed as follows:
where
and
Q-forward:
The partial derivatives of w.r.t. and can be computed as follows:
Appendix A.2. The PR Model:
Liability:
Since that in the PR model, we have
Therefore, if is selected to be population 1, the value of can be computed as
Similarly, if is selected to be population 2, we have
In the following derivation, we assume is population 1 and is population 2. It can be easily modified to adapt different situations.
At time , we project the life table. This is denoted by
We have
The partial derivatives with respect to , and can then be computed as follows:
where
and
Q-forward:
As previously mentioned, we assume to be population 2. Therefore, can be computed as
The partial derivatives of with respect to and can be computed as follows:
Appendix B. Simulation Procedure
The simulation procedure of the value of the liability being hedged is summarized as follows:
- Simulate M sample paths of and . We denote these simulated paths as , for . Accordingly, for each simulated path , the values of the corresponding state variables are and .
- For each simulated path , , we project the life table at time , based on the simulated and . The methodology of how we project the life table is summarized as follows:
- 1.
- Based on and , we first compute the central death rate of an individual aged x, :
- –
- ACF Model
- –
- PR Model
- 2.
- Then we compute the death probability , based on the value of . Throughout this study, we assume constant force of mortality. Therefore, can be computed through the following equation:and accordingly
- 3.
- We use to denote the probability that an individual aged x at time survives to age , for a particular path . The survival probability is computed as
- For each projected life table, we calculate the value of the life annuity , which is
Similarly, the value of the q-forward is
where
and is the pre-defined forward mortality rate at time .
Notes
| 1 | Data source: Human Mortality Database (HMD). |
| 2 | For an expanded data set, the same MLE method can be used. |
References
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, and Marwa Khalaf-Allah. 2011. Bayesian stochastic mortality modelling for two populations. ASTIN Bulletin: The Journal of the IAA 41: 29–59. [Google Scholar]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from england and wales and the united states. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., Malene Kallestrup Lamb, Carsten Rosenskjold, David P. Blake, and Kevin Dowd. 2019. Modelling Socio-Economic Differences in the Mortality of Danish Males Using a New Affluence Index. London: Pensions Institute, Cass Business School, City University London. [Google Scholar]
- Chen, Hua, Richard MacMinn, and Tao Sun. 2015. Multi-population mortality models: A factor copula approach. Insurance: Mathematics and Economics 63: 135–46. [Google Scholar] [CrossRef]
- Dong, Yumo, Fei Huang, Honglin Yu, and Steven Haberman. 2020. Multi-population mortality forecasting using tensor decomposition. Scandinavian Actuarial Journal 8: 754–75. [Google Scholar] [CrossRef]
- Dowd, Kevin, Andrew J. G. Cairns, David Blake, Guy D. Coughlan, and Marwa Khalaf-Allah. 2011. A gravity model of mortality rates for two related populations. North American Actuarial Journal 15: 334–56. [Google Scholar] [CrossRef]
- Graziani, George. 2014. Longevity risk—A fine balance. Journal of Retirement 1: 35–37. [Google Scholar]
- Hunt, Andrew, and David Blake. 2020. Identifiability in age/period mortality models. Annals of Actuarial Science 14: 461–99. [Google Scholar] [CrossRef]
- Hyndman, Rob. 2023. Demography: Forecasting Mortality, Fertility, Migration and Population Data. R Package Version 2.0. Available online: https://CRAN.R-project.org/package=demography (accessed on 30 September 2023).
- Hyndman, Rob J., Heather Booth, and Farah Yasmeen. 2013. Coherent mortality forecasting: The product-ratio method with functional time series models. Demography 50: 261–83. [Google Scholar] [CrossRef] [PubMed]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting u. s. mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar]
- Li, Johnny Siu-Hang, and Yanxin Liu. 2020. The heat wave model for constructing two-dimensional mortality improvement scales with measures of uncertainty. Insurance: Mathematics and Economics 93: 1–26. [Google Scholar] [CrossRef]
- Li, Nan, and Ronald Lee. 2005. Coherent mortality forecasts for a group of populations: An extension of the lee-carter method. Demography 42: 575–94. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Pintao, Anja De Waegenaere, and Bertrand Melenberg. 2021. A multipopulation approach to forecasting all-cause mortality using cause-of-death mortality data. North American Actuarial Journal 25: S421–56. [Google Scholar] [CrossRef]
- Michaelson, Avery, and Jeff Mulholland. 2014. Strategy for increasing the global capacity for longevity risk transfer: Developing transactions that attract capital markets investors. Journal of Alternative Investment 17: 18–27. [Google Scholar] [CrossRef]
- Plat, Richard. 2009. On stochastic mortality modeling. Insurance: Mathematics and Economics 45: 393–404. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the lee-carter model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
- Russolillo, Maria, Giuseppe Giordano, and Steven Haberman. 2011. Extending the lee–carter model: A three-way decomposition. Scandinavian Actuarial Journal 2011: 96–117. [Google Scholar] [CrossRef]
- Tsai, Cary Chi-Liang, and Ying Zhang. 2019. A multi-dimensional bühlmann credibility approach to modeling multi-population mortality rates. Scandinavian Actuarial Journal 5: 406–31. [Google Scholar] [CrossRef]
- Zhou, Rui, Guangyu Xing, and Min Ji. 2019. Changes of relation in multi-population mortality dependence: An application of threshold vecm. Risks 7: 14. [Google Scholar] [CrossRef]
- Zhou, Rui, Yujiao Wang, Kai Kaufhold, Johnny Siu-Hang Li, and Ken Seng Tan. 2014. Modeling period effects in multi-population mortality models: Applications to solvency ii. North American Actuarial Journal 18: 150–67. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).