1. Introduction
Risk minimization is the underlying principle of portfolio construction. The main themes of portfolio construction in investment are asset allocation and portfolio selection. As the portfolio consists of more than one asset, determining the assets included in the portfolio is crucial. To minimize portfolio risk, the assets, such as stocks, should be negatively correlated (
Markowitz 1952;
Robiyanto 2018). Notwithstanding the importance of correlation in constructing portfolios, most of the time the retail investors in the Indonesia Stock Exchange do not pay attention to the effect of stock correlation when investing in banking stocks. The existing general assumption explains that state-owned enterprise (SOE) stocks in the banking sector have different characteristics and are unrelated to each other.
In practice, each stock will have different characteristics, although they tend to have the same movement (co-movement) that is due to similar factors influencing them. According to
Bandyopadhyay and Ganguly (
2012), the economic cycle affects the mutual dependence or the same co-movement of firms’ stocks. When a country experiences a recession, it will affect many firms simultaneously. Hence, there is a tendency to include stocks with the same driving factors in the same portfolio. In modern portfolio theory, similar factors are called systematic risk.
In contrast to systematic risk, the unsystematic component of portfolio risk is diversifiable. Thus, it raises the importance of correlation consideration (
Atahau 2014). This study aims to determine the co-movement in question using the OGARCH method. This method can simplify examining the same risk factors on various financial instruments to produce a covariance matrix. The importance of co-movement of banking stocks for investors allows them to choose stocks in their investment portfolio that cannot be combined in one portfolio based on the more straightforward method of the variance-covariance matrix, which is still considered a challenge for capital market players in Indonesia. In addition, it also facilitates the formulation of better investment strategies since it prevents combining stocks with co-movements in a portfolio. Meanwhile, the importance of co-movement of banking stocks for policymakers (especially the State Ministry of State-Owned Enterprises) also provides inputs in formulating policies related to the potential for banks with a systemic impact on the SOEs in the banking sector, especially those related to the co-movement of SOE stocks. Moreover, it serves as a basis for formulating the policies for establishing SOE banking holding.
There have been several studies that empirically examined co-movement. For example, the studies by
Bai (
2011);
Byström (
2004);
Muharam et al. (
2020);
Robiyanto (
2017);
De la Torre Torres (
2013);
Robiyanto et al. (
2017) use the dynamic conditional correlation-GARCH (DCC-GARCH) method to form a portfolio of stocks in Indonesia and Malaysia with gold. The DCC-GARCH can overcome the problem of abnormal data distribution commonly found in the distribution pattern of stock returns on the Indonesian stock market. In stock co-movement research, an OGARCH application is required because in the application of the OGARCH model, linearly observed time-series data can be converted into independent time-series data using PCA (
Luo et al. 2015). In addition, the OGARCH method is a method that can be used to simplify the process of examining the same risk factor on various financial instruments to produce a covariance matrix. However, this method was still relatively rarely used in previous research.
The banking sector is one of the drivers of the Indonesian capital market. The application of multivariate GARCH in the banking sector has been studied by
Elyasiani and Mansur (
2004) in measuring bank stock return sensitivities to long-term and short-term interest rates.
Bandyopadhyay and Ganguly (
2012) reviewed the co-movement study in large corporations and the banking sector and found bank stock portfolio return sensitivities that were due to changes in both long-term and short-term interest rates. Furthermore,
Byström (
2004) examined the co-movement between the Nordic stock markets during the Asian Financial Crisis using the OGARCH method. The results indicated that the OGARCH produced the right degree of co-movement compared to other methods. It means OGARCH can create a positive definite covariance to overcome the estimation problems using different GARCH models. Meanwhile,
Bai (
2011) studied the co-movement of the world’s leading energy sector stocks—such as BP, Chevron, Conoco Phillips, Exxon Mobil, and Shell—using the OGARCH. The author confirmed that it could simplify highly complex calculations and even calculate the volatility and correlation of the stocks studied. In other fields, such as pension funds,
De la Torre Torres (
2013) simplified the investment portfolio calculation using the OGARCH. Furthermore, in the studies using the regional-level stock market,
Robiyanto (
2017) and
Muharam et al. (
2020) used the method previously used by
Byström (
2004). They found that their results supported the research conclusions (
Byström 2004).
By implementing the OGARCH method, this research is expected to produce a more straightforward approach to predicting the SOE stocks’ co-movement in Indonesia’s banking sector since the capital market players are unfamiliar with this method. Instead, they use the heuristic methods such as correlation coefficient in constructing stock portfolios. The objects studied are the state-owned banks because they are the dominant players in the Indonesian banking industry. According to the industry profile report of December 2019, during the 2018–2019 period, banking SOEs accounted for a 43 to 44% market share in terms of total assets compared to all banking industry players in Indonesia. In addition, the method is expected to facilitate the formulation of investment strategies for stocks in the banking sector in Indonesia. The findings of this study are expected to provide valuable input for investors to select appropriate banking stocks to be included in their investment portfolio. Hence, the objectives of this study are to apply the OGARCH method for calculating the variance–covariance matrix to predict the co-movement of stocks of SOEs engaged in the banking sector in Indonesia and to formulate the right investment strategy for the SOE banks in Indonesia. Understanding the co-movement of these stocks helps to understand the types of banking stocks that cannot be combined in one portfolio. As a result, the investors can improve their stock portfolio formulation since an active investment strategy for the stock portfolio of SOEs in the banking sector can be formulated by avoiding the inclusion of stocks with co-movements. For the state-owned regulators, this research is expected to serve as the basis for formulating the policies regarding the establishment of SOE banking holding. This research also provides a novelty in predicting the co-movement of SOE stocks in the banking sector in Indonesia since most researchers still use heuristic measures such as multivariate GARCH, which possess some estimation problems. This research is arranged into five sections: introduction, literature review, methodology (including materials), results (including discussion), and conclusions.
3. Research Methodology
The data used in this study was the daily closing price data of SOE stocks in the banking sector listed on the Indonesia Stock Exchange before the COVID-19 pandemic from 2 January 2013 to 30 December 2019 with 1699 observations. This particular period shows no changes in the number of banking state-owned enterprises. Besides, none of these SOEs held a seasonal equity offering through the right issue, which could affect the theoretical price of the stock to avoid the confounding effect. There are four SOE stocks in the banking sector whose stocks were owned directly by the Government of the Republic of Indonesia. They are BBNI (PT. Bank Negara Indonesia (Persero) Tbk), BBRI (PT. Bank Rakyat Indonesia (Persero) Tbk), BBTN (PT. Bank Tabungan Negara (Persero) Tbk), and BMRI (PT. Bank Mandiri (Persero) Tbk). The data was obtained from both Bloomberg and the Indonesia Stock Exchange.
Before analyzing the data using the OGARCH, the return on the SOE stocks were calculated. The authors refer to
Gitman and Zutter (
2015) in calculating the stock price return. The formula used is as follows:
Most financial modeling researchers agree that the GARCH method is the most widely used and accepted model for time-varying volatility models in finance. The following is a typical GARCH (1,1) model (
Duncan and Liu 2009):
where:
.
Returns are assumed to be dependent on their (zero) mean observation. The (error term) is assumed to be conditioned on previous information () and normally distributed with a zero expected value and conditional variance ().
Apart from GARCH, the OGARCH method would be best applied in a highly correlated series (
Bai 2011). Therefore, a correlation analysis of the SOE stock price return of the banking sector was examined. The OGARCH analysis was done using the Eviews 12 program. The authors employed the OGARCH method since a portfolio analysis requires a calculation of the correlation matrix and covariance between assets involving a more complex calculation as the number of assets increases. In other words, a method can be used to simplify examining the same risk factors on various financial instruments to produce a covariance matrix. It combines principal component analysis (PCA) with the GARCH technique. The PCA is often described as a set of procedures that uses changes in orthogonal variables to simplify important information from a series of highly correlated variables into variables that are not/poorly correlated (
Robiyanto 2017).
Luo et al. (
2015) explained that using the PCA in an OGARCH model, the observed time-series data are linearly transformed into independent time-series data. These new orthogonal variables are then referred to as principal components (PC), and the number of PCs will be less than the number of initial variables (
Bai 2011). Several studies highlighting the superiority of the OGARCH method in comparison to other available methods include (
Alexander 2000,
2001;
Klemm 2013;
Robiyanto 2017;
Bai 2011).
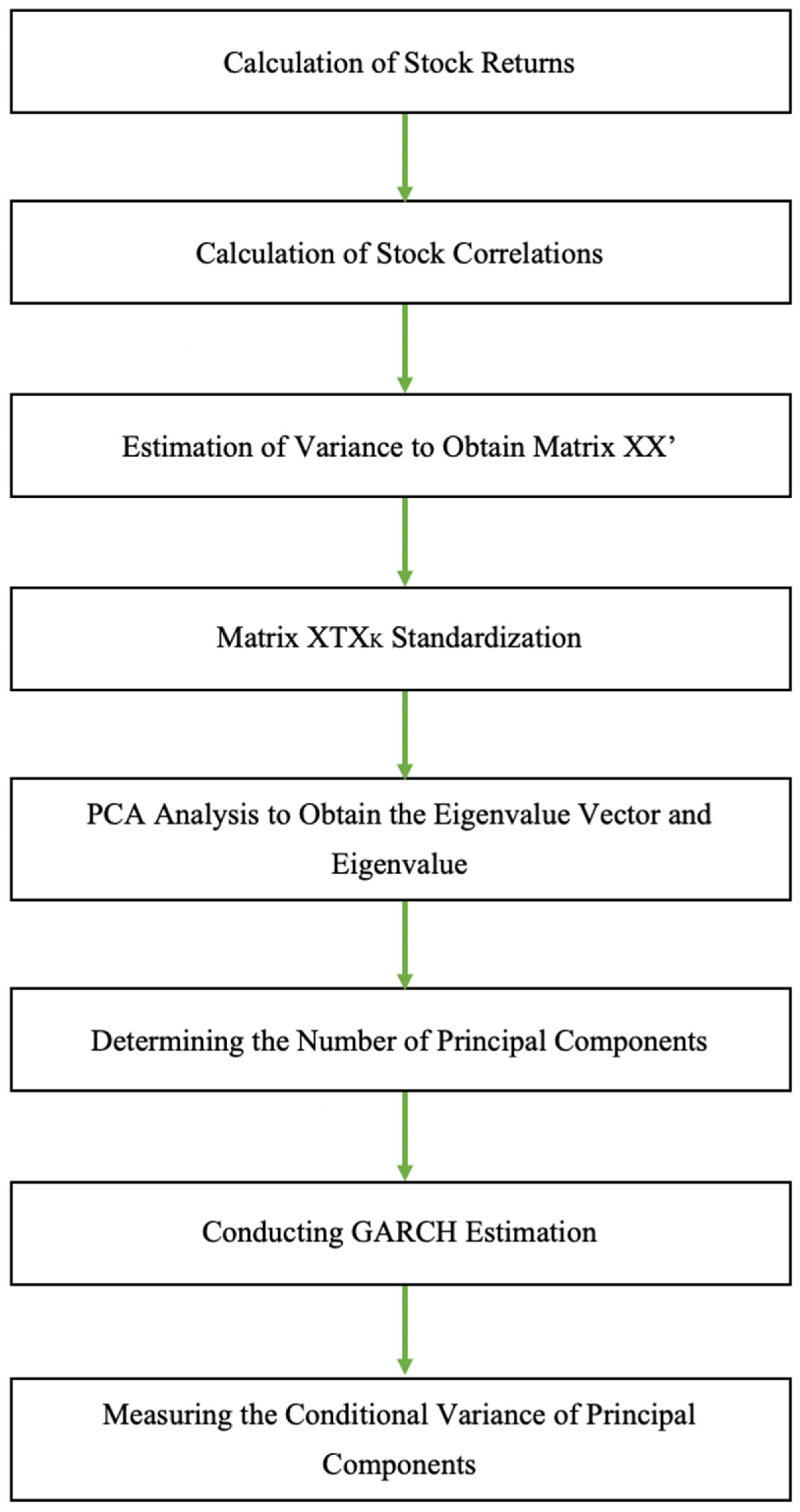
In conducting the estimation using the OGARCH, several steps are conducted. First, a correlation analysis of the SOE stock price return of the banking sector was examined since the OGARCH method would be best applied in a highly correlated series (
Bai 2011). Thus, the data should be standardized into matrix XTX
k, formerly YTX
k (TX
k: daily return k of SOE banking stocks at T day) by estimating the variance averaged for each y
i to obtain matrix XX’. Then, the PCA analysis is conducted based on matrix XX’ to obtain the eigenvalue vector and eigenvalue.
The resulted eigenvalue matrix (denoted by L with m
th refer to its column 1
m = (m
1,m,...,l
k,m), 1 KX eigenvector associated eigenvalue λ
m) is transformed into columns λ
1> λ
2 >...> λ
k. The following step is to determine the number of principal components. When the first principal component has been selected, the resulting m
th principal component is as follows:
From the equation,
xi =
ith column of
Xn column; TX
n matrix is taken out from
X and represents the principal component matrix
P =
XnWn. After employing the PCA, the next step is conducting the GARCH estimation: measuring the conditional variance of the principal components i
th pi, i = 1, N is estimated by GARCH(1,1), and conditional variance matrix of
Xn with the following formulas:
The conditional covariance matrix of X
n is
=
and the conditional variance matrix of Y is
=
, where
=
(
). The amount of components of n chosen to reflect the current system determines the precision of the conditional covariance matrix V
t from the initial return (
Robiyanto 2017). Based on the previous narration regarding steps to estimate co-movement using OGARCH, the research flow diagram below is depicted in
Figure 1. To verify the findings, the authors ran vector autoregression (VAR) on the sample of state-owned banks’ returns. The co-movement exists if the time series involved is bi-directional.
4. Results and Discussion
Table 1 presents the statistic descriptive of all SOE banking stocks in this study: BBNI, BBRI, BBTN, and BMRI.
In
Table 1, BBRI shows the highest average daily stock return (0.0877%) compared to other banking stocks. It might relate to its strong fundamental conditions, as indicated by BBRI being the most SOE banking stocks held by foreign investors. BBRI has the widest outreach, with its coverage scattered all over Indonesia. It focuses on SME lending compared to other SOE banking stocks. In contrast, BBTN has the lowest average daily return (0.0499%) over the research period. It also has the highest deviation (2.35%) compared to other SOE banking stocks. Focusing on mortgage loans differentiates BBTN substantially from other SOE banks. The focus strategy might contribute to its low return and high daily stock fluctuation.
Prior to OGARCH analysis, correlation analysis should be done to measure the correlation between stocks (
Robiyanto 2018) stated that OGARCH will be working appropriately if the data set correlates.
Table 2 presents the correlation analysis of the SOE stock returns of the banking sector listed on the Indonesia Stock Exchange. Overall, the results show a significant correlation. Thus, OGARCH analysis is suitable for the dataset used in this study.
OGARCH analysis combines GARCH and PCA. It also uses the conditional variances of stocks that are then formed into several main principal components (PC). The analysis results using the OGARCH method involving GARCH and PCA analysis for returns of SOE stock in the banking sector indicate that two principal components explain the variance. The details can be seen in the following
Table 3 and
Table 4.
The scree plot in
Figure 2 shows that the first and the second components have eigenvalues of more than one, while the eigenvalues of the third and the fourth components are less than one. Based on the eigenvalue results, only two components are appropriate to be formed. These components are named PC1 and PC2.
Table 4 and
Figure 2 show that the three SOE stocks in the banking sector consisting of BBNI, BBRI, and BMRI can form PC1. The PC1 has an eigenvalue of 2.68 with a proportion of 0.6711, which means that the returns of the three SOE stocks in the banking sector have a co-movement. This first factor can explain 67.11% of the three stocks’ returns variance. The eigenvalue cumulative proportion shown in
Figure 2 depicts this proportion, along with other PCs with a low proportion. It indicates that the three stocks had the same main risk factor and contributed 67.11% to the conditional variance of each stock. Meanwhile, the BBTN stock forms PC2 with a proportion of 15.29%. It indicates that the BBTN stock did not have the same movements and variances as the others.
In addition, the authors verified the findings by conducting robustness testing using vector autoregression (VAR) to reinforce the main estimation of this study. Since the OGARCH model is a member of the multivariate GARCH family, it can handle large covariance matrices and ease the computational burden on the volatility estimates and VAR-type calculations. The results of VAR testing with optimal lag can be seen in
Table 5 below.
When the BBNI(−1) stock return increases on a previous day, the BBRI and BMRI stock returns also rise significantly. Nevertheless, when the BBNI(−2) stock return increased in the last two days, it significantly impacted the BMRI. A similar trend was also found for BBRI and BMRI. When the BBRI(−1) stock return increases on a previous day, it has a positive and significant impact on BMRI. Conversely, when the BBRI(−2) stock return rises in the last two days, it negatively and significantly impacts the BBNI and BMRI. Analogous to the other two banks, when the BMRI(−1) stock return rises on a previous day, it has a positive and significant impact on the BBNI and itself (BMRI). However, when the BMRI(−2) stock return rises in the last two days, it negatively and significantly impacts itself (BMRI). A different effect is found for BBTN. When the BBTN(−1) stock return rises on a previous day, the BBNI, BBTN (itself), and BMRI all suffer. In contrast, when the BBTN(−2) stock return rises in the last two days, it negatively and significantly impacts itself (BBTN).
The authors also ran impulse response functions (IRF) to highlight the VAR test results. In general, the IRF’s results support the main findings. There is a large deviation of stock movement between BBTN and the rest of the state-owned banking stocks. In contrast, only a small deviation pattern of stocks’ movement among the rest of state-owned banking was found during the observation period. It implies that the co-movement of stocks persisted between the BBRI, BMRI, and BBNI, which contradicted the BBTN stock movement during the observation period. The so-called impulse response function (IRF) is one way to investigate a model’s dynamics.
Equation (8) shows how a shock
ϵt =
δ at time
t impacts a system at time
t +
h, assuming no further shocks,
ϵt + h = 0 ∀
h. IRF is considered a practical way of representing the behavior of economic variables (stock returns) in response to shocks to the vector (
δt). An IRF represents the effect of an unanticipated one-unit change in the impulse variable on the response variable over several subsequent periods (typically 10). In the IRFs graph, one impulse is located in each row, and one response variable is positioned in each column. Each graph’s horizontal axis is in the unit of time (daily). In contrast, the vertical axis represents the variable units in the VAR (percentage points). It can be displayed in
Figure 3 and
Figure 4 below.
Figure 3 illustrates the impact of a one-standard-deviation impulse on the BBNI, BBRI, BBTN, and BMRI equation in IRF. Almost one standard deviation shock to BBNI, BBRI, BBTN, and BMRI causes a significant increase and decrease on BBNI, BBRI, BBTN, and BMRI stock return on the 2nd and 3rd day. Unlike the three banking sectors (BBNI, BBRI, and BMRI), one standard deviation shock to BBNI, BBRI, and BMRI resulted in a stable BBTN stock return. Except for one standard deviation shock to BBTN that causes significant decreases on BBTN (itself) on the 2nd and 3rd day.
Figure 4 shows that the shock of BBTN stock has a greater influence than other state-owned banking (BBNI, BBRI, and BMRI) shocks. Overall,
Figure 3 and
Figure 4 (multiple and combined) supported the main findings that BBTN movement patterns and volatility are different from the rest of state-owned banking stocks’ movement and volatility. BBTN focused on mortgage loans, evident from its type composition, where mortgage loans dominate other loans. Thus, the property market and economic cycle mainly affect the pricing of loans and their return. It becomes concentrated and no longer diversified when focused primarily on mortgage loans. Pricing and return are lower than other diversified banks, but it is backed by definite collateral, provided that the property market is in a stable condition (does not collapse).
The three state-owned stocks in the banking sector (BBNI, BBRI, and BMRI) have a similar principal component influencing their conditional variance. On the contrary, the BBTN stock has different principal components. The different principal components of BBTN might be related to its focus on mortgage loans, which were the opposite of the other three state-owned banks in this research. Its stock return sensitivity to common factors such as inflation, interest rate, and economic cycle (systematic risk) was mainly caused by those factors’ impact on the property and real estate sector. In addition, the BBTN also has the smallest capital compared to the other sample banks (evidenced by its relative portion in a different capital category), which might implicate its operation and returns. The findings are also supported by the VAR analysis, where the returns of the three SOE stocks in the banking sector move together but not with the returns of BBTN stock.
Furthermore, the IRFs’ graphs show that the BBTN tends to move differently from the rest of the state-owned banking stocks. In addition, its volatility is also different from the BBNI, BBRI, and BMRI. Besides, both principal components in this study contribute 84.61% toward explaining the conditional variance return of the four SOE stocks studied in the banking sector.
Based on the findings of this study, it can be concluded that the hypothesis is supported empirically. The OGARCH method can predict the co-movement of Indonesia’s state-owned banking sector stocks before the COVID-19 pandemic. It summarizes the covariance matrix to be simplified so that further application could facilitate the portfolio calculation. As stated by
Paolella et al. (
2021), the OGARCH model was suitable for a specified number of leading principal components of the covariance matrix. The results of this study are consistent with the findings by (
Bai 2011;
Muharam et al. 2020;
Robiyanto 2017).
In addition, it is also quite interesting that the remaining 17.6% of the conditional variance return of the four stocks studied could be explained by other components not formed in this study. It implies that undetectable and random factors could affect the conditional variance return of the four stocks studied. Within the capital asset pricing model (CAPM) framework, this finding proves that 82.4% of the risk in the four stocks is systematic risk, while the remaining 17.6% of the total risk is a non-systematic risk.
5. Conclusions
This study finds that the OGARCH method can simplify the covariance matrix of the examined four SOE stocks in the banking sector. Three stocks (BBNI, BBRI, and BMRI) with the same principal component influence their conditional variance. However, the BBTN stock has different principal components. Meanwhile, it is found that 82.4% of the risk of the four stocks is systematic risk, and the remaining 17.6% is a non-systematic risk.
The theoretical implication of this research is providing empirical evidence from the Indonesian banking sector in the ability of OGARCH to remedy the inherent estimation problems found in multivariate ARCH modeling. The findings also imply that investment managers or investors should not put the BBNI, BBRI, and BMRI stocks in the same portfolio as they have the same risk factors. Furthermore, the BBTN stock can be combined with other SOE stocks in other banking sectors. Hence, considering the co-movement of SOE banking stocks in constructing the stock portfolio is crucial for reducing the portfolio risk. In the context of ASEAN countries, this research contributes to the knowledge related to portfolio construction involving SOE banking stocks since there is a similarity in banking industry structure in some ASEAN countries where a few SOE banks dominate the banking industry.
The regulators formulating the policy on holding banks may use the results of this study by considering the potential merging of the SOE banks with similar stock returns co-movement. The policy implication of this research is related to the importance of addressing the specific characteristics of each SOE bank under consideration when aiming to form a bank holding company. It is advisable to place banks with similar characteristics in terms of co-movement into one holding company instead of placing banks with different co-movement into one holding company. Future researchers are suggested to conduct studies on other SOE stocks so that the results can be used to form optimal portfolios, considering that the SOE stocks are often regarded as attractive to be included in a portfolio.