BRICS Capital Markets Co-Movement Analysis and Forecasting
Abstract
:1. Introduction
2. Review of Literature
3. Data and Methodology
- Methodology
- Wavelet Analysis
- Wavelet Coherence
- Wavelet Clustering
- Forecasting
- Artificial Neural Network Forecasting
4. Main Results
- Explanatory Variables
- Wavelet Analysis
- Wavelet Coherence
- Wavelet Clustering
- Forecasting
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://cran.r-project.org/web/packages/biwavelet/biwavelet.pdf (accessed on 1 March 2022). |
References
- Aggarwal, Shalini, and Abhay Raja. 2019. Stock market interlinkages among the BRIC economies. International Journal of Ethics and Systems 35: 59–74. [Google Scholar] [CrossRef]
- Ahlgren, Niklas, and Jan Antell. 2002. Testing For Cointegration Between International Stock Prices. Applied Financial Economics 12: 851–61. [Google Scholar] [CrossRef]
- Aloui, Chaker, and Besma Hkiri. 2014. Co-movements of GCC emerging stock markets: New evidence from wavelet coherence analysis. Economic Modelling 36: 421–31. [Google Scholar] [CrossRef]
- Arshanapalli, Bala, and John Doukas. 1993. International stock market linkages: Evidence from the pre- and post-1987 period. Journal of Banking and Finance 17: 193–208. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Campbell R. Harvey. 1995. Time-varying world market integration. Journal of Finance 50: 403–44. [Google Scholar] [CrossRef]
- Brooks, Robin, and Marco Del Negro. 2004. The rise in co-movement across national stock markets: Market integration or IT bubble. Journal of Empirical Finance 11: 659–80. [Google Scholar] [CrossRef] [Green Version]
- Chan, Kam C., Benton E. Gup, and Ming-Shiun Pan. 1997. International Stock Market Efficiency And Integration: A Study of Eighteen Nations. Journal of Business Finance and Accounting 24: 803–13. [Google Scholar] [CrossRef]
- Chaudhuri, Kausik. 1997. Cointegration, Error Correction And Granger Causality: An Application with Latin American Stock Markets. Applied Economics Letters 4: 469–71. [Google Scholar] [CrossRef]
- Chavent, Marie, Vanessa Kuentz-Simonet, Amaury Labenne, and Jérôme Saracco. 2018. ClustGeo: An R package for hierarchical clustering with spatial constraints. Computational Statistics 33: 1799–822. [Google Scholar] [CrossRef] [Green Version]
- Dai, Wensheng, Jui-Yu Wu, and Chi-Jie Lu. 2012. Combining nonlinear independent component analysis and neural network for the prediction of Asian stock market indexes. Expert Systems with Applications 39: 4444–52. [Google Scholar] [CrossRef]
- De Jong, Frank, and Frans A. De Roon. 2005. Time-varying market integration and expected returns in emerging markets. Journal of Financial Economics 78: 583–613. [Google Scholar] [CrossRef] [Green Version]
- Dima, B., Ş. M. Dima, and Flavia Barna. 2015. A wavelet analysis of capital markets’ integration in Latin America. Applied Economics 47: 1019–36. [Google Scholar] [CrossRef]
- Dimitriou, Dimitrios, Dimitris Kenourgios, and Theodore Simos. 2013. Global financial crisis and emerging stock market contagion: A multivariate FIAPARCH–DCC approach. International Review of Financial Analysis 30: 46–56. [Google Scholar] [CrossRef]
- Eakins, Stanley G., and Stanley R. Stansell. 2003. Can value-based stock selection criteria yield superior risk-adjusted returns: An application of neural networks. International Review of Financial Analysis 12: 83–97. [Google Scholar] [CrossRef]
- Fernández, Alberto, and Sergio Gómez. 2007. Portfolio selection using neural networks. Computers & Operations Research 34: 1177–91. [Google Scholar] [CrossRef] [Green Version]
- Forbes, Kristin J., and Roberto Rigobon. 2002. No contagion, only interdependence: Measuring stock market comovements. Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Forti, Mauro, Paolo Nistri, and Marc Quincampoix. 2004. Generalized neural network for nonsmooth nonlinear programming problems. IEEE Transactions on Circuits and Systems-I 51: 1741–54. [Google Scholar] [CrossRef]
- Goetzmann, William N., Lingfeng Li, and K. Geert Rouwenhorst. 2005. Long-term global market correlations. Journal of Business 78: 1–38. [Google Scholar] [CrossRef] [Green Version]
- Granger, Clive William John, and Oskar Morgenstern. 1970. The Predictability of Stock Market Prices. Lexington: Heath Lexington Books, Heath & Co. [Google Scholar]
- Grubel, Herbert G. 1968. Internationally diversified portfolios: Welfare gains and capital flows. American Economic Review 58: 1299–314. [Google Scholar]
- Hung, Ngo Thai. 2019. Equity market integration of China and Southeast Asian countries: Further evidence from MGARCH-ADCC and wavelet coherence analysis. Quantitative Finance and Economics 3: 201–20. [Google Scholar] [CrossRef]
- Johnson, Robert, and Luc Soenen. 2003. Economic integration and stock market co-movement in the Americas. Journal of Multinational Financial Management 13: 85–100. [Google Scholar] [CrossRef]
- Kang, Sang Hoon, and Seong-Min Yoon. 2011. The global financial crises and the integartion of emerging stock markets in Asia. Journal of East Asian Economic Integration 15: 49–73. [Google Scholar]
- Kao, Wei-Shun, Tzu-Chuan Kao, Chang-Cheng Changchien, Li-Hsun Wang, and Kuei-Tzu Yeh. 2018. Contagion in International Stock Markets After the Subprime Mortgage Crisis. The Chinese Economy 51: 130–53. [Google Scholar] [CrossRef]
- Karim, Muhammad Mahmudul, Mohammad Ashraful Ferdous Chowdhury, and Mansur Masih. 2021. Re-examining oil and BRICS’stock markets: New evidence from wavelet and MGARCH-DCC. Macroeconomics and Finance in Emerging Market Economies, 1–19. [Google Scholar] [CrossRef]
- Kasa, Kenneth. 1992. Common stochastic trends in international stock markets. Journal of Monetary Economics 29: 95–124. [Google Scholar] [CrossRef]
- Ko, Po-Chang, and Ping-Chen Lin. 2006. An evolution-based approach with modularized evaluations to forecast financial distress. Knowledge Based Systems 19: 84–91. [Google Scholar] [CrossRef]
- Ko, Po-Chang, and Ping-Chen Lin. 2008. Resource allocation neural network in portfolio selection. Expert Systems with Applications 35: 330–37. [Google Scholar] [CrossRef]
- Lau, Chi Keung Marco, and Xin Sheng. 2018. Inter-and intra-regional analysis on spillover effects across international stock markets. Research in International Business and Finance 46: 420–29. [Google Scholar] [CrossRef] [Green Version]
- Lehkonen, Heikki, and Kari Heimonen. 2014. Timescale-dependent stock market comovement: BRICs vs. developed markets. Journal of Empirical Finance 28: 90–103. [Google Scholar] [CrossRef] [Green Version]
- Levy, Haim, and Marshall Sarnat. 1970. International diversification of investment portfolios. American Economic Review 60: 668–75. [Google Scholar]
- Liu, Qingshan, and Jun Wang. 2006. A recurrent neural network for non-smooth convex programming subject to linear equality and bound constraints. In LNCS: Processing 13th International Conference on Neural Information Processing. Berlin and Heidelberg: Springer, vol. 4233, pp. 1004–13. [Google Scholar]
- Maake, Witness, and Terence Van Zyl. 2020. Applications of Machine Learning to Estimating the Sizes and Market Impact of Hidden Orders in the BRICS Financial Markets. Journal Financial Economics 11: 223–49. [Google Scholar] [CrossRef]
- Maiti, Moinak. 2021. Quantile regression, asset pricing and investment decision. IIMB Management Review 33: 28–37. [Google Scholar] [CrossRef]
- Maiti, Moinak, and A. Balakrishnan. 2018. Is human capital the sixth factor? Journal of Economic Studies 45: 710–37. [Google Scholar] [CrossRef]
- Maiti, Moinak, and A. Balakrishnan. 2020. Can leverage effect coexist with value effect? IIMB Management Review 32: 7–23. [Google Scholar] [CrossRef]
- Maiti, Moinak, Darko Vukovic, Viktor Krakovich, and Maneesh Kumar Pandey. 2020a. How integrated are cryptocurrencies. International Journal of Big Data Management 1: 64–80. [Google Scholar] [CrossRef]
- Maiti, Moinak, Yaroslav Vyklyuk, and Darko Vuković. 2020b. Cryptocurrencies Co-movement Forecasting with Neural Networks. Internet Technology Letters 3: e157. [Google Scholar] [CrossRef]
- Majhi, Ritanjah, Ganapati Panda, Gadadhar Sahoo, Pradipta K. Dash, and Debi Prasad Das. 2007. Stock market prediction of S&P 500 and DJIA using bacterial foraging optimization technique. Paper presented at the 2007 IEEE Congress on Evolutionary Computation (CEC 2007), Singapore, September 25–28; pp. 2569–75. [Google Scholar]
- Malliaris, Anastasios G., and Jorge L. Urrutia. 1992. The international crash of October 1987: Causality tests. Journal of Financial and Quantitative Analysis 27: 353–63. [Google Scholar] [CrossRef] [Green Version]
- Markowitz, Harry M. 1952. Portfolio selection. The Journal of Finance 7: 77–91. [Google Scholar]
- Mensi, Walid, Shawkat Hammoudeh, and Sang Hoon Kang. 2017. Dynamic linkages between developed and BRICS stock markets: Portfolio risk analysis. Finance Research Letters 21: 26–33. [Google Scholar] [CrossRef]
- Mensi, Walid, Besma Hkiri, Khamis H. Al-Yahyaee, and Sang Hoon Kang. 2018. Analyzing time–frequency co-movements across gold and oil prices with BRICS stock markets: A VaR based on wavelet approach. International Review of Economics and Finance 54: 74–102. [Google Scholar] [CrossRef]
- Patel, Ritesh J. 2017. Co-movement and integration among stock markets: A study of 14 countries. Indian Journal of Finance 11: 53–66. [Google Scholar] [CrossRef]
- Qureshi, Fiza, Saba Qureshi, Sobia Shafaq Shah, Ijaz Ur Rehman, and Faisal Shahzad. 2020. Further evidence on co-movement between equity funds and business cycle variables in BRICS: A Wavelet analysis. Borsa Istanbul Review 20: S93–S102. [Google Scholar] [CrossRef]
- Islam, Raisul. 2014. A comparison of the long term interdependence of Southeast Asian equity markets. Journal of East Asian Economic Integration 18: 187–221. [Google Scholar] [CrossRef]
- Ramos-Requena, José Pedro, Juan Evangelista Trinidad-Segovia, and Miguel Ángel Sánchez-Granero. 2020. An Alternative Approach to Measure Co-Movement between Two Time Series. Mathematics 8: 261. [Google Scholar] [CrossRef] [Green Version]
- Ratanapakorn, Orawan, and Subhash C. Sharma. 2002. Interrelationships among regional stock indices. Review of Financial Economics 11: 91–108. [Google Scholar] [CrossRef]
- Raza, Syed Ali, Nida Shah, and Arshian Sharif. 2019. Time frequency relationship between energy consumption, economic growth and environmental degradation in the United States: Evidence from transportation sector. Energy 173: 706–20. [Google Scholar] [CrossRef]
- Rikhotso, Prayer M., and Beatrice D. Simo-Kengne. 2022. Dependence structures between Sovereign credit default swaps and global risk factors in BRICS countries. Journal of Risk and Financial Management 15: 109. [Google Scholar] [CrossRef]
- Rua, António, and Luís C. Nunes. 2009. International co-movement of stock market returns: A wavelet analysis. Journal of Empirical Finance 16: 632–39. [Google Scholar] [CrossRef] [Green Version]
- Shik Lee, Hahn. 2004. International transmission of stock market movements: A wavelet analysis. Applied Economics Letters 11: 197–201. [Google Scholar] [CrossRef]
- Syriopoulos, Theodore. 2007. Dynamic linkages between emerging European and developed stock markets: Has the EMU any impact? International Review of Financial Analysis 16: 41–60. [Google Scholar] [CrossRef]
- Sznajderska, Anna. 2019. The role of China in the world economy: Evidence from a global VAR model. Applied Economics 51: 1574–87. [Google Scholar] [CrossRef]
- Torrence, Christopher, and Peter J. Webster. 1999. Interdecadal changes in the ESNO—Monsoon system. Journal of Climate 12: 2679–90. [Google Scholar] [CrossRef] [Green Version]
- Vukovic, Darko B., Kseniya A. Lapshina, and Moinak Maiti. 2019. European Monetary Union bond market dynamics: Pre & post crisis. Research in International Business and Finance 50: 369–80. [Google Scholar]
- Vukovic, Darko, Yaroslav Vyklyuk, Natalia Matsiuk, and Moinak Maiti. 2020. Neural network forecasting in prediction Sharpe ratio: Evidence from EU debt market. Physica A: Statistical Mechanics and Its Applications 542: 123331. [Google Scholar] [CrossRef]
- Vukovic, Darko B., Kseniya A. Lapshina, and Moinak Maiti. 2021. Wavelet Coherence Analysis of Returns, Volatility and Interdependence of the US and the EU Money markets: Pre & Post Crisis. The North American Journal of Economics and Finance 58: 101457. [Google Scholar] [CrossRef]
- Vyklyuk, Yaroslav, Darko Vukovic, and Ana Jovanovic. 2013. Forex prediction with neural network: Usd/eur currency pair. Actual Problem of Economics 10: 251–61. [Google Scholar]
- Wang, Z., Jian Yang, and David A. Bessler. 2003. Financial crisis and African stock market integration. Applied Economics Letters 10: 527–33. [Google Scholar] [CrossRef]
- Xu, Haifeng, and Shigeyuki Hamori. 2012. Dynamic linkages of stock prices between the BRICs and the United States: Effects of the 2008–2009 financial crisis. Journal of Asian Economics 23: 344–52. [Google Scholar] [CrossRef]
- Yang, Lu, Xiao Jing Cai, and Shigeyuki Hamori. 2017. Does the crude oil price influence the exchange rates of oil-importing and oil-exporting countries differently? A wavelet coherence analysis. International Review of Economics & Finance 49: 536–47. [Google Scholar]
- Zhang, Yudong, and Lenan Wu. 2009. Stock market prediction of S&P 500 via combination of improved BCO approach and BP neural network. Expert Systems with Applications 36: 8849–54. [Google Scholar]

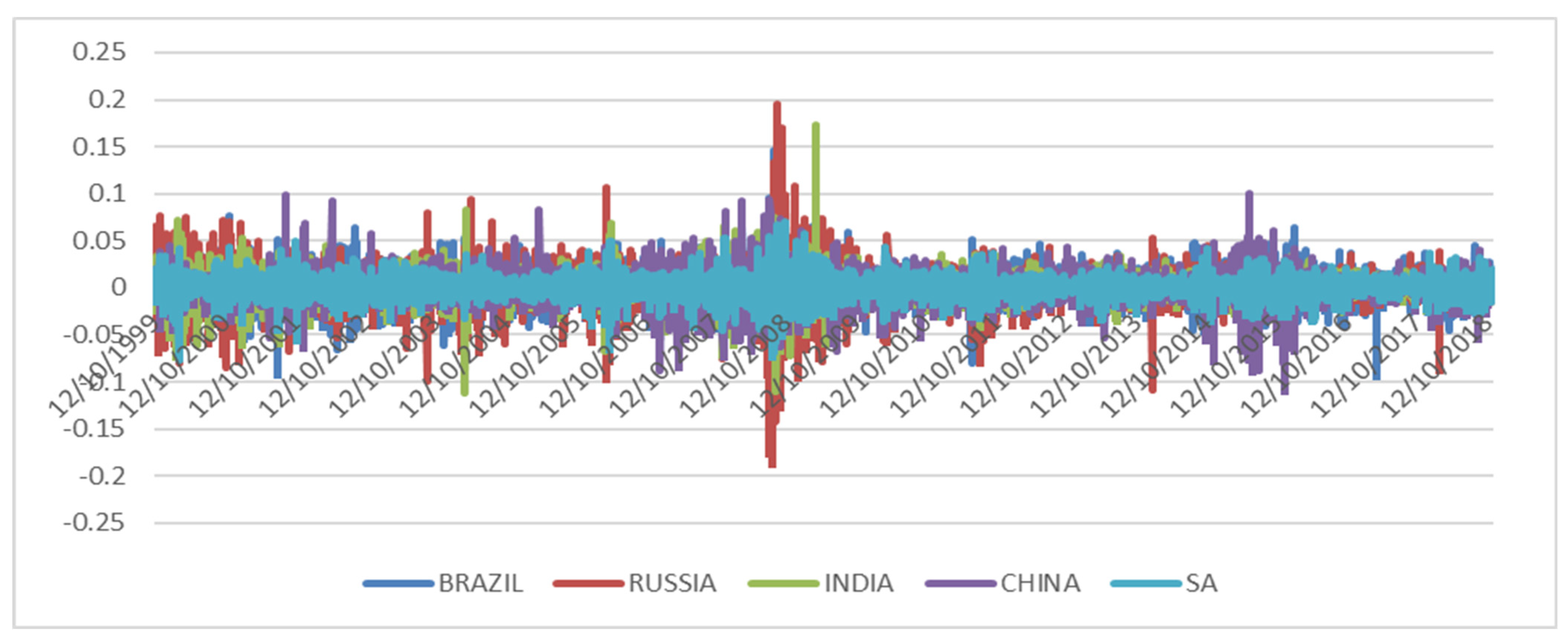
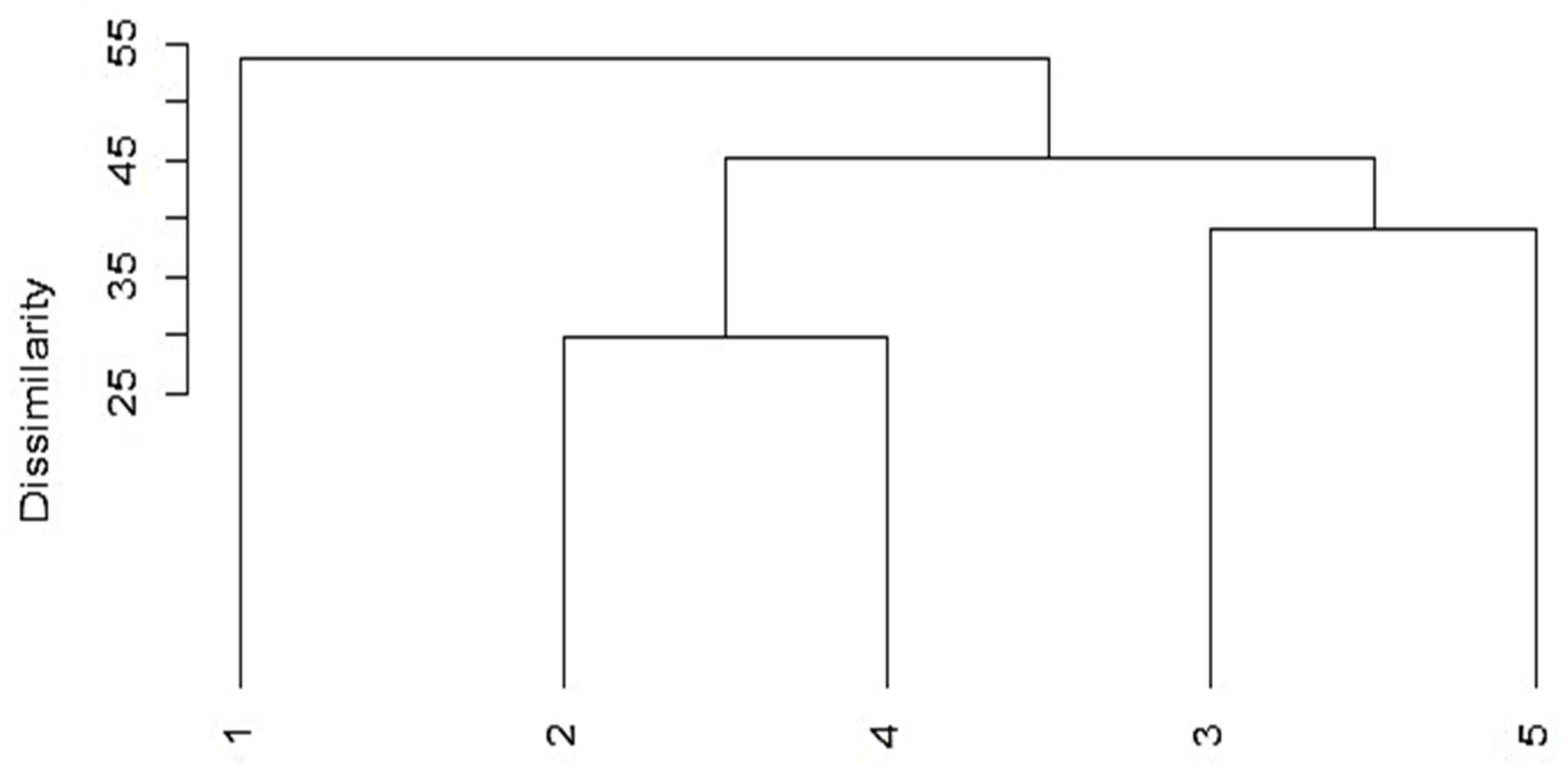
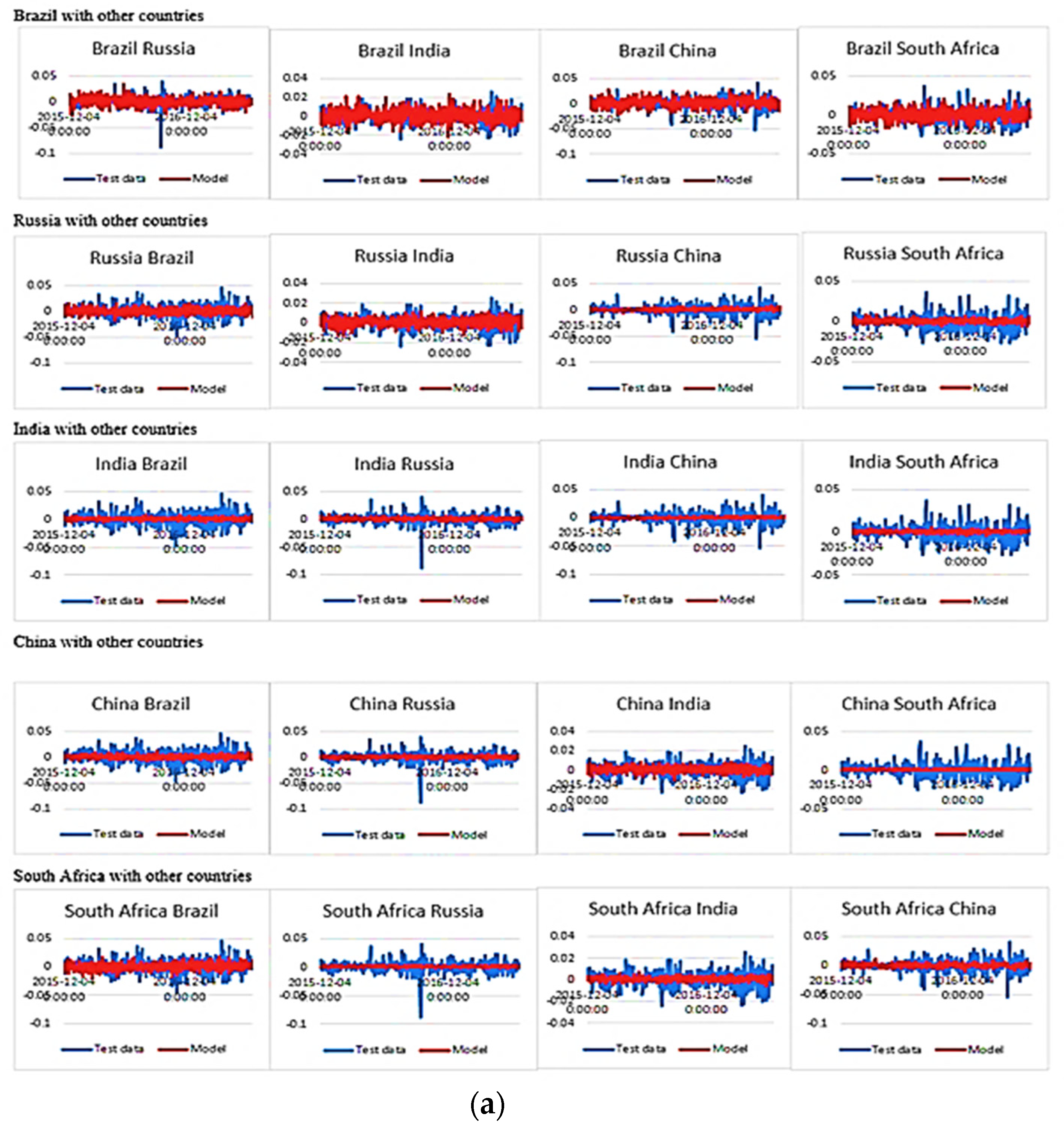
| Brazil | Russia | India | China | SA | |
|---|---|---|---|---|---|
| Mean | 0.0005 | 0.00059 | 0.00039 | 0.00013 | 0.00036 |
| Standard Deviation | 0.01723 | 0.01931 | 0.01401 | 0.01514 | 0.01168 |
| Sample Variance | 0.0003 | 0.00037 | 0.0002 | 0.00023 | 0.00014 |
| Kurtosis | 4.5916 | 12.044 | 9.70844 | 6.29822 | 3.81758 |
| Skewness | 0.02419 | −0.2957 | 0.00564 | −0.2399 | −0.0968 |
| Range | 0.26051 | 0.38127 | 0.28478 | 0.20878 | 0.14713 |
| Minimum | −0.1139 | −0.1866 | −0.1114 | −0.1083 | −0.0764 |
| Maximum | 0.14658 | 0.19464 | 0.17339 | 0.10045 | 0.07073 |
| Sum | 2.38308 | 2.8248 | 1.86007 | 0.6203 | 1.72307 |
| Count | 4765 | 4765 | 4765 | 4765 | 4765 |
| Countries | Weekly | Yearly | Countries | Weekly | Yearly |
|---|---|---|---|---|---|
| BRAZIL->RUSSIA | 0.0098 | 0.0133 | INDIA->CHINA | 0.0098 | 0.0103 |
| BRAZIL->INDIA | 0.0074 | 0.0105 | INDIA->SA | 0.0092 | 0.0096 |
| BRAZIL->CHINA | 0.0097 | 0.0134 | CHINA->BRAZIL | 0.0124 | 0.0128 |
| BRAZIL->SA | 0.0081 | 0.0127 | CHINA->RUSSIA | 0.0103 | 0.0101 |
| RUSSIA->BRAZIL | 0.0078 | 0.0134 | CHINA->INDIA | 0.0112 | 0.008 |
| RUSSIA->INDIA | 0.0066 | 0.009 | CHINA->SA | 0.0087 | 0.0095 |
| RUSSIA->CHINA | 0.0081 | 0.0105 | SA->BRAZIL | 0.0143 | 0.0141 |
| RUSSIA->SA | 0.0094 | 0.0098 | SA->RUSSIA | 0.0168 | 0.01 |
| INDIA->BRAZIL | 0.0082 | 0.0126 | SA->INDIA | 0.009 | 0.0078 |
| INDIA->RUSSIA | 0.0086 | 0.0102 | SA->CHINA | 0.0084 | 0.0107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maiti, M.; Vukovic, D.; Vyklyuk, Y.; Grubisic, Z. BRICS Capital Markets Co-Movement Analysis and Forecasting. Risks 2022, 10, 88. https://doi.org/10.3390/risks10050088
Maiti M, Vukovic D, Vyklyuk Y, Grubisic Z. BRICS Capital Markets Co-Movement Analysis and Forecasting. Risks. 2022; 10(5):88. https://doi.org/10.3390/risks10050088
Chicago/Turabian StyleMaiti, Moinak, Darko Vukovic, Yaroslav Vyklyuk, and Zoran Grubisic. 2022. "BRICS Capital Markets Co-Movement Analysis and Forecasting" Risks 10, no. 5: 88. https://doi.org/10.3390/risks10050088
APA StyleMaiti, M., Vukovic, D., Vyklyuk, Y., & Grubisic, Z. (2022). BRICS Capital Markets Co-Movement Analysis and Forecasting. Risks, 10(5), 88. https://doi.org/10.3390/risks10050088







