EM Estimation for the Bivariate Mixed Exponential Regression Model
Abstract
:1. Introduction
- finite mixture models: see, for example, (Fung et al. 2021; Lee and Lin 2010; Miljkovic and Grün 2016; Tzougas et al. 2014, 2018, 2019);
- composite or splicing models: see for instance, (Bakar et al. 2015; Calderín-Ojeda and Kwok 2016; Cooray and Ananda 2005; Grün and Miljkovic 2019; Nadarajah and Bakar 2014; Parodi 2020; Pigeon and Denuit 2011; Scollnik 2007; Scollnik and Sun 2012).
- combinations of finite mixtures and composite models: see Reynkens et al. (2017).
2. The Bivariate Mixed Exponential Regression Model
2.1. Bivariate Pareto Regression Model
2.2. Bivariate Exponential-Inverse Gaussian Regression Model
3. The EM Algorithm for the Bivariate Mixed Exponential Regression Model
- E-step: The Q-function, , which is the conditional posterior expectation of Equation (11), is given bywhere and where the conditional expectation for any real value function, , is defined as followswhere the posterior density function is defined as
- M-step: After calculating the Q-function, we find its maximum global point, , i.e., we update the parameters by computing the gradient function, , and the Hessian matrix, , of the Q-function. In particular, the Newton–Raphson algorithm is used for maximizing the Q-function and the parameters for the Exponential part and the parameter for the randnom effect part are updated separately as shown below.
- -
- For the Exponential part,where is the design matrix for .
- -
- For the random effect part, we derive the first and second order derivatives of and then we take the posterior expectations to construct its gradient functions and the Hessian matrix. In what follows, we derive the derivatives for the IGA and IG densities which were defined in the previous section. Finally, we update using the one-step ahead Newton iterationIn what follows, we will show how Equation (11) can be modified in the case of the IGA and IG mixing densities.
- Inverse Gamma mixing densityThe first and second derivatives of the term are given bywhere the is the digamma function and is the corresponding first derivative. Furthermore, it is easy to observe that at iteration r, the posterior density would be an IGA. Thus, the expectations involved in the E-step of the algorithm are given by
- Inverse Gaussian densityIn the case of the IG mixing density, the first and second derivatives of the term are given byFurthermore, one can easily see that at iteration r, the posterior density in this case is a GIG. Therefore, the expectations involved in the E-step of the algorithm are given bywhere .
4. Empirical Analysis
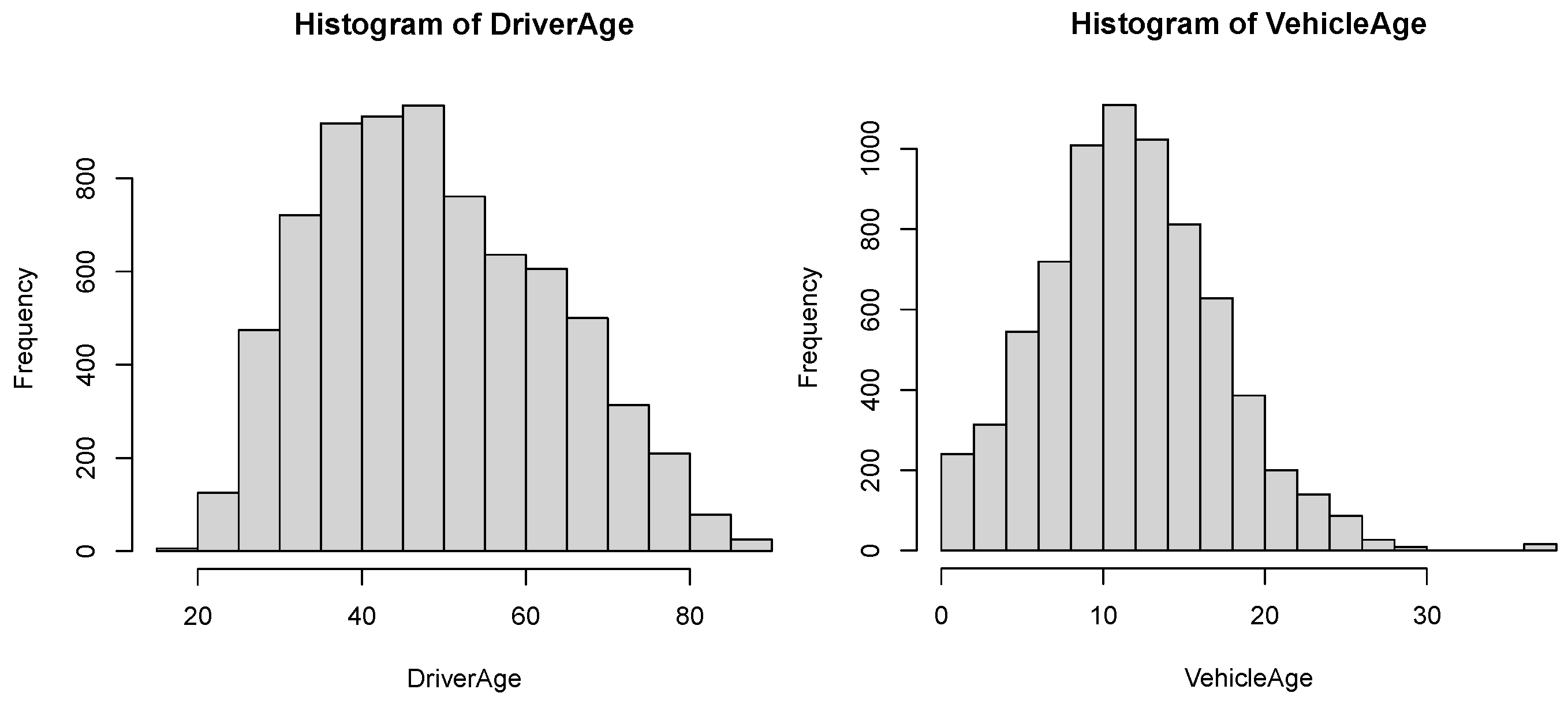
- The variable Driver’s age. Policyholders aged 18 to 90 years old.
- The variable Vehicle’s age. Vehicles aged 0 to 60 years old.
- The variable Car cubism, ’CC’, consists of four categories. Vehicles with horse power ’0–1299 cc’ (C1), ’1300–1399 cc’ (C2), ’1400–1599 cc’ and ’greater or equal 1600 cc’ (C3).
- The variable ’PT’ consisted of three types of policy, ’Economic type which includes only MTPL coverage’ (C1) , ’Middle type which includes apart from MTPL coverage other types of coverage’ (C2), and ’Expensive type—Own coverage’ (C3).
- The variable ’Region’ consisted of three board regions, ’Capital city’ (C1), ’province cities of the mainland’ (C2), and ’province cities of the island area’ (C3).
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EM | Expectation—Maximization |
| IGA | Inverse Gamma |
| IG | Inverse Gaussian |
| GIG | Generalized Inverse Gaussian |
| BPA | Bivariate Pareto |
| BEIG | Bivariate Exponential-Inverse Gaussian |
| 1 | Please note that the EM algorithms which are used for fitting the BPA and BEIG regression models are direct extensions from the univariate to the multivariate case of the EM algorithms which were developed by Tzougas and Karlis (2020). |
References
- Abdallah, Anas, Jean-Philippe Boucher, and Hélène Cossette. 2016. Sarmanov family of multivariate distributions for bivariate dynamic claim counts model. Insurance: Mathematics and Economics 68: 120–33. [Google Scholar] [CrossRef] [Green Version]
- Anderson, David R., and Kenneth P. Burnham. 2004. Model Selection and Multi-Model Inference, 2nd ed. New York: Springer, vol. 63, p. 10. [Google Scholar]
- Bakar, S. A. Abu, Nor A. Hamzah, Mastoureh Maghsoudi, and Saralees Nadarajah. 2015. Modeling loss data using composite models. Insurance: Mathematics and Economics 61: 146–54. [Google Scholar]
- Baumgartner, Carolin, Lutz F. Gruber, and Claudia Czado. 2015. Bayesian total loss estimation using shared random effects. Insurance: Mathematics and Economics 62: 194–201. [Google Scholar] [CrossRef]
- Bermúdez, Lluís, Montserrat Guillén, and Dimitris Karlis. 2018. Allowing for time and cross dependence assumptions between claim counts in ratemaking models. Insurance: Mathematics and Economics 83: 161–69. [Google Scholar] [CrossRef]
- Bermúdez, Lluís, and Dimitris Karlis. 2011. Bayesian multivariate poisson models for insurance ratemaking. Insurance: Mathematics and Economics 48: 226–36. [Google Scholar] [CrossRef] [Green Version]
- Bermúdez, Lluís, and Dimitris Karlis. 2012. A finite mixture of bivariate poisson regression models with an application to insurance ratemaking. Computational Statistics & Data Analysis 56: 3988–99. [Google Scholar]
- Bermúdez, Lluís, and Dimitris Karlis. 2017. A posteriori ratemaking using bivariate poisson models. Scandinavian Actuarial Journal 2017: 148–58. [Google Scholar] [CrossRef] [Green Version]
- Bermúdez, Lluís, and Dimitris Karlis. 2021. Multivariate inar (1) regression models based on the sarmanov distribution. Mathematics 9: 505. [Google Scholar] [CrossRef]
- Blostein, Martin, and Tatjana Miljkovic. 2019. On modeling left-truncated loss data using mixtures of distributions. Insurance: Mathematics and Economics 85: 35–46. [Google Scholar] [CrossRef]
- Bolancé, Catalina, Montserrat Guillen, and Albert Pitarque. 2020. A Sarmanov distribution with beta marginals: An application to motor insurance pricing. Mathematics 8: 2020. [Google Scholar] [CrossRef]
- Bolancé, Catalina, and Raluca Vernic. 2019. Multivariate count data generalized linear models: Three approaches based on the Sarmanov distribution. Insurance: Mathematics and Economics 85: 89–103. [Google Scholar] [CrossRef] [Green Version]
- Calderín-Ojeda, Enrique, and Chun Fung Kwok. 2016. Modeling claims data with composite Stoppa models. Scandinavian Actuarial Journal 2016: 817–36. [Google Scholar] [CrossRef]
- Cockriel, William M., and James B. McDonald. 2018. Two multivariate generalized beta families. Communications in Statistics-Theory and Methods 47: 5688–701. [Google Scholar] [CrossRef]
- Cooray, Kahadawala, and Malwane M. A. Ananda. 2005. Modeling actuarial data with a composite lognormal-Pareto model. Scandinavian Actuarial Journal 2005: 321–34. [Google Scholar] [CrossRef]
- Denuit, Michel, Montserrat Guillen, and Julien Trufin. 2019. Multivariate credibility modelling for usage-based motor insurance pricing with behavioural data. Annals of Actuarial Science 13: 378–99. [Google Scholar] [CrossRef] [Green Version]
- Frees, Edward W. 2009. Regression Modeling with Actuarial and Financial Applications. Cambridge: Cambridge University Press. [Google Scholar]
- Fung, Tsz Chai, Andrei L. Badescu, and X. Sheldon Lin. 2019. A class of mixture of experts models for general insurance: Application to correlated claim frequencies. ASTIN Bulletin: The Journal of the IAA 49: 647–88. [Google Scholar] [CrossRef]
- Fung, Tsz Chai, Andrei L. Badescu, and X. Sheldon Lin. 2021. A new class of severity regression models with an application to ibnr prediction. North American Actuarial Journal 25: 206–31. [Google Scholar] [CrossRef]
- Gómez-Déniz, Emilio, and Enrique Calderín-Ojeda. 2021. A priori ratemaking selection using multivariate regression models allowing different coverages in auto insurance. Risks 9: 137. [Google Scholar] [CrossRef]
- Grün, Bettina, and Tatjana Miljkovic. 2019. Extending composite loss models using a general framework of advanced computational tools. Scandinavian Actuarial Journal 2019: 642–60. [Google Scholar] [CrossRef]
- Jeong, Himchan, and Dipak K. Dey. 2021. Multi-Peril Frequency Credibility Premium via Shared Random Effects. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3825435 (accessed on 13 April 2021).
- Jeong, Himchan, and Emiliano A. Valdez. 2020. Predictive compound risk models with dependence. Insurance: Mathematics and Economics 94: 182–95. [Google Scholar] [CrossRef]
- Laudagé, Christian, Sascha Desmettre, and Jörg Wenzel. 2019. Severity modeling of extreme insurance claims for tariffication. Insurance: Mathematics and Economics 88: 77–92. [Google Scholar] [CrossRef]
- Lee, Simon C. K., and X. Shelson Lin. 2010. Modeling and evaluating insurance losses via mixtures of Erlang distributions. North American Actuarial Journal 14: 107–30. [Google Scholar] [CrossRef]
- Miljkovic, Tatjana, and Bettina Grün. 2016. Modeling loss data using mixtures of distributions. Insurance: Mathematics and Economics 70: 387–396. [Google Scholar] [CrossRef]
- Nadarajah, Saralees, and S. A. Abu Bakar. 2014. New composite models for the Danish fire insurance data. Scandinavian Actuarial Journal 2014: 180–87. [Google Scholar] [CrossRef]
- Oh, Rosy, Himchan Jeong, Jae Youn Ahn, and Emiliano A. Valdez. 2021. A multi-year microlevel collective risk model. Insurance: Mathematics and Economics 100: 309–28. [Google Scholar] [CrossRef]
- Parodi, Pietro. 2020. A generalised property exposure rating framework that incorporates scale-independent losses and maximum possible loss uncertainty. Astin Bulletin 50: 513–53. [Google Scholar] [CrossRef]
- Pechon, Florian, Michel Denuit, and Julien Trufin. 2019. Multivariate modelling of multiple guarantees in motor insurance of a household. European Actuarial Journal 9: 575–602. [Google Scholar] [CrossRef] [Green Version]
- Pechon, Florian, Michel Denuit, and Julien Trufin. 2021. Home and motor insurance joined at a household level using multivariate credibility. Annals of Actuarial Science 15: 82–114. [Google Scholar] [CrossRef]
- Pechon, Florian, Julien Trufin, and Michel Denuit. 2018. Multivariate modelling of household claim frequencies in motor third-party liability insurance. Astin Bulletin 48: 969–93. [Google Scholar] [CrossRef] [Green Version]
- Pigeon, Mathieu, and Michel Denuit. 2011. Composite lognormal-Pareto model with random threshold. Scandinavian Actuarial Journal 2011: 177–92. [Google Scholar] [CrossRef]
- Raftery, Adrian E. 1995. Bayesian model selection in social research. Sociological Methodology 25: 111–163. [Google Scholar] [CrossRef]
- Reynkens, Tom, Roel Verbelen, Jan Beirlant, and Katrien Antonio. 2017. Modelling censored losses using splicing: A global fit strategy with mixed Erlang and extreme value distributions. Insurance: Mathematics and Economics 77: 65–77. [Google Scholar] [CrossRef] [Green Version]
- Scollnik, David P. M. 2007. On composite lognormal-Pareto models. Scandinavian Actuarial Journal 2007: 20–33. [Google Scholar] [CrossRef]
- Scollnik, David P. M., and Chenchen Sun. 2012. Modeling with Weibull-Pareto models. North American Actuarial Journal 16: 260–72. [Google Scholar] [CrossRef]
- Shi, Peng, and Emiliano A. Valdez. 2014a. Longitudinal modeling of insurance claim counts using jitters. Scandinavian Actuarial Journal 2014: 159–79. [Google Scholar] [CrossRef]
- Shi, Peng, and Emiliano A. Valdez. 2014b. Multivariate negative binomial models for insurance claim counts. Insurance: Mathematics and Economics 55: 18–29. [Google Scholar] [CrossRef]
- Tzougas, George, and Alice Pignatelli di Cerchiara. 2021a. Bivariate mixed poisson regression models with varying dispersion. North American Actuarial Journal, 1–31. [Google Scholar] [CrossRef]
- Tzougas, George, and Alice Pignatelli di Cerchiara. 2021b. The multivariate mixed negative binomial regression model with an application to insurance a posteriori ratemaking. Insurance: Mathematics and Economics 101: 602–25. [Google Scholar] [CrossRef]
- Tzougas, George, and Himchan Jeong. 2021. An expectation-maximization algorithm for the exponential-generalized inverse gaussian regression model with varying dispersion and shape for modelling the aggregate claim amount. Risks 9: 19. [Google Scholar] [CrossRef]
- Tzougas, George, and Dimitris Karlis. 2020. An em algorithm for fitting a new class of mixed exponential regression models with varying dispersion. Astin Bulletin 50: 555–83. [Google Scholar] [CrossRef]
- Tzougas, George, Spyridon Vrontos, and Nicholas Frangos. 2014. Optimal bonus-malus systems using finite mixture models. Astin Bulletin 44: 417–44. [Google Scholar] [CrossRef] [Green Version]
- Tzougas, George, Spyridon Vrontos, and Nicholas Frangos. 2018. Bonus-malus systems with two-component mixture models arising from different parametric families. North American Actuarial Journal 22: 55–91. [Google Scholar] [CrossRef]
- Yang, Xipei, Edward W. Frees, and Zhengjun Zhang. 2011. A generalized beta copula with applications in modeling multivariate long-tailed data. Insurance: Mathematics and Economics 49: 265–84. [Google Scholar] [CrossRef]
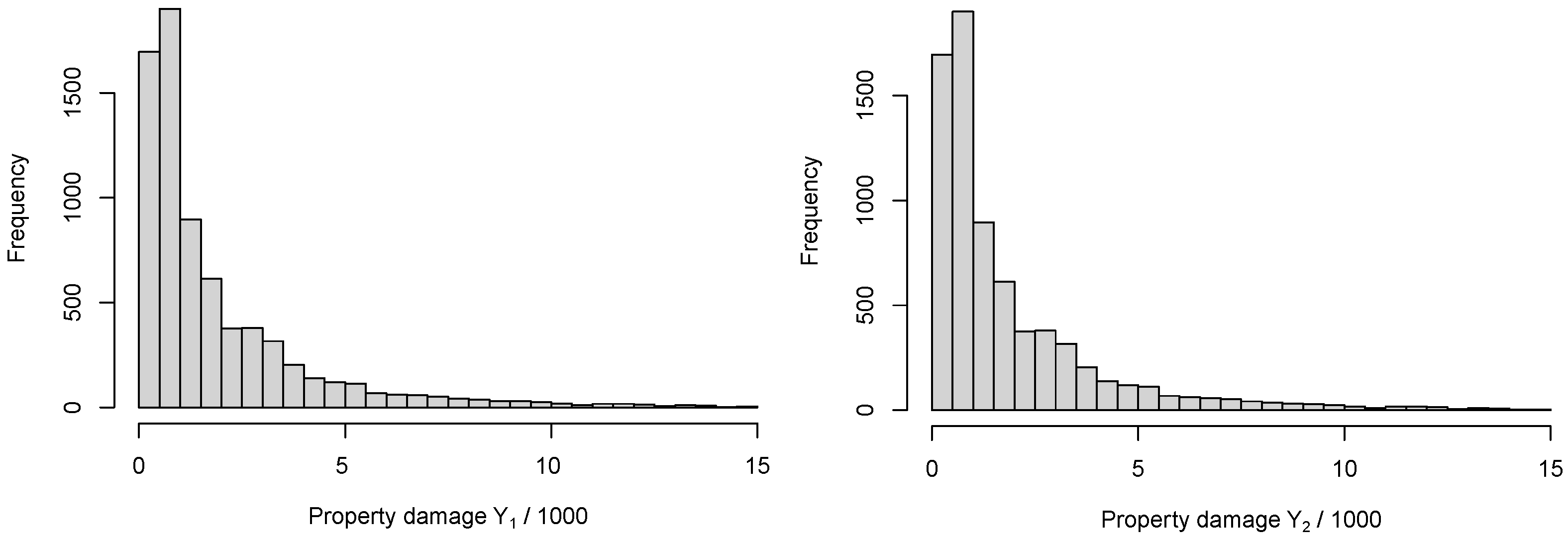
| Aggregated Claim | Min | Median | Mean | Max | Standard Deviation | Correlation | p-Value |
|---|---|---|---|---|---|---|---|
| 0.9 | 2413.4 | 11,017.3 | 251,958.2 | 27,128.85 | 0.1095 | 0.000 | |
| 6.2 | 1012.4 | 1871.2 | 14,818.2 | 2217.138 |
| Horse Power (CC) | Policy Type (PT) | Region | |
|---|---|---|---|
| C1 | 2036 | 1144 | 4220 |
| C2 | 2417 | 1940 | 2333 |
| C3 | 1833 | 4179 | 710 |
| C4 | 977 | - | - |
| BPA | BEIG | |||
|---|---|---|---|---|
| Response | ||||
| 0.5258 | 0.7905 | |||
| (0.0394) | (0.016) | |||
| Intercept | 8.6756 | 8.0076 | 8.5108 | 7.8137 |
| (0.0979) | (0.0905) | (0.0905) | (0.0861) | |
| Driver’s Age | 0.0010 | 0.0028 | 0.0007 | 0.0028 |
| (0.0014) | (0.0012) | (0.0014) | (0.0013) | |
| CC: C2 | −0.0854 | 0.0761 | −0.0523 | 0.0918 |
| (0.0486) | (0.0431) | (0.0481) | (0.0455) | |
| CC: C3 | 0.0517 | 0.0661 | 0.0498 | 0.0615 |
| (0.0517) | (0.0463) | (0.0517) | (0.0489) | |
| CC: C4 | −0.0064 | 0.1104 | 0.0238 | 0.1183 |
| (0.0633) | (0.0564) | (0.0625) | (0.0595) | |
| PT: C2 | 0.4555 | −0.0352 | 0.3859 | −0.0684 |
| (0.0614) | (0.0535) | (0.0599) | (0.0564) | |
| PT: C3 | 0.4057 | −0.0764 | 0.3622 | −0.0989 |
| (0.0559) | (0.0482) | (0.0540) | (0.0506) | |
| Vehcle’s Age | 0.0155 | −0.0015 | 0.0139 | −0.0021 |
| (0.0035) | (0.0031) | (0.0035) | (0.0033) | |
| Region: C2 | −0.1552 | 0.0502 | −0.1125 | 0.0736 |
| (0.0417) | (0.0369) | (0.0411) | (0.0389) | |
| Region: C3 | 0.2422 | −0.0306 | 0.2493 | −0.0189 |
| (0.0644) | (0.0577) | (0.0643) | (0.0609) | |
| AIC | 267,937.7 | 267,843.1 | ||
| BIC | 268,082.4 | 267,987.8 | ||
| True | Copula with PA | BPA | True | Copula with PA | BPA | ||
| 2 | 2.0713 | 2.6455 | 3 | 3.0353 | 2.6455 | ||
| Intercept | −1 | −1.0445 | −1.0447 | Intercept | −1.5 | −1.5936 | −1.5675 |
| 0.0003 | 0.0012 | 0.0008 | 0.003 | 0.0065 | 0.0070 | ||
| −0.4 | −0.3527 | −0.3603 | −0.3 | −0.3182 | −0.3152 | ||
| −0.05 | 0.0125 | −0.0089 | −0.2 | −0.2113 | −0.2205 | ||
| 0.1 | 0.0385 | 0.0190 | −0.05 | −0.0329 | −0.0227 | ||
| 0.2 | 0.1422 | 0.1651 | 0.15 | 0.1675 | 0.1628 | ||
| 0.3 | 0.2438 | 0.2571 | 0.25 | 0.2746 | 0.2700 | ||
| 0.4 | 0.3157 | 0.3216 | 0.35 | 0.4538 | 0.4366 | ||
| 0.45 | 0.5197 | 0.5063 | |||||
| 0.2 | 0.1941 | ||||||
| AIC | −4486.499 | −4418.983 | BIC | −4356.155 | −4301.673 | ||
| True | Copula with EIG | BEIG | True | Copula with EIG | BEIG | ||
| 2 | 2.0168 | 2.1322 | 3 | 2.7243 | 2.1322 | ||
| Intercept | −1 | −1.0676 | −1.0694 | Intercept | −1.5 | −1.4777 | −1.4709 |
| 0.0003 | 0 | −0.0002 | 0.003 | −0.0020 | -0.0008 | ||
| −0.4 | −0.3679 | −0.0002 | −0.3 | −0.2583 | −0.2654 | ||
| −0.05 | −0.0411 | −0.0348 | −0.2 | −0.1480 | −0.1601 | ||
| 0.1 | 0.1598 | 0.1676 | −0.05 | −0.0230 | −0.0279 | ||
| 0.2 | 0.2485 | 0.2507 | 0.15 | 0.1724 | 0.1661 | ||
| 0.3 | 0.3525 | 0.3589 | 0.25 | 0.2030 | 0.2083 | ||
| 0.4 | 0.4232 | 0.4334 | 0.35 | 0.3321 | 0.3378 | ||
| 0.45 | 0.4537 | 0.4450 | |||||
| 0.2 | 0.1920 | ||||||
| AIC | −3310.483 | −3260.53 | BIC | −3180.139 | −3143.22 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Dassios, A.; Tzougas, G. EM Estimation for the Bivariate Mixed Exponential Regression Model. Risks 2022, 10, 105. https://doi.org/10.3390/risks10050105
Chen Z, Dassios A, Tzougas G. EM Estimation for the Bivariate Mixed Exponential Regression Model. Risks. 2022; 10(5):105. https://doi.org/10.3390/risks10050105
Chicago/Turabian StyleChen, Zezhun, Angelos Dassios, and George Tzougas. 2022. "EM Estimation for the Bivariate Mixed Exponential Regression Model" Risks 10, no. 5: 105. https://doi.org/10.3390/risks10050105
APA StyleChen, Z., Dassios, A., & Tzougas, G. (2022). EM Estimation for the Bivariate Mixed Exponential Regression Model. Risks, 10(5), 105. https://doi.org/10.3390/risks10050105








