Risk Assessment of Polish Joint Stock Companies: Prediction of Penalties or Compensation Payments
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Analysis of Variables
3.2. Sample Selection for the Modelling Process
3.3. Supervised Learning
3.4. Model Evaluation and Interpretation (SHAP Approach)
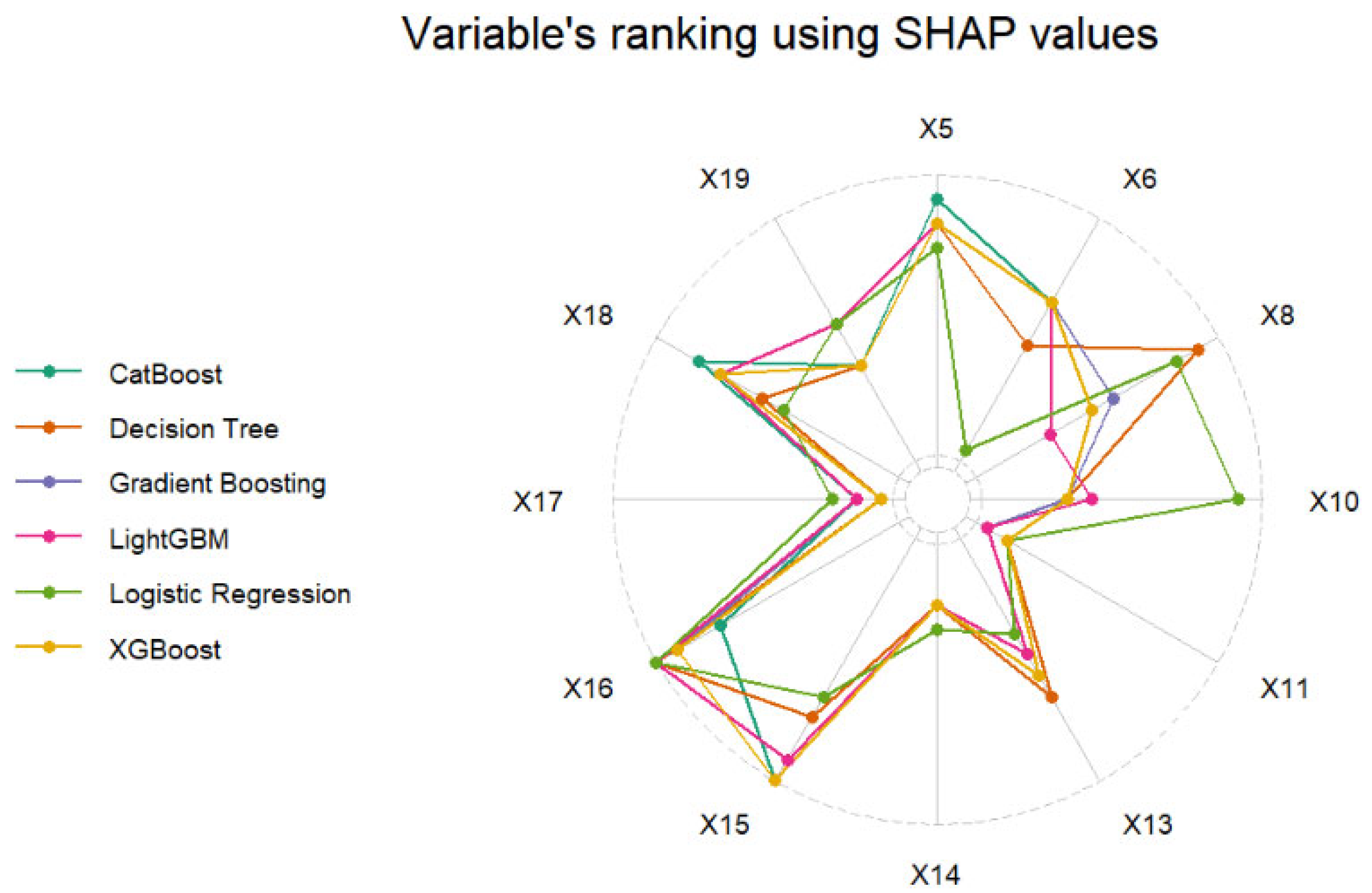
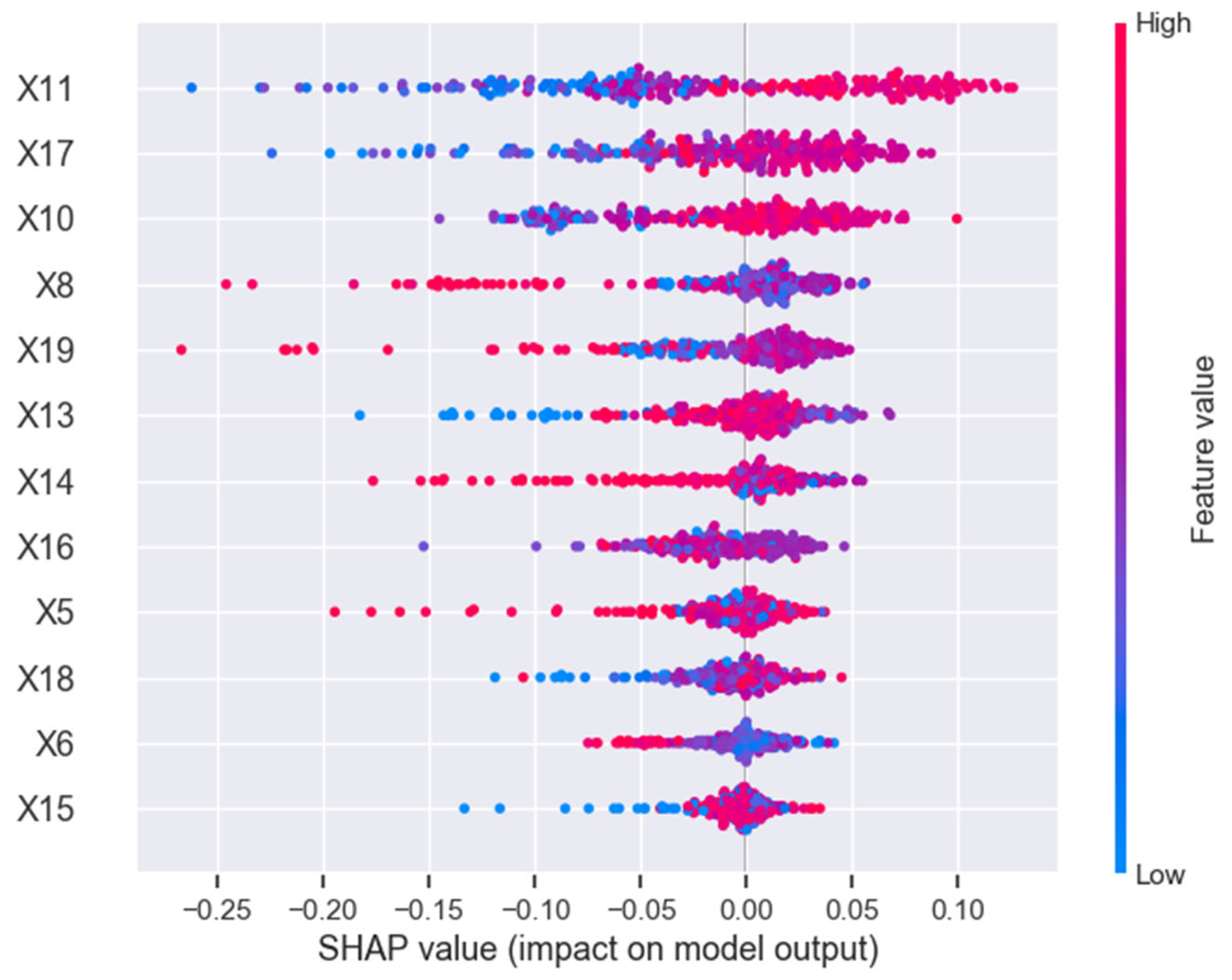
4. Results
4.1. Description of Data
4.1.1. Dependent Variable
4.1.2. Independent Variables
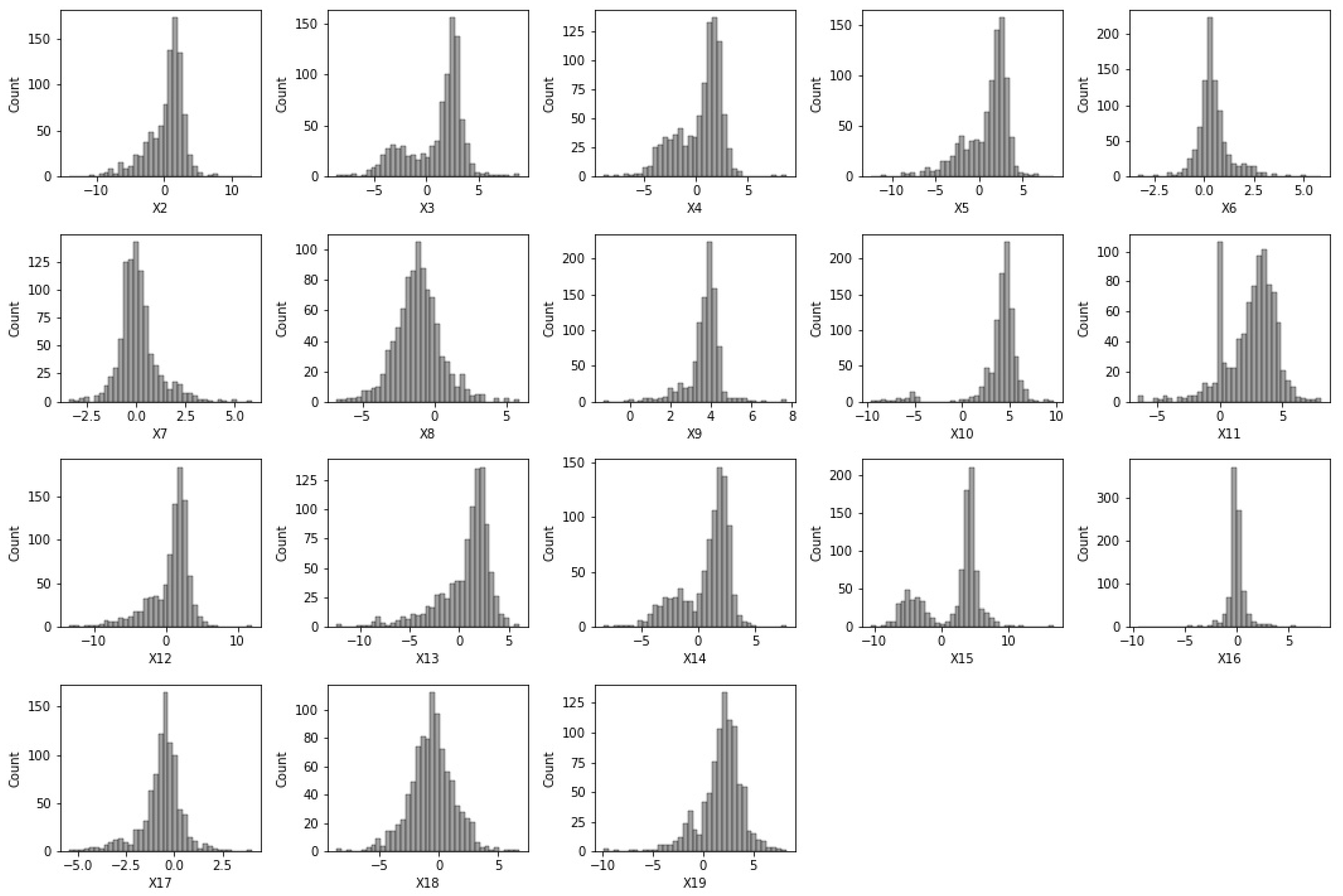
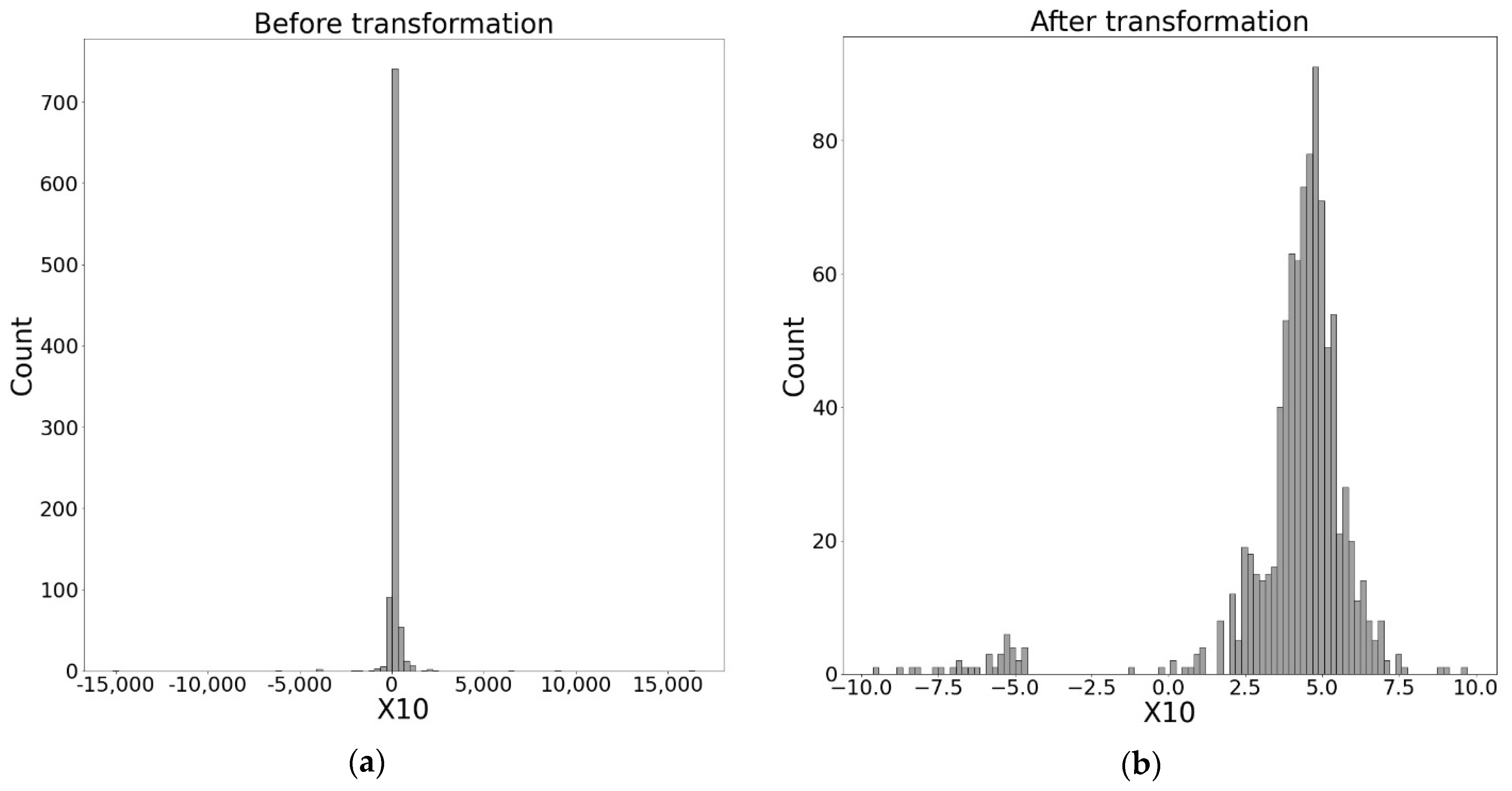
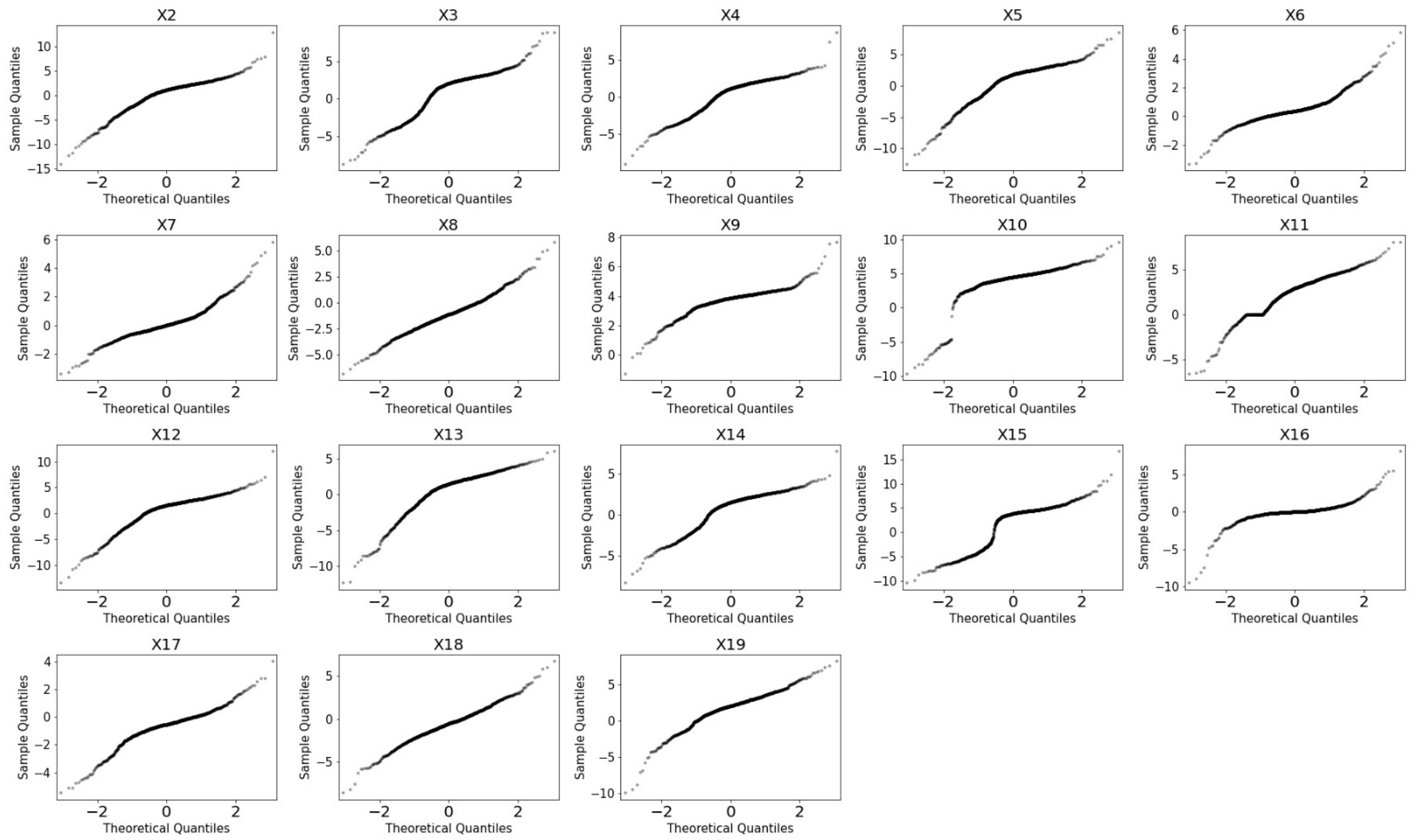
4.2. Analysis of Independent Variables
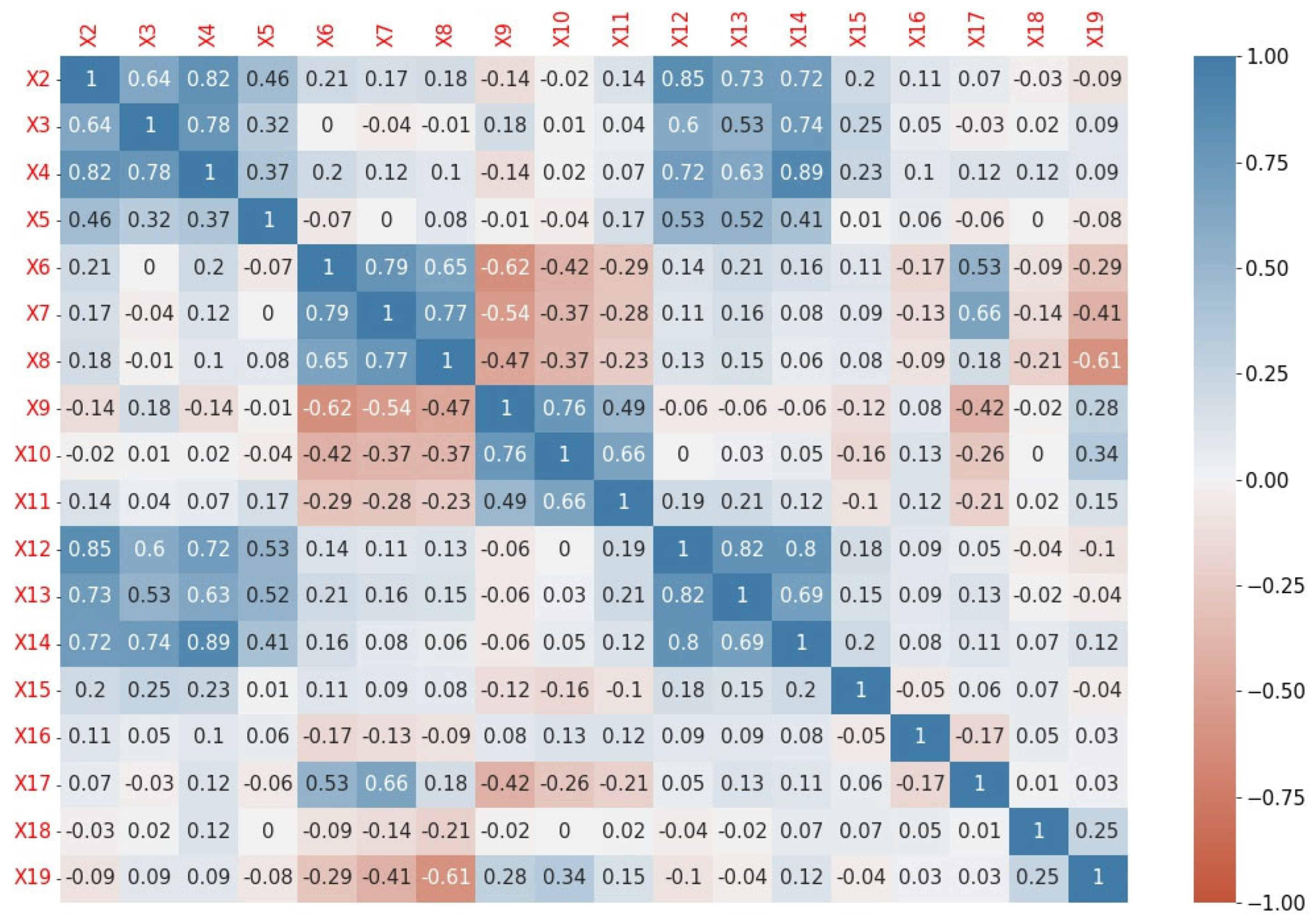
4.3. Correlation Analysis
- Step 1: Similar to the case of X12, the X2 variable correlated in accordance with the approved threshold with three other variables. There was also a strong correlation between X12 and X2, but X2 had a lower impact on the dependent variable than X12 based on the value of the Phi coefficient;
- Step 2: the X7 and X12 variables correlated in accordance with the approved threshold with two other variables;
- Step 3: X9 correlated with one variable (labelled X10), but its correlation with the dependent variable based on the value of the Phi coefficient was weaker than for X10.
4.4. Division of Data into a Training Set and a Test Set
- I group: <minimum value; I quartile>
- II group: (I quartile; median>
- III group: (median; III quartile>
- IV group: (III quartile; maximum value>
4.5. Supervised Learning
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | Elektrobudowa SA financial situation (in Polish) is available on: https://www.rynekelektryczny.pl/spor-elektrobudowy-i-orlenu-dotyczacy-metatezy/ (accessed on 21 January 2022). |
| 2 | Documentations of these libraries are available on the official websites dedicated to these packages: https://scikit-learn.org/stable/index.html, https://xgboost.readthedocs.io/en/latest/python/python_intro.html, https://catboost.ai/en/docs/, https://lightgbm.readthedocs.io/en/latest/index.html (accessed on 21 January 2022). |
| 3 | This information was available on the website: https://lightgbm.readthedocs.io/en/latest/Features.html#references (accessed on 21 January 2022). |
| 4 | Information about the payment of penalties by companies is available on: https://www.knf.gov.pl/o_nas/Kary_nalozone_przez_KNF (accessed on 21 January 2022). |
| 5 | The explanation of Elektrobudowa SA situation (in Polish) is available on: https://wysokienapiecie.pl/39649-elektrobudowa-idzie-pod-mlotek/ (accessed on 21 January 2022). |
References
- Ala’raj, Maher, and Maysam F. Abbod. 2016. Classifiers consensus system approach for credit scoring. Knowledge-Based Systems 104: 89–105. [Google Scholar] [CrossRef]
- Al-Hashedi, Khaled Gubran, and Pritheega Magalingam. 2021. Financial fraud detection applying data mining techniques: A comprehensive review from 2009 to 2019. Computer Science Review 40: 100402. [Google Scholar] [CrossRef]
- Almamy, Jeehan, John Aston, and Leonard N. Ngwa. 2016. An evaluation of Altman’s Z-score using cash flow ratio to predict corporate failure amid the recent financial crisis: Evidence from the UK. Journal of Corporate Finance 36: 278–85. [Google Scholar] [CrossRef]
- Altman, Edward I. 1968. Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. The Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Awad, Mariette, and Rahul Khanna. 2015. Efficient Learning Machines. Theories, Concepts, and Applications for Engineers and System Designers. New York: Apress Open. [Google Scholar]
- Bakouregui, Abdoulaye Sanni, Hamdy M. Mohamed, Ammar Yahia, and Brahim Benmokrane. 2021. Explainable extreme gradient boosting tree-based prediction of load-carrying capacity of FRP-RC columns. Engineering Structures 245: 112836. [Google Scholar] [CrossRef]
- Barboza, Flavio, Herbert Kimura, and Edward Altman. 2017. Machine learning models and bankruptcy prediction. Expert Systems with Applications 83: 405–17. [Google Scholar] [CrossRef]
- Beaver, William H. 1966. Financial Ratios As Predictors of Failure. Journal of Accounting Research 4: 71–111. [Google Scholar] [CrossRef]
- Bequé, Artem, and Stefan Lessmann. 2017. Extreme learning machines for credit scoring: An empirical evaluation. Expert Systems with Applications 86: 42–53. [Google Scholar] [CrossRef]
- Betz, Frank, Silviu Opricǎ, Tuomas A. Peltonen, and Peter Sarlin. 2014. Predicting distress in European banks. Journal of Banking and Finance 45: 225–41. [Google Scholar] [CrossRef] [Green Version]
- Chang, Yung-Chia, Kuei-Hu Chang, and Guan-Jhih Wu. 2018. Application of eXtreme gradient boosting trees in the construction of credit risk assessment models for financial institutions. Applied Soft Computing 73: 914–20. [Google Scholar] [CrossRef]
- Chawla, Nitesh V., Kevin W. Bowyer, Lawrence O. Hall, and W. Philip Kegelmeyer. 2002. SMOTE: Synthetic Minority Over-sampling Technique. Journal of Artificial Intelligence Research 16: 321–57. [Google Scholar] [CrossRef]
- Chen, Tianqi, and Carlos Guestrin. 2016. XGBoost: A scalable tree boosting system. Paper presented at the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13–17; New York: ACM, pp. 785–94. [Google Scholar] [CrossRef] [Green Version]
- Chollet, Francois. 2018. Deep Learning. Praca z Językiem Python i Biblioteką Keras. Gliwice: Helion. [Google Scholar]
- de Roux, Daniel, Boris Perez, Andrés Moreno, Maria del Pilar Villamil, and César Figueroa. 2018. Tax Fraud Detection for Under-Reporting Declarations Using an Unsupervised Machine Learning Approach. Paper presented at the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, August 19–23; New York: ACM, pp. 215–22. [Google Scholar] [CrossRef]
- Dietterich, Thomas G. 1997. Machine-Learning Research. AI Magazine 18: 97–136. [Google Scholar] [CrossRef]
- Dumitrescu, Elena-Ivona, Sullivan Hué, Christophe Hurlin, and Sessi Tokpavi. 2020. Machine Learning or Econometrics for Credit Scoring: Let’s Get the Best of Both Worlds. SSRN Electronic. [Google Scholar] [CrossRef]
- Fawcett, Tom, and Foster Provost. 2014. Analiza Danych w Biznesie. Sztuka Podejmowania Skutecznych Decyzji. Gliwice: Helion. [Google Scholar]
- Feng, Changyong, Hongyue Wang, Naiji Lu, Tian Chen, Hua He, Ying Lu, and Xin M. Tu. 2014. Log-transformation and its implications for data analysis. Shanghai Archives of Psychiatry 26: 105–9. [Google Scholar] [CrossRef]
- Friedman, Jerome H. 2002. Stochastic gradient boosting. Computational Statistics & Data Analysis 38: 367–78. [Google Scholar] [CrossRef]
- Futagami, Katsuya, Yusuke Fukazawa, Nakul Kapoor, and Tomomi Kito. 2021. Pairwise acquisition prediction with SHAP value interpretation. The Journal of Finance and Data Science 7: 22–44. [Google Scholar] [CrossRef]
- Geng, Ruibin, Indranil Bose, and Xi Chen. 2015. Prediction of financial distress: An empirical study of listed Chinese companies using data mining. European Journal of Operational Research 241: 236–47. [Google Scholar] [CrossRef]
- Harris, Terry. 2015. Credit scoring using the clustered support vector machine. Expert Systems with Applications 42: 741–50. [Google Scholar] [CrossRef] [Green Version]
- Jabeur, Sami Ben, Cheima Gharib, Salma Mefteh-Wali, and Wissal Ben Arfi. 2021. CatBoost model and artificial intelligence techniques for corporate failure prediction. Technological Forecasting and Social Change 166: 120658. [Google Scholar] [CrossRef]
- Ke, Guolin, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, and Tie Yan Liu. 2017. LightGBM: A highly efficient gradient boosting decision tree. Paper presented at the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, December 4–9; Red Hook: Curran Associates Inc., pp. 3149–57. [Google Scholar] [CrossRef]
- Le, Hong Hanh, and Jean-Laurent Viviani. 2018. Predicting bank failure: An improvement by implementing a machine-learning approach to classical financial ratios. Research in International Business and Finance 44: 16–25. [Google Scholar] [CrossRef]
- Lundberg, Scott M., and Su-In Lee. 2017. A Unified Approach to Interpreting Model Predictions. Paper presented at the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, December 4–9; Red Hook: Curran Associates Inc., pp. 4768–77. [Google Scholar] [CrossRef]
- Maldonado, Sebastián, Julio López, and Carla Vairetti. 2019. An alternative SMOTE oversampling strategy for high-dimensional datasets. Applied Soft Computing 76: 380–89. [Google Scholar] [CrossRef]
- Mangalathu, Sujith, Seong-Hoon Hwang, and Jong-Su Jeon. 2020. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Engineering Structures 219: 110927. [Google Scholar] [CrossRef]
- Marqués, A. I., V. García, and J. S. Sánchez. 2012. Exploring the behaviour of base classifiers in credit scoring ensembles. Expert Systems with Applications 39: 10244–50. [Google Scholar] [CrossRef]
- Matthews, Spencer, and Brian Hartman. 2021. mSHAP: SHAP Values for Two-Part Models. Risks 10: 3. [Google Scholar] [CrossRef]
- Monedero, Iñigo, Félix Biscarri, Carlos León, Juan I. Guerrero, Jesús Biscarri, and Rocío Millán. 2012. Detection of frauds and other non-technical losses in a power utility using Pearson coefficient, Bayesian networks and decision trees. International Journal of Electrical Power & Energy Systems 34: 90–98. [Google Scholar] [CrossRef]
- Mselmi, Nada, Amine Lahiani, and Taher Hamza. 2017. Financial distress prediction: The case of French small and medium-sized firms. International Review of Financial Analysis 50: 67–80. [Google Scholar] [CrossRef]
- Ng, Wing W.Y., Zhengxi Liu, Jianjun Zhang, and Witold Pedrycz. 2021. Maximizing minority accuracy for imbalanced pattern classification problems using cost-sensitive Localized Generalization Error Model. Applied Soft Computing 104: 107178. [Google Scholar] [CrossRef]
- Ohlson, James A. 1980. Financial Ratios and the Probabilistic Prediction of Bankruptcy. Journal of Accounting Research 18: 109–31. [Google Scholar] [CrossRef] [Green Version]
- Park, Sunghwa, Hyunsok Kim, Janghan Kwon, and Taeil Kim. 2021. Empirics of Korean Shipping Companies’ Default Predictions. Risks 9: 159. [Google Scholar] [CrossRef]
- Patel, Harsh H., and Purvi Prajapati. 2018. Study and Analysis of Decision Tree Based Classification Algorithms. International Journal of Computer Sciences and Engineering 6: 74–78. [Google Scholar] [CrossRef]
- Petropoulos, Anastasios, Vasilis Siakoulis, Evangelos Stavroulakis, and Nikolaos E. Vlachogiannakis. 2020. Predicting bank insolvencies using machine learning techniques. International Journal of Forecasting 36: 1092–1113. [Google Scholar] [CrossRef]
- Pham, Xuan T. T., and Tin H. Ho. 2021. Using boosting algorithms to predict bank failure: An untold story. International Review of Economics & Finance 76: 40–54. [Google Scholar] [CrossRef]
- Pisula, Tomasz. 2017. Zastosowanie ensemble klasyfikatorów do oceny ryzyka upadłości przedsiębiorstw na przykładzie firm sektora produkcyjnego działających na Podkarpaciu. Zarządzanie i Finanse 15: 279–93. [Google Scholar]
- Prokhorenkova, Liudmila, Gleb Gusev, Aleksandr Vorobev, Anna Veronika Dorogush, and Andrey Gulin. 2018. Catboost: Unbiased boosting with categorical features. Paper presented at the 32nd International Conference on Neural Information Processing Systems (NIPS’18), Montréal, QC, Canada, December 3–8; Red Hook: Curran Associates Inc., pp. 6639–49. [Google Scholar] [CrossRef]
- Rachakonda, Aditya Ramana, and Ayush Bhatnagar. 2021. ARatio: Extending area under the ROC curve for probabilistic labels. Pattern Recognition Letters 150: 265–71. [Google Scholar] [CrossRef]
- Sagi, Omer, and Lior Rokach. 2021. Approximating XGBoost with an interpretable decision tree. Information Sciences 572: 522–42. [Google Scholar] [CrossRef]
- Sahin, Yusuf, Serol Bulkan, and Ekrem Duman. 2013. A cost-sensitive decision tree approach for fraud detection. Expert Systems with Applications 40: 5916–23. [Google Scholar] [CrossRef]
- Sesmero, M. Paz, José Antonio Iglesias, Elena Magán, Agapito Ledezma, and Araceli Sanchis. 2021. Impact of the learners diversity and combination method on the generation of heterogeneous classifier ensembles. Applied Soft Computing 111: 107689. [Google Scholar] [CrossRef]
- Severino, Matheus Kempa, and Yaohao Peng. 2021. Machine learning algorithms for fraud prediction in property insurance: Empirical evidence using real-world microdata. Machine Learning with Applications 5: 100074. [Google Scholar] [CrossRef]
- Shrivastav, Santosh Kumar, and P. Janaki Ramudu. 2020. Bankruptcy Prediction and Stress Quantification Using Support Vector Machine: Evidence from Indian Banks. Risks 8: 52. [Google Scholar] [CrossRef]
- Sun, Jie, Hui Li, Hamido Fujita, Binbin Fu, and Wenguo Ai. 2020. Class-imbalanced dynamic financial distress prediction based on Adaboost-SVM ensemble combined with SMOTE and time weighting. Information Fusion 54: 128–44. [Google Scholar] [CrossRef]
- Tian, Zhenya, Jialiang Xiao, Haonan Feng, and Yutian Wei. 2020. Credit Risk Assessment based on Gradient Boosting Decision Tree. Procedia Computer Science 174: 150–60. [Google Scholar] [CrossRef]
- Tsai, C, and J Wu. 2008. Using neural network ensembles for bankruptcy prediction and credit scoring. Expert Systems with Applications 34: 2639–49. [Google Scholar] [CrossRef]
- Wang, Shutao, Shiyu Liu, Jingkun Zhang, Xiange Che, Yuanyuan Yuan, Zhifang Wang, and Deming Kong. 2020. A new method of diesel fuel brands identification: SMOTE oversampling combined with XGBoost ensemble learning. Fuel 282: 118848. [Google Scholar] [CrossRef]
- Xia, Yufei, Chuanzhe Liu, Bowen Da, and Fangming Xie. 2018. A novel heterogeneous ensemble credit scoring model based on bstacking approach. Expert Systems with Applications 93: 182–99. [Google Scholar] [CrossRef]
- Zhao, Huimin, Atish P. Sinha, and Wei Ge. 2009. Effects of feature construction on classification performance: An empirical study in bank failure prediction. Expert Systems with Applications 36: 2633–44. [Google Scholar] [CrossRef]
- Zhou, Ligang. 2013. Performance of corporate bankruptcy prediction models on imbalanced dataset: The effect of sampling methods. Knowledge-Based Systems 41: 16–25. [Google Scholar] [CrossRef]
- Zizi, Youssef, Amine Jamali-Alaoui, Badreddine El Goumi, Mohamed Oudgou, and Abdeslam El Moudden. 2021. An Optimal Model of Financial Distress Prediction: A Comparative Study between Neural Networks and Logistic Regression. Risks 9: 200. [Google Scholar] [CrossRef]
- Zizi, Youssef, Mohamed Oudgou, and Abdeslam El Moudden. 2020. Determinants and Predictors of SMEs’ Financial Failure: A Logistic Regression Approach. Risks 8: 107. [Google Scholar] [CrossRef]
- Zmijewski, Mark E. 1984. Methodological Issues Related to the Estimation of Financial Distress Prediction Models. Journal of Accounting Research 22: 59–82. [Google Scholar] [CrossRef]

| Year | Number of Companies |
|---|---|
| 2017 | 305 |
| 2018 | 311 |
| 2019 | 312 |
| Year | Number of “Bad” | Percentage of “Bad” [%] |
|---|---|---|
| 2017 | 93 | 30.49 |
| 2018 | 95 | 30.55 |
| 2019 | 96 | 30.77 |
| Variable | Variable Name | Character of Variable |
|---|---|---|
| X1 | Net profit | Dichotomous |
| X2 | Return on sales | Continuous |
| X3 | Return on equity | Continuous |
| X4 | Return on assets | Continuous |
| X5 | Operating cash flow margin | Continuous |
| X6 | Current Ratio | Continuous |
| X7 | Quick Ratio | Continuous |
| X8 | Absolute liquidity ratio | Continuous |
| X9 | Debt ratio | Continuous |
| X10 | Debt to equity ratio | Continuous |
| X11 | Long-term debt to equity ratio | Continuous |
| X12 | Operating profit margin | Continuous |
| X13 | Sales profit margin | Continuous |
| X14 | Basic earning power ratio | Continuous |
| X15 | Net income to operating cash flow | Continuous |
| X16 | Indicator of overall financial standing | Continuous |
| X17 | Receivables to payables coverage ratio | Continuous |
| X18 | Return on investment | Continuous |
| X19 | Investment turnover ratio | Continuous |
| Category | Number of Occurrences | Percentage of Occurrences [%] |
|---|---|---|
| 0—loss | 263 | 28.34 |
| 1—profit | 665 | 71.66 |
| Variable | Mean | Minimum Value | Maximum Value | Median | Coefficient of Variation [%] | Skewness Coefficient |
|---|---|---|---|---|---|---|
| X2 | −1387.96 | −1,216,550.00 | 445,611.11 | 2.94 | −3123.11 | −22.71 |
| X3 | 13.76 | −5658.89 | 7278.58 | 7.70 | 3464.02 | 6.96 |
| X4 | −6.78 | −7758.00 | 6325.71 | 3.05 | −5122.08 | −5.74 |
| X5 | −480.07 | −246,550.00 | 5228.21 | 5.79 | −1783.38 | −26.17 |
| X6 | 3.35 | 0.04 | 358.67 | 1.41 | 438.60 | 17.99 |
| X7 | 2.86 | 0.03 | 358.67 | 1.01 | 512.24 | 18.20 |
| X8 | 1.95 | 0.00 | 358.67 | 0.32 | 730.08 | 19.56 |
| X9 | 55.73 | 0.28 | 2262.17 | 47.92 | 188.37 | 16.80 |
| X10 | 129.55 | −15,158.62 | 16,453.24 | 89.90 | 692.44 | 2.04 |
| X11 | 46.34 | −686.19 | 3314.26 | 18.74 | 388.58 | 12.59 |
| X12 | −986.23 | −699,000.00 | 162,711.11 | 4.74 | −2496.28 | −24.90 |
| X13 | −581.19 | −233,300.00 | 361.05 | 4.23 | −1761.10 | −21.28 |
| X14 | −1.86 | −3998.00 | 2309.78 | 4.54 | −8464.50 | −14.40 |
| X15 | 20,047.12 | −35,700.00 | 18,374,400.00 | 46.37 | 3008.83 | 30.36 |
| X16 | −22.47 | −13,123.06 | 3202.08 | 0.99 | −2307.00 | −20.48 |
| X17 | 0.91 | 0.00 | 56.19 | 0.59 | 245.68 | 17.60 |
| X18 | −1.00 | −292.41 | 146.86 | 0.20 | −1859.29 | −8.05 |
| X19 | 36.83 | −2.99 | 3866.35 | 7.99 | 474.30 | 14.70 |
| X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| −1.20 | −0.86 | −0.84 | −1.37 | 1.05 | 1.05 | 0.22 | −1.19 | −3.21 |
| X11 | X12 | X13 | X14 | X15 | X16 | X17 | X18 | X19 |
| −0.94 | −1.43 | −1.58 | −1.09 | −0.79 | −1.51 | −0.85 | −0.15 | −1.04 |
| X5 | X6 | X8 | X10 | X11 | X13 | X14 | X15 | X16 | X17 | X18 | X19 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0000 | 0.0000 | 0.0197 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.5602 | 0.2839 | 0.0000 | 0.0000 |
| Year | Companies | “Bad” |
|---|---|---|
| 2017 | 305 | 93 |
| 2018 | 311 | 95 |
| 2019 | 312 | 96 |
| Category | I Group | II Group | III Group | IV Group |
|---|---|---|---|---|
| 0 | 67 | 55 | 43 | 47 |
| 1 | 10 | 21 | 33 | 29 |
| Category | I Group | II Group | III Group | IV Group |
|---|---|---|---|---|
| 0 | 69 | 54 | 44 | 49 |
| 1 | 9 | 24 | 33 | 29 |
| Category | I Group | II Group | III Group | IV Group |
|---|---|---|---|---|
| 0 | 73 | 51 | 43 | 49 |
| 1 | 5 | 27 | 35 | 29 |
| Character of Set | Category | Number of Records |
|---|---|---|
| Training set | 1 | 206 |
| 0 | 478 | |
| Test set | 1 | 78 |
| 0 | 166 |
| Character of Set | Category | Number of Records |
|---|---|---|
| Training set | 1 | 478 |
| 0 | 478 | |
| Test set | 1 | 78 |
| 0 | 166 |
| Method | AUC | Cohen’s Kappa |
|---|---|---|
| Logistic regression | 0.6522 | 0.1903 |
| Decision tree | 0.5913 | 0.1767 |
| XGBoost | 0.7159 | 0.2754 |
| Gradient boosting | 0.7100 | 0.2925 |
| LightGBM | 0.7178 | 0.2716 |
| CatBoost | 0.7321 | 0.3027 |
| Method | Standard Deviation of AUC | Standard Deviation of Cohen’s Kappa |
|---|---|---|
| Logistic regression | 0.0244 | 0.0425 |
| Decision tree | 0.0347 | 0.0657 |
| XGBoost | 0.0194 | 0.0162 |
| Gradient boosting | 0.0181 | 0.0319 |
| LightGBM | 0.0210 | 0.0566 |
| CatBoost | 0.0195 | 0.0393 |
| Ranking | Variable |
|---|---|
| 1 | X11 |
| 2 | X17 |
| 3 | X14 |
| 4 | X10 |
| 5 | X19 |
| 6 | X13 |
| 7 | X8 |
| 8 | X6 |
| 9 | X18 |
| 10 | X5 |
| 11 | X16 |
| 12 | X15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szymura, A. Risk Assessment of Polish Joint Stock Companies: Prediction of Penalties or Compensation Payments. Risks 2022, 10, 102. https://doi.org/10.3390/risks10050102
Szymura A. Risk Assessment of Polish Joint Stock Companies: Prediction of Penalties or Compensation Payments. Risks. 2022; 10(5):102. https://doi.org/10.3390/risks10050102
Chicago/Turabian StyleSzymura, Aleksandra. 2022. "Risk Assessment of Polish Joint Stock Companies: Prediction of Penalties or Compensation Payments" Risks 10, no. 5: 102. https://doi.org/10.3390/risks10050102
APA StyleSzymura, A. (2022). Risk Assessment of Polish Joint Stock Companies: Prediction of Penalties or Compensation Payments. Risks, 10(5), 102. https://doi.org/10.3390/risks10050102





