A Novel Implementation of Siamese Type Neural Networks in Predicting Rare Fluctuations in Financial Time Series
Abstract
:1. Introduction
1.1. Literature Review on Classification of Tabular Data Using CNNs
1.2. Motivation
2. Materials and Methods
2.1. A Brief Mathematical Survey on Financial Analytics
- , where a short-term upward share movement is expected:
- , where not much short-term share movement is expected:
- , where a short-term downward share movement is expected:
2.2. Materials: Data
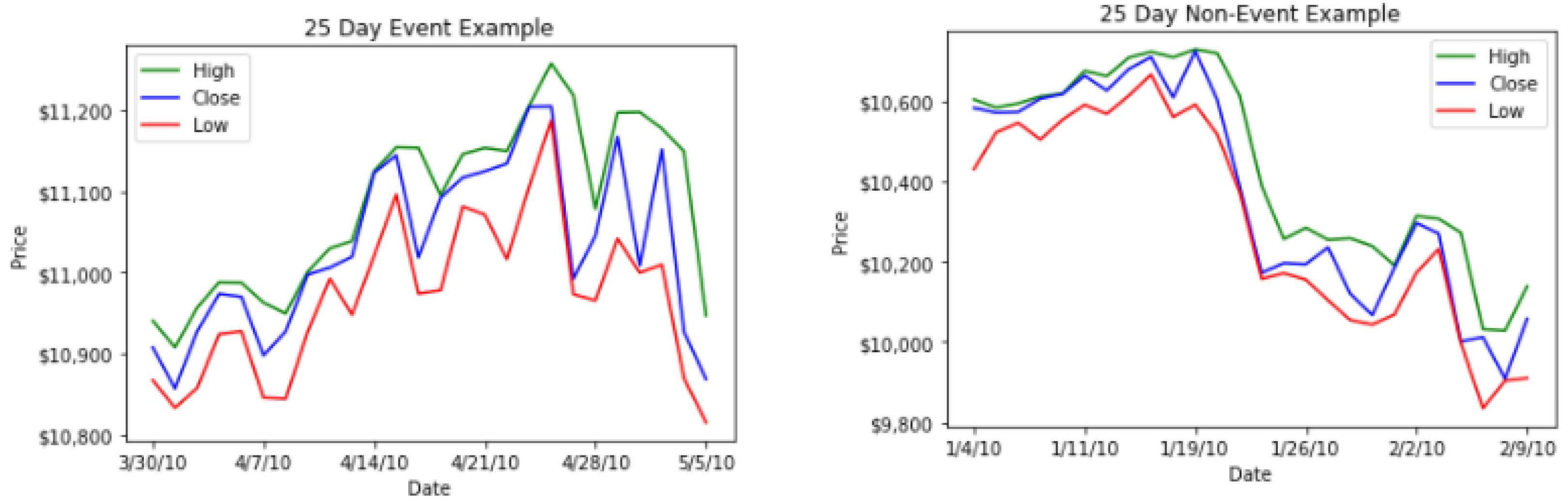
- We collect High, Low and Close price for a 25 day period. This results in tabular data that can be arranged in a matrix. The columns of this matrix represent the High, Low and Close price of the day and the ith row of the matrix represents the ith day in the 25 day window.
- The values across each row are converted to an 8 bit integer between 0 and 255 and stored in the vector below.where and represents the transformed values of High, Low and Close price of the day.
- We then arrange the ’s in a way that allows us to represent the temporal relationship spatially.
- This allows us to create an image corresponding to the matrix as shown in Figure 1 below.
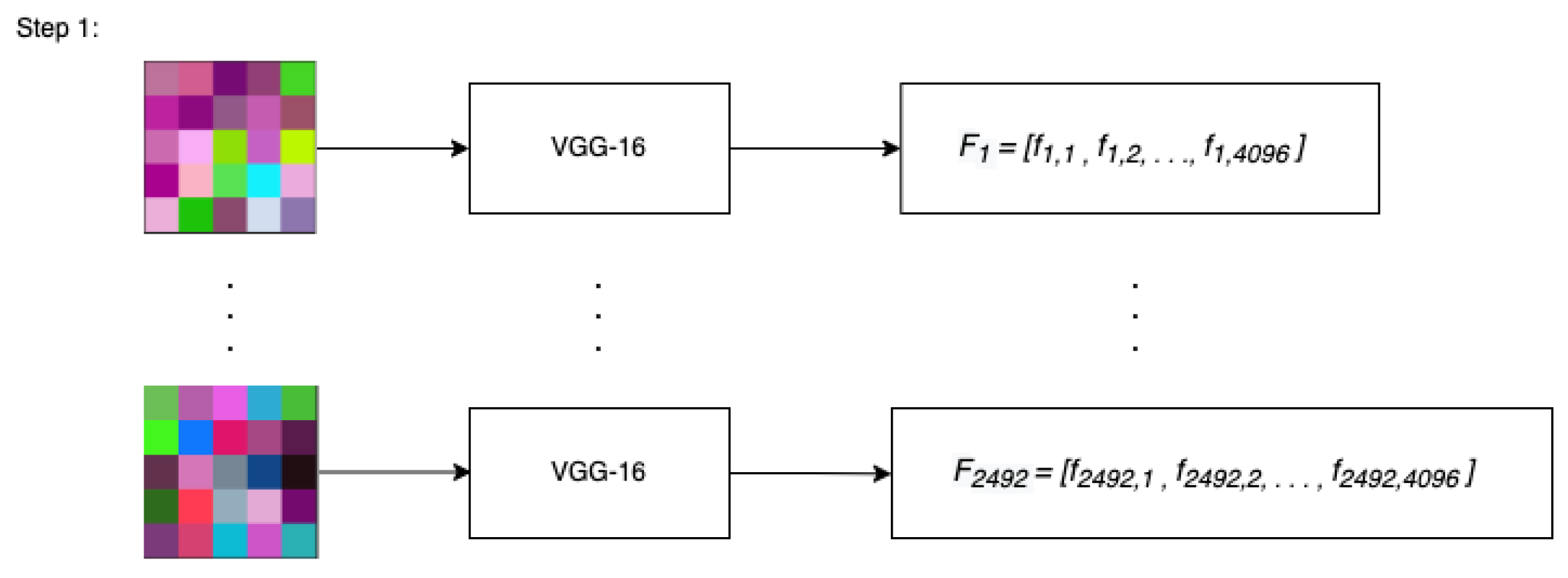
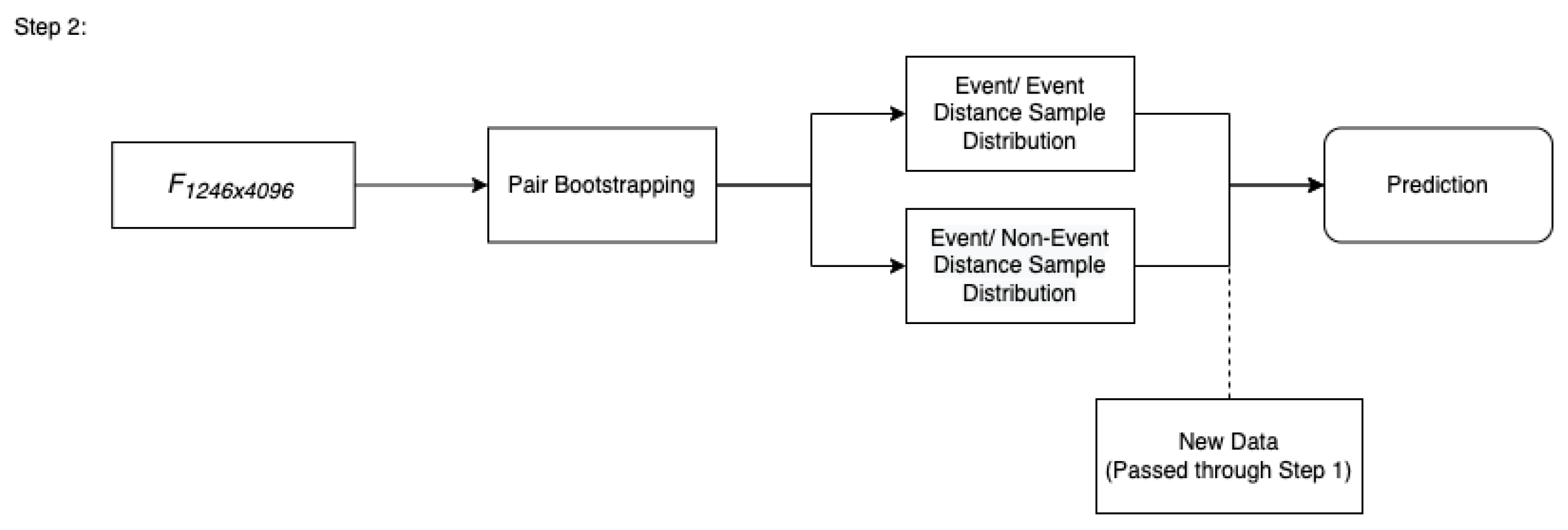
2.3. Methods
3. Results
4. Discussion
- Limited data resulting in production of limited images
- Extreme class imbalance (99-1, 95-5, 90-10) as is common with rare event prediction.
- image size, class imbalance level and training and testing split ratios were varied
- Principal Component Analysis (PCA) on the matrix before training and testing was performed
- different types of re-sampling techniques were used and
- hyperparameter variations were considered.
5. Conclusions
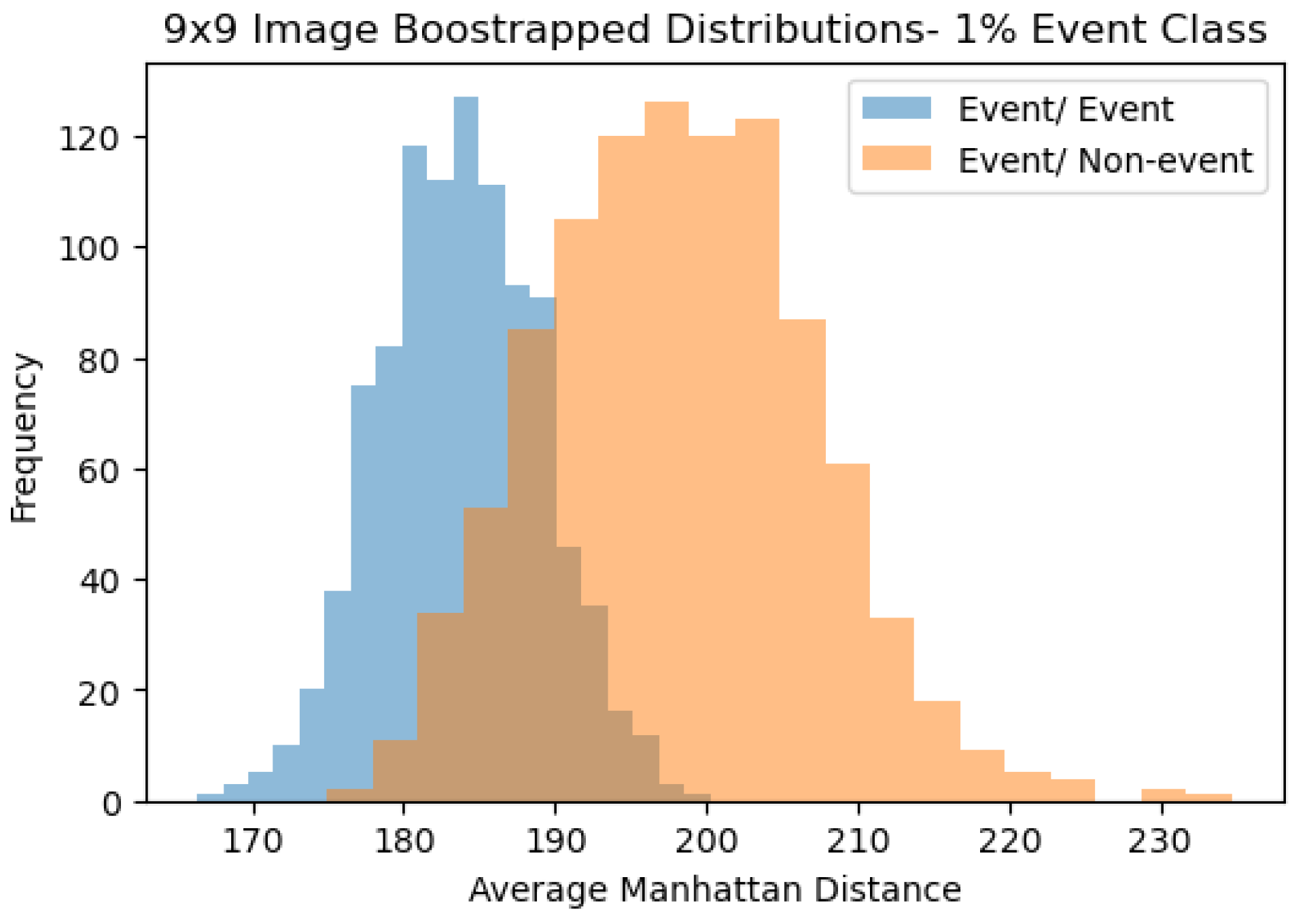
- The first is that an active learning approach (Malialis et al. 2020) can be applied to this method in which after every day, the two bootstraps are retaken to include the new observation. While this method may be computationally expensive, it could lead to a more pronounced separation in the event/event and event/non-event distributions, thereby leading to better predictions.
- In this paper we proposed a “snake" method to transform time series into images. Since there a variety of ways to visualize tabular data as an image (Hatami et al. 2017; Sezer and Ozbayoglu 2018; Sharma et al. 2019; Sharma and Kumar 2020a; Sun et al. 2019), we note this as a means to parameterize or tune our method for other future applications. For instance, the research presented in this paper made use of square images. However, one could consider circular images (Wang and Oates 2015), textured images (Sharma and Kumar 2020b) or images created through Markov Transition Field (MTF) (Wang and Oates 2015). Further research can be done to compare image shape or similarly develop new transformation techniques that result in other types of images.
- We believe different image classification frameworks such as ResNet50 (https://arxiv.org/abs/1512.03385, accessed on 7 November 2021) can be experimented with to further improve results as they can effect the image resizing as well as the output feature vector that is used for similarity comparisons.
- For this research we used time series data from only the S&P 500 index. The combination of S&P 500 with other time series data such as Dow Jones (https://finance.yahoo.com/quote/%5EDJI/, accessed on 7 November 2021) or Nasdaq (https://finance.yahoo.com/quote/%5EIXIC/, accessed on 7 November 2021) could help to identify further patterns to improve prediction accuracy, or related derived metrics such as volatility indexes.
- Lastly, although this paper investigated daily financial time series data (HLC) to predict and identify patterns for rare event prediction, the proposed approach could also be applied to intra-day trading applications as technical analyses are even more relevant there.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, Ozden Gur, and Umut Ariturk. 2014. Dynamic churn prediction framework with more effective use of rare event data: The case of private banking. Expert Systems with Applications 17: 7889–903. [Google Scholar]
- Bettman, Jenni L., Stephen J. Sault, and Emma L. Schultz. 2009. Fundamental and technical analysis: Substitutes or complements? Accounting & Finance 49: 21–36. [Google Scholar]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2001a. Non-Gaussian Ornstein-Uhlenbeck-based models and some of their uses in financial economics. Journal of the Royal Statistical Society Series B (Statistical Methodology) 63: 167–241. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2001b. Modelling by Lévy processes for financial econometrics. In Lévy Processes: Theory and Applications. Edited by Ole E. Barndorff-Nielsen, Thomas Mikosch and Sidney I. Resnick. Basel: Birkhäuser, pp. 283–318. [Google Scholar]
- Buturovic, Ljubomir, and Dejan Miljkovic. 2020. A novel method for classification of tabular data using convolutional neural networks. bioRxiv. [Google Scholar] [CrossRef]
- Chavarnakul, Thira, and David Enke. 2008. Intelligent technical analysis based equivolume charting for stock trading using neural networks. Expert Systems with Applications 34: 1004–17. [Google Scholar] [CrossRef]
- Cheng, Ching-Hsue, and You-Shyang Chen. 2007. Fundamental Analysis of Stock Trading Systems using Classification Techniques. Paper presented at International Conference on Machine Learning and Cybernetics, Hong Kong, China, August 19–22; pp. 1377–82. [Google Scholar] [CrossRef]
- Cheon, Seong-Pyo, Sungshin Kim, So-Young Lee, and Chong-Bum Lee. 2009. Bayesian networks based rare event prediction with sensor data. Knowledge-Based Systems 22: 336–43. [Google Scholar] [CrossRef]
- Drakopoulou, Veliota. 2016. A Review of Fundamental and Technical Stock Analysis Techniques. Journal of Stock Forex Trading 5. [Google Scholar] [CrossRef]
- Ekapure, Shubham, Nuruddin Jiruwala, Sohan Patnaik, and Indranil SenGupta. 2021. A data-science-driven short-term analysis of Amazon, Apple, Google, and Microsoft stocks. arXiv arXiv:2107.14695. [Google Scholar]
- Esteva, Andre, Brett Kuprel, Roberto A. Novoa, Justin Ko, Susan M. Swetter, Helen M. Blau, and Sebastian Thrun. 2017. Dermatologist-level classification of skin cancer with deep neural networks. Nature 542: 115–18. [Google Scholar] [CrossRef]
- Gumbel, Emil Julius. 1958. Statistics of Extremes. New York: Columbia University Press. [Google Scholar]
- Habtemicael, Semere, and Indranil SenGupta. 2016. Pricing variance and volatility swaps for Barndorff-Nielsen and Shephard process driven financial markets. International Journal of Financial Engineering 3: 165002. [Google Scholar] [CrossRef]
- Hatami, Nima, Yann Gavet, and Johan Debayle. 2017. Classification of time series images using deep convolutional neural networks. Paper presented at International Conference on Machine Vision, Tenth International Conference on Machine Vision (ICMV), Vienna, Austria, November 13–15. [Google Scholar]
- Hu, Zexin, Yiqi Zhao, and Matloob Khushi. 2021. A Survey of Forex and Stock Price Prediction Using Deep Learning. Applied System Innovation 4: 9. [Google Scholar] [CrossRef]
- Issaka, Aziz, and Indranil SenGupta. 2017. Analysis of variance based instruments for Ornstein-Uhlenbeck type models: Swap and price index. Annals of Finance 13: 401–34. [Google Scholar] [CrossRef]
- Janjuaa, Zaffar Haider, Massimo Vecchioa, Mattia Antonini, and Fabio Antonelli. 2019. Antoniniab. Antonelli IRESE: An intelligent rare-event detection system using unsupervised learning on the IoT edge. Engineering Applications of Artificial Intelligence 84: 41–50. [Google Scholar] [CrossRef] [Green Version]
- Johnson, Justin M., and Taghi M. Khoshgoftaar. 2019. Survey on deep learning with class imbalance. Journal of Big Data 6. [Google Scholar] [CrossRef]
- Koch, Gregory, Richard Zemel, and Ruslan Salakhutdinov. 2015. Siamese neural networks for one- shot image recognition. Presented at the Deep Learning Workshop at the 2015 International Conference on Machine Learning, Lille, France; Available online: https://www.cs.cmu.edu/~rsalakhu/papers/oneshot1.pdf (accessed on 1 November 2021).
- Li, Jinyan, Lian-sheng Liu, Simon Fong, Raymond K. Wong, Sabah Mohammed, Jinan Fiaidhi, Yunsick Sung, and Kelvin K. L. Wong. 2017. Adaptive swarm balancing algorithms for rare-event prediction in imbalanced healthcare data. PLoS ONE 12: e0180830. [Google Scholar] [CrossRef] [Green Version]
- Li, Xuhong, Yves Grandvalet, and Franck Davoine. 2018. Explicit inductive bias for transfer learning with convolutional networks. Paper presented at International Conference on Machine Learning, Stockholm, Sweden, July 10–15; pp. 2825–34. [Google Scholar]
- Lin, Minglian, and Indranil SenGupta. 2021. Analysis of optimal portfolio on finite and small time horizons for a stochastic volatility market model. SIAM Journal on Financial Mathematics 12: 1596–624. [Google Scholar] [CrossRef]
- Liu, Jiaming, Yali Wang, and Yu Qiao. 2017. Sparse deep transfer learning for convolutional neural network. Paper presented at Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, February 4–9. [Google Scholar]
- Malialis, kleanthis, Christos G. Panayiotou, and Marios M. Polycarpou. 2020. Data-efficient Online Classification with Siamese Networks and Active Learning. Paper presented at International Joint Conference on Neural Networks (IJCNN 2020), Glasgow, UK, July 19–24. [Google Scholar]
- Murphy, John J. 1999. Technical Analysis of the Financial Markets: A Comprehensive Guide to Trading Methods and Applications. New York: New York Institute of Finance. [Google Scholar]
- Nazário, Rodolfo Toríbio Farias, Lima e Silva, Jéssica, Vinicius Amorim Sobreiro, and Herbert Kimura. 2017. A literature review of technical analysis on stock markets. The Quality Review of Economics and Finance 66: 115–26. [Google Scholar]
- Rao, Vishwas, Romit Maulik, Emil Constantinescu, and Mihai Anitescu. 2020. A Machine-Learning-Based Importance Sampling Method to Compute Rare Event Probabilities. In Computational Science-ICCS. Lecture Notes in Computer Science. Cham: Springer, volume 12142. [Google Scholar]
- Roberts, Michael, and Indranil SenGupta. 2020. Sequential hypothesis testing in machine learning, and crude oil price jump size detection. Applied Mathematical Finance 27: 374–95. [Google Scholar] [CrossRef]
- Salmon, Nicholas, and Indranil SenGupta. 2021. Fractional Barndorff-Nielsen and Shephard model: Applications in variance and volatility swaps, and hedging, Annals of Finance. Annals of Finance 17: 529–558. [Google Scholar] [CrossRef]
- SenGupta, Indranil. 2016. Generalized BN-S stochastic volatility model for option pricing. International Journal of Theoretical and Applied Finance 19: 1650014. [Google Scholar] [CrossRef]
- SenGupta, Indranil, William Nganje, and Erik Hanson. 2021. Refinements of Barndorff-Nielsen and Shephard model: An analysis of crude oil price with machine learning. Annals of Data Science 8: 39–55. [Google Scholar] [CrossRef] [Green Version]
- Sezer, Omer Berat, and Ahmet Murat Ozbayoglu. 2018. Algorithmic financial trading with deep convolutional neural networks: Time series to image conversion approach. Applied Soft Computing 70: 525–538. [Google Scholar] [CrossRef]
- Sharma, Alok, Edwin Vans, Daichi Shigemizu, Keith A. Boroevich, and Tatsuhiko Tsunoda. 2019. DeepInsight: A methodology to transform a non-image data to an image for convolution neural network architecture. Scientific Reports 9: 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharma, Anuraganand, and Dinesh Kumar. 2020a. Classification with 2-D Convolutional Neural Networks for breast cancer diagnosis. arXiv arXiv:2007.03218v2. [Google Scholar]
- Sharma, Anuraganand, and Dinesh Kumar. 2020b. Non-image data classification with convolutional neural networks. arXiv arXiv:2007.03218. [Google Scholar]
- Shen, Shunrong, Haomiao Jiang, and Tongda Zhang. 2012. Stock Market Forecasting Using Machine Learning Algorithms. Stanford: Department of Electrical Engineering, Stanford University, pp. 1–5. [Google Scholar]
- Shoshi, Humayra, and Indranil SenGupta. 2021. Hedging and machine learning driven crude oil data analysis using a refined BarndorffNielsen and Shephard model. International Journal of Financial Engineering 8: 2150015. [Google Scholar] [CrossRef]
- Simonyan, Karen, and Andrew Zisserman. 2014. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv arXiv:1409.1556. [Google Scholar]
- Stine, Robert. 1989. An Introduction to Bootstrap Methods: Examples and Ideas. Sociological Methods & Research 18: 243–91. [Google Scholar]
- Sun, Baohua, Lin Yang, Wenhan Zhang, Michael Lin, Patrick Dong, Charles Young, and Jason Dong. 2019. Supertml: Two-dimensional word embedding for the precognition on structured tabular data. Paper presented at IEEE Conference on Computer Vision and Pattern Recognition Workshops, Nashville, TN, USA, June 19–25. [Google Scholar]
- Taigman, Yaniv, Ming Yang, Marc’Aurelio Ranzato, and Lior Wolf. 2014. DeepFace: Closing the Gap to Human-Level Performance in Face Verification. Paper presented at the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, June 23–28; pp. 1701–8. [Google Scholar]
- Tsai, Chih-Fong, and S. P. Wang. 2009. Stock Price Forecasting by Hybrid Machine Learning Techniques. Paper presented at International MultiConference of Engineers and Computer Scientists, Hong Kong, China, March 18–20. [Google Scholar]
- Vijh, Mehar, Deeksha Chandola, Vinay Anand Tikkiwal, and Arun Kumar. 2020. Stock Closing Price Prediction using Machine Learning Techniques. Procedia Computer Science 167: 599–606. [Google Scholar] [CrossRef]
- Wang, Zhiguang, and Tim Oates. 2015. Imaging time series to improve classification and imputation. Paper presented at 24th International Conference on Artificial Intelligence, Buenos Aires, Argentina, July 25–31; pp. 3939–45. [Google Scholar]
- Weiss, Gary M., and Haym Hirsh. 2000. Learning to Predict Extremely Rare Events. Technical Report WS-00-05. Paper presented at Learning from Imbalanced Data Sets, AAAI Workshop, Menlo Park, CA, USA, July 31; pp. 64–68. [Google Scholar]

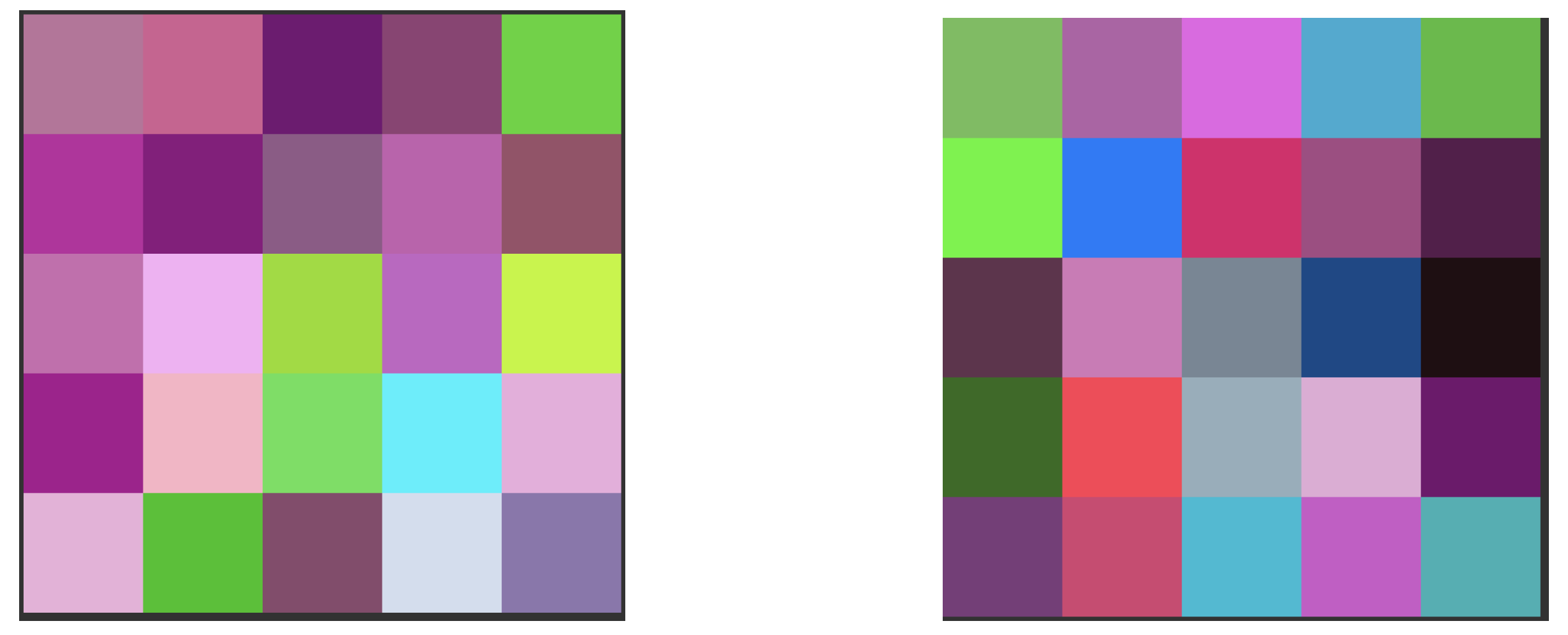
| Image Size | Class Imbalance | Accuracy | Precision | Recall | Score |
|---|---|---|---|---|---|
| 5 × 5 | 1% | 0.691 | 0.010 | 0.364 | 0.020 |
| 5% | 0.763 | 0.024 | 0.105 | 0.039 | |
| 10% | 0.819 | 0.086 | 0.109 | 0.096 | |
| 6 × 6 | 1% | 0.687 | 0.005 | 0.182 | 0.010 |
| 5% | 0.776 | 0.041 | 0.179 | 0.067 | |
| 10% | 0.808 | 0.083 | 0.121 | 0.098 | |
| 7 × 7 | 1% | 0.580 | 0.008 | 0.364 | 0.015 |
| 5% | 0.795 | 0.067 | 0.259 | 0.106 | |
| 10% | 0.826 | 0.131 | 0.159 | 0.144 | |
| 8 × 8 | 1% | 0.678 | 0.008 | 0.273 | 0.015 |
| 5% | 0.708 | 0.048 | 0.267 | 0.082 | |
| 10% | 0.707 | 0.086 | 0.239 | 0.127 | |
| 9 × 9 | 1% | 0.765 | 0.011 | 0.273 | 0.021 |
| 5% | 0.782 | 0.044 | 0.167 | 0.070 | |
| 10% | 0.835 | 0.123 | 0.138 | 0.130 |
| Image Size | Imbalance | Event Images | Non-Event Images | Total |
|---|---|---|---|---|
| 1% | 11 | 1235 | 1246 | |
| 5% | 57 | 1189 | ||
| 10% | 110 | 1136 | ||
| 1% | 11 | 1230 | 1241 | |
| 5% | 56 | 1185 | ||
| 10% | 107 | 1134 | ||
| 1% | 11 | 1216 | 1227 | |
| 5% | 58 | 1169 | ||
| 10% | 113 | 1114 | ||
| 1% | 11 | 1216 | 1227 | |
| 5% | 60 | 1167 | ||
| 10% | 109 | 1118 | ||
| 1% | 11 | 1207 | 1219 | |
| 5% | 60 | 1158 | ||
| 10% | 109 | 1110 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basu, T.; Menzer, O.; Ward, J.; SenGupta, I. A Novel Implementation of Siamese Type Neural Networks in Predicting Rare Fluctuations in Financial Time Series. Risks 2022, 10, 39. https://doi.org/10.3390/risks10020039
Basu T, Menzer O, Ward J, SenGupta I. A Novel Implementation of Siamese Type Neural Networks in Predicting Rare Fluctuations in Financial Time Series. Risks. 2022; 10(2):39. https://doi.org/10.3390/risks10020039
Chicago/Turabian StyleBasu, Treena, Olaf Menzer, Joshua Ward, and Indranil SenGupta. 2022. "A Novel Implementation of Siamese Type Neural Networks in Predicting Rare Fluctuations in Financial Time Series" Risks 10, no. 2: 39. https://doi.org/10.3390/risks10020039
APA StyleBasu, T., Menzer, O., Ward, J., & SenGupta, I. (2022). A Novel Implementation of Siamese Type Neural Networks in Predicting Rare Fluctuations in Financial Time Series. Risks, 10(2), 39. https://doi.org/10.3390/risks10020039







