1. Introduction
Financial time series modeling is an essential aspect of forecasting and risk evaluation in financial markets. In this paper, we consider the case of copper, which, according to the NYMEX, is the third most used metal, which makes it important to assess the nature of its price fluctuations. Further, the likely pressure on copper prices due to its possible scarcity is a cause for concern
Gordon et al. (
2006);
Tilton and Lagos (
2007), especially in light of its importance for the growing network industry.
Our previous works,
Mastroeni and Vellucci (
2019);
Mastroeni et al. (
2018), showed that a significant level of noise is usually present in the time series of copper futures intraday prices, supporting the conclusion that logarithmic returns have both a stochastic and deterministic nature. Hence, the use of stochastic models appears to be a natural choice.
In this paper, we develop a novel stochastic differential equation (SDE) that models the data and is based on the whitening filter approach
Wiener (
1949), a method characterizing linear time-variant systems. From a statistical point of view, we assume that the time series of prices can be described by autocorrelation. This property is obtained by means of statistical analyses of the historical data recorded for the futures copper closing prices (HG1 ticker) as exchanged on the COMEX market (CMX). Starting from a model of the empirical autocorrelation shown by the time series of prices, we introduce an SDE, which is characterized by this autocorrelation, and fits the model to the data. To the best of our knowledge, there have been no papers following this approach.
The purpose of the developed SDE model is to move one step further concerning the analysis started in our previous paper
Mastroeni et al. (
2018). In that paper, we showed that the time series of copper prices (the same studied in the present paper but for a shorter interval) exhibited both stochastic and chaotic features. At the same time, the recurrence plot of the time series revealed a pattern typical of intermittency phenomena.
The presence of stochastic features and intermittency phenomena called for a second step of the time series analysis started in
Mastroeni et al. (
2018), i.e., a new approach to short-term modeling for copper futures prices.
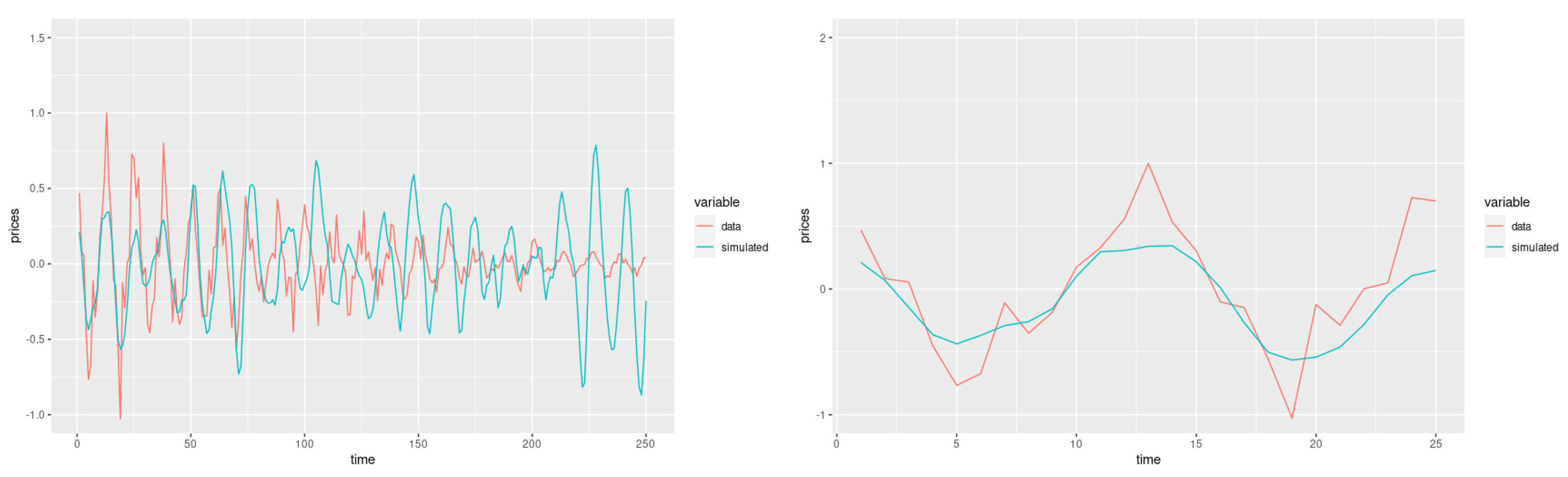
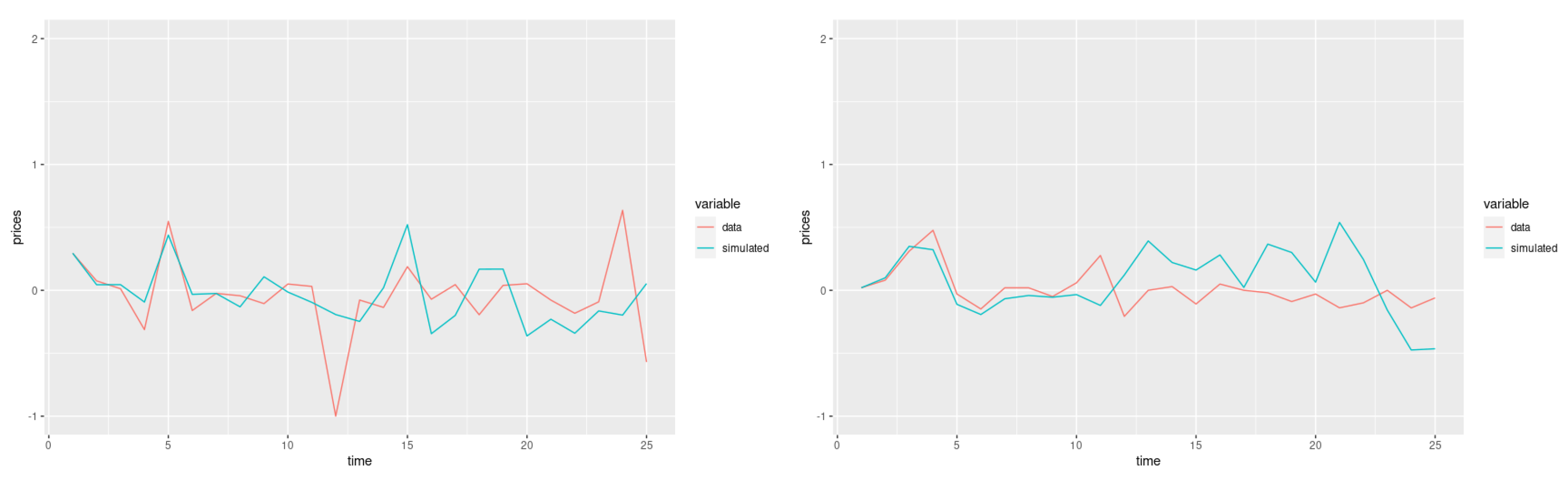
Our model produced trajectories close to the real data only in the short run. This is due, on the one hand, to the fitted model from the empirical autocorrelation and, on the other, to the predominantly stochastic behavior of the copper price time series, which can only be predicted in the short term
Mastroeni and Vellucci (
2019,
2022). To investigate the stochastic (vs deterministic) nature of the data, we follow the intuition behind recurrence analysis
Eckmann et al. (
1987);
Marwan et al. (
2007). In the
Appendix A, we show that the performance of the model improved significantly when the time series had an empirical autocorrelation function close to the damped cosine model and a determinism measure (DET), based on a recurrence plot, close to one. In the numerical section, we show that the presence of a large stochastic component produced a poorer performance than that obtained for time intervals with a large deterministic component.
So far, the literature does not seem to have focused on mathematical modeling of the copper futures market, following econometric and statistical approaches instead. The following is a brief review of the literature supporting this claim.
In
Jin et al. (
2021), the authors analyzed the effect of the price correlation between domestic and foreign copper futures contracts.
Guo et al. (
2020) investigated the nonlinear correlation between the spot and futures prices in China’s copper market using nonlinear Granger causality and multifractal methods.
Gong and Lin (
2018) examined whether structural breaks contained incremental information for forecasting the volatility of copper futures. In
Zheng et al. (
2022), the authors conducted a comparative exploration of the chaotic characteristics of Chinese and international copper futures prices, showing the differences in those series through recurrence plots and correlation dimensions.
The co-movements of the dynamic correlations between copper futures and spot prices on a scale by scale basis were analyzed in
Yu et al. (
2021), using grey correlation analysis and wavelet analysis. In
Galán-Gutiérrez and Martín-García (
2022), Granger causality was exploited to test whether, during the first COVID-19 wave, the evolution of the pandemic was cointegrated with the price structure of copper futures, on the one hand, and with incremental levels of copper stocks, on the other. The authors of
Idrovo-Aguirre and Contreras-Reyes (
2021) proposed the impulse–response functions of a vector autoregressive model to capture the dynamic between copper prices and house building permits.
As for the development of a model that fit the same copper time series considered in
Mastroeni et al. (
2018), the paper
Rivero and Vellucci (
2022) modeled the copper price time series with a matching pursuit algorithm, which used a waveform dictionary with rectangular window functions introduced in
De Carli and Vellucci (
2018). The novelty of the present paper is the introduction of an SDE for the copper futures market: to the best of our knowledge, this is the only paper in the literature that attempts to provide a mathematical model for the copper futures market.
This paper is organized as follows.
Section 2 describes the state space reconstruction by introducing a formal definition of determinism for time series. In
Section 3, we recall the whitening filter approach and prove some preliminary useful results.
Section 4 contains a brief exploratory analysis of the data, whereas in
Section 5, we give the main results of the paper, constructing an SDE characterized by a damped cosine autocorrelation function. In
Section 6.2, we perform some numerical simulations on the SDE obtained in the preceding sections for copper futures prices’ time series and, in the
Appendix A, we compare them with the results obtained from an artificial time series.
Section 7 is devoted to our conclusions.
3. Preliminary Results: The Whitening Filter Approach
Let us recall the whitening filter approach and introduce some preliminary results that we need to achieve the mathematical results in the subsequent sections.
One of the most commonly used methods to characterize a linear time-variant system, that is, to specify its input–output relationship, is based on the impulse response of the system. For example, a two-terminal pair system, with input
and output
is depicted in
Figure 1. The impulse response of the linear time-variant system is denoted by
. It is the output at time
t to an input applied at time
. Given
, for a physically realizable system, we assume that
is zero outside the range
. Then, the input–output relation assumes the form:
Let us consider now a nonstationary noise
that can be characterized by its autocorrelation
. The whitening filter problem consists in finding the system
for a given
, such that the output spectrum is
. Let us introduce the following Proposition.
Proposition 1. Let be the set of eigenfunctions of ,Then, the filter given by the expansion of equation:solves the whitening filter problem. Proof. Given the expression of noise output
we can compute its autocorrelation function as:
and then,
If
is real
, it is symmetric; therefore, a standard eigenfunction approach can be used to solve the integral Equation (
15).
Let
be the set of eigenfunctions of
,
Since the set of eigenfunctions is complete, the system functions can be expanded as
where
By using the expansion (
17), Equation (
15) becomes:
If one first considers making the output noise spectrum only stationary:
then
is identified as
, where
and
are the eigenfunction and eigenvalue associated with
, respectively:
□
Now, we denote by or simply the bilateral Laplace transform of a function .
If a random (wide-sense stationary) process
passes through a time-invariant filter
, such as the one depicted in
Figure 1, then the autocorrelation function given by Equation (
15) becomes
For white noise input,
, and
The power spectrum of the output is the Laplace transform of
:
By integrating first with respect to
t:
and then with respect to
, we obtain:
Let us now explain what the relation is between a pole or zero of and the corresponding pole or zero of . The poles and zeros of are those of mirrored across the imaginary axis of a complex plane. Therefore, the poles and zeros of are paired across the imaginary axis. With N pole pairs and M zero pairs in , we have (in principle) different choices of whitening filter that produce . However, imposing the causality/stability of the whitening filter, we have to place all the poles in the left-hand-side complex plane. After that, we have just choices. Then, to impose a minimum phase, we place all zeros in the left-hand-side complex plane. At the end, the filter is stable, causal, and minimum phase. Here, we refer to a strictly stable linear system as being one with all the poles of its transfer function in the open left-hand-side complex plane , and we refer to a stable linear system as being one with poles in the closed left-hand-side complex plane.
4. Exploratory Data Analysis
The dataset employed in our analysis was the time series of intraday Generic 1st Futures Copper closing prices (HG1 ticker) as exchanged on the COMEX market (CMX) and retrieved from the Bloomberg website. The dataset consisted of 2864 observations and spanned from 8 June 2021 to 8 June 2022.
We denoted the time series of intraday prices by
, with
, and the logarithmic returns by
. The overall time series is shown in
Figure 2 and
Figure 3.
The data were not equally spaced intraday prices, i.e., the number of intraday observations was not constant but varied over time. See
Figure 4.
The Hurst exponent of the series was 0.53, which meant that the time series was trending. This value was near to (i.e., the time series was generated by a geometric Brownian motion).
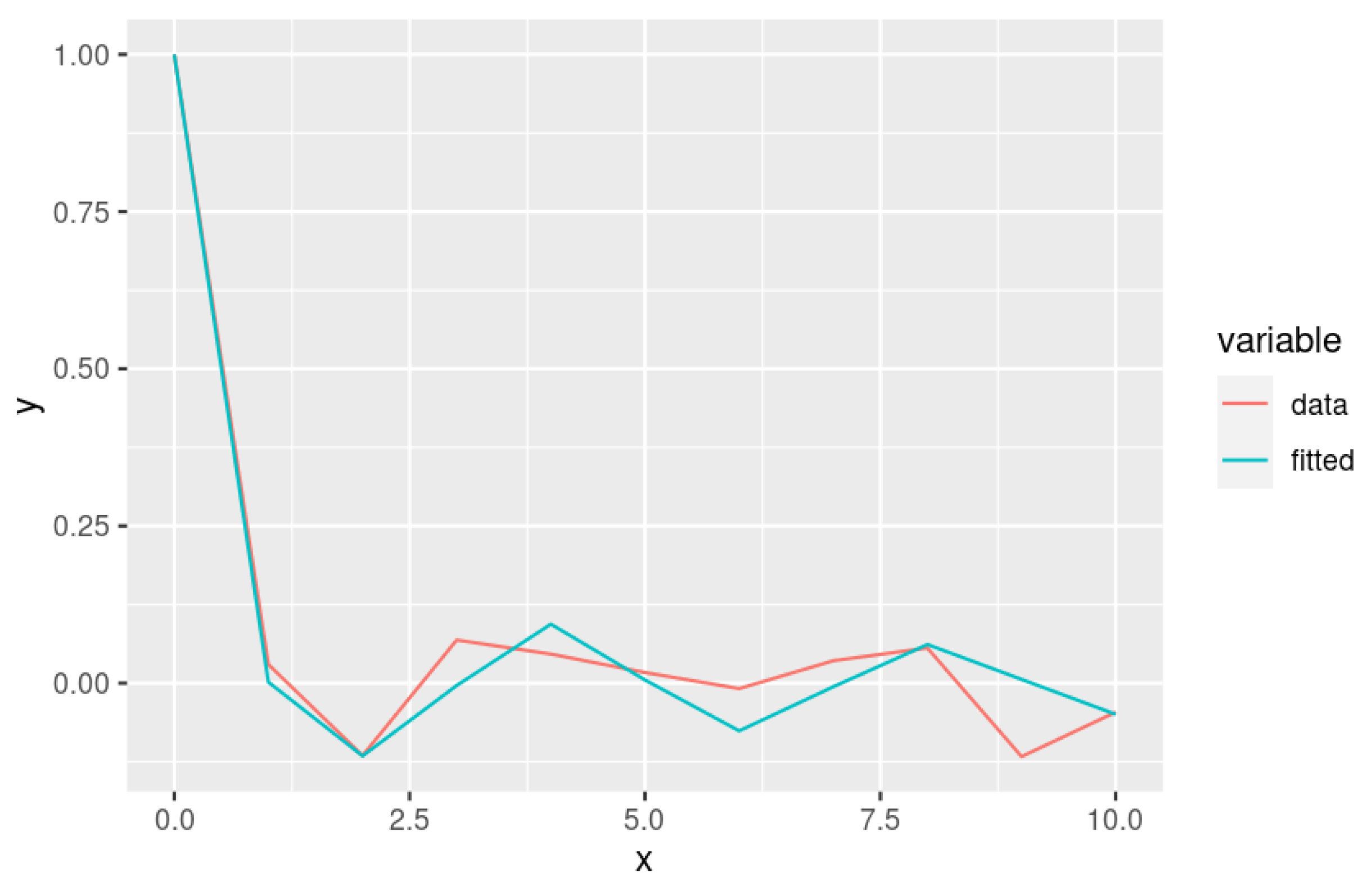
Figure 5 shows the autocorrelation of the considered data set for time lags up to points in time 10 (number of observations, recall that we have intraday prices). The red line is the autocorrelation computed from the data, while the green line corresponds to the nonlinear fit according to the expression
The damped cosine function was a good approximation to the autocorrelation for time lags up to approximately 10 observations.
5. Construction of the SDE-Based Model
Let us assume the logarithmic returns
were characterized by the damped cosine autocorrelation
described by (
27), whose decay rate is governed by the coefficient
.
Since we know that the autocorrelation price process
fits a function such as (
27), the problem was to derive an SDE that describes a process with this autocorrelation. Theorem 3 answers this question:
Theorem 3. Let be the white noise. Let also , , and . If is the autocorrelation of log-price described by (27), then the SDE that results from the whitening filter procedure iswhere δ is the Dirac delta function, , and the variance of is . Proof. The Wiener–Kolmogorov whitening procedure from
Wiener (
1949) is used on
to represent the log-price
as a function of time, driven by a white noise input
. The procedure is used in the proof to decompose the Laplace transform of
into the product of white noise and a system function:
. Here, the quantity
is the transfer function of the whitening filter for the log-price
, and
is the transform of the white noise
that drives
.
The Laplace transform of the autocorrelation function
is
Splitting the module,
solving the integrals,
and factorizing the resulting expression, we obtain
where
. Hence, we have
and
Indeed, the autocorrelation function
of the white noise input is found by taking the inverse Laplace transform of (
34) as
where
is the variance of
.
From the definition of a transfer function, we have that
, where
is the Laplace transform of
. Moreover, it is well known that for a generic function
,
Applying these last considerations to Equation (
33), and recalling that
,
, and
, we obtain the differential Equation (
28). □
Remark 1. As anticipated in Section 3, it can be easily demonstrated that the whitening filter, whose transfer function is described by Equation (33) in the proof of Theorem 3, is unique, stable, causal, and minimum phase. At this stage, we do not yet have the formulation of a standard SDE, i.e., a rigorously defined equivalent implicit Ito’s integral equation. For instance,
where
B denotes a Wiener process (the standard Brownian motion). Instead, the approach followed in Theorem 3 presents us with these mathematical problems
Evans (
2012):
However, we can start from (
28) with a heuristic explanation: we could think of the white noise introduced in Theorem 3 as the “derivative” of Brownian motion. It is just heuristic reasoning because the standard Brownian motion is nowhere differentiable with probability one, but it is a way to start and move intuitively from (
28). To formalize this rigorously, we use the theory of generalized functions.
As we know, a generalized function is a continuous linear function on the set of infinitely differentiable functions with bounded support, which we denote with
or simply
. The space of generalized functions on
is denoted by
. We write
We define the generalized derivative of
to be the generalized function
, so that
Thinking of Brownian motion as a random function, we can define a white noise as its generalized derivative. Hence:
Lemma 1. Let be a real-valued Brownian motion on a probability space . Then, Proof. Formally, according to
Evans (
2012);
Lord et al. (
2014), white noise
is a stochastic process on a probability space
with
and
for all
, where
denotes the Dirac delta function.
We define
for some
. Then,
is a stochastic process on
with
and for all
,
Let
. Then, we have
i.e., replacing
,
Therefore, in distribution, we can write
Thus, we have that the derivative of the covariance matrix for the Brownian motion is the same as the covariance matrix for the white noise; thus, the derivative of the Brownian motion is the white noise. □
In a similar manner, we introduce the second time derivative on a Wiener process (or just the time derivative on a white noise):
Lemma 2. Let be a real-valued Brownian motion on a probability space . Then, the stochastic processhas the following statistics: Proof. Similar to the proof of Lemma 1, we define
and we take
at the last step.
For the expected value of
we have that
. For the covariance, we have instead
i.e.,
From the statistics of a white noise,
we have that
as
. □
Corollary 1. The Ito’s integral form of Equation (28) iswhere Θ is the Heaviside step function with the distributional derivative . Equation (54) has the unique solution: Proof. From Lemmas 1 and 2, we can rewrite Equation (
28) as
To reduce the order in Equation (
56), we combine the derivative terms shifting some of them around. Hence, we obtain a first-order system with the substitution
, i.e.,
. Accordingly,
With simple algebra, we obtain
and thus the corresponding well-defined Ito’s integral form (
54).
By passing to the vectorial form and neglecting the Heaviside terms, Equation (
54) can be rewritten as
where
Given any initial value
, from the linearity of the SDE, we know that Equation (
59) has the unique solution
Mao (
2007)
To consider the neglected terms, let us replace the Brownian motion
by the process
such that
whose quadratic variation is
Now, for a one-dimensional Brownian motion
, we have
Hence, a Brownian motion is a martingale with respect to the filtration
. Moreover, using the definition of the total variation of a real-valued function, it is possible to show that the variation of
is 0 on every interval in
and 1 on every larger interval. This means that the total variation of
is
itself; hence, it is a càdlàg adapted process of finite variation. Thus,
is a semi martingale
Rogers and Williams (
2000).
Hence, Equation (
54) can be rewritten as
Ito’s formula gives us the solution of (
66), i.e.,
The matrix
A has the property that
so we can use it to define sequences
as
where
, and
The general closed formula for
, when the discriminant of the quadratic polynomial
is not zero, is in terms of
. In our case,
, which is by definition different from 0. Thus,
, and
So:
which is the right column of
The left column is similarly calculated as:
Equation (
54) then has the unique solution:
Thus, since , we have the claim. □
7. Conclusions
In this paper, we developed a novel stochastic differential equation (SDE) that fit the model of intraday copper futures prices and was based on the whitening filter approach
Wiener (
1949), a method characterizing linear time-variant systems. We assumed that the time series of prices could be described by its autocorrelation. This property was obtained through statistical analyses of historical data. Starting from an empirical autocorrelation model obtained from the price time series, we introduced an SDE that was characterized by this autocorrelation and fit the model to the data.
The model we developed produced trajectories close to the real data only in the short run. This was due, on the one hand, to the model fitted by empirical autocorrelation and, on the other, to the predominantly stochastic behavior of the copper price time series, which can only be predicted in the short term
Mastroeni and Vellucci (
2019,
2022). To investigate the stochastic (vs. deterministic) nature of the data, we followed the intuition behind the recurrence analysis
Eckmann et al. (
1987);
Marwan et al. (
2007). In the
Appendix A, we also show that the performance of the model improved significantly, when the time series had an empirical autocorrelation function close to the damped cosine model and a determinism measure (DET) based on the recurrence plot close to one. Therefore, future work will include the assumption of more complex functions to model the autocorrelation function of intraday copper futures prices.
Based on the numerical results presented in
Section 6.2 regarding the level of determinism through the recurrence plot and the performance of the SDE model, this paper showed that the predictability of copper futures prices is rather weak. In fact, as already said, the model we derived produced trajectories close to the actual data only in the short term. Consequently, the investment risk of copper futures is high, which confirms the results in
Mastroeni et al. (
2018). Based on the reconstructed copper price phase space, the recurrence plot confirmed that deterministic features coexisted with stochastic ones in copper futures prices. In the intervals considered, the level of determinism was often zero, indicating that the copper futures prices were not predictable.
Compared to other metal futures such as aluminum and nickel, copper futures seem to have a higher investment risk. For instance, the prices considered by
Sun et al. (
2022) were highly deterministic. In any case, the time series considered here were different in terms of granularity and time span, and intraday copper futures are probably a riskier investment than daily ones. Investigating this aspect could be an interesting issue for a future work.
Additional further research would be to generalize the SDE model to the multivariate case. In fact, since copper prices are correlated with other commodities (such as steel, gold, and oil), it would be interesting to know whether this model could use this information. In any case, co-movements among these series did not arise from the model, but it is necessary to use ad hoc methodologies, e.g., those employed in our previous papers
Mastroeni et al. (
2021,
2022);
Benedetto et al. (
2020,
2021),
Benedetto et al. (
2016). A possible generalization of the SDE model proposed in this paper should integrate these methodologies in the whitening filter approach.