Limited Performance of Machine Learning Models Developed Based on Demographic and Laboratory Data Obtained Before Primary Treatment to Predict Coronary Aneurysms
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Data Processing
2.3. Supervised Machine Learning
2.4. Performance Evaluation
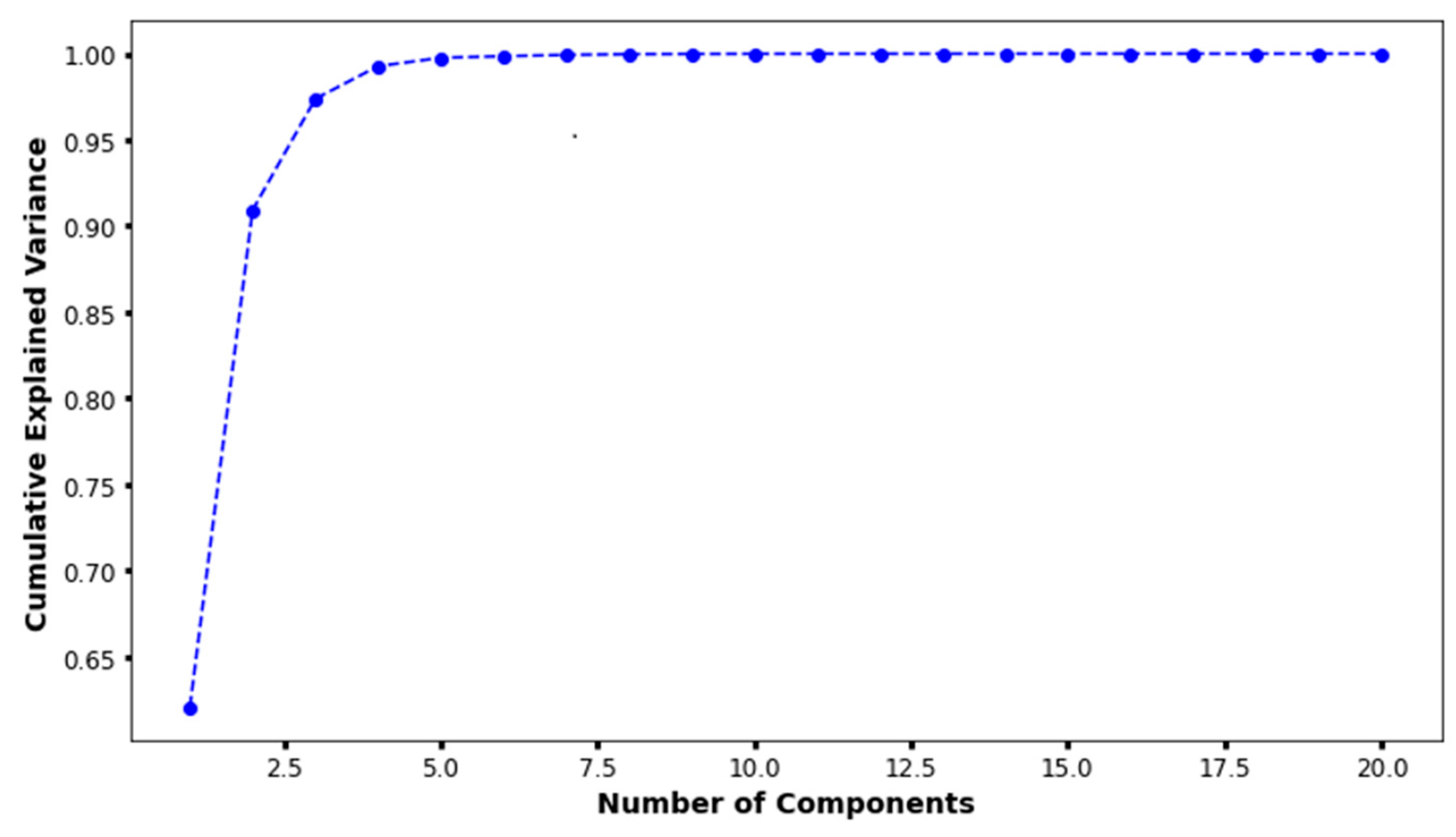
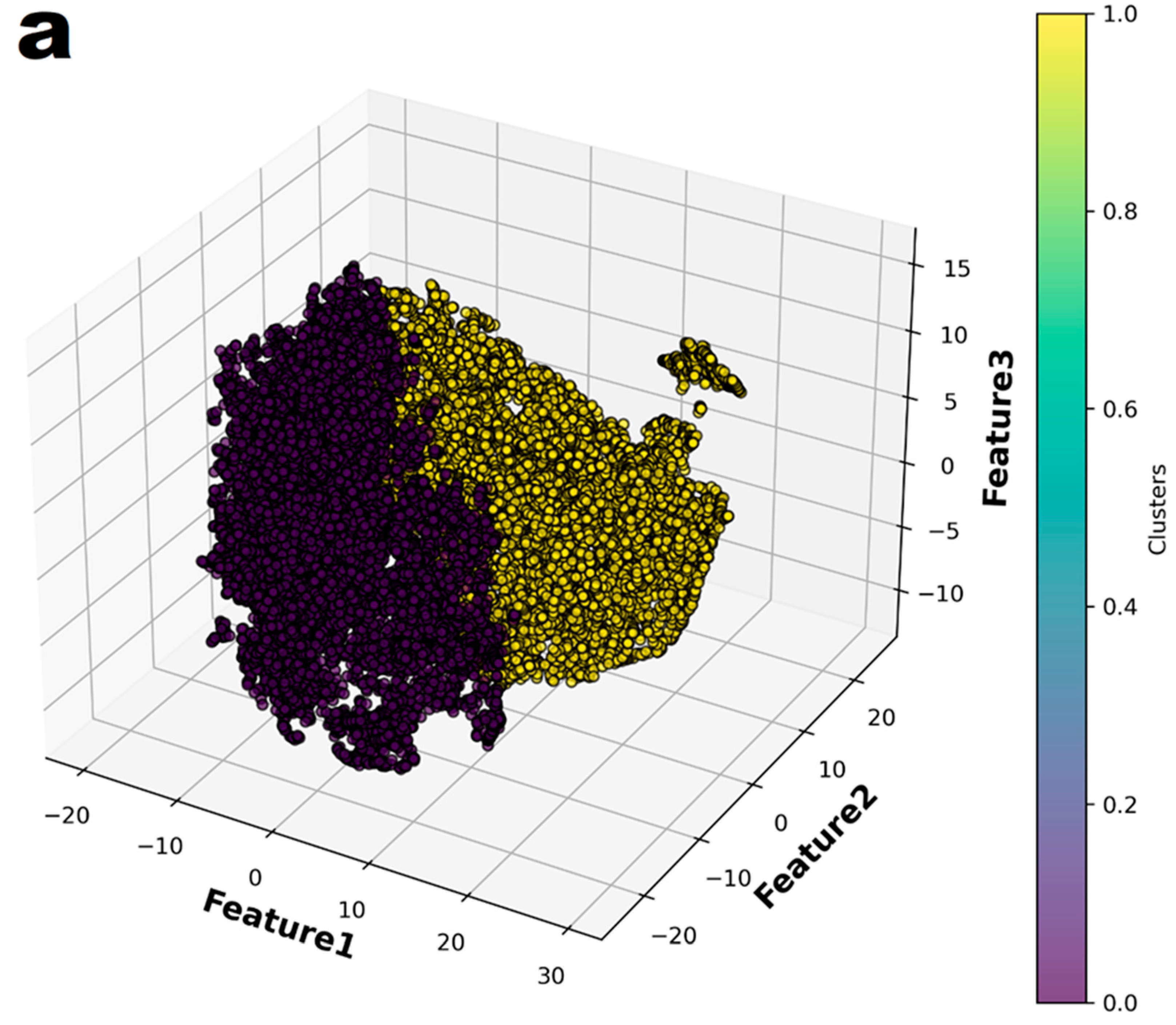
2.5. Unsupervised Machine Learning
3. Results
3.1. Supervised Machine Learning
3.2. Unsupervised Machine Learning
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McCrindle, B.W.; Rowley, A.H.; Newburger, J.W.; Burns, J.C.; Bolger, A.F.; Jackson, M.A.; Takahashi, M.; Shah, P.B.; Kobayashi, T.; Wu, M.H.; et al. Diagnosis, Treatment, and Long-Term Management of Kawasaki Disease: A Scientific Statement for Health Professionals from the American Heart Association. Circulation 2017, 135, e927–e999. [Google Scholar] [CrossRef] [PubMed]
- Jone, P.N.; Tremoulet, A.; Choueiter, N.; Dominguez, S.R.; Harahsheh, A.S.; Mitani, Y.; Zmmerman, M.; Lin, M.T.; Friedman, K.G. Update on Diagnosis and Management of Kawasaki Disease: A Scientific Statement from the American Heart Association. Circulation 2024, 150, e481–e500. [Google Scholar] [CrossRef]
- Sagi, T.; Ayusawa, M.; Miura, M.; Kobayashi, T.; Suzuki, H.; Mori, M.; Terai, M.; Ogawa, S. Guidelines for Medical Treatment of Acute Kawasaki Disease: Report of the Research Committee of the Japanese Society of Pediatric Cardiology and Cardiac Surgery (2012 Revised Version). Pediatr. Int. 2014, 56, 135–158. [Google Scholar]
- Sleeper, L.A.; Minich, L.L.; McCrindle, B.M.; Li, J.S.; Mason, W.; Colan, S.D.; Atz, A.M.; Printz, B.F.; Baker, A.; Vetter, V.; et al. Pediatric Heart Network Investigators. Evaluation of Kawasaki Disease Risk-Scoring Systems for Intravenous Immunoglobulin Resistance. J. Pediatr. 2011, 158, 831–835. [Google Scholar] [CrossRef]
- Kobayashi, T.; Inoue, Y.; Takeuchi, K.; Okada, Y.; Tamura, K.; Tomomasa, T.; Kobayashi, T.; Morikawa, A. Prediction of Intravenous Immunoglobulin Unresponsiveness in Patients with Kawasaki Disease. Circulation 2006, 113, 2606–2612. [Google Scholar] [CrossRef] [PubMed]
- Egami, K.; Muta, H.; Ishii, M.; Suda, K.; Sugahara, Y.; Iemura, M.; Matsuishi, T. Prediction of Resistance to Intravenous Immunoglobulin Treatment in Patients with Kawasaki Disease. J. Pediatr. 2006, 149, 237–240. [Google Scholar] [CrossRef]
- Sano, T.; Kurotobi, S.; Matsuzaki, K.; Yamamoto, T.; Maki, I.; Miki, K.; Kogaki, S.; Hara, J. Prediction of Non-Responsiveness to Standard High-Dose Gamma-Globulin Therapy in Patients with Acute Kawasaki Disease Before Starting Initial Treatment. Eur. J. Pediatr. 2007, 166, 131–137. [Google Scholar] [CrossRef]
- Son, M.B.F.; Gauvreau, K.; Tremoulet, A.H.; Lo, M.; Baker, A.L.; de Ferranti, S.; Dedeoglu, F.; Sundel, R.P.; Friedman, K.G.; Burns, J.C.; et al. Risk Model Development and Validation for Prediction of Coronary Artery Aneurysms in Kawasaki Disease in a North American Population. J. Am. Heart Assoc. 2019, 8, e011319. [Google Scholar] [CrossRef]
- Harada, K. Intravenous Gamma-Globulin Treatment in Kawasaki Disease. Acta Paediatr. Jpn. 1991, 33, 805–810. [Google Scholar] [CrossRef]
- Malek, A.; Ghodsi, A.; Hamedi, A. The Negative Predictive Value of Harada Scoring for Coronary Artery Dilatation or Aneurysm in Children with Kawasaki Disease: A Cross-Sectional Study. Iran. J. Med. Sci. 2022, 47, 379–384. [Google Scholar]
- Tewelde, H.; Yoon, J.; Van Ittersum, W.; Worley, S.; Preminger, T.; Godfarb, J. The Harada score in the US population of children with Kawasaki disease. Hosp. Pediatr. 2014, 4, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Yu, J.J. Recent Machine Learning Applications in Kawasaki Disease Research. Kawasaki Dis. 2024, 2, e6. [Google Scholar] [CrossRef]
- Kim, G.B.; Park, S.; Eun, L.Y.; Han, J.W.; Lee, S.Y.; Yoon, K.L.; Yu, J.J.; Choi, J.W.; Lee, K.Y. Epidemiology and Clinical Features of Kawasaki Disease in South Korea, 2012–2014. Pediatr. Infect. Dis. J. 2017, 36, 482–485. [Google Scholar] [CrossRef]
- Kim, G.B.; Eun, L.Y.; Han, J.W.; Kim, S.H.; Yoon, K.L.; Han, M.Y.; Yu, J.J.; Choi, J.W.; Rhim, J.W. Epidemiology of Kawasaki Disease in South Korea: A Nationwide Survey 2015–2017. Pediatr. Infect. Dis. J. 2020, 39, 1012–1016. [Google Scholar] [CrossRef]
- Yu, J.J.; Choi, H.J.; Cho, H.J.; Kim, S.H.; Cheon, E.J.; Kim, G.B.; Eun, L.Y.; Jung, S.Y.; Jun, H.O.; Woo, H.O.; et al. Newly Developed Sex-Specific Z Score Model for Coronary Artery Diameter in a Pediatric Population. J. Korean Med. Sci. 2024, 39, e144. [Google Scholar] [CrossRef]
- Research Committee on Kawasaki Disease. Report of Subcommittee on Standardization of Diagnostic Criteria and Reporting of Coronary Artery Lesions in Kawasaki Disease; Ministry of Health and Welfare: Tokyo, Japan, 1984. [Google Scholar]
- Fukazawa, R.; Kobayashi, J.; Ayusawa, M.; Hamada, H.; Miura, M.; Mitani, Y.; Tsuda, E.; Nakajima, H.; Matsuura, H.; Ikeda, K.; et al. JCS/JSCS 2020 Guideline on Diagnosis and Management of Cardiovascular Sequelae in Kawasaki Disease. Circ. J. 2020, 84, 1348–1407. [Google Scholar] [CrossRef]
- Lee, H.; Eun, Y.; Hwang, J.Y.; Eun, L.Y. Explainable deep learning algorithm for distinguishing incomplete Kawasaki disease by coronary artery lesions on echocardiographic imaging. Comput. Methods Programs Biomed. 2022, 223, 106970. [Google Scholar] [CrossRef] [PubMed]
- Kuo, H.C.; Shen, S.H.; Chen, Y.H.; Lin, Y.C.; Chang, C.Y.; Wu, Y.C.; Wang, T.D.; Chang, L.S.; Tai, I.H.; Hsieh, K.S. Detection of coronary lesions in Kawasaki disease by scaled-YOLOv4 with HarDNet backbone. Front. Cardiovasc. Med. 2023, 9, 1000374. [Google Scholar] [CrossRef]
- Xu, D.; Feng, C.H.; Cao, A.M.; Yang, S.; Tang, Z.C.; Li, X.H. Progression prediction of coronary artery lesions by echocardiography-based ultrasomics analysis in Kawasaki disease. Ital. J. Pediatr. 2024, 50, 185. [Google Scholar] [CrossRef]
- Azuma, J.; Yamamoto, T.; Nitta, M.; Hasegawa, Y.; Kijima, E.; Shimotsuji, T.; Mizoguchi, Y. Structure Equation Model and Neural Network Analyses to Predict Coronary Artery Lesions in Kawasaki Disease: A Single-Centre Retrospective Study. Sci. Rep. 2020, 10, 11868. [Google Scholar] [CrossRef]
- Burns, J.C.; Capparelli, E.V.; Brown, J.A.; Newburger, J.W.; Glode, M.P. Intravenous Gamma-Globulin Treatment and Retreatment in Kawasaki Disease: US/Canadian Kawasaki Syndrome Study Group. Pediatr. Infect. Dis. J. 1998, 17, 1144–1148. [Google Scholar] [CrossRef] [PubMed]
- Durongpisitkul, K.; Soongswang, J.; Laohaprasitiporn, D.; Nana, A.; Prachuabmoh, C.; Kangkagate, C. Immunoglobulin Failure and Retreatment in Kawasaki Disease. Pediatr. Cardiol. 2003, 24, 145–148. [Google Scholar] [CrossRef] [PubMed]
- Uehara, R.; Belay, E.D.; Maddox, R.A.; Holman, R.C.; Nakamura, Y.; Yashiro, M.; Oki, I.; Ogino, H.; Schonberger, L.B.; Yanagawa, H. Analysis of Potential Risk Factors Associated with Nonresponse to Initial Intravenous Immunoglobulin Treatment Among Kawasaki Disease Patients in Japan. Pediatr. Infect. Dis. J. 2008, 27, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Lam, J.Y.; Song, M.S.; Kim, G.B.; Shimizu, C.; Bainto, E.; Tremoulet, A.H.; Nemati, S.; Burns, J.C. Intravenous Immunoglobulin Resistance in Kawasaki Disease Patients: Prediction Using Clinical Data. Pediatr. Res. 2024, 95, 692–697. [Google Scholar] [CrossRef]
- Friedman, K.G.; Gauvreau, K.; Hamaoka-Okamoto, A.; Tang, A.; Berry, E.; Tremoulet, A.H.; Mahavadi, V.S.; Baker, A.; deFerranti, S.D.; Fulton, D.R.; et al. Coronary Artery Aneurysms in Kawasaki Disease: Risk Factors for Progressive Disease and Adverse Cardiac Events in the US Population. J. Am. Heart Assoc. 2016, 5, e003289. [Google Scholar] [CrossRef]

| WBC count > 12,000/µL |
| Hemoglobin < 11.6 g/dL |
| Platelets < 350,000/µL |
| C-reactive protein > 3 mg/dL |
| Albumin < 3.5 g/dL |
| Age ≤ 12 months |
| Male sex |
| Characteristics | Frequency of Sample | Value |
|---|---|---|
| Age, months | all | 32.9 ± 24.4 |
| Male | all | 10,023 (58.3) |
| Family history | 13,008 (75.7) | 152 (1.2) |
| Recurrence | 16,537 (96.2) | 817 (4.9) |
| Body weight, kg | all | 13.9 ± 5.7 |
| Height, cm | all | 91.7 ± 17.1 |
| Body surface area, m2 | all | 0.58 ± 0.17 |
| Complete presentation | all | 12,211 (71.0) |
| Duration of fever, days | 16,823 (97.9) | 6.2 ± 2.2 |
| Spontaneous defervescence | all | 474 (2.8) |
| Unresponse to initial IVIG | 10,000 (58.2) | 2260 (22.6) |
| Laboratory findings | ||
| WBC, ×103/µL | all | 14.1 ± 5.6 |
| Neutrophil, % | all | 63.0 ± 16.5 |
| Hemoglobin, g/dL | all | 11.4 ± 1.0 |
| Platelet, ×103/µL | all | 352.6 ± 115.0 |
| Protein, g/dL | 17,037 (99.1) | 6.6 ± 1.6 |
| Albumin, g/dL | all | 3.9 ± 0.4 |
| AST, IU/L | all | 87.1 ± 163.2 |
| ALT, IU/L | all | 93.1 ± 148.3 |
| Total bilirubin, mg/dL | 16,744 (97.4) | 0.68 ± 2.7 |
| Na+, mmol/L | 16,968 (98.7) | 136.5 ± 2.7 |
| C-reactive protein, mg/dL | all | 8.0 ± 6.4 |
| Pyuria | 16,831 (97.9) | 3998 (23.8) |
| Echocardiographic results | ||
| LMCA, mm | all | 2.50 ± 0.61 |
| Z score | all | 0.71 ± 1.45 |
| LAD, mm | all | 1.98 ± 0.68 |
| Z score | all | 0.58 ± 1.62 |
| LCx, mm | 5741 (33.4) | 1.68 ± 0.53 |
| Z score | 0.31 ± 1.38 | |
| RCA, mm | all | 2.11 ± 0.67 |
| Z score | all | 0.82 ± 1.55 |
| CAA | all | 3088 (18.0) |
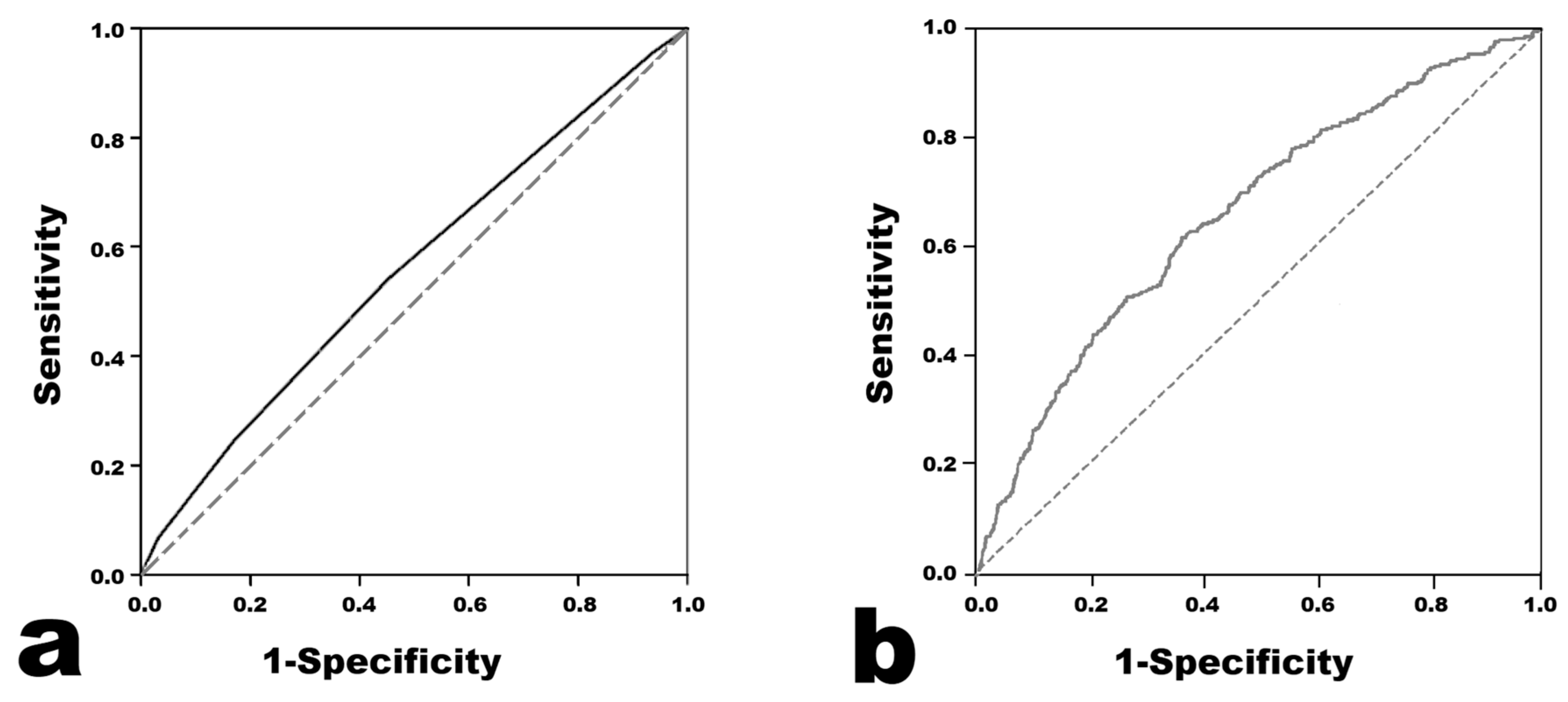
| AUC (95% CI) | Accuracy | Sensitivity | Specificity | PPV | NPV | F1-Score | MCC | CV | |
|---|---|---|---|---|---|---|---|---|---|
| Logistic Regression (Lasso Regularization) | 0.650 (0.615–0.684) | 0.589 | 0.689 | 0.567 | 0.258 | 0.893 | 0.376 | 0.197 | 0.624 |
| Logistic Regression (Ridge Regression) | 0.650 (0.617–0.685) | 0.589 | 0.689 | 0.567 | 0.259 | 0.893 | 0.376 | 0.197 | 0.624 |
| Support Vector Machine | 0.559 (0.521–0.597) | 0.659 | 0.434 | 0.709 | 0.246 | 0.851 | 0.314 | 0.117 | 0.565 |
| Ensemble Method | 0.641 (0.607–0.676) | 0.666 | 0.534 | 0.695 | 0.277 | 0.872 | 0.365 | 0.185 | 0.636 |
| Random Forest | 0.621 (0.584–0.654) | 0.573 | 0.625 | 0.562 | 0.238 | 0.872 | 0.347 | 0.143 | 0.617 |
| Gradient Boosting Machine | 0.655 (0.619–0.687) | 0.591 | 0.676 | 0.572 | 0.257 | 0.890 | 0.373 | 0.191 | 0.637 |
| Light Gradient Boosting Machine | 0.661 (0.630–0.695) | 0.633 | 0.615 | 0.637 | 0.271 | 0.883 | 0.376 | 0.197 | 0.628 |
| Multi-Layer Perceptron (3 hidden layers) | 0.545 (0.510–0.584) | 0.756 | 0.217 | 0.874 | 0.273 | 0.836 | 0.242 | 0.100 | 0.539 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-J.; Kim, G.-B.; Yang, D.; Jang, Y.-J.; Yu, J.-J. Limited Performance of Machine Learning Models Developed Based on Demographic and Laboratory Data Obtained Before Primary Treatment to Predict Coronary Aneurysms. Biomedicines 2025, 13, 1073. https://doi.org/10.3390/biomedicines13051073
Kim M-J, Kim G-B, Yang D, Jang Y-J, Yu J-J. Limited Performance of Machine Learning Models Developed Based on Demographic and Laboratory Data Obtained Before Primary Treatment to Predict Coronary Aneurysms. Biomedicines. 2025; 13(5):1073. https://doi.org/10.3390/biomedicines13051073
Chicago/Turabian StyleKim, Mi-Jin, Gi-Beom Kim, Dongha Yang, Yeon-Jin Jang, and Jeong-Jin Yu. 2025. "Limited Performance of Machine Learning Models Developed Based on Demographic and Laboratory Data Obtained Before Primary Treatment to Predict Coronary Aneurysms" Biomedicines 13, no. 5: 1073. https://doi.org/10.3390/biomedicines13051073
APA StyleKim, M.-J., Kim, G.-B., Yang, D., Jang, Y.-J., & Yu, J.-J. (2025). Limited Performance of Machine Learning Models Developed Based on Demographic and Laboratory Data Obtained Before Primary Treatment to Predict Coronary Aneurysms. Biomedicines, 13(5), 1073. https://doi.org/10.3390/biomedicines13051073






