Medical Professional Enhancement Using Explainable Artificial Intelligence in Fetal Cardiac Ultrasound Screening
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Preparation
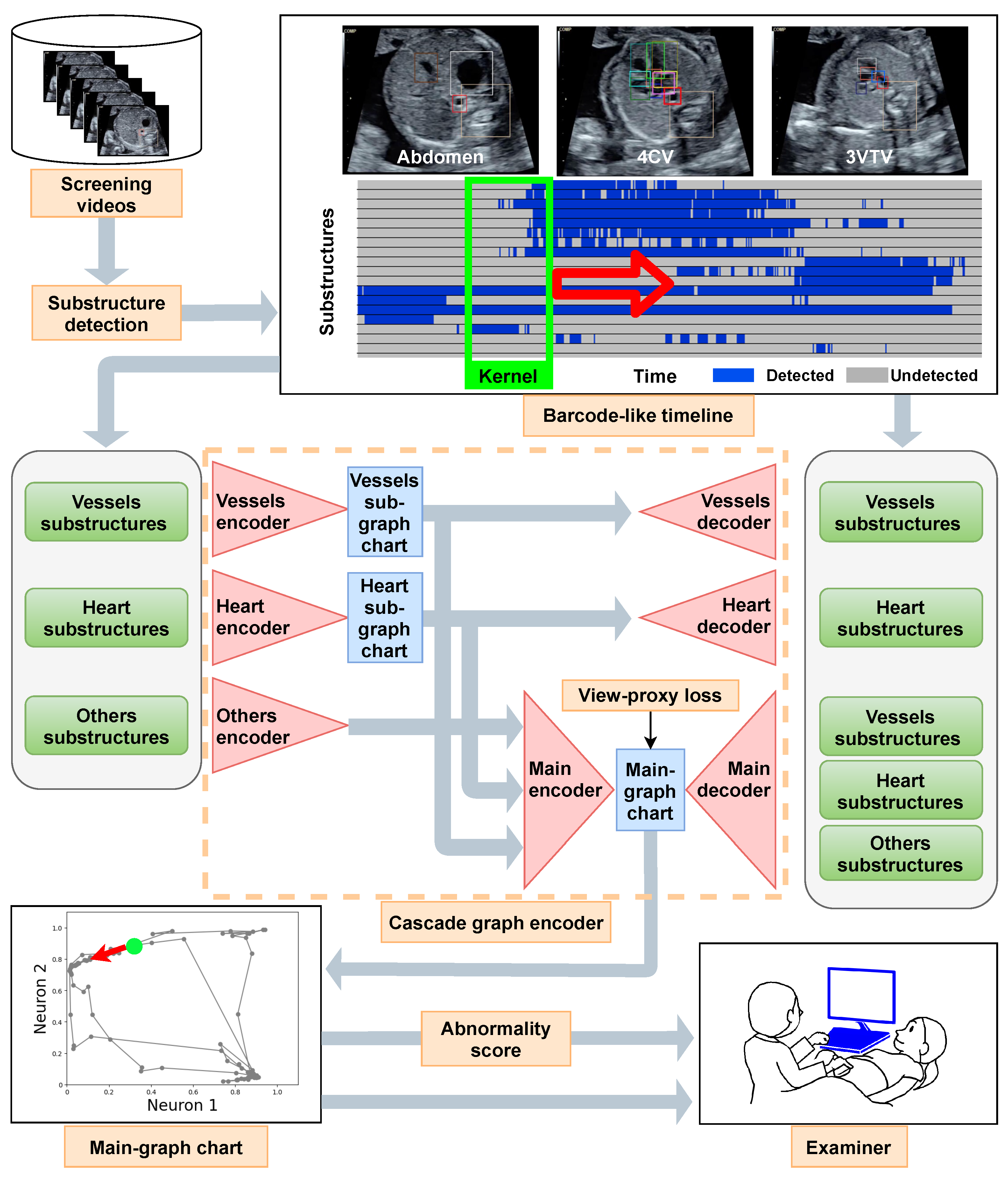
2.2. Proposed Method
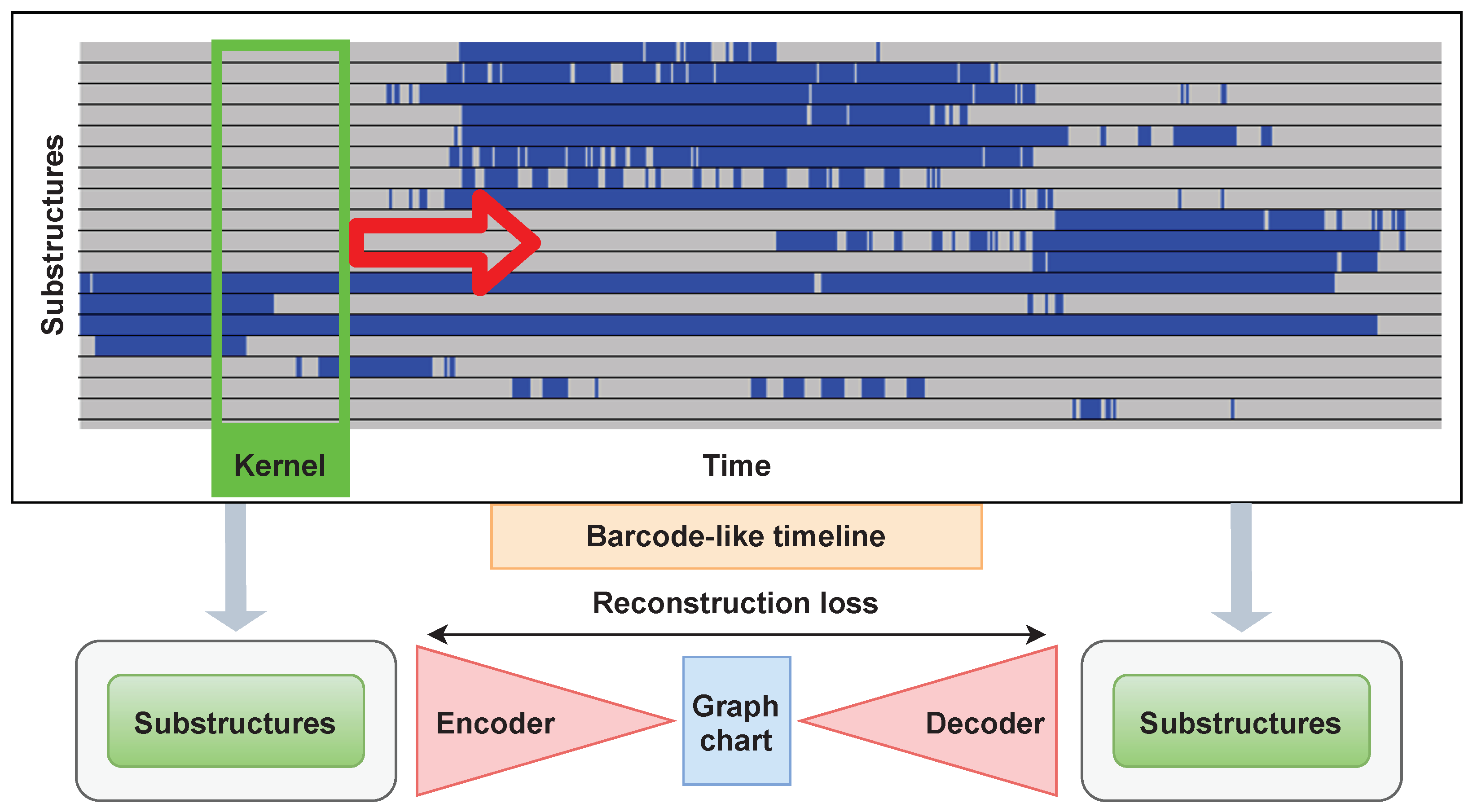
2.2.1. Graph Chart Diagram
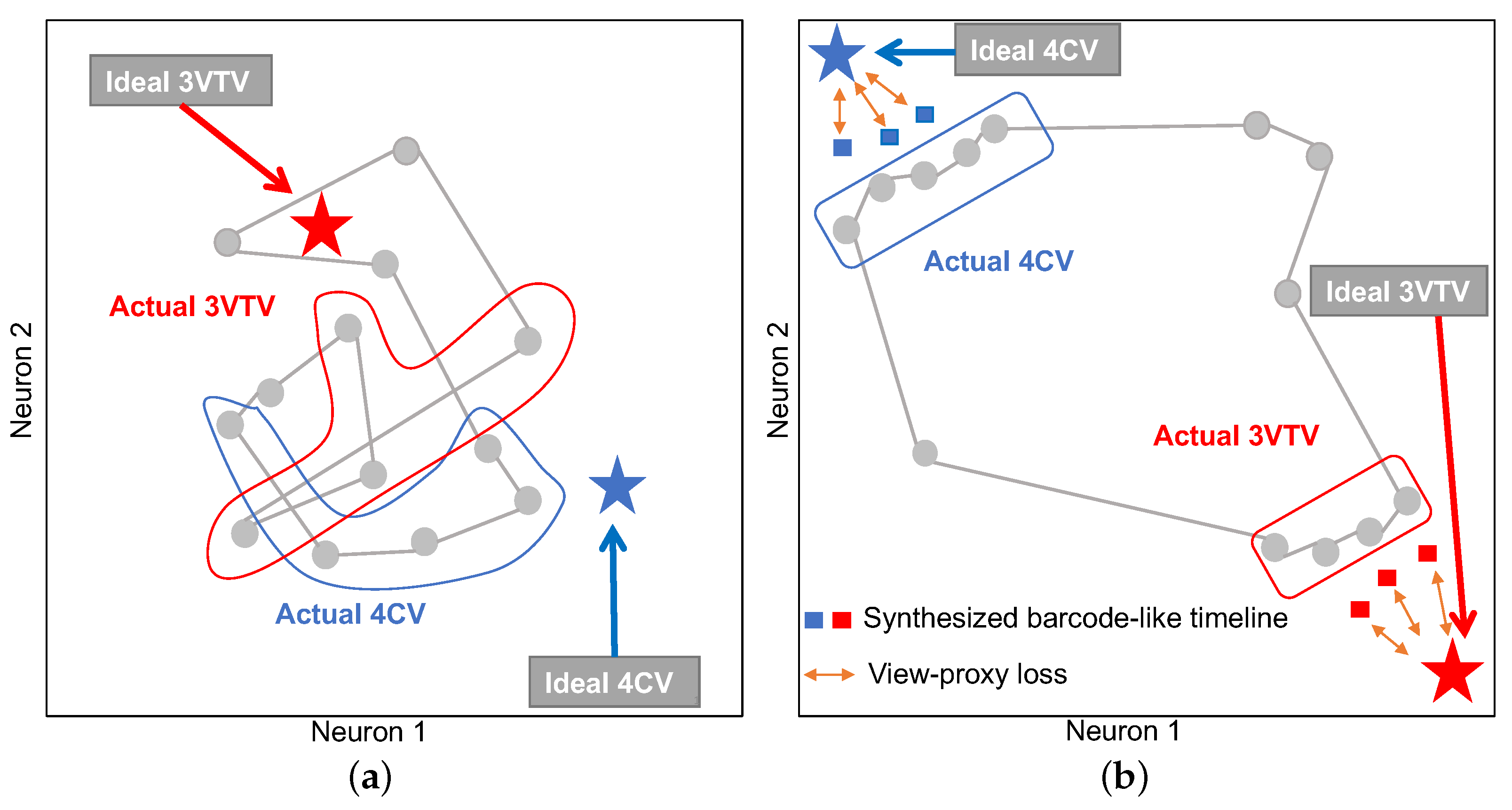
2.2.2. View-Proxy Loss and Cascade Graph Encoder
2.2.3. Abnormality Score
2.3. Evaluation of Medical Professional Enhancement
- Instruction part ⋯ The examiners were instructed on how to perform the test, and a graph chart diagram was explained. The examiners were given samples of the main-graph chart diagrams of a pair of normal and abnormal videos. We used a different model and different videos for testing to generate these main-graph chart diagrams. The performance of AI was not explained to examiners. Regarding the types of CHDs, the examiners were not informed what types of diseases would be included. Considering the ratio of normal to abnormal cases, we did not inform the examiners of the amounts of each.
- First block ⋯ The examiners were given 40 randomly numbered videos and an Excel file to fill in the answers. They played the videos on a laptop computer and filled in the Excel file with their decisions and confidence levels. No protocol was provided on how to assess the videos in detail to allow the examiners to perform this test as they usually would perform fetal cardiac ultrasound screening in a clinical setting. Therefore, the first block was performed depending on each examiner’s education and skill level.
- Second block ⋯ The examiners evaluated the same dataset independently of the first block, referring to graph chart diagrams G and abnormality scores for each video. The graph chart diagrams were given as PNG files, and the anomaly scores were given in an Excel sheet. The decisions of the AI between the normal and abnormal cases were not presented. Shapes created by the Shapely package were also not provided to the examiners. Considering the choice of graph chart diagrams G and abnormality scores , we adopted the results with the third-best AUC of the ROC curve among the five trials.
2.4. Statistical Analysis
3. Results
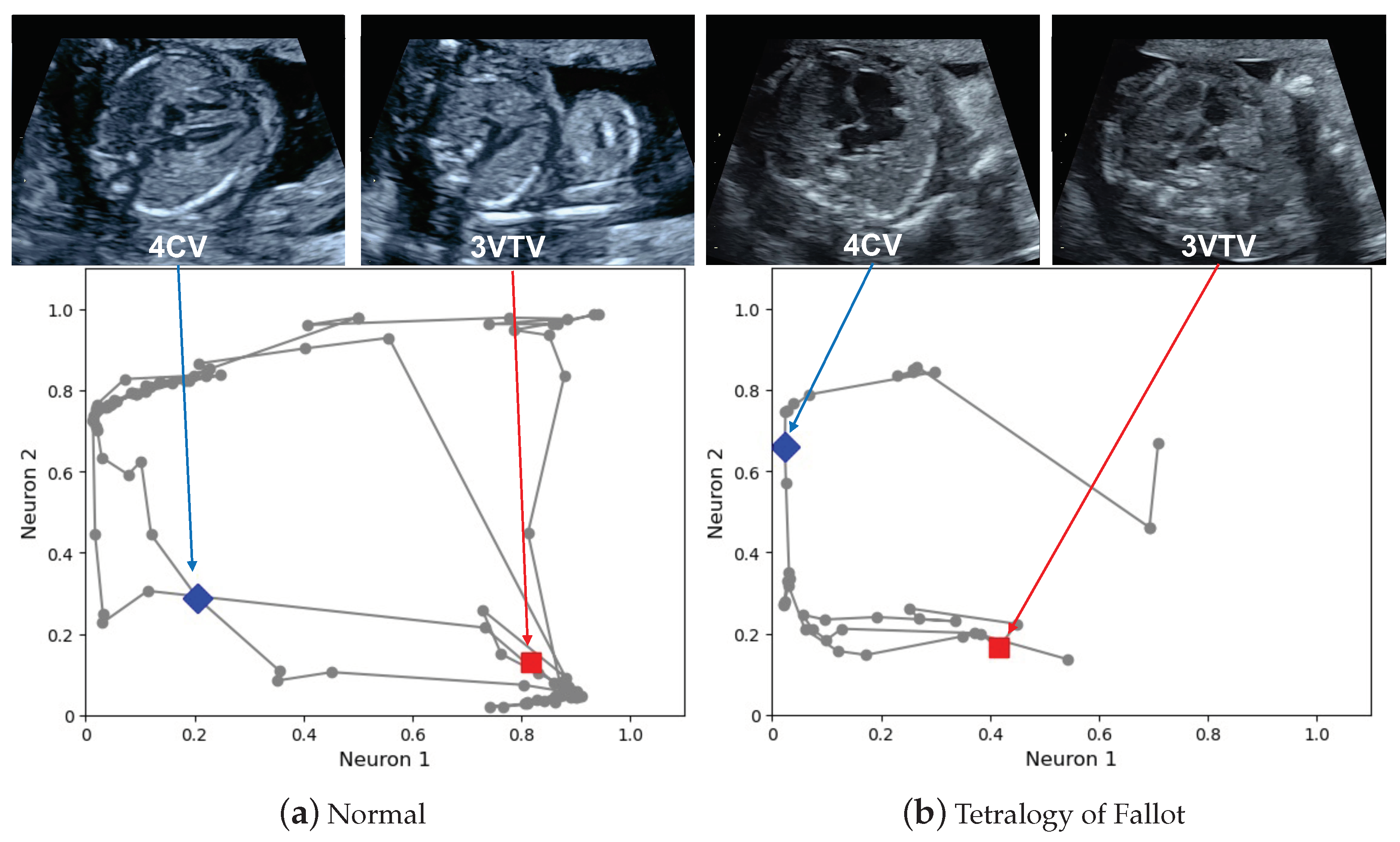
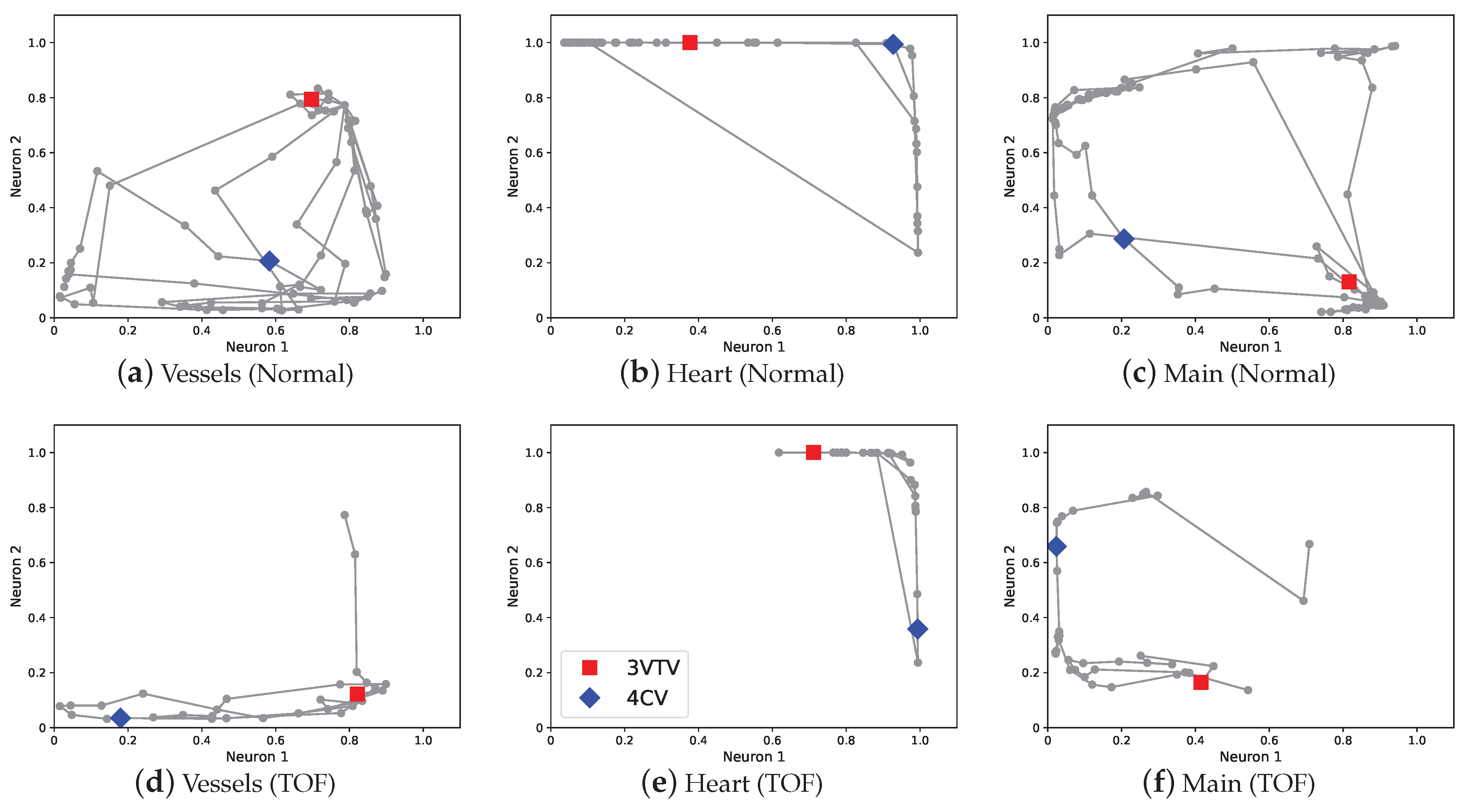
3.1. Examples of Graph Chart Diagram
3.2. Screening Performance Using Only AI
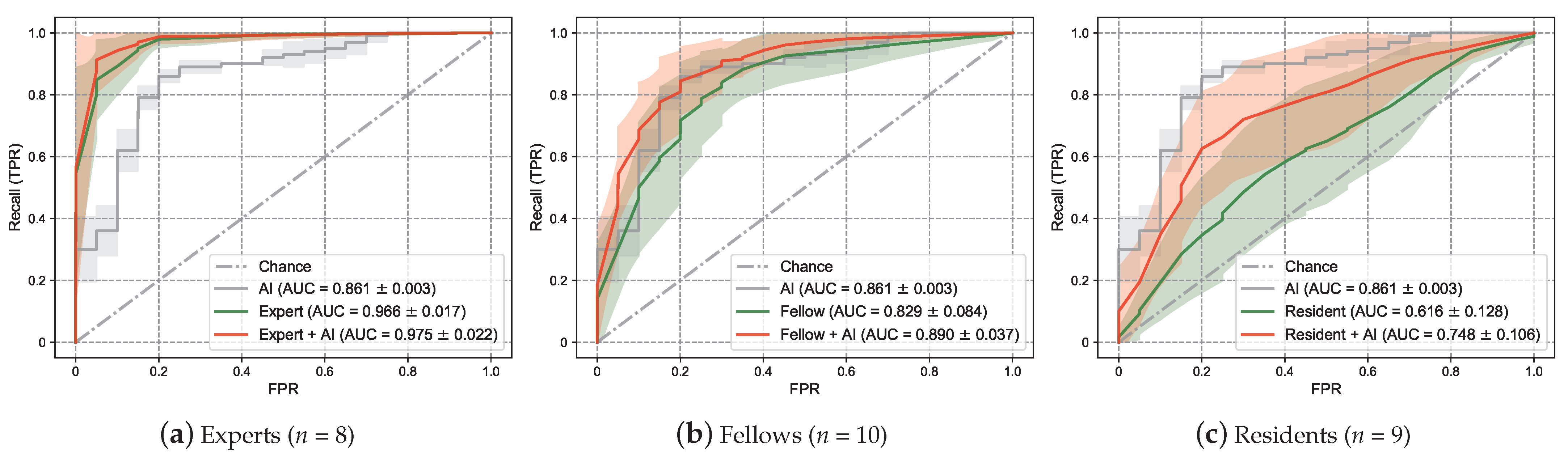
3.3. Screening Performance Enhancement Using the Examiner and AI Collaboration
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| AUC | area under the curve |
| CHD | congenital heart disease |
| DNN | deep neural network |
| FPR | false-positive rate |
| GE | General Electronic |
| Grad-CAM | Gradient-weighted Class Activation Mapping |
| ROC | receiver operating characteristic |
| SD | standard deviation |
| TOF | tetralogy of Fallot |
| TPR | true-positive rate |
| USA | United States of America |
| YOLO | You Only Look Once |
| 3VTV | three-vessel trachea view |
| 4CV | four-chamber view |
Appendix A. Formula of the Proposed Method
Appendix A.1. Simple Auto-Encoder for Graph Chart Diagram
Appendix A.2. View-Proxy Loss
Appendix A.3. Cascade Graph Encoder
| Algorithm A1 Inference algorithm of the cascade graph encoder. |
|
| Algorithm A2 Training algorithm of the cascade graph encoder. |
|
Appendix B. Experimental Details
References
- Hamamoto, R.; Suvarna, K.; Yamada, M.; Kobayashi, K.; Shinkai, N.; Miyake, M.; Takahashi, M.; Jinnai, S.; Shimoyama, R.; Sakai, A.; et al. Application of artificial intelligence technology in oncology: Towards the establishment of precision medicine. Cancers 2020, 12, 3532. [Google Scholar] [CrossRef] [PubMed]
- Komatsu, M.; Sakai, A.; Dozen, A.; Shozu, K.; Yasutomi, S.; Machino, H.; Asada, K.; Kaneko, S.; Hamamoto, R. Towards clinical application of artificial intelligence in ultrasound imaging. Biomedicines 2021, 9, 720. [Google Scholar] [CrossRef] [PubMed]
- Liao, Q.; Zhang, Q.; Feng, X.; Huang, H.; Xu, H.; Tian, B.; Liu, J.; Yu, Q.; Guo, N.; Liu, Q.; et al. Development of deep learning algorithms for predicting blastocyst formation and quality by time-lapse monitoring. Commun. Biol. 2021, 4, 415. [Google Scholar] [CrossRef] [PubMed]
- Shad, R.; Cunningham, J.P.; Ashley, E.A.; Langlotz, C.P.; Hiesinger, W. Designing clinically translatable artificial intelligence systems for high-dimensional medical imaging. Nat. Mach. Intell. 2021, 3, 929–935. [Google Scholar] [CrossRef]
- Jain, P.K.; Gupta, S.; Bhavsar, A.; Nigam, A.; Sharma, N. Localization of common carotid artery transverse section in B-mode ultrasound images using faster RCNN: A deep learning approach. Med. Biol. Eng. Comput. 2020, 58, 471–482. [Google Scholar] [CrossRef]
- Ellahham, S.; Ellahham, N.; Simsekler, M.C.E. Application of artificial intelligence in the health care safety context: Opportunities and challenges. Am. J. Med. Qual. 2019, 35, 341–348. [Google Scholar] [CrossRef]
- Garcia-Canadilla, P.; Sanchez-Martinez, S.; Crispi, F.; Bijnens, B. Machine learning in fetal cardiology: What to expect. Fetal Diagn. Ther. 2020, 47, 363–372. [Google Scholar] [CrossRef]
- Carvalho, D.V.; Pereira, E.M.; Cardoso, J.S. Machine learning interpretability: A survey on methods and metrics. Electronics 2019, 8, 832. [Google Scholar] [CrossRef] [Green Version]
- Rudin, C.; Radin, J. Why are we using black box models in AI when we don’t need to? A lesson from an explainable AI Competition. Harvard Data Sci. Rev. 2019, 1. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar] [CrossRef] [Green Version]
- Fong, R.C.; Vedaldi, A. Interpretable explanations of black boxes by meaningful perturbation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 3449–3457. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Yune, S.; Mansouri, M.; Kim, M.; Tajmir, S.H.; Guerrier, C.E.; Ebert, S.A.; Pomerantz, S.R.; Romero, J.M.; Kamalian, S.; et al. An explainable deep-learning algorithm for the detection of acute intracranial haemorrhage from small datasets. Nat. Biomed. Eng. 2019, 3, 173–182. [Google Scholar] [CrossRef]
- Ahsan, M.M.; Nazim, R.; Siddique, Z.; Huebner, P. Detection of COVID-19 patients from CT scan and chest X-ray data using modified MobileNetV2 and LIME. Healthcare 2021, 9, 1099. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, M.; Yeasin, M. Eigen-CAM: Visual explanations for deep convolutional neural networks. SN Comput. Sci. 2021, 2, 47. [Google Scholar] [CrossRef]
- Montavon, G.; Lapuschkin, S.; Binder, A.; Samek, W.; Müller, K.R. Explaining nonlinear classification decisions with deep Taylor decomposition. Pattern Recognit. 2017, 65, 211–222. [Google Scholar] [CrossRef]
- Lauritsen, S.M.; Kristensen, M.; Olsen, M.V.; Larsen, M.S.; Lauritsen, K.M.; Jørgensen, M.J.; Lange, J.; Thiesson, B. Explainable artificial intelligence model to predict acute critical illness from electronic health records. Nat. Commun. 2020, 11, 3852. [Google Scholar] [CrossRef] [PubMed]
- Han, S.H.; Kwon, M.S.; Choi, H.J. EXplainable AI (XAI) approach to image captioning. J. Eng. 2020, 2020, 589–594. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, Y.; Shu, L.; Li, J.; Duan, H.; Shu, Q.; Li, H. Explainable machine-learning predictions for complications after pediatric congenital heart surgery. Sci. Rep. 2021, 11, 17244. [Google Scholar] [CrossRef] [PubMed]
- Budd, S.; Sinclair, M.; Day, T.; Vlontzos, A.; Tan, J.; Liu, T.; Matthew, J.; Skelton, E.; Simpson, J.; Razavi, R.; et al. Detecting hypo-plastic left heart syndrome in fetal ultrasound via disease-specific atlas maps. In Proceedings of the Medical Image Computing and Computer Assisted Intervention (MICCAI), Strasbourg, France, 27 September–1 October 2021; pp. 207–217. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Bei, Y.; Rudin, C. Concept whitening for interpretable image recognition. Nat. Mach. Intell. 2020, 2, 772–782. [Google Scholar] [CrossRef]
- Wu, R.; Fujita, Y.; Soga, K. Integrating domain knowledge with deep learning models: An interpretable AI system for automatic work progress identification of NATM tunnels. Tunn. Undergr. Space Technol. 2020, 105, 103558. [Google Scholar] [CrossRef]
- Blazek, P.J.; Lin, M.M. Explainable neural networks that simulate reasoning. Nat. Comput. Sci. 2021, 1, 607–618. [Google Scholar] [CrossRef]
- Barić, D.; Fumić, P.; Horvatić, D.; Lipic, T. Benchmarking attention-based interpretability of deep learning in multivariate time series predictions. Entropy 2021, 23, 143. [Google Scholar] [CrossRef] [PubMed]
- Donofrio, M.; Moon-Grady, A.; Hornberger, L.; Copel, J.; Sklansky, M.; Abuhamad, A.; Cuneo, B.; Huhta, J.; Jonas, R.; Krishnan, A.; et al. Diagnosis and treatment of fetal cardiac disease a scientific statement from the american heart association. Circulation 2014, 129, 2183–2242. [Google Scholar] [CrossRef] [PubMed]
- Tegnander, E.; Williams, W.; Johansen, O.; Blaas, H.G.; Eik-Nes, S. Prenatal detection of heart defects in a non-selected population of 30 149 fetuses—detection rates and outcome. Ultrasound Obstet. Gynecol. 2006, 27, 252–265. [Google Scholar] [CrossRef] [PubMed]
- Cuneo, B.F.; Curran, L.F.; Davis, N.; Elrad, H. Trends in prenatal diagnosis of critical cardiac defects in an integrated obstetric and pediatric cardiac imaging center. J. Perinatol. 2004, 24, 674–678. [Google Scholar] [CrossRef] [Green Version]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Rajpurkar, P.; Irvin, J.A.; Ball, R.L.; Zhu, K.; Yang, B.; Mehta, H.; Duan, T.; Ding, D.; Bagul, A.; Langlotz, C.; et al. Deep learning for chest radiograph diagnosis: A retrospective comparison of the CheXNeXt algorithm to practicing radiologists. PLoS Med. 2018, 15, e1002686. [Google Scholar] [CrossRef]
- De Fauw, J.; Ledsam, J.R.; Romera-Paredes, B.; Nikolov, S.; Tomasev, N.; Blackwell, S.; Askham, H.; Glorot, X.; O’Donoghue, B.; Visentin, D.; et al. Clinically applicable deep learning for diagnosis and referral in retinal disease. Nat. Med. 2018, 24, 1342–1350. [Google Scholar] [CrossRef]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef]
- Yamada, M.; Saito, Y.; Imaoka, H.; Saiko, M.; Yamada, S.; Kondo, H.; Takamaru, H.; Sakamoto, T.; Sese, J.; Kuchiba, A.; et al. Development of a real-time endoscopic image diagnosis support system using deep learning technology in colonoscopy. Sci. Rep. 2019, 9, 14465. [Google Scholar] [CrossRef] [Green Version]
- Bressem, K.K.; Vahldiek, J.L.; Adams, L.; Niehues, S.M.; Haibel, H.; Rodriguez, V.R.; Torgutalp, M.; Protopopov, M.; Proft, F.; Rademacher, J.; et al. Deep learning for detection of radiographic sacroiliitis: Achieving expert-level performance. Arthritis Res. Ther. 2021, 23, 106. [Google Scholar] [CrossRef]
- Kusunose, K.; Abe, T.; Haga, A.; Fukuda, D.; Yamada, H.; Harada, M.; Sata, M. A deep learning approach for assessment of regional wall motion abnormality from echocardiographic images. JACC Cardiovasc. Imaging 2020, 13, 374–381. [Google Scholar] [CrossRef] [PubMed]
- Arnaout, R.; Curran, L.; Zhao, Y.; Levine, J.C.; Chinn, E.; Moon-Grady, A.J. An ensemble of neural networks provides expert-level prenatal detection of complex congenital heart disease. Nat. Med. 2021, 27, 882–891. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Yang, Y.; Yu, C.; Liu, J.; Duan, X.; Weng, Z.; Chen, D.; Liang, Q.; Fang, Q.; Zhou, J.; et al. Ensembled deep learning model outperforms human experts in diagnosing biliary atresia from sonographic gallbladder images. Nat. Commun. 2021, 12, 1259. [Google Scholar] [CrossRef]
- Shad, R.; Quach, N.; Fong, R.; Kasinpila, P.; Bowles, C.; Castro, M.; Guha, A.; Suarez, E.E.; Jovinge, S.; Lee, S.; et al. Predicting post-operative right ventricular failure using video-based deep learning. Nat. Commun. 2021, 12, 5192. [Google Scholar] [CrossRef] [PubMed]
- Chan, W.K.; Sun, J.H.; Liou, M.J.; Li, Y.R.; Chou, W.Y.; Liu, F.H.; Chen, S.T.; Peng, S.J. Using Deep Convolutional Neural Networks for Enhanced Ultrasonographic Image Diagnosis of Differentiated Thyroid Cancer. Biomedicines 2021, 9, 1771. [Google Scholar] [CrossRef]
- Hekler, A.; Utikal, J.; Enk, A.; Hauschild, A.; Weichenthal, M.; Maron, R.; Berking, C.; Haferkamp, S.; Klode, J.; Schadendorf, D.; et al. Superior skin cancer classification by the combination of human and artificial intelligence. Eur. J. Cancer 2019, 120, 114–121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salim, M.; Wåhlin, E.; Dembrower, K.; Azavedo, E.; Foukakis, T.; Liu, Y.; Smith, K.; Eklund, M.; Strand, F. External evaluation of 3 commercial artificial intelligence algorithms for independent assessment of screening mammograms. JAMA Oncol. 2020, 6, 1581–1588. [Google Scholar] [CrossRef]
- Uchino, E.; Suzuki, K.; Sato, N.; Kojima, R.; Tamada, Y.; Hiragi, S.; Yokoi, H.; Yugami, N.; Minamiguchi, S.; Haga, H.; et al. Classification of glomerular pathological findings using deep learning and nephrologist–AI collective intelligence approach. Int. J. Med. Inform. 2020, 141, 104231. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Tsuzuki, T.; Akatsuka, J.; Ueki, M.; Morikawa, H.; Numata, Y.; Takahara, T.; Tsuyuki, T.; Tsutsumi, K.; Nakazawa, R.; et al. Automated acquisition of explainable knowledge from unannotated histopathology images. Nat. Commun. 2019, 10, 5642. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, P.; McGough, M.; Xing, F.; Wang, C.; Bui, M.; Xie, Y.; Sapkota, M.; Cui, L.; Dhillon, J.; et al. Pathologist-level interpretable whole-slide cancer diagnosis with deep learning. Nat. Mach. Intell. 2019, 1, 236–245. [Google Scholar] [CrossRef]
- Tschandl, P.; Rinner, C.; Apalla, Z.; Argenziano, G.; Codella, N.; Halpern, A.; Janda, M.; Lallas, A.; Longo, C.; Malvehy, J.; et al. Human–computer collaboration for skin cancer recognition. Nat. Med. 2020, 26, 1229–1234. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–27 July 2017; pp. 6517–6525. [Google Scholar] [CrossRef] [Green Version]
- Komatsu, M.; Sakai, A.; Komatsu, R.; Matsuoka, R.; Yasutomi, S.; Shozu, K.; Dozen, A.; Machino, H.; Hidaka, H.; Arakaki, T.; et al. Detection of cardiac structural abnormalities in fetal ultrasound videos Using Deep Learning. Appl. Sci. 2021, 11, 371. [Google Scholar] [CrossRef]
- Baldominos, A.; Saez, Y.; Isasi, P. A Survey of Handwritten Character Recognition with MNIST and EMNIST. Appl. Sci. 2019, 9, 3169. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- van der Voort, S.R.; Incekara, F.; Wijnenga, M.M.; Kapas, G.; Gardeniers, M.; Schouten, J.W.; Starmans, M.P.; Nandoe Tewarie, R.; Lycklama, G.J.; French, P.J.; et al. Predicting the 1p/19q codeletion status of presumed low-grade glioma with an externally validated machine learning algorithm. Clin. Cancer Res. 2019, 25, 7455–7462. [Google Scholar] [CrossRef] [Green Version]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
- Velliangiri, S.; Alagumuthukrishnan, S.; Thankumar joseph, S.I. A review of dimensionality reduction techniques for efficient computation. Procedia Comput. Sci. 2019, 165, 104–111. [Google Scholar] [CrossRef]
- Huang, X.; Wu, L.; Ye, Y. A review on dimensionality reduction techniques. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1950017. [Google Scholar] [CrossRef]
- Ali, M.; Alqahtani, A.; Jones, M.W.; Xie, X. Clustering and classification for time series data in visual analytics: A survey. IEEE Access 2019, 7, 181314–181338. [Google Scholar] [CrossRef]
- Ali, M.; Jones, M.W.; Xie, X.; Williams, M. TimeCluster: Dimension reduction applied to temporal data for visual analytics. Vis. Comput. 2019, 35, 1013–1026. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Kim, D.; Cho, M.; Kwak, S. Proxy anchor loss for deep metric learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 3235–3244. [Google Scholar] [CrossRef]
- Aziere, N.; Todorovic, S. Ensemble deep manifold similarity learning using hard proxies. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7291–7299. [Google Scholar] [CrossRef]
- Movshovitz-Attias, Y.; Toshev, A.; Leung, T.K.; Ioffe, S.; Singh, S. No fuss distance metric learning using proxies. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 360–368. [Google Scholar] [CrossRef] [Green Version]
- Fukami, K.; Nakamura, T.; Fukagata, K. Convolutional neural network based hierarchical autoencoder for nonlinear mode decomposition of fluid field data. Phys. Fluids 2020, 32, 095110. [Google Scholar] [CrossRef]
- Liu, G.; Bao, H.; Han, B. A Stacked autoencoder-based deep neural network for achieving gearbox fault diagnosis. Math. Probl. Eng. 2018, 2018, 5105709. [Google Scholar] [CrossRef] [Green Version]
- Baumgartner, C.F.; Kamnitsas, K.; Matthew, J.; Fletcher, T.P.; Smith, S.; Koch, L.M.; Kainz, B.; Rueckert, D. SonoNet: Real-time detection and localisation of fetal standard scan planes in freehand ultrasound. IEEE Trans. Med. Imaging 2017, 36, 2204–2215. [Google Scholar] [CrossRef] [Green Version]
- Madani, A.; Arnaout, R.; Mofrad, M.; Arnaout, R. Fast and accurate view classification of echocardiograms using deep learning. NPJ Digit. Med. 2018, 1, 6. [Google Scholar] [CrossRef]
- Dong, J.; Liu, S.; Liao, Y.; Wen, H.; Lei, B.; Li, S.; Wang, T. A generic quality control framework for fetal ultrasound cardiac four-chamber planes. IEEE J. Biomed. Health Inform. 2020, 24, 931–942. [Google Scholar] [CrossRef]
- Pu, B.; Li, K.; Li, S.; Zhu, N. Automatic fetal ultrasound standard plane recognition based on deep Learning and IIoT. IEEE Trans. Ind. Inform. 2021, 17, 7771–7780. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, H.; Luo, H.; Li, K. Automatic quality assessment for 2D fetal sonographic standard plane based on multitask learning. Medicine 2021, 100, e24427. [Google Scholar] [CrossRef]
- Day, T.G.; Kainz, B.; Hajnal, J.; Razavi, R.; Simpson, J.M. Artificial intelligence, fetal echocardiography, and congenital heart disease. Prenat. Diagn. 2021, 41, 733–742. [Google Scholar] [CrossRef]
- Hasan, M.; Choi, J.; Neumann, J.; Roy-Chowdhury, A.K.; Davis, L.S. Learning temporal regularity in video sequences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 733–742. [Google Scholar] [CrossRef] [Green Version]
- Narasimhan, M.G.; Sowmya, S.K. Dynamic video anomaly detection and localization using sparse denoising autoencoders. Multimed. Tools Appl. 2018, 77, 13173–13195. [Google Scholar] [CrossRef]
- Nayak, R.; Pati, U.C.; Das, S.K. A comprehensive review on deep learning-based methods for video anomaly detection. Image Vis. Comput. 2021, 106, 104078. [Google Scholar] [CrossRef]
- Dozen, A.; Komatsu, M.; Sakai, A.; Komatsu, R.; Shozu, K.; Machino, H.; Yasutomi, S.; Arakaki, T.; Asada, K.; Kaneko, S.; et al. Image segmentation of the ventricular septum in fetal cardiac ultrasound videos based on deep learning using time-series information. Biomolecules 2020, 10, 1526. [Google Scholar] [CrossRef] [PubMed]
- Shozu, K.; Komatsu, M.; Sakai, A.; Komatsu, R.; Dozen, A.; Machino, H.; Yasutomi, S.; Arakaki, T.; Asada, K.; Kaneko, S.; et al. Model-agnostic method for thoracic wall segmentation in fetal ultrasound Videos. Biomolecules 2020, 10, 1691. [Google Scholar] [CrossRef] [PubMed]
- Vargas-Quintero, L.; Escalante-Ramírez, B.; Camargo Marín, L.; Guzmán Huerta, M.; Arámbula Cosio, F.; Borboa Olivares, H. Left ventricle segmentation in fetal echocardiography using a multi-texture active appearance model based on the steered Hermite transform. Comput. Methods Programs Biomed. 2016, 137, 231–245. [Google Scholar] [CrossRef] [PubMed]
- Yasutomi, S.; Arakaki, T.; Matsuoka, R.; Sakai, A.; Komatsu, R.; Shozu, K.; Dozen, A.; Machino, H.; Asada, K.; Kaneko, S.; et al. Shadow estimation for ultrasound images using auto-encoding structures and synthetic shadows. Appl. Sci. 2021, 11, 1127. [Google Scholar] [CrossRef]
| Cascade Graph Encoder | View-Proxy Loss | Mean (SD) | Median (Min–Max) |
|---|---|---|---|
| √ | √ | 0.861 (0.003) | 0.860 (0.858–0.865) |
| √ | 0.819 (0.013) | 0.813 (0.803–0.835) | |
| √ | 0.833 (0.002) | 0.833 (0.830–0.835) | |
| 0.798 (0.007) | 0.803 (0.790–0.805) |
| Method | Mean (SD) | Median (Min–Max) |
|---|---|---|
| Expert | – | |
| Expert + AI | – | |
| Fellow | – | |
| Fellow + AI | – | |
| Resident | – | |
| Resident + AI | – | |
| Examiner | – | |
| Examiner + AI | – |
| Method | Accuracy (SD) | FPR (SD) | Recall (SD) | Precision (SD) | F1 Score (SD) |
|---|---|---|---|---|---|
| Expert | |||||
| Expert + AI | |||||
| Fellow | |||||
| Fellow + AI | |||||
| Resident | |||||
| Resident + AI | |||||
| Examiners | |||||
| Examiners + AI |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakai, A.; Komatsu, M.; Komatsu, R.; Matsuoka, R.; Yasutomi, S.; Dozen, A.; Shozu, K.; Arakaki, T.; Machino, H.; Asada, K.; et al. Medical Professional Enhancement Using Explainable Artificial Intelligence in Fetal Cardiac Ultrasound Screening. Biomedicines 2022, 10, 551. https://doi.org/10.3390/biomedicines10030551
Sakai A, Komatsu M, Komatsu R, Matsuoka R, Yasutomi S, Dozen A, Shozu K, Arakaki T, Machino H, Asada K, et al. Medical Professional Enhancement Using Explainable Artificial Intelligence in Fetal Cardiac Ultrasound Screening. Biomedicines. 2022; 10(3):551. https://doi.org/10.3390/biomedicines10030551
Chicago/Turabian StyleSakai, Akira, Masaaki Komatsu, Reina Komatsu, Ryu Matsuoka, Suguru Yasutomi, Ai Dozen, Kanto Shozu, Tatsuya Arakaki, Hidenori Machino, Ken Asada, and et al. 2022. "Medical Professional Enhancement Using Explainable Artificial Intelligence in Fetal Cardiac Ultrasound Screening" Biomedicines 10, no. 3: 551. https://doi.org/10.3390/biomedicines10030551
APA StyleSakai, A., Komatsu, M., Komatsu, R., Matsuoka, R., Yasutomi, S., Dozen, A., Shozu, K., Arakaki, T., Machino, H., Asada, K., Kaneko, S., Sekizawa, A., & Hamamoto, R. (2022). Medical Professional Enhancement Using Explainable Artificial Intelligence in Fetal Cardiac Ultrasound Screening. Biomedicines, 10(3), 551. https://doi.org/10.3390/biomedicines10030551








