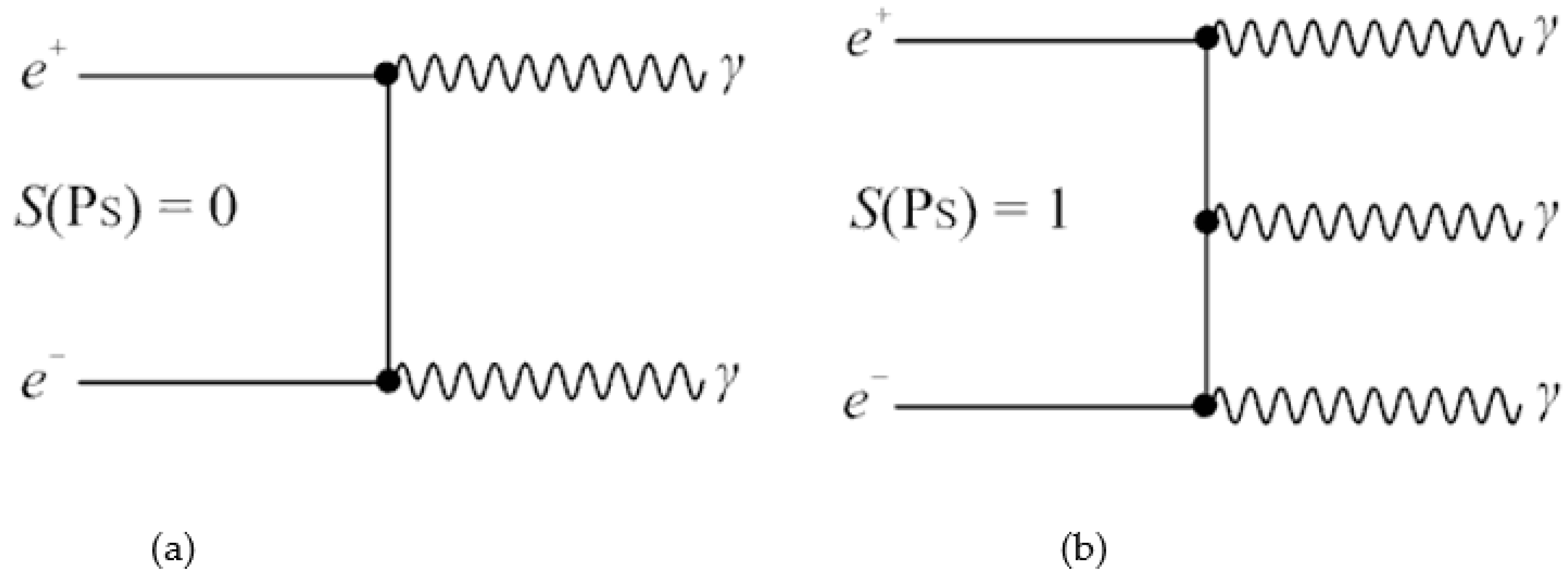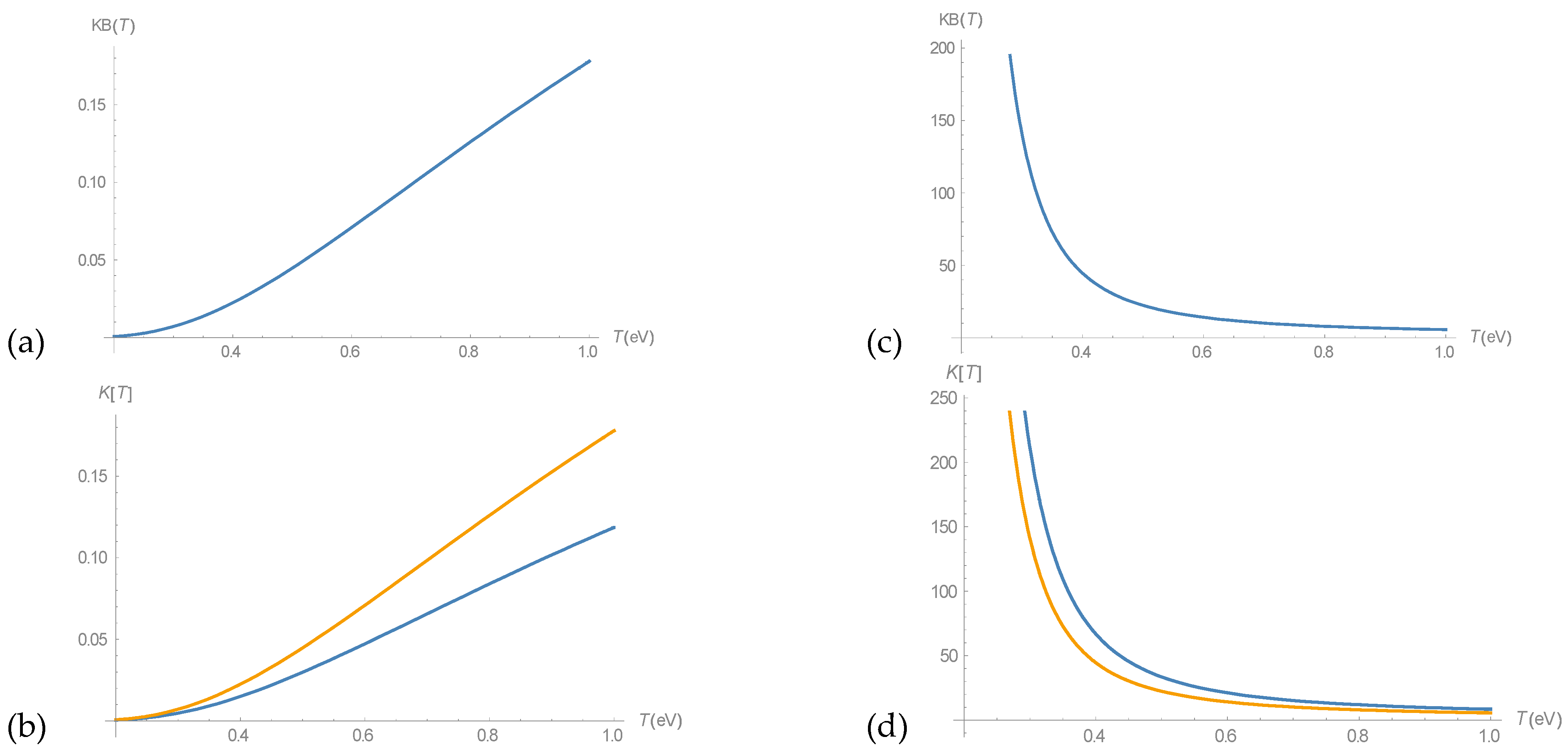Collision of a Positron with the Capture of an Electron from Lithium and the Effect of a Magnetic Field on the Particles Balance

Abstract

The processes of scattering slow positrons with the possible formation of positronium play an important role in the diagnosis of both composite materials, including semiconductor materials, and for the analysis of images obtained by positron tomography of living tissues. In this paper, we consider the processes of scattering positrons with the capture of an electron and the formation of positronium. When calculating the cross-section for the capture reaction, exchange effects caused by the rearrangement of electrons between colliding particles are taken into account. Comparison of the results of calculating the cross-section with a similar problem of electron capture by a proton showed that the mass effect is important in such a collision process. The loss of an electron by a lithium atom is more effective when it collides with a positron than with a proton or alpha particles. The dynamic equilibrium of the formation of positronium in the presence of a strong magnetic field is considered. It is shown that a strong magnetic field during tomography investigation shifts the dynamic equilibrium to the positronium concentration followed by positron annihilation with radiation of three gamma-quants.

1. Introduction

Low energy positron beams are widely used in material physics, as well as in biophysics and medical physics. Positron beams obtained at accelerators are collected in a storage ring and pass through a moderator, which reduces the positron velocity to thermal velocities. Descriptions of the positrons scattering processes in moderators of various types and in living tissue during when used for medical purposes for conducting positron therapy, as well as understanding the processes taking place with the participation of positrons, play a key role in research and diagnostics. Various mechanisms of deceleration are studied, associated both with inelastic collisions with atoms with the formation of positronium, and with the formation [1,2] and the processes of interaction of a positron with phonons of the crystal lattice [3].

The advent of positron emission tomography (PET) [4] has changed the capabilities and role of nuclear medicine, not because the images it produces are better than conventional single-photon imaging (flat and single-photon emission computed tomography (SPECT)), but also because it is the fastest growing diagnostic specialty.

After radiation from the nucleus, the positron passes through the substance and constantly loses kinetic energy due to interaction with other nuclei, in acts of ionization with other atoms and due to radiation during inelastic scattering, while constantly deviating from its original path. Thus, the positron will make an extremely tortuous passage through matter. Because of this, it is difficult to estimate the range of positrons based on their energy alone; therefore, empirical measurements are usually carried out to determine the average range of positrons in a given material. The positron eventually combines with an electron to form a positronium. The processes of scattering positrons with the possible formation of positronium play an important role in diagnosis, and for the analysis of the images obtained in positron tomography of living tissues. That is why the detailed theoretical analysis of each step and each process during the positron pass is very important for understanding the total picture of positron scattering. In the last decade, significant progress has been observed in the creation of positron beams based on low-energy traps [5] New high-resolution experimental measurements were performed for a number of atomic and molecular targets, including He [6], Ne and Ar [7,8], Xe [9] and Kr [10]. The cross-sections for the production of positronium are especially important, see recent work [11].

In the scattering of a positron with capture of an electron from the outer shell of an atom in a dielectric and in living tissue, exchange effects in the electronic system play an important role. It is especially important during the slow-scattering of atomic particles, where the electron shells belonging to the different centers are overlapping over a long duration. This also occurs during the scattering of elementary particles, such as an alpha particle, proton or positron, when an electron is captured by this particle from the shell of the atom. In this case, the electron states of the atomic ion and a new bearing atom (hydrogen-atom or positronium) are strongly overlapping. Such an overlapping occurs for the non-orthogonal states, belonging to the different centers. It is necessary to take into account the exchange effects in slow collisions. Moreover, the overlap of electron shells and the associated exchange effects, in fact, determine the rearrangement of the electron shells themselves in the course of charge exchange or a chemical reaction.

Commonly in the formulation of the general theory of scattering on the basis of invariant perturbation theory, in the algorithm for obtaining expressions for the S-scattering matrix, as well as the T-matrix of scattering on the energy surface, there is initially no method that allows taking into account the exchange effects caused by the overlapping of the electron shells themselves for the colliding complex particles [12,13]. This is done by the method of obtaining corrections, taken out of the context of perturbation theory, where first the curve of the adiabatic interaction potential of particles is calculated, and then the problem of the scattering of structureless particles in the resulting potential is considered. In such a setting, obtaining an analytical result is impossible, the problem can be solved only numerically. In recent decades various highly sophisticated methods including the exterior complex scaling (ECS) [14], R-matrix with pseudo-states (RMPS) [15], time-dependent close-coupling (TDCC) [16] and convergent close coupling (CCC) [17] have been used for the theoretical description of electron-impact ionization (and excitation) processes. Electron scattering by atomic center problems are examples of a cases where there is only one “natural” center, namely the atomic center. All coordinates are readily written with the origin set at the atomic center. Yet, there are many atomic collision systems that involve at least two centers, such as the positron–hydrogen scattering system. This is a three-body system where all the particles are distinguishable, and which allows for their rearrangement. There have two “natural” centers, the atomic center and the positronium (Ps) center. Commonly, for positron–hydrogen scattering ionization the problem splits into two separate components: the rearrangement process of Ps-formation and the three-body breakup process. In this case a proper formulation of Ps-formation processes requires a combined basis consisting of two independent basis sets for each of the centers which makes theoretical studies considerably more challenging than for electron scattering. Furthermore, the positron-atom system is an ideal prototype of the ubiquitous collision systems such as proton-atom scattering, where charge-exchange processes also require a two-center treatment. The description of intercenter exchange effects leads to the fact that the problem of electron redistribution between centers always leads to ambiguity of solutions, both in the formulation and solution of integral equations for the scattering amplitude, and in the invariant formalism, in the construction of the S-scattering matrix and calculating its matrix elements [13]. Integral and differential cross-sections for the Ps-formation channel for e+–alkali–metal–atom collisions was calculated by using a model optical potential by Gianturco and Melissa [18]. The atomic targets discussed there were Li, Na, and K. The potential was obtained without empirical parameters by global modeling of the dynamic polarization potential and short-range correlation forces using generalized damping functions. The absorption part of the potential is obtained by means of a dispersion relation. Another sophisticated approach was developed by King and Gribakin based on the many body perturbation theory. They used an approximation by considering virtual Ps formation only in the ground state. Gribakin and Ludlow [19] have further improved the method by introducing the techniques for the exact summation of the electron–positron ladder diagram series. One of the most complex and commonly used methods is he close-coupling (CC) [20], based on the expansion of the total wave function using the wave functions of the target state. Substitution of this expansion into the Schrödinger equation leads to coupled differential equations in coordinate space or Lippmann–Schwinger integral equations for the T-matrix in momentum space. Solving these equations, we obtain the transition amplitudes for all open channels. For instance, CC refers to close-coupling calculations with a combined basis made of pseudostates for the atomic center supplemented by Ps eigenstates. It should be noted that this consideration of scattering problem for two-electronic system (Helium and positron) is based on one-electron Green function without taking into account the identity of electrons belonging to the different centers, in contrary to the consideration [21,22,23].

To describe the scattering of complex atomic particles we use the scattering theory algorithm, which basically takes into account the indicated exchange effects; this is a formalism based on the invariant exchange perturbation theory (IEPT) [21]. EPT formalism has developed in a general form [21]. It uses an antisymmetric basis, which takes into account all possible rearrangements of electrons between scattering centers. It is shown that this basis is not orthogonal; nevertheless, it possesses the completeness property. The representation of energy corrections and wave function corrections is unique and contains a special symmetric form of the perturbation operator. We take into account the principle of indistinguishability of identical particles when describing the scattering of atomic particles in general terms. As shown in [21,23], the EPT formalism for the nonstationary case has the form of an invariant exchange perturbation theory (IEPT). The general expressions obtained for the scattering matrix (S) and the transition matrix (T) for arbitrary types of interactions consistently take into account the permutations of electrons between overlapping nonorthogonal states. This formalism was used to describe the process of collision of atomic particles in connection with the rearrangement of the electronic structure between scattered particles, taking into account exchange effects [21,22,23,24,25]. All exchange effects that contribute to the first-order corrections to the amplitude and scattering cross-section are taken into account sequentially. It takes into account the entanglement of the channels already in the first approximation of the exchange perturbation theory.

Theoretical studies of the scattering of positrons by a multielectron atom are associated with additional difficulties due to the complexity of the target structure. Additionally, helium, which is a two-electron system, has excitation (or excitation ionization) channels that are usually excluded. This is a good approximation, since the contribution of these channels is usually two orders of magnitude less than the contribution of the corresponding one-electron excitation processes. Massey and Moussa [26] at the first-order Born approximation (FBA) performed the first calculations of e+–He scattering. They used only ground states for He and Ps and obtained cross-sections for elastic scattering and formation of Ps in its ground state. These studies showed the importance of the Ps-channel coupling with the elastic channel and motivated further researches. FBA studies have also shown that more sophisticated approaches to this problem are required. The distorted-wave Born approximation (DWBA) results are obtained by using distorted wavefunctions in first-order calculations. This method gives more accurate results than the FBA down to lower energies. DWBA was used in early works [27], applied to the excitation of helium by positrons in the energy range from the threshold to 150 eV. Although the agreement with the experimental data was not entirely satisfactory, the method showed the importance of taking into account the polarization potential in the excitation channels at low energies. The most systematic study of the ionization process within the framework of DWBA was carried out by Campeanu [28].

The aim of this work is to consistently take into account exchange effects in the problem of scattering of slow atomic particles with possible processes of rearrangement of electron shells (chemical reactions). In this case, the main emphasis is placed precisely on the exchange effects associated with the overlap of the electron shells of the atomic particles themselves. This circumstance requires correction of the general formulas for the invariant perturbation theory and the quantum theory of scattering (T–S scattering matrices) taking into account the principle of indistinguishability of identical particles for electrons belonging to colliding atoms. The attempts to consider scattering processes with taking into account the exchange effects were made in [23,24,25] for description of an inelastic coherent electron scattering by disordered media and for the problem of proton scattering by lithium atom with electron capture [24].

One of the flagships of technological progress in medical diagnostic is the new GE SIGNA hybrid PET/MRI machine, which provides simultaneous magnetic resonance imaging and positron emission tomography. Both MRI and PET are methods for examining internal organs and tissues, based on various physical principles and having their own characteristics. Magnetic resonance imaging is based on the response of atomic nuclei in a powerful magnetic field. Under the influence of a strong magnetic field, the positively charged protons of the nuclei line up along the magnetic lines. Then a radio frequency signal is applied, under the influence of which the protons temporarily change their position, and then, returning to their original position, they emit a signal, which is recorded by an MRI tomography. The result is a high-quality color image with fine details of the studied part of the body, with clear boundaries of pathological formations. Unlike MRI, PET does not provide a clear picture of tissues and organs, but it allows to recognize the course pathological processes literally at the cellular level. For example, a PET scan shows the spread of metastases in cancer. In 1983, GE introduced the first tunnel-type MRI scanner for examining a patient’s entire body. It was a pipe, in the walls of which magnets were mounted, which created a strong field with an induction of 1.5 T. The tunnel had a diameter of 60 cm, which at that time was considered sufficient for placing people of any build inside the apparatus. Later, the designers proposed a new version—an MRI machine with a large tube diameter. On the one hand, this increased the level of patient comfort, on the other hand, it provided the technical possibility of adding a ring for PET detectors to the tunnel. Now it was possible to obtain a combined image, where detailed anatomical information about the boundaries and volumes was combined with data on the biological functions of the regions of interest in the body at the molecular level. It is important to note that the strong magnetic fields of MRI can uncontrollably affect the processes in PET, while simultaneously adding additional information by changing the spectrum of gamma radiation. Such processes need to be investigated.

Then, the tasks of our work are:

(1) Consideration of the problem of scattering of a positron by a Lithium atom with the possibility of charge exchange. Detailed quantum-mechanical calculation of the differential cross-section of this process as a function of scattering angle. Establishing the effect of the mass of a charged particle on the cross-section of the recharge process.

(2) Investigation of the equilibrium concentration of positronium in the presence of a strong magnetic field. It is shown that the magnetic field changes the ratio of the concentration of free electrons and positrons to the bound states of positronium. This equilibrium is shifted towards positronium components. Then during the following annihilation of positrons three gamma-quants instead of two will be radiated.

2. Capture of an Electron by a Positron with Ionization of Lithium

We consider a process of positron scattering on Lithium atom: $Li+e^{+}\to L{i}^{+}+Ps$ with a positronium creation. The relative motion of the positron and the atom is determined by the operator of kinetic energy $-\frac{{\hslash }^2}{2\mu }{\nabla }_R^2$, where $R$ is vector directed from the positron to the nucleus of the Lithium atom and $\mu =\frac{M_{Li}{m}_{e^{+}}}{\left(M_{Li}+m_{e^{+}}\right)}$ is a reduced mass, where $M_{Li}$ is Lithium atom mass and $m_{e^{+}}$ is a positron mass. Interaction between positron and the atom is determined by the operator:

$$V(1,2,3)=-\frac{e^2}{r_{e^{+}1}}-\frac{e^2}{r_{e^{+}2}}-\frac{e^2}{r_{e^{+}3}}+\frac{3e^2}{R}$$

(1)

where terms $-\frac{e^2}{r_{e^{+}n}}$ (n = 1, 2, 3) describe an interaction of positron with electrons, numbered 1, 2, 3, belonging to the lithium atom, and the term $\frac{3e^2}{R}$ describes an interaction of positron with lithium’s nucleus. The motion of electrons in lithium atom is described by the Hamiltonian:

$$H(1,2,3)=-\frac{{\hslash }^2}{2m}({\nabla }_1^2+{\nabla }_2^2+{\nabla }_3^2)-\frac{Z{e}^2}{r_{\mathrm{Li}1}}-\frac{Z{e}^2}{r_{\mathrm{Li}2}}-\frac{Z{e}^2}{r_{\mathrm{Li}3}}$$

(2)

In our consideration of the scattering process, we will pay especial attention to questions of the electron permutation symmetry during the scattering process with an electron capture of the problem. So, an antisymmetric eigenfunction of the Hamiltonian, correspondent to the energy ${\epsilon }_n$ eigenvalue with respect to intra-atomic electron permutations is given by:

$${\mathsf{\Phi }}_{Li}\otimes {\chi }_{Li}=\frac{1}{f_{Li}}\left({\mathsf{\Psi }}_{Li1}{\mathsf{{\rm X}}}_{Li1}+{\mathsf{\Psi }}_{Li2}{\mathsf{{\rm X}}}_{Li2}\right)$$

(3)

where ${\mathsf{\Psi }}_{Li1}$ is a spatial part and ${\mathsf{{\rm X}}}_{Li1}$ is spin part of the antisymmetrized wave function. The antisymmetrization is performed by using Young’s operators ${\omega }_{11}^{[21]}$, ${\omega }_{12}^{[21]}$, ${\omega }_{21}^{[21]}$, ${\omega }_{22}^{[21]}$ [29], where the indices [21] correspond to the type of a Young diagram with two cells in the first row and one in the second. We use antisymmetrization of the wave function using Young’s method:

$$\begin{array}{c}{\mathsf{\Psi }}_{\mathrm{Li}1}={\omega }_{11}^{[21]}{\phi }_{1s}(R-r_1){\phi }_{1s}(R-r_2){\phi }_{2s}(R-r_3),\\ {\mathsf{{\rm X}}}_{\mathrm{Li}1}={\omega }_{22}^{[21]}{\alpha }_1{\beta }_2{\alpha }_3=\frac{\sqrt{3}}{2}({\alpha }_1{\beta }_2{\alpha }_3-{\beta }_1{\alpha }_2{\alpha }_3).\end{array}$$

(4)

The second term of (3) is equal to zero due to:

$$\begin{array}{c}{\mathsf{\Psi }}_{\mathrm{Li}2}={\omega }_{21}^{[21]}{\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_3\right)=\\ =(P_{23}-P_{13}-P_{123}+P_{132}){\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_3\right)=0,\\ P_{23}{\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_3\right)={\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_3\right){\phi }_{2s}\left(R-r_2\right)=\\ P_{123}{\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_3\right),\\ P_{13}{\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_3\right)={\phi }_{1s}\left(R-r_3\right){\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_1\right)=\\ =P_{132}{\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_3\right),\end{array}$$

The Hamiltonian of the unperturbed system, corresponding to the initial rearrangement of electrons, describes the relative motion of a lithium atom and a positron in the center-of-mass system:

$$H_0^{p=0}=H(1,2,3)-\frac{{\hslash }^2}{2\mu }{\nabla }_R^2$$

(5)

In the initial state, the motion of proton and Lithium atom in the center of mass system is described as plane wave with the wave vector of relative motion $k_i$. In the same way, in the final state, the motion of a Lithium ion is described as a plane wave with a wave vector of relative motion $k_f$. Thus, the initial state is described by the vector:

$$|{\mathsf{\Phi }}_i^0)=\frac{1}{f_{\mathrm{Li}}}{\mathsf{\Psi }}_{\mathrm{Li}1}{\mathsf{{\rm X}}}_{\mathrm{Li}1}\exp (i{k}_i·R).$$

(6)

Here, a normalization factor $f_{Li}=\sqrt{3}$ is found from the condition,

$$\frac{1}{f_{\mathrm{Li}}{}^2}\langle {\mathsf{\Psi }}_{\mathrm{Li}1}|{\mathsf{\Psi }}_{\mathrm{Li}1}\rangle \langle {\mathsf{{\rm X}}}_{\mathrm{Li}1}|{\mathsf{{\rm X}}}_{\mathrm{Li}1}\rangle =1$$

(7)

The antisymmetric vector of the final state is obtained by applying the normalized Young operator [4] to the wave function of the Ps–lithium-ion system in the open channel $\frac{{\hslash }^2{k}_f^2}{2\mu }={\epsilon }_i-{\epsilon }_n+\frac{{\hslash }^2{k}_i^2}{2\mu }\ge 0$:

$$|{\mathsf{\Psi }}_f^0\rangle =\frac{1}{f_0}\left({\mathsf{\Psi }}_1{\mathsf{{\rm X}}}_1+{\mathsf{\Psi }}_2{\mathsf{{\rm X}}}_2\right)\exp \left(i{k}_{f}R\right)$$

(8)

where

$$\begin{array}{l}{\mathsf{\Psi }}_1={\omega }_{11}^{[21]}{\psi }_{1s}(R-r_1){\psi }_{1s}(R-r_2)\psi (r_3),\\ {\mathsf{\Psi }}_2={\omega }_{21}^{[21]}{\psi }_{1s}\left(R-r_1\right){\psi }_{1s}\left(R-r_2\right)\psi (r_3)=0,\\ {\mathsf{{\rm X}}}_1={\omega }_{22}^{[21]}\frac{1}{\sqrt{2}}({\alpha }_1{\beta }_2-{\beta }_1{\alpha }_2){\chi }_3=\\ =\frac{1}{\sqrt{6}}(2{\alpha }_1{\beta }_2{\chi }_3-2{\alpha }_2{\beta }_1{\chi }_3+{\alpha }_1{\beta }_3{\chi }_2+{\alpha }_3{\beta }_2{\chi }_1-{\alpha }_3{\beta }_1{\chi }_2-{\alpha }_2{\beta }_3{\chi }_1)\end{array}$$

(9)

And a normalization factor

$$\begin{array}{l}{f}_0=\langle {\mathsf{{\rm X}}}_1|{\chi }_{L{i}^{+}}{\chi }_{Ps}\rangle {\displaystyle \int \langle {\mathsf{\Psi }}_1|{\mathsf{\Phi }}_{L{i}^{+}}{\mathsf{\Phi }}_{Ps})d^{3}R}=\\ =\frac{4}{\sqrt{3}}{\displaystyle \int (\langle {\psi }_{1s}{|{\phi }_{1s}\rangle }^2\langle {\psi }_{1s}|{\phi }_{2s}\rangle -\langle {\psi }_{1s}|{\phi }_{1s}\rangle \langle {\psi }_{1s}|{\phi }_{2s}\rangle \langle {\psi }_{1s}|{\phi }_{1s}\rangle )}{d}^{3}R\end{array}$$

(10)

A differential cross-section of the scattering events taking into account identity principle for electrons belonging to the different atomic centers has a general form, based on the applying of the formalism of invariant exchange perturbation theory [21,25]:

$$\frac{d{\sigma }_{fi}}{d\mathsf{\Omega }}=j^{-1}\frac{d{w}_{fi}}{d\mathsf{\Omega }}=\frac{{\mu }_i{\mu }_f{k}_f}{{\left(2\pi {\hslash }^2\right)}^2{k}_i}{\left|\langle {\mathsf{\Psi }}_f^0|\widehat{T}|{\mathsf{\Phi }}_i^0)\right|}^2$$

(11)

where bra-vector $\langle {\mathsf{\Psi }}_f^0|$ is antisymmetrized with respect to electron permutations among the incident atomic centers, ket-vector $|{\mathsf{\Phi }}_i^0)$ corresponds to the initial electrons arrangement (initial permutation p = 0), ${\mu }_i=\frac{m_{e^{+}}{M}_{Li}}{m_{e^{+}}+M_{Li}}$ and ${\mu }_f=\frac{m_{Ps}{M}_{L{i}^{+}}}{m_{Ps}+M_{L{i}^{+}}}$ are reduces masses in the center of masses system, i.e., the lithium atom and positron at the beginning of scattering process and the lithium ion and Ps at the end of the scattering process. There, the T-matrix is the operator of transition on the energy surface [21,25] and an operator equation accounting electron permutations:

$$\widehat{T}=V_0^{\mathbb{N}}+V_0^{\mathbb{N}}{\left(\frac{\widehat{f}}{P}\right)}^{-1}{\left(E_i-H+i\eta \right)}^{-1}{V}_0^{\mathbb{N}}$$

(12)

The solution of this operator equation has the form [21]:

$$\begin{array}{l}\widehat{T}=V^{\mathbb{N}}+V^{\mathbb{N}}{\left(E_i-H_0+i\eta \right)}^{-1}{\left(\frac{\widehat{f}}{\mathrm{N}}\right)}^{-1}{V}^{\mathbb{N}}+\\ +V^{\mathbb{N}}{\left(E_i-H_{p=0}^0+i\eta \right)}^{-1}{\left(\frac{\widehat{f}}{\mathrm{N}}\right)}^{-1}{V}^{\mathbb{N}}{\left(E_i-H_{p=0}^0+i\eta \right)}^{-1}{\left(\frac{\widehat{f}}{\mathrm{N}}\right)}^{-1}{V}^{\mathbb{N}}+\dots \end{array}$$

Here with agreement to the general formalism IEPT [21], a renormalized perturbation operator $V_0^{\mathbb{N}}$ has the following form $V^{\mathbb{N}}=V\left(\frac{\widehat{f}}{\mathrm{N}}\right)$, where $\langle {\mathsf{\Psi }}_i^0|\widehat{f}|{\mathsf{\Phi }}_i^0)=f_i$ and $\langle {\mathsf{\Psi }}_f^0|\widehat{f}|{\mathsf{\Phi }}_f^0)=f_f$. It takes into account a specific normalization of antisymmetric wave vectors: $\langle {\mathsf{\Psi }}_i^0|{\mathsf{\Phi }}_i^0)=\langle {\mathsf{\Psi }}_f^0|{\mathsf{\Phi }}_f^0)=1$.

We use the Equation (11) in the first approximation, then for our case:

$$\frac{d{\sigma }_{fi}}{d\mathsf{\Omega }}=\frac{{\mu }_i{\mu }_f{k}_f}{{\left(2\pi {\hslash }^2\right)}^2{k}_i}{\left|\frac{f_i^2}{P}\langle {\mathsf{\Psi }}_f^0|V(1,2,3)|{\mathsf{\Phi }}_i^0)\right|}^2$$

(13)

where bra-vector $\langle {\mathsf{\Psi }}_f^0|$ has the form (8), and ket-vector $|{\mathsf{\Phi }}_i^0)$ is determined by expression (6), perturbation operator is (3). The initial states of electrons of a lithium atom have the form [25,30]:

$$\begin{array}{l}{\varphi }_{1s}(R-r_i)=\sqrt{\frac{{\alpha }_1^3}{\pi }}\exp (-{\alpha }_1|R-r_i|),\\ {\alpha }_1=2.698.\\ {\varphi }_{2s}(R-r_i)=\sqrt{\frac{{\alpha }_2^3}{8\pi }}(1-\frac{{\alpha }_2}{2}|R-r_i|)\exp (-\frac{{\alpha }_2}{2}|R-r_i|),\\ {\alpha }_2=1.594.\end{array}$$

(14)

To describe the final states of electrons in a helium-like lithium ion, we use the functions:

$$\begin{array}{l}{\psi }_{is}(R-r_i)=\sqrt{\frac{{\alpha }_3^3}{\pi }}\exp (-{\alpha }_3|R-r_i|),\\ {\alpha }_3=1.692,\_\_i=1,2\end{array}$$

(15)

We describe the final state of an electron in positronium (Ps) as a one-electron hydrogen-like wave function:

$$\begin{array}{l}\psi (r_3)=\sqrt{\frac{{\beta }^3}{\pi }}\exp \left(-\beta r_3\right),\\ \beta =1/2.\end{array}$$

(16)

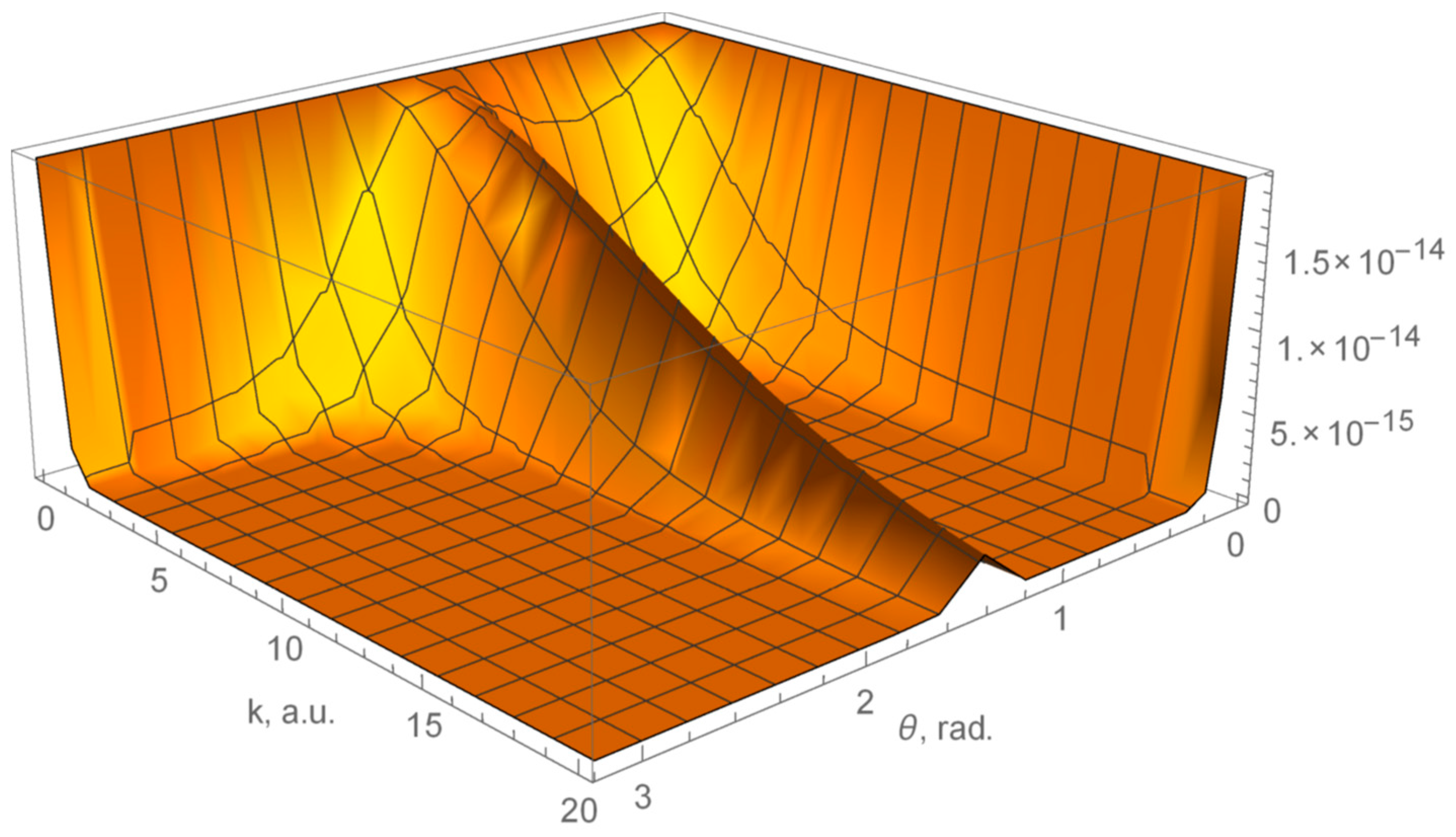
The differential cross-section calculated using analytical Expression (13) is shown in Figure 1.

It is easy to see from Figure 1 that the process of electron capture is most efficient at small scattering angles θ = 0 and θ~π/2. A similar situation occurs during the scattering of a proton with electron capture [24], differential cross-section is calculated by using (13); the capture efficiency has a pronounced peak at small scattering angles. But in the case of positron scattering, this process is seven orders of magnitude less efficient. The isotopic effect is clearly visible, due to the difference between the masses of the proton and the positron by a factor of 1600.

Table 1. Total positronium-formation cross-section (10⁻¹⁶ cm²).

Energy eV	1 Exp [31]	2 Exp [32]	Theor-1 [33]	Theor-2 [34]	CCC [35]	Authors E(eV) K = K/a	Authors Crossection
0.4	32 ± 3		32	33	31	K = 2 E = 0.4	46
0.5	35 ± 3		36	35	33
0.6	32 ± 3		37	36	34	K = 2.5 E = 0.63	37
0.7	41 ± 3		42	40	38
0.8	36 ± 3		40	40	38
0.9	30 ± 3	25 ± 2	39	39	39	K = 3 E = 0.9	31
1	35 ± 3		29	40	38	K = 3.5 E = 1.225
2	37 ± 3	27± 2	27	41	37	K = 4 E = 1.6	23
3	33 ± 3	18 ± 2	31	33	30	K = 5 E = 2.5	19
4	25 ± 3	17 ± 2	22	31	25	K = 6 E = 3.6	16
5	18 ± 3	9 ± 2	20	25	20	K = 7 E = 4.9	14
8	11 ± 3		16	19	17	K = 8 E = 6.4	12
10		4 ± 2	9	10	10	K = 9 E = 8.1 K = 10 E = 10	10.6 9.6

gives a comparison of results for the total cross-section of the process positronium formation obtained from experiments [31,32] and from theoretical investigations [33,34] and calculations by using CCC with truncated basis [35].

3. Dynamic Equilibrium of Electron–Positron–Positronium

After emission from the nucleus and losing kinetic energy by interactions with the surrounding matter the positron eventually combines with an electron when both are essentially at rest. A metastable intermediate species called positronium may be formed by the positron and electron combining. The cross-section of this process for scattering by atomic centers, which determines the probability of positronium production per unit time, was discussed above. The positronium is a hydrogen-like element composed of the positron and electron that revolve around their combined centre of mass. Due to this, a moving electron in the Coulomb potential of a positron has a reduced mass ${\mu }_e=\frac{m_e{m}_{e^{+}}}{m_e + m_{e^{+}}}=\frac{m_e}{2}$, which means that the energy spectrum and the ionization potential differ from the hydrogen atom by a factor of two $E_{nPs}=-\frac{{\mu }_e{e}^4}{2{\hslash }^2{n}^2}=\frac{1}{2}{E}_{nH}$.

The positronium has a mean life of around 10⁻⁷ s. The ground state of positronium, like that of hydrogen, has two possible configurations depending on the total spin of the electron and the positron. The singlet state with total spin equal to zero, ¹S₀, (S = 0, M_s = 0) is known as para-positronium (p-Ps). It has a mean lifetime of 0.12 ns and decays preferentially into two gamma rays with energy of 511 keV each (in the center-of-mass frame), see Figure 2. By detecting these photons the position at which the decay occurred can be determined. This process is used in positron-emission tomography. Para-positronium can decay into any even number of photons (2, 4, 6, ...), but the probability quickly decreases with the number: the branching ratio for decay into 4 photons is 1.439(2) × 10⁻⁶. Para-positronium lifetime in vacuum is approximately [36]

$${\tau }_{pp}=\frac{2\hslash }{m{c}^2{\alpha }^5}=0.1244ns$$

Here $\alpha =\frac{e^2}{\hslash c}=\frac{1}{137}$ is the fine-structure constant.

The triplet state with total spin S = 1(M_s = −1, 0, 1), ³S₁, is known as ortho-positronium (o-Ps). It has a mean lifetime of 142.05 ± 0.02 ns, and the leading decay is three gammas. Other modes of decay are negligible; for instance, the five-photons mode has branching ratio of ≈10⁻⁶ [37]. The ortho-positronium lifetime in a vacuum can be calculated approximately as:

$${\tau }_{pp}=\frac{\frac{1}{2}9\hslash }{2m{c}^2{\alpha }^6({\pi }^2-9)}=138.6 ns,$$

For more accurate calculations with corrections to O(α²), which has a value of 7.040 μs⁻¹ for the decay rate, gives a lifetime 142 ns [38,39]. It is mentioned also about positronium in the 2S state, which is metastable having a lifetime of 1100 ns against annihilation [40].

Positronium formation occurs with a higher probability in gases and metals, but only in about one-third of cases in water or human tissue where direct annihilation of the electron and the positron is more favorable.

3.1. Equilibrium Constant K(T) of the Reaction

We consider the ionization reaction at a given temperature T:

$$e^{+}+Li=Ps+L{i}^{+}$$

(17)

Then the condition of dynamic equilibrium will have the form:

$${\mu }_{e^{+}}+{\mu }_{Li}={\mu }_{Ps}+{\mu }_{L{i}^{+}}$$

(18)

where µ_n (n = e⁺, Li, Ps, Li⁺-positron, lithium, positronium, lithium-ion, respectively) is a chemical potential. We consider each component as a perfect gas. This model is appropriate both for the semiconductor materials, and for the living tissues due to the screening effect. Then, we have a chemical potential for the perfect gas in the following form:

$$\mu =-T\ln \left(\frac{g_0}{n}{\left(\frac{mT}{2\pi {\hslash }^2}\right)}^{3/2}\right)+{\epsilon }_0$$

(19)

where ε₀ is the internal ground state energy and g₀ is the factor of the ground state degeneration. Then, from (18) and (19) we have the following:

$$-T\ln \left(\frac{g_{e^{+}}{g}_{Li}}{g_{L{i}^{+}}{g}_{Ps}}\frac{n_{Ps}{n}_{L{i}^{+}}}{n_{e^{+}}{n}_{Li}}{\left(\frac{m_{e^{+}}{M}_{Li}}{M_{L{i}^{+}}{m}_{Ps}}\right)}^{3/2}\right)+\left[{\epsilon }_{0e^{+}}+{\epsilon }_{0Li}-{\epsilon }_{0Ps}-{\epsilon }_{0L{i}^{+}}\right]=0$$

(20)

where ${\epsilon }_{0L{i}^{+}}-{\epsilon }_{0Li}=I= 5.39 \mathrm{eV}$ is the first ionization potential of lithium, ${\epsilon }_{0e^{+}}-{\epsilon }_{0Ps}=E_{bond}$—is a value of bond energy of electron in positronium atom. Its ionization potential from the ground state is 6.77 eV (half the ionization potential of hydrogen, the radius of the positronium atom in the ground state is 0.106 nm (twice the hydrogen atom), $E_{bond}-I=\Delta =6.77-5.39=1.38 \mathrm{eV}$ is an energy profit of the process.

Then we have for the concentrations relation:

$$\frac{n_{e^{+}}{n}_{Li}}{n_{Ps}{n}_{L{i}^{+}}}=\frac{g_{e^{+}}{g}_{Li}}{g_{L{i}^{+}}{g}_{Ps}}{\left(\frac{m_{e^{+}}{M}_{Li}}{M_{L{i}^{+}}{m}_{Ps}}\right)}^{3/2}{e}^{-\frac{\Delta }{T}}.$$

(21)

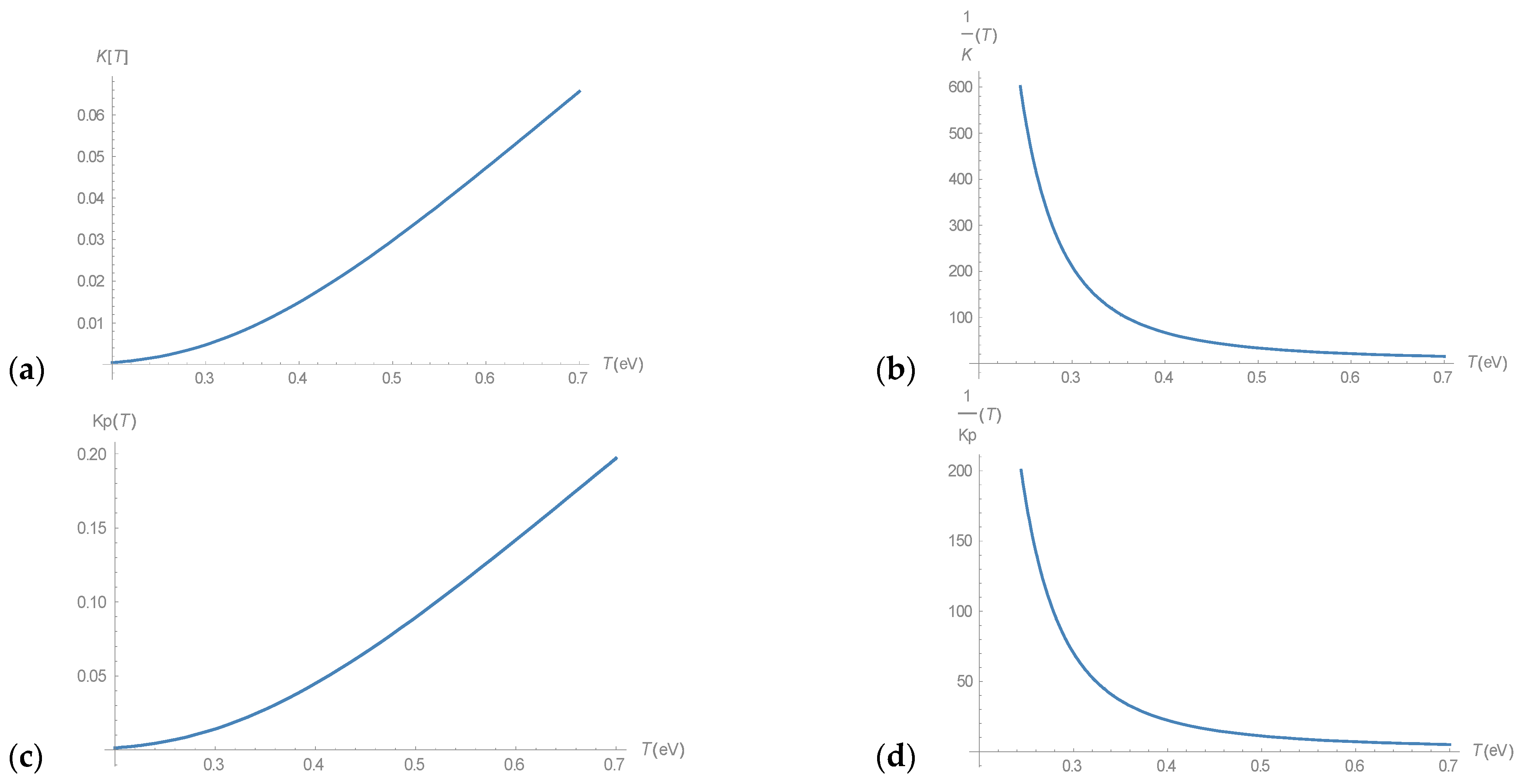
In our consideration, $g_{e^{+}}=2,\_g_{Li}=2,\_g_{L{i}^{+}}=1,\_g_{Ps/p}=1,\_g_{Ps/o}=3$

$$\frac{n_{e^{+}}{n}_{Li}}{n_{Ps}{n}_{L{i}^{+}}}=\frac{4}{g_{Ps}}{\left(\frac{m_{e^{+}}{M}_{Li}}{M_{L{i}^{+}}{m}_{Ps}}\right)}^{3/2}{e}^{-\frac{\Delta }{T}}.$$

(22)

Then, for o-Ps we have

$$K_o(T)=\frac{n_{e^{+}}{n}_{Li}}{n_{Ps}{n}_{L{i}^{+}}}=\frac{\sqrt{2}}{3}{e}^{-\frac{\Delta }{T}}$$

(23)

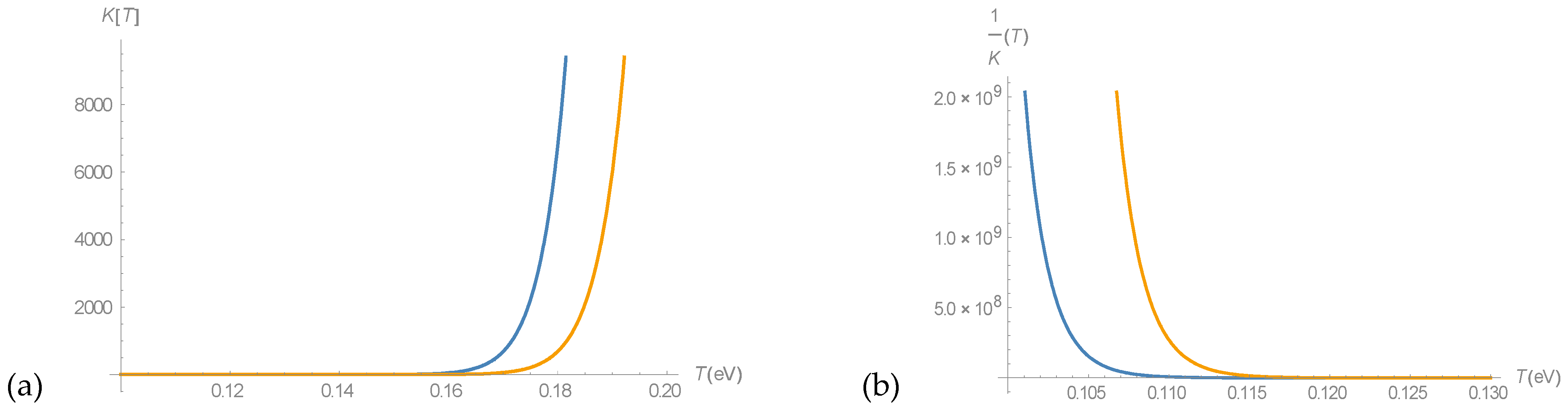
Figure 3 shows the dependence of the temperature for this balance constant.

For p-Ps we have:

$$K_p(T)=\frac{n_{e^{+}}{n}_{Li}}{n_{Ps}{n}_{L{i}^{+}}}=\sqrt{2}{e}^{-\frac{\Delta }{T}}.$$

(24)

Here we use as a temperature parameter T a mean-temperature of expositional tissue, which is about ten times the room temperature.

3.2. Equilibrium Constant in Magnetic Field

To calculate a chemical potential of charged particles, like as electron and positron in the presence of strong magnetic field it is necessary to consider a statistical sum z with taking into account magnetic field. This statistical sum has the following form (for details of calculations, see Appendix A: Derivation of the chemical potential in a magnetic field).

$$\begin{array}{l}{z}_n=\frac{1}{N!}{\left(\frac{Vg{e}^{-\frac{{\epsilon }_0}{T}}}{{\left(2\pi \hslash \right)}^3}{\displaystyle \underset{p}{\int }{e}^{-\frac{{\epsilon }_{\nu }(p_z,{\sigma }_z)}{T}}{d}^{3}p}\right)}^N={\left(\frac{eV{e}^{-\frac{{\epsilon }_0}{T}}}{N{\left(2\pi \hslash \right)}^3}{\displaystyle \underset{p}{\int }{e}^{-\frac{{\epsilon }_{\nu }(p_z,{\sigma }_z)}{T}}{d}^{3}p}\right)}^N=\\ ={\left(\frac{eV{e}^{-\frac{{\epsilon }_0}{T}}}{N{\left(2\pi \hslash \right)}^3}{\left(2\pi mT\right)}^{3/2}\frac{\hslash {\omega }_B}{T}\frac{ch\left(\frac{{\mu }_{B}B}{T}\right)}{sh\left(\frac{\hslash {\omega }_B}{2T}\right)}\right)}^N,\\ {\omega }_B=\frac{eB}{mc},\_\_\_{\mu }_B=\frac{e\hslash }{2mc},\\ \frac{\hslash {\omega }_B}{2}={\mu }_{B}B\sim 1.5·{10}^6·{10}^{-20}=1.5·{10}^{-14}Erg\approx 0.009 \mathrm{eV}\end{array}$$

(25)

Then, the free energy F and chemical potential μ have the form accounting the influence of the magnetic field:

$$\begin{array}{l}F=-T\ln z=-NT\ln \left(\frac{Ve}{N{\left(2\pi \hslash \right)}^3}{\left(2\pi mT\right)}^{3/2}\frac{\hslash {\omega }_c}{T}\frac{2ch\left(\frac{{\mu }_{B}H}{T}\right)}{2sh\frac{\hslash {\omega }_c}{2T}}{e}^{-\frac{{\epsilon }_0}{T}}\right)=\\ =-NT\ln \left(\frac{Ve}{N{\left(2\pi \hslash \right)}^3}{\left(2\pi mT\right)}^{3/2}\frac{\hslash {\omega }_c}{T}\frac{2ch\left(\frac{{\mu }_{B}H}{T}\right)}{2sh\frac{\hslash {\omega }_c}{2T}}\right)+N{\epsilon }_0,\\ \mu =-T\ln \left(\frac{1}{n}{\left(\frac{mT}{2\pi {\hslash }^2}\right)}^{3/2}\frac{\hslash {\omega }_c}{T}\frac{2ch\left(\frac{{\mu }_{B}H}{T}\right)}{2sh\frac{\hslash {\omega }_c}{2T}}\right)+{\epsilon }_0,\end{array}$$

(26)

For the positronium and for the lithium-atom we take into account only the Zeeman energy splitting of sublevels:

$$\begin{array}{l}{\mu }_{Ps}=-T\ln \left(\frac{1}{n_{Ps}}{\left(\frac{M_{Ps}T}{2\pi {\hslash }^2}\right)}^{3/2}2ch\left(\frac{{\mu }_{B}H}{T}\right)\right)+{\epsilon }_{0Ps},\\ {\mu }_{Li}=-T\ln \left(\frac{1}{n_{Li}}{\left(\frac{M_{Li}T}{2\pi {\hslash }^2}\right)}^{3/2}2ch\left(\frac{{\mu }_{B}H}{T}\right)\right)+{\epsilon }_{0Li}\end{array}$$

(27)

Then for (18) in the magnetic field instead of (20) we have the following expressions:

$$\begin{array}{l}-T\ln \left(\frac{g_{e^{+}}{g}_{Li}}{g_{L{i}^{+}}{g}_{Ps}}\frac{n_{Ps}{n}_{L{i}^{+}}}{n_{e^{+}}{n}_{Li}}{\left(\frac{m_{e^{+}}{M}_{Li}}{M_{L{i}^{+}}{m}_{Ps}}\right)}^{3/2}\right)+\left[{\epsilon }_{0e^{+}}+{\epsilon }_{0Li}-{\epsilon }_{0Ps}-{\epsilon }_{0L{i}^{+}}\right]=0\\ {\mu }_{e^{+}}+{\mu }_{Li}={\mu }_{Ps}+{\mu }_{L{i}^{+}}\\ -T\ln \left(\frac{\hslash {\omega }_{c^{+}}}{T}\frac{2ch\left(\frac{{\mu }_{e^{+}}H}{T}\right)}{2sh\frac{\hslash {\omega }_{e^{+}}}{2T}}\frac{2ch\left(\frac{{\mu }_{B}H}{T}\right)}{2ch\left(\frac{{\mu }_{B}H}{T}\right)}\frac{g_{Li3+}}{2ch\left(\frac{{\mu }_{e+}H}{T}\right)}\frac{n_{Ps}{n}_{L{i}^{+}}}{n_{e^{+}}{n}_{Li}}{\left(\frac{m_{e^{+}}{M}_{Li}}{m_{Ps}{M}_{L{i}^{+}}}\right)}^{3/2}\right)+\\ +\left[{\epsilon }_{0e^{+}}+{\epsilon }_{0Li}-{\epsilon }_{0Ps}-{\epsilon }_{0L{i}^{+}}\right]=0,\\ \frac{n_{e^{+}}{n}_{Li}}{n_{Ps}{n}_{L{i}^{+}}}={\left(\frac{m_{e^{+}}{M}_{Li}}{m_{Ps}{M}_{L{i}^{+}}}\right)}^{3/2}\frac{\frac{\hslash {\omega }_{c^{+}}}{T}}{sh\frac{\hslash {\omega }_c}{2T}}{e}^{-\frac{\Delta }{T}}.\\ \frac{\hslash {\omega }_c}{T}\ge 1\\ \frac{n_{e^{+}}{n}_{Li}}{n_{Ps}{n}_{L{i}^{+}}}=\frac{2\hslash {\omega }_c}{T}{e}^{-\frac{\hslash {\omega }_c}{2T}}{\left(\frac{m_{e^{+}}{M}_{Li}}{m_{Ps}{M}_{L{i}^{+}}}\right)}^{3/2}{e}^{-\frac{\Delta }{T}}.\end{array}$$

(28)

It is easy to see that the magnetic field changes the ratio of the concentration of free electrons and positrons to the bound states of positronium. This equilibrium is shifted towards positronium components. A dependence of the equilibrium constant K_B(T) in the magnetic field as a function of mean-temperature is shown in Figure 4.

In addition to the described process with the participation of lithium, one more process of the formation of positronium can occur, in a magnetic field and without it. We consider a process of positronium formation from the ordinarily process:

$$\begin{array}{l}{e}^{+}+e=P{s}_o\\ {\mu }_{e^{+}}+{\mu }_e={\mu }_{oPs}\end{array}$$

(29)

Using expression (20) for chemical potentials for the system without magnetic field we have:

$$-T\ln \left(\frac{g_{e^{+}}{g}_e}{g_{Ps}}\frac{n_{Ps}}{n_{e^{+}}{n}_e}{\left(\frac{m_{e^{+}}{m}_e}{m_{Ps}}\right)}^{3/2}{\left(\frac{T}{2\pi {\hslash }^2}\right)}^{3/2}\right)+\left[{\epsilon }_{0e^{+}}+{\epsilon }_{0e}-{\epsilon }_{0Ps}\right]=0$$

(30)

where the relations for the energies give us:

$$\left[{\epsilon }_{0e^{+}}+{\epsilon }_{0e}-{\epsilon }_{0Ps}\right]=I=6.77 \mathrm{eV}.$$

Then we have the following concentration ratio:

$$\frac{n_{e^{+}}{n}_e}{n_{Ps}}=\frac{g_{e^{+}}{g}_e}{g_{Ps}}{\left(\frac{m_{e^{+}}{m}_e}{m_{Ps}}\right)}^{3/2}{\left(\frac{T}{2\pi {\hslash }^2}\right)}^{3/2}{e}^{-\frac{I}{T}}.$$

(31)

For the temperature in eV and for the Kelvin scale in our case, respectively:

$$\begin{array}{l}\frac{n_{e^{+}}{n}_e}{n_{Ps}}=\frac{32}{3}{10}^{21}{\left(\frac{T}{\pi }\right)}^{3/2}{e}^{-\frac{6.77}{T}},\\ \frac{n_{e^{+}}{n}_e}{n_{Ps}}=\frac{4}{3}{10}^{15}{\left(T^o\right)}^{3/2}{e}^{-\frac{7.7·{10}^4}{T^o}}.\end{array}$$

(32)

In the presence of a magnetic field for (29), taking into account Expression (26) for the chemical potentials of an electron and a positron, and (27), for positronium, we have:

$$\begin{array}{l}-T\ln \left(\frac{\hslash {\omega }_{c^{+}}}{T}\frac{2ch\left(\frac{{\mu }_{e^{+}}H}{T}\right)}{2sh\frac{\hslash {\omega }_{e^{+}}}{2T}}\frac{\hslash {\omega }_c}{T}\frac{2ch\left(\frac{{\mu }_{e}H}{T}\right)}{2sh\frac{\hslash {\omega }_e}{2T}}\frac{1}{2ch\left(\frac{{\mu }_{B}H}{T}\right)}\frac{1}{2ch\left(\frac{{\mu }_{e+}H}{T}\right)}\frac{n_{Ps}}{n_{e^{+}}{n}_e}{\left(\frac{m_{e^{+}}{m}_e}{m_{Ps}}\right)}^{3/2}{\left(\frac{T}{2\pi {\hslash }^2}\right)}^{3/2}\right)+\\ +\left[{\epsilon }_{0e^{+}}+{\epsilon }_{0e}-{\epsilon }_{0Ps}\right]=0,\end{array}$$

From here we come to the following concentration ratio:

$$\frac{n_{e^{+}}{n}_e}{n_{Ps}}=\frac{\frac{\hslash {\omega }_{c^{+}}}{T}}{2sh\frac{\hslash {\omega }_{e^{+}}}{2T}}\frac{\frac{\hslash {\omega }_c}{T}}{2sh\frac{\hslash {\omega }_e}{2T}}{\left(\frac{m_{e^{+}}{m}_e}{m_{Ps}}\right)}^{3/2}{\left(\frac{T}{2\pi {\hslash }^2}\right)}^{3/2}{e}^{-\frac{I_H}{T}}$$

(33)

Equation (33) takes into account the change in the value of the ionization potential I in a magnetic field [41]. Just like a hydrogen atom in a magnetic field, the energy spectrum in positronium must also change in a magnetic field. The ground state energy of positronium in magnetic field has the following energy correction [42,43]:

$$\begin{array}{l}\Delta {\epsilon }_{0H}\simeq -\frac{e^2}{2r_H}=-5.76·{10}^{-13}erg=-0.36 \mathrm{eV}\\ r_H=\sqrt{\frac{\hslash }{m{\omega }_H}}=\sqrt{\frac{\hslash c}{eH}}=2·{10}^{-7}\mathrm{cm}\end{array}$$

where we used $r_H=\sqrt{\frac{\hslash }{m{\omega }_H}}=\sqrt{\frac{\hslash c}{eH}}$ and $a_{BPs}=\frac{{\hslash }^2}{\mu e^2}$ are Lamoure radius and Bohr radius for positronium, respectively. So that ionization potential I in a magnetic field [41,42]

$$I_H=\left(6.77+0.36\right) \mathrm{eV}=7.13 \mathrm{eV}$$

$$\hslash {\omega }_c=\hslash \frac{eH}{mc}=\frac{1.6·{10}^{-10}1.5·{10}^6}{{10}^{10}}=1.6·{10}^{-14}·1.5Erg=0.015 \mathrm{eV}$$

Figure 5 shows comparison of equilibrium constants dependent on mean-temperature T for direct electron–positron reaction with formation of positronium in magnetic field and without magnetic field.

4. Discussion

Understanding and describing the processes of scattering positrons plays a key role both in obtaining positron beams and in using positron therapy. The mechanism of deceleration associated with inelastic collisions with atoms on the example of the lithium atom with the formation of positronium and ion is studied in present work. In the process of slow scattering, exchange effects are very important. We took into account the strong overlap of electronic states during scattering and the adiabatic transition of an electron from the lithium center to the positron center. Analytical consideration and calculations using IEPT show that the highest efficiency of the electron capture process for a positron and a proton [43] occurs at different scattering angles. After electron capture fragments of reaction scatter on angle around π/2 for the case of positronium and lithium ion (see Figure 1) and under the angle around zero for hydrogen atom and lithium ion. For higher energy positrons (see Figure 1) the electron capture process is more efficient for small angles, around zero. A maximal efficiency of positronium creation is for the positron initial energy $\epsilon \sim 400a.u=\mathrm{10,800} \mathrm{eV}$. It is a one of the possible mechanisms of positron deceleration: first, an electron capture and then decay of positronium without annihilation.

Consideration of the various types of reactions of slow positrons with the formation of positronium allows us to conclude that the direct formation of positronium in the absence of a magnetic field occurs in the low-temperature limit T < 0.1 eV, but already at T > 0.16 eV, the equilibrium shifts towards free electrons and positrons. This is due to the fact that the temperature factor, which is proportional to T^3/2 in Relation (31), begins to prevail over the exponential contribution that enhances the bound state. At the same time magnetic field H~1.5 Tesla influence on this relation and move it to the positronium formation (see Figure 5). A participation of the atomic ionization process during positron scattering with electron capture makes positronium creation probable not only for room temperatures but also for temperatures 0.4–1 eV. Because of the absence of factor T^3/2 in the Relationship (21), in (22) for reaction (18) this constant of dynamic equilibrium is dependent of the exponential factor with energy profit. The influence of the magnetic field on this process is the same, as in previous case, it shifts the equilibrium to the positronium. It is important to note that a strong magnetic field (H~1.5 Tesla) interacts both with the intrinsic magnetic moment of the electron and with a positron with an energy (${\epsilon }_H={\mu }_{B}H\sim 1.5·{10}^{-14}Erg\approx 0.01 \mathrm{eV}$) exceeding the hyperfine interaction of the magnetic moments of an electron and a positron in the positronium (${\epsilon }_{sf}=\frac{{\left|{\mu }_B\right|}^2}{a_{BPs}^3}\sim {10}^{-16}Erg\sim {10}^{-4} \mathrm{eV}$). Since the magnetic moments of an electron and a positron have the opposite sign, and because of the interaction with the magnetic field, the most preferable spin state for both particles is the state with the total spin S = 1, that is, ortho-positronium. The magnetic field reduces the probability of formation of para-positronium to zero. It is very easy to prove this by censoring the annihilation radiation, which should be with 3-gamma quanta (Figure 1).

5. Conclusions

We used the method of the invariant exchange perturbation theory in the first approach (see Equation (11)). It allowed us correctly take into account the intercentre exchange effects. But we understand, that at the considered low impact energies, higher order interactions (couplings to other channels such as target excitation and excited-state Ps-formation) are important. The first approximation of the exchange perturbation theory describes well a coherent entanglement of channels due to the exchange in the elastic scattering channels, for a more detailed consideration of excited states, second-order corrections of the EPT formalism are required. Other methods (close-coupling, distorted-wave, etc.) have already been applied to the problem for calculations of integrated cross-sections.

Both processes under consideration, involving positrons, can help in the analysis of the results of tomographic studies. The process of scattering of a positron with the capture of an electron from an atom, described quantum mechanically with the correct allowance for the exchange contributions, gives detailed results for the magnitude and angular dependence of the scattering cross-section. It determines the probability of formation of the positronium and the actual probability of “launching” the process of establishing dynamic equilibrium in the system in the statistical sense. Another conclusion is concerned with the influence of magnetic fields on the mentioned equilibrium. It is shown that the magnetic field not only shifts the dynamic equilibrium, or a balance towards the formation of a positronium, but also leaves only the ortho-positronium, making the existence of the para-positronium impossible.