Online Inertial Machine Learning for Sensor Array Long-Term Drift Compensation
Abstract
:1. Introduction
2. Data Preprocessing
2.1. Data Acquisition
2.2. Feature Extraction
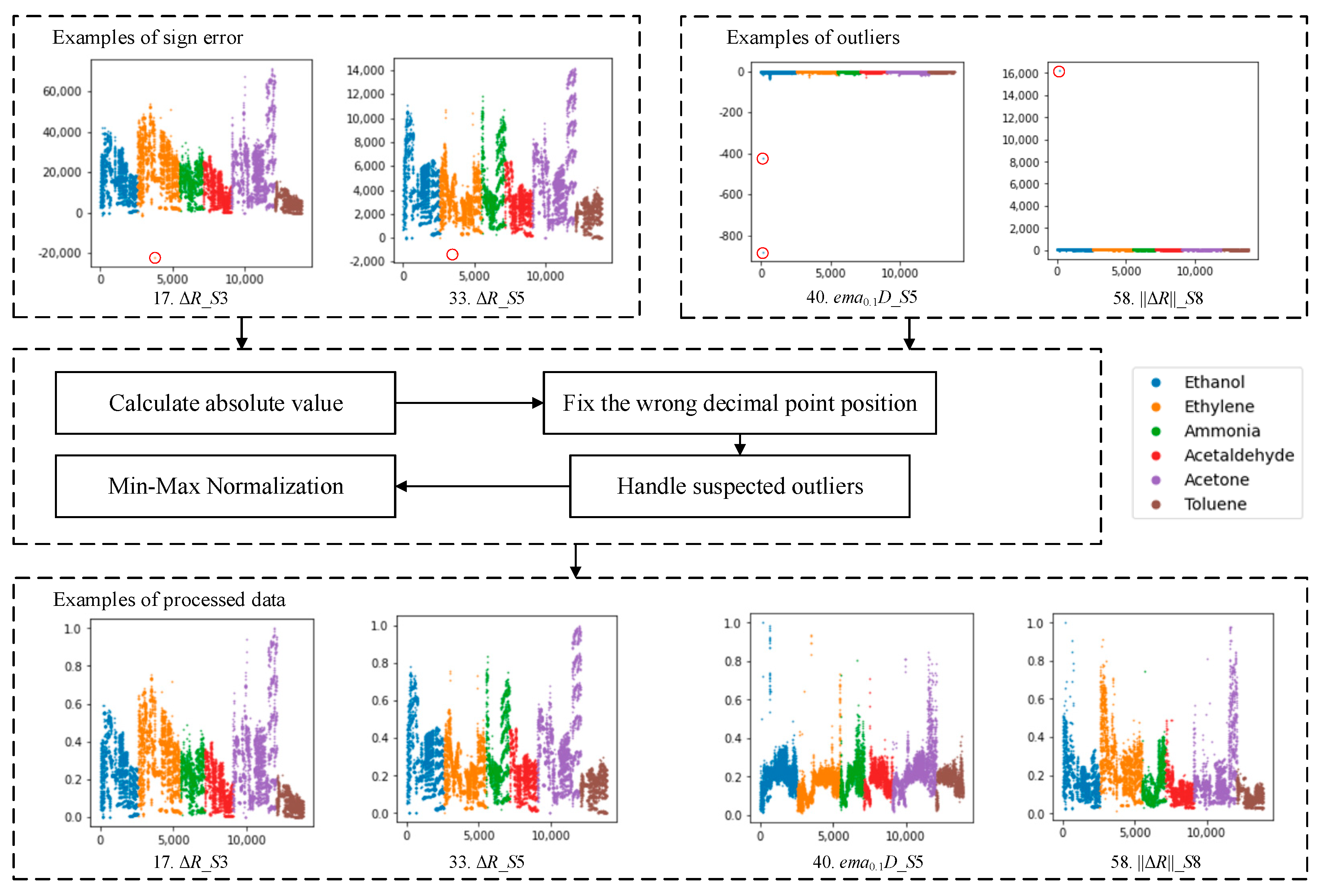
2.3. Data Cleaning and Normalization
2.4. Additional Notes
3. Inertial Machine Learning Method
3.1. Online Inertial Learning Framework
3.2. Description of Each Phase and Algorithm Design
- Initially, the storage queues are empty. Data items are queued in time series to build the initial sample set. In real applications, this process is the data initialization phase, which can be done in the lab or using calibration data to populate the queue. The end milestone of this phase is that the number of data items in all queues reaches the start learning coefficient.
- In this phase, the starting learning conditions are reached, the classifier starts to be trained, and no real sample data will be queued. The pseudo-label data enter the queues sequentially as real samples. If the number of data items in a queue reaches the upper limit, every time the pseudo-label data enters the queue, the queue of the corresponding category will perform the dequeue operation accordingly. The end milestone of this phase is that the number of data items in all queues reaches the upper limit (i.e., queue capacity).
- All storage queues in this phase are full. The classifier will continue to work and continuously enqueue the pseudo-label data predicted by the classifier, and each enqueue is accompanied by a dequeue operation.
3.3. Evaluation Method
3.4. Base Classifier
4. Experiments and Results
4.1. Experimental Datasets and Environment
- dataset1: Use batch 1 as the training set and batch k as the test set, where k = 2, 3, 4, 5, 6, 7, 8, 9, 10.
- dataset2: Use batch 1–2 as the training set and batch k as the test set, where k = 3, 4, 5, 6, 7, 8, 9, 10.
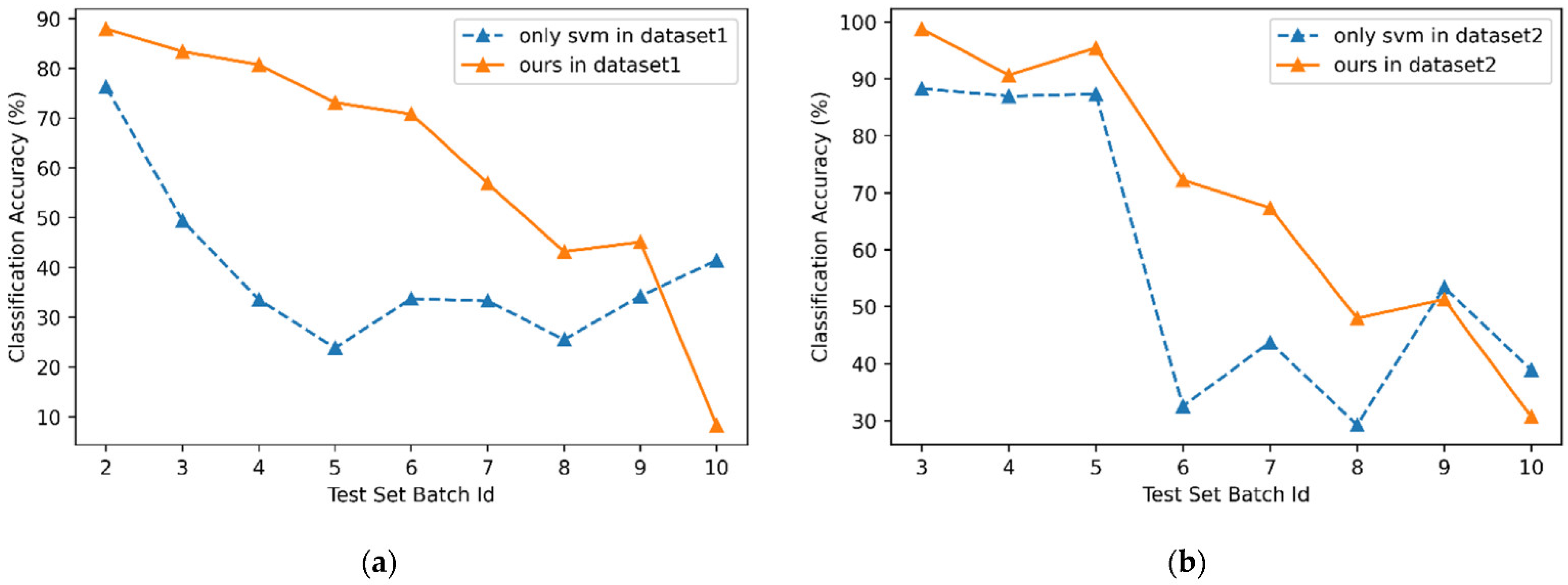
4.2. Experimental Results for Dataset1
4.3. Experimental Results for Dataset2
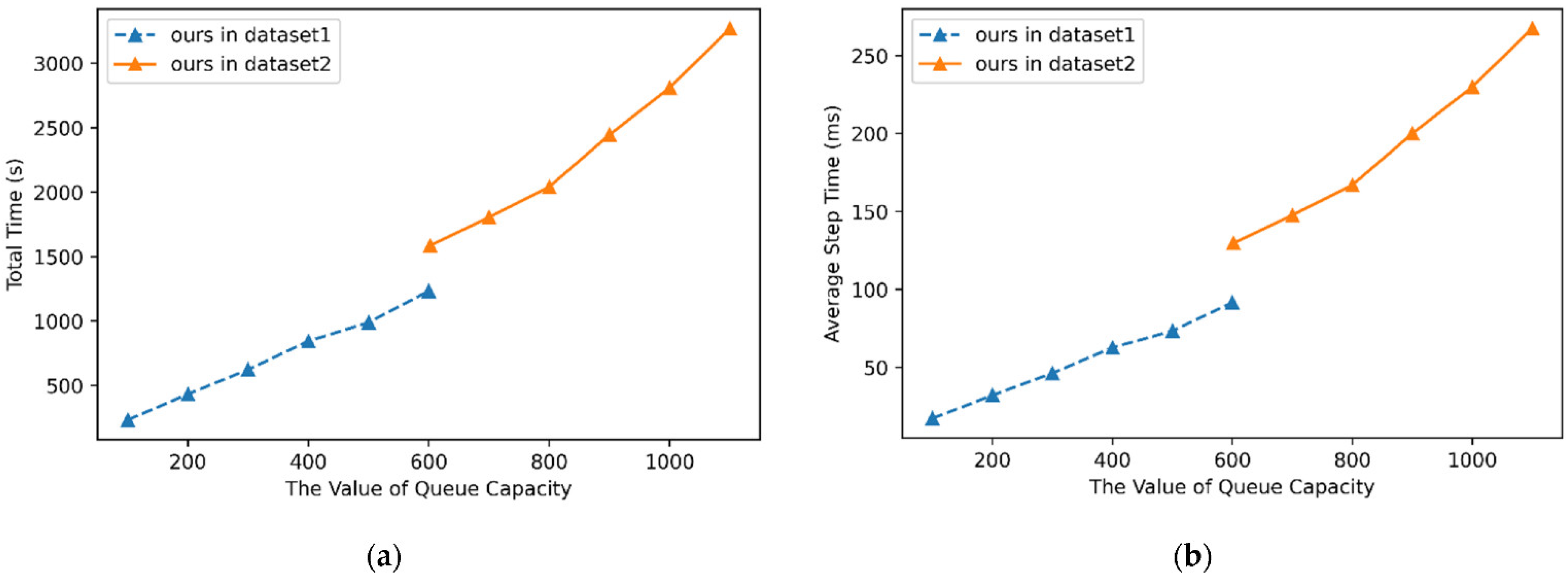
4.4. Experimental Comparison and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Gutierrez-Osuna, R. Pattern Analysis for Machine Olfaction: A Review. IEEE Sens. J. 2002, 2, 189–202. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Gu, J.; Zhang, R.; Mao, Y.; Tian, S. Freshness Evaluation of Three Kinds of Meats Based on the Electronic Nose. Sensors 2019, 19, 605. [Google Scholar] [CrossRef] [Green Version]
- Pajot-Augy, E. Medical diagnosis by breath analysis: Odor sensors. Médecine/Sciences 2019, 35, 123–131. [Google Scholar] [CrossRef]
- Zarra, T.; Cimatoribus, C.; Naddeo, V.; Reiser, M.; Belgiorno, V.; Kranert, M. Environmental odour monitoring by electronic nose. Glob. Nest J. 2018, 20, 664–668. [Google Scholar] [CrossRef]
- Salvato, M.; De Vito, S.; Massera, E.; Buonanno, A.; Miglietta, M.; Fattoruso, G.; Di Francia, G. Combining Real Time Classifiers for Fast and Reliable Electronic Nose response analysis for Aerospace NDTs. In Proceedings of the 28th European Conference on Solid-State Transducers (Eurosensors 2014), Brescia, Italy, 7–10 September 2014; pp. 859–862. [Google Scholar]
- Ait Si Ali, A.; Djelouat, H.; Amira, A.; Bensaali, F.; Benammar, M.; Bermak, A. Electronic nose system on the Zynq SoC platform. Microprocess. Microsyst. 2017, 53, 145–156. [Google Scholar] [CrossRef]
- Cheng, L.; Meng, Q.-H.; Lilienthal, A.J.; Qi, P.-F. Development of compact electronic noses: A review. Meas. Sci. Technol. 2021, 32. [Google Scholar] [CrossRef]
- Développement, Y. Gas and Particle Sensors—Technology and Market Trends 2021. Available online: https://www.i-micronews.com/products/gas-and-particle-sensors-technology-and-market-trends-2021/ (accessed on 20 July 2021).
- Chilo, J.; Pelegri-Sebastia, J.; Cupane, M.; Sogorb, T. E-Nose Application to Food Industry Production. IEEE Instrum. Meas. Mag. 2016, 19, 27–33. [Google Scholar] [CrossRef]
- Feng, S.; Farha, F.; Li, Q.; Wan, Y.; Xu, Y.; Zhang, T.; Ning, H. Review on Smart Gas Sensing Technology. Sensors 2019, 19, 3760. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, Y.-C.; Yao, D.-J. Intelligent gas-sensing systems and their applications. J. Micromech. Microeng. 2018, 28, 093001. [Google Scholar] [CrossRef]
- Lotsch, J.; Kringel, D.; Hummel, T. Machine Learning in Human Olfactory Research. Chem. Senses 2019, 44, 11–22. [Google Scholar] [CrossRef]
- Cao, J.; Liu, T.; Chen, J.; Yang, T.; Zhu, X.; Wang, H. Drift Compensation on Massive Online Electronic-Nose Responses. Chemosensors 2021, 9, 78. [Google Scholar] [CrossRef]
- Zhao, X.; Li, P.; Xiao, K.; Meng, X.; Han, L.; Yu, C. Sensor Drift Compensation Based on the Improved LSTM and SVM Multi-Class Ensemble Learning Models. Sensors 2019, 19, 3844. [Google Scholar] [CrossRef] [Green Version]
- Vergara, A.; Vembu, S.; Ayhan, T.; Ryan, M.A.; Homer, M.L.; Huerta, R. Chemical gas sensor drift compensation using classifier ensembles. Sens. Actuators B-Chem. 2012, 166–167, 320–329. [Google Scholar] [CrossRef]
- Carmel, L.; Levy, S.; Lancet, D.; Harel, D. A feature extraction method for chemical sensors in electronic noses. Sens. Actuators B-Chem. 2003, 93, 67–76. [Google Scholar] [CrossRef]
- Distante, C.; Leo, M.; Siciliano, P.; Persaud, K.C. On the study of feature extraction methods for an electronic nose. Sens. Actuators B-Chem. 2002, 87, 274–288. [Google Scholar] [CrossRef]
- Rehman, A.U.; Bermak, A. Heuristic Random Forests (HRF) for Drift Compensation in Electronic Nose Applications. IEEE Sens. J. 2019, 19, 1443–1453. [Google Scholar] [CrossRef]
- Feng, L.; Dai, H.; Song, X.; Liu, J.; Mei, X. Gas identification with drift counteraction for electronic noses using augmented convolutional neural network. Sens. Actuators B-Chem. 2021, 351, 130986. [Google Scholar] [CrossRef]
- Sasago, Y.; Nakamura, H.; Anzai, Y.; Moritsuka, T.; Odaka, T.; Usagawa, T. FET-type hydrogen sensor with short response time and high drift immunity. In Proceedings of the 37th Symposium on VLSI Technology, Kyoto, Japan, 5–8 June 2017; pp. T106–T107. [Google Scholar]
- Zhu, X.; Liu, T.; Chen, J.; Cao, J.; Wang, H. One-Class Drift Compensation for an Electronic Nose. Chemosensors 2021, 9, 208. [Google Scholar] [CrossRef]
- Ma, Z.; Luo, G.; Qin, K.; Wang, N.; Niu, W. Online Sensor Drift Compensation for E-Nose Systems Using Domain Adaptation and Extreme Learning Machine. Sensors 2018, 18, 742. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Li, D.; Chen, J.; Chen, Y.; Yang, T.; Cao, J. Active Learning on Dynamic Clustering for Drift Compensation in an Electronic Nose System. Sensors 2019, 19, 3601. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Xu, P.; Du, Y.; Yuan, F.; Song, K. Balanced Distribution Adaptation for Metal Oxide Semiconductor Gas Sensor Array Drift Compensation. Sensors 2021, 21, 3403. [Google Scholar] [CrossRef]
- Dongrong, Z.; Bin, Y.E.; Jin, D. The Realization of High Precision Platform Inertial Navigation System. J. Proj. Rocket. Missiles Guid. 2011, 31, 59–62. [Google Scholar]
- Diaz, E.M.; Caamano, M.; Sanchez, F.J.F. Landmark-Based Drift Compensation Algorithm for Inertial Pedestrian Navigation. Sensors 2017, 17, 1555. [Google Scholar] [CrossRef] [Green Version]
- Bro, R.; Smilde, A.K. Principal component analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef] [Green Version]
- Puth, M.-T.; Neuhaeuser, M.; Ruxton, G.D. Effective use of Pearson’s product-moment correlation coefficient Comment. Anim. Behav. 2014, 93, 183–189. [Google Scholar] [CrossRef]
- Yang, Z. Kernel-based support vector machines. Comput. Eng. Appl. 2008, 44, 1–6, 24. [Google Scholar]

| Batch Id | Month Ids | Quantity and Proportion of Each Gas in the Batch | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ethanol | Ethylene | Ammonia | Acetaldehyde | Acetone | Toluene | ||||||||
| batch1 | 1, 2 | 90 | 20.2% | 98 | 22.0% | 83 | 18.7% | 30 | 6.7% | 70 | 15.7% | 74 | 16.6% |
| batch2 | 3, 4, 8, 9, 10 | 164 | 13.2% | 334 | 26.8% | 100 | 8.0% | 109 | 8.8% | 532 | 42.8% | 5 | 0.4% |
| bacth3 | 11, 12, 13 | 365 | 23.0% | 490 | 30.9% | 216 | 13.6% | 240 | 15.1% | 275 | 17.3% | 0 | 0.0% |
| batch4 | 14, 15 | 64 | 39.8% | 43 | 26.7% | 12 | 7.5% | 30 | 18.6% | 12 | 7.5% | 0 | 0.0% |
| batch5 | 16 | 28 | 14.2% | 40 | 20.3% | 20 | 10.2% | 46 | 23.4% | 63 | 32.0% | 0 | 0.0% |
| batch6 | 17, 18, 19, 20 | 514 | 22.3% | 574 | 25.0% | 110 | 4.8% | 29 | 1.3% | 606 | 26.3% | 467 | 20.3% |
| batch7 | 21 | 649 | 18.0% | 662 | 18.3% | 360 | 10.0% | 744 | 20.6% | 630 | 17.4% | 568 | 15.7% |
| batch8 | 22, 23 | 30 | 10.2% | 30 | 10.2% | 40 | 13.6% | 33 | 11.2% | 143 | 48.6% | 18 | 6.1% |
| batch9 | 24, 30 | 61 | 13.0% | 55 | 11.7% | 100 | 21.3% | 75 | 16.0% | 78 | 16.6% | 101 | 21.5% |
| batch10 | 36 | 600 | 16.7% | 600 | 16.7% | 600 | 16.7% | 600 | 16.7% | 600 | 16.7% | 600 | 16.7% |
| Features (S1) | Features (S2) | Features (S3) | … | Features (S16) |
|---|---|---|---|---|
| 1. | 9. | 17. | … | 121. |
| 2. | 10. | 18. | … | 122. |
| 3. | 11. | 19. | … | 123. |
| 4. | 12. | 20. | … | 124. |
| 5. | 13. | 21. | … | 125. |
| 6. | 14. | 22. | … | 126. |
| 7. | 15. | 23. | … | 127. |
| 8. | 16. | 24. | … | 128. |
| Train Set Batch | ACC (%) of Test Set Batch | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 76.21 | 49.43 | 33.54 | 23.85 | 33.73 | 33.29 | 25.51 | 34.25 | 41.41 |
| 2 | 90.16 | 86.95 | 68.02 | 42.04 | 42.56 | 31.29 | 59.36 | 37.47 | |
| 3 | 69.56 | 94.92 | 72.17 | 73.45 | 40.81 | 61.7 | 49.66 | ||
| 4 | 86.29 | 45.56 | 39.8 | 17.68 | 22.97 | 14.77 | |||
| 5 | 56.43 | 44.45 | 39.79 | 43.61 | 19.27 | ||||
| 6 | 78.24 | 75.17 | 36.8 | 51.77 | |||||
| 7 | 86.05 | 65.31 | 62.61 | ||||||
| 8 | 61.27 | 20.02 | |||||||
| 9 | 25.05 | ||||||||
| Train Set Batch | ACC (%) of Test Set Batch | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 76.21 | 49.43 | 33.54 | 23.85 | 33.73 | 33.29 | 25.51 | 34.25 | 41.41 |
| 1–2 | 88.27 | 86.95 | 87.3 | 32.52 | 43.75 | 29.25 | 53.4 | 38.91 | |
| 1–3 | 87.57 | 95.43 | 69.69 | 68.44 | 55.1 | 74.25 | 43.08 | ||
| 1–4 | 96.95 | 69.6 | 66.95 | 52.72 | 72.34 | 42.58 | |||
| 1–5 | 72.39 | 72.57 | 54.08 | 72.97 | 43.91 | ||||
| 1–6 | 85.8 | 90.13 | 67.44 | 54.3 | |||||
| 1–7 | 90.81 | 76.38 | 65.19 | ||||||
| 1–8 | 77.02 | 67.75 | |||||||
| 1–9 | 66.77 | ||||||||
| ACC (%) of Test Set Batch | TT (s) | AST (ms) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 100 | 68.09 | 47.29 | 38.51 | 33.50 | 46.96 | 19.07 | 19.39 | 11.91 | 37.72 | 231.85 | 17.22 |
| 200 | 75.08 | 76.23 | 45.96 | 63.45 | 69.74 | 22.53 | 11.22 | 0.0 | 22.86 | 431.94 | 32.08 |
| 300 | 87.94 | 83.35 | 45.96 | 64.97 | 56.91 | 29.69 | 39.12 | 11.70 | 23.39 | 622.45 | 46.23 |
| 400 | 87.94 | 83.35 | 80.74 | 73.10 | 57.09 | 46.50 | 33.00 | 23.62 | 17.22 | 843.44 | 62.64 |
| 500 | 87.94 | 83.35 | 80.75 | 73.10 | 70.83 | 56.88 | 43.20 | 45.11 | 8.31 | 988.20 | 73.39 |
| 600 | 87.94 | 83.42 | 62.73 | 73.10 | 70.83 | 60.92 | 43.54 | 45.74 | 10.64 | 1232.71 | 91.55 |
| ACC (%) of Test Set Batch | TT (s) | AST (ms) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 602 | 98.80 | 91.93 | 96.45 | 69.87 | 60.20 | 37.07 | 38.09 | 23.22 | 1584.59 | 129.66 |
| 700 | 98.80 | 90.68 | 96.45 | 72.04 | 65.65 | 46.26 | 51.28 | 26.81 | 1804.33 | 147.64 |
| 800 | 98.80 | 90.68 | 96.45 | 72.04 | 65.57 | 46.94 | 50.85 | 25.94 | 2040.36 | 166.96 |
| 900 | 98.80 | 90.68 | 95.43 | 72.04 | 59.56 | 42.86 | 45.74 | 32.14 | 2444.38 | 200.01 |
| 1000 | 98.80 | 90.68 | 95.43 | 72.04 | 59.75 | 43.54 | 46.17 | 23.86 | 2809.77 | 229.91 |
| 1100 | 98.80 | 90.68 | 95.43 | 72.22 | 67.37 | 47.96 | 51.28 | 30.67 | 3269.14 | 267.50 |
| ACC (%) of Test Set Batch | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Only SVM | 76.21 | 49.43 | 33.54 | 23.85 | 33.73 | 33.29 | 25.51 | 34.25 | 41.41 |
| Ours () | 87.94 | 83.35 | 80.75 | 73.1 | 70.83 | 56.88 | 43.2 | 45.11 | 8.31 |
| improvement value | 11.73 | 33.92 | 47.21 | 49.25 | 37.1 | 23.59 | 17.69 | 10.86 | −33.1 |
| improvement ratio (%) | 15.39 | 68.62 | 140.76 | 206.5 | 109.99 | 70.86 | 69.35 | 31.71 | −79.93 |
| ACC (%) of Test Set Batch | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Only SVM | 88.27 | 86.95 | 87.3 | 32.52 | 43.75 | 29.25 | 53.4 | 38.91 |
| Ours () | 98.8 | 90.68 | 95.43 | 72.22 | 67.37 | 47.96 | 51.28 | 30.67 |
| improvement value | 10.53 | 3.73 | 8.13 | 39.7 | 23.62 | 18.71 | −2.12 | −8.24 |
| improvement ratio (%) | 11.93 | 4.29 | 9.31 | 122.08 | 53.99 | 63.97 | −3.97 | −21.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Han, S.; Wang, A.; Shang, K. Online Inertial Machine Learning for Sensor Array Long-Term Drift Compensation. Chemosensors 2021, 9, 353. https://doi.org/10.3390/chemosensors9120353
Dong X, Han S, Wang A, Shang K. Online Inertial Machine Learning for Sensor Array Long-Term Drift Compensation. Chemosensors. 2021; 9(12):353. https://doi.org/10.3390/chemosensors9120353
Chicago/Turabian StyleDong, Xiaorui, Shijing Han, Ancheng Wang, and Kai Shang. 2021. "Online Inertial Machine Learning for Sensor Array Long-Term Drift Compensation" Chemosensors 9, no. 12: 353. https://doi.org/10.3390/chemosensors9120353
APA StyleDong, X., Han, S., Wang, A., & Shang, K. (2021). Online Inertial Machine Learning for Sensor Array Long-Term Drift Compensation. Chemosensors, 9(12), 353. https://doi.org/10.3390/chemosensors9120353






