Abstract
This study aims to develop a refractive-index sensor operating in the visible region using an all-dielectric metasurface, which was chosen for its advantages of low optical loss and narrow spectral bandwidth, compared to those of conventional metallic metasurfaces. COMSOL software was utilized as a calculation tool to simulate the resonant properties of an all-dielectric metasurface composed of a circular nanohole-structured titanium oxide (TiO2) thin film, with the aim of enhancing the sensitivity of the refractive index for sensing targets. The simulation focused on finding the best geometrical conditions for the all-dielectric metasurface to achieve high sensitivity. Two resonance modes observed in this metasurface were considered: the quasi-bound-state-in-the-continuum (qBIC) mode and the perfect-reflection (PR) mode. The simulated results demonstrated that high sensitivities of 257 nm/RIU at the PR mode and 94 nm/RIU at the qBIC mode in the visible spectral range could be obtained by periodically constructing the metasurface with a unit cell having a lattice constant of 350 nm, a nanohole radius of 160 nm, and a nanohole depth of 250 nm. Furthermore, the study showed that the resonance mode that enabled high sensitivity was the PR mode, with a sensitivity nearly three times larger than that of the qBIC mode and the ability to reach the highest reflectance at the resonance wavelength. The optimized feature had the highest reflectance at a resonant wavelength of 570.19 nm, and although the quality factor was 25.50, these designed parameters were considered sufficient for developing a refractive index biosensor with high sensitivity and optical efficiency when operating in the visible spectral range.
1. Introduction
Optical chemical sensors and biosensors play a vital role in quantitatively analyzing the concentration of analytes, including chemical molecules and biomarkers. These sensors find applications in drug discovery, clinical diagnosis, and the detection of toxic industrial chemicals [1,2,3]. The sensor surface immobilizes specific analytes via ligands, which induce signal changes in various optical transducers such as surface-plasmon-resonance (SPR) sensors, surface-enhanced Raman spectroscopy (SERS) [4], potentiometric sensors (e.g., the light-addressable potentiometric sensor—LAPS [5]), and metasurface-based sensors [6,7,8]. Optical sensors offer advantages, including high sensitivity, low susceptibility to environmental fluctuations, and label-free detection, that make them ideal for chemical and biological molecule detection [2].
Metamaterials have gained popularity in recent years for sensor applications, due to their exceptional sensitivity compared to that of other materials [9]. Metamaterials consist of periodically arranged nanostructures, a concept initially proposed by Smith et al. in 2000 [10]. These materials allow manipulation of energy flux, propagation, and the polarization state of incident electromagnetic waves at nanoscale dimensions [11,12,13,14,15]. A two-dimensional (2D) version of metamaterials, known as metasurfaces, consists of a nanostructured thin-film layer on a solid substrate. Generally, the solid substrate material for metasurfaces is recommended as a dielectric for optical lossless properties. The nanostructured thin-film layer on the dielectric substrate can be made of either metal [16,17,18], resulting in a metallic metasurface, or dielectric materials [13,19,20], leading to an all-dielectric metasurface. The resonant properties of the designed and fabricated metasurface significantly dictate its working principle and performance.
The resonance in metallic metasurfaces is based on SPR and the corresponding free electron oscillation [21]. However, this process dissolves heat [22], leading to optical losses and low efficiency [12]. On the other hand, all-dielectric metasurfaces achieve resonance through specific dielectric materials with high refractive indices and low extinction coefficients [23]. Mie theory [24,25,26,27,28,29,30,31,32] explains the resonant mechanism of all-dielectric metasurfaces, involving multipole oscillations from electric dipoles, magnetic dipoles, electric quadrupoles, magnetic quadrupoles, and higher-order even multipoles generated in the dielectric nanostructured layer. The dielectric material has low optical losses, so the extinction coefficient approaches zero in the optically transparent spectrum, making it ideal for supporting Mie resonance [33]. For instance, titanium dioxide (TiO2), known for its high refractive index and its optical transparency in the visible spectral range, is a potential candidate for developing all-dielectric metasurfaces [19,33,34]. Similarly, silicon exhibits low losses in the infrared spectral range, and when combined with a germanium thin-film layer between the metasurface and substrate, it enables super absorption, exceeding the 50% absorption limit and achieving a high-quality factor in the absorptance spectrum [35,36].
Multiple resonance modes can be observed in an all-dielectric metasurface, due to multipole oscillations [13,23,37]. One such resonance condition is the bound state in a continuum (BIC), which can occur in the all-dielectric metasurface [13,23,37]. In an ideal scenario, BIC resonance would have an infinite quality factor, implying that the electromagnetic field at the resonant wavelength is entirely confined to the area near the interface between the metasurface and the ambient medium. However, practical implementations cannot achieve perfect BIC resonance, due to the finite dimensions and the fabrication variations in the metasurface [13]. These inevitable defects create leakage channels, causing the resonant electromagnetic wave to radiate into the far field and enabling spectral monitoring using a spectrometer. This phenomenon is known as a quasi-bound-state-in-the-continuum (qBIC) mode [13,37]. Mie’s theory also interprets the qBIC resonance in all-dielectric metasurfaces [38,39].
The resonant wavelength of the qBIC mode is determined by the geometrical shape and size of the metasurface and the refractive index of the surrounding medium. Consequently, the qBIC resonance mode in an all-dielectric metasurface exhibits sensitivity to changes in the refractive index of the surrounding medium. However, the detected spectrum resulting from the far-field wave of the qBIC mode belongs to the leaky waves that are radiated from the resonance mode. In practical applications, this characteristic can limit the optical efficiency to a relatively low level.
According to Mie theory, an all-dielectric metasurface can exhibit resonance modes that enhance light-scattering efficiency from a dielectric nanostructured thin-film layer under resonant wavelength excitation [31,32,39]. It can also enhance the fluorescence intensity from a dielectric nanostructure thin-film layer supported on the tip of a large core fiber, serving as an optical fiber meta-tip [40]. Previous research utilized a silicon metasurface, one of the all-dielectric metasurfaces with a high-quality factor, for refractive-index sensing [41,42,43]. The metasurface’s unit cell comprises two nanocylinders separated by a tiny gap and suspended in air. Operating under monochromatic light-source illumination and an intensity-based refractive-index-sensing scheme, this designed metasurface sensor can detect refractive-index changes of the order of 10−6 [41].
Another study focused on the perfect-reflection (PR) mode excited at a specific wavelength, which can be generated by an all-dielectric metasurface composed of a TiO2 nanosphere array or a TiO2 nanocylinder array embedded in an air background environment [19]. This near-perfect reflection phenomenon corresponds to a resonance mode that exhibits the highest reflectance (close to 1) at the central wavelength of the resonance bandwidth. The all-dielectric metasurface’s optical efficiency is significantly increased, due to the backscattering light’s generation of PR at the resonant wavelength supported by Mie resonance [19]. However, these proposed all-dielectric metasurfaces lack a supporting substrate; therefore, they do not fulfill the basic requirement of a real sensor [19].
As mentioned earlier, an all-dielectric metasurface can exhibit multiple resonance modes, such as qBIC and PR modes, which respond sensitively to changes in the refractive index of the surrounding medium. However, to develop an effective refractive-index sensor, it is crucial to identify the resonance mode with the highest sensitivity and the highest optical efficiency. The sensor’s working principle revolves around monitoring the shift in resonant wavelength that results from changes in the refractive index of the surrounding medium.
This study aimed to determine the optimal geometric conditions for an all-dielectric metasurface composed of a periodic structure of circular nanohole arrays to achieve high sensitivity in the visible spectral range at the best resonance mode.
To achieve this goal, a systematic investigation of the resonance modes of the all-dielectric metasurface is necessary, including the resonant wavelength, the spectral profile, the location of enhanced field enhancement, and the optical efficiency for obtaining the highest transmittance or reflectance at the resonant wavelength. These resonant properties are highly dependent on the materials used and the geometric shape and physical size of the metasurface nanostructure. By analyzing and understanding these factors, this study aimed to identify the most suitable resonance mode for a nanohole all-dielectric metasurface with high sensitivity to changes in the refractive index.
This study aimed to design a high-sensitivity refractive-index sensor utilizing an all-dielectric metasurface operating in the visible range. This purpose of this focus on the visible range was to avoid water absorption, which occurs when biomolecule solutions are detected in the near-infrared range [44]. Additionally, light sources and photodetectors in the visible range are more cost-effective than other electromagnetic spectra [45]. Our research extensively investigated the potential resonance modes in an all-dielectric metasurface and carefully analyzed them to determine the optimized geometric conditions that yield high sensing performance and optical efficiency, especially for detecting small changes in the refractive index. Computer numerical simulations were employed to carry out this analysis. The simulated results indicate that the resonance mode for the designed metasurface to achieve high sensitivity is the PR mode, which exhibits a sensitivity nearly three times greater than that of the qBIC mode and reaches the highest reflectance at the resonance wavelength.
2. Design and Method
This section provides a detailed description of the simulated all-dielectric metasurface’s geometrical shape and physical size. Figure 1a illustrates the geometric model and its parameters for the all-dielectric metasurface designed using the finite-element method (FEM) to simulate its spectral response. Previous studies showed that nanoparticles and a nanostructured dielectric layer with a high refractive index can effectively generate Mie resonance [27,31,39]. To enhance the efficiency of the Mie resonance and achieve high sensitivity and optical efficiency, it was suggested that the refractive index of the substrate material be lower than that of the nanostructured layer [46].
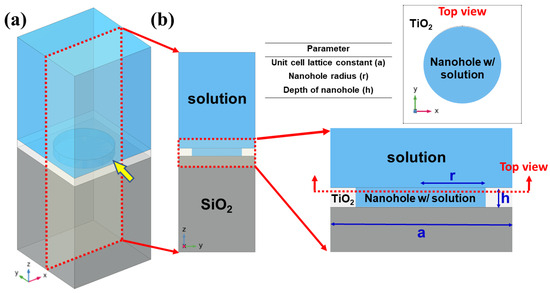
Figure 1.
(a) Schematic 3D plot and (b) cross-sectional and top views with designed geometric parameters of the designed unit cell of the all-dielectric metasurface composed of a dielectric nanohole-structured thin layer on a solid dielectric substrate.
To meet this requirement, the proposed all-dielectric metasurface’s three-dimensional (3D) unit cell structure consists of a periodic arrangement of circular nanoholes constructed by a thin TiO2 layer (white region) on a glass substrate (gray region). The remaining region, including the ambient medium and circular nanohole region, is filled with a solution (blue region). The refractive indices of the materials used, TiO2, SiO2, and solution, are 2.648, 1.479, and 1.331 at 550 nm, respectively [47]. The unit cell model is extended to form an infinite 2D array by applying Floquet-periodic boundary conditions on the surrounding four sides in the x- and y-axes. Perfectly matched layers (PMLs) are placed on the top and bottom of the unit cell in the computational domain to absorb emergent waves [48,49]. The unit cell of the metasurface is positioned on the x–y plane, with the z-direction perpendicular to the metasurface.
The reflectance spectrum is calculated from the x-plane polarized component of the backscattering light, obtained by illuminating the all-dielectric metasurface with y-plane polarized waves (transverse electronic mode (TE mode)) under normal incidence with port boundary conditions. The dispersion relationship of the glass substrate (SiO2) and the structured TiO2 layer is determined using the Cauchy equation [47]. All simulations use commercial FEM software (COMSOL Multiphysics, ANSYS, Burlington, MA, USA).
In the following simulation, the physical properties of the designed all-dielectric metasurface are modified by three geometric parameters of the unit cell: the lattice constant (a), the nanohole radius (r), and the nanohole depth (h), as shown in Figure 1b. The resonant wavelength and sensitivity are calculated and compared for various combinations of these geometric parameters (a, r, and h). The numerical simulation in this study aimed to determine an optimized geometric condition that achieved reasonable sensitivity and higher optical efficiency in the visible spectrum.
To identify all possible resonance modes in the all-dielectric metasurface, simulations were initially conducted by illuminating the design with y-polarized light in the visible spectrum (400–700 nm) under normal incidence. The spectrum of the scattered light was then calculated, and it was found that the overall spectrum of the scattered light can be categorized into two ranges. The first range, situated near the resonant wavelength, was designated as the resonant spectrum; the second range, farther from the resonant wavelength, was considered the background spectrum. When resonance occurs, the scattered light at the resonant wavelength exhibits a partially polarized state with both x- and y-polarized electric-field components [13]. On the other hand, the scattering light far from the resonant wavelength retains its polarization, consisting only of y-polarized electric field components.
The resonant spectrum proved to be of particular interest in this simulation. To filter out the background spectrum (the nonresonant spectrum), the spectrum of the emergent light was calculated, considering only the x-polarized component of the electric field. This process obtained the purely resonant spectrum by removing the nonresonant components. In this simulation, the calculated values of the transmittance throughout the visible spectrum were close to zero (data not shown). This was due to the scattering lights generated from Mie resonance being strongly scattered in the backward direction but weakly scattered in the forward direction [19].
The next section of this article focuses on the backscattering light to illustrate the geometric parameters that impact the resonant behavior. The reflectance spectrum, obtained by individually varying the lattice constant, the radius, and the depth of the unit cell in the nanohole-structured metasurface, is presented and discussed.
3. Results and Discussion
3.1. The Reflectance Spectrum Determined by the Lattice Constant
Based on previous findings [50], the resonant wavelength highly depends on the lattice constant of the all-dielectric metasurface’s unit cell. Figure 2a displays the reflectance spectrum of the metasurface with the unit cell lattice constant ranging from 300 to 450 nm in increments of 1 nm, while keeping the radius (r) and the depth (h) fixed at 130 nm and 40 nm, respectively. As depicted in Figure 2a, multiple resonance modes are evident. To further investigate these resonance modes, the reflectance spectra at specific lattice constants of a = 350 nm and a = 410 nm are replotted in Figure 2b. Several reflectance peaks can be observed, representing a resonant mode excited by Mie resonance in the all-dielectric metasurface [24,25,26,27,28,29,30,31,32]. Among these resonance modes, one stands out with the highest reflectance, approximately 1, at the central wavelength. This high-reflectance resonance mode at the central wavelength is considered a candidate for achieving optimal conditions in sensing applications and is referred to as the “PR mode” [19]. By analyzing the reflectance peaks, the wavelength peak shift of the PR mode can be identified when the analyte interacts with the metasurface.
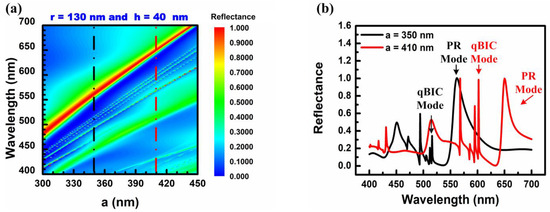
Figure 2.
(a) The reflectance spectrum of the nanohole all-dielectric metasurface by varying the nanohole-structured thin-film layer’s lattice constant of the all-dielectric metasurface with fixed r = 130 nm and h = 40 nm. (b) The reflectance spectrum of the nanohole-structured thin-film layer of the all-dielectric metasurface with lattice constants (a) of 350 and 410 nm (black and red dashed line in Figure 2a). Multiple resonance modes can be found, including the PR and qBIC modes.
Another resonance mode with a sharp reflectance bandwidth but lower reflectance than the PR mode is observed, known as the “qBIC mode”. The qBIC mode of the all-dielectric metasurface has been widely employed for refractive-index sensing applications [51]. Both the PR mode and qBIC mode were of interest in this study to evaluate the performance of the designed all-dielectric metasurface for biosensing, with the former offering higher reflectance and the latter exhibiting a sharper resonant bandwidth. To illustrate the effect of varying the lattice constant on the wavelength shift, the resonant properties for these two lattice constants are summarized in Table 1. The choice of results with a = 350 nm was made because the resonant wavelength is near visible light’s central wavelength. For comparison, results with a significantly larger lattice constant increment (e.g., 60 nm difference from the original lattice constant) were considered, and thus results with a = 410 nm were selected. When the lattice constant increased from 350 nm to 410 nm, the resonant wavelengths of the PR and qBIC modes shifted from 562 nm to 650 nm and 516 nm to 602 nm, respectively. While the reflectance of the PR mode remained at 1 regardless of the lattice constant changes, the reflectance of the qBIC mode varied with the lattice constant, indicating that the resonant scattering efficiency of the qBIC mode is highly dependent on the lattice constant, whereas the PR mode is independent of it. The PR mode exhibited a more stable reflectance response than that of the qBIC mode, ensuring that the resonant signal of the PR mode could be readily identified.

Table 1.
The resonant properties of the PR and qBIC modes at two different lattice constants.
While the lattice constant is dominant in determining the resonant wavelength, it is important to ascertain whether variations in the nanohole structure’s radius and depth influence the resonant wavelength. The radius and the depth are critical factors, as they define the ensemble volume of the high refractive index region occupied by the resonant fields [52]. Therefore, the following two subsections discuss the impact of individually varying the radius and the depth on the resonant wavelength of the resonance modes. Considering that the desired resonant wavelength of the designed metasurface is intended to be near the central wavelength of the visible range, the lattice constant was initially fixed at 350 nm, since the perfect resonant wavelength is approximately 550 nm.
3.2. The Reflectance Spectrum Determined by the Radius of the Nanohole-Structured Layer
To investigate the intrinsic effect of the central wavelength of the resonance mode with changes in the radius, the lattice constant and depth were kept fixed at 350 nm and 40 nm, respectively. Figure 3a displays the reflectance spectrum of the all-dielectric metasurface, with the radius of the circular nanohole-structured layer varying from 10 to 170 nm in increments of 1 nm, while maintaining the lattice constant and the depth at a = 350 nm and h = 40 nm, respectively. Multiple resonance modes are evident in Figure 3a. To analyze the wavelength shift resulting from variations in the radius, the reflectance spectra for two different radii, r = 70 nm and r = 130 nm, were replotted, as shown in Figure 3b. The choice of these two radii allowed for a comparison of the effective areas of the high refractive index in the x–y plane.
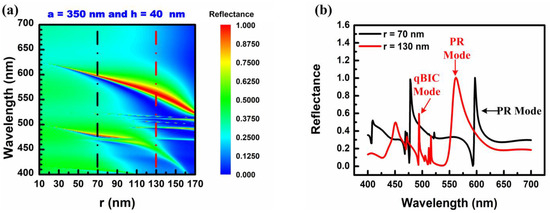
Figure 3.
(a) The reflectance spectrum of the nanohole all-dielectric metasurface by varying the radius of the nanohole-structured thin-film layer of the all-dielectric metasurface with a = 350 nm and h = 40 nm. (b) The reflectance spectrum of the nanohole-structured thin-film layer of the all-dielectric metasurface with radius (r) of 70 nm and 130 nm (black and red dashed line in Figure 3a).
The resonant properties obtained for these two different radii are summarized in Table 2. When the radius decreased from 130 nm to 70 nm, the resonant wavelength of the PR mode shifted from 562 nm to 597 nm. Meanwhile, the qBIC mode vanished as the radius decreased from 130 to 70 nm. Compared with the resonant properties influenced by the lattice constant and the radius at the PR mode, the shift in the resonant wavelength was 35 nm and 88 nm, due to changes in the radius and lattice constant, respectively. This indicated that changes in the resonant wavelength due to the radius effect were less significant than those that were due to the lattice constant. However, the resonant bandwidth of the PR mode decreased by 23 nm and 12 nm due to changes in the radius and lattice constant, respectively. This suggested that the radius influenced the resonant bandwidth more than the lattice constant. These results demonstrate that the resonant bandwidth is highly dependent on the radius, as it is determined by the effective area of the high refractive index in the nanostructure, where the resonant wave is confined [53]. Additionally, the disappearance of the qBIC mode is attributed to this resonance mode being more dependent than the PR mode on the radius of the unit cell [53].

Table 2.
The resonant properties of the PR and qBIC modes at two different radii.
3.3. The Reflectance Spectrum Determined by the Depth of the Nanohole-Structured Layer
Finally, to explore the impact of the central wavelength of the resonance mode with changes in the depth, the lattice constant and radius were kept fixed at 350 nm and 130 nm, respectively. Figure 4a presents the reflectance spectrum of the all-dielectric metasurface, with the depth of the circular nanohole-structured layer varying from 10 to 400 nm in increments of 10 nm, while maintaining the lattice constant and the radius at a = 350 nm and r = 130 nm, respectively. As shown in Figure 4a, as the depth increases, longitudinal resonant waves may also be generated when the film thickness thickens; thus, longitudinal resonance modes are observed in the reflectance spectrum.
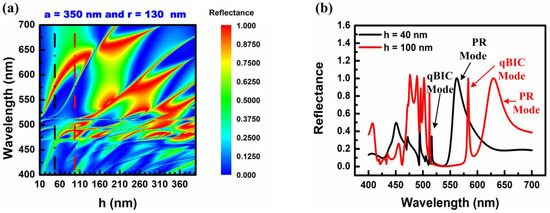
Figure 4.
(a) The reflectance spectrum of the nanohole all-dielectric metasurface by varying the depth of the nanohole-structured thin-film layer of the all-dielectric metasurface with a = 350 nm and h = 40 nm. (b) The reflectance spectrum of the nanohole-structured thin-film layer of the all-dielectric metasurface with depths (h) of 40 and 100 nm (black and red dashed lines in Figure 4a).
To analyze the wavelength shift resulting from variations in the depth, the reflectance spectra for two different depths, h = 40 nm and h = 100 nm, were replotted, as shown in Figure 4b. The choice of these two depths allowed for a comparison of the thinner film thickness (h = 40 nm) and the thicker film thickness (h = 100 nm) of the high-refractive-index thin-film layer.
The resonant properties obtained for these two different depths are summarized in Table 3. When the depth increased from 40 nm to 100 nm, the resonant wavelength of the PR mode shifted from 562 nm to 629 nm. The reflectance of the PR mode remained at 1 while the depth changed. Meanwhile, the resonant wavelength of the qBIC mode shifted from 516 nm to 583 nm as the depth increased from 40 nm to 100 nm. The reflectances of the PR mode and qBIC mode at a depth of 40 nm were 1 and 0.34, respectively, with the reflectance of the qBIC mode significantly lower than that of the PR mode.

Table 3.
The resonant properties of the PR and qBIC modes at two different depths.
Comparing the resonant properties affected by changing the lattice constant and the radius, the resonant wavelength changed by 67 nm in the PR mode when varying the depth, whereas it changed by 88 nm and 36 nm when changing the lattice constant and the radius, respectively, in the PR mode. This indicated that changes in the resonant wavelength were less significant as the lattice constant changes.
Regarding the effect on the resonant bandwidth by varying the depth and comparing it with the effect of changing the lattice constant and the radius, the resonant bandwidth changed by 12 nm, 23 nm, and 17 nm in the PR mode as the lattice constant, the radius, and the depth changed, respectively. These results revealed that the resonant bandwidth is highly dependent on the radius and depth, as both are determined by the effective area of the high refractive index in the nanostructure where the resonant wave is confined [53].
3.4. The Electric Field and Magnetic Field Distribution on the Interface of the Metasurface
The localized field distributions of the PR mode and the qBIC mode are analyzed below to assess the field enhancement with the electric field distribution, considering the geometric parameters a = 350 nm, r = 130 nm, and h = 40 nm. The z-directional electric-field distributions of the PR mode and the qBIC mode on the top surface of the nanostructured layer (x-y plane) are depicted as colored plots in Figure 5a,b, respectively. The arrows’ directions and colors indicate the combined vector direction and field strength of the x and y electric-field components, respectively. To facilitate the identification and comparison of vector intensities in the x–y plane for both electric and magnetic fields, maintaining the original consistent color gradient representation is a more suitable approach for visualizing the field distribution.
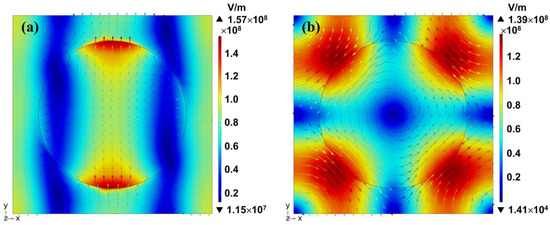
Figure 5.
The distribution of the electric field on the top of the nanohole-structured thin-film layer (e.g., the x–y plane) in (a) the PR mode and (b) the qBIC mode under the simulation conditions at a = 350 nm, r = 130 nm, and h = 40 nm.
The electric fields of both the PR mode and the qBIC mode were primarily located at the sidewall and the outside of the nanohole. The highest electric field of the PR mode was greater than that of the qBIC mode. Moving on to the magnetic field distributions on the top surface of the nanostructured layer (the x–y plane), illustrated in Figure 6a,b for the PR mode and the qBIC mode, respectively, the magnetic fields of both modes were found outside the nanohole, with the highest magnetic field of the PR mode larger than that of the qBIC mode. Consequently, the PR mode exhibited a higher field enhancement effect in the electric and magnetic fields than the qBIC mode.
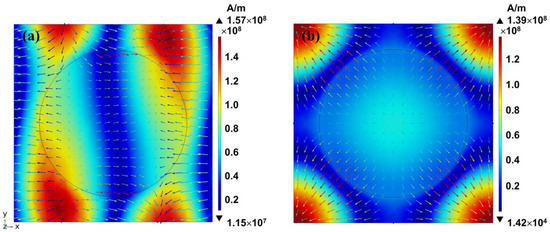
Figure 6.
The distribution of the magnetic field on the top of the nanohole-structured thin-film layer (e.g., the x–y plane) in (a) the PR mode and (b) the qBIC mode under the simulation conditions at a = 350 nm, r = 130 nm, and h = 40 nm.
3.5. Geometrical Optimization for High Sensitivity in the Visible Spectral Range
According to the definition of the sensitivity, while the reaction of the sensor response X is linear with an offset relative to the input measurand M, the sensitivity can be expressed as follows [54]:
The working principle of refractive-index sensing is that the resonant wavelength of the metasurface can be linearly changed with the refractive index of the ambient medium. The sensitivity in the case of the linear with offset is a well-used factor to evaluate the sensing performance of the designed metasurface sensor, which is determinedas follows:
In Equation (2), the sensor response, , is equal to the shift () in the resonant wavelength from an initial resonant wavelength, , , resulting from the changes in the input measured, as well as the change in the refractive index (∆n) of the ambient medium. The sensitivity is evaluated in order to simulate the spectral response. In this work, the eigenfrequency solver [55] is a COMSOL calculating tool that predicts the complex eigenfrequency by considering two different refractive indices, n1 = 1.331 and n2 = 1.332, to find the resonant frequency shifted by changing the refractive index of the solution, where is the resonant angular frequency and is the resonant bandwidth. The resonant wavelength shift can be obtained from the resonant wavelength at two different refractive indices, and , where and are the phase velocity and resonant frequency of the resonant wave, respectively and is equal to 0.001. Finally, by substituting and into Equation (2), the sensitivity can be calculated. The reason for choosing the narrower range of the refractive index was to determine a set of the optimum geometrical parameters of the all-dielectric metasurface for achieving the highest sensitivity via a fast convergence, without a time-consuming process. The optimized geometric condition for high sensitivity in the visible spectral range was investigated by varying the radius and the depth, and the lattice constant was fixed at 350 nm, as shown in Table 4. In this simulation, the qBIC and PR modes were considered to calculate the sensitivity of the corresponding geometric condition. Finally, the best resonance mode for gaining high sensitivity in the visible spectral range could be determined.

Table 4.
The geometrical parameter design table to obtain the high sensitivity.
Figure 7a–c shows the calculated values of the sensitivity, resonant wavelength, and quality factor () of the metasurface constructed by considering different radii of the nanohole structure under the qBIC mode. In Figure 7a, the sensitivity calculated at different depths of the nanohole structure and different radii of the nanohole structure with a lattice constant of 350 nm is presented. The highest sensitivity of the qBIC was 94 nm/refractive-index unit (RIU), while the optimized geometric parameters were a = 350 nm, r = 160 nm, and h = 250 nm. In this geometrical condition, the resonant wavelength and the quality factor were 618.73 nm and 3.73 × 106, respectively. This optimal condition was able to utilize a commercialized high-power LED light source, in which the central wavelength was 620 nm and the designed resonant wavelength was close to 620 nm.
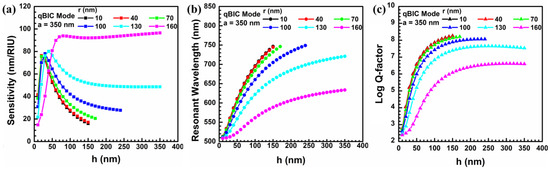
Figure 7.
The (a) sensitivity, (b) resonant wavelength, and (c) quality factor are determined by different combinations of radii and depths of the nanohole-structured metasurface under the qBIC mode.
Figure 8a–c shows the calculated values of the sensitivity, resonant wavelength, and quality factor by considering different radii of the nanohole structure under the PR mode. As shown in Figure 8a, the highest sensitivity of the PR mode was 258 nm/RIU, while the optimized geometric parameters were a = 350 nm, r = 160 nm, and h = 250 nm. In this geometrical condition, the resonant wavelength and quality factor were 570.19 nm and 25.50, respectively. Because the quality factor was much larger than that of the qBIC mode in this optimal condition, the resonance mode was able to utilize a commercialized broadband light source in the visible region. Comparing the calculated values of the discrete point in each colored curve piloted in Figure 7a–c and Figure 8a–c, the calculated results of the resonant properties and the sensitivity of these two resonant modes are summarized in Table 5. In Table 5, these calculated results show that a set of optimized geometric dimensions with r = 160 nm and h = 250 nm achieved the highest sensitivity when the lattice constant was fixed at a = 350 nm. The PR mode should be selected to reach this highest sensitivity in this geometric dimension.
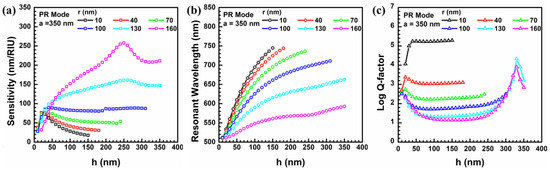
Figure 8.
The (a) sensitivity, (b) resonant wavelength, and (c) quality factor are determined by different combinations of radius and depth of the nanohole-structured metasurface under the PR mode.

Table 5.
The resonant properties and optimized geometric parameters for obtaining the highest sensitivity of the qBIC mode and the PR mode.
To verify the accuracy of the sensitivity, which was quickly calculated using the eigenfrequency solver in COMSOL, the sensitivity was recalculated by considering an investigation range that incorporated a refractive index change from n = 1.331 to 1.340, with an increment of 0.001 RIU, as the refractive-index distribution. The selection of the refractive-index range for the solution investigation was based on the typical location of the refractive index of the protein solution within this range [56]. The jth wavelength shift (j = 1, 2, 3, …,9) was sequentially calculated from the resonant wavelength differences between the refractive index nj (= 1.332, = 1.333, n3 = 1.334, …, and n9 = 1.340) and the initial refractive index (n0 = 1.331). Finally, the calculated sensitivity values were obtained by a linear-curve-fitting procedure; the slope of the fitted curve was equal to the sensitivity. Figure 9 shows the sensor response curve, which clearly indicates that the linearity of the sensitivity operated at the qBIC mode (indicated by the open symbol) and the PR mode (indicated by solid symbols) under the lattice constant was fixed at a = 350 nm, the radii of the circular hole thin-film structure layer were, respectively, r = 130 nm (light blue-colored lines and symbols) and r = 160 nm (pink-colored lines and symbols) and the depths of the circular hole thin-film structure layer were h = 200 nm (Figure 9a), h = 250 nm (Figure 9b), and h = 300 nm (Figure 9c). As shown in Figure 9, the refractive index was linearly proportional to the wavelength in the refractive-index region between n = 1.331 and 1.340 and the range of the refraction index region was an interval of the various concentrations of the protein solution from 0 to several tens of ng/mL [57,58,59]. The calculated values of the sensitivity, by considering that the refractive index was from the investigation range (n = 1.331–1.340) and narrow range (n = 1.331–1.332) at different geometrical parameters and resonance modes, are summarized in Table 6; all the calculated values obtained from the investigation range were close to the ones obtained from the narrow refractive index range. The highest sensitivity was 257.22 nm/RIU obtained from the investigation range, which was also close to the value of the 257.90 nm/RIU calculated from the narrow range.
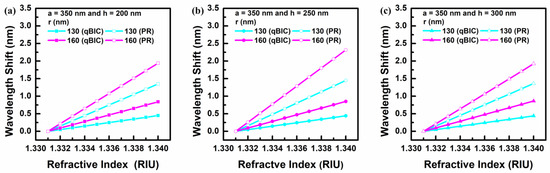
Figure 9.
The sensor response curves of the proposed all-dielectric metasurface refractive-index sensor operated at the qBIC (solid symbol) mode and the PR mode (open symbol) and radii of the circular hole thin-film structure layer are respectively given as r = 130 nm (light blue-colored symbols) and 160 nm (pink-colored symbols), while the depths of the circular hole thin-film structure layer are at (a) h = 200 nm, (b) h = 250 nm, and (c) h = 300 nm.

Table 6.
Comparison of the calculated sensitivity values by considering that the refractive index changes from the investigation range and narrow range.
3.6. Comparison of Sensitivity with the Previous Study on Metasurface Sensors
To ensure that the simulation results of the designed metasurface yielded a sufficiently high sensitivity for refractive-index sensing in the visible and near-infrared spectral range, a comparison of sensitivities with previous studies in recent years and the proposed all-dielectric metasurface is summarized in Table 7. The sensitivity of the designed all-dielectric metasurface was higher than that of the metasurfaces in the cited references [43,60,61,62,63,64]. Notably, only two other metasurfaces using a dielectric hybrid disk [65] and an Si crescent-shaped nanoparticle as the unit cells exhibited higher sensitivity than the proposed designed metasurface. However, the dielectric hybrid disk metasurface operates in the near-infrared range, with the dielectric hybrid disks embedded in the air background, lacking a solid substrate and making physical realization challenging.

Table 7.
Comparison of different values of refractive-index sensitivity of different types of metasurface refractive-index sensors.
On the other hand, the Si crescent metasurface boasts higher sensitivity and operates in the visible spectral range. Nonetheless, the fabrication process poses difficulties in producing unit cells with identical crescent shapes, thinner width (60 nm), and thicker film thickness (200–300 nm) [Figure 1a in ref]. In contrast, the proposed design features a simpler geometrical shape, facilitating fabrication and resulting in a high-sensitivity metasurface in the visible spectral range.
In conclusion, the simulation results demonstrate that the designed all-dielectric metasurface significantly improves sensitivity and fabrication complexity, compared to matasurfaces in previous work. This advancement paves the way for enhanced technology in refractive-index sensing applications in the visible and near-infrared spectral ranges.
4. Conclusions
This study utilized a computer numerical simulation to determine the optimized geometric parameters of a nanohole-structured all-dielectric metasurface with high refractive-index sensitivity in the visible spectral range. The unit cell was designed with a circular nanohole structure, using a higher-refractive-index material, TiO2. The simulation results revealed that the lattice constant primarily determines the resonant wavelength, while the radius and depth of the metasurface influence the resonant bandwidth. Notably, modifications in the depth of the nanostructures had a more pronounced impact than that of changes in the radius. The resonance mode displayed its strongest electric-field distribution on the sidewall of the nanohole and its highest magnetic-field distribution outside the nanohole, which is reasonable, as the resonance mainly occurs in the high-refractive-index region, due to field confinement.
After a systematic simulation and analysis, the optimal condition for the highest sensitivity, reaching 257 nm/RIU, was achieved with a lattice constant of 350 nm, a nanohole radius of 160 nm, and a nanohole depth of 250 nm, resulting in a resonant wavelength of 570.19 nm. These investigations into the geometric parameters contribute significantly to the future development of a refractive-index sensor with high sensitivity and optical efficiency that is operable in the visible region. This metasurface device’s fabrication and measurement setup can be suggested by following the previous work [13,34]. Appendix A provides a brief overview of the fabrication process of the nanohole all-dielectric metasurface and current fabricated results. However, it should be noted that the quality and uniformity of this fabricated metasurface did not match the expectation of the design. No available and clear behavior can be measured in our system, leaving room for technical improvements in the future. Efforts to control the uniformity of the nanohole array should be intensified for process optimization.
Author Contributions
Conceptualization, Y.-J.L. and C.-J.Y.; methodology, C.-T.C., C.-C.H., Y.-J.L. and C.-J.Y.; formal analysis, C.-T.C.; investigation, C.-T.C., C.-M.Y., I.-H.C. and Y.-J.L.; data curation, C.-M.Y. and I.-H.C.; writing—original draft, C.-J.Y.; writing—review and editing, C.-M.Y. and C.-J.Y.; visualization, C.-C.H.; supervision, Y.-J.L. and C.-J.Y.; funding acquisition, C.-J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Chang Gung Memorial Hospital, Taiwan, under grant numbers CMRPD2L0121, CMRPD2L0171, CORPG3M0112, CMRPG3N0501, and CMRPG3M1361 and by the National Science and Technology Council of Taiwan, under grant numbers NSTC 111-2221-E-182-026, 111-2221-E-182-023-MY3, 111-2923-E-182-001-MY3, and 111-2314-B-182-054-MY3. And The APC was funded by National Science and Technology Council of Taiwan, under grant numbers NSTC 111-2221-E-182-026.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Fabrication Process of the Nanohole All-Dielectric Metasurface
The fabrication of this metasurface was attempted in our group using atomic layer deposition (ALD) for the TiO2 layer to achieve good thickness and uniformity control on a glass substrate. Subsequently, a Cr layer was thermally evaporated to serve as the hard mask layer, facilitating the transfer of nanohole array patterns via an e-beam lithography and metal reactive ion etching process (RIE) [34]. Another RIE process was employed to remove the TiO2 layer with nanohole arrays. Finally, a wet etching process was used to remove the Cr hard mask. The suggested process flow and the currently obtained fabricated results are shown in Figure A1a,b, respectively.
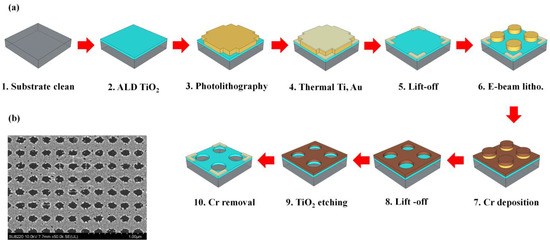
Figure A1.
(a). The fabrication process of all-dielectric metasurface and (b) scanning electron microscope (SEM) image of the fabricated result of the metasurface.
References
- Anas, N.A.A.; Fen, Y.W.; Omar, N.A.S.; Daniyal, W.M.E.M.M.; Ramdzan, N.S.M.; Saleviter, S. Development of graphene quantum dots-based optical sensor for toxic metal ion detection. Sensors 2019, 19, 3850. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Wang, J. Optical biosensors: An exhaustive and comprehensive review. Analyst 2020, 145, 1605–1628. [Google Scholar] [CrossRef]
- Esfahani Monfared, Y. Overview of recent advances in the design of plasmonic fiber-optic biosensors. Biosensors 2020, 10, 77. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z. Surface-enhanced Raman spectroscopy: Advancements and applications. J. Raman Spectrosc. 2005, 36, 466–470. [Google Scholar] [CrossRef]
- Yang, C.-M.; Yen, T.H.; Liu, H.-L.; Lin, Y.-J.; Lin, P.-Y.; Tsui, L.S.; Chen, C.-H.; Chen, Y.-P.; Hsu, Y.-C.; Lo, C.-H. A real-time mirror-LAPS mini system for dynamic chemical imaging and cell acidification monitoring. Sens. Actuators B Chem. 2021, 341, 130003. [Google Scholar] [CrossRef]
- Qin, J.; Jiang, S.; Wang, Z.; Cheng, X.; Li, B.; Shi, Y.; Tsai, D.P.; Liu, A.Q.; Huang, W.; Zhu, W. Metasurface micro/nano-optical sensors: Principles and applications. ACS Nano 2022, 16, 11598–11618. [Google Scholar] [CrossRef]
- Kumari, S.; Tripathi, S.M. Hybrid plasmonic SOI ring resonator for bulk and affinity bio-sensing applications. Silicon 2022, 14, 11577–11586. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B. Photonic and plasmonic metasensors. Laser Photonics Rev. 2022, 16, 2100328. [Google Scholar] [CrossRef]
- Salim, A.; Lim, S. Recent advances in the metamaterial-inspired biosensors. Biosens. Bioelectron. 2018, 117, 398–402. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.; Nemat-Nasser, S.C.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184. [Google Scholar] [CrossRef]
- Tang, C.; Yang, J.; Wang, Y.; Cheng, J.; Li, X.; Chang, C.; Hu, J.; Lü, J. Integrating terahertz metamaterial and water nanodroplets for ultrasensitive detection of amyloid β aggregates in liquids. Sens. Actuators B Chem. 2021, 329, 129113. [Google Scholar] [CrossRef]
- Liu, B.; Song, K.; Xiao, J. Two-dimensional optical metasurfaces: From plasmons to dielectrics. Adv. Condens. Matter Phys. 2019, 2019, 2329168. [Google Scholar] [CrossRef]
- Romano, S.; Zito, G.; Torino, S.; Calafiore, G.; Penzo, E.; Coppola, G.; Cabrini, S.; Rendina, I.; Mocella, V. Label-free sensing of ultralow-weight molecules with all-dielectric metasurfaces supporting bound states in the continuum. Photonics Res. 2018, 6, 726–733. [Google Scholar] [CrossRef]
- Moitra, P.; Yang, Y.; Anderson, Z.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Realization of an all-dielectric zero-index optical metamaterial. Nat. Photonics 2013, 7, 791–795. [Google Scholar] [CrossRef]
- Gil, M.; Bonache, J.; Martin, F. Metamaterial filters: A review. Metamaterials 2008, 2, 186–197. [Google Scholar] [CrossRef]
- Mubeen, S.; Zhang, S.; Kim, N.; Lee, S.; Kramer, S.; Xu, H.; Moskovits, M. Plasmonic properties of gold nanoparticles separated from a gold mirror by an ultrathin oxide. Nano Lett. 2012, 12, 2088–2094. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Consales, M.; Quero, G.; Spaziani, S.; Principe, M.; Micco, A.; Galdi, V.; Cutolo, A.; Cusano, A. Metasurface-Enhanced Lab-on-Fiber Biosensors. Laser Photonics Rev. 2020, 14, 2000180. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, H.; Lu, Y.; Chen, Y. All-dielectric metasurface for achieving perfect reflection at visible wavelengths. J. Phys. Chem. C 2018, 122, 2990–2996. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef]
- Cui, S.; Tian, C.; Mao, J.; Wu, W.; Fu, Y. Nanopillar array-based plasmonic metasurface for switchable multifunctional biosensing. Opt. Commun. 2022, 506, 127548. [Google Scholar] [CrossRef]
- Galvez, F.; de Lara, D.P.; Spottorno, J.; García, M.; Vicent, J. Heating effects of low power surface plasmon resonance sensors. Sens. Actuators B Chem. 2017, 243, 806–811. [Google Scholar] [CrossRef]
- Tian, J.; Li, Q.; Belov, P.A.; Sinha, R.K.; Qian, W.; Qiu, M. High-Q all-dielectric metasurface: Super and suppressed optical absorption. ACS Photonics 2020, 7, 1436–1443. [Google Scholar] [CrossRef]
- Kivshar, Y. All-dielectric meta-optics and non-linear nanophotonics. Natl. Sci. Rev. 2018, 5, 144–158. [Google Scholar] [CrossRef]
- Kruk, S.; Kivshar, Y. Functional meta-optics and nanophotonics governed by Mie resonances. Acs Photonics 2017, 4, 2638–2649. [Google Scholar] [CrossRef]
- Decker, M.; Staude, I. Resonant dielectric nanostructures: A low-loss platform for functional nanophotonics. J. Opt. 2016, 18, 103001. [Google Scholar] [CrossRef]
- Decker, M.; Staude, I.; Falkner, M.; Dominguez, J.; Neshev, D.N.; Brener, I.; Pertsch, T.; Kivshar, Y.S. High-efficiency dielectric Huygens’ surfaces. Adv. Opt. Mater. 2015, 3, 813–820. [Google Scholar] [CrossRef]
- Cheng, J.; Ansari-Oghol-Beig, D.; Mosallaei, H. Wave manipulation with designer dielectric metasurfaces. Opt. Lett. 2014, 39, 6285–6288. [Google Scholar] [CrossRef]
- Staude, I.; Miroshnichenko, A.E.; Decker, M.; Fofang, N.T.; Liu, S.; Gonzales, E.; Dominguez, J.; Luk, T.S.; Neshev, D.N.; Brener, I. Tailoring directional scattering through magnetic and electric resonances in subwavelength silicon nanodisks. ACS Nano 2013, 7, 7824–7832. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Reinhardt, C.; Chichkov, B.N. Multipole light scattering by nonspherical nanoparticles in the discrete dipole approximation. Phys. Rev. B 2011, 84, 235429. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Reinhardt, C.; Seidel, A.; Luk’yanchuk, B.S.; Chichkov, B.N. Optical response features of Si-nanoparticle arrays. Phys. Rev. B 2010, 82, 045404. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wu, Y.; Yang, W.; Fan, Y.; Song, Q.; Xiao, S. TiO2 metasurfaces: From visible planar photonics to photochemistry. Sci. Adv. 2019, 5, eaax0939. [Google Scholar] [CrossRef] [PubMed]
- Semmlinger, M.; Zhang, M.; Tseng, M.L.; Huang, T.-T.; Yang, J.; Tsai, D.P.; Nordlander, P.; Halas, N.J. Generating third harmonic vacuum ultraviolet light with a TiO2 metasurface. Nano Lett. 2019, 19, 8972–8978. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Ma, B.; Qin, R.; Ghosh, P.; Qiu, M.; Li, Q. High-Q Absorption in All-Dielectric Photonics Assisted by Metamirrors. ACS Photonics 2022, 9, 3391–3397. [Google Scholar] [CrossRef]
- Yu, J.; Ma, B.; Ouyang, A.; Ghosh, P.; Luo, H.; Pattanayak, A.; Kaur, S.; Qiu, M.; Belov, P.; Li, Q. Dielectric super-absorbing metasurfaces via PT symmetry breaking. Optica 2021, 8, 1290–1295. [Google Scholar] [CrossRef]
- Koshelev, K.; Bogdanov, A.; Kivshar, Y. Meta-optics and bound states in the continuum. Sci. Bull. 2019, 64, 836–842. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Novikov, S.M.; Zywietz, U.; Eriksen, R.L.; Reinhardt, C.; Bozhevolnyi, S.I.; Chichkov, B.N. Demonstration of Magnetic Dipole Resonances of Dielectric Nanospheres in the Visible Region. Nano Lett. 2012, 12, 3749–3755. [Google Scholar] [CrossRef]
- Babicheva, V.E.; Evlyukhin, A.B. Resonant Lattice Kerker Effect in Metasurfaces With Electric and Magnetic Optical Responses. Laser Photonics Rev. 2017, 11, 1700132. [Google Scholar] [CrossRef]
- Alhalaby, H.; Principe, M.; Zaraket, H.; Vaiano, P.; Aliberti, A.; Quero, G.; Crescitelli, A.; Di Meo, V.; Esposito, E.; Consales, M. Design and optimization of all-dielectric fluorescence enhancing metasurfaces: Towards advanced metasurface-assisted optrodes. Biosensors 2022, 12, 264. [Google Scholar] [CrossRef]
- Tognazzi, A.; Rocco, D.; Gandolfi, M.; Locatelli, A.; Carletti, L.; De Angelis, C. High quality factor silicon membrane metasurface for intensity-based refractive index sensing. Optics 2021, 2, 193–199. [Google Scholar] [CrossRef]
- Ollanik, A.J.; Oguntoye, I.O.; Hartfield, G.Z.; Escarra, M.D. Highly sensitive, affordable, and adaptable refractive index sensing with silicon-based dielectric metasurfaces. Adv. Mater. Technol. 2019, 4, 1800567. [Google Scholar] [CrossRef]
- Yavas, O.; Svedendahl, M.; Dobosz, P.; Sanz, V.; Quidant, R. On-a-chip biosensing based on all-dielectric nanoresonators. Nano Lett. 2017, 17, 4421–4426. [Google Scholar] [CrossRef]
- Romano, S.; Zito, G.; Yépez, S.N.L.; Cabrini, S.; Penzo, E.; Coppola, G.; Rendina, I.; Mocellaark, V. Tuning the exponential sensitivity of a bound-state-in-continuum optical sensor. Opt. Express 2019, 27, 18776–18786. [Google Scholar] [CrossRef]
- Conteduca, D.; Barth, I.; Pitruzzello, G.; Reardon, C.P.; Martins, E.R.; Krauss, T.F. Dielectric nanohole array metasurface for high-resolution near-field sensing and imaging. Nat. Commun. 2021, 12, 3293. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yang, Q.; Shao, T.; Xu, Y.; Wang, L.; Xu, Q.; Zhang, X.; Kravchenko, I.; Gu, J.; Han, J. Terahertz bound state in the continuum in dielectric membrane metasurfaces. New J. Phys. 2022, 24, 053010. [Google Scholar] [CrossRef]
- Available online: refractiveindex.info (accessed on 5 September 2023).
- Berenger, J.-P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Bérenger, J.-P. Perfectly matched layer (PML) for computational electromagnetics. Synth. Lect. Comput. Electromagn. 2007, 2, 1–117. [Google Scholar]
- Lee, Y.; Park, M.-K.; Kim, S.; Shin, J.H.; Moon, C.; Hwang, J.Y.; Choi, J.-C.; Park, H.; Kim, H.-R.; Jang, J.E. Electrical broad tuning of plasmonic color filter employing an asymmetric-lattice nanohole array of metasurface controlled by polarization rotator. Acs Photonics 2017, 4, 1954–1966. [Google Scholar] [CrossRef]
- Hsiao, H.H.; Hsu, Y.C.; Liu, A.Y.; Hsieh, J.C.; Lin, Y.H. Ultrasensitive Refractive Index Sensing Based on the Quasi-Bound States in the Continuum of All-Dielectric Metasurfaces. Adv. Opt. Mater. 2022, 10, 2200812. [Google Scholar] [CrossRef]
- Malekfar, M.R.; Shokooh-Saremi, M.; Mirsalehi, M.M. Design of highly transmissive all-dielectric metasurface based on silicon nanodisks. Photonics Nanostructures-Fundam. Appl. 2018, 31, 140–146. [Google Scholar] [CrossRef]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing action from photonic bound states in continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef]
- D’Amico, A.; Di Natale, C. A contribution on some basic definitions of sensors properties. IEEE Sens. J. 2001, 1, 183–190. [Google Scholar] [CrossRef]
- Mohamady, S.; Raja Ahmad, R.K.; Montazeri, A.; Zahari, R.; Abdul Jalil, N.A. Modeling and eigenfrequency analysis of sound-structure interaction in a rectangular enclosure with finite element method. Adv. Acoust. Vib. 2009, 2009, 371297. [Google Scholar] [CrossRef]
- Tan, C.-Y.; Huang, Y.-X. Dependence of refractive index on concentration and temperature in electrolyte solution, polar solution, nonpolar solution, and protein solution. J. Chem. Eng. Data 2015, 60, 2827–2833. [Google Scholar] [CrossRef]
- Antony, A.; Mitra, J. Refractive index-assisted UV/Vis spectrophotometry to overcome spectral interference by impurities. Anal. Chim. Acta 2021, 1149, 238186. [Google Scholar] [CrossRef]
- Xu, W.; Zhuo, Y.; Song, D.; Han, X.; Xu, J.; Long, F. Development of a novel label-free all-fiber optofluidic biosensor based on Fresnel reflection and its applications. Anal. Chim. Acta 2021, 1181, 338910. [Google Scholar] [CrossRef]
- Cole, T.; Kathman, A.; Koszelak, S.; McPherson, A. Determination of local refractive index for protein and virus crystals in solution by Mach-Zehnder interferometry. Anal. Biochem. 1995, 231, 92–98. [Google Scholar] [CrossRef]
- Li, Z.; Panmai, M.; Zhou, L.; Li, S.; Liu, S.; Zeng, J.; Lan, S. Optical sensing and switching in the visible light spectrum based on the bound states in the continuum formed in GaP metasurfaces. Appl. Surf. Sci. 2023, 620, 156779. [Google Scholar] [CrossRef]
- Ray, D.; Raziman, T.; Santschi, C.; Etezadi, D.; Altug, H.; Martin, O.J. Hybrid metal-dielectric metasurfaces for refractive index sensing. Nano Lett. 2020, 20, 8752–8759. [Google Scholar] [CrossRef]
- He, K.; Liu, Y.; Fu, Y. Transmit-array, metasurface-based tunable polarizer and high-performance biosensor in the visible regime. Nanomaterials 2019, 9, 603. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Luo, M.; Zhao, X.; Li, Y.; Wang, Q.; Liu, Z.; Guo, J.; Guo, Z.; Liu, J.; Wu, X. Asymmetric tetramer metasurface sensor governed by quasi-bound states in the continuum. Nanophotonics 2023, 12, 1295–1307. [Google Scholar] [CrossRef]
- Wu, P.; Qu, S.; Zeng, X.; Su, N.; Chen, M.; Yu, Y. High-Q refractive index sensors based on all-dielectric metasurfaces. RSC Adv. 2022, 12, 21264–21269. [Google Scholar] [CrossRef] [PubMed]
- Chao, M.; Liu, Q.; Zhang, W.; Zhuang, L.; Song, G. Mutual coupling of corner-localized quasi-BICs in high-order topological PhCs and sensing applications. Opt. Express 2022, 30, 29258–29270. [Google Scholar] [CrossRef]
- Wang, J.; Kühne, J.; Karamanos, T.; Rockstuhl, C.; Maier, S.A.; Tittl, A. All-dielectric crescent metasurface sensor driven by bound states in the continuum. Adv. Funct. Mater. 2021, 31, 2104652. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).