Next Article in Journal
Dissolved Gas Analysis in Transformer Oil Using Ni Catalyst Decorated PtSe2 Monolayer: A DFT Study
Next Article in Special Issue
Detection of Polynitro Compounds at Low Concentrations by SERS Using Ni@Au Nanotubes
Previous Article in Journal
Materials for Chemical Sensing: A Comprehensive Review on the Recent Advances and Outlook Using Ionic Liquids, Metal–Organic Frameworks (MOFs), and MOF-Based Composites
Previous Article in Special Issue
Fabrication and Magneto-Structural Properties of Co2-Based Heusler Alloy Glass-Coated Microwires with High Curie Temperature
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemosensors
Volume 10
Issue 8
10.3390/chemosensors10080291
chemosensors-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Review of Helical Magnetic Structures in Magnetic Microwires

by
Alexander Chizhik
1,*,
Julian Gonzalez
1,
Arcady Zhukov
1,2,3 and
Przemyslaw Gawronski
4
1
Department Advanced Polymers and Materials: Physics, Chemistry and Technology, Faculty of Chemistry, University of Basque Country, UPV/EHU, 20018 San Sebastian, Spain
2
Department of Applied Physics I, EIG, University of Basque Country, UPV/EHU, 20018 San Sebastian, Spain
3
IKERBASQUE, Basque Foundation for Science, 48011 Bilbao, Spain
4
Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, 30-059 Krakow, Poland
*
Author to whom correspondence should be addressed.
Chemosensors 2022, 10(8), 291; https://doi.org/10.3390/chemosensors10080291
Submission received: 17 June 2022 / Revised: 19 July 2022 / Accepted: 20 July 2022 / Published: 23 July 2022
(This article belongs to the Special Issue Innovative Materials, Technologies, and Sensors)
Browse Figures
Review Reports Versions Notes

Abstract

:
We provide an overview of the helical magnetic structures in magnetic microwires. Having analyzed the experimental data describing the magnetic behavior of magnetic microwires since the 1990s, we found indirect evidence of the existence of various types of helical magnetic structures. Purposeful research has allowed us to discover the spiral magnetic structure as one of the most unusual helical structures. A comparison of the spiral structure with another type of helical structure—elliptical—was carried out. In the analysis, emphasis was placed on the length of the domain wall as one of the most important parameters. The difference in the dynamic properties of the spiral and elliptical domain walls has been demonstrated.

1. Introduction

Non-destructive testing is one of the rapidly developing areas of magneto-chemical sensors. In particular, the use of Giant magneto-resistance (GMR) sensors is one of the most promising lines for active elements in the sensors, which gives information about the corrosion of pipes occurring under various climatic influences.
Generally, testing using the eddy current is a traditional method for studying the properties of metallic objects. In particular, bursting and corrosion is a common purpose of this type of study [1]. The principle of action is that eddy currents are induced in the metallic body when the AC electric current passes through it. The key point is the defects of different types, which bring the fluctuation of the eddy current. It, in turn, causes the transformation of such properties of the magnetic field as amplitude and phase. An essential detail is the low frequency of excitation. It permits a good penetration of the exiting field inside the metallic pipe. We could control the magnetic field by controlling the change in the impedance in the system [2]. It is the basis of the testing functioning. There are advantages and disadvantages with the application of the eddy current method associated with this [3]. The disadvantage is that natural changes in the pipe, not related to the presence of defects, can interfere with the standard operation of the testing system, which appears in the errors and noise of the useful signal. The solution to the problem is the use of a spatial system of the sensors, which makes it possible to implement a systematic approach to the analysis of the defects and to increase the reliability of the work. The advantage of the eddy current method is determined by its non-contact nature itself.
Within the framework of the indicated problem of creating a sensor system, GMR active elements are the most suitable elements. GMR sensors have the following advantages: a high signal-to-noise ratio at a low excitation frequency, small dimensions and associated with it low consumption of power. As a result, they are the almost ideal basis for creating the said sensor system.
Thus, there is a whole series of using GMR sensors as elements in the non-intrusive control of a wide range of objects. In particular, these can be small cracks close to the surface, cracks both in large objects such as aircrafts or metal supports, and small objects such as printed electronic circuit boards [4,5,6,7,8,9,10,11,12,13]. In addition, the volumetric systems of sensors of this type make it possible to detect areas with metal corrosion with a size of the order of units of mm [14,15,16,17].
It is also worth mentioning the technique of using pulsed eddy currents [18,19,20,21,22]. The high accuracy of this method is because the jump transitions in the eddy current are coupled with electromagnetic jumps. This is also related to the shortcomings of the method, which increase the characteristic size of the detected defect to tens of mm. This is due to the need for signal averaging.
As for Giant Magneto-impedance (GMI) sensors, they are also widely used in chemical and, largely, biochemical sensors. Along with Hall sensors, Fluxgate sensors, GMR sensors and spin valve sensors, GMI sensors find their rightful niche in this variety of the active elements [23,24,25,26]. The widespread use of GMI sensors received a significant boost after their potential in this area was established [27,28]. As is known, the GMI effect manifests itself in a significant increase in the impedance at high frequencies during the application of an external magnetic field. In ribbons, microwires and thin films, this is in turn due to changes in the penetration depth caused by the field [29,30,31,32,33,34].
In recent years, several types of soft magnetic materials have been studied in detail as candidates for GMI active elements for magnetic biosensors. Thin films, tapes and microwires are the main materials of them [35,36,37,38,39,40,41]. GMI biochemical sensors logically attract considerable attention due to their well-known advantages: low cost, relatively high sensitivity and small geometric parameters. It is necessary to note a special stage in the development of GMI biosensors, when they were included as prototypes in a bioanalytical system [42,43,44,45,46].
One of the most important ways of using magnetic structures in micro- and nanowires is the “magnetic domain-wall racetrack memory”. This use was conceptually shown in a famous work [47] and then was developed in other works.
The idea was to use the controlled motion of domain walls in magnetic nanowires. The control was supposed to be carried out by the method of short pulses of a spin-polarized electric current. This was to allow the creation of a storage device with a high performance and reliability. At the same time, the low cost of these storages was also assumed. A series of magnetic nanowires had to be created on a silicon basis. In this case, there should be spintronic reading and writing nanodevices that store a series of bits. This is the so-called “hippodrome memory”.
More than ten years of active research has allowed us to get closer to the creation of model prototypes. For example, the article [48] mentions “chiral domain wall (DW) motions based racetrack memory”. Read–write heads are created with the help of tunnel junctions. A single layer (CoFeB) or multi-layer (Co/Ni) magnetic nanowire can store information because the magnetic domains have different magnetizations (the “up” direction is “0” and the “down” direction represents “1”). To separate the data, direct currents, or artificial potentials, are used. An essential condition is the control of domain nucleation. Nucleation does not interfere with propagation if the nucleation process is determined mainly by the switching mechanism. The charge current directed in the plane of the magnetic nanowires is generated by the DW propagation circuit.
At a certain stage of research, scientists came to significant technical solutions that allow the creation of the real prototypes. Initially, it was proposed [47] that a magneto-resistive sensor performs the reading. It was located near the track. This was proposed in order to be able to use the emanating fringing fields to distinguish the magnetic states. Another method involved placing the magnetic tunnel junction (MTJ) sensor directly on the racetrack. The use of MTJ sensors [49] is promising. The size and compactness allow metal–oxide–semiconductors (CMOS) to be compatible with racetrack memory (RTM) applications. In addition, the real values of the tunneling magneto-resistance (TMR) are much higher than the values of the Giant magneto-resistance (GMR).
It is important to note such a property of tunneling currents as spin polarization. It is this property that allows the magnetic bit to be reoriented by spin transfer torques (STT). In addition, the polarity of the current allows one to determine the orientation of the bit being written, which is also an essential practical step.
In addition to the technical details, conceptual modeling is also essential. In the paper [50] it is shown by means of simulation how a domain wall can pass through an inhomogeneity. In particular, it demonstrated the passage through such inhomogeneity as the corner of the intersection of an L-shaped three-dimensional nanowire. The passage of the inhomogeneity was accompanied by the transformation of the domain wall. Namely, the domain wall was transformed from a head-to-head type into a Neel-type domain wall or vice versa. The direction of the transformation depended on the direction of the movement. An important way out for practical applications is to consider the threshold current density required to push the domain wall through the corner. It is this parameter that carries information about the technical details of the recording information.
The conducted studies have shown the particular importance of understanding the magnetic structure of the active elements in the search for optimal modes of their operation. For many years, our experimental and theoretical studies have been devoted to the study of the magnetic structure and the nature of its transformations in one of the most promising objects—amorphous glass-covered magnetic microwires.
Since the first observations of the domain structure in microwires, the need to classify these structures has become of key importance both for fundamental research and for applications. The results of our first extensive systematic magneto-optical studies made it possible to identify two main types of these structures [51]. These results are fully consistent with the known model [52,53].
At some point, it became clear to us that the circular magnetic structure is a particular case of some more general structure. It was logical to assume that such a structure should have been a helical structure. In our work [54], we confirmed this assumption, experimentally and with calculations. From that moment on, we focused on this magnetic structure. We managed to show its diversity and unusual properties. In particular, our attention was drawn to the helical domain structure and the magnetization reversal processes in which it was involved. The most unusual properties were shown by the spiral magnetic structure, which is one of the two helical structures. We have studied the basic processes of its existence: the processes of its origin, movement and disappearance. In addition, in accordance with one another, a spiral structure and a magnetization reversal process were put. A detailed comparison of the elliptical and helical domain walls was also carried out.
In the last stage of research, we studied the effect of external mechanical stress and thermal annealing conditions. By extensively conducting theoretical rackets, we were able to predict the features of the transformation of the helical structures in the presence of external influences of various types. In this review, we focused precisely on the description of these latest studies of ours.

2. Materials and Methods

2.1. Materials

We studied glass-coated amorphous microwires with different chemical compositions and geometric ratios. The cobalt- and iron-rich amorphous microwires were prepared using the Taylor–Ulitovsky method [55,56] and the rotating-water quenching technique (Unitika Ltd., Osaka, Japan). The amorphous structure of the samples was confirmed by X-ray Diffraction. The morphology of the samples was evaluated using a Carl Zeiss microscope.
As prepared and annealed microwires were studied. Annealing was carried out in a conventional furnace. The temperature, Tann, inside the furnace was set to 350 °C. The tensile stress was applied during the annealing and slow cooling of the microwire inside the furnace (stress-annealing configuration).

2.2. Magneto-Optical Kerr Effect Technique

To observe the cylindrically shaped surface magnetic domains and the magnetization reversal, we applied the magneto-optical Kerr effect (MOKE) [51,57]. Surface hysteresis loops were obtained with a MOKE magnetometer. The contrast images of the cylindrically shaped domains were obtained with an optical polarizing microscope (Carl Zeiss, reflective version) [51,57]. The high contrast images of the domain structure were the result of the digital processing of the original images. Reference images corresponding to the saturation magnetic states were used in this process. The geometry of the experiment was chosen in such a way that the rotation of the plane of the reflected light was proportional to the magnetic field component which in turn was parallel to the axis of the cylindrically shaped microwire and the plane of the incident light.
To apply the axial magnetic field parallel to the microwire axis, Helmholtz coils were used. To apply the circular magnetic field lying in a plane perpendicular to the axis, an electric current that did not exceed the boundary values was passed through the microwire. The direction of the circular field depended on the direction of the electric current. In some experiments, the magnetic fields of these two types were used simultaneously, resulting in an exotic configuration of the helicoidal field. The helicoidal angle of this field could be controlled by the ratio of the amplitudes of the two magnetic fields making up the total field.

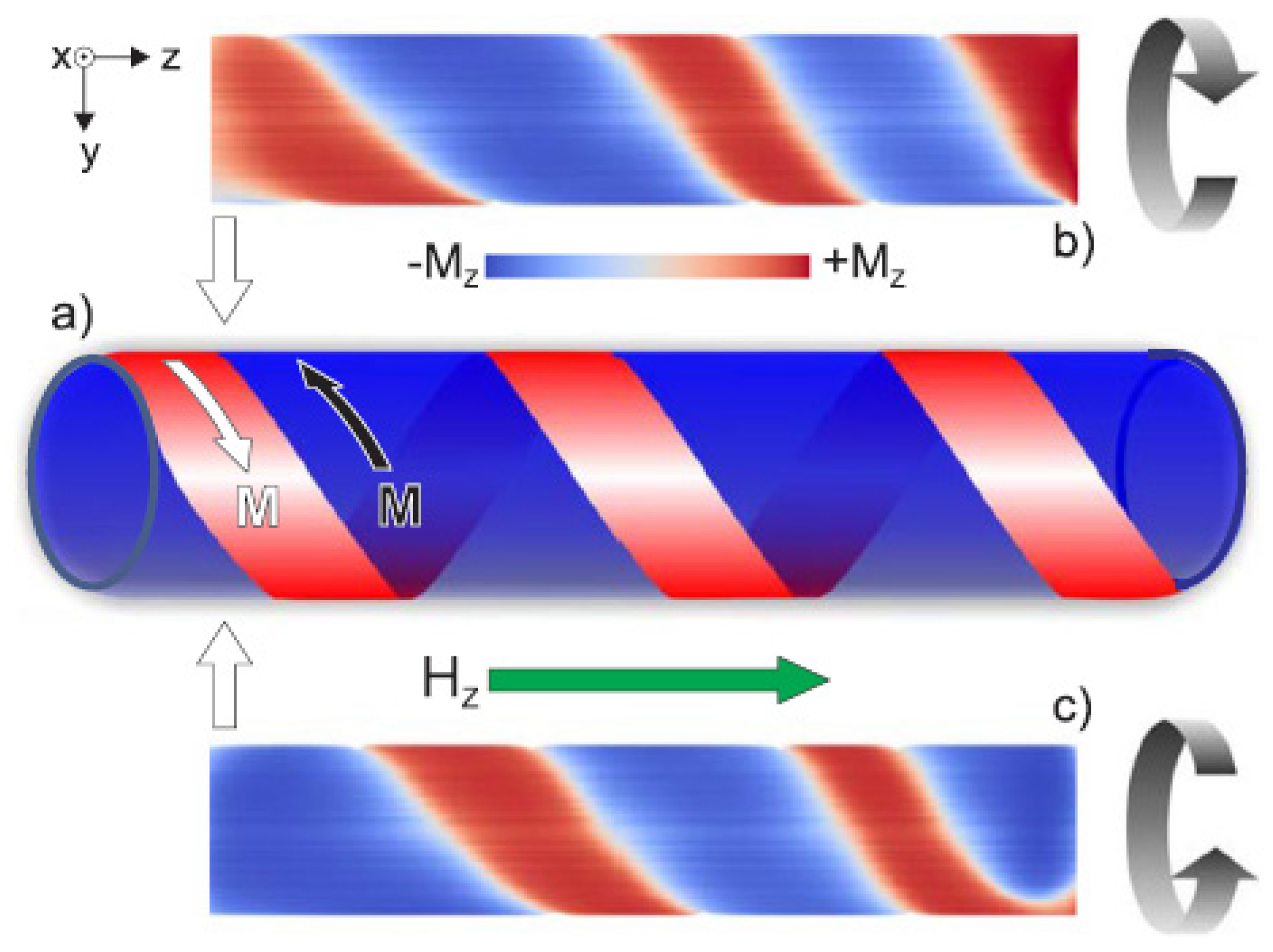
3. Background: Helical, Elliptical, Spiral and Vortex Magnetic Structures

The main characteristic feature of magnetic vortexes is the presence of an axis around which the magnetization smoothly rotates [58,59,60,61]. The simplest version of a vortex is a flat vortex with a centrally located axis. The ordinary vortex is mentioned in article [62]. There, the experimentally observed difference between a domain wall in the form of a plane vortex and a transversal domain wall was shown. The domain wall dynamics were measured with the classical Sixtus–Tonks experiments [51]. The energy difference between the two formations led to the difference in the mobile properties of the domain walls observed in the Fe-rich microwires. It was found that the transversal domain wall had no time to de-pin. Instead, the vortex-type domain wall nucleated at the end of the microwire.
The energy of the vortex-type domain wall is much higher than transversal ones since the exchange is higher. Therefore, it does not appear at a low applied field. However, the vortex-type domain wall does not create the free poles at its surface and it can propagate without an interaction with the radial domain structure below the surface. Therefore, its domain wall mobility is higher and it can reach very high velocities. A more complex version of the vortex is shown in [63]. Magnetic configuration consists of a periodic series of anti-parallel transverse domain-like regions separated by transverse vortex states with opposite alternating chirality.
As for the helical magnetic structure, the main feature is the inclination effect with a fixed inclination angle. In turn, the helical structure is divided into elliptical and spiral structures. The length of the domain wall in the form of an ellipse is limited only by the length of the ellipse and is determined precisely by the angle of the ellipse inclination. The limiting case of an elliptic domain structure is the classical circular bamboo structure. In this case, the angle of the inclination from the circular direction is equal to 0.
The main feature of the spiral magnetic structure is its “infinity”. In other words, only the length of the real sample determines its length. The limiting version of the spiral structure is the longitudinal structure, when the angle of the deviation from the axial axis becomes equal to zero. In this case, the domain wall is directed strictly along the microwire axis. This exotic structure was observed in the work [64].
When the vortex becomes non-flat, it merges with the helical structure and the distinctions between them are blurred. If the plane cross-section of this structure continues to be a vortex, then in the general distributed form, the helicity of the structure is more pronounced [63,65,66].
A wide range of different structures have been demonstrated in the works [66,67], both experimentally (with CoNi nanowires) and as a result of simulations. It was shown experimentally and theoretically the existence of such structures as longitudinaly distributed vortexes of a positive and negative chirality, chiral domain walls and two divided vortexes, smoothly passing one into another. The transformation of a multi-domain cylindrical structure into a compact series of transverse-vortex chains is shown in detail. Particular attention is paid to longitudinal vortex domains.
In work [67], a pure helical structure was shown. A complex and inhomogeneous magnetic configuration is revealed, consisting of a periodic configuration of exotic antiparallel transverse domain-like regions separated by transverse-vortex states of alternating chirality and polarity in a region rich in hexagonal close-packed (hcp) crystal structures. In turn, axial domains predominate in some areas. A transition between these two regions has also been identified. The experimental results were compared with micromagnetic simulations showing that a vortex chain is formed inside the cobalt-rich CoNi alloy. Correlated local changes in the composition and crystal structure were identified as the source of different magnetic configurations: the vortex chain is the result of the hcp phase.

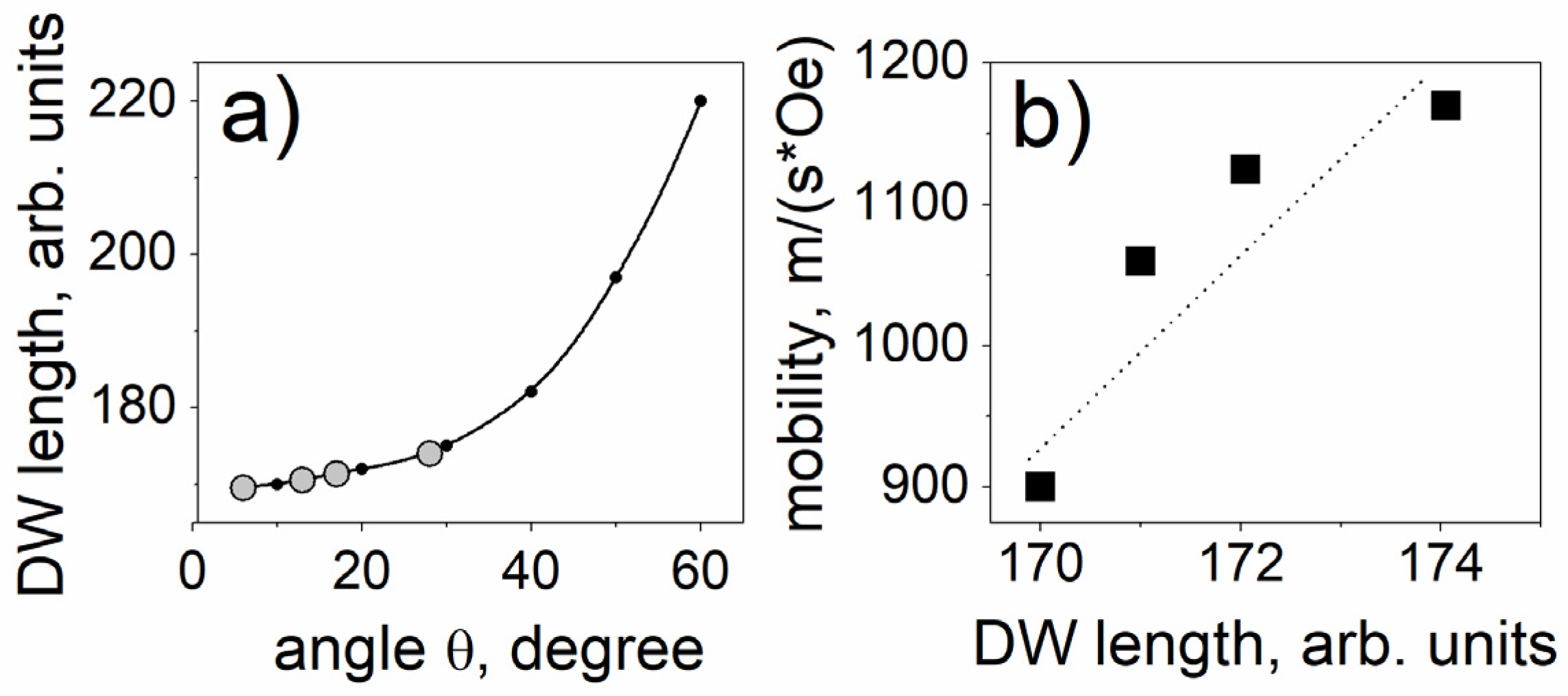
4. Background: Magnetic Structure in Magnetic Microwires

Initially, we followed the pioneer works [68,69,70] devoted to the study of the surface magnetic structure in Fe- and Co-rich microwires. These studies were carried out both by the classical MOKE and by the dilute, ferro-fluid-based colloid (Bitter technique). In these studies, for the first time, magnetic domains were clearly demonstrated on the surface of magnetic microwires.
Following the experimental foundations laid down in these articles, we, together with Yamasaki′s laboratory, observed both the formation of magnetic vortexes and the transformation of surface domains under the action of mechanical stress [71,72]. An independent confirmation of the vortex structure was demonstrated in the work [73].
Further studies using MOKE microscopy [74], a MOKE magnetometer [75] and the Bitter technique [76] made it possible to discover a series of interesting effects that led us to understanding the peculiarities of the magnetization reversal process in microwires. These effects include the effects of axial and circular surface bistability, as well as the relationship of the surface magnetic structure with the GMI effect [77,78,79]. All these effects are directly related to the use of magnetic wires in magnetic sensors [80].
It is also necessary to note the studies that have shown the existence of helical structures. In the work, where the experiments were performed with the Bitter technique [81], it was shown that the inclination of the helical magnetic structure correlates with the external mechanical stress applied to the magnetic microwire. We also paid attention to the work in which the authors, using the classical MOKE [82,83], independently observed inclined DWs and the walls directed parallel to the microwire axis. As we will see below, these structures are a manifestation of the general helical structure, which transforms depending on the conditions of the experiment. Additional studies of interest were the original studies that made it possible to observe the fine structure of the domain walls [83]. The idea of the determination of a magnetic profile turned out to be useful for our further research. These experiments [84] allowed us to study in detail the transformation of the surface magnetic structure in the microwire. It is impossible not to leave without mentioning the use of the magneto-optical method of indicator films [85]. Under certain conditions, such studies make it possible to obtain the magnetic images in the samples with a low optical surface quality.
Research cannot be complete without the development of an adequate theoretical model. Such a model was once proposed [86] and developed for many years [87]. It is based on an idea that the domain structure of the microwire consists of an inner core with axial magnetization (observed by a Barkhausen jump at a low field) and a shell domain structure mostly circumferentially or radially magnetized. In the case of the radially magnetized outer shell, the surface magnetic structure is complemented by the closure domains with the magnetization directed along the microwire axis.
This model has found, in particular, its indirect confirmation in our work [88].
In this case, we studied 7 cm-long ferromagnetic wires obtained with the in-rotating-water quenching technique ((Co94Fe6)72.5Si12.5B15, diameter 120 µm). The sample was partially polished prior to testing. Because of this, a flat wedge-shaped surface was created with a varying width of the wedge [88].
The transformation of the domain structure was studied in two different places in the wedge-shaped plane surface of the microwire. The polarization geometry was chosen in such a way that the black–white contrast reflected the perpendicular direction of the magnetization in the surface of the microwire (marked in Figure 1 and Figure 2 by the black–white arrows). Figure 1 demonstrates the surface magnetization reversal in the point of the surface corresponding to the narrow wedge.
First, we can see here an inclination of the axially directed component of the magnetization towards the perpendicular direction (Figure 1b). Then, the formation of circular surface domains was observed (in the form of a black–white contrast).
The domain walls’ motion marks the second phase (Figure 1b–d). These domain walls separate the previously formed surface circular domains. This process culminated in the formation of the circular mono-domain. In the remaining images, we see a similar process occurring in a negative magnetic field. A further increase in the magnetic field leads to the deviation of the magnetic system towards the axial direction.
In the case of a wider wedge, the process of the magnetization reversal is different from that described above. This is because a wider wedge shows the process at a greater depth in the microwire (Figure 2).
First, we could simultaneously see a black–white–grey contrast that testifies the coexistence of magnetic domains with three different directions of magnetization. Second, the magnetization reversal comes in the form of a jump-like rearrangement of the domain structure, while the regular motion of the domain walls does not occur (Figure 2c–e). As before, at the first step, the simultaneous rotation of the magnetization and the formation of the domain structure take place. It should be noted that the change in contrast can occur abruptly without changing the geometric configuration of the domains (Figure 2d,e). Finally, magnetization reversal finishes with the motion of the small domains towards the border of the wedged plane.

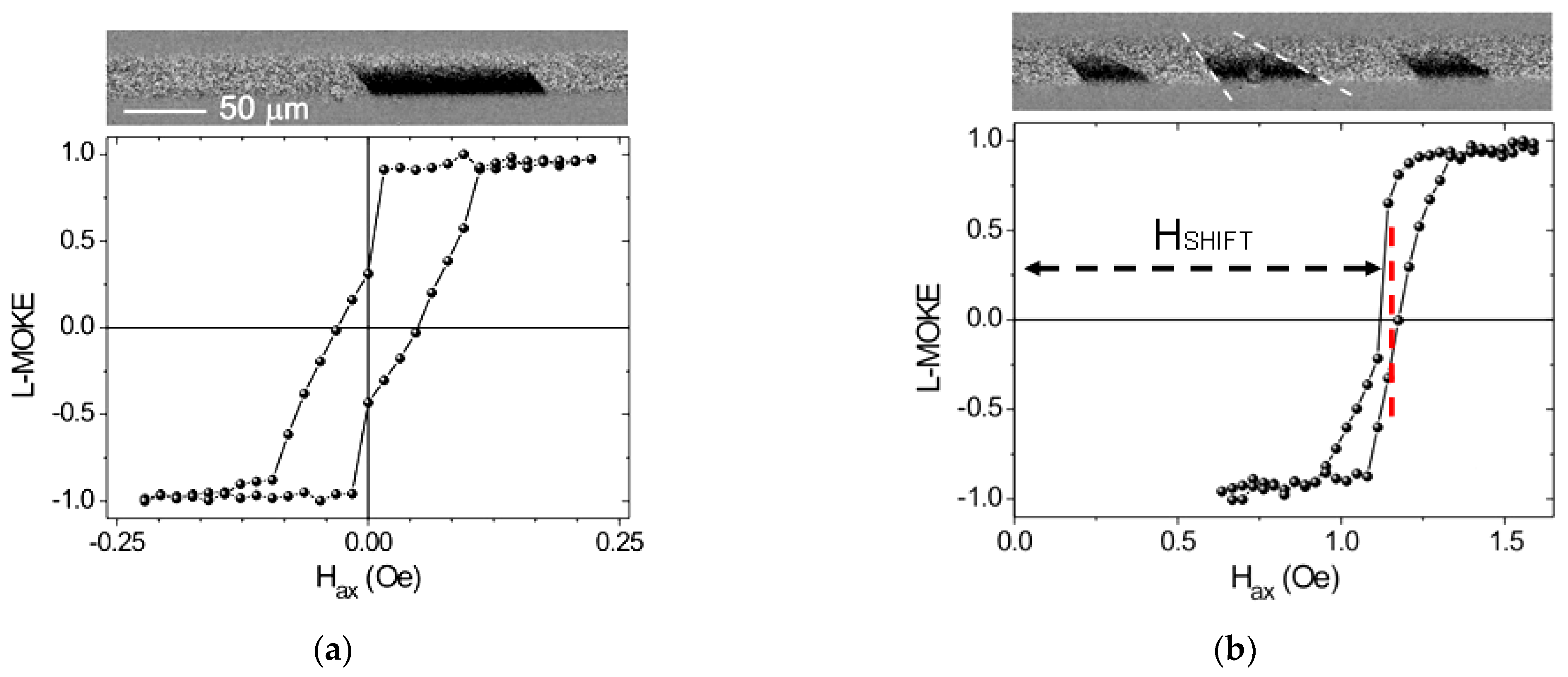
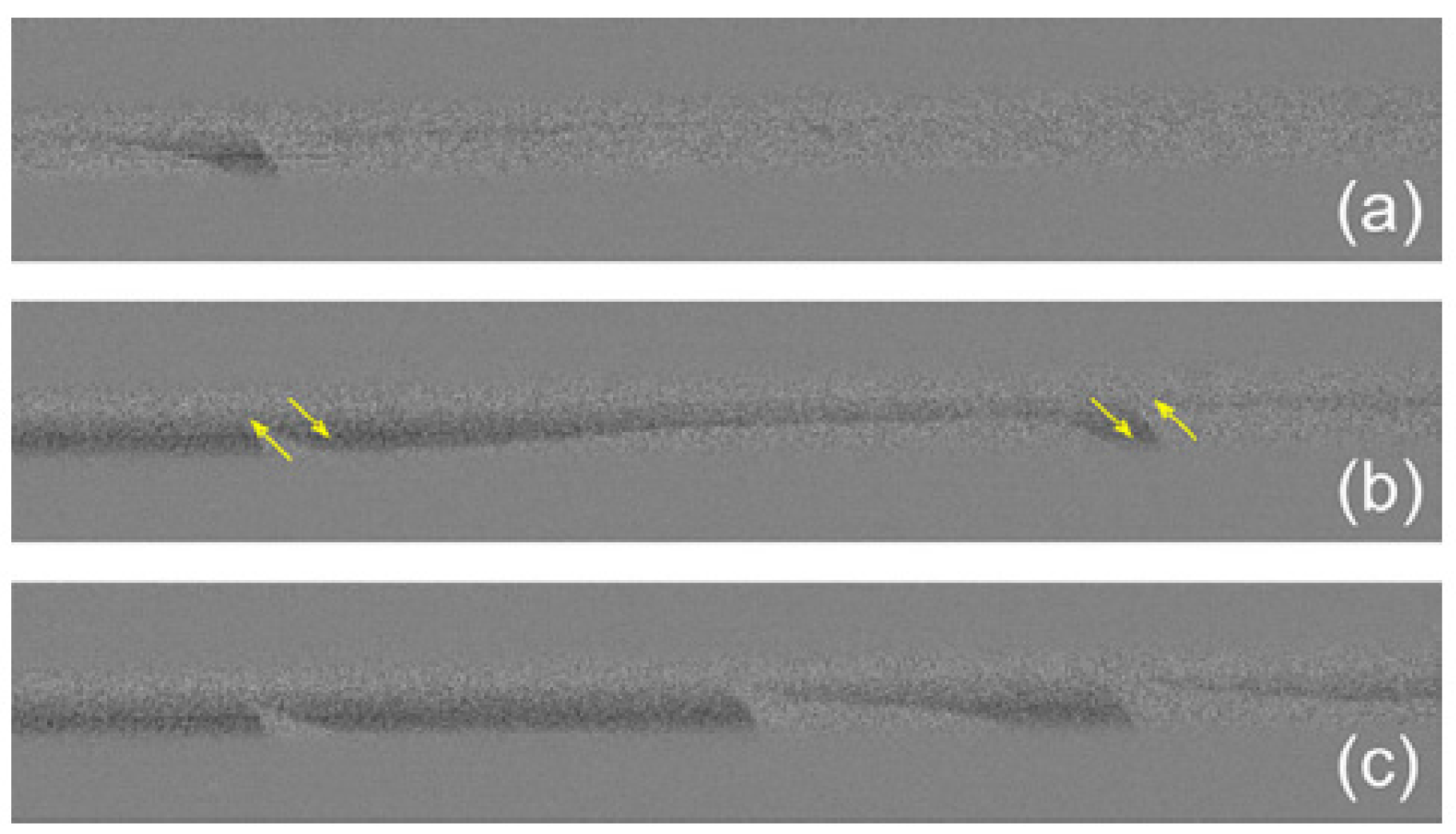
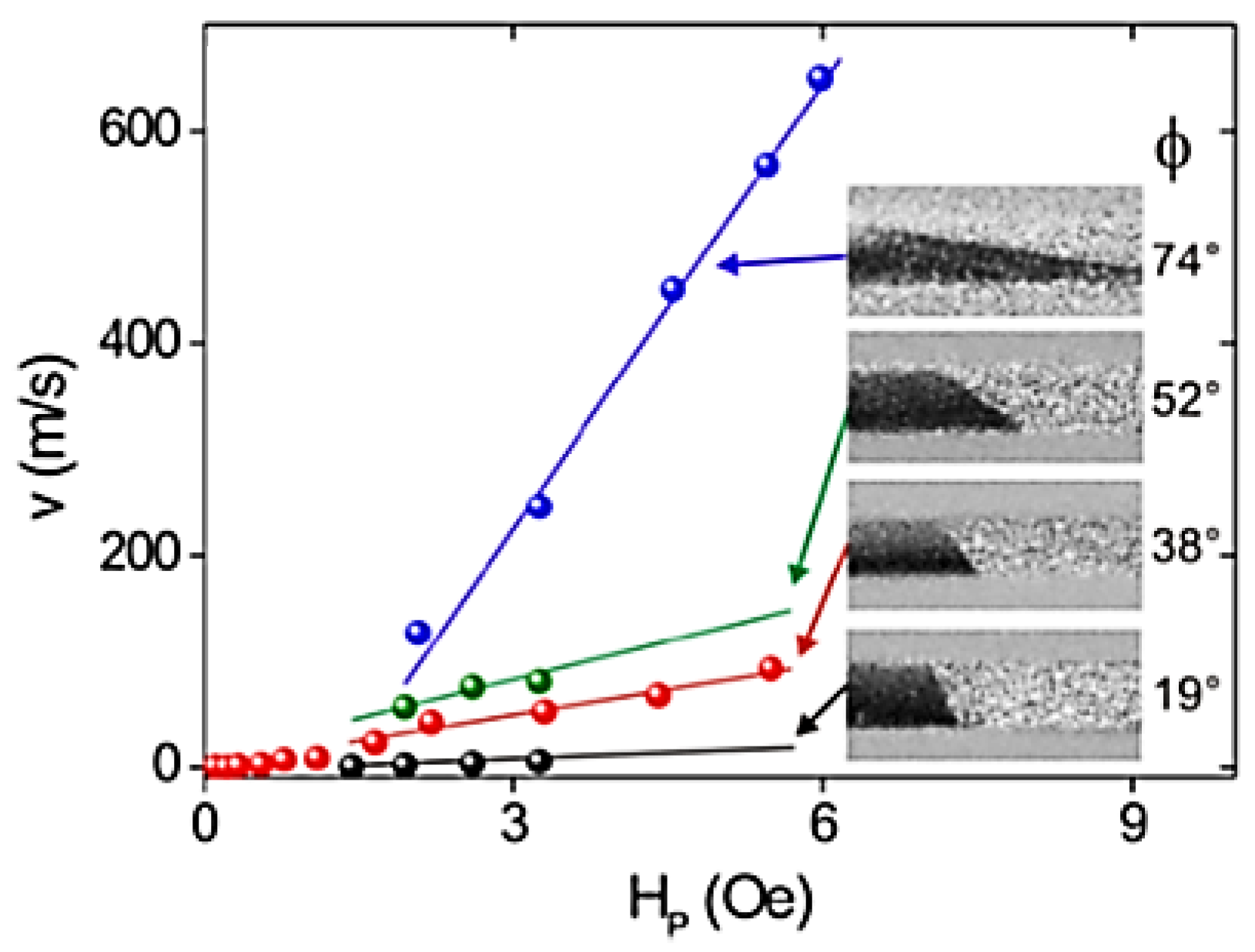
5. MOKE Study of Helical Magnetic Structures in Microwires

The division of the helical structure into elliptical and helical structures was demonstrated in our paper [54]. The inference about the presence of two different helical structures was prompted by a number of our studies with the response of the magnetic system of the microwires to various external influences.
The first type of the additional external influence was a circular magnetic field (HCIRC). An electric current flowing through a microwire [89] produced this field. We studied glass-coated amorphous microwires with the nominal composition of Fe5.71Co64.04B15.88Si10.94Cr3.40Ni0.03 (metallic nucleus radius 50 μm, glass coating thickness 20 μm).
Here (Figure 3) the longitudinal MOKE dependencies on the axial magnetic field (Hax) are shown. We also demonstrate the transformation of the magnetic structure caused by the circular magnetic field. Surface hysteresis loops also change in the presence of the HCIRC, as well as the helical magnetic structure (here it was the elliptic structure with the helicity angle of about 45°). An important detail is the parallel direction of all the observed domain walls. It confirms that this structure is namely an elliptic one. The shape of the MOKE hysteresis loop (Figure 3a) also confirms the mechanism of the magnetization reversal: it occurs mainly by the regular motion of the elliptic domain walls.
The application of the circular magnetic field transforms the MOKE hysteresis loop and the surface domain structure (Figure 3b). The non-symmetric shape and shift of the hysteresis loop and the different angle of inclination of the domain walls is the manifestation of this transformation. The difference in the angle of the DW inclination depends on the amplitude of the HCIRC. Analyzing these images in hindsight, we could state the presence of a multi-domain spiral domain structure in this wire. The shift of the hysteresis loop shows that in order to form a stable domain, the magnetic system needs to overcome a much larger energy barrier compared to the case of HCIRC. = 0. Additionally adding up with a periodically changing axial field, a DC circular magnetic field changes the magnetization reversal mechanism. Preferred may be the mode of the domain nucleation or the motion of the domain walls.
The experimental configuration of the combination of the crossed axial-circular magnetic fields realized in the Fe-rich microwires (Fe71.7B13.4Si11Nb3Ni0.9, metallic nucleus radius 50 μm, glass coating thickness 20 μm) gives another interesting type of helical domain structure [90]. Fixing the DC circular magnetic field, we changed the axial magnetic field in a narrow range of 2.75 Oe–2.85 Oe (Figure 4).
Here are two equal explanations of the observed effect, not contradicting one another. First, we could state that we observe here the formation of the non-planar vortex structure observed earlier in [88]. We see the formation of the wedged domain (Figure 4a) which transforms to the vortex structure (Figure 4b). The fact that this is a vortex confirms the directions of the four white arrows. Although the vortex appears to be somewhat stretched in space, the 360-degree turn of the magnetization and smooth domain walls are indicative of a vortex. A smooth change in the sign of the curvature of the domain walls also attracted our attention as a characteristic feature of the vortex.
The second explanation lies within our search for a spiral magnetic structure. The formation of a spatial system of wedge-shaped domains is a characteristic feature of one of the scenarios for the formation of a spiral structure. The motion of the wedge-shaped domain over the surface of the microwire was one of the characteristic features attributed by us to the spiral structure [54]. There is no conflict between the two explanations. At a certain stage of the magnetization reversal process, it is possible to observe the transformation of the vortex into a periodic system of wedge-shaped domains (Figure 4c).
By focusing on a very narrow range of the applied axial field, we can conclude that both the vortex structure and the spiral structure, being attractive for detailed study, exist within a very narrow energy range. Thus, the stable fixation of these domain structures requires the fine tuning of the entire experimental system.
Focusing separately on the elliptical wall, we found [91] that the velocity of the elliptically shaped domain wall significantly increases with an increasing domain wall inclination with respect to the axis of the wire.
Here are the main stages of our experiments, which allowed us to discover the relationship between the structure of the elliptic domain walls and their mobility. Following our preliminary developments, we set the angle of inclination of a single isolated elliptical domain wall (inset Figure 5). The range of the inclination angle of the domain wall was from 19 degrees to 74 degrees. The combination of the dc axial-circular magnetic fields allowed us to place the domain wall in an advantageous starting position on the surface of the microwire. To make the domain wall move, a pulsed circular field was applied in the form of an electric current pulse (the time duration of the pulse was about 10 ns to 1 ms). The magnitude of the current did not exceed the limits associated with possible thermal Joule overheating. The displacement of the domain walls was uniform and regular. The displacement values depended on the amplitude of the circular field pulse. The result of the experiments was a system of the dependences of the velocity of the motion of the domain walls of various inclinations on the magnitude of the magnetic field (Figure 5). By analyzing the figure, we can conclude that the mobility of the inclined elliptic domain walls with the incitation close to the circular direction is two orders smaller than for the case of the domain wall almost parallel to the microwire axis. We assumed that, in the general case, the domain wall has the shape of an ellipse. Therefore, this effect is associated both with the length of the domain wall, which depends on the inclination, and with the change in the magnetic pressure, which also depends on the angle of the inclination of the domain wall.
Another type of the external influence was the torsion mechanical stress [92]. Fe-rich and Co-rich microwires were studied here: Fe71.7B13.4Si11Nb3Ni0.9, metallic nucleus diameter 80 μm, glass coating 20 μm, and Co64.04Fe5.71B15.88Si10.94Cr3.4Ni0.3 metallic nucleus diameter 95 μm, glass coating 16 μm). The torsion stress of two opposite directions is the source of the surface domain structure transformation (Figure 6 and Figure 7). The applied stress did not exceed the limit values, which could cause irreversible mechanical changes. These values were chosen experimentally in advance. In the two types of microwires studied, the stress-induced changes were similar in scenario but differed in their details. In two cases, the application of the torsion stress caused the expected deviation from the equilibrium positions. The amplitude of the deviation depended on the magnitude of the applied torsion stress. The type of the equilibrium magnetic state determined the difference in the magnetic behavior. Due to the difference in the value and the sign of magnetostriction, in the Co wire it was a transverse multi-domain structure (a circular domain structure), while in the Fe wire it was a two-domain structure with a domain wall parallel to the wire axis (a longitudinal domain structure).
Thus, because of the performed wide series of the studies with a combination of different types of external influences, we fixed the possibility of the existence of the spiral magnetic structure, marked its difference from the elliptical magnetic structure, and confirmed its existence with theoretical calculations [54].
Specifically, the existence of a spiral magnetic structure was determined in the sample of Fe71.7B13.4Si11Nb3Ni0.9 composition (diameter of the metallic nucleus 103 μm, total diameter 158 μm) which was preliminarily stress annealed (the annealing temperature was 350 °C).
During the experiment, torsion stress was applied. As can be seen, the application of torsion stress is often the key episode in the discovery of the spiral magnetic structure.
The scenario of magnetization reversal, taking into account the presence of a spiral magnetic structure, was as follows. Starting from the saturation magnetic state, we applied an axial field, turning the magnetization in the opposite direction. At a certain stage, the alone wedge-shaped domain appeared (Figure 8a). This we considered the first sign of a spiral magnetic structure. Then, there were more domains of this type on the curved surface of the microwire. At this stage, two parallel processes took place: the co-directional motion of the wedge tips and the expansion of the domains themselves (Figure 8b). Thus, a system of infinite helical domains was formed, circularly encircling the entire sample. The infinite length of the domain walls is the second characteristic feature of the spiral structure. By using the term “infinite”, we mean that the length of the domain walls was limited only by the boundaries of the real sample. The surface magnetization reversal process ends with the fact that the spiral domains, expanding, fill the entire sample, forming a homogeneous mono-domain, thereby replacing the unfavorable magnetic state.
To facilitate the analysis, we present three main domain structures that we observed on the surface of the microwire: circular, elliptical and spiral (Figure 9). The circular structure is the simplest and is often the basis for experiments. Applying the external influence, we deviated from it in search of helical structures. The elliptical magnetic structure is one of the two helical structures known to us. Its main characteristic is the angle of inclination. The inclination angle is directly related to the length of the elliptical domain wall, which in this case is finite. The third structure is the spiral structure. Often being metastable, it nevertheless attracted our close attention due to its many unusual properties.
To reinforce the experimental results, the demonstrated the spiral magnetic structure, we performed a theoretical analysis. It was based on the statement that the internal stresses inside the microwire are distributed in different way along different directions: radial, circumferential and axial [93,94]. The details of the calculations are described in the work [54].
The results of the simulations are presented in the Figure 10 and Figure 11. The red–blue contrast corresponds to the axial directions of the magnetization MZ inside the microwire and in the surface. Figure 10 clearly shows the spiral structure on the surface of the microwire. To eliminate the ambiguous interpretation of the presented images, we demonstrated two-sided calculated images of the microwire (Figure 10b,c). It is significant that the direction of the inclination of the helical structure did not change the sign. Otherwise, we would be talking about an elliptical magnetic structure [90].
Figure 11, showing detailed transversal cross sections of the microwire wire, completes the picture of the calculations. Here we present the results of the calculations corresponding to two different experimental configurations: the variation in the amplitude of the external axial magnetic field in the fixed narrow cross-section plane of the microwire (Figure 11a–e) and the variation in the position of the cross-sections at the fixed value of HAX.
Here are the main most significant results of the calculations to which we pay attention. In the case of the spiral magnetic structure, the distribution of magnetization both inside and on the surface of the microwire is almost completely different from the classical core–shell model. The existing magnetic spiral is accompanied by an asymmetric distribution of magnetization inside the cylinder. The actual magnetic spiral is located not only on the surface but also largely in the volume of the microwire. Only at sufficiently large amplitudes of the external magnetic field does the magnetization distribution closely correspond to the classical core–shell model. This indirectly defines the range of magnetic fields where this model can actually be used.
The main conclusion that we draw from the results of the calculations presented in the series shown in Figure 11f–j is the presence of a clearly marked migration of the spiral domain inside the microwire and in the surface. It is unusual that cyclic spiral migration in some cases can occur only inside the microwire but without appearing on the surface. In this case, the microwire, outwardly looking like a nearly saturated and uniformly magnetized cylinder, retains all the unusual properties that characterize the spiral magnetic structure.
Having recognized three main types of magnetic structures that can be observed on the surface of a microwire (Figure 9), we focused on finding an experimental configuration where these three structures could exist simultaneously. As a result, we found that such a configuration exists and is feasible, albeit complex. This is a combination of the three main external influences: torsion mechanical stress, the axial magnetic field and the circular magnetic field [95].
Simultaneously varying the amplitude and sign of these parameters, we found a narrow range where we managed to observe the coexistence of cylindrical–elliptic–spiral structures (Fe71.7B13.4Si11Nb3Ni0.9 d = 103 μm, D = 158 μm). Previously, these structures were observed only separately [96,97,98]. As can be seen (Figure 12), each of the structures occupies a local limited space on the surface of the microwire and the boundary between them is quite sharp. Such a coexistence indicates that, being variations of the helical structure, they are energetically close enough and can reversibly transform into one another.
As we have seen, the essential difference in the spiral and elliptical magnetic structures is the significant difference in the length of the domain wall. In this regard, we decided to find out how this difference in length affects the mobile properties of the domain walls in the microwire [99]. To do this, we investigated two microwires: Fe71.7B13.4Si11Nb3Ni0.9 (microwire I), d = 103 μm, D = 158 μm; and Fe5.71Co64.04B15.88Si10.94Cr3.40Ni0.03 (microwire II), d = 100 μm, D = 140 μm. A comparative analysis of experiments and calculations of the mobile properties of the spiral and elliptical domain walls showed the following (Figure 13 and Figure 14).
Direct studies on the motion of domain walls using the Sixtus–Tonks [51] method have shown a real possibility of fixing a dynamic transition between the three designated types of domain walls. As in the case of static observations, the external torsion stress leads to a jump-like transition between different types of domain walls. As a result of the experiments, we obtained magnetic field dependences of the velocity in the presence of the torsion stress of various magnitudes and signs. In the absence of stress, a trivial linear dependence was obtained, which we associate with the motion of a circular domain wall. A relatively small torsion stress changed the field dependence of the velocity. A sharp jump appeared on it, which, according to our understanding, is related to the transition to a spiral domain wall type. It is interesting to note that, in fact, a series of jumps was observed in a narrow range of fields but not exactly one jump. This effect is an indirect confirmation of our earlier conclusion that domain walls of different types are very close energetically. In a narrow range of fields, a series of reversible transitions between walls of two types takes place. A further increase in the magnetic field makes the spiral domain wall stable and the jumps disappear.
Some increase in torsion stress changes the angle of inclination of the spiral domain wall, which manifests itself in an increase in the amplitude of the jump and, accordingly, an increase in the velocity on the field dependence. Without reaching the limiting stress values associated with irreversible mechanical damage to the glass shell, we are nevertheless remote to reach the next limiting stress value. This value was already associated with the transitions of the domain wall to the state of the elliptical structure. In this case, a series of reversible hops between two types of domain wall was also observed. A further increase in the external magnetic field led to the establishment of a regime of uniform motion of a stable elliptical domain wall.
First, we established a relationship between the inclination angle of the domain wall and the length of the domain wall (Figure 11a and Figure 12a). In the case of an elliptical wall, we used the equation for the normalized length of the inclined ellipse:
L = 4(πab + (ab)2)/((a + b)(2πb))
“b” and “a” are the semi-axes of an elliptically closed line. The angle φ is the angle of the ellipse inclination, which was measured from the axial direction of the microwire. For the spiral wall, the calculations given in [54,100] were used.
Subsequently, we studied the mobile properties of the samples I and II using the Sixtus–Tonks method [101,102]. The first conclusion from the performed experiments is that the velocity of domain wall motion increases with an increasing magnetic field in the two types of studied microwires. During the analysis, the following logical chain was built. (a) There is a direct relationship between the angle of inclination of the domain wall and its length. (b) There is a direct correlation between the angle of inclination of the domain wall and its velocity (mobility). Thus, DW mobility was put in direct correspondence with its length for two types of the studied magnetic structure. We built these dependences based on the results of the calculations and experiments (Figure 13b and Figure 14b). The clearly pronounced difference in the obtained dependences of the domain wall mobility on their length finds its explanation in the fact that the length of the elliptic domain wall is limited while the length of the spiral domain wall is “infinite”. Another notable difference in the magnetic behavior of the two studied magnetic systems is the following. During the field-induced displacement of the elliptic domain wall, the value of the angle of the domain wall inclination is stable, while for the spiral domain wall, the angle of the domain wall inclination changes slightly from the initial direction.
It is impossible not to mention one more area of our research, which we consider quite promising. We are talking about the study of very long microwires with magnetic properties distributed along the length. This type of sample has not previously been developed. We obtained this type of sample following to the original method. The method is based on annealing in a furnace under tension stress. The temperature inside the furnace was set to 350 °C. Due to its large length, part of the sample was placed inside the annealing furnace and part of the sample was outside. As a result, different parts of the sample were annealed at different temperatures, but in the presence of the same external stress.
We see three zones in a sample that has undergone this kind of heat treatment. Zone “A” corresponds to the part of the sample that was completely inside the annealing furnace during the annealing process. Zone “B” is the zone where the temperature smoothly changed from the temperature inside the annealing furnace to room temperature. Finally, zone “C” corresponds to room temperature. The length of zone “B” was about 5 cm, which allowed us to study it in sufficient detail. At the initial stage, we built the dependence of the temperature at which the parts of the sample were in the process of annealing on the length of the studied sample. As expected, the temperature gradually decreased with distance from the annealing furnace. Further, using the fluxmetric method, we obtained a series of field dependences of the magnetization corresponding to different regions of the studied sample. The resulting hysteresis loops were characterized by both different coercivity values and different loop squareness. The change in squareness is associated with the disappearance of the so-called bistability effect. It occurs when the secondary measuring coil moves along the sample from room temperature towards a high temperature. At relatively low temperatures, magnetic bistability persisted. However, with an increase in temperature, the hysteresis loop sharply changed its shape, which indicated the disappearance of the effect.
The main reason for the observed processes is the distribution of anisotropy along the wire, caused by the process of non-uniform annealing along the length. In this case, when analyzing the obtained experimental data, we used the mentioned “core–shell” model. In the analysis, we followed the ratio Mr/M0, which changed as we moved along the sample. Mr is the remanent magnetization and M0 is the magnetic moment of the maximum value of the external magnetic field. The distribution of magnetic anisotropy finds its manifestation in the form of its continuous spatial gradient along the length of the microwire, mainly in zone “B”. This dependence is due to the spatial transformation of the domain structure inside the surface of the microwire. We believe that there is a simultaneous increase in the outer near-surface region, which has transverse magnetic anisotropy, and a decrease in the inner volume region. This is evidenced by the change in the ratio Mr/M0.
The discovered longitudinal distribution of the magnetic properties prompted us to study the dynamics of the domain walls. It was found that in the longitudinal areas with a large induced anisotropy, the velocity of the DW displacement is higher. This is due precisely to the transverse projection of the magnetic anisotropy in the surface zone of the microwire. We believe that in this case the transverse component of the magnetic anisotropy of names has a similar effect on the dynamics with a transverse magnetic field. We believe that in this case the transverse component of the magnetic anisotropy has a similar effect of the transverse magnetic field on the DW dynamics.
We used the features of the experiments of Sixtus–Tonks [51] to obtain additional information about the DW transformation. As is known, the motion of the DW through the measuring coil is accompanied by a jump in the electromotive force (EMF) signal associated with this motion. The transformation of the DW was estimated from the transformation of the EMF peaks. In the area of the microwire where the temperature of the annealing was changed, the following effect was observed. Faster DW motion is accompanied by the decrease in the DW length.
In order to obtain a complete picture of the transformation of the magnetic structure along the length of the microwire, we carried out MOKE studies in three designated temperature zones of the sample under study. Particular attention was paid to the minor loops, which carried detailed information about the surface bistability effect. An analysis of the hysteresis loops obtained by the MOKE showed the following. Several types of surface magnetic structures were found as we moved along the microwire. In the room temperature zone, the bistability effect was recorded. The helical magnetic structure attracted the most attention. The degree of its helicity varied along the length. This effect has not been observed before. The application of torsion stress, traditional for such experiments, showed that this stress both leads to the gradual disappearance of bistability and changes the twist angle of the helical magnetic structure. In zone B, where, as we believe, there is a helicoidal structure unfolded along the wire length, the minor loops demonstrate clear jumps between two magnetic states with magnetization inclined from the axial direction, but not reaching the circular direction. Thus, we have fixed a metastable helical state, which stably exists in a narrow range of external axial magnetic fields during the magnetization reversal.
A joint analysis of the volume and surface hysteresis loops allowed us to modify the model of the magnetic structure in the microwire, taking into account the existence of a helical structure. On the one hand, we have a clear confirmation of the change in the ratio of the inner and outer parts with length of microwires. On the other hand, as we found out from the calculations, the helicoidal inner core performs cyclic migration along the microwire associated with the periodical nature of the helical structure. Combining these two statements, we believe that in the case of a microwire subjected to longitudinally distributed annealing, the cyclic migration of the inner core is naturally accompanied by a change in its characteristic cross section.

6. Conclusions

Here we present the review of last year’s study on the magnetic structure in magnetic microwires. We focused in particular on the formation and transformation of the helical magnetic structure. First, we analyzed the results of other authors obtained earlier, based on which we assumed the existence of two types of helical magnetic structures, spiral and elliptical. After that, we carried out our preparatory studies, manipulating such external influences as the DC electric current, DC axial magnetic field and torsion mechanical stress. Finally, we established the existence of a spiral magnetic structure. Having described its main properties, we outlined its main differences with the elliptical magnetic structure. The performed calculations confirmed the reality of the existence of a spiral magnetic structure in microwires. It was shown that an essential feature of the spiral magnetic structure is the migration of the spiral domain inside the microwire volume and in the surface of the microwire.
The simultaneous existence of spiral, elliptical and circular magnetic structures was also found, which indicates the energetic closeness of these structures. In addition, we paid special attention to the comparing of the lengths of the spiral and elliptical domain elliptical domain walls. Only the length of the real sample limits the length of the spiral domain wall. The difference in the length finds its manifestation in the difference of the dynamic properties of two types of studied magnetic structures.

Author Contributions

A.C.: conceptualization, formal analysis, investigation, writing—original draft, writing—review and editing. A.Z.: conceptualization, formal analysis, funding acquisition, investigation, project administration, resources, supervision, validation, writing—original draft, writing—review and editing. J.G.: writing—original draft, writing—review and editing. P.G.: formal analysis, investigation, methodology. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Spanish MCIU, under PGC2018-099530-B-C31 (MCIU/AEI/FEDER, UE), by the EU under the “INFINITE”(Horizon 2020) project, by the Government of the Basque Country, under the PUE_2021_1_0009 and Elkartek (MINERVA, ZE-KONP and COMPONENS) projects, by the University of the Basque Country, under the scheme of “Ayuda a Grupos Consolidados” (Ref.: GIU18/192) and under the COLAB20/15 project and by the Diputación Foral de Gipuzkoa in the frame of Programa “Red guipuzcoana de Ciencia, Tecnología e Innovación 2021” under the 2021-CIEN-000007-01 project.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Garcıa-Martın, J.; Gomez-Gil, J.; Vazquez-Sanchez, E. Non-destructive techniques based on eddy current testing. Sensors 2011, 11, 2525–2565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Uzal, E.; Rose, J. The impedance of eddy current probes above layered metals whose conductivity and permeability vary continuously. IEEE Trans. Magn. 1993, 29, 1869–1873. [Google Scholar] [CrossRef]
  3. Stutzke, N.; Russek, S.; Pappas, P. Low-frequency noise measurements on commercial magnetoresistive magnetic field sensors. J. Appl. Phys. 2005, 97, 10Q107. [Google Scholar] [CrossRef]
  4. Dogaru, T.; Smith, S.T. Giant magnetoresistence-based eddy-current sensor. IEEE Trans. Magn. 2002, 37, 3831–3838. [Google Scholar] [CrossRef]
  5. Rifai, D.; Abdalla, A.; Ali, A.; Razali, R. Giant Magnetoresistance Sensors: A Review on Structures and Non-Destructive Eddy Current Testing Applications. Sensors 2016, 16, 298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Nair, N.; Melapudi, V.; Hector, J.; Liu, X.; Deng, Y.; Zeng, Z.; Udpa, L.; Thomas, J.; Udpa, S. A GMR-based eddy current system for NDE of aircraft structures. IEEE Trans. Magn. 2016, 42, 3312–3314. [Google Scholar] [CrossRef]
  7. Yang, G.; Zeng, Z.; Deng, Y.; Liu, X.; Udpa, L.; Tamburrino, A. 3D EC-GMR sensor system for detection of subsurface defects at steel fastener sites. NDT E Int. 2012, 50, 20–28. [Google Scholar] [CrossRef]
  8. Lo, C.; Nakagawa, N. Evaluation of eddy current and magnetic techniques for inspecting rebars in bridge barrier rails. AIP Conf. Proc. 2013, 1511, 1371–1377. [Google Scholar]
  9. Yamada, S.; Chomsuwan, K.; Fukuda, Y.; Iwahara, M.; Wakiwaka, H.; Shoji, S. Eddy-current testing probe with spin-valve type GMR sensor for printed circuit board inspection. IEEE Trans. Magn. 2004, 40, 2676–2678. [Google Scholar] [CrossRef]
  10. Wang, R.; Kawamura, Y. An automated sensing system for steel bridge inspection using GMR sensor array and magnetic wheels of climbing robot. J. Sens. 2016, 1, 1. [Google Scholar] [CrossRef] [Green Version]
  11. Du, W.; Nguyen, H.; Dutt, A.; Scallion, K. Design of a GMR sensor array system for robotic pipe inspection. In Proceedings of the 2010 IEEE Sensors, Kona, HI, USA, 1–4 November 2010; pp. 2551–2554. [Google Scholar]
  12. Chen, L.; Que, P.; Jin, T. A giant-magnetoresistance sensor for magnetic-flux-leakage nondestructive testing of a pipe. Russ. J. Nondestruct. Test. 2005, 41, 462–465. [Google Scholar] [CrossRef]
  13. Kaack, M.; Orth, T.; Fischer, G.; Weingarten, W.; Koka, S.; Arzt, N. Application of GMR sensors for the industrial inspection of seamless steel pipes. In Proceedings of the 11th Symposium on Magnetoresistive Sensors and Magnetic Systems, Wetzlar, Germany, 29–30 March 2011. [Google Scholar]
  14. Rifai, D.; Abdalla, A.; Razali, R.; Ali, K.; Faraj, M. An eddy current testing platform system for pipe defect inspection based on an optimized eddy current technique probe design. Sensors 2017, 17, 579. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Zilberstein, V.; Walrath, K.; Grundy, D.; Schlicker, D.; Goldfine, N.; Abramovici, E.; Yentzer, T. MWM eddy-current arrays for crack initiation and growth monitoring. Int. J. Fatigue 2003, 25, 1147–1155. [Google Scholar] [CrossRef]
  16. Farea, S.; Hammad, R.; Dawoud, F.; Dossary, S.; Alzarani, S.; Binqorsain, A.; Minachi, A.; Goldfine, N.; Denenberg, S.; Manning, B.; et al. Field Demonstrations of MR-MWM-Array Solution for Detection, Imaging and Sizing of Corrosion under Fireproofing (CUF) with Wire Mesh. In Proceedings of the 15th Middle East Corrosion Conference, Manama, Bahrain, 2–5 February 2014. [Google Scholar]
  17. Bailey, J.; Long, N.; Hunze, A. Eddy Current Testing with Giant Magnetoresistance (GMR) Sensors and a Pipe-Encircling Excitation for Evaluation of Corrosion under Insulation. Sensors 2017, 17, 2229. [Google Scholar] [CrossRef] [Green Version]
  18. Brett, C.; de Raad, J. Validation of pulsed eddy current system for measuring wall thinning trough insulation. In Proceedings of the SPIE 2947, Nondestructive Evaluation of Utilities and Pipes, Scottsdale, AZ, USA, 14 November 1996. [Google Scholar]
  19. Cheng, W. Pulsed Eddy Current Testing of Carbon Steel Pipes Wall-thinning Through Insulation and Cladding. J. Nondestruct. Eval. 2012, 31, 215–224. [Google Scholar] [CrossRef]
  20. Greiner, M.; Demers-Carpeneter, V.; Rochette, M.; Hardy, F. Pulsed Eddy Current: New Developments for Corrosion under Insulation Examinations. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar]
  21. Majidnia, S.; Rudlin, J.; Nilavalan, R. A pulsed eddy current system for flaw detection using an encircling coil on a steel pipe. In Proceedings of the First International Conference on Welding and Non-Destructive Testing (ICWNDT2014), Karaj, Iran, 25–26 February 2014. [Google Scholar]
  22. Majidnia, S.; Rudlin, J.; Nilavalan, R. Investigations on a pulsed eddy current system for flaw detection using an encircling coil on a steel pipe. Insight Non Destr. Test. Cond. Monit. 2014, 56, 560–565. [Google Scholar] [CrossRef]
  23. Heim, E.; Ludwig, F.; Schilling, M. Binding assays with streptavidin-functionalized superparamagnetic nanoparticles and biotinylated analytes using fluxgate magnetorelaxometry. J. Magn. Magn. Mater. 2009, 321, 1628–1631. [Google Scholar] [CrossRef]
  24. Lee, Y.M.; Jeong, Y.; Kang, H.J.; Chung, S.J.; Chung, B.H. Cascade enzyme-linked immunosorbent assay (CELISA). Biosens. Bioelectron. 2009, 25, 332–337. [Google Scholar] [CrossRef]
  25. Lee, W.; Joo, S.J.; Sun, U.K.; Rhie, K.W.; Hong, J.K.; Shin, K.H.; Kim, K.H. Magnetic bead counter using a micro-Hall sensor for biological applications. Appl. Phys. Lett. 2009, 94, 153903. [Google Scholar] [CrossRef]
  26. Pannetier, L.M.; Parkkonen, L.; Sergeeva, C.N.; Polovy, H.; Fermon, C.; Fowley, C. Magnetocardiography with sensors based on giant magnetoresistance. Appl. Phys. Lett. 2011, 98, 153705. [Google Scholar] [CrossRef] [Green Version]
  27. Ferreira, H.A.; Graham, D.L.; Freitas, P.P.; Cabral, J.M.S. Biodetection using magnetically labeled biomolecules and arrays of spin valve sensors. J. Appl. Phys. 2003, 93, 7281–7286. [Google Scholar] [CrossRef]
  28. Vacher, F.; Alves, F.; Gilles, C. Eddy current nondestructive testing with giant magneto-impedance sensor. NDT EInt. 2007, 40, 439–442. [Google Scholar] [CrossRef]
  29. Phan, M.H.; Peng, H.X. Giant magnetoimpedance materials: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 323–420. [Google Scholar] [CrossRef]
  30. Tehranchi, M.M.; Ranjbaran, M.; Eftekhari, H. Double core giant magneto-impedance sensors for the inspection of magnetic flux leakage from metal surface cracks. Sens. Actuators A 2011, 170, 55–61. [Google Scholar] [CrossRef]
  31. Moulin, J.; Shahosseini, I.; Alves, F.; Mazaleyrat, F. Ultrasoft Finemet thin films for magneto-impedance microsensors. J. Micromech. Microeng. 2011, 21, 074010–074017. [Google Scholar] [CrossRef]
  32. Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar] [CrossRef]
  33. Panina, L.V.; Mohri, K.; Uchiyama, T.; Noda, M. Giant magneto-impedance in Co-rich amorphous wires and films. IEEE Trans. Magn. 1995, 31, 1249–1260. [Google Scholar] [CrossRef]
  34. Jackson, J.D. Classical Electrodynamics; John Wiley &Sons, Inc.: Hoboken, NJ, USA, 1975. [Google Scholar]
  35. Qin, F.X.; Peng, H.X.; Phan, M.H. Wire-length effect on GMI in Co70.3Fe3.7B10Si13Cr3 amorphous glass-coated microwires. Mater. Sci. Eng. 2010, 167, 129–132. [Google Scholar] [CrossRef]
  36. Ripka, P.; Kraus, L. Magnetic Sensors and Magnetometers; Artech House: Boston, MA, USA, 2001; pp. 350–358. [Google Scholar]
  37. Zhou, Y.; Yu, J.Q.; Zhao, X.L.; Cai, B.C. Simulation of giant magnetoimpedance in single layer and sandwiched thin films. J. Appl. Phys. 2001, 89, 1816–1819. [Google Scholar] [CrossRef]
  38. Peksoz, A.; Kaya, Y.; Taysioglu, A.A.; Derebasi, N.; Kaynak, G. Giant magneto-impedance effect in diamagnetic organic thin film coated amorphous ribbons. Sens. Actuators A 2010, 159, 69–72. [Google Scholar] [CrossRef]
  39. NazariNejad, S.; Fomani, A.A.; Mansour, R. Giant Magneto-Impedance Thin Film Magnetic Sensor. IEEE Trans. Magn. 2013, 49, 3874–3877. [Google Scholar] [CrossRef]
  40. Dwevedi, S.; Markandeyulu, G. Giant magnetoimpedance effect in nanocrystalline ribbons for sensitive magnetic sensors. J. Appl. Phys. 2010, 107, 09A328. [Google Scholar] [CrossRef]
  41. Laurita, N.; Chaturvedi, A.; Bauer, C.; Jayathilaka, P.; Leary, A.; Miller, C.; Phan, M.H.; McHenry, M.E.; Srikanth, H. Enhanced giant magnetoimpedance effect and field sensitivity in Co-coated soft ferromagnetic amorphous ribbons. J. Appl. Phys. 2011, 109, 07C706. [Google Scholar] [CrossRef] [Green Version]
  42. Chiriac, H.; Tibu, M.; Moga, A.; Herea, D. Magnetic GMI sensor for detection of biomolecules. J. Magn. Magn. Mater. 2005, 293, 671–676. [Google Scholar] [CrossRef]
  43. Chiriac, H.; Herea, D.; Corodeanu, S. Microwire array for giant magneto-impedance detection of magnetic particles for biosensor prototype. J. Magn. Magn. Mater. 2007, 311, 425–428. [Google Scholar] [CrossRef]
  44. Chiriac, H.; Herea, D. Magneto-impedance sensor for biomedical applications. Int. J. Appl. Electromagn. Mech. 2007, 25, 453–459. [Google Scholar] [CrossRef]
  45. Kim, D.; Kim, H.; Park, S.; Lee, W.; Jeung, W.Y. Operating Field Optimization of Giant Magneto Impedance (GMI) Devices in Micro Scale for Magnetic Bead Detection. IEEE Trans. Magn. 2008, 44, 3985–3988. [Google Scholar]
  46. Blanc-Béguin, F.; Nabily, S.; Gieraltowski, J.; Turzo, A.; Querellou, S.; Salaun, P. Cytotoxicity and GMI bio-sensor detection of maghemite nanoparticles internalized into cells. J. Magn. Magn. Mater. 2009, 321, 192–197. [Google Scholar] [CrossRef]
  47. Parkin, S.S.P.; Hayashi, M.; Thomas, L. Magnetic domain-wall racetrack memory. Science 2008, 320, 190. [Google Scholar] [CrossRef]
  48. Zhang, Y.; Zhao, W.; Klein, J.O.; Claude Chappert, C.; Ravelosona, D. Peristaltic perpendicuar-magnetic anisotropy racetrack memory based on chiral domain wall motions. J. Phys. D Appl. Phys. 2015, 48, 105001. [Google Scholar] [CrossRef]
  49. Bläsing, R.; Khan, A.A.; Filippou, P.C.; Garg, C.; Hameed, F.; Castrillon, J.; Parkin, S.S.P. From physics to the cusp of applications within a decade. Proc. IEEE 2020, 108, 1303. [Google Scholar] [CrossRef]
  50. Honda, S.; Sonobe, Y.; Greaves, S.J. Transforming domain motion for 3D racetrack memory with perpendicular magnetic anisotropy. J. Phys. D Appl. Phys. 2021, 54, 135002. [Google Scholar] [CrossRef]
  51. Chizhik, A.; Gonzalez, J. Magnetic Microwires. A Magneto-Optical Study; Pan Stanford Publishing: Singapore, 2014. [Google Scholar]
  52. Melo, L.G.C.; Menard, D.; Ciureanu, P.; Yelon, A.; Cochrane, R.W. Coupled core–shell model of magnetoimpedance in wires. J. Appl. Phys. 2004, 95, 1331. [Google Scholar] [CrossRef]
  53. Torrejon, J.; Thiaville, A.; Adenot-Engelvin, A.L.; Vazquez, M.; Acher, O. Cylindrical magnetization model for glass-coated microwires with circular anisotropy: Statics. J. Magn. Magn. Mater. 2011, 323, 283. [Google Scholar] [CrossRef]
  54. Chizhik, A.; Zhukov, A.; Gonzalez, J.; Gawronski, P.; Kułakowski, K.; Stupakiewicz, A. Spiral magnetic domain structure in cylindrically-shaped microwires. Sci. Rep. 2018, 8, 15090. [Google Scholar] [CrossRef] [Green Version]
  55. Zhukov, A.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Hernando, B.; Gonzalez-Legarreta, L.; Suñol, J.J.; Zhukova, V. Correlation of Crystalline Structure with Magnetic and Transport Properties of Glass-Coated Microwires. Crystals 2017, 7, 41. [Google Scholar] [CrossRef]
  56. Baranov, S.A.; Larin, V.S.; Torcunov, A.V. Technology, Preparation and Properties of the Cast Glass-Coated Magnetic Microwires. Crystals 2017, 7, 136. [Google Scholar] [CrossRef]
  57. Stupakiewicz, A.; Chizhik, A.; Tekielak, M.; Zhukov, A.; Gonzalez, J.; Maziewski, A. Direct imaging of the magnetization reversal in microwires using all-MOKE microscopy. Rev. Sci. Instrum. 2014, 85, 103702. [Google Scholar] [CrossRef]
  58. Vock, S.; Hengst, C.; Wolf, M.; Tschulik, K.; Uhlemann, M.; Sasvari, Z.; Makarov, D.; Schmidt, O.G.; Schultz, L.; Neu, V. Magnetic vortex observation in FeCo nanowires by quantitative magnetic force microscopy. Appl. Phys. Lett. 2014, 105, 172409. [Google Scholar] [CrossRef]
  59. Moreno, J.; Bran, C.; Vazquez, M.; Kosel, J. Cylindrical magnetic nanowires applications. IEEE Trans. Magn. 2021, 57, 800317. [Google Scholar] [CrossRef]
  60. Geng, L.D.; Jin, Y.M. Magnetic vortex racetrack memory. J. Magn. Magn. Mater. 2017, 423, 84. [Google Scholar] [CrossRef] [Green Version]
  61. Janutka, A.; Brzuszek, K. Giant magnetoreactance in magnetic nanowires. J. Magn. Magn. Mater. 2020, 515, 167297. [Google Scholar] [CrossRef]
  62. Richter, K.; Kostyk, Y.; Varga, R.; Zhukov, A.; Larin, V. Domain Wall Dynamics in Amorphous Microwires. Acta Physica Polonica A 2008, 113, 7. [Google Scholar] [CrossRef]
  63. Andersen, I.M.; Rodríguez, L.A.; Bran, C.; Marcelot, C.; Joulie, S.; Hungria, T.; Vazquez, M.; Gatel, C.; Snoeck, E. Exotic Transverse-Vortex Magnetic Configurations in CoNi Nanowires. ACS Nano 2020, 14, 1399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  64. Richter, K.; Thiaville, A.; Varga, R.; McCord, J. The role of uniaxial magnetic anisotropy distribution on domain wall tilting in amorphous glass-coated microwires. J. Appl. Phys. 2020, 127, 193905. [Google Scholar] [CrossRef]
  65. Fernandez-Roldan, J.A.; del Real, R.P.; Bran, C.; Vazquez, M.; Chubykalo-Fesenko, O. Electric current and field control of vortex structures in cylindrical magnetic nanowires. Phys. Rev. B 2020, 102, 024421. [Google Scholar] [CrossRef]
  66. Andersen, I.M.; Wolf, D.; Rodriguez, L.A.; Lubk, A.; Oliveros, D.; Bran, C.; Niermann, T.; Rößler, U.K.; Vazquez, M.; Gatel, C.; et al. Field tunable three-dimensional magnetic nanotextures in cobalt-nickel nanowires. Phys. Rev. Res. 2021, 3, 033085. [Google Scholar] [CrossRef]
  67. Fernandez-Roldan, J.A.; Ivanov, Y.P.; Chubykalo-Fesenko, O. 4—Micromagnetic modeling of magnetic domain walls and domains in cylindrical nanowires. In Magnetic Nano- and Microwires. (Second Edition) Design, Synthesis, Properties and Applications; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Cambridge, UK, 2020; pp. 403–426. [Google Scholar]
  68. Mohri, K.; Humphrey, F.B.; Yamasaki, J.; Kinoshita, F. Large barkhausen effect and matteucci effect in amorphous magnetostrictive wires for pulse generator elements. IEEE Trans. Magn. 1985, 21, 2017. [Google Scholar] [CrossRef]
  69. Takajo, M.; Yamasaki, J.; Humphrey, F.B. Domain observations of Fe and Co based amorphous wires. IEEE Trans. Magn. 1993, 29, 3484. [Google Scholar] [CrossRef]
  70. Yamasaki, J.; Humphrey, F.B.; Mohri, K.; Kawamura, H.H. Takamur, H.; Mälmhäll, R. Large Barkhausen discontinuities in Co-based amorphous wires with negative magnetostriction. J. Appl. Phys. 1988, 63, 3949. [Google Scholar] [CrossRef]
  71. Chizhik, A.; Gonzalez, J.; Yamasaki, J.; Zhukov, A.; Blanco, J.M. Vortex-type domain structure in Co-rich amorphous wires. J. Appl. Phys. 2004, 95, 2933. [Google Scholar] [CrossRef] [Green Version]
  72. Chizhik, A.; Yamasaki, J.; Zhukov, A.; Gonzalez, J.; Blanco, J.M. Magnetization reversal and magnetic domain structure in glass-covered Co-rich microwires in presence of tensile stress. J. Magn. Magn. Mater. 2004, 272–276, e499–e500. [Google Scholar] [CrossRef]
  73. Ivanov, Y.P.; del Real, R.P.; Chubykalo-Fesenko, O.; Vazquez, M. Vortex magnetic structure in circularly magnetized microwires as deduced from magneto-optical Kerr measurements. J. Appl. Phys. 2014, 115, 063909. [Google Scholar] [CrossRef] [Green Version]
  74. Richter, K.; Thiaville, A.; Varga, R. Magneto-optical study of the surface reversal process in amorphous glass-coated microwires with positive magnetostriction. IEEE Trans. Magn. 2014, 50, 2501404. [Google Scholar] [CrossRef]
  75. Chiriac, H.; Lostun, M.; Óvári, T.A. Surface Magnetization Processes in Amorphous Microwires. IEEE Trans. Magn. 2010, 46, 383. [Google Scholar] [CrossRef]
  76. Hernando, B.; Sánchez, M.L.; Prida, V.M.; Santos, J.D.; Olivera, J.; Belzunce, F.J.; Badini, G.; Vázquez, M. Magnetic domain structure of amorphous Fe73.5Si13.5B9Nb3Cu1 wires under torsional stress. J. Appl. Phys. 2008, 103, 07E716. [Google Scholar] [CrossRef]
  77. Chiriac, H.T.; Óvári, T.A.; Ţibu, M. Effect of surface domain structure on wall mobility in amorphous microwires. J. Appl. Phys. 2009, 105, 07A310. [Google Scholar] [CrossRef]
  78. Chizhik, A.; Gonzalez, J.; Zhukov, A.; Blanco, J.M. Circular magnetic bistability in Co-rich amorphous microwires. J. Phys. D Appl. Phys. 2003, 36, 419. [Google Scholar] [CrossRef]
  79. Ipatov, M.; Chizhik, A.; Zhukova, V.; Gonzalez, J.; Zhukov, A. Correlation of surface domain structure and magneto-impedance in amorphous microwires. J. Appl. Phys. 2011, 109, 113924. [Google Scholar] [CrossRef]
  80. Chiriac, H.; Óvári, T.A. Amorphous glass-covered magnetic wires: Preparation, properties, applications. Prog. Mater. Sci. 2011, 40, 333. [Google Scholar] [CrossRef]
  81. Sanchez, M.L.; Santos, J.D.; Olivera, J.; Prida, V.M.; Hernando, B. Influence of magnetic field and torsional stress on the skin penetration depth of Finemet wires. J. Magn. Magn. Mater. 2007, 316, 475. [Google Scholar] [CrossRef]
  82. McCord, J. Progress in magnetic domain observation by advanced magneto-optical microscopy. J. Phys. D Appl. Phys. 2015, 48, 333001. [Google Scholar] [CrossRef]
  83. Vahovsky, O.; Richter, K.; Varga, R.; McCord, J. Local distortions of surface domain walls in cylindrical microwires observed by magneto-optics. J. Magn. Magn. Mater. 2021, 537, 168168. [Google Scholar] [CrossRef]
  84. Ye, J.; del Real, R.P.; Infante, G.; Vázquez, M. Local magnetization profile and geometry magnetization effects in microwires as determined by magneto-optical Kerr effect. J. Appl. Phys. 2013, 113, 043904. [Google Scholar] [CrossRef] [Green Version]
  85. Aksenov, O.I.; Aronin, A.S. Investigation of the Domain Structure of Co-Based Microwires by Magneto-Optical Indicator Films Method. Phys. Solid State 2021, 63, 513. [Google Scholar] [CrossRef]
  86. Menard, D.; Frankland, D.; Ciureanu, P.; Yelon, A.; Rouabhi, M.; Cochrane, R.W.; Chiriac, H.; Ovari, T.A. Modeling of domain structure and anisotropy in glass-covered amorphous wires. J. Appl. Phys. 1998, 83, 6566. [Google Scholar] [CrossRef]
  87. Torrejon, J.; Thiaville, A.; Adenot-Engelvin, A.L.; Vazquez, M. Cylindrical magnetization model for glass-coated microwires with circumferencial anisotropy: Dynamics. J. Magn. Magn. Mater. 2013, 333, 144. [Google Scholar] [CrossRef] [Green Version]
  88. Chizhik, A.; Gonzalez, J.; Zhukov, A.; Blanco, J.M. Transformation of surface domain structure in Co-rich amorphous wires. Sens. Actuators B 2007, 126, 235. [Google Scholar] [CrossRef]
  89. Chizhik, A.; Stupakiewicz, A.; Zhukov, A.; Maziewski, A.; Gonzalez, J.; Zablotskii, V. Manipulation of Magnetic Domain Structures with Helical Magnetization in Magnetic Microwires. IEEE Trans. Magn. 2014, 50, 2005903. [Google Scholar] [CrossRef]
  90. Chizhik, A.; Stupakiewicz, A.; Zhukov, A.; Gonzalez, J. On mechanisms of domain switching in amorphous glass-coated wires. Phys. Status Solidi A 2016, 213, 350. [Google Scholar] [CrossRef]
  91. Chizhik, A.; Zhukov, A.; Gonzalez, J.; Stupakiewicz, A. Control of the domain wall motion in cylindrical magnetic wires. A. Appl. Phys. Lett. 2016, 109, 052405. [Google Scholar] [CrossRef]
  92. Chizhik, A.; Gonzalez, J.; Zhukov, A.; Stupakiewicz, A. Torsion stress induced magnetic switching in amorphous microwires. IEEE Magn. Lett. 2017, 8, 5106805. [Google Scholar] [CrossRef]
  93. Chizhik, A.; Zhukova, V.; Zhukov, A.J.; Gonzalez, J.; Gawronski, P.; Kułakowski, K.; Stupakiewicz, A. Surface magnetic structures induced by mechanical stresses in Co-rich Microwires. J. Alloys Compd. 2018, 735, 1449. [Google Scholar] [CrossRef]
  94. Vazquez, M.; Gomez Polo, C.; Velazquez, J.; Hernando, A. Bending stresses and bistable behavior in Fe-rich amorphous wire. J. Appl. Phys. 1994, 75, 5791. [Google Scholar] [CrossRef]
  95. Chizhik, A.; Zhukov, A.; Corte-León, P.; Blanco, J.M.; Gonzalez, J.; Gawroński, P. Torsion induced acceleration of domain wall motion in magnetic microwires. J. Magn. Magn. Mater. 2019, 489, 165420. [Google Scholar]
  96. Chizhik, A.; Zhukov, A.; Gonzalez, J.; Stupakiewicz, A. Basic study of magnetic microwires for sensor applications: Variety of magnetic structures. J. Magn. Magn. Mater. 2017, 422, 299. [Google Scholar] [CrossRef]
  97. Chizhik, A.; Zhukov, A.; Gonzalez, J.; Stupakiewicz, A. Control of reversible magnetization switching by pulsed circular magnetic field in glass-coated amorphous microwires. Appl. Phys. Lett. 2018, 112, 072407. [Google Scholar] [CrossRef]
  98. Chizhik, A.; Zhukov, A.; Blanco, J.M.; Gonzalez, J.; Gawronski, P. Experimental determination of limit angle of helical anisotropy in amorphous magnetic microwires. J. Magn. Magn. Mater. 2009, 321, 803. [Google Scholar] [CrossRef]
  99. Chizhik, A.; Zhukov, A.; Gonzalez, J.; Gawronski, P. Study of length of domain walls in cylindrical magnetic microwires. J. Magn. Magn. Mater. 2020, 512, 167060. [Google Scholar] [CrossRef]
  100. Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of mumax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef] [Green Version]
  101. Hudak, J.; Blazek, J.; Cverha, A.; Gonda, P.; Varga, R. Improved Sixtus–Tonks method for sensing the domain wall propagation direction. Sens. Actuators A 2009, 156, 292. [Google Scholar] [CrossRef]
  102. Calle, E.; Jiménez, A.; Vázquez, M.; del Real, R.P. Time-resolved velocity of a domain wall in a magnetic microwire. J. Alloys Compd. 2018, 767, 106. [Google Scholar] [CrossRef]
Chemosensors 10 00291 g001 550
Figure 1. Surface magnetic domain structures transformation in narrow wedge. (a) −10 Oe, (b) −2 Oe, (c) −0.3 Oe, (d) 0.03 Oe, (e) 0.3 Oe, (f) 1.3 Oe, (g) 2 Oe, (h) 10 Oe. Reprinted with permission from [88].
Figure 1. Surface magnetic domain structures transformation in narrow wedge. (a) −10 Oe, (b) −2 Oe, (c) −0.3 Oe, (d) 0.03 Oe, (e) 0.3 Oe, (f) 1.3 Oe, (g) 2 Oe, (h) 10 Oe. Reprinted with permission from [88].
Chemosensors 10 00291 g001
Chemosensors 10 00291 g002 550
Figure 2. Surface magnetic domain structures transformation in wide wedge. (a) −10 Oe, (b) −2 Oe, (c) −0.8 Oe, (d) −0.4 Oe, (e) 0.14 Oe, (f) 2 Oe, (g) 10 Oe. Reprinted with permission from [88].
Figure 2. Surface magnetic domain structures transformation in wide wedge. (a) −10 Oe, (b) −2 Oe, (c) −0.8 Oe, (d) −0.4 Oe, (e) 0.14 Oe, (f) 2 Oe, (g) 10 Oe. Reprinted with permission from [88].
Chemosensors 10 00291 g002
Chemosensors 10 00291 g003 550
Figure 3. MOKE hysteresis loops and surface domain structures (a) Hax = 0.04 Oe, HCIRC = 0; (b) Hax = 1.25 Oe, HCIRC = 0.6 Oe. Reprinted with permission from [89].
Figure 3. MOKE hysteresis loops and surface domain structures (a) Hax = 0.04 Oe, HCIRC = 0; (b) Hax = 1.25 Oe, HCIRC = 0.6 Oe. Reprinted with permission from [89].
Chemosensors 10 00291 g003
Chemosensors 10 00291 g004 550
Figure 4. Axial magnetic field transformation of surface magnetic domain structure (HCIRC DC 1.12 Oe) (a) HAX = 2.75 Oe; (b) HAX = 2.8 Oe; (c) HAX = 2.85 Oe. Image size is 150 × 720 μm2. Reprinted with permission from [90].
Figure 4. Axial magnetic field transformation of surface magnetic domain structure (HCIRC DC 1.12 Oe) (a) HAX = 2.75 Oe; (b) HAX = 2.8 Oe; (c) HAX = 2.85 Oe. Image size is 150 × 720 μm2. Reprinted with permission from [90].
Chemosensors 10 00291 g004
Chemosensors 10 00291 g005 550
Figure 5. Dependencies of the velocity of the DW on pulsed magnetic field. Insets: domain structure images for different angles of the DW inclination. Reprinted with permission from [91].
Figure 5. Dependencies of the velocity of the DW on pulsed magnetic field. Insets: domain structure images for different angles of the DW inclination. Reprinted with permission from [91].
Chemosensors 10 00291 g005
Chemosensors 10 00291 g006 550
Figure 6. Co-rich microwire. Torsion-stress-induced transformation of surface domain structure (a) −21π rad·m−1; (b) 5π rad·m−1; (c) +21π rad·m−1. Reprinted with permission from [92].
Figure 6. Co-rich microwire. Torsion-stress-induced transformation of surface domain structure (a) −21π rad·m−1; (b) 5π rad·m−1; (c) +21π rad·m−1. Reprinted with permission from [92].
Chemosensors 10 00291 g006
Chemosensors 10 00291 g007 550
Figure 7. Fe-rich microwire. Torsion-stress-induced transformation of surface domain structure (a) 34π rad·m−1; (b) 27π rad·m−1; (c) −7π rad·m−1. Reprinted with permission from [92].
Figure 7. Fe-rich microwire. Torsion-stress-induced transformation of surface domain structure (a) 34π rad·m−1; (b) 27π rad·m−1; (c) −7π rad·m−1. Reprinted with permission from [92].
Chemosensors 10 00291 g007
Chemosensors 10 00291 g008 550
Figure 8. Nucleation and displacement of wedge-shaped domains along the curved surface of microwire in the presence of axial magnetic field. Hax: (a) 0.1 Oe, (b) 0.2 Oe and (c) 0.4 Oe. Reprinted with permission from [54].
Figure 8. Nucleation and displacement of wedge-shaped domains along the curved surface of microwire in the presence of axial magnetic field. Hax: (a) 0.1 Oe, (b) 0.2 Oe and (c) 0.4 Oe. Reprinted with permission from [54].
Chemosensors 10 00291 g008
Chemosensors 10 00291 g009 550
Figure 9. Three typical domain structures existing in microwires. (a) Circular structure, (b) elliptical structure, (c) spiral structure. Arrows show the direction of magnetization in domains. Dashed lines show the domain walls. Reprinted with permission from [54].
Figure 9. Three typical domain structures existing in microwires. (a) Circular structure, (b) elliptical structure, (c) spiral structure. Arrows show the direction of magnetization in domains. Dashed lines show the domain walls. Reprinted with permission from [54].
Chemosensors 10 00291 g009
Chemosensors 10 00291 g010 550
Figure 10. Result of calculation. (a) Schematic picture of spiral structure. (b,c) Plane images of the (b) front and (c) back part of the calculated structure. Reprinted with permission from [54].
Figure 10. Result of calculation. (a) Schematic picture of spiral structure. (b,c) Plane images of the (b) front and (c) back part of the calculated structure. Reprinted with permission from [54].
Chemosensors 10 00291 g010
Chemosensors 10 00291 g011 550
Figure 11. Result of calculation. Sections of microwire (a–e) fixed position Z = 5.27 μm and varying axial field. Hax (a) 28 Oe, (b) 15 Oe, (c) 0, (d) −28 Oe and (e) −40 kA/m. (f–j) fixed axial field Hax = −30 kA/m and varying position. Z (f) 0.64 μm, (g) 1.85 μm, (h) 2.43 μm, (i) 3.65 μm and (j) 4.82 μm. Reprinted with permission from [54].
Figure 11. Result of calculation. Sections of microwire (a–e) fixed position Z = 5.27 μm and varying axial field. Hax (a) 28 Oe, (b) 15 Oe, (c) 0, (d) −28 Oe and (e) −40 kA/m. (f–j) fixed axial field Hax = −30 kA/m and varying position. Z (f) 0.64 μm, (g) 1.85 μm, (h) 2.43 μm, (i) 3.65 μm and (j) 4.82 μm. Reprinted with permission from [54].
Chemosensors 10 00291 g011
Chemosensors 10 00291 g012 550
Figure 12. Experimental picture of coexistence of three types of surfaces of domain structure: cylindrical (I), spiral (II), elliptic (III). Reprinted with permission from [95].
Figure 12. Experimental picture of coexistence of three types of surfaces of domain structure: cylindrical (I), spiral (II), elliptic (III). Reprinted with permission from [95].
Chemosensors 10 00291 g012
Chemosensors 10 00291 g013 550
Figure 13. Dependence of DW length of angle of inclination (a) and dependence of mobility on DW length in elliptic domain wall. (a) Line—results of the calculation (Equation (1)) and points taken from the experiments. (b) experimental points. Reprinted with permission from [99].
Figure 13. Dependence of DW length of angle of inclination (a) and dependence of mobility on DW length in elliptic domain wall. (a) Line—results of the calculation (Equation (1)) and points taken from the experiments. (b) experimental points. Reprinted with permission from [99].
Chemosensors 10 00291 g013
Chemosensors 10 00291 g014 550
Figure 14. Dependence of DW length of angle of inclination (a) and dependence of mobility on DW length in spiral domain wall. (a) Line—results of the calculation, points taken from the experiments. (b) experimental points. Reprinted with permission from [99].
Figure 14. Dependence of DW length of angle of inclination (a) and dependence of mobility on DW length in spiral domain wall. (a) Line—results of the calculation, points taken from the experiments. (b) experimental points. Reprinted with permission from [99].
Chemosensors 10 00291 g014
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Chizhik, A.; Gonzalez, J.; Zhukov, A.; Gawronski, P. Review of Helical Magnetic Structures in Magnetic Microwires. Chemosensors 2022, 10, 291. https://doi.org/10.3390/chemosensors10080291

AMA Style

Chizhik A, Gonzalez J, Zhukov A, Gawronski P. Review of Helical Magnetic Structures in Magnetic Microwires. Chemosensors. 2022; 10(8):291. https://doi.org/10.3390/chemosensors10080291

Chicago/Turabian Style

Chizhik, Alexander, Julian Gonzalez, Arcady Zhukov, and Przemyslaw Gawronski. 2022. "Review of Helical Magnetic Structures in Magnetic Microwires" Chemosensors 10, no. 8: 291. https://doi.org/10.3390/chemosensors10080291

APA Style

Chizhik, A., Gonzalez, J., Zhukov, A., & Gawronski, P. (2022). Review of Helical Magnetic Structures in Magnetic Microwires. Chemosensors, 10(8), 291. https://doi.org/10.3390/chemosensors10080291

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop