Next Article in Journal / Special Issue
An Improved Design for Chemomechanical Sensors: A Piezoresistive Pressure Sensor with a Mechanical Boss
Previous Article in Journal / Special Issue
Autonomous Oscillation of Nonthermoresponsive Polymers and Gels Induced by the Belousov–Zhabotinsky Reaction
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemosensors
Volume 1
Issue 3
10.3390/chemosensors1030021
chemosensors-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Hydrophobic Pollution on Response of Thermo-Sensitive Hydrogel

by
Hideo Tajima
*,
Fumiaki Sato
† and
Kazuaki Yamagiwa
†
Graduate School of Science & Technology, Niigata University, 2-8050 Ikarashi, Nishi-ku, Niigata 950-2181, Japan
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Chemosensors 2013, 1(3), 21-32; https://doi.org/10.3390/chemosensors1030021
Submission received: 1 July 2013 / Revised: 10 September 2013 / Accepted: 16 September 2013 / Published: 30 September 2013
(This article belongs to the Special Issue Hydrogel-Based Chemosensors)
Browse Figures
Versions Notes

Abstract

:
Hydrogels are widely studied for chemical sensors. However, they are known to adsorb organic compound and metal ions. The adsorption abilities of hydrogels against organic compounds and metal ions will negatively affect the performance of a hydrogel based chemical sensor. To clarify the effect of hydrophobic pollution on swelling behavior of temperature-sensitive gel, the temperature-responses of spherical N,N-diethylacrylamide (DEAA) gel in phenol solution were evaluated using the collective polymer diffusion constant. Phenol was selected as a model hydrophobic pollution. The equilibrium radius of DEAA gel changed discontinuously at about 874 g/m3 phenol solution, and the collective polymer diffusion constant decreased sharply between 874 and 916 g/m3, suggesting a “critical slowing down”. The phenol concentration difference EC was successfully used to correlate phenol concentration with the collective polymer diffusion constant. The correlation will be useful as an estimation of hydrogel response reduction associated with hydrophobic pollution.

1. Introduction

Hydrogels are widely studied for chemical sensors [1,2,3,4,5,6,7] because of their large, reversible changes in volume and other properties in response to small changes in temperature. Shin et al. prepared an inverse opal hydrogel pH sensor. This pH sensor showed rapid response time [1]. Lee et al. detected dissolved oxygen and pH with a hydrogel microarray sensor [2]. Selective detection of heavy metal ions was investigated with microcapsules consisting of a hydrogel and crown ether derivative by Pi et al. [3]. Hydrogel based sensors are also applied to a detection of gaseous material such as CO2 [4], Cl2 [5], NO [6], and VOCs [7]. On the other hand, hydrogels have a good performance for recyclable adsorbents [8,9,10,11,12] and biomedical applications (including drug delivery) [13,14,15]. They are not only organic compounds but also absorb metal ions. The adsorption of metal ions by hydrogels has recently attracted increasing attention over the past several years [10,11,16]. These adsorption abilities of hydrogels against organic compounds and metal ions will negatively affect a performance of hydrogel based chemical sensor.
In applications of thermo-response hydrogels as a chemical sensor, the important gel characteristics are not only selectivity but also the kinetics of stimulus-response. It is well known the hydrogel kinetics depends on the hydrogel particle radius [17] and shape [18]. In addition, the swelling and shrinking rates of hydrogel change depending on the initial and final temperatures in the temperature swing process [19]. However, limited information is available on the effect of volume change and adsorption process on hydrogel response kinetics. Hydrogels as chemical sensors must operate in a solution included in the target material. However, the swelling ratios of hydrogels vary with changing solute concentrations [20].
Our previous study [21] has already elucidated the dominant factors governing the temperature-response rate of spherical poly(N,N-diethylacrylamide) (DEAA) in pure water. The aim of this study was to elucidate the effects of hydrophobic pollution on the temperature response of hydrogel. This study used polyDEAA gel as a hydrogel and phenol as a model hydrophobic pollution. Phenol is representative of possible contamination in biological and chemical substances. At the same time, phenol gives very specific interaction with polymeric gels. Spherical polyDEAA particles with radii of less than 1 mm were prepared by the method developed in our previous work [22] and used to measure the temperature response rate because small spherical gel particles have isotropic and rapid volume changes [18,21].

2. Experimental Section

2.1. Temperature-Response of a Single Spherical DEAA Gel Particle in Dilute Phenol Solution

The temperature-sensitive monomer N,N-diethylacrylamide (DEAA, Kojin Co. Ltd., Japan) was used to prepare the hydrogel materials. DEAA gels were prepared from a liquid-liquid dispersion using static mixing technology, and photo-crosslinked by UV irradiation. The preparation method for polyDEAA particles has been reported in detail previously [22]. Some sample gel particles (single spherical gels) were collected from the resultant polyDEAA gels after the gels were swollen in deionized water at 293 K.
The calculation theory and method are the same as reported previously [21]. The details are given in the reference and described briefly here.
Because the lower critical solution temperature (LCST) of polyDEAA in water is about 306 K [23], the initial and final temperatures for swelling were fixed at 313 K and 293 K, respectively, to include the LCST for adsorption operation. The apparatus consisted of the measuring cell, two thermostatted water baths for initial and final temperature setting, a video microscope, and a PC for video capture. The temperatures of the water baths were controlled to within ±0.1 K. The measuring cell contained a polyDEAA gel particle (the circularity of the gel particle was 1.107) and solution (deionized water or phenol solution). The time course of the volume change of the polyDEAA gel particle was observed with the video microscope and recorded as a digital movie. The swelling experiments described above were carried out at least twice under the same conditions. Photographic images of the sample particle were taken from the digital movie, and the digitalized images were analyzed with a PC. The Heywood diameter was used to evaluate the representative length of the polyDEAA gel particle.
The swelling behavior was analyzed by the following equation based on the Tanaka-Fillmore theory [17]:
Chemosensors 01 00021 i001
Chemosensors 01 00021 i002
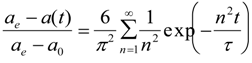
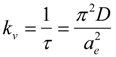where ae, a0 and a(t) are the hydrogel characteristic length at equilibrium, initially and at time t, and τ is the relaxation time of the polymer network. When τ is smaller than time t (that is t/τ> 1), we can assume n = 1. It has been already confirmed for the DEAA gel used in this study that linear behavior was within t/τ > 0.25 in water [21]. Then we assumed n = 1, and calculated kv of polyDEAA gel by fitting the experimental data to Equation (1). The collective polymer diffusion constant D could be obtained from the kv value according to Equation (2). To validate the swelling rate of the polyDEAA gel prepared in this study, its response rate was measured in pure water. The kv values are in agreement with the literature data [21]. The collective polymer diffusion constant in pure water, D0, was evaluated as 3.95 × 10−11 m2·s−1 for swelling. This study used polyDEAA gel particles with radii of 0.35–0.50 mm (as measured in pure water at 293 K).

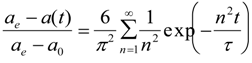
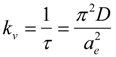
2.2. Phenol Adsorption Isotherm

Phenol (99%, Wako Pure Chemical Industries, Ltd., Osaka, Japan) was used as a model hydrophobic pollution. Phenol adsorption isotherms were measured at 313 K and 293 K. Gel particles 0.25 g in dry weight were packed into a filter made of polyterephthalate, and then the packed gels were swollen in deionized water at a given temperature before adsorption isotherm measurement. Before use, we confirmed that the polyterephthalate filter did not adsorb phenol. The packed gels were placed in 50 cm3 of aqueous phenol solution in a vial at the given temperature and allowed to sit for at least a day, with occasional shaking, to reach equilibrium. The phenol concentration in the bulk solution was determined by measuring the UV-absorbance at 270 nm with a spectrophotometer. The phenol adsorption amount in equilibrium qphenol was calculated from the material balance of the bulk phenol solution. In this study, the volume change of aqueous phenol solution by the water content in swollen hydrogel was ignored because the volume change was estimated to be less than 1%. Although there has been an example reported of the Hill equation approximation for the adsorption isotherm of phenol on a hydrogel [24], the phenol adsorption isotherm was approximately expressed by a Freundlich type equation from an engineering viewpoint:
Chemosensors 01 00021 i003
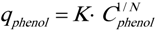where K and N are experimentally determined parameters.
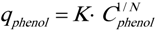
Adsorption isotherm data are shown in Figure 1. At the phenol concentrations used in this study, the phenol adsorption isotherm could be approximately expressed by a Freundlich type equation. The parameter values were estimated as K = 3.34 × 10−4, 1/N = 1.74 at 293 K and K = 1.57 × 10−2, 1/N = 1.27 at 313 K. Because there is one polyDEAA gel particle in an excess amount of phenol solution in this study, the temperature swing operation at a constant bulk phenol concentration will be as indicated by arrow (a) in Figure 1. The arrow (b) in Figure 1 shows the temperature swing operation when the amount of phenol adsorbed is kept constant. The given Freundlich type equation was used to calculate suitable phenol concentrations for swelling of DEAA gel under a constant amount of adsorbed phenol.
Chemosensors 01 00021 g001 1024
Figure 1. Adsorption isotherm data for N,N-diethylacrylamide (DEAA) gel and phenol solution system. Solid lines are fits to a Freundlich type equation.
Figure 1. Adsorption isotherm data for N,N-diethylacrylamide (DEAA) gel and phenol solution system. Solid lines are fits to a Freundlich type equation.
Chemosensors 01 00021 g001

2.3. Swelling Behavior of DEAA Gel at Fixed amount of Adsorption Phenol

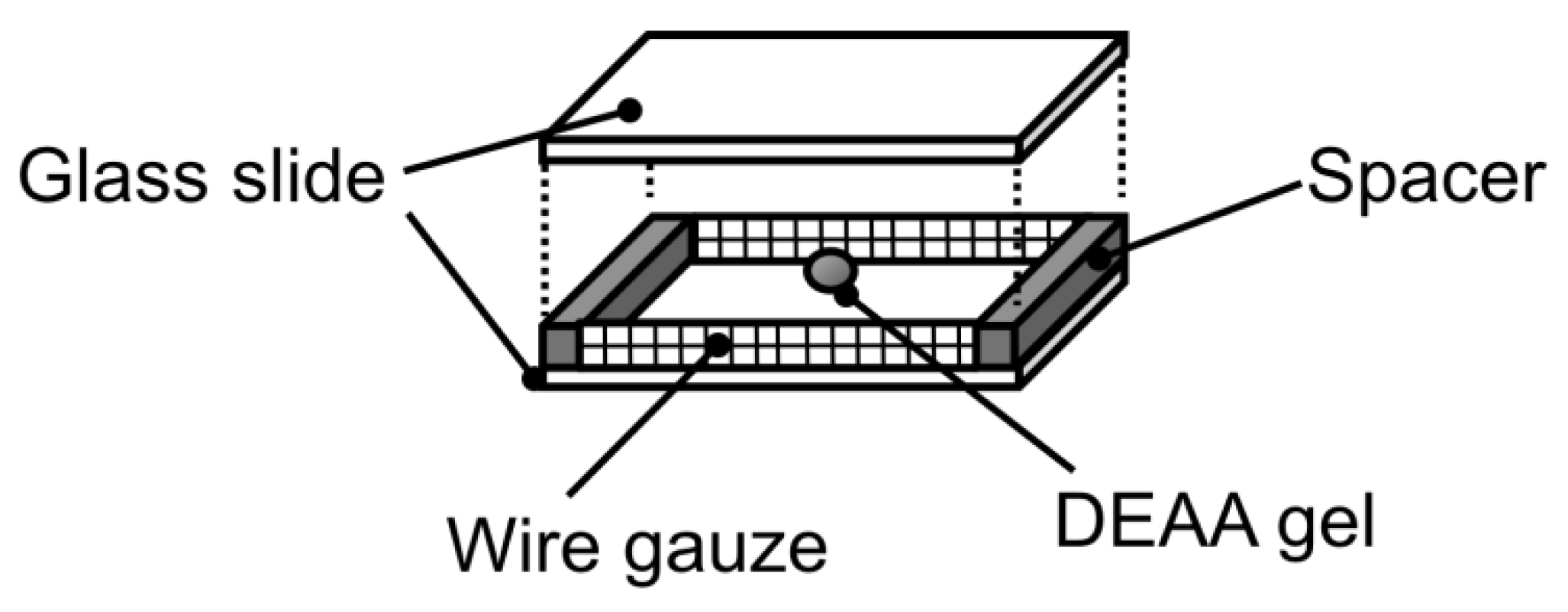
To evaluate the effect of adsorbed phenol amount on swelling behavior of hydrogel, the adsorbed phenol amount needs to be fixed during the swelling process. This can be done by measuring the swelling behavior with simultaneous changing the bulk phenol concentration and temperature. The bulk phenol concentration, which qphenol at 293 K is equal to that at 313 K, was calculated from Equation (3). A specially designed measuring cell was made to easily change the phenol solution, as shown in Figure 2. The cell containing a polyDEAA gel particle was placed in a phenol solution in a Petri dish at 313 K until it reached a state of equilibrium. When the cell was quickly transferred to the other phenol solution set at 293 K, the polyDEAA gel was exposed to the other phenol solution. That is, only temperature was varied, and the amount of adsorbed phenol was fixed. The other parts of the experimental procedure were carried out as described previously in Section 2.2.
Chemosensors 01 00021 g002 1024
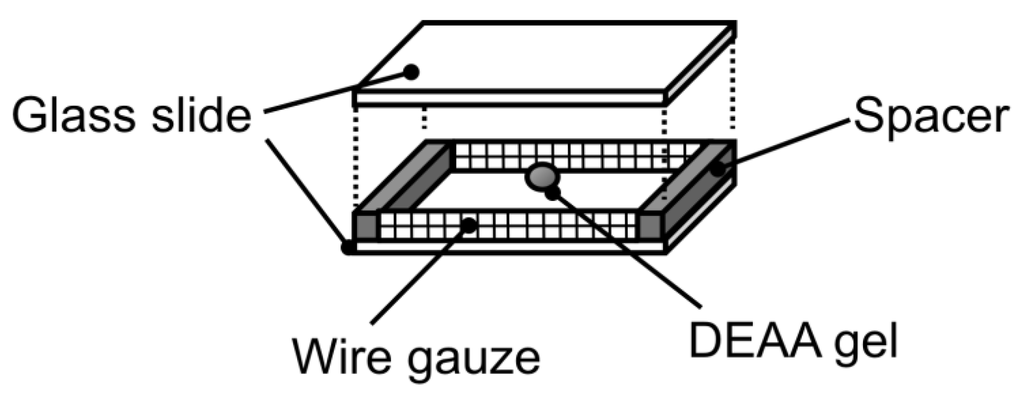
Figure 2. Special design of observation cell for temperature swing with simultaneous change of phenol solution.
Figure 2. Special design of observation cell for temperature swing with simultaneous change of phenol solution.
Chemosensors 01 00021 g002

3. Results and Discussion

3.1. Equilibrium Radius and Swelling Behavior of DEAA Gel in Phenol Solution

The equilibrium radius of the DEAA gel particle was measured at various bulk phenol concentrations. Figure 3 shows the equilibrium radius change with bulk phenol concentration. The equilibrium radius ae of this DEAA gel particle in pure water (0 g/m3 phenol) was 0.417 mm at 293 K. The ae value decreased slightly with increasing bulk phenol concentration, and was 0.381 mm at a bulk phenol concentration of 802 g/m3. Between 874 and 916 g/m3, the ae value was discontinuously changed. The ae was less than 0.3 mm at phenol concentrations above 950 g/m3. A discontinuous change in characteristic length of DEAA gel at a certain phenol concentration has also been observed at a different temperature in the literature [25]. The temperature induced volume phase transition of hydrogels depends on the solute concentration (NIPA-phenol system) [26] and that the phenol concentration required to induce the volume phase transition for DEAA gel is lower than that for NIPA gel [25]. Our results imply that the phenol concentration required to induce a volume phase transition at 293 K is about 874 g/m3 for the DEAA gel used in this study. At 313 K, changing the phenol concentration only causes a small change in ae. The DEAA gel remains in the shrunken state at 313 K. The reduction of the ae value with increasing the bulk phenol concentration is attributed to the increase in hydrophobic interactions caused by the adsorption of phenol molecules onto the DEAA gel network. High hydrophobic interaction of DEAA and phenol promotes the hydrogen bond formation between amide group of gel and the hydroxyl group of phenol, and subsequent the adsorption of phenol divests the amide group of hydrated water molecules [20,24]. We now know that hydrophobic pollution is capable of reducing hydrogel size in a chemical sensor. Furthermore, temperature sensitivity of DEAA gel is also changed because the phenol adsorption to DEAA gel lowers the transition temperature [20,25].
Chemosensors 01 00021 g003 1024
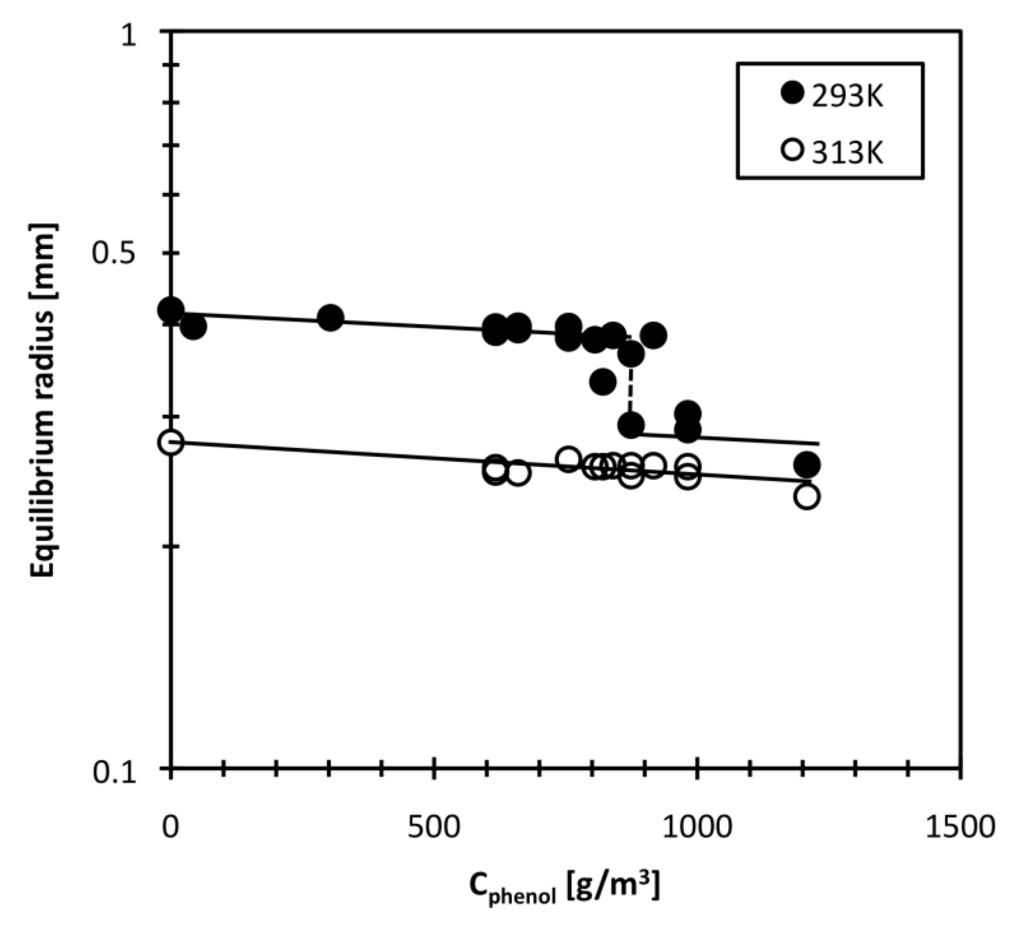
Figure 3. Effect of phenol concentration on DEAA gel radius.
Figure 3. Effect of phenol concentration on DEAA gel radius.
Chemosensors 01 00021 g003
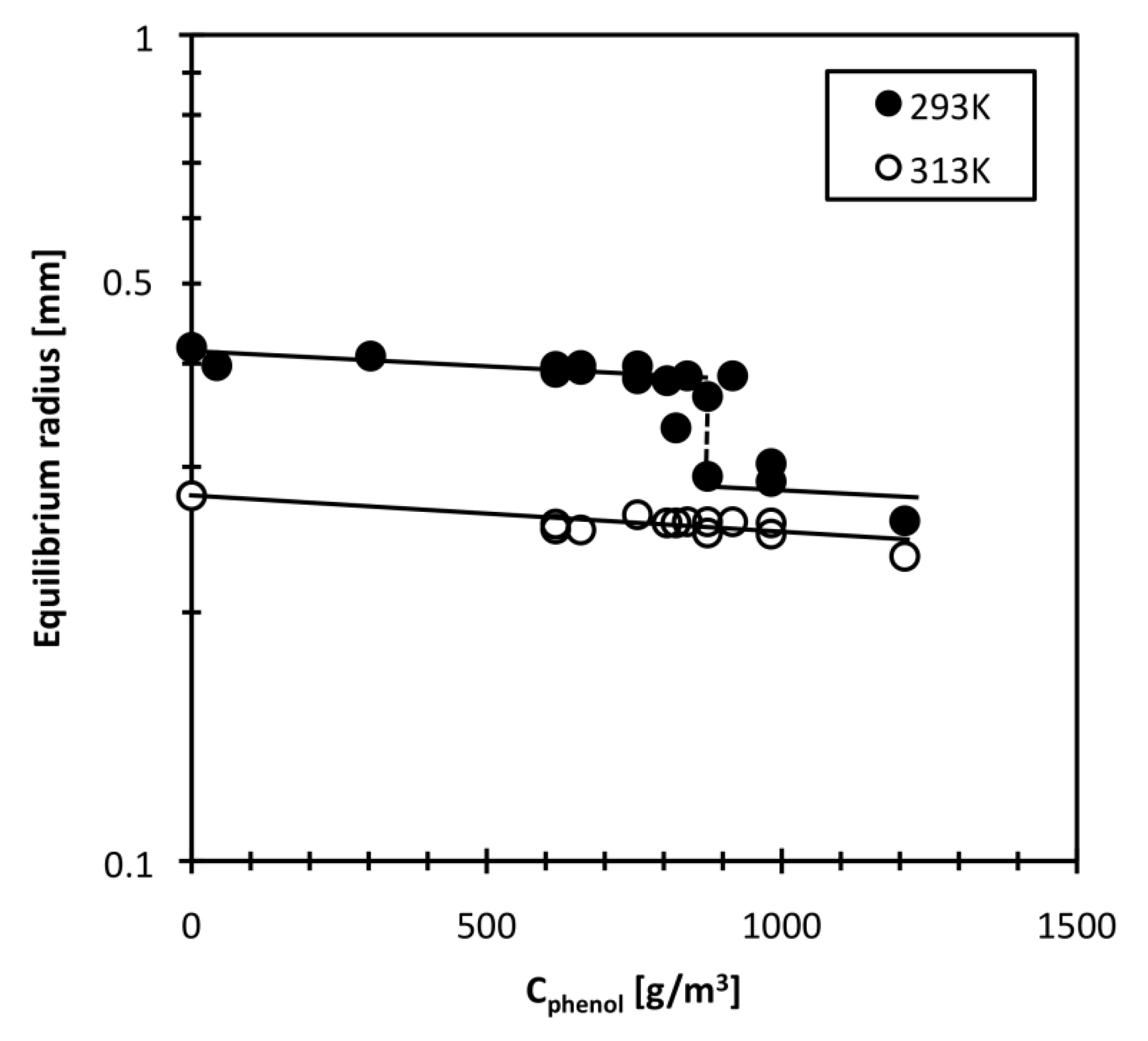
Figure 4 shows typical kinetic curves for the DEAA gel in phenol solution during the swelling process at 293 K. In phenol solution, the kinetic curve showed three distinct stages with different slopes. The entire kinetic curve in phenol solution, therefore, could not be fitted with Equation (1), although the kinetic curve data below 306 K corresponded approximately to the theoretical curve for swelling in water [21]. A linear approximation could be fitted to the later stages of the curve, 1–2 h after the start of swelling process (stage (C) in Figure 4). Both the phenol adsorption onto DEAA gel and desorption from the gel processes were almost finished within 2 h (data not shown). This time, range is very similar to the time of the change from stages (B) to (C) shown in Figure 4. The lack of fitting during the earlier stages suggests attributions of phenol adsorption-desorption process and subsequent polymer chain network relaxation during stages (A) and/or (B). The effect of hydrophobic pollution on hydrogel behavior changes with time.
Chemosensors 01 00021 g004 1024
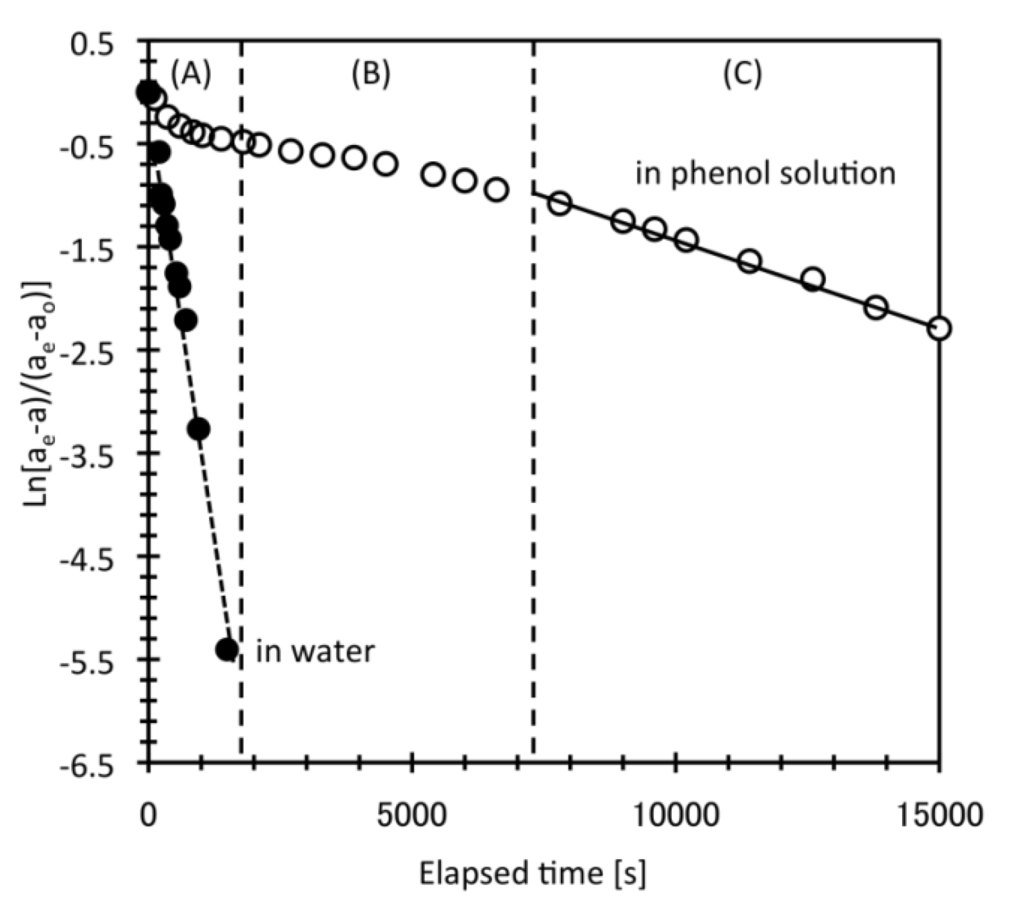
Figure 4. Typical kinetic curve of DEAA gel during swelling in phenol solution. Conditions: bulk phenol concentrations 755 g/m3; temperature swing from 313 K to 293 K.
Figure 4. Typical kinetic curve of DEAA gel during swelling in phenol solution. Conditions: bulk phenol concentrations 755 g/m3; temperature swing from 313 K to 293 K.
Chemosensors 01 00021 g004

3.2. Effect of Phenol Adsorption-Desorption Process on Swelling Behavior

If the temperature swings from 313 K to 293 K under an excess phenol concentration (that is, when the bulk phenol concentration is constant as indicated by arrow (a) in Figure 1), the amount of adsorbed phenol on the DEAA gel is reduced according to the adsorption isotherm. To elucidate the effect of the phenol adsorption-desorption process on swelling behavior, the temperature swing experiment was performed under conditions that the amount of adsorbed phenol is fixed. As indicated by arrow (b) in Figure 1, the bulk phenol concentration was simultaneously changed with temperature swing to keep the amount of adsorbed phenol constant, at qphenol = 42 g/kg of dry gel. The phenol concentration Cphenol was changed from 520 g/m3 at 313 K to 850 g/m3 at 293 K.
Figure 5 shows the radius change of a DEAA gel particle and kinetic curve for temperature swing from 313 K to 293 K under fixed qphenol condition. The data obtained with fixed bulk phenol concentration (Cphenol = 850 g/m3) were also plotted for comparison. The final DEAA gel radius under fixed qphenol condition finally reached same length as the radius obtained at phenol concentration of 850 g/m3 because the final amount of adsorbed phenol was the same for both fixed qphenol and fixed Cphenol conditions (Figure 5a). The initial amount of adsorbed phenol under fixed qphenol condition is lower than that under fixed Cphenol conditions as shown in Figure 1. During the initial stages, therefore, the DEAA gel radius under fixed qphenol condition was rapidly varied. The kinetic curve under fixed qphenol condition was a typical curve that could be described by the Tanaka and Fillmore theory [17,18], and consequently the linear approximation based on Equation (1) was successful (Figure 5b). This result implies that phenol was not eliminated from the DEAA gel and the polymer network decorated with fixed amount of adsorbed phenol apparently diffused. The slope of the approximately linear region obtained under fixed qphenol condition was very similar to the slope of the curve obtained under fixed Cphenol condition. This result is evidence that the polymer network decorated with fixed amount of phenol is undergoing collective diffusion in the later stage (C) of the curves obtained under fixed bulk phenol concentration and that the phenol adsorption-desorption process has finished before the start of stage (C). Phenol adsorption-desorption proceeds during the earlier stages of swelling, while the DEAA gel continues to swell after the phenol adsorption-desorption has reached a state of equilibrium. This is attributed to the slower kinetics of polymer network diffusion and relaxation compared with those of phenol adsorption.
The above results in phenol solution can be explained as follows. In the first stage (A), the volume change in the DEAA gel is extreme as a result of the sudden change in surrounding temperature. In the second stage (B), the volume change is suppressed by the adsorption-desorption of phenol molecules. After the phenol adsorption-desorption process and polymer network relaxation are almost complete, the DEAA polymer network decorated with phenol molecules [27,28] swells during the last stage (C). The apparent collective polymer diffusion constant obtained from the data in stage (C), therefore, can be regarded as the collective diffusion constant of the DEAA polymer network decorated with phenol molecules.
Chemosensors 01 00021 g005 1024
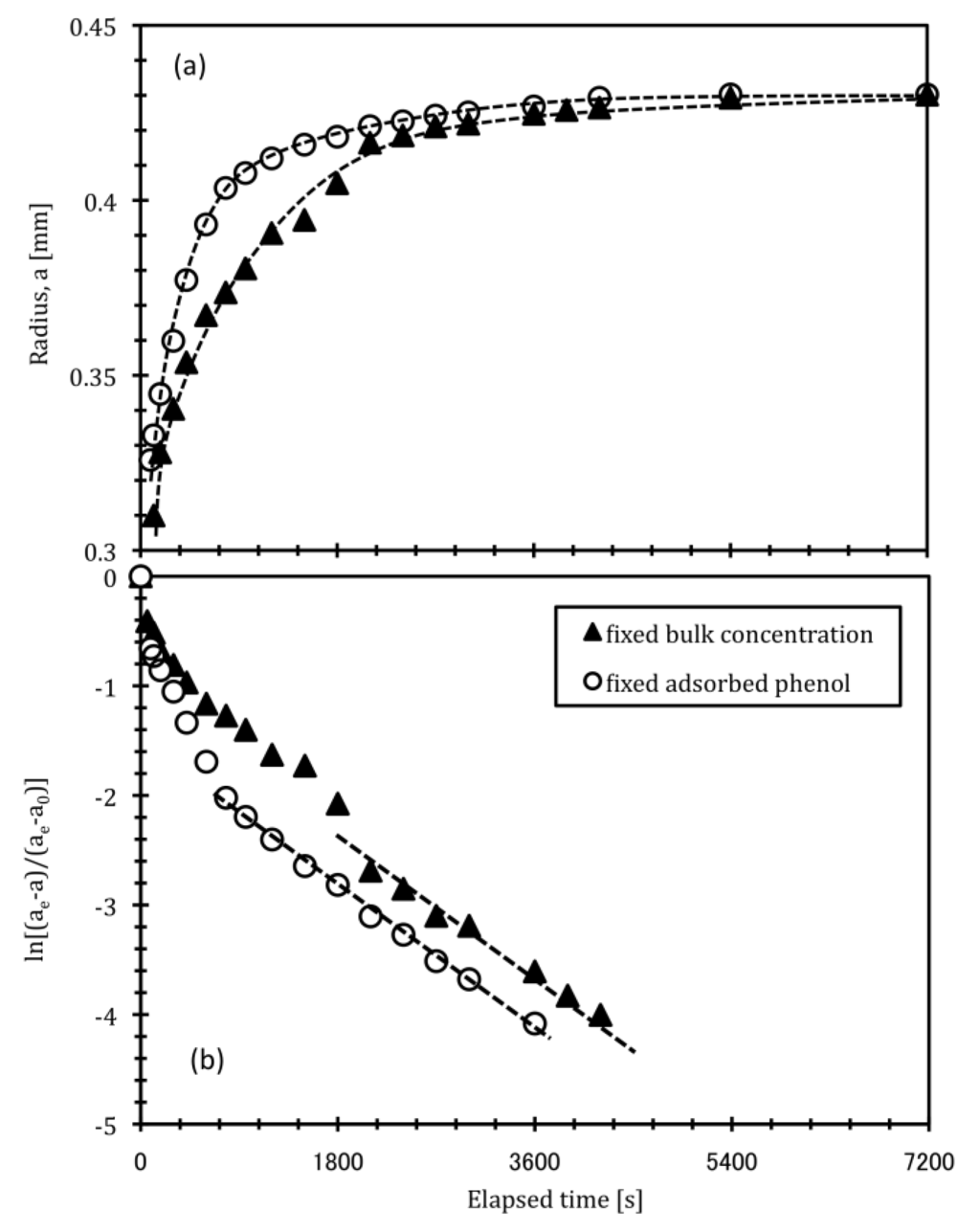
Figure 5. Comparison of kinetic curve for DEAA gel swelling process under two different types of conditions: fixed qphenol or fixed Cphenol. (a) Time-course of DEAA gel radius (b) Kinetic curve during swelling process. Conditions: bulk phenol concentration 850 g/m3; temperature swing from 313 K to 293 K.
Figure 5. Comparison of kinetic curve for DEAA gel swelling process under two different types of conditions: fixed qphenol or fixed Cphenol. (a) Time-course of DEAA gel radius (b) Kinetic curve during swelling process. Conditions: bulk phenol concentration 850 g/m3; temperature swing from 313 K to 293 K.
Chemosensors 01 00021 g005

3.3. Effect of Phenol Adsorption on Collective Polymer Diffusion Constant

By fitting the data in stage (C) to Equation (1), the apparent collective polymer chain diffusion constant was obtained. Figure 6 shows the ratio of collective polymer diffusion constant in phenol solution, D, to that in pure water, D0, as a function of bulk phenol concentration Cphenol. As shown and discussed in earlier sections, the phenol concentration changed the ae value of the DEAA gel discontinuously at the transition concentration Ctr, about 874 g/m3. The D value decreased strongly with increase in bulk phenol concentration up to Ctr (open circles). When the phenol concentration was higher than Ctr, the D value increased (closed circles). This behavior is quite similar to the “critical slowing down” of the D value with swelling temperature found for NIPA gel [19,29]. The volume phase transition of DEAA gel is continuous with temperature [21,25], but the volume changes discontinuously with phenol adsorption. Although the swing temperature is fixed, the amount of adsorbed phenol varies with phenol concentration, as shown in Figure 1. The behavior of the D value will be affected by the amount of adsorbed phenol and the phenol distribution in the DEAA gel particle.
Chemosensors 01 00021 g006 1024
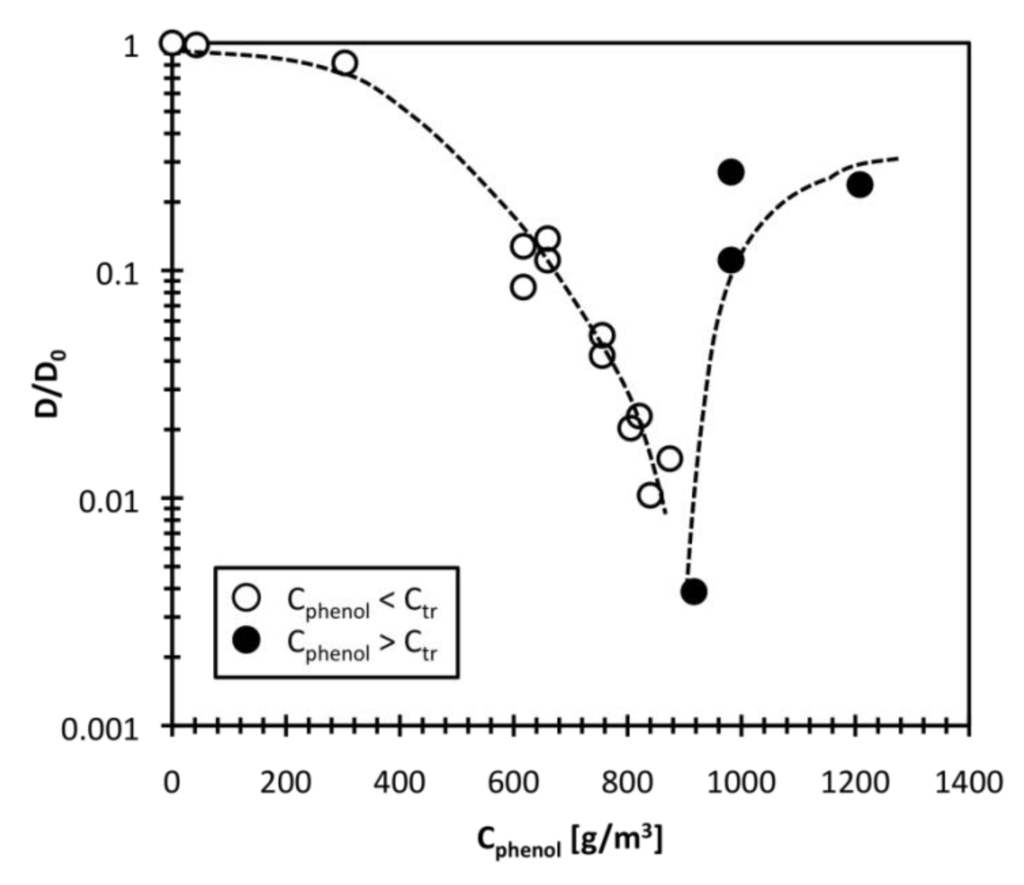
Figure 6. Relationship between collective diffusion constant and bulk phenol concentration.
Figure 6. Relationship between collective diffusion constant and bulk phenol concentration.
Chemosensors 01 00021 g006
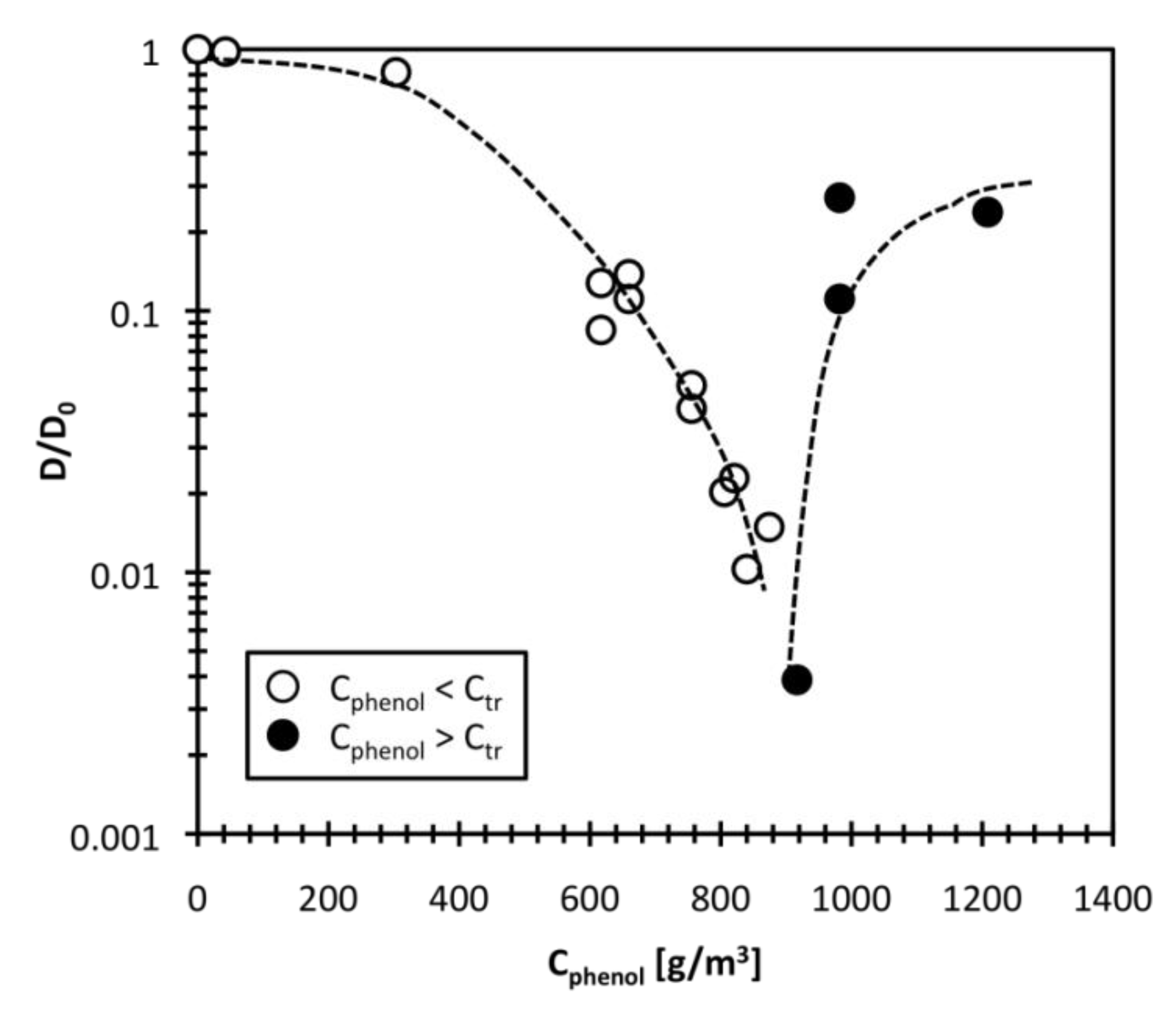
When considering the temperature dependence of the collective polymer diffusion constant, we can use the reduced temperature, E [29,30]:
Chemosensors 01 00021 i004
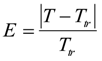where Ttr is the transition temperature. The D value is related to E by Equation (5):
Chemosensors 01 00021 i005
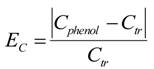
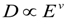where v is a fitted exponent. This equation is shown to be associated with the mesh size of polymer networks, friction coefficient f, and solution viscosity η [29]. Here, an analogous relation is defined using the bulk phenol concentration instead of temperature. The phenol concentration difference EC is analogous to the reduced temperature, E:
Chemosensors 01 00021 i006
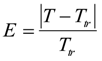
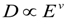
The phenol adsorption amount qphenol depends on the phenol concentration Cphenol from Equation (1).
Chemosensors 01 00021 i007
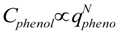
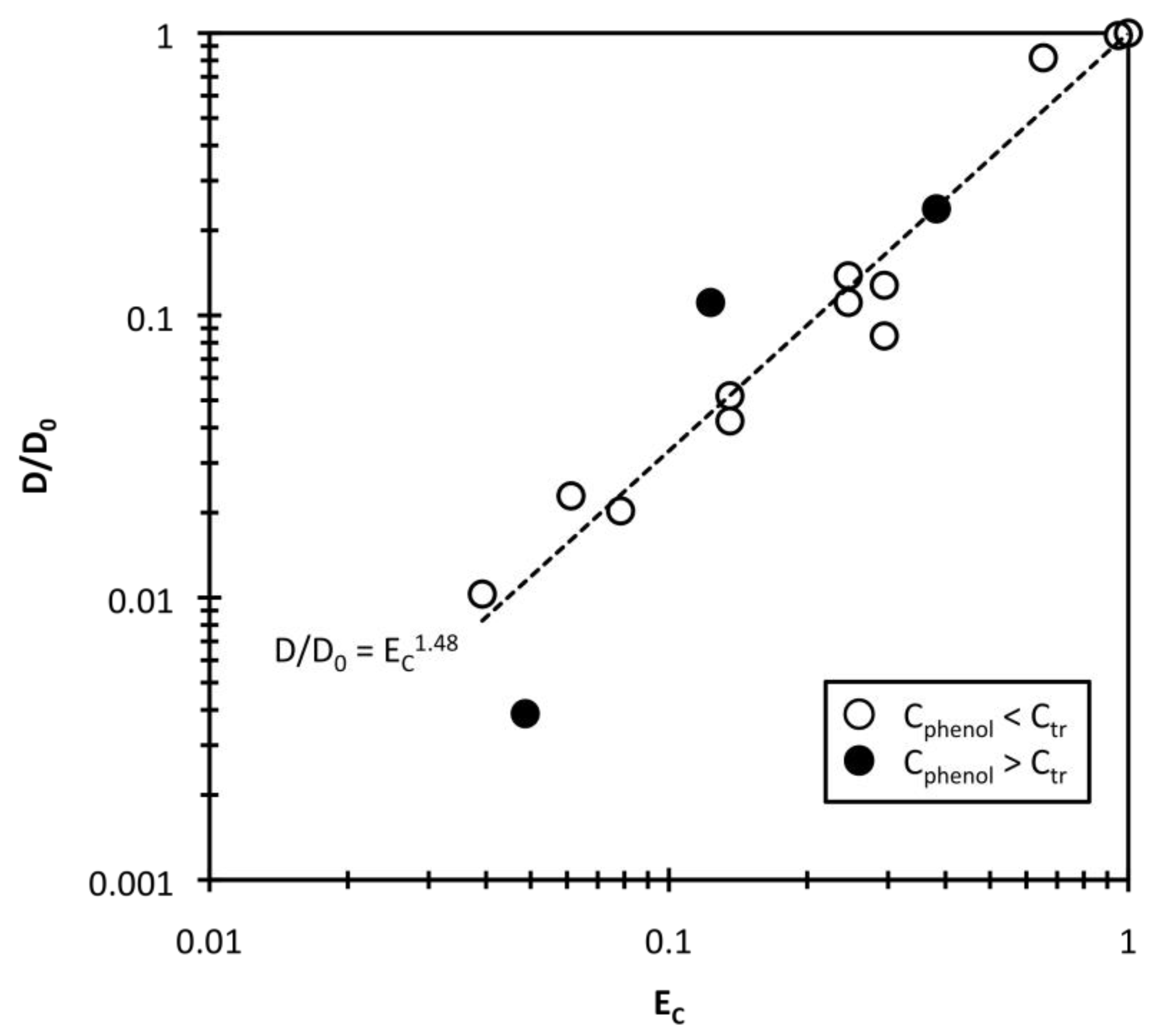
Therefore, the phenol concentration difference EC is also a function of qphenol. Assuming that Ctr = 874 g/m3, the diffusion constant ratio D/D0 was log-log plotted against EC in Figure 7. In principle, the D value may have to be normalized with the solution viscosity η to be able to examine the influence of mesh size, as shown in previous research [21]. In this study, the solution viscosity change with phenol concentration is negligible because the solution viscosity at low phenol concentrations (η) can be approximated as the water viscosity (η0) [27]. Therefore, the diffusion constant ratio D/D0 is equal to Dη/D0η0 and the effect of solution viscosity is eliminated. As shown in Figure 7, the D value depends strongly on EC, especially when Cphenol < Ctr (open circles). When Cphenol > Ctr, the D data may be scattered (closed circles) because the gel size change is very small and complicated. From the fitted curves, v = 1.48 for swelling. The collective polymer diffusion constant in phenol solution is correlated well with the phenol concentration difference based on the transition concentration, which indicates that the diffusion constant is mainly affected in phenol solution by the amount of adsorbed phenol and the mesh size of the polymer networks.
Chemosensors 01 00021 g007 1024
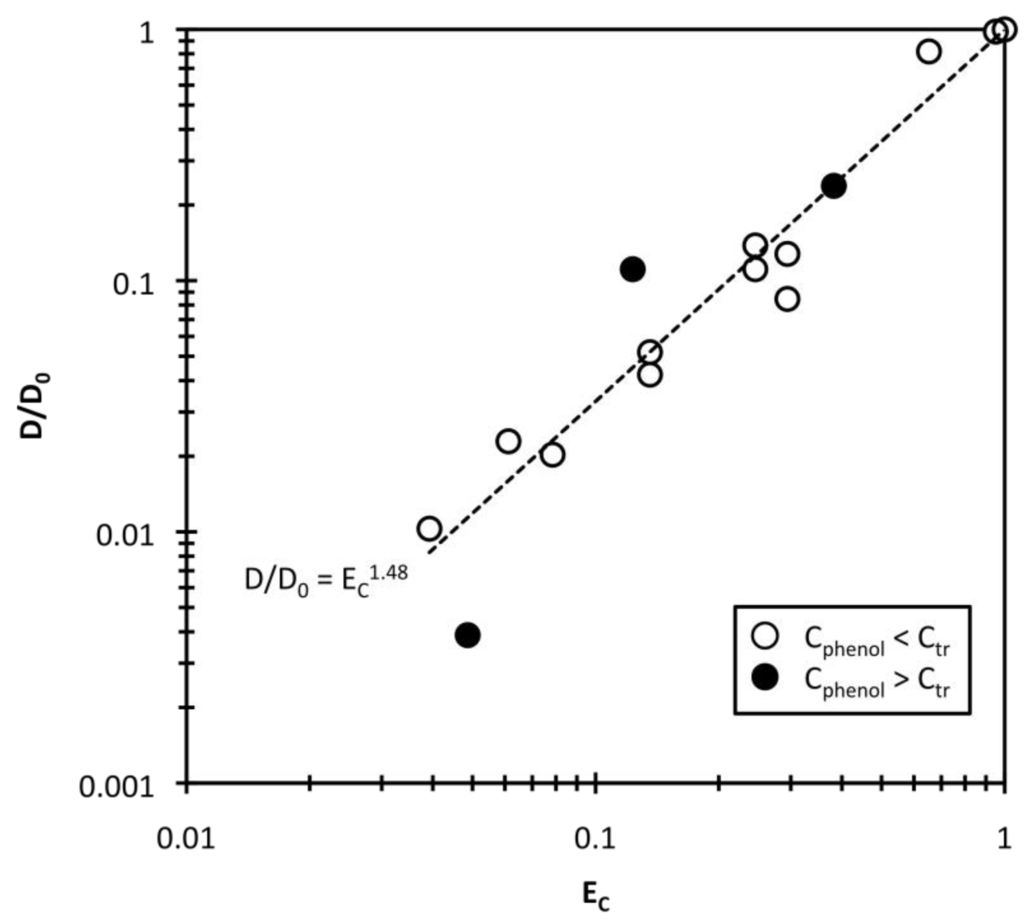
Figure 7. Effect of the reduced concentration EC on the collective diffusion constant.
Figure 7. Effect of the reduced concentration EC on the collective diffusion constant.
Chemosensors 01 00021 g007

4. Conclusions

We investigated the effect of hydrophobic pollution on hydrogel response in aqueous solution with use of N,N-diethylacrylamide gel as a hydrogel and phenol as a hydrophobic pollution. The equilibrium radius of DEAA gel in dilute phenol solution changed discontinuously at phenol concentration of about 874 g/m3. The collective polymer diffusion constant was dramatically decreased in the range of 874–916 g/m3, suggesting a “critical slowing down”. When comparing kinetic curves, we find that the slope of the approximately linear region obtained under conditions of fixed qphenol is very similar to the slope of the curve obtained under conditions of fixed Cphenol. During the latter stages of swelling, we found that a polymer network decorated with a constant amount of phenol exhibits collective diffusion. Phenol adsorption-desorption proceeds during the earlier stages of swelling, while the DEAA gel continues to swell after the phenol adsorption-desorption finished. 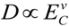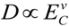Using the phenol concentration difference EC (analogous to the reduced temperature, E) we find that the D value depends strongly on EC, Chemosensors 01 00021 i008, and that the exponent v = 1.48. The correlation will be useful as estimation of hydrogel response reduction associated with hydrophobic pollution.

Acknowledgments

The authors are grateful to the Sasaki Environment Tech. Foundation, Japan, for supporting a part of this research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shin, J.; Braun, P.V.; Lee, W. Fast response photonic crystal pH sensor based on templated photo-polymerized hydrogel inverse opal. Sens. Actuators B 2010, 150, 183–190. [Google Scholar] [CrossRef]
  2. Lee, S.; Ibey, B.L.; Coté, G.L.; Pishko, M.V. Measurement of pH and dissolved oxygen within cell culture media using a hydrogel microarray sensor. Sens. Actuators B 2008, 128, 388–398. [Google Scholar] [CrossRef]
  3. Pi, S.; Ju, X.; Wu, H.; Xie, R.; Chu, L. Smart responsive microcapsules capable of recognizing heavy metal ions. J. Colloid Interface Sci. 2010, 349, 512–518. [Google Scholar] [CrossRef]
  4. Herber, S.; Olthuis, W.; Bergveld, P. A swelling hydrogel-based PCO2 sensor. Sens. Actuators B 2003, 91, 378–382. [Google Scholar] [CrossRef]
  5. Meskath, S.; Urban, G.; Heinzea, J. A new optochemical chlorine gas sensor based on the application of amphiphilic co-networks as matrices. Sens. Actuators B 2011, 151, 327–332. [Google Scholar] [CrossRef]
  6. Zguris, J.; Pishko, M.V. Nitric oxide sensitive fluorescent poly(ethylene glycol) hydrogel microstructures. Sens. Actuators B 2006, 115, 503–509. [Google Scholar] [CrossRef]
  7. Endo, T.; Yanagida, Y.; Hatsuzawa, T. Colorimetric detection of volatile organic compounds using a colloidal crystal-based chemical sensor for environmental applications. Sens. Actuators B 2007, 125, 589–595. [Google Scholar] [CrossRef]
  8. Yamagiwa, K.; Komi, T.; Kumakura, A.; Yokoyama, S.; Yoshida, M.; Ohkawa, A. Photo-crosslinked copolymer gel as an adsorbent for temperature-swing adsorption process. J. Chem. Eng. Jpn. 2004, 37, 1274–1278. [Google Scholar] [CrossRef]
  9. Yamagiwa, K.; Komi, T.; Yoshida, M.; Ohkawa, A.; Iida, T. Temperature-swing adsorption of nonionic surfactant with photo-crosslinked polymeric gel. J. Chem. Eng. Jpn. 2001, 34, 1171–1176. [Google Scholar] [CrossRef]
  10. Tokuyama, H.; Yanagawa, K.; Sakohara, S. Temperature swing adsorption of heavy metals on novel phosphate-type adsorbents using thermosensitive gels and/or polymers. Sep. Purif. Technol. 2006, 50, 8–14. [Google Scholar] [CrossRef]
  11. Tokuyama, H.; Kanehara, A. Temperature swing adsorption of gold(III) ions on poly(N-isopropylacrylamide) gel. React. Funct. Polym. 2007, 67, 136–143. [Google Scholar] [CrossRef]
  12. Takeshita, K.; Matsumura, T.; Nakao, Y. Separation of americium(III) and europium(III) by thermal-swing extraction using thermosensitive polymer gel. Prog. Nucl. Energy 2008, 50, 466–469. [Google Scholar] [CrossRef]
  13. Huber, D.L.; Manginell, R.P.; Samara, M.A.; Kim, B.; Bunker, B.C. Programmed adsorption and release of proteins in a microfluidic device. Science 2003, 301, 352–354. [Google Scholar] [CrossRef]
  14. Klouda, L.; Mikos, A.G. Thermoresponsive hydrogels in biomedical applications. Eur. J. Pharm. Biopharm. 2008, 68, 34–45. [Google Scholar] [CrossRef]
  15. Sershen, S.; West, J. Implantable, polymeric systems for modulated drug delivery. Adv. Drug Deliv. Rev. 2002, 54, 1225–1235. [Google Scholar] [CrossRef]
  16. Tokuyama, H.; Kanazawa, R.; Sakohara, S. Equilibrium and kinetics for temperature swing adsorption of a target metal on molecular imprinted thermosensitive gel adsorbents. Sep. Purif. Technol. 2005, 44, 152–159. [Google Scholar] [CrossRef]
  17. Tanaka, T.; Fillmore, J. Kinetics of swelling of gels. J. Chem. Phys. 1979, 70, 1214–1218. [Google Scholar] [CrossRef]
  18. Li, Y.; Tanaka, T. Kinetics of swelling and shrinking of gels. J. Chem. Phys. 1990, 92, 1365–1371. [Google Scholar] [CrossRef]
  19. Sato Matsuo, E.; Tanaka, T. Kinetics of discontinuous volume-phase transition of gels. J. Chem. Phys. 1988, 89, 1695–1703. [Google Scholar] [CrossRef]
  20. Kosik, K.; Wilk, E.; Geissler, E.; Laszlo, K. Interaction of phenols with thermo-responsive hydrogels. Colloids Surf. A Physicochem. Eng. Aspects 2008, 319, 159–164. [Google Scholar] [CrossRef]
  21. Tajima, H.; Yoshida, Y.; Yamagiwa, K. Experimental study of swelling and shrinking kinetics of spherical poly (N,N-diethylacrylamide) gel with continuous phase transition. Polymer 2011, 52, 732–738. [Google Scholar] [CrossRef]
  22. Tajima, H.; Yoshida, Y.; Abiko, S.; Yamagiwa, K. Size adjustment of spherical temperature-sensitive hydrogel beads by liquid–liquid dispersion using a Kenics static mixer. Chem. Eng. J. 2010, 156, 479–486. [Google Scholar] [CrossRef]
  23. Idziak, I.; Avoce, D.; Lessaed, D.; Grabel, D.; Zhu, X.X. Thermosensitivity of aqueous solutions of poly(N,N-diethylacrylamide). Macromolecules 1999, 32, 1260–1263. [Google Scholar] [CrossRef]
  24. Kawashima, T.; Koga, S.; Annaka, M.; Sasaki, S. Roles of hydrophobic interaction in a volume transition of alkylacrylamide gel induced by the hydrogen-bond-driving alkylphenol binding. J. Phys. Chem. B 2005, 109, 1055–1062. [Google Scholar] [CrossRef]
  25. Koga, S.; Kawashima, T.; Sasaki, S. Elastic relaxation of collapsed poly(alkylacrylamide) gels and their complexes with phenol. J. Phys. Chem. B 2004, 108, 10838–10844. [Google Scholar] [CrossRef]
  26. Suzuki, Y.; Suzuki, N.; Takasu, Y.; Nishio, I. A study on the structure of water in an aqueous solution by the solvent effect on a volume phase transition of N-isopropylacrylamide gel and low-frequency Raman spectropy. J. Chem. Phys. 1997, 107, 5890–5897. [Google Scholar] [CrossRef]
  27. Laszio, K.; Kosik, K.; Rochas, C.; Geissler, E. Phase transition in Poly (N-isopropylacrylamide) hydrogels induced by phenols. Macromolecules 2003, 36, 7771–7776. [Google Scholar] [CrossRef]
  28. Kosik, K.; Geissler, E.; Zrinyi, M.; Laszlo, K. Interaction of non-ionic hydrogels with small aromatic molecules. Polym. Adv. Technol. 2003, 14, 771–775. [Google Scholar] [CrossRef]
  29. Takahashi, K.; Takigawa, T.; Masuda, T. Swelling and deswelling kinetics of poly(N-isopropylacrylamide) gels. J. Chem. Phys. 2004, 120, 2972–2979. [Google Scholar] [CrossRef] [Green Version]
  30. Tokita, M.; Tanaka, T. Reversible decrease of gel-solvemt friction. Science 1991, 253, 1121–1123. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Tajima, H.; Sato, F.; Yamagiwa, K. Effect of Hydrophobic Pollution on Response of Thermo-Sensitive Hydrogel. Chemosensors 2013, 1, 21-32. https://doi.org/10.3390/chemosensors1030021

AMA Style

Tajima H, Sato F, Yamagiwa K. Effect of Hydrophobic Pollution on Response of Thermo-Sensitive Hydrogel. Chemosensors. 2013; 1(3):21-32. https://doi.org/10.3390/chemosensors1030021

Chicago/Turabian Style

Tajima, Hideo, Fumiaki Sato, and Kazuaki Yamagiwa. 2013. "Effect of Hydrophobic Pollution on Response of Thermo-Sensitive Hydrogel" Chemosensors 1, no. 3: 21-32. https://doi.org/10.3390/chemosensors1030021

APA Style

Tajima, H., Sato, F., & Yamagiwa, K. (2013). Effect of Hydrophobic Pollution on Response of Thermo-Sensitive Hydrogel. Chemosensors, 1(3), 21-32. https://doi.org/10.3390/chemosensors1030021

Article Metrics

Back to TopTop