Prioritization of Medical Errors in Patient Safety Management: Framework Using Interval-Valued Intuitionistic Fuzzy Sets
Abstract
1. Introduction
1.1. Definition of Medical Error
1.2. Current State of the System in Turkey
1.3. Aim of the Study
2. Patient Safety Management Methodologies
- Move Your Dot: In 2003, the Institute of Healthcare Improvement (IHI) in the USA [42] generated this model for safety management in hospitals, in which mortality rates are measured and evaluated, with the aim of reducing them. In this method, mortality rates, which are standardized based on several variables, are used to improve care by comparing hospitals with each other and the national average. After standardized mortality rates are calculated, mortality rates in determined hospitals can be measured and improvements can be planned to reduce them.
- Bow-tie model: A systematic model is generated, in which risks, preventive barriers, and recovery barriers of processes are detailed as a whole picture [45]. In the model, risk factors, preventive barriers, and recovery barriers are integrated. The route of an incident can be tracked, from the beginning to the consequences, by presenting the failures in preventive and recovery barriers [46].
- Health failure mode and effect analysis (H), FMEA: FMEA is a simple and widely used methodology, which basically prioritizes risks based on a calculated risk number. The main reason for the method’s extensive use is the simple structure of the method, which is focused on preventing deficiencies and improving safety [47,48].
- Root cause analysis (RCA): This method is generally used to evaluate an incident using two basic questions: “what happened?” and “why did it happen?” The main aim is to prevent the occurrence of similar accidents in the future by learning from the experience [49].
- Preventive and Recovery Information System for Monitoring and Analysis (PRISMA): The model is focused on processes, rather than individuals. A casual tree, which is a visual presentation of the related error and all of the information about it, is used as a starting point to classify basic causes. Then, the findings are translated into preventive measures [50].
- Benchmarking can be used to measure and compare the quality and safety of care. After the indicators are determined, the healthcare institution can make an assessment of its processes and take action accordingly. However, the main problem in benchmarking is the comparison of different populations. In these cases, external accountability is dangerous [51]. La Fata et al. [52] used benchmarking to compare the service performance of hospitals under a fuzzy evaluation environment and generated a hybrid decision-making model.
- Bundles, which is defined as a set of precautions, which are used collectively. Smorenburg [53] stated that caregivers generally tend to use simple bundles of care processes to make changes. The application of the bundle will be a successful and effective method in reaching a set of objectives. However, a limited number of interventions can be used to create bundles.
- Rapid response teams are used to improve communication between several care providers as supporting functions. Studies show that rapid response teams can be called if a nurse or doctor suspects that a patient is at risk. However, the critical issue is that the original care providers must continue to be involved [54].
- The time-out procedure is a simple check with a standardized questionnaire to ensure that the right operation is being performed. The Joint Commission in the USA included time-out procedures in operating rooms as accreditation criteria. Roos [55] stated that time-out procedures should be used to ensure that all checkpoints are summarized and checked with the entire team before surgery.
- Harten et al. [56] stated that there should be risk analysis, preventive measures, and evaluation processes to prevent risks, as well as controlling mechanisms, in safety management systems. In their study, the minimum requirements of a safety management system include: (i) pro-active periodic risk inventory, (ii) incident and complication reporting, (iii) systematic and structured approach for improvements, and (iv) strategic and operational activities.
3. Materials and Methods
3.1. Preliminaries
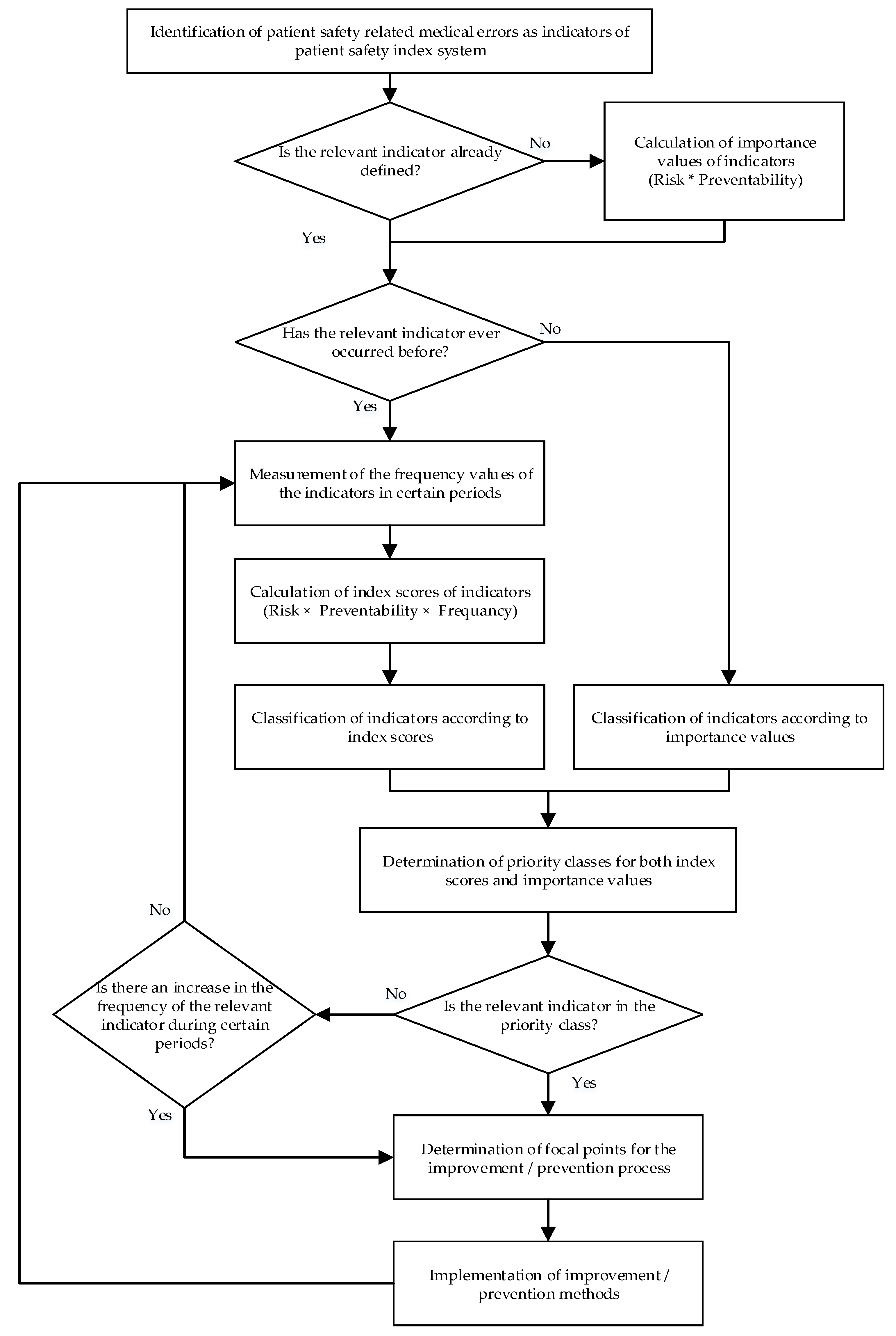
3.2. Steps of the Proposed Model
3.2.1. Step 1: Analyze the Actual Problem and Determine the Set of Attributes
3.2.2. Step 2: Collection of Opinions of Decision-Makers
3.2.3. Step 3: Aggregation of Opinions of Decision-Makers
4. Results
4.1. Calculation of Index Scores
4.2. Calculation of Importance Scores
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yucesan, M.; Gul, M. Hospital Service Quality Evaluation: An Integrated Model Based on Pythagorean Fuzzy AHP and Fuzzy TOPSIS. Soft Comput. 2020, 24, 3237–3255. [Google Scholar] [CrossRef]
- Simpson, D.; Hamilton, S.; McSherry, R.; McIntosh, R. Measuring and Assessing Healthcare Organisational Culture in the England’s National Health Service: A Snapshot of Current Tools and Tool Use. Healthcare 2019, 7, 127. [Google Scholar] [CrossRef] [PubMed]
- Tuzkaya, G.; Sennaroglu, B.; Kalender, Z.T.; Mutlu, M. Hospital Service Quality Evaluation with IVIF-PROMETHEE and a Case Study. Socio Econ. Plan. Sci. 2019, 68, 100705. [Google Scholar] [CrossRef]
- Chassin, M.R.; Galvin, R.W.; Donaldson, M.S. The Urgent Need to Improve Health Care Quality: Institute of Medicine National Roundtable on Health Care Quality. J. Am. Med. Assoc. 1998, 280, 1000–1005. [Google Scholar] [CrossRef]
- Kohn, L.T.; Corrigan, J.M.; Donaldson, M.S. To Err Is Human. Building a Safer Health System, Volume 6; National Academies Press: Washington, DC, USA, 1999; Volume 2. [Google Scholar] [CrossRef]
- Institute of Medicine. Shaping the Future. Crossing the Quality Chasm: A New Health System for the 21th Century; National Academies Press: Washington, DC, USA, 2001. [Google Scholar] [CrossRef]
- Donaldson, L. An Organisation with a Memory. Clin. Med. 2002, 2, 452–457. [Google Scholar] [CrossRef]
- Carinci, F.; Van Gool, K.; Mainz, J.; Veillard, J.; Pichora, E.C.; Januel, J.M.; Arispe, I.; Kim, S.M.; Klazinga, N.S. Towards Actionable International Comparisons of Health System Performance: Expert Revision of the OECD Framework and Quality Indicators. Korea Int. J. Qual. Health Care 2015, 27, 137–146. [Google Scholar] [CrossRef] [PubMed]
- Stelfox, H.T.; Palmisani, S.; Scurlock, C.; Orav, E.J.; Bates, D.W. The ‘To Err Is Human’ Report and the Patient Safety Literature. Qual. Saf. Health Care 2006, 15, 174–178. [Google Scholar] [CrossRef] [PubMed]
- OCDE. Measuring Patient Safety: Opening the Black Box; OECD Publishing: Paris, France, 2018. [Google Scholar]
- Makary, M.A.; Daniel, M. Medical Error-the Third Leading Cause of Death in the US. BMJ 2016, 353, i2139. [Google Scholar] [CrossRef] [PubMed]
- Donaldson, L.J.; Kelley, E.T.; Dhingra-Kumar, N.; Kieny, M.P.; Sheikh, A. Medication Without Harm: WHO’s Third Global Patient Safety Challenge. Lancet 2017, 389, 1680–1681. [Google Scholar] [CrossRef]
- NSQHS. Australian Commission on Safety and Quality in Health Care: NSQHS Standards; NSQHS: Sydney, Australia, 2017. [Google Scholar]
- National Health Service. Learning from Patient Safety Incidents|NHS Improvement; NHS Improvement: London, UK, 2020. [Google Scholar]
- Canadian Patient Safety Institute. Canadian Disclosure Guidelines: Being Open and Honest with Patients and Families; Canadian Patient Safety Institute: Edmonton, AB, Canada, 2011. [Google Scholar]
- Slawomirski, L.; Auraaen, A.; Klazinga, N. The Economics of Patient Safety Strengthening a Value-Based Approach to Reducing Patient Harm at National Level; OECD Publishing: Paris, France, 2017. [Google Scholar]
- Xu, K.; Soucat, A.; Kutzin, J.; Siroka, A.; Garcia, M.A.; Dupuy, J.; Eigo, N.; Li, D.; Indikadahena, C.; Touré, H.; et al. Global Spending on Health: A World in Transition. Available online: http://apps.who.int/bookorders (accessed on 10 July 2020).
- Van Geest, J.B.; Cummins, D.S. An Educational Needs Assessment for Improving Patient Safety. Natl. Patient Saf. Found. White Pap. Rep. 2003, 3, 1–28. [Google Scholar]
- National Patient Safety Foundation at the AMA (NPSF). Free from Harm Accelerating Patient Safety Improvement Fifteen Years after To Err Is Human Report of an Expert Panel Convened by The National Patient Safety Foundation; IHI: Boston, MA, USA, 2015. [Google Scholar]
- Blendon, R.J.; DesRoches, C.M.; Brodie, M.; Benson, J.M.; Rosen, A.B.; Schneider, E.; Altman, D.E.; Zapert, K.; Herrmann, M.J.; Steffenson, A.E. Views of Practicing Physicians and the Public on Medical Errors. N. Engl. J. Med. 2002, 347, 1933–1940. [Google Scholar] [CrossRef] [PubMed]
- Schoen, C.; Osborn, R.; Huynh, P.T.; Doty, M.; Zapert, K.; Peugh, J.; Davis, K. Taking the Pulse of Health Care Systems: Experiences of Patients with Health Problems in Six Countries. Health Aff. (Millwood) 2005, 24 (Suppl. S1), W5-509-25. [Google Scholar] [CrossRef] [PubMed]
- King, H.B.; Battles, J.; Baker, D.P.; Alonso, A.; Salas, E.; Webster, J.; Toomey, L.; Salisbury, M. TeamSTEPPSTM: Team Strategies and Tools to Enhance Performance and Patient Safety; Agency for Healthcare Research and Quality: Rockville, MD, USA, 2008. [Google Scholar]
- Carayon, P.; Schoofs Hundt, A.; Karsh, B.T.; Gurses, A.P.; Alvarado, C.J.; Smith, M.; Brennan, P.F. Work System Design for Patient Safety: The SEIPS Model. Qual. Saf. Health Care 2006, 15, i50–i58. [Google Scholar] [CrossRef] [PubMed]
- Dhamanti, I.; Leggat, S.G.; Barraclough, S. The Role of Governments in the Implementation of Patient Safety and Patient Safety Incident Reporting in Indonesia: A Qualitative Study. Healthcare 2019, 7, 64. [Google Scholar] [CrossRef]
- Wolf, Z.R.; Hughes, R.G. Error Reporting and Disclosure; Agency for Healthcare Research and Quality (US): Rockville, MD, USA, 2008.
- Ministry of Health Turkey. Safety Reporting System 2016 Statistics and Analysis Report; Ministry of Health Turkey: Ankara, Turkey, 2016.
- Ministry of Health Turkey. Başbakanlık Mevzuatı Geliştirme ve Yayın Genel Müdürlüğü. Available online: https://www.resmigazete.gov.tr/eskiler/2011/04/20110406-3.htm (accessed on 12 July 2020).
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Intuitionistic Fuzzy Sets in Some Medical Applications. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2001; Volume 2206 LNCS, pp. 148–151. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. A Similarity Measure for Intuitionistic Fuzzy Sets and Its Application in Supporting Medical Diagnostic Reasoning. In Lecture Notes in Artificial Intelligence (Subseries of Lecture Notes in Computer Science); Springer: Berlin/Heidelberg, Germany, 2004; Volume 3070, pp. 388–393. [Google Scholar] [CrossRef]
- Atanassov, K.; Pasi, G.; Yager, R. Intuitionistic Fuzzy Interpretations of Multi-Criteria Multi-Person and Multi-Measurement Tool Decision Making. Int. J. Syst. Sci. 2005, 36, 859–868. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. An Intuitionistic Fuzzy Set Based Approach to Intelligent Data Analysis: An Application to Medical Diagnosis; Physica: Heidelberg, Germany, 2003; pp. 57–70. [Google Scholar] [CrossRef]
- Xu, Z. Some Similarity Measures of Intuitionistic Fuzzy Sets and Their Applications to Multiple Attribute Decision Making. Fuzzy Optim. Decis. Mak. 2007, 6, 109–121. [Google Scholar] [CrossRef]
- Li, Y.; Olson, D.L.; Qin, Z. Similarity Measures between Intuitionistic Fuzzy (Vague) Sets: A Comparative Analysis. Pattern Recognit. Lett. 2007, 28, 278–285. [Google Scholar] [CrossRef]
- Dengfeng, L.; Chuntian, C. New Similarity Measures of Intuitionistic Fuzzy Sets and Application to Pattern Recognitions. Pattern Recognit. Lett. 2002, 23, 221–225. [Google Scholar] [CrossRef]
- Wang, W.; Xin, X. Distance Measure between Intuitionistic Fuzzy Sets. Pattern Recognit. Lett. 2005, 26, 2063–2069. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Wang, Y.; Ma, P.; Su, X. Multiattribute Decision Making Based on Entropy under Interval-Valued Intuitionistic Fuzzy Environment. Math. Probl. Eng. 2013, 2013, 526871. [Google Scholar] [CrossRef]
- Mukherjee, A.; Sarkar, S. Similarity Measures for Interval-Valued Intuitionistic Fuzzy Soft Sets and Its Application in Medical Diagnosis Problem. New Trends Math. Sci. 2014, 2, 159–165. [Google Scholar]
- Mukherjee, A.; Sarkar, S. Distance Based Similarity Measures for Interval-Valued Intuitionistic Fuzzy Soft Sets and Its Application. New Trends Math. Sci. 2015, 3, 34–42. [Google Scholar]
- Reason, J. Human Error: Models and Management. BMJ Clin. Res. 2000, 320, 768–770. [Google Scholar] [CrossRef]
- EC/DG SANCO Sponsored Safety IMprovement for PATients In Europe Project Findings, Lessons and Future. Available online: https://ec.europa.eu/health/archive/ph_systems/docs/%20ev_20071122_co04_en.pdf (accessed on 10 September 2019).
- Institute for Healthcare Improvement. Move Your Dot—Measuring, Evaluating, and Reducing Hospital Mortality Rates; IHI: Boston, MA, USA, 2003. [Google Scholar]
- Classen, D.C.; Lloyd, R.C.; Provost, L.; Griffin, F.A.; Resar, R. Development and Evaluation of the Institute for Healthcare Improvement Global Trigger Tool. J. Patient Saf. 2008, 4, 169–177. [Google Scholar] [CrossRef]
- Adler, L.; Denham, C.R.; McKeever, M.; Purinton, R.; Guilloteau, F.; Moorhead, J.D.; Resar, R. Global Trigger Tool. J. Patient Saf. 2008, 4, 245–249. [Google Scholar] [CrossRef]
- Abdi, Z.; Ravaghi, H.; Abbasi, M.; Delgoshaei, B.; Esfandiari, S. Application of Bow-Tie Methodology to Improve Patient Safety. Int. J. Health Care Qual. Assur. 2016, 29, 425–440. [Google Scholar] [CrossRef]
- Moran, J.W.; Armbruster, S. Bow Tie Diagram. 2016. Available online: http://www.phf.org/resourcestools/Documents/Bow_Tie_Diagram.pdf (accessed on 22 July 2020).
- De Rosier, J.; Stalhandske, E.; Bagian, J.P.; Nudell, T. Using Health Care Failure Mode and Effect Analysis: The VA National Center for Patient Safety’s Prospective Risk Analysis System. Jt. Comm. J. Qual. Improv. 2002, 28, 248–267. [Google Scholar] [CrossRef]
- Institute for Healthcare Improvement. QI Essentials Toolkit: Failure Modes and Effects Analysis; IHI: Boston, MA, USA, 2017. [Google Scholar] [CrossRef]
- National Patient Safety Foundation. RCA2 Improving Root Cause Analyses and Actions to Prevent Harm; National Patient Safety Foundation: Boston, MA, USA, 2015; p. 51. [Google Scholar]
- Reijnders-Thijssen, P.M.J. 21 Prisma: Instrument Voor Reactieve Analyse van Meldingen. In Praktijkboek Patiëntveiligheid; Bohn Stafleu van Loghum: Houten, The Netherlands, 2006; pp. 261–267. [Google Scholar] [CrossRef]
- Storms, F. 22 Benchmark/Vergelijking Indicatoren: Instrument Voor Meten En Vergelijken van Kwaliteit En Veiligheid van Zorg. In Praktijkboek Patiëntveiligheid; Bohn Stafleu van Loghum: Houten, The Netherlands, 2006; pp. 269–274. [Google Scholar] [CrossRef]
- La Fata, C.M.; Lupo, T.; Piazza, T. Service Quality Benchmarking via a Novel Approach Based on Fuzzy ELECTRE III and IPA: An Empirical Case Involving the Italian Public Healthcare Context. Health Care Manag. Sci. 2019, 22, 106–120. [Google Scholar] [CrossRef]
- Smorenburg, S.M. 27 Bundels. In Praktijkboek Patiëntveiligheid; Bohn Stafleu van Loghum: Houten, The Netherlands, 2006; pp. 295–299. [Google Scholar] [CrossRef]
- Salm, E.F. 29 Rapid Response Teams. In Praktijkboek Patiëntveiligheid; Bohn Stafleu van Loghum: Houten, The Netherlands, 2006; pp. 307–310. [Google Scholar] [CrossRef]
- Roos, W.D.M.H. 30 Time-Outprocedure. In Praktijkboek Patiëntveiligheid; Bohn Stafleu van Loghum: Houten, The Netherlands, 2006; pp. 311–313. [Google Scholar] [CrossRef]
- Van Harten, W.H.; Schellekens, W.M.L.C.M.; Kievit, J.; Smorenburg, S.M. 6 Het Veiligheidsmanagementsysteem: De Aanpak Op Organisatieniveau. In Praktijkboek Patiëntveiligheid; Bohn Stafleu van Loghum: Houten, The Netherlands, 2006; pp. 75–85. [Google Scholar] [CrossRef]
- Maheswaran, K.; Loganathan, T. A Novel Approach for Prioritization of Failure Modes in FMEA Using MCDM. Int. J. Eng. Res. Appl. 2013, 3, 733–739. [Google Scholar]
- Su, C.T.; Chou, C.J. A Systematic Methodology for the Creation of Six Sigma Projects: A Case Study of Semiconductor Foundry. Expert Syst. Appl. 2008, 34, 2693–2703. [Google Scholar] [CrossRef]
- Luo, C.M.; Chang, H.F. Safety Process Innovation in Medical Service Industry. Qual. Quant. 2013, 47, 2915–2931. [Google Scholar] [CrossRef]
- Chang, K.H.; Chang, Y.C.; Lai, P.T. Applying the Concept of Exponential Approach to Enhance the Assessment Capability of FMEA. J. Intell. Manuf. 2014, 25, 1413–1427. [Google Scholar] [CrossRef]
- Chen, S.H. Determining the Service Demands of an Aging Population by Integrating QFD and FMEA Method. Qual. Quant. 2016, 50, 283–298. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Ding, X.F.; Su, Q. Improving Risk Evaluation in FMEA with a Hybrid Multiple Criteria Decision Making Method. Int. J. Qual. Reliab. Manag. 2015, 32, 763–782. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Liu, H.C. New Approach for Failure Mode and Effect Analysis Using Linguistic Distribution Assessments and TODIM Method. Reliab. Eng. Syst. Saf. 2017, 167, 302–309. [Google Scholar] [CrossRef]
- Tofallis, C. Add or Multiply? A Tutorial on Ranking and Choosing with Multiple Criteria. INFORMS Trans. Educ. 2014, 14, 109–119. [Google Scholar] [CrossRef]
- Karasan, A.; Ilbahar, E.; Cebi, S.; Kahraman, C. A New Risk Assessment Approach: Safety and Critical Effect Analysis (SCEA) and Its Extension with Pythagorean Fuzzy Sets. Saf. Sci. 2018, 108, 173–187. [Google Scholar] [CrossRef]
- Toker, D.; Tozan, H.; Vayvay, O. A Decision Model for Pharmaceutical Marketing and a Case Study in Turkey. Ekon. Istraz. 2013, 26, 101–114. [Google Scholar] [CrossRef]
- Öztürk, N.; Tozan, H. A Fuzzy-Based Decision Support Model for Selecting the Best Dialyser Flux in Haemodialysis. J. Healthc. Eng. 2015, 6, 303–324. [Google Scholar] [CrossRef]
- Karatas, M.; Karacan, I.; Tozan, H. An Integrated Multi-Criteria Decision Making Methodology for Health Technology Assessment. Eur. J. Ind. Eng. 2018, 12, 504–534. [Google Scholar] [CrossRef]
- Öztürk, N.; Tozan, H.; Vayvay, Ö. A New Decision Model Approach for Health Technology Assessment and a Case Study for Dialysis Alternatives in Turkey. Int. J. Environ. Res. Public Health 2020, 17, 3608. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval Valued Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Ze-shui, X. Methods for Aggregating Interval-Valued Intuitionistic Fuzzy Information and Their Application to Decision Making. Control Decis. 2007, 22, 215–219. [Google Scholar]
- Oztaysi, B.; Onar, S.C.; Goztepe, K.; Kahraman, C. Evaluation of Research Proposals for Grant Funding Using Interval-Valued Intuitionistic Fuzzy Sets. Soft Comput. 2017, 21, 1203–1218. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria Fuzzy Decision-Making Method Based on a Novel Accuracy Function under Interval-Valued Intuitionistic Fuzzy Environment. Expert Syst. Appl. 2009, 36, 6899–6902. [Google Scholar] [CrossRef]
- Lakshmana Gomathi Nayagam, V.; Muralikrishnan, S.; Sivaraman, G. Multi-Criteria Decision-Making Method Based on Interval-Valued Intuitionistic Fuzzy Sets. Expert Syst. Appl. 2011, 38, 1464–1467. [Google Scholar] [CrossRef]
- Joshi, B.P.; Kharayat, P.S. Generalized Intuitionistic Fuzzy Einstein Weighted Averaging Aggregation Operator. In IEEE International Conference on Computer Communication and Control, IC4 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Garg, H. A New Generalized Improved Score Function of Interval-Valued Intuitionistic Fuzzy Sets and Applications in Expert Systems. Appl. Soft Comput. 2016, 38, 988–999. [Google Scholar] [CrossRef]
- Nguyen, H. A New Interval-Valued Knowledge Measure for Interval-Valued Intuitionistic Fuzzy Sets and Application in Decision Making. Expert Syst. Appl. 2016, 56, 143–155. [Google Scholar] [CrossRef]
- Zhai, Y.; Xu, Z.; Liao, H. Measures of Probabilistic Interval-Valued Intuitionistic Hesitant Fuzzy Sets and the Application in Reducing Excessive Medical Examinations. IEEE Trans. Fuzzy Syst. 2018, 26, 1651–1670. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, J. An Overview of Distance and Similarity Measures of Intuitionistic Fuzzy Sets. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2008, 16, 529–555. [Google Scholar] [CrossRef]
- Wu, C.; Luo, P.; Li, Y.; Ren, X. A New Similarity Measure of Interval-Valued Intuitionistic Fuzzy Sets Considering Its Hesitancy Degree and Applications in Expert Systems. Math. Probl. Eng. 2014, 2014, 1–16. [Google Scholar] [CrossRef]
- Wei, C.P.; Wang, P.; Zhang, Y.Z. Entropy, Similarity Measure of Interval-Valued Intuitionistic Fuzzy Sets and Their Applications. Inf. Sci. 2011, 181, 4273–4286. [Google Scholar] [CrossRef]
- Pang, Q.; Wang, H.; Xu, Z. Probabilistic Linguistic Term Sets in Multi-Attribute Group Decision Making. Inf. Sci. 2016, 369, 128–143. [Google Scholar] [CrossRef]
- Touwen, L.; Tervoort, M.A.; Van Dijk, H.; Orsini, M. 16 Move Your Dot: Het Verbeteren van Patiëntveiligheid. In Praktijkboek Patiëntveiligheid; Bohn Stafleu van Loghum: Houten, The Netherlands, 2006; pp. 219–236. [Google Scholar] [CrossRef]
- Paling, J. Strategies to Help Patients Understand Risks. BMJ 2003, 327, 745. [Google Scholar] [CrossRef] [PubMed]
- Onar, S.C.; Oztaysi, B.; Otay, I.; Kahraman, C. Multi-Expert Wind Energy Technology Selection Using Interval-Valued Intuitionistic Fuzzy Sets. Energy 2015, 90, 274–285. [Google Scholar] [CrossRef]
- Anderson, J.G.; Abrahamson, K. Your Health Care May Kill You: Medical Errors. In Studies in Health Technology and Informatics; IOS Press: Amsterdam, The Netherlands, 2017; Volume 234, pp. 13–17. [Google Scholar] [CrossRef]
- Pérez-Francisco, D.H.; Duarte-Clíments, G.; Del Rosario-Melián, J.M.; Gómez-Salgado, J.; Romero-Martín, M.; Sánchez-Gómez, M.B. Influence of Workload on Primary Care Nurses’ Health and Burnout, Patients’ Safety, and Quality of Care: Integrative Review. Healthcare 2020, 8, 12. [Google Scholar] [CrossRef]
- Marşap, A. Sağlık İşletmelerinde Kalite: Sağlıkta Kaliteşim Sistemi ve Sağlıkta Mükemmellikte Süreklilik; BETA Yayınları: Istanbul, Turkey, 2015. [Google Scholar]
- Global Health Care Sector Outlook: Making Progress Against Persistent Challenges. Available online: https://www2.deloitte.com/tr/en/pages/life-sciences-and-healthcare/articles/2017-global-health-care-sector-outlook.html (accessed on 4 March 2019).
- Stephanie Allen, P.; Hammett, D.R.; De Vettori, E.; Purdy, L.; Qun, Z.; Krolop, S.; Sehgal, C.; Wada, Y.; Van Bergen, M.; Suboh, A.; et al. 2019 Global Health Care Outlook Shaping the Future. Des. Issues 2019. [Google Scholar] [CrossRef]
| Methodology | Advantages | Disadvantages |
|---|---|---|
| Move your Dot | Detailed analysis (miscommunication, scheduling errors, adverse events, and non-response to a question are also evaluated). | Filling records is not a controlled process and requires improvements. Many problems can be encountered during the data collection phase. |
| Tracking errors in the system. | ||
| Inter-hospital variation can be tracked. | ||
| Trigger tool | Suitable for monitoring the number of adverse events (at the department level or a specific care level). | Screening and assessment take time, as assessment should ideally be made by two individuals independently and agreed upon. |
| Bow-tie model | Useful for analyzing the current safety management model. | Creating a complete model for each risk takes too much time and a number of sessions in which multidisciplinary focus is needed. Moreover, the success of the analysis highly depends on the motivation of the participants. Thus, it is too easy to set the wrong priorities. |
| Easy determination of root causes. | ||
| Health failure mode and effect analysis—(H)FMEA | Visible risks. | (H)FMEA takes too much time, as a minimum of four participants is needed. For this reason, the model is time-intensive. Time, resources, and space must be made available to implement the method properly. |
| Helps to take precautions before an incident takes place. | ||
| Root cause analysis (RCA) | Objective description | RCA is a time-consuming approach and not every employee is suitable to carry out the analysis. Moreover, the contributions of RCA to improving patient safety have not been scientifically presented. |
| Create recommendations to prevent the occurrence of similar errors. | ||
| Creates insight into the employees. | ||
| PRISMA | Detailed analysis with quantitative and qualitative insights. | In the model, after a casual tree and the classifications of the basic causes are made, a link with context variables for each basic cause should be created. If PRISMA is planned for use in comparing data between organizations, it is vital to design variables uniformly. |
| Visible conclusions. |
| Code | Definition |
|---|---|
| 1 | Easily Preventable (control charts etc.) |
| 2 | Can be preventable with small system improvements |
| 3 | Can be preventable with training |
| 4 | Can be preventable with radical improvements |
| 5 | Unpreventable but side effects can be preventable |
| 6 | Unpreventable |
| Code | Definition |
|---|---|
| LI | Grade 0: Without repercussion for the patient (near miss) |
| MLI | Grade 1: Adverse events contributed to temporary harm to the patient and intervention was needed |
| MI | Grade 2: Contributed to temporary harm to the patient, thereby resulting in longer admission being necessary |
| I | Grade 3: Contributed to or resulted in permanent harm to the patient |
| VI | Grade 4: Intervention was needed to keep the patient alive |
| EI | Grade 5: Contributed to the death of the patient |
| Linguistic Term (Code) | Membership Values | Non-Membership Values | |
|---|---|---|---|
| Preventability | Severity | ||
| 1 | EI | (0.65; 0.75) | (0.1; 0.25) |
| 2 | VI | (0.60; 0.70) | (0.15; 0.30) |
| 3 | I | (0.55; 0.65) | (0.20; 0.35) |
| 4 | MI | (0.50; 0.60) | (0.25; 0.40) |
| 5 | MLI | (0.45; 0.55) | (0.30; 0.45) |
| 6 | LI | (0.25; 0.40) | (0.50; 0.60) |
| Code | Definition |
|---|---|
| Rare | Less than 1 in 100,000,000 (probability of being x < 0.00000001) |
| Very Low | 1 in 100,000,000 (probability of being 0.00000001 < x < 0.0000001) |
| Low | 1 in 10,000,000 (probability of being 0.0000001 < x < 0.000001) |
| Medium-Low | 1 in 1,000,000 (probability of being 0.000001 < x < 0.0001) |
| Medium | 1 in 100,000 (probability of being 0.00001 < x < 0.0001) |
| Medium High | 1 in 10,000 (probability of being 0.0001 < x < 0.001) |
| High | 1 in 1,000 (probability of being 0.001 < x < 0.01) |
| Very High | 1 in 100 (probability of being 0.01 < x < 0.1) |
| Extremely High | 1 in 10 (probability of being 0.1 < x < 1) |
| Linguistic Term for Occurrence/Frequency | ||
|---|---|---|
| Rare | (0; 0.2) | (0.5; 0.8) |
| Very Low | (0.1; 0.3) | (0.4; 0.7) |
| Low | (0.2; 0.4) | (0.3; 0.6) |
| Medium-Low | (0.3; 0.5) | (0.2; 0.5) |
| Medium | (0.4; 0.6) | (0.2; 0.4) |
| Medium High | (0.5; 0.7) | (0.1; 0.3) |
| High | (0.6; 0.8) | (0; 0.2) |
| Very High | (0.7; 0.9) | (0; 0.1) |
| Extremely High | (0.8; 1) | (0; 0) |
| Error Type | Code | Error Name | ||
|---|---|---|---|---|
| Laboratory | L18 | Clotted sample | (0.472; 0.572) | (0.277; 0.428) |
| L17 | Sample with hemolysis | (0.485; 0.585) | (0.264; 0.415) | |
| L16 | Insufficient sample | (0.466; 0.570) | (0.281; 0.430) | |
| L05 | Wrong record | (0.432; 0.550) | (0.303; 0.450) | |
| L01 | Wrong test request | (0.415; 0.530) | (0.328; 0.470) | |
| Medication | I1g | Erroneous dosing | (0.537; 0.637) | (0.211; 0.363) |
| I1a | Wrong drug demand | (0.505; 0.605) | (0.244; 0.395) | |
| I0a | Inappropriate temperature and humidity | (0.410; 0.528) | (0.331; 0.472) | |
| I2b | Preparation of wrong drug | (0.538; 0.643) | (0.202; 0.357) | |
| I3c | Transferring wrong drug from pharmacy | (0.486; 0.590) | (0.259; 0.410) | |
| General/Surgical | di | Non-marking of operation area/side | (0.551; 0.651) | (0.197; 0.349) |
| kd | Unverified Patient ID, location of operation and surgical procedure | (0.529; 0.630) | (0.219; 0.370) | |
| gd | Not confirming removal of make-up, prosthesis and valuable items | (0.483; 0.585) | (0.264; 0.415) | |
| tr | The operation area has not been shaved | (0.491; 0.595) | (0.254; 0.406) | |
| ts | Health worker does not accompany patient transfer | (0.482; 0.582) | (0.267; 0.418) | |
| Patient Related | HRHc | Patient Falls | (0.596; 0.697) | (0.146; 0.303) |
| TKHg | Incorrect report of patient basic information | (0.531; 0.631) | (0.217; 0.369) | |
| TKHa | Incorrect identification of patients | (0.582; 0.684) | (0.157; 0.316) |
| Error Type | Code | Error Name | ||
|---|---|---|---|---|
| Laboratory | L18 | Clotted sample | (0.553; 0.654) | (0.193; 0.346) |
| L17 | Sample with hemolysis | (0.555; 0.656) | (0.190; 0.344) | |
| L16 | Insufficient sample | (0.586; 0.687) | (0.160; 0.313) | |
| L05 | Wrong record | (0.559; 0.660) | (0.188; 0.340) | |
| L01 | Wrong test request | (0.618; 0.718) | (0.130; 0.282) | |
| Medication | I1g | Erroneous dosing | (0.511; 0.619) | (0.227; 0.382) |
| I1a | Wrong drug demand | (0.533; 0.636) | (0.212; 0.364) | |
| I0a | Inappropriate temperature and humidity | (0.560; 0.700) | (0.147; 0.300) | |
| I2b | Preparation of wrong drug | (0.527; 0.631) | (0.217; 0.369) | |
| I3c | Transferring wrong drug from pharmacy | (0.566; 0.667) | (0.181; 0.333) | |
| General/Surgical | di | Non-marking of operation area/side | (0.554; 0.658) | (0.183; 0.342) |
| kd | Unverified Patient ID, location of operation and surgical procedure | (0.558; 0.663) | (0.180; 0.337) | |
| gd | Not confirming removal of make-up, prosthesis and valuable items | (0.576; 0.682) | (0.160; 0.318) | |
| tr | The operation area has not been shaved | (0.591; 0.696) | (0.146; 0.304) | |
| ts | Health worker does not accompany patient transfer | (0.572; 0.678) | (0.166; 0.322) | |
| Patient Related | HRHc | Patient Falls | (0.543; 0.645) | (0.199; 0.356) |
| TKHg | Incorrect report of patient basic information | (0.566; 0.671) | (0.175; 0.329) | |
| TKHa | Incorrect identification of patients | (0.547; 0.656) | (0.186; 0.344) |
| RPN | Ideal Case | Similarity | ||||
|---|---|---|---|---|---|---|
| Code | Score | Ranking | ||||
| L18 | (0.532; 0.657) | (0.179; 0.343) | (0; 0.446) | (0.323; 0.554) | 0.638 | 2 |
| L17 | (0.538; 0.663) | (0.172; 0.337) | (0; 0.451) | (0.318; 0.549) | 0.635 | 1 |
| L16 | (0.513; 0.642) | (0.193; 0.358) | (0; 0.453) | (0.315; 0.547) | 0.662 | 5 |
| L05 | (0.516; 0.649) | (0.189; 0.351) | (0; 0.441) | (0.331; 0.559) | 0.644 | 4 |
| L01 | (0.525; 0.658) | (0.181; 0.342) | (0; 0.447) | (0.325; 0.553) | 0.640 | 3 |
| I1g | (0.486; 0.620) | (0.213; 0.380) | (0; 0.457) | (0.310; 0.543) | 0.691 | 11 |
| I1a | (0.482; 0.614) | (0.221; 0.386) | (0; 0.452) | (0.317; 0.548) | 0.693 | 14 |
| I0a | (0.462; 0.601) | (0.237; 0.399) | (0; 0.443) | (0.331; 0.557) | 0.701 | 15 |
| I2b | (0.492; 0.627) | (0.206; 0.373) | (0; 0.461) | (0.304; 0.539) | 0.689 | 10 |
| I3c | (0.484; 0.618) | (0.217; 0.382) | (0; 0.455) | (0.313; 0.545) | 0.692 | 13 |
| di | (0.505; 0.639) | (0.193; 0.361) | (0; 0.470) | (0.292; 0.530) | 0.684 | 8 |
| kd | (0.498; 0.632) | (0.201; 0.368) | (0; 0.465) | (0.299; 0.535) | 0.686 | 9 |
| gd | (0.486; 0.620) | (0.213; 0.380) | (0; 0.456) | (0.310; 0.544) | 0.692 | 12 |
| tr | (0.455; 0.597) | (0.204; 0.403) | (0; 0.462) | (0.302; 0.538) | 0.719 | 17 |
| ts | (0.447; 0.587) | (0.216; 0.413) | (0; 0.455) | (0.312; 0.545) | 0.723 | 18 |
| HRHc | (0.517; 0.651) | (0.179; 0.349) | (0; 0.479) | (0.280; 0.521) | 0.679 | 6 |
| TKHg | (0.462; 0.604) | (0.198; 0.396) | (0; 0.468) | (0.297; 0.532) | 0.716 | 16 |
| TKHa | (0.513; 0.650) | (0.179; 0.350) | (0; 0.479) | (0.280; 0.521) | 0.680 | 7 |
| Code | Ranking Based on Index Score | Ranking Based on the Reported Number of Events |
|---|---|---|
| L18 | 2 | 1 |
| L17 | 1 | 2 |
| L16 | 5 | 5 |
| L05 | 4 | 4 |
| L01 | 3 | 3 |
| I1g | 11 | 7 |
| I1a | 14 | 9 |
| I0a | 15 | 12 |
| I2b | 10 | 10 |
| I3c | 13 | 14 |
| di | 8 | 6 |
| kd | 9 | 11 |
| gd | 12 | 13 |
| tr | 17 | 17 |
| ts | 18 | 18 |
| HRHc | 6 | 8 |
| TKHg | 16 | 16 |
| TKHa | 7 | 15 |
| Degree of Hesitancy | k1 = 0 | k1 = 0.25 | k1 = 0.50 | k1 = 0.75 | k1 = 1 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| k2 = 1 | k2 = 0.75 | k2 = 0.50 | k2 = 0.25 | k2 = 0 | ||||||
| Code | Score | Ranking | Score | Ranking | Score | Ranking | Score | Ranking | Score | Ranking |
| L18 | 0.559 | 15 | 0.591 | 15 | 0.623 | 15 | 0.655 | 15 | 0.687 | 15 |
| L17 | 0.567 | 14 | 0.600 | 14 | 0.632 | 14 | 0.665 | 14 | 0.698 | 14 |
| L16 | 0.570 | 12 | 0.603 | 12 | 0.636 | 12 | 0.669 | 12 | 0.702 | 12 |
| L05 | 0.543 | 18 | 0.575 | 18 | 0.607 | 18 | 0.639 | 18 | 0.670 | 18 |
| L01 | 0.555 | 16 | 0.587 | 16 | 0.620 | 16 | 0.652 | 16 | 0.684 | 16 |
| I1g | 0.576 | 9 | 0.610 | 9 | 0.644 | 9 | 0.678 | 9 | 0.711 | 9 |
| I1a | 0.569 | 13 | 0.601 | 13 | 0.634 | 13 | 0.667 | 13 | 0.700 | 13 |
| I0a | 0.546 | 17 | 0.578 | 17 | 0.610 | 17 | 0.641 | 17 | 0.673 | 17 |
| I2b | 0.585 | 7 | 0.619 | 7 | 0.654 | 7 | 0.688 | 7 | 0.723 | 7 |
| I3c | 0.573 | 11 | 0.606 | 11 | 0.640 | 11 | 0.673 | 11 | 0.706 | 11 |
| di | 0.603 | 3 | 0.639 | 3 | 0.674 | 3 | 0.710 | 3 | 0.745 | 3 |
| kd | 0.594 | 5 | 0.628 | 5 | 0.663 | 5 | 0.698 | 5 | 0.733 | 5 |
| gd | 0.576 | 8 | 0.610 | 8 | 0.644 | 8 | 0.678 | 8 | 0.712 | 8 |
| tr | 0.588 | 6 | 0.622 | 6 | 0.657 | 6 | 0.692 | 6 | 0.726 | 6 |
| ts | 0.573 | 10 | 0.607 | 10 | 0.640 | 10 | 0.674 | 10 | 0.707 | 10 |
| HRHc | 0.621 | 1 | 0.658 | 1 | 0.695 | 1 | 0.732 | 1 | 0.769 | 1 |
| TKHg | 0.598 | 4 | 0.633 | 4 | 0.668 | 4 | 0.703 | 4 | 0.738 | 4 |
| TKHa | 0.618 | 2 | 0.655 | 2 | 0.693 | 2 | 0.730 | 2 | 0.767 | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalender, Z.T.; Tozan, H.; Vayvay, O. Prioritization of Medical Errors in Patient Safety Management: Framework Using Interval-Valued Intuitionistic Fuzzy Sets. Healthcare 2020, 8, 265. https://doi.org/10.3390/healthcare8030265
Kalender ZT, Tozan H, Vayvay O. Prioritization of Medical Errors in Patient Safety Management: Framework Using Interval-Valued Intuitionistic Fuzzy Sets. Healthcare. 2020; 8(3):265. https://doi.org/10.3390/healthcare8030265
Chicago/Turabian StyleKalender, Zeynep Tugce, Hakan Tozan, and Ozalp Vayvay. 2020. "Prioritization of Medical Errors in Patient Safety Management: Framework Using Interval-Valued Intuitionistic Fuzzy Sets" Healthcare 8, no. 3: 265. https://doi.org/10.3390/healthcare8030265
APA StyleKalender, Z. T., Tozan, H., & Vayvay, O. (2020). Prioritization of Medical Errors in Patient Safety Management: Framework Using Interval-Valued Intuitionistic Fuzzy Sets. Healthcare, 8(3), 265. https://doi.org/10.3390/healthcare8030265






