Eliciting Distributive Preferences in Health Care Resource Allocation: A Person Trade-Off Study
Abstract
1. Introduction
1.1. Background and Significance
1.2. Literature Review
1.2.1. Theoretical Foundations of Distributive Preferences
1.2.2. Empirical Evidence
1.2.3. Methodological Advances and Challenges
1.2.4. Dynamic Contexts and Policy Implications
1.2.5. Research Gaps
1.3. Research Objectives and Contribution
2. Materials and Methods
2.1. Person Trade-Off Methodology
2.2. Survey Design
2.3. Person Trade-Off Tasks
2.4. Study Sample and Data Collection
2.5. Statistical Analysis
2.5.1. Distributive Preference Type Analysis
2.5.2. Testing the Hypotheses
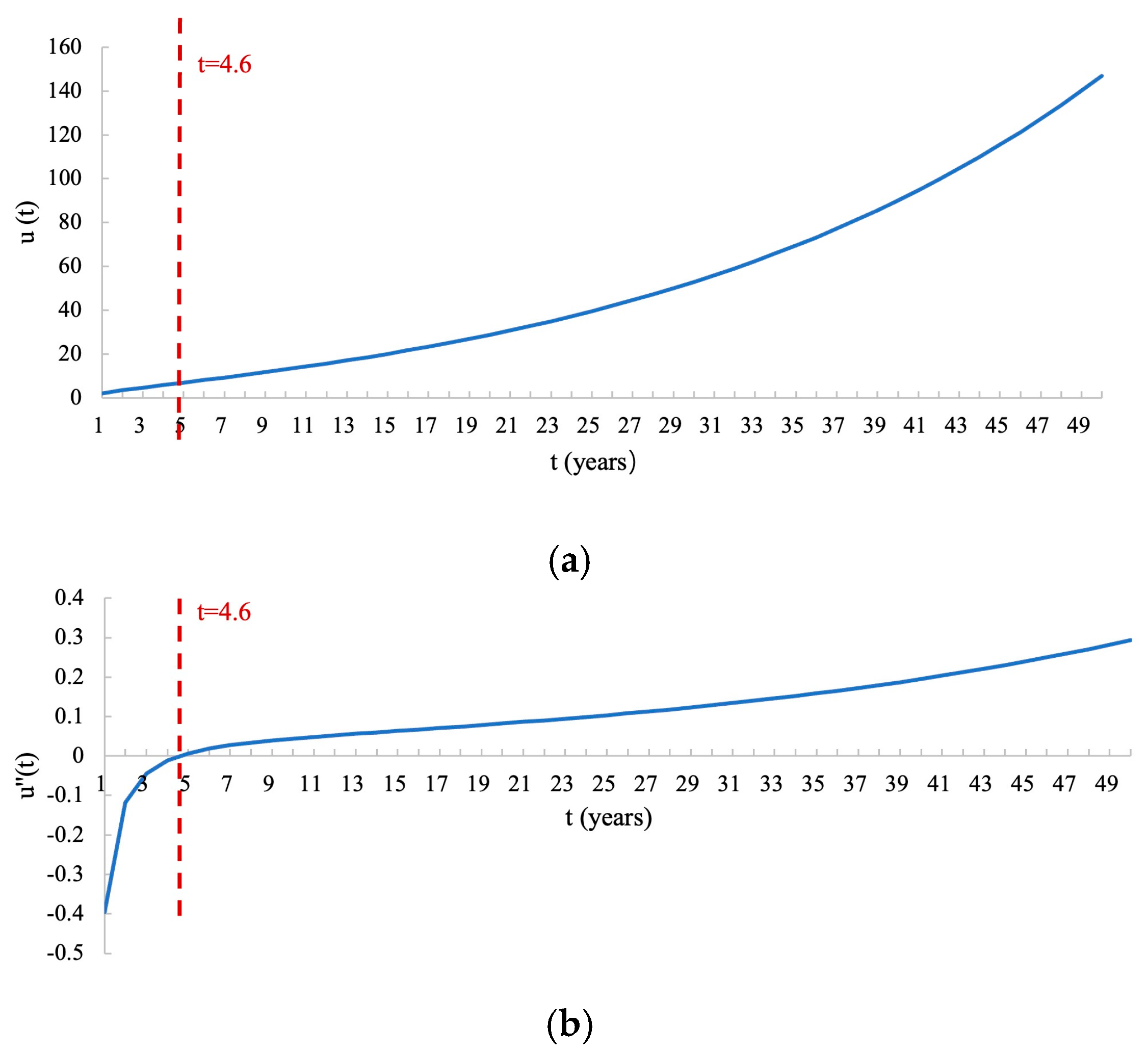
2.5.3. Estimating the Threshold
2.5.4. Consistency Analysis and the Test–Retest Reliability
2.5.5. Subgroup Analysis
3. Results
3.1. Distributive Preference Type
3.2. Regression Analysis Results and Threshold
3.3. Test–Retest Analysis and Subgroup Analysis Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QALYs | Quality-adjusted life years |
| CEA | Cost-effectiveness analysis |
| SWF | Social welfare function |
| HRSWF | Health-related social welfare function |
| LE | Life expectancy |
| UK | United Kingdom |
| PTO | Person trade-off |
References
- Lockwood, M. Quality of life and resource allocation. R. Inst. Philos. Suppl. 1988, 23, 33–55. [Google Scholar] [CrossRef]
- Dolan, P. The measurement of individual utility and social welfare. J. Health Econ. 1998, 17, 39–52. [Google Scholar] [CrossRef]
- Dolan, P.; Shaw, R.; Tsuchiya, A.; Williams, A. QALY maximisation and people’s preferences: A methodological review of the literature. Health Econ. 2005, 14, 197–208. [Google Scholar] [CrossRef]
- Nord, E.; Richardson, J.; Street, A.; Kuhse, H.; Singer, P. Maximizing health benefits vs egalitarianism: An Australian survey of health issues. Soc. Sci. Med. 1995, 41, 1429–1437. [Google Scholar] [CrossRef]
- Rand, L.Z.; Kesselheim, A.S. Controversy Over Using Quality-Adjusted Life-Years in Cost-Effectiveness Analyses: A Systematic Literature Review. Health Aff. 2021, 40, 1402–1410. [Google Scholar] [CrossRef]
- McGuire, A.; Fenn, P.; Mayhew, K. Providing Health Care: The Economics of Alternative Systems of Finance and Delivery; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Nord, E. The QALY—A measure of social value rather than individual utility? Health Econ. 1994, 3, 89–93. [Google Scholar] [CrossRef]
- Wagstaff, A. QALYs and the equity-efficiency trade-off. J. Health Econ. 1991, 10, 21–41. [Google Scholar] [CrossRef]
- Atkinson, A.B. On the Measurement of Inequality. J. Econ. Theory 1970, 2, 244–263. [Google Scholar] [CrossRef]
- Mæstad, O.; Norheim, O.F. A universal preference for equality in health? Reasons to reconsider properties of applied social welfare functions. Soc. Sci. Med. 2012, 75, 1836–1843. [Google Scholar] [CrossRef]
- Choudhry, N.; Slaughter, P.; Sykora, K.; Naylor, C.D. Distributional dilemmas in health policy: Large benefits for a few or smaller benefits for many? J. Health Serv. Res. Policy 1997, 2, 212–216. [Google Scholar] [CrossRef]
- Olsen, J.A. A note on eliciting distributive preferences for health. J. Health Econ. 2000, 19, 541–550. [Google Scholar] [CrossRef]
- Rodríguez-Míguez, E.; Pinto-Prades, J.L. Measuring the social importance of concentration or dispersion of individual health benefits. Health Econ. 2002, 11, 43–53. [Google Scholar] [CrossRef]
- Dolan, P.; Edlin, R.; Tsuchiya, A. The Relative Societal Value of Health Gains to Different Beneficiaries; The University of Leeds: Woodhouse, UK; The University of Sheffield: Western Bank, UK, 2008. [Google Scholar]
- Gyrd-Hansen, D.; Kristiansen, I.S. Preferences for ‘life-saving’programmes: Small for all or gambling for the prize? Health Econ. 2008, 17, 709–720. [Google Scholar] [CrossRef]
- Patrick, D.L.; Bush, J.W.; Chen, M.M. Methods for measuring levels of well-being for a health status index. Health Serv. Res. 1973, 8, 228. [Google Scholar]
- Attema, A.E.; Brouwer, W.B.F.; Pinto-Prades, J.L. Reference-dependent age weighting of quality-adjusted life years. Health Econ. 2022, 31, 2515–2536. [Google Scholar] [CrossRef]
- Sheen, D.; Peasgood, T.; Goranitis, I. Eliciting Societal Preferences for Non-health Outcomes: A Person Trade-Off Study in the Context of Genomics. Clin. Ther. 2023, 45, 710–718. [Google Scholar] [CrossRef]
- Damschroder, L.J.; Baron, J.; Hershey, J.C.; Asch, D.A.; Jepson, C.; Ubel, P.A. The validity of person tradeoff measurements: Randomized trial of computer elicitation versus face-to-face interview. Med. Decis. Mak. 2004, 24, 170–180. [Google Scholar] [CrossRef]
- Al-Janabi, H.; Wittenberg, E.; Donaldson, C.; Brouwer, W. The relative value of carer and patient quality of life: A person trade-off (PTO) study. Soc. Sci. Med. 2022, 292, 114556. [Google Scholar] [CrossRef]
- Damschroder, L.J.; Roberts, T.R.; Zikmund-Fisher, B.J.; Ubel, P.A. Why people refuse to make tradeoffs in person tradeoff elicitations: A matter of perspective? Med. Decis. Mak. 2007, 27, 266–280. [Google Scholar] [CrossRef] [PubMed]
- Ubel, P.A.; Richardson, J.; Baron, J. Exploring the role of order effects in person trade-off elicitations. Health Policy 2002, 61, 189–199. [Google Scholar] [CrossRef]
- NICE. NICE Health Technology Evaluations: The Manual (PMG36). Available online: https://www.nice.org.uk/process/pmg36/chapter/introduction-to-health-technology-evaluatio (accessed on 1 May 2024).
- Love-Koh, J.; Griffin, S.; Kataika, E.; Revill, P.; Sibandze, S.; Walker, S. Methods to promote equity in health resource allocation in low- and middle-income countries: An overview. Glob. Health 2020, 16, 6. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Lancsar, E.; Ghijben, P.; Butler, J.R.; Donaldson, C. Attributes and weights in health care priority setting: A systematic review of what counts and to what extent. Soc. Sci. Med. 2015, 146, 41–52. [Google Scholar] [CrossRef]
- Schwappach, D.L. Resource allocation, social values and the QALY: A review of the debate and empirical evidence. Health Expect. 2002, 5, 210–222. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Song, Z.; Zong, Q. Urban-Rural Inequality of Opportunity in Health Care: Evidence from China. Int. J. Environ. Res. Public Health 2021, 18, 7792. [Google Scholar] [CrossRef]
- Wang, F.; Gillani, S.; Razzaq, A.; Nazir, R.; Shafiq, M.N.; Li, B. Synergistic impacts of technological advancement and environmental hazards on social change and human well-being in South Asia. Technol. Forecast. Soc. Change 2024, 208, 123721. [Google Scholar] [CrossRef]
- Nord, E. The person-trade-off approach to valuing health care programs. Med. Decis. Mak. 1995, 15, 201–208. [Google Scholar] [CrossRef]
- Pinto Prades, J.L. Is the person trade-off a valid method for allocating health care resources? Health Econ. 1997, 6, 71–81. [Google Scholar] [CrossRef]
- Green, C. On the societal value of health care: What do we know about the person trade-off technique? Health Econ. 2001, 10, 233–243. [Google Scholar] [CrossRef]
- Olsen, J.A. Persons vs years: Two ways of eliciting implicit weights. Health Econ. 1994, 3, 39–46. [Google Scholar] [CrossRef]
- McHugh, N.; van Exel, J.; Mason, H.; Godwin, J.; Collins, M.; Donaldson, C.; Baker, R. Are life-extending treatments for terminal illnesses a special case? Exploring choices and societal viewpoints. Soc. Sci. Med. 2018, 198, 61–69. [Google Scholar] [CrossRef]
- Reckers-Droog, V.; van Exel, J.; Brouwer, W. Equity weights for priority setting in healthcare: Severity, age, or both? Value Health 2019, 22, 1441–1449. [Google Scholar] [CrossRef] [PubMed]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Dolan, P.; Cookson, R. A qualitative study of the extent to which health gain matters when choosing between groups of patients. Health Policy 2000, 51, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Linley, W.G.; Hughes, D.A. Societal views on NICE, cancer drugs fund and value-based pricing criteria for prioritising medicines: A cross-sectional survey of 4118 adults in Great Britain. Health Econ. 2013, 22, 948–964. [Google Scholar] [CrossRef]

| Program A | Program B | ||
|---|---|---|---|
| t | P | T | p |
| 1 year | 100 patients | 10 years | ? |
| 2 years | 50 patients | 10 years | ? |
| 5 years | 20 patients | 10 years | ? |
| 20 years | 5 patients | 10 years | ? |
| 50 years | 2 patients | 10 years | ? |
| Preference Category | Preference Definition |
|---|---|
| Concentration 1 | If t < T, p < Pt/T If t > T, p > Pt/T |
| Diffusion 2 | If t < T, p > Pt/T If t > T, p < Pt/T |
| Maximizing 3 | p = Pt/T |
| Extreme egalitarianism 4 | If t < T, p = upper limit If t > T, p = lower limit |
| Extreme inequality seeking 4 | If t < T, p = lower limit If t > T, p = upper limit |
| Pairs | Program 1 | Program 2 | Distributive Preference | t-Test (p Value) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 100 | 38.0 | 2 | 50 | 17.4 | −1 | D * | <0.001 |
| 2 | 1 | 100 | 38.0 | 5 | 20 | 9.4 | −4 | D * | <0.001 |
| 3 | 1 | 100 | 38.0 | 10 | 10 | 10.0 | −9 | D * | <0.001 |
| 4 | 1 | 100 | 38.0 | 20 | 5 | 32.2 | −19 | D * | <0.001 |
| 5 | 1 | 100 | 38.0 | 50 | 2 | 37.7 | −49 | D | 0.42 |
| 6 | 2 | 50 | 17.4 | 5 | 20 | 9.4 | −3 | D * | <0.001 |
| 7 | 2 | 50 | 17.4 | 10 | 10 | 10.0 | −8 | D * | <0.001 |
| 8 | 2 | 50 | 17.4 | 20 | 5 | 32.2 | −18 | C * | <0.001 |
| 9 | 2 | 50 | 17.4 | 50 | 2 | 37.7 | −48 | C * | <0.001 |
| 10 | 5 | 20 | 9.4 | 10 | 10 | 10.0 | −5 | C * | <0.001 |
| 11 | 5 | 20 | 9.4 | 20 | 5 | 32.2 | −15 | C * | <0.001 |
| 12 | 5 | 20 | 9.4 | 50 | 2 | 37.7 | −45 | C * | <0.001 |
| 13 | 10 | 10 | 10 | 20 | 5 | 32.2 | −10 | C * | <0.001 |
| 14 | 10 | 10 | 10 | 50 | 2 | 37.7 | −40 | C * | <0.001 |
| 15 | 20 | 5 | 32.2 | 50 | 2 | 37.7 | −30 | C * | <0.001 |
| Preference Category | t = 1 Year | t = 2 Years | t = 5 Years | t = 20 Years | t = 50 Years |
|---|---|---|---|---|---|
| Concentration | 7.2% | 24.0% | 37.0% | 78.0% | 74.6% |
| Diffusion | 89.0% | 63.2% | 33.6% | 4.0% | 17.4% |
| Maximizing | 3.4% | 9.6% | 21.2% | 14.4% | 4.0% |
| Extreme egalitarianism | 0.2% | 1.2% | 6.8% | 2.0% | 1.6% |
| Extreme inequality seeking | 0.2% | 2.0% | 1.4% | 1.6% | 2.4% |
| Total | 100% | 100% | 100% | 100% | 100% |
| Health Gain (t) in Program A | Number of People (P) in Program A | Health Gain (T) in Program B | Indifference Number of People in Program B (Mean [SD]) | |||
|---|---|---|---|---|---|---|
| Version 1 () 1 | Version 2 () 1 | t-Test (p Value) 2 | Total () | |||
| 1 | 100 | 10 | 38.5 [1.3] | 37.8 [1.4] | 0.3736 | 38.0 [20.2] * |
| 2 | 50 | 10 | 18.4 [0.7] | 17.3 [0.7] | 0.155 | 17.4 [10.8] * |
| 5 | 20 | 10 | 9.5 [0.3] | 10.2 [0.3] | 0.9475 | 9.4 [3.9] * |
| 20 | 5 | 10 | 32.5 [2.2] | 35.1 [2.2] | 0.7900 | 32.2 [27.7] * |
| 50 | 2 | 10 | 38.7 [2.6] | 41.1 [2.8] | 0.7390 | 37.7 [35.6] * |
| ln u(t) | Coef. | SE | p | 95%CI |
|---|---|---|---|---|
| t | 0.035 | 0.002 | <0.000 | (0.030, 0.039) |
| ln t | 0.646 | 0.030 | <0.000 | (0.587, 0.705) |
| constant | 0.735 | 0.032 | <0.000 | (0.672, 0.798) |
| R2(adjusted) | 0.771 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, N.; Su, C.; Wu, J. Eliciting Distributive Preferences in Health Care Resource Allocation: A Person Trade-Off Study. Healthcare 2025, 13, 1309. https://doi.org/10.3390/healthcare13111309
Fang N, Su C, Wu J. Eliciting Distributive Preferences in Health Care Resource Allocation: A Person Trade-Off Study. Healthcare. 2025; 13(11):1309. https://doi.org/10.3390/healthcare13111309
Chicago/Turabian StyleFang, Nan, Chang Su, and Jing Wu. 2025. "Eliciting Distributive Preferences in Health Care Resource Allocation: A Person Trade-Off Study" Healthcare 13, no. 11: 1309. https://doi.org/10.3390/healthcare13111309
APA StyleFang, N., Su, C., & Wu, J. (2025). Eliciting Distributive Preferences in Health Care Resource Allocation: A Person Trade-Off Study. Healthcare, 13(11), 1309. https://doi.org/10.3390/healthcare13111309







