Managing Mortality and Aging Risks with a Time-Varying Lee–Carter Model
Abstract
1. Introduction
2. Data and Methods
2.1. Database
2.2. The Lee–Carter and Related Models
2.3. Issues with the Lee–Carter Model and Related Literature
2.4. A Time-Varying Coefficients Extension of the Lee–Carter Model
2.4.1. A Time-Varying Framework Using Kernels
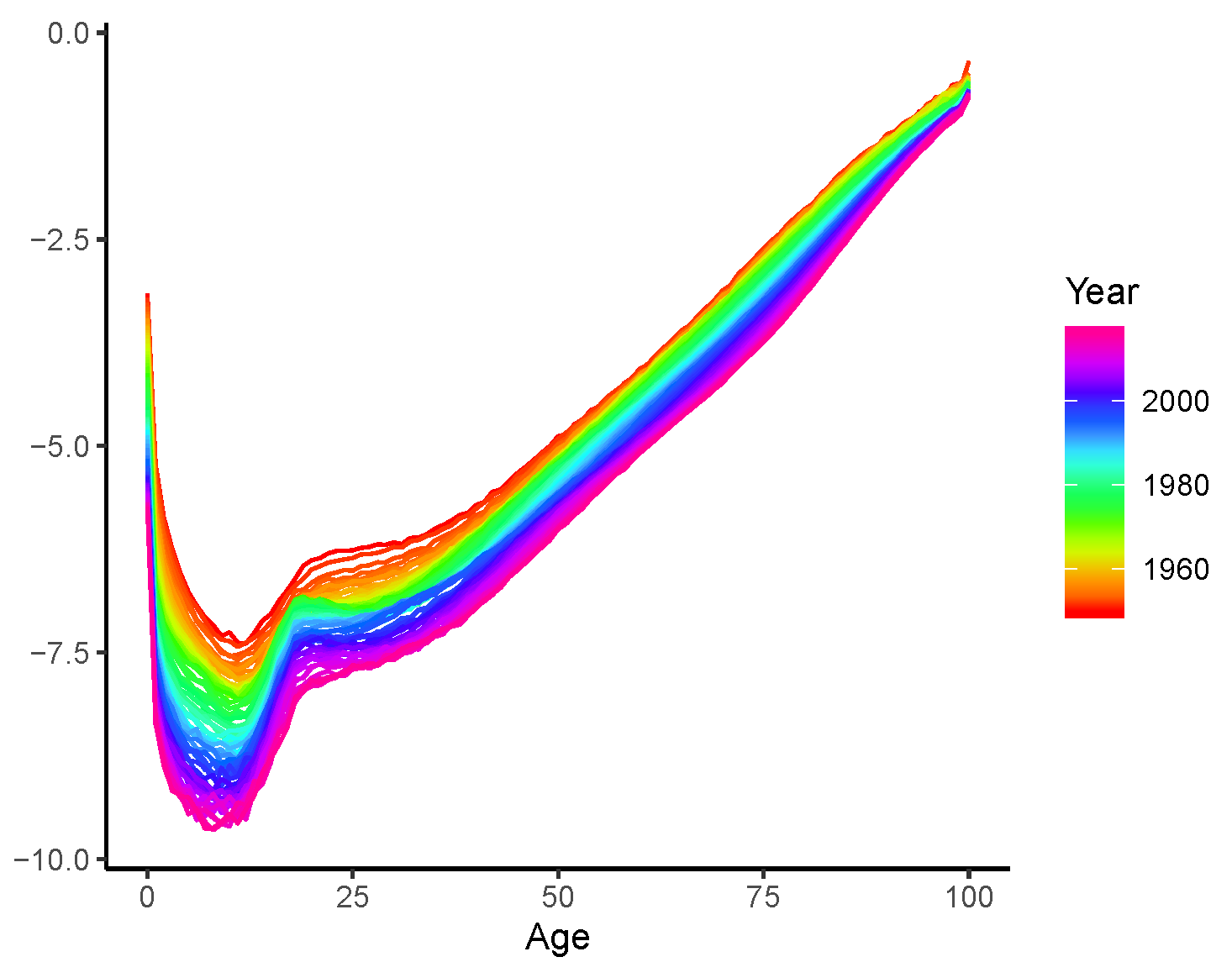
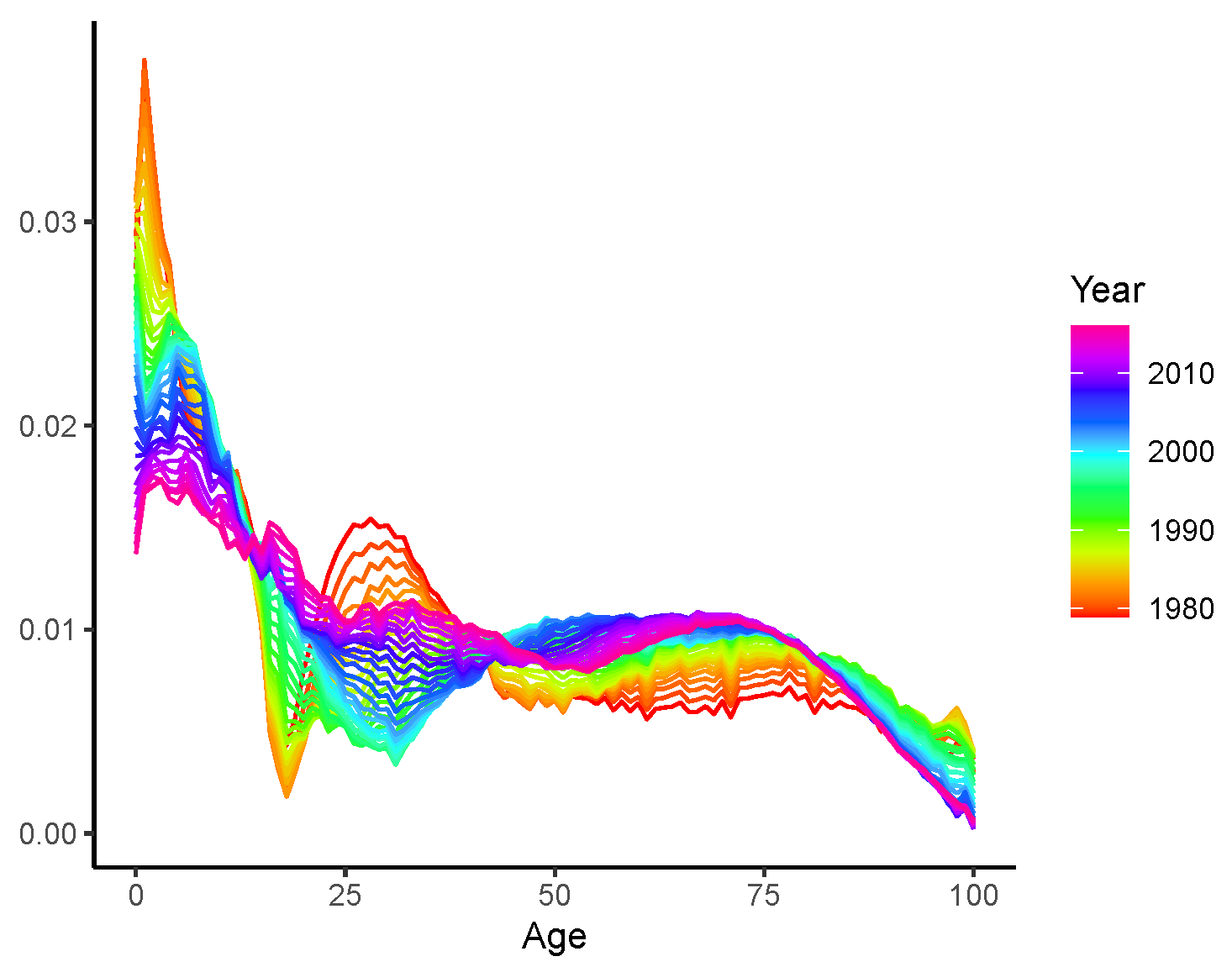
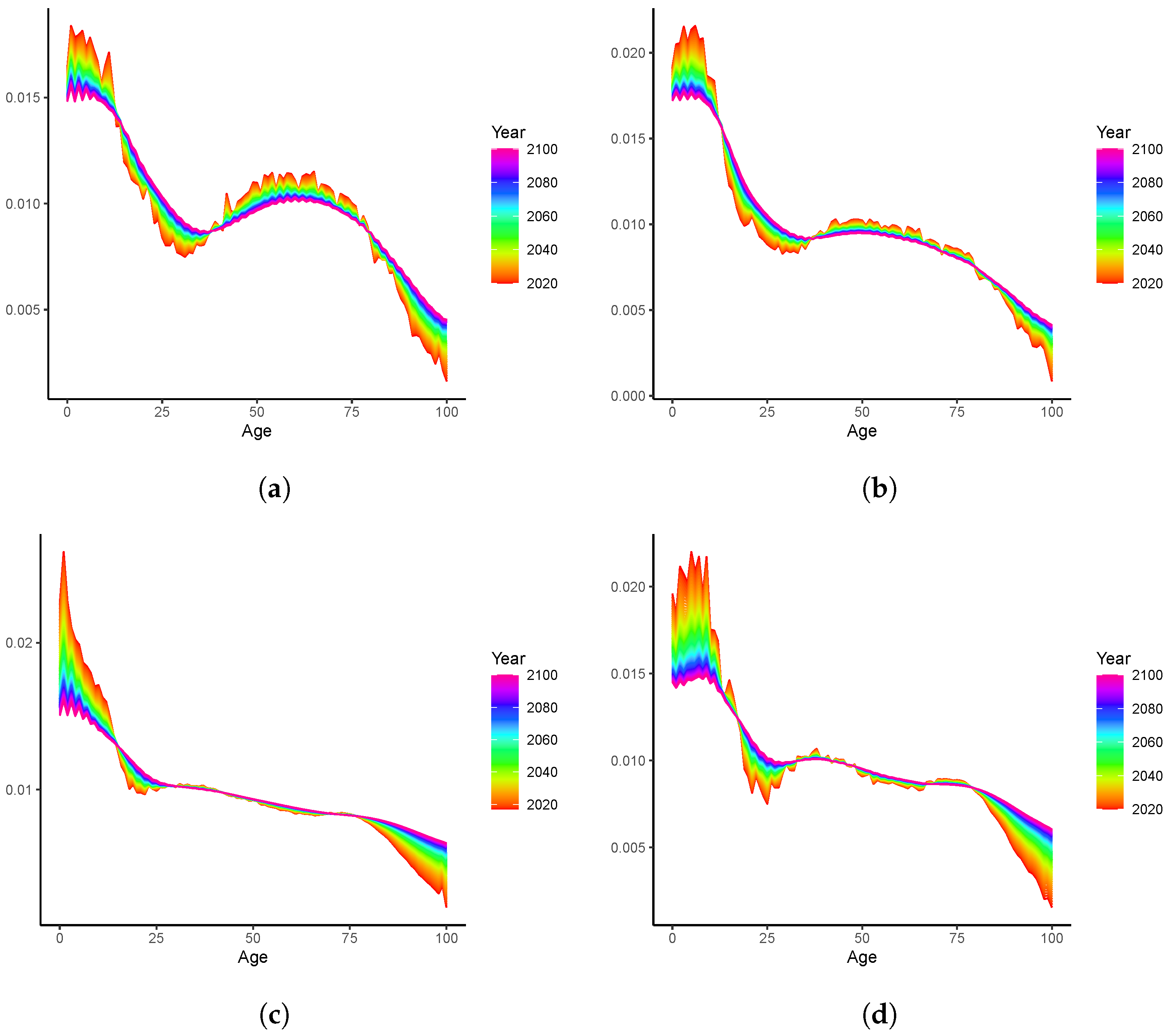
2.4.2. Coherent Modelling of the Dynamic Age-Specific Mortality Declines
2.4.3. Tuning Parameters Selection and the Estimation Procedure
- Fit the original LC model with the full sample to obtain , , and d;
- For the training sample spanning , use the Epanechnikov (LC-E) or Gaussian (LC-G) kernel to obtain , based on which the constrained VAR model of Equation (6) is fitted for ;
- Select the optimal tuning parameters b, , , and via a grid search, such that the RMSFE of the test sample over is minimized;
- With the selected tuning parameters, fit the LC-E or LC-G model for the full sample;
- Forecast with the fitted model, and then produce with Equation (5), where and sourced from Step 1.
2.5. Related Mortality Models
3. Results and Discussion
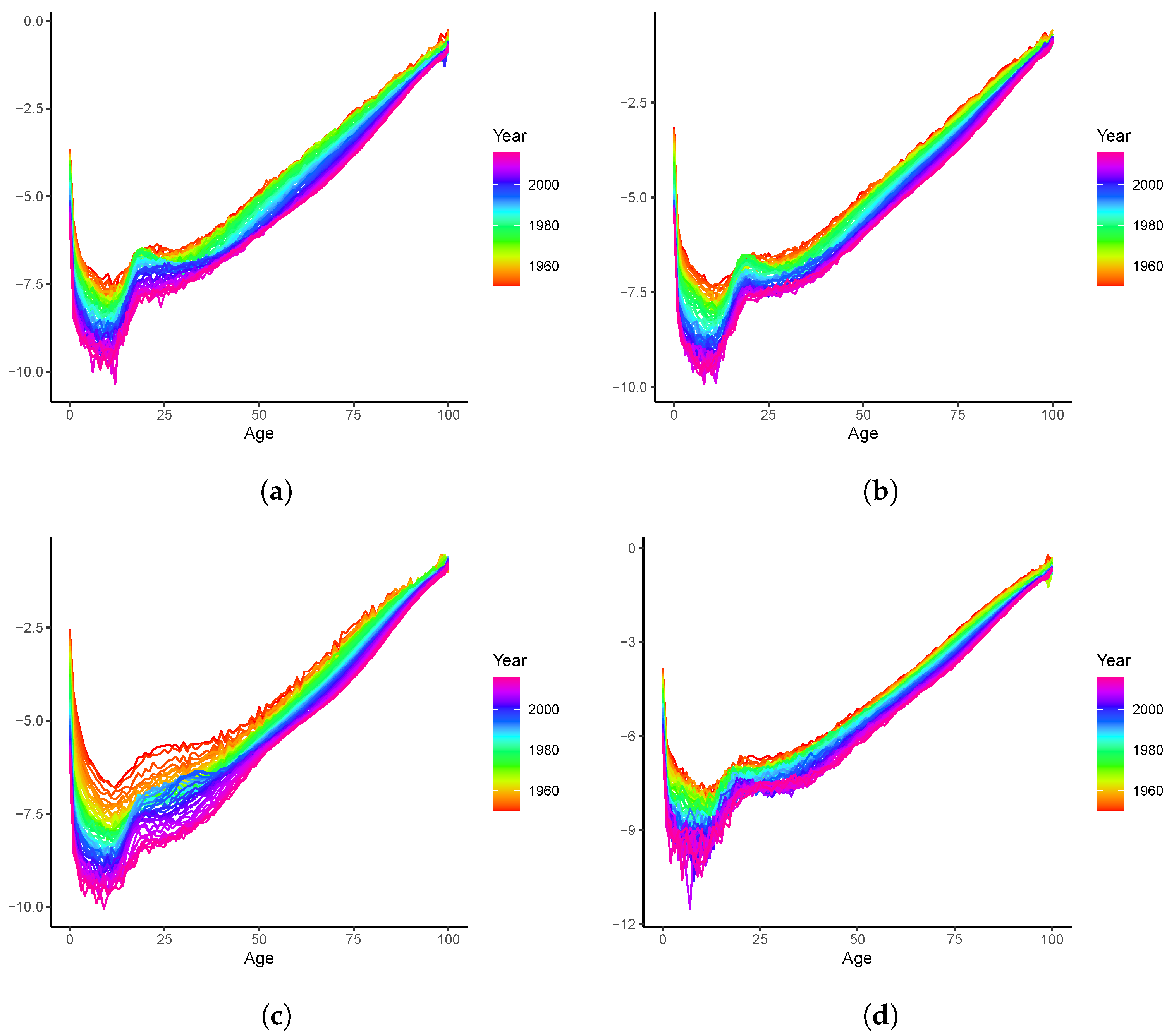
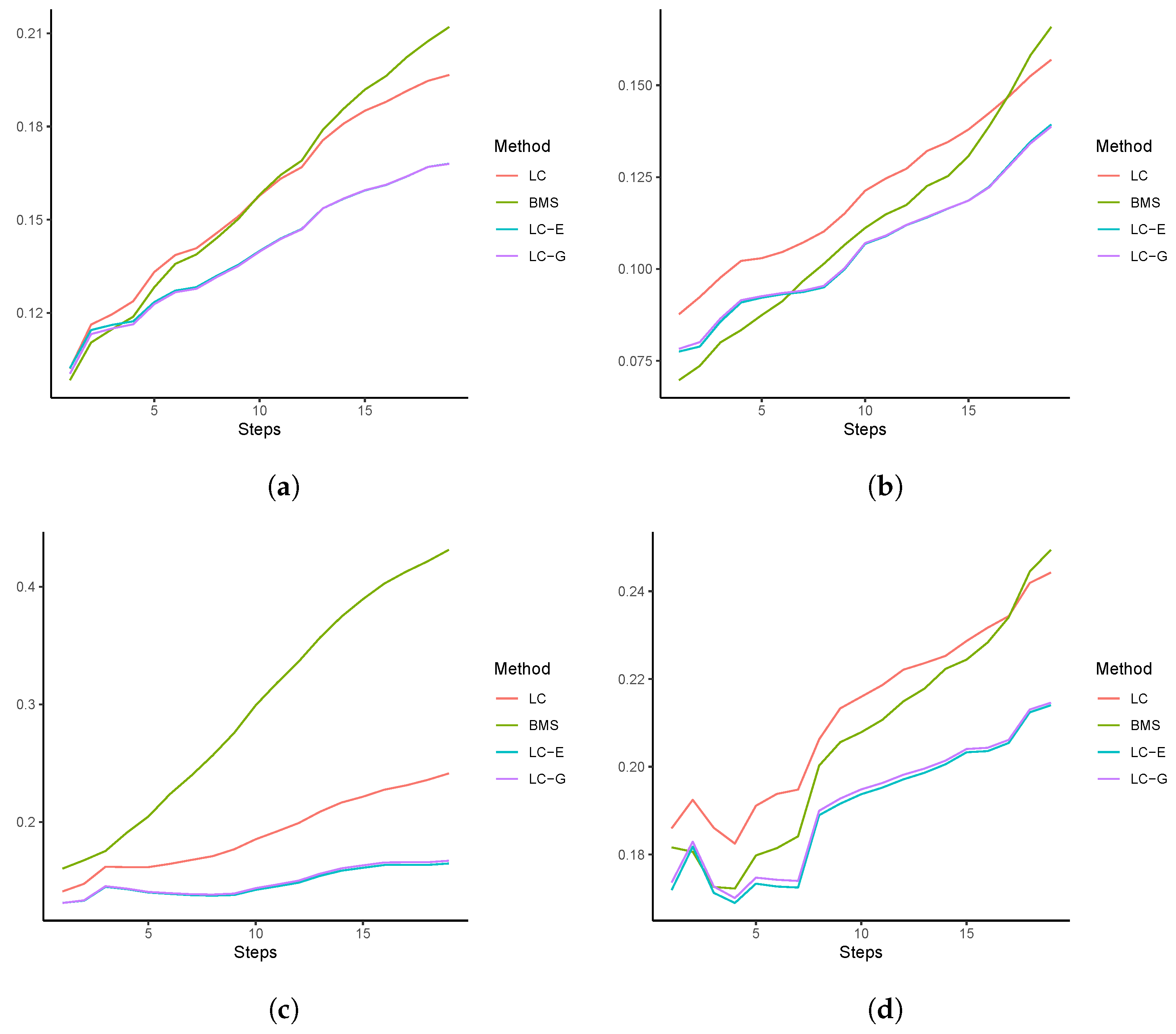
3.1. Out-of-Sample Forecasting Analysis
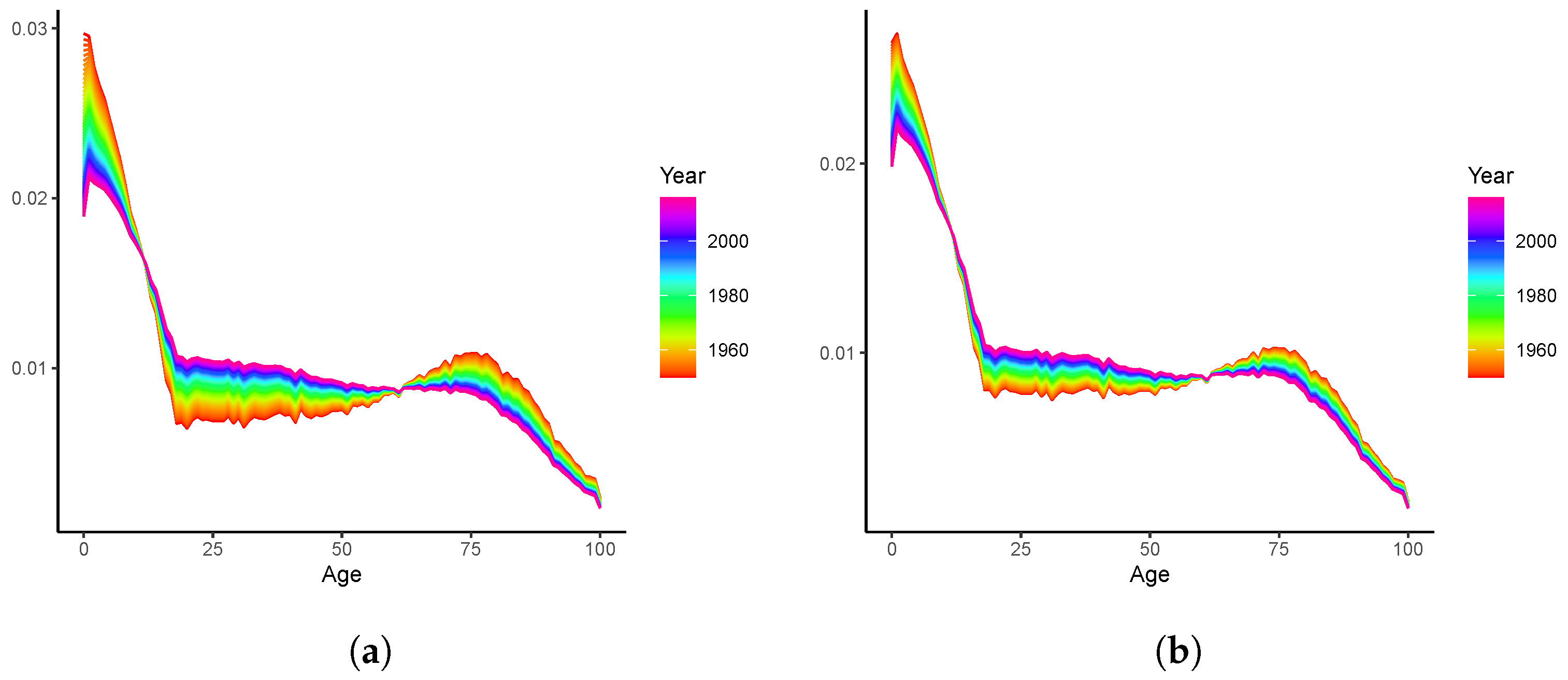
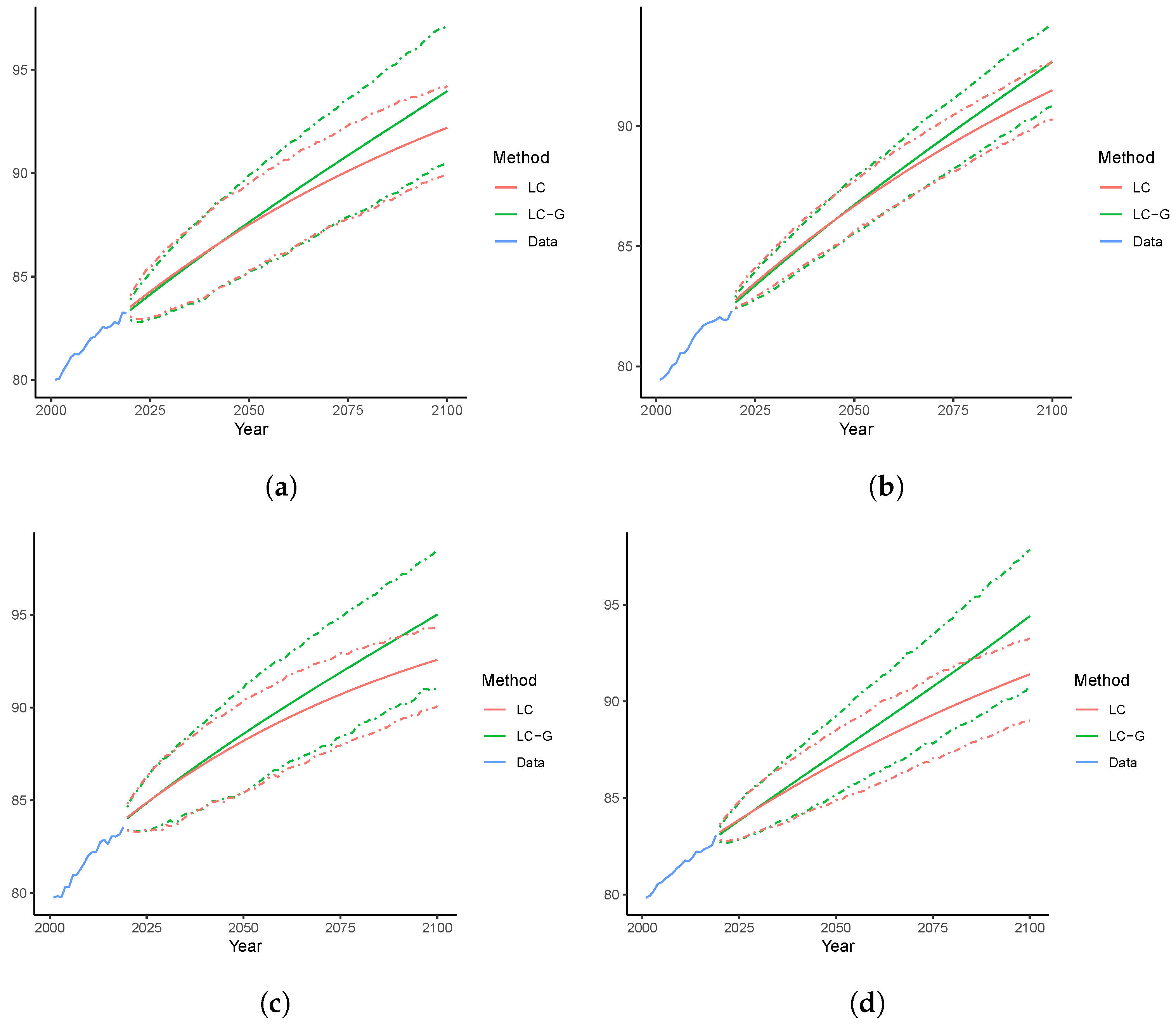
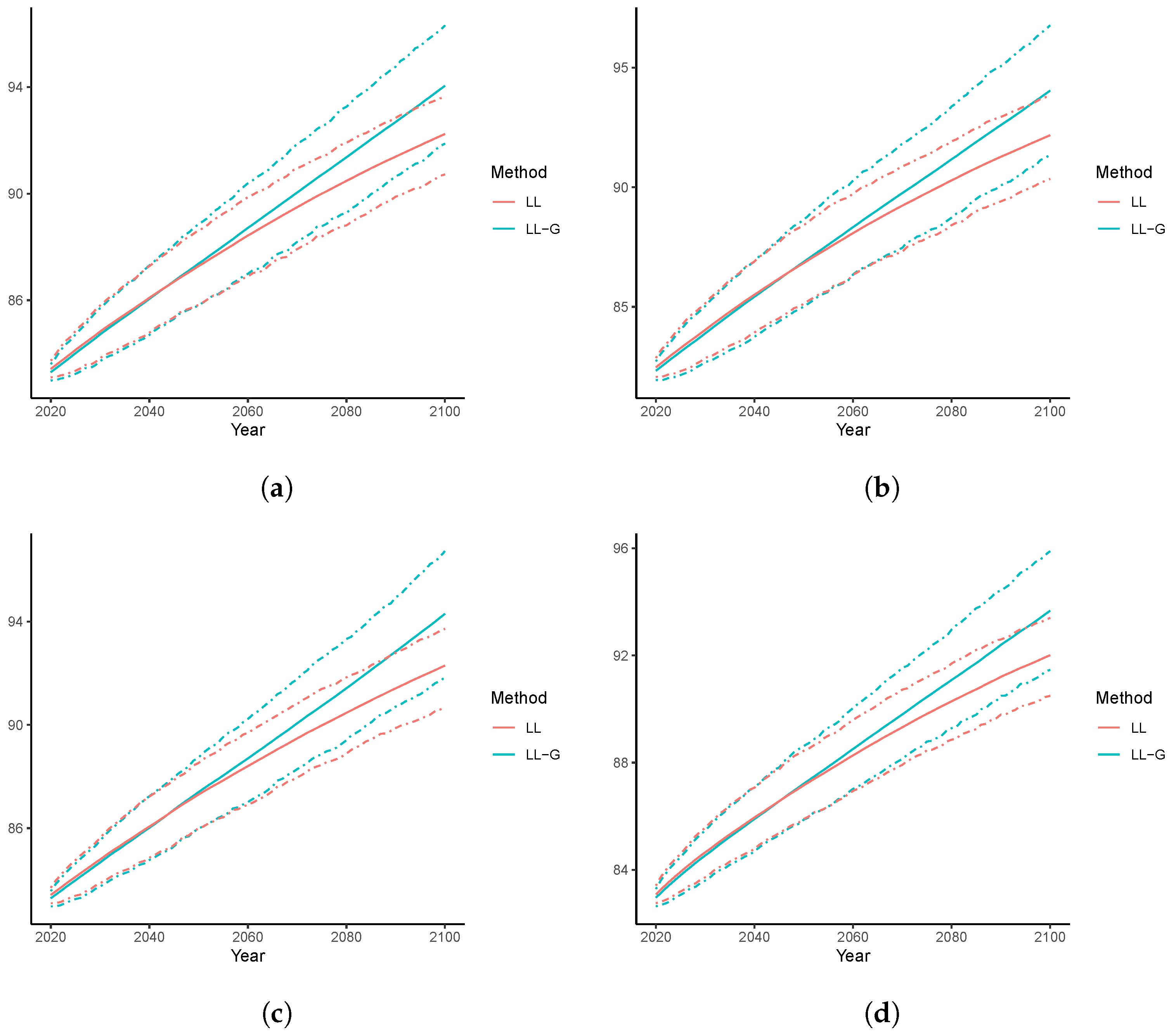
3.2. Long-Term Analyses: 2020–2100
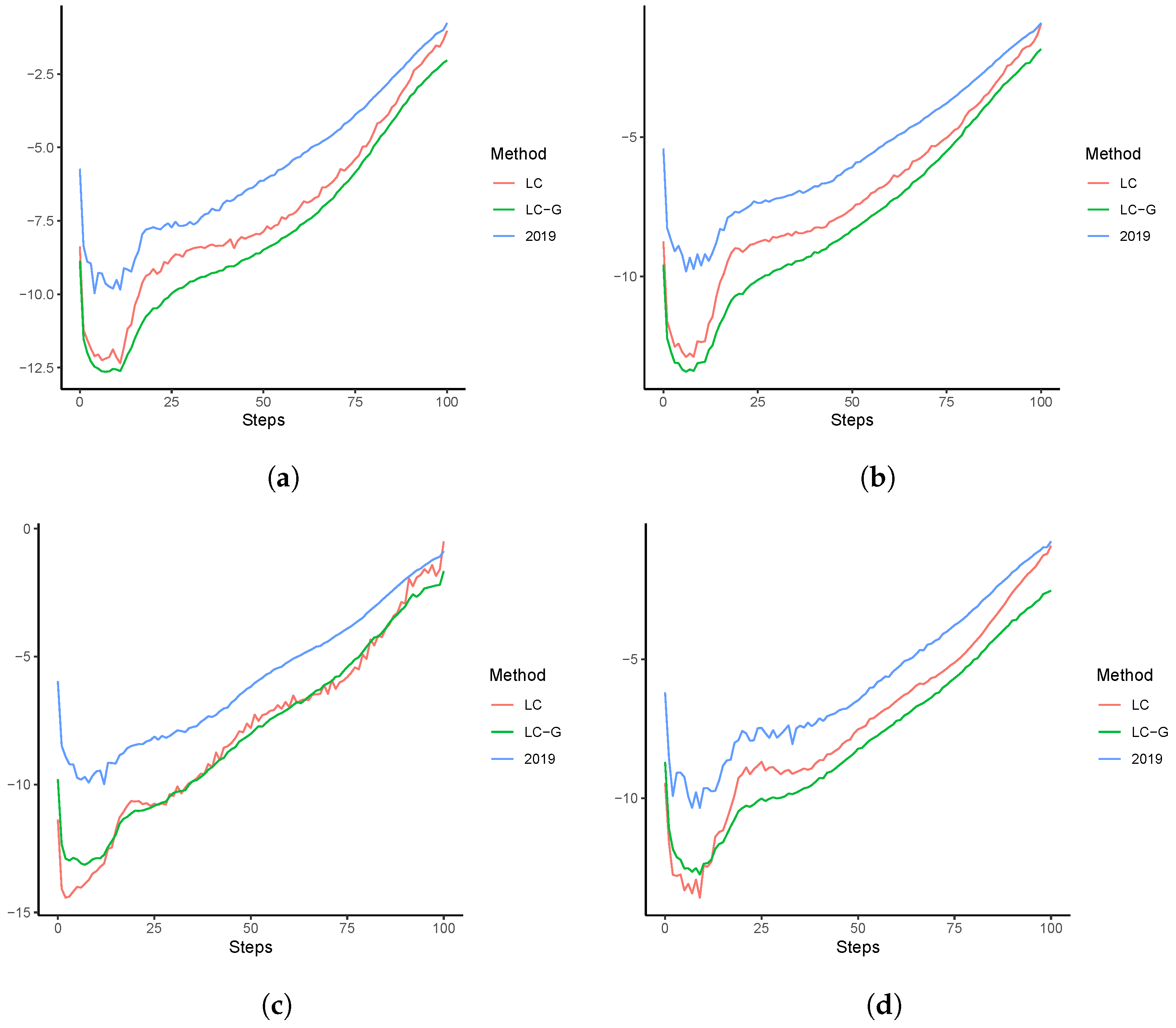
4. Extensions to the Multi-Population Modelling: An Illustrative Example
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maestas, N.; Mullen, K.J.; Powell, D. The Effect of Population Aging on Economic Growth, the Labor Force and Productivity; Technical report; National Bureau of Economic Research: Cambridge, MA, USA, 2016. [Google Scholar]
- Fenton, J.J.; Jerant, A.F.; Bertakis, K.D.; Franks, P. The cost of satisfaction: A national study of patient satisfaction, health care utilization, expenditures, and mortality. Arch. Intern. Med. 2012, 172, 405–411. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Zhang, C. The power of social pensions: Evidence from China’s new rural pension scheme. Am. Econ. J. Appl. Econ. 2021, 13, 179–205. [Google Scholar] [CrossRef]
- Lee, R.D.; Carter, L.R. Modeling and forecasting US mortality. J. Am. Stat. Assoc. 1992, 87, 659–671. [Google Scholar]
- Li, N.; Lee, R.; Gerland, P. Extending the Lee–Carter method to model the rotation of age patterns of mortality decline for long-term projections. Demography 2013, 50, 2037–2051. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Lu, Y. Coherent Forecasting of Mortality Rates: A Sparse Vector-Autoregression Approach. ASTIN Bull. J. IAA 2017, 47, 563–600. [Google Scholar] [CrossRef]
- Fan, J.; Gijbels, I. Local Polynomial Modelling and Its Applications: Monographs on Statistics and Applied Probability; CRC Press: Boca Raton, FL, USA, 1996; Volume 66. [Google Scholar]
- Human Mortality Database. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). 2023. Available online: https://www.mortality.org/ (accessed on 28 January 2023).
- Li, N.; Lee, R. Coherent mortality forecasts for a group of populations: An extension of the Lee–Carter method. Demography 2005, 42, 575–594. [Google Scholar] [CrossRef]
- Booth, H.; Hyndman, R.; Tickle, L.; De Jong, P. Lee–Carter mortality forecasting: A multi-country comparison of variants and extensions. Demogr. Res. 2006, 15, 289–310. [Google Scholar] [CrossRef]
- Li, H.; Li, J.S.H. Optimizing the Lee–Carter approach in the presence of structural changes in time and age patterns of mortality improvements. Demography 2017, 54, 1073–1095. [Google Scholar] [CrossRef]
- Boonen, T.J.; Li, H. Modeling and forecasting mortality with economic growth: A multipopulation approach. Demography 2017, 54, 1921–1946. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Forecasting mortality with international linkages: A global vector-autoregression approach. Insur. Math. Econ. 2021, 100, 59–75. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Mortality forecasting with an age-coherent sparse var model. Risks 2021, 9, 35. [Google Scholar] [CrossRef]
- Renshaw, A.E.; Haberman, S. Lee–Carter mortality forecasting with age-specific enhancement. Insur. Math. Econ. 2003, 33, 255–272. [Google Scholar] [CrossRef]
- Li, H.; De Waegenaere, A.; Melenberg, B. The choice of sample size for mortality forecasting: A Bayesian learning approach. Insur. Math. Econ. 2015, 63, 153–168. [Google Scholar] [CrossRef]
- Booth, H.; Maindonald, J.; Smith, L. Applying Lee–Carter under conditions of variable mortality decline. Popul. Stud. 2002, 56, 325–336. [Google Scholar] [CrossRef] [PubMed]
- Brouhns, N.; Denuit, M.; Vermunt, J.K. A Poisson log-bilinear regression approach to the construction of projected lifetables. Insur. Math. Econ. 2002, 31, 373–393. [Google Scholar] [CrossRef]
- Chang, L.; Shi, Y. Dynamic modelling and coherent forecasting of mortality rates: A time-varying coefficient spatial-temporal autoregressive approach. Scand. Actuar. J. 2020, 843–863. [Google Scholar] [CrossRef]
- Huang, J.Z.; Wu, C.O.; Zhou, L. Polynomial spline estimation and inference for varying coefficient models with longitudinal data. Stat. Sin. 2004, 14, 763–788. [Google Scholar]
- Huang, J.Z.; Shen, H. Functional coefficient regression models for non-linear time series: A polynomial spline approach. Scand. J. Stat. 2004, 31, 515–534. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Varying-coefficient models. J. R. Stat. Soc. Ser. B Methodol. 1993, 55, 757–779. [Google Scholar] [CrossRef]
- Chiang, C.T.; Rice, J.A.; Wu, C.O. Smoothing spline estimation for varying coefficient models with repeatedly measured dependent variables. J. Am. Stat. Assoc. 2001, 96, 605–619. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, W. Statistical estimation in varying coefficient models. Ann. Stat. 1999, 27, 1491–1518. [Google Scholar] [CrossRef]
- Wand, M.P.; Jones, M.C. Kernel Smoothing; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Theodoridis, S. Machine Learning: A Bayesian and Optimization Perspective; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Feng, L.; Shi, Y. Forecasting mortality rates: Multivariate or univariate models? J. Popul. Res. 2018, 35, 289–318. [Google Scholar] [CrossRef]
- Feng, L.; Shi, Y.; Chang, L. Forecasting mortality with a hyperbolic spatial temporal VAR model. Int. J. Forecast. 2020, 37, 255–273. [Google Scholar] [CrossRef]
- Li, H.; Lu, Y.; Lyu, P. Coherent mortality forecasting for less developed countries. Risks 2021, 9, 151. [Google Scholar] [CrossRef]
- Guibert, Q.; Lopez, O.; Piette, P. Forecasting mortality rate improvements with a high-dimensional VAR. Insur. Math. Econ. 2019, 88, 255–272. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Li, J. A quantitative comparison of simulation strategies for mortality projection. Ann. Actuar. Sci. 2014, 8, 281. [Google Scholar] [CrossRef]
- Cairns, A.J.; Blake, D.; Dowd, K. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. J. Risk Insur. 2006, 73, 687–718. [Google Scholar] [CrossRef]
- Renshaw, A.E.; Haberman, S. A cohort-based extension to the Lee–Carter model for mortality reduction factors. Insur. Math. Econ. 2006, 38, 556–570. [Google Scholar] [CrossRef]
- Plat, R. On stochastic mortality modeling. Insur. Math. Econ. 2009, 45, 393–404. [Google Scholar] [CrossRef]
- Currie, I.D.; Durban, M.; Eilers, P.H. Smoothing and forecasting mortality rates. Stat. Model. 2004, 4, 279–298. [Google Scholar] [CrossRef]
- Wang, D.; Lu, P. Modelling and forecasting mortality distributions in England and Wales using the Lee–Carter model. J. Appl. Stat. 2005, 32, 873–885. [Google Scholar] [CrossRef]
- Debón, A.; Montes, F.; Mateu, J.; Porcu, E.; Bevilacqua, M. Modelling residuals dependence in dynamic life tables: A geostatistical approach. Comput. Stat. Data Anal. 2008, 52, 3128–3147. [Google Scholar] [CrossRef]
- Hainaut, D. A neural-network analyzer for mortality forecast. ASTIN Bull. J. IAA 2018, 48, 481–508. [Google Scholar] [CrossRef]
- Levantesi, S.; Pizzorusso, V. Application of machine learning to mortality modeling and forecasting. Risks 2019, 7, 26. [Google Scholar] [CrossRef]
- Nigri, A.; Levantesi, S.; Marino, M.; Scognamiglio, S.; Perla, F. A deep learning integrated Lee–Carter model. Risks 2019, 7, 33. [Google Scholar] [CrossRef]
- Richman, R.; Wüthrich, M.V. A neural network extension of the Lee–Carter model to multiple populations. Ann. Actuar. Sci. 2021, 15, 346–366. [Google Scholar] [CrossRef]
- Haberman, S.; Renshaw, A. A comparative study of parametric mortality projection models. Insur. Math. Econ. 2011, 48, 35–55. [Google Scholar] [CrossRef]
- Cadena, M. Mortality Models based on the Transform ∖log (-∖log x). arXiv 2015, arXiv:1502.07199. [Google Scholar]
- Doukhan, P.; Pommeret, D.; Rynkiewicz, J.; Salhi, Y. A class of random field memory models for mortality forecasting. Insur. Math. Econ. 2017, 77, 97–110. [Google Scholar] [CrossRef]
- Vékás, P. Rotation of the age pattern of mortality improvements in the European Union. Cent. Eur. J. Oper. Res. 2020, 28, 1031–1048. [Google Scholar] [CrossRef]
| LC-E | LC-G | |||||
|---|---|---|---|---|---|---|
| ADF | GC | BW | ADF | GC | BW | |
| Australia | 3 | 4 | 5.07 | 3 | 3 | 3.73 |
| Austria | 6 | 5 | 3.13 | 5 | 5 | 2.18 |
| Canada | 3 | 6 | 5.23 | 3 | 6 | 3.55 |
| Denmark | 7 | 4 | 4.26 | 7 | 5 | 2.73 |
| UK | 3 | 3 | 9.79 | 3 | 3 | 9.81 |
| Finland | 3 | 3 | 5.15 | 3 | 3 | 1.55 |
| France | 4 | 3 | 3.37 | 4 | 4 | 2.27 |
| Italy | 4 | 4 | 3.21 | 4 | 5 | 2.18 |
| Japan | 6 | 7 | 9.71 | 6 | 6 | 9.88 |
| Netherlands | 5 | 6 | 5.96 | 5 | 7 | 4.18 |
| Norway | 5 | 4 | 5.23 | 5 | 4 | 3.73 |
| Spain | 5 | 3 | 3.21 | 5 | 3 | 2.18 |
| Sweden | 4 | 3 | 3.86 | 4 | 4 | 2.64 |
| Switzerland | 4 | 4 | 2.57 | 4 | 5 | 1.82 |
| USA | 4 | 4 | 9.92 | 4 | 4 | 8.18 |
| Mean | 4.4 | 4.2 | - | 4.3 | 4.5 | - |
| RMSFE | Ranking | |||||||
|---|---|---|---|---|---|---|---|---|
| Country | LC | BMS | LC-E | LC-G | LC | BMS | LC-E | LC-G |
| Australia | 0.197 | 0.212 | 0.175 | 0.175 | 3 | 4 | 2 | 1 |
| Austria | 0.250 | 0.191 | 0.183 | 0.183 | 4 | 3 | 1 | 2 |
| Canada | 0.157 | 0.166 | 0.140 | 0.141 | 3 | 4 | 1 | 2 |
| Denmark | 0.389 | 0.413 | 0.345 | 0.345 | 3 | 4 | 1 | 2 |
| UK | 0.171 | 0.167 | 0.166 | 0.164 | 4 | 3 | 2 | 1 |
| Finland | 0.266 | 0.280 | 0.253 | 0.248 | 3 | 4 | 2 | 1 |
| France | 0.230 | 0.201 | 0.168 | 0.168 | 4 | 3 | 2 | 1 |
| Italy | 0.230 | 0.295 | 0.129 | 0.129 | 3 | 4 | 2 | 1 |
| Japan | 0.468 | 0.354 | 0.460 | 0.460 | 4 | 1 | 3 | 2 |
| Netherlands | 0.234 | 0.220 | 0.223 | 0.223 | 4 | 1 | 3 | 2 |
| Norway | 0.297 | 0.271 | 0.264 | 0.264 | 4 | 3 | 2 | 1 |
| Spain | 0.241 | 0.431 | 0.163 | 0.163 | 3 | 4 | 1 | 2 |
| Sweden | 0.244 | 0.249 | 0.215 | 0.215 | 3 | 4 | 1 | 2 |
| Switzerland | 0.359 | 0.331 | 0.296 | 0.296 | 4 | 3 | 1 | 2 |
| USA | 0.130 | 0.133 | 0.123 | 0.122 | 3 | 4 | 2 | 1 |
| Mean | 0.258 | 0.261 | 0.220 | 0.220 | 3 | 4 | 2 | 1 |
| Mean | Std. Dev. | Median | Q | Q | |
|---|---|---|---|---|---|
| Panel A: five-year age groups | |||||
| LC | 0.256 | 0.089 | 0.239 | 0.198 | 0.288 |
| BMS | 0.265 | 0.090 | 0.237 | 0.202 | 0.326 |
| LC-E | 0.220 | 0.083 | 0.189 | 0.168 | 0.265 |
| LC-G | 0.219 | 0.082 | 0.189 | 0.167 | 0.262 |
| Panel B: 1970–2000 | |||||
| LC | 0.240 | 0.080 | 0.218 | 0.192 | 0.262 |
| BMS | 0.239 | 0.084 | 0.220 | 0.180 | 0.288 |
| LC-E | 0.200 | 0.062 | 0.187 | 0.153 | 0.240 |
| LC-G | 0.200 | 0.062 | 0.187 | 0.152 | 0.238 |
| Error Measure | Ranking | |||||||
|---|---|---|---|---|---|---|---|---|
| Country | LL | LL-BMS | LL-E | LL-G | LL | LL-BMS | LL-E | LL-G |
| Australia | 0.185 | 0.179 | 0.176 | 0.175 | 4 | 3 | 2 | 1 |
| Austria | 0.244 | 0.234 | 0.214 | 0.210 | 4 | 3 | 2 | 1 |
| Canada | 0.163 | 0.127 | 0.143 | 0.136 | 4 | 1 | 3 | 2 |
| Denmark | 0.276 | 0.299 | 0.252 | 0.250 | 3 | 4 | 2 | 1 |
| UK | 0.167 | 0.120 | 0.158 | 0.153 | 4 | 1 | 3 | 2 |
| Finland | 0.268 | 0.252 | 0.263 | 0.260 | 4 | 1 | 3 | 2 |
| France | 0.195 | 0.204 | 0.147 | 0.135 | 3 | 4 | 2 | 1 |
| Italy | 0.233 | 0.226 | 0.217 | 0.216 | 4 | 3 | 2 | 1 |
| Japan | 0.184 | 0.108 | 0.168 | 0.169 | 4 | 1 | 2 | 3 |
| Netherlands | 0.179 | 0.165 | 0.151 | 0.141 | 4 | 3 | 2 | 1 |
| Norway | 0.247 | 0.244 | 0.233 | 0.232 | 4 | 3 | 2 | 1 |
| Spain | 0.271 | 0.268 | 0.249 | 0.248 | 4 | 3 | 2 | 1 |
| Sweden | 0.236 | 0.221 | 0.211 | 0.198 | 4 | 3 | 2 | 1 |
| Switzerland | 0.304 | 0.313 | 0.271 | 0.263 | 3 | 4 | 2 | 1 |
| USA | 0.185 | 0.175 | 0.171 | 0.169 | 4 | 3 | 2 | 1 |
| Mean | 0.222 | 0.209 | 0.202 | 0.197 | 4 | 3 | 2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Shi, Y.; Shu, A. Managing Mortality and Aging Risks with a Time-Varying Lee–Carter Model. Healthcare 2023, 11, 743. https://doi.org/10.3390/healthcare11050743
Chen Z, Shi Y, Shu A. Managing Mortality and Aging Risks with a Time-Varying Lee–Carter Model. Healthcare. 2023; 11(5):743. https://doi.org/10.3390/healthcare11050743
Chicago/Turabian StyleChen, Zhongwen, Yanlin Shi, and Ao Shu. 2023. "Managing Mortality and Aging Risks with a Time-Varying Lee–Carter Model" Healthcare 11, no. 5: 743. https://doi.org/10.3390/healthcare11050743
APA StyleChen, Z., Shi, Y., & Shu, A. (2023). Managing Mortality and Aging Risks with a Time-Varying Lee–Carter Model. Healthcare, 11(5), 743. https://doi.org/10.3390/healthcare11050743







