Optimizing Large-Scale COVID-19 Nucleic Acid Testing with a Dynamic Testing Site Deployment Strategy
Abstract
1. Introduction
2. Literature Review
3. Problem Statement and Model Formulation
4. Case Study
4.1. Parameter Settings
4.2. Optimal Results
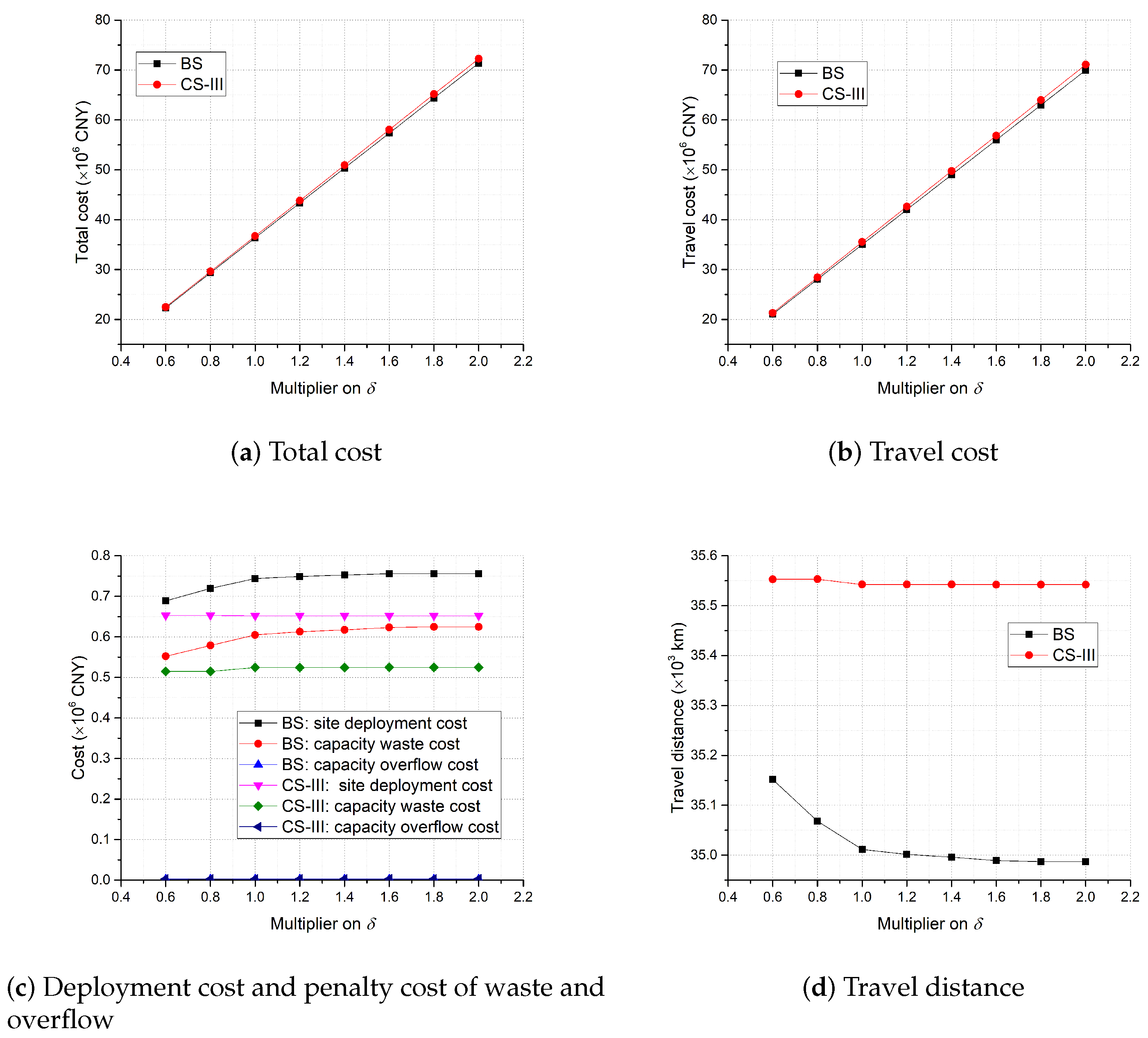
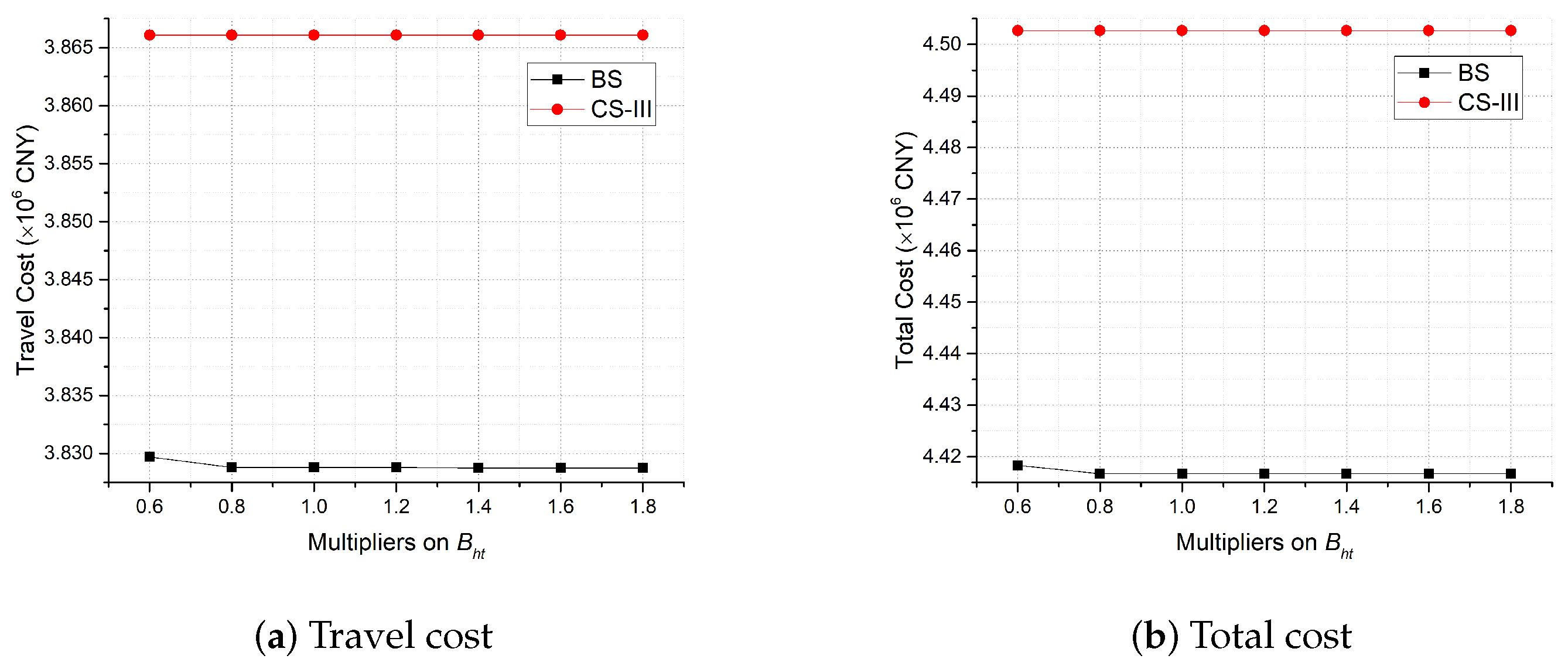
4.3. Sensitivity Analysis
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NAT | Nucleic acid testing |
| EHF | Emergency healthcare facility |
| BS | Base strategy |
| CS | Comparison strategy |
References
- World Health Organization. WHO Coronavirus (COVID-19) Dashboard. 2022. Available online: https://covid19.who.int/ (accessed on 2 October 2022).
- Wikipedia. Lockdown. 2022. Available online: https://en.wikipedia.org/wiki/Lockdown (accessed on 2 October 2022).
- Bezerra, A.C.V.; Silva, C.E.M.d.; Soares, F.R.G.; Silva, J.A.M.d. Factors associated with people’s behavior in social isolation during the COVID-19 pandemic. Cienc. Saude Coletiva 2020, 25, 2411–2421. [Google Scholar] [CrossRef] [PubMed]
- Dinleyici, E.C.; Borrow, R.; Safadi, M.A.P.; van Damme, P.; Munoz, F.M. Vaccines and routine immunization strategies during the COVID-19 pandemic. Hum. Vaccines Immunother. 2021, 17, 400–407. [Google Scholar] [CrossRef] [PubMed]
- Jordan-Martin, N.C.; Madad, S.; Alves, L.; Wang, J.; O’Gere, L.; Smith, Y.G.; Pressman, M.; Shure, J.A.; Cosmi, M. Isolation hotels: A community-based intervention to mitigate the spread of the COVID-19 pandemic. Health Secur. 2020, 18, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Fang, D.; Pan, S.; Li, Z.; Yuan, T.; Jiang, B.; Gan, D.; Sheng, B.; Han, J.; Wang, T.; Liu, Z. Large-scale public venues as medical emergency sites in disasters: Lessons from COVID-19 and the use of Fangcang shelter hospitals in Wuhan, China. BMJ Glob. Health 2020, 5, e002815. [Google Scholar] [CrossRef] [PubMed]
- Esbin, M.N.; Whitney, O.N.; Chong, S.; Maurer, A.; Darzacq, X.; Tjian, R. Overcoming the bottleneck to widespread testing: A rapid review of nucleic acid testing approaches for COVID-19 detection. RNA 2020, 26, 771–783. [Google Scholar] [CrossRef]
- Chandrashekhar, V. 1.3 billion people. A 21-day lockdown. Can India curb the coronavirus. Science 2020, 10. [Google Scholar]
- Lewis, D. What scientists have learnt from COVID lockdowns. Nature 2022, 609, 236–239. [Google Scholar] [CrossRef]
- Cao, S.; Gan, Y.; Wang, C.; Bachmann, M.; Wei, S.; Gong, J.; Huang, Y.; Wang, T.; Li, L.; Lu, K.; et al. Post-lockdown SARS-CoV-2 nucleic acid screening in nearly ten million residents of Wuhan, China. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef]
- Yan, Y.; Chang, L.; Wang, L. Laboratory testing of SARS-CoV, MERS-CoV, and SARS-CoV-2 (2019-nCoV): Current status, challenges, and countermeasures. Rev. Med. Virol. 2020, 30, e2106. [Google Scholar] [CrossRef]
- Lavezzo, E.; Franchin, E.; Ciavarella, C.; Cuomo-Dannenburg, G.; Barzon, L.; Del Vecchio, C.; Rossi, L.; Manganelli, R.; Loregian, A.; Navarin, N.; et al. Suppression of a SARS-CoV-2 outbreak in the Italian municipality of Vo’. Nature 2020, 584, 425–429. [Google Scholar] [CrossRef]
- Gollier, C.; Gossner, O. Group Testing against COVID-19; Technical Report; EconPol Policy Brief: Munich, Germany, 2020. [Google Scholar]
- Holt, E. Slovakia to test all adults for SARS-CoV-2. Lancet 2020, 396, 1386–1387. [Google Scholar] [CrossRef] [PubMed]
- Reuters. Luxembourg Starts Mass COVID-19 Testing, Aims to Cover Everyone Soon. 2020. Available online: https://www.reuters.com/article/us-health-coronavirus-luxembourg-testing-idUSKBN22W1PL (accessed on 2 October 2022).
- Iacobucci, G. Covid-19: Mass population testing is rolled out in Liverpool. BMJ 2020, 371, m4268. [Google Scholar] [CrossRef] [PubMed]
- Basso, L.J.; Salinas, V.; Sauré, D.; Thraves, C.; Yankovic, N. The effect of correlation and false negatives in pool testing strategies for COVID-19. Health Care Manag. Sci. 2022, 25, 146–165. [Google Scholar] [CrossRef]
- Huang, F.; Guo, P.; Wang, Y. Optimal group testing strategy for the mass screening of SARS-CoV-2. Omega 2022, 112, 102689. [Google Scholar] [CrossRef]
- China Daily. Nucleic Acid Testing Capacity, Efficiency Further Improved. 2022. Available online: https://www.chinadaily.com.cn/a/202204/18/WS625cba5ea310fd2b29e577b0.html (accessed on 2 October 2022).
- U.S. Department of Health and Human Services. COVID-19 Strategic Testing Plan. 24 May 2020. Available online: https://www.democrats.senate.gov/imo/media/doc/COVID%20National%20Diagnostics%20Strategy%2005%2024%202020%20v%20FINAL.pdf (accessed on 2 October 2022).
- Hosseini-Motlagh, S.M.; Samani, M.R.G.; Farokhnejad, P. Designing a testing kit supply network for suspected COVID-19 cases under mixed uncertainty approach. Appl. Soft Comput. 2021, 111, 107696. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Xie, X. A distributionally robust optimisation for COVID-19 testing facility territory design and capacity planning. Int. J. Prod. Res. 2022, 60, 4229–4252. [Google Scholar] [CrossRef]
- Liu, K.; Liu, C.; Xiang, X.; Tian, Z. Testing facility location and dynamic capacity planning for pandemics with demand uncertainty. Eur. J. Oper. Res. 2023, 304, 150–168. [Google Scholar] [CrossRef]
- U.S. Department of Health and Human Services. Community-Based Testing Sites for COVID-19. 2022. Available online: https://www.hhs.gov/coronavirus/community-based-testing-sites/index.html (accessed on 2 October 2022).
- Center for Disease Control and Prevention. Guidance for SARS-CoV-2 Rapid Testing Performed in Point-of-Care Settings. 2022. Available online: https://www.cdc.gov/coronavirus/2019-ncov/lab/point-of-care-testing.html (accessed on 2 October 2022).
- GOV.UK. List of General Population COVID-19 Testing Providers. 2022. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/1105694/covid-private-testing-providers-general-testing-22.9.22.csv/preview (accessed on 2 October 2022).
- Fox Business. COVID Testing Sites Search Part of Google, Biden Partnership. 2021. Available online: https://www.foxbusiness.com/politics/biden-administration-worked-with-google-to-help-people-track-down-covid-testing-sites (accessed on 2 October 2022).
- BBC News. Coronavirus: Bradford Walk-in Testing Centre Opening. 2020. Available online: https://www.bbc.com/news/uk-england-leeds-53247897 (accessed on 2 October 2022).
- The New York Times. I’m Overseas and I’ve Tested Positive. What Now? 2022. Available online: https://www.nytimes.com/2022/05/04/travel/covid-test-positive-traveling-overseas.html (accessed on 2 October 2022).
- Li, Z.; Gao, J. 15-Minute nucleic acid test circles strategy in large cities in China. J. Biosaf. Biosecurity 2022, 4, 84–85. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Seyedi, P.; Syam, S.S. A survey of healthcare facility location. Comput. Oper. Res. 2017, 79, 223–263. [Google Scholar] [CrossRef]
- Kim, D.G.; Kim, Y.D. A branch and bound algorithm for determining locations of long-term care facilities. Eur. J. Oper. Res. 2010, 206, 168–177. [Google Scholar] [CrossRef]
- Galvao, R.D.; Espejo, L.G.A.; Boffey, B. A hierarchical model for the location of perinatal facilities in the municipality of Rio de Janeiro. Eur. J. Oper. Res. 2002, 138, 495–517. [Google Scholar] [CrossRef]
- Griffin, P.M.; Scherrer, C.R.; Swann, J.L. Optimization of community health center locations and service offerings with statistical need estimation. IIE Trans. 2008, 40, 880–892. [Google Scholar] [CrossRef]
- Şahin, G.; Süral, H.; Meral, S. Locational analysis for regionalization of Turkish Red Crescent blood services. Comput. Oper. Res. 2007, 34, 692–704. [Google Scholar] [CrossRef]
- Ndiaye, M.; Alfares, H. Modeling health care facility location for moving population groups. Comput. Oper. Res. 2008, 35, 2154–2161. [Google Scholar] [CrossRef]
- Mestre, A.M.; Oliveira, M.D.; Barbosa-Póvoa, A.P. Location–allocation approaches for hospital network planning under uncertainty. Eur. J. Oper. Res. 2015, 240, 791–806. [Google Scholar] [CrossRef]
- Shishebori, D.; Babadi, A.Y. Robust and reliable medical services network design under uncertain environment and system disruptions. Transp. Res. Part E Logist. Transp. Rev. 2015, 77, 268–288. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Z.; Jiang, P.; Luo, L. A stochastic programming model for emergency supplies pre-positioning, transshipment and procurement in a regional healthcare coalition. Socio-Econ. Plan. Sci. 2022, 82, 101279. [Google Scholar] [CrossRef] [PubMed]
- Akıncılar, A.; Akıncılar, E. A new idea for ambulance location problem in an environment under uncertainty in both path and average speed: Absolutely robust planning. Comput. Ind. Eng. 2019, 137, 106053. [Google Scholar] [CrossRef]
- Toro-Díaz, H.; Mayorga, M.E.; Chanta, S.; McLay, L.A. Joint location and dispatching decisions for emergency medical services. Comput. Ind. Eng. 2013, 64, 917–928. [Google Scholar] [CrossRef]
- Silva, F.; Serra, D. Locating emergency services with different priorities: The priority queuing covering location problem. J. Oper. Res. Soc. 2008, 59, 1229–1238. [Google Scholar] [CrossRef]
- Syam, S.S.; Côté, M.J. A location–allocation model for service providers with application to not-for-profit health care organizations. Omega 2010, 38, 157–166. [Google Scholar] [CrossRef]
- Cho, S.H.; Jang, H.; Lee, T.; Turner, J. Simultaneous location of trauma centers and helicopters for emergency medical service planning. Oper. Res. 2014, 62, 751–771. [Google Scholar] [CrossRef]
- Chan, T.C.; Demirtas, D.; Kwon, R.H. Optimizing the deployment of public access defibrillators. Manag. Sci. 2016, 62, 3617–3635. [Google Scholar] [CrossRef]
- Nasrollahzadeh, A.A.; Khademi, A.; Mayorga, M.E. Real-time ambulance dispatching and relocation. Manuf. Serv. Oper. Manag. 2018, 20, 467–480. [Google Scholar] [CrossRef]
- Mete, H.O.; Zabinsky, Z.B. Stochastic optimization of medical supply location and distribution in disaster management. Int. J. Prod. Econ. 2010, 126, 76–84. [Google Scholar] [CrossRef]
- Jenkins, P.R.; Lunday, B.J.; Robbins, M.J. Robust, multi-objective optimization for the military medical evacuation location-allocation problem. Omega 2020, 97, 102088. [Google Scholar] [CrossRef]
- Alghanmi, N.; Alotaibi, R.; Alshammari, S.; Alhothali, A.; Bamasag, O.; Faisal, K. A survey of location-allocation of points of dispensing during public health emergencies. Front. Public Health 2022, 10, 811858. [Google Scholar] [CrossRef]
- Alinaghian, M.; Goli, A. Location, allocation and routing of temporary health centers in rural areas in crisis, solved by improved harmony search algorithm. Int. J. Comput. Intell. Syst. 2017, 10, 894–913. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, N.; Zhang, J. Integrated temporary facility location and casualty allocation planning for post-disaster humanitarian medical service. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 1–16. [Google Scholar] [CrossRef]
- Caunhye, A.M.; Li, M.; Nie, X. A location-allocation model for casualty response planning during catastrophic radiological incidents. Socio-Econ. Plan. Sci. 2015, 50, 32–44. [Google Scholar] [CrossRef]
- Ramirez-Nafarrate, A.; Lyon, J.D.; Fowler, J.W.; Araz, O.M. Point-of-dispensing location and capacity optimization via a decision support system. Prod. Oper. Manag. 2015, 24, 1311–1328. [Google Scholar] [CrossRef]
- Chen, A.Y.; Yu, T.Y. Network based temporary facility location for the Emergency Medical Services considering the disaster induced demand and the transportation infrastructure in disaster response. Transp. Res. Part B Methodol. 2016, 91, 408–423. [Google Scholar] [CrossRef]
- Sharma, B.; Ramkumar, M.; Subramanian, N.; Malhotra, B. Dynamic temporary blood facility location-allocation during and post-disaster periods. Ann. Oper. Res. 2019, 283, 705–736. [Google Scholar] [CrossRef]
- Tang, L.; Li, Y.; Bai, D.; Liu, T.; Coelho, L.C. Bi-objective optimization for a multi-period COVID-19 vaccination planning problem. Omega 2022, 110, 102617. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Wan, X.; Wang, Q. A multi-period location–allocation model for integrated management of emergency medical supplies and infected patients during epidemics. Comput. Ind. Eng. 2022, 2022, 108640. [Google Scholar] [CrossRef]
- Devi, Y.; Patra, S.; Singh, S.P. A location-allocation model for influenza pandemic outbreaks: A case study in India. Oper. Manag. Res. 2021, 15, 487–502. [Google Scholar] [CrossRef]
- Risanger, S.; Singh, B.; Morton, D.; Meyers, L.A. Selecting pharmacies for COVID-19 testing to ensure access. Health Care Manag. Sci. 2021, 24, 330–338. [Google Scholar] [CrossRef]
- Villicaña-Cervantes, D.; Ibarra-Rojas, O.J. Accessible location of mobile labs for COVID-19 testing. Health Care Manag. Sci. 2022. [Google Scholar] [CrossRef] [PubMed]
- Chenghua Release. Normalized Nucleic Acid Detection Sites in Chenghua District (In Chinese). 2022. Available online: https://mp.weixin.qq.com/s/KToBszRHqTU-py29x9ndHA (accessed on 2 October 2022).
- Baidu Map. Dynamic Thermodynamic Diagram (In Chinese). 2022. Available online: https://lbs.baidu.com/index.php?title=androidsdk/guide/render-map/DynamicThermodynamicDiagram (accessed on 2 October 2022).
- Gaode Map. Gaode Open Platform (In Chinese). 2022. Available online: https://lbs.amap.com/api/cooperation/about/us (accessed on 2 October 2022).

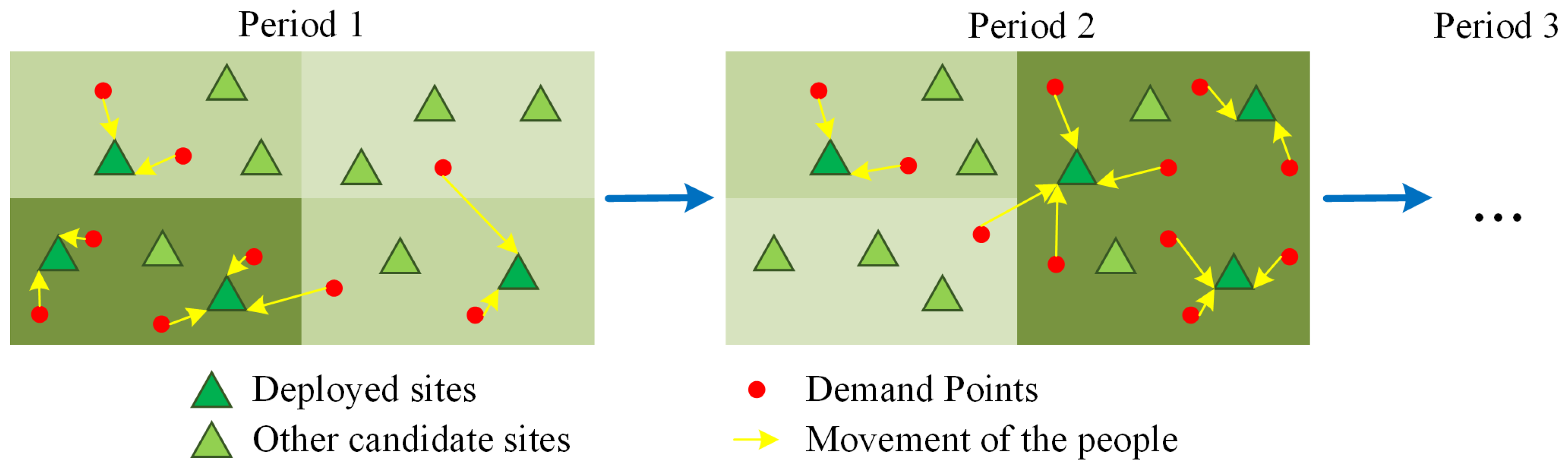


| Sets |
|---|
| , periods, indexed by t |
| I, COVID-19 NAT demand points, indexed by i |
| J, candidate COVID-19 NAT sites, indexed by j |
| K, types of medical supplies for COVID-19 NAT, indexed by k |
| H, types of staff for COVID-19 NAT, indexed by h |
| Parameters |
| , demand amount, number of target people needing COVID-19 NAT, at demand point i in period t |
| , distance between demand point i and candidate NAT site j |
| , amount of types k medical supplies required to run candidate NAT site j per period |
| , number of type h staff required to run candidate NAT site j per period |
| , the maximum amount of demand that can be served per period at candidate NAT site j |
| , fixed cost of deploying NAT site j |
| , total amount of types k medical supplies available in period t |
| , total number of type h staff available in period t |
| , unit penalty cost of wasting NAT capacity of opened candidate NAT site j |
| , unit penalty cost of NAT capacity overflow of opened candidate NAT site j |
| , a factor transferring distance into cost |
| M, a huge positive number |
| Decision Variables |
| , equals 1 if candidate NAT site j opens in period t; 0, otherwise |
| , number of target people of demand point i moving to candidate NAT site j in period t |
| , amount of capacity left at opened candidate NAT site j in period t |
| , amount of capacity overflow at opened candidate NAT site j in period t |
| Type | Capacity | Cost | ||||||
|---|---|---|---|---|---|---|---|---|
| I | 2000 | 2000 | 1 | 4 | 10 | 800 | 3 | 5 |
| II | 800 | 1400 | 1 | 4 | 8 | 500 | 2 | 3 |
| III | 400 | 800 | 3 | 2 | 3 | 300 | 1 | 1 |
| IV | 400 | 800 | 3 | 2 | 4 | 300 | 1 | 2 |
| V | 400 | 1000 | 5 | 2 | 5 | 300 | 1 | 3 |
| Period | ||||
|---|---|---|---|---|
| 1 | 2000 | 60,000 | 400 | 600 |
| 2 | 2000 | 80,000 | 300 | 800 |
| 3 | 2000 | 80,000 | 300 | 800 |
| 4 | 2000 | 60,000 | 400 | 600 |
| Strategies | Cost Components ( CNY) | Total Cost ( CNY) | |||
|---|---|---|---|---|---|
| Deployment | Capacity Waste | Capacity Overflow | Travel | ||
| BS | 0.364 | 0.221 | 0.003 | 3.829 | 4.417 |
| CS-I | - | - | - | - | (infeasible) |
| CS-I (3.5 km) | 0.557 | 0.448 | 0.011 | 4.182 | 5.198 |
| CS-II | 0.380 | 0.242 | 0.008 | 3.874 | 4.504 |
| CS-III | 0.386 | 0.245 | 0.006 | 3.866 | 4.503 |
| Strategies | Periods | Hospitals (57) | Clinics (68) | HCs (41) | Pharmacies (44) | Other Sites (22) |
|---|---|---|---|---|---|---|
| BS | 0 | 13 | 17 | 33 | 1 | |
| 3 | 28 | 26 | 29 | 8 | ||
| 10 | 37 | 31 | 34 | 14 | ||
| 2 | 20 | 21 | 30 | 5 | ||
| CS-I (3.5 km) | - | 25 | 28 | 17 | 18 | 22 |
| CS-II | - | 3 | 27 | 24 | 30 | 8 |
| CS-III | - | 3 | 28 | 24 | 30 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Luo, L.; Tang, X.; Wang, Q. Optimizing Large-Scale COVID-19 Nucleic Acid Testing with a Dynamic Testing Site Deployment Strategy. Healthcare 2023, 11, 393. https://doi.org/10.3390/healthcare11030393
He X, Luo L, Tang X, Wang Q. Optimizing Large-Scale COVID-19 Nucleic Acid Testing with a Dynamic Testing Site Deployment Strategy. Healthcare. 2023; 11(3):393. https://doi.org/10.3390/healthcare11030393
Chicago/Turabian StyleHe, Xiaozhou, Li Luo, Xuefeng Tang, and Qingyi Wang. 2023. "Optimizing Large-Scale COVID-19 Nucleic Acid Testing with a Dynamic Testing Site Deployment Strategy" Healthcare 11, no. 3: 393. https://doi.org/10.3390/healthcare11030393
APA StyleHe, X., Luo, L., Tang, X., & Wang, Q. (2023). Optimizing Large-Scale COVID-19 Nucleic Acid Testing with a Dynamic Testing Site Deployment Strategy. Healthcare, 11(3), 393. https://doi.org/10.3390/healthcare11030393






