Abstract
To simulate the behaviors of photovoltaic (PV) systems properly, the best values of the uncertain parameters of the PV models must be identified. Therefore, this paper proposes a novel optimization framework for estimating the parameters of the triple-diode model (TDM) of PV units with different technologies. The proposed methodology is based on the generalized normal distribution optimization (GNDO) with two novel strategies: (i) a premature convergence method (PCM), and (ii) a ranking-based updating method (RUM) to accelerate the convergence by utilizing each individual in the population as much as possible. This improved version of GNDO is called ranking-based generalized normal distribution optimization (RGNDO). RGNDO is experimentally investigated on three commercial PV modules (Kyocera KC200GT, Ultra 85-P and STP 6-120/36) and a solar unit (RTC Si solar cell France), and its extracted parameters are validated based on the measured dataset points extracted at generalized operating conditions. It can be reported here that the best scores of the objective function are equal to 0.750839 mA, 28.212810 mA, 2.417084 mA, and 13.798273 mA for RTC cell, KC200GT, Ultra 85-P, and STP 6-120/36; respectively. Additionally, the principal performance of this methodology is evaluated under various statistical tests and for convergence speed, and is compared with a number of the well-known recent state-of-the-art algorithms. RGNDO is shown to outperform the other algorithms in terms of all the statistical metrics as well as convergence speed. Finally, the performance of the RGNDO is validated in various operating conditions under varied temperatures and sun irradiance levels.
1. Introduction
Over the last decades, due to the significant financial and environmental issues with conventional energy sources, such as fossil fuels, there has been considerable interest in clean, renewable energy sources (RESs) [1,2]. Among the RESs, solar energy—using photovoltaic (PV) systems to convert solar energy into electricity—is the second most used RES worldwide, after wind energy [3]. Since PV systems rely on solar energy, their performance is significantly influenced by variations in solar irradiance levels and in temperature. Therefore, to optimize the performance of these systems before installation, suitable mathematical models are required to accurately simulate the behavior of the PV system under different operation conditions [4,5,6]. The three most common PV system models found in the literature are the single-diode model (SDM) [7,8], the double-diode model (DDM) [7,8], and the triple-diode model (TDM) [9,10].
The SDM needs only five parameters to be estimated, which is straightforward, but its performance deteriorates at low irradiance levels and under temperature variations [11]. To overcome those drawbacks, the DDM with seven unknown parameters was proposed, using an additional diode to recombine the current and manage other non-idealities [11]. However, the DDM still suffers from some defects in recombining the current and the other non-idealities. Thus, the TDM with nine unknown parameters was proposed using an additional diode [12]. Regrettably, the nine unknown parameters are not directly provided by the manufacturers, so they need to be accurately estimated to optimize the PV systems. The problem is converted to an optimization problem with a non-linear objective function (OF) with a large count of local minima in order to minimize the difference between the measured and estimated I-V and P-V curves.
Due to the significant success of meta-heuristic algorithms in solving many real-world optimization problems [13,14,15,16], they have attracted the interest of researchers to solve the parameter extraction problems of PV models. A new parameter estimation technique based on the Interior Search Optimization Algorithm has been recently proposed for estimating the unknown parameters of the supercapacitor (SC) as an energy storage device for different applications like electric vehicles and hybrid renewable systems [17]. Allam [10] adapted the moth-flame optimization (MFO) algorithm to identify the nine parameters of the TDM for the multi-crystalline solar cell/module. Experimentally, MFO was compared with a number of recent robust state-of-the-art algorithms: differential evolution with integrated mutation per iteration and flower pollination (FPA) algorithms to verify its efficacy. Moreover, MFO was investigated at different operation conditions to identify its ability to extract the unknown parameters of the PV models at different irradiance levels and temperatures. The experimental studies confirm the superiority of MFO in minimizing the Root Mean Square Error (RMSE) within the least execution time.
El-Hameed [6] employed the manta-rays foraging optimizer (MRFO) to estimate the nine unknown parameters of the TDM and used two datasets to validate its performance: the measured data and the three key points taken from the manufacturer’s datasheets. They used two test cases—Kyocera polycrystalline KC200GT solar module and the Ultra 85-P—to investigate the performance of MRFO, which was compared with a number of the well-known optimization algorithms. The grasshopper optimization algorithm (GOA) [18] was proposed to estimate the parameters of the TDM Kyocera KC200GT and Solarex MSX-60 PV cells. Its performance was validated under different irradiance and temperature levels and compared with a number of the other parameter estimation algorithms under the same condition to ensure a fair comparison.
Yousri, D. et al. [19] proposed a new parameter extraction technique based on fractional chaotic ensemble particle swarm optimizer (FC-EPSO) to estimate the parameters of SDM, DDM, and TDM based on measured data extracted under different irradiance and temperature levels. In FC-EPSO, the factional chaos maps are integrated with the PSO to improve its performance in reaching accurate and reliable outcomes. FC-EPSO was validated on three different experimental datasets: two are extensively used in commercial applications and the third was measured in the laboratory at different irradiance and temperature levels. Finally, FC-EPSO was compared with a number of state-of-the-art algorithms to verify its efficacy.
In [20], the coyote optimization algorithms (COA) were proposed for estimating the parameters of the various PV models: SDM, DDM, and TM. The COA was investigated on various types of PV modules: mono-crystalline, multi-crystalline, and thin-film under various operation conditions. Further, Selem [3] proposed the artificial electric field algorithm (AEFA) to extract the unknown TDM parameters. AEFA was investigated on two commercial models, validated on measured dataset points, and compared with a range of other techniques to determine its superiority. Additionally, Ibrahim [21] proposed the improved wind-driven optimization algorithm (IWDO) to find unidentified parameters of the TDM based on improving the performance of IWDO by using the mutation strategy of the differential evolution algorithm to boost the exploration operator of the standard algorithm. The proposed approach was used to find the parameters of three commercial PV models and, to verify its efficacy, it was compared with a number of algorithms, such as the standard wind-driven optimization, the MFO, the sunflower optimization, the adaptive wind-driven optimization, and the improved opposition-based whale optimization algorithms. Two additional algorithms have been recently proposed for tackling these problems: the Harris hawks optimization (HHO) algorithm [22], and the interval branch and bound global optimization algorithm [23]. Some of the other recent optimization algorithms proposed for the different PV models: SDM, DDM, TDM, and PV modules are reviewed in Table 1.

Table 1.
Survey of the existing state-of-the-art algorithms for parameter estimation of different PV models.
According to the small amount of the research addressing parameter selection for TDM the techniques investigated are prone to becoming trapped in local minima and are generally slow in converging to the near-optimal solution. Recently, a new meta-heuristic algorithm known as the generalized normal distribution optimization (GNDO) was proposed to address the parameter extraction of SDM and DDM [40]. Although significant success was achieved by this algorithm for SDM and DDM, it still suffers from the low premature convergence caused by:
- ❖
- Relating its exploitation capability with the average of the current mean position of the population, the best-so-far solution, and the position of the current individual, and that may cause low convergence toward the best-so-far solution for reaching better solutions quickly whether the best-so-far solution is not a local minimum one.
- ❖
- Relating its exploration capability with three solutions selected randomly from the population and may make the algorithm explore regions that may already have been explored.
To help the algorithm to explore more regions, while increasing its convergence speed, two improvements are proposed:
- ❖
- A novel ranking-based position updating method (RUM) to help the algorithm in exploring as many regions as possible; and
- ❖
- A premature convergence method (PCM) to help accelerate its convergence speed toward the near-optimal solution.
Those two methods: RUM and PCM, are integrated with the GNDO to accelerate its convergence toward the near-optimal solution for triple-diode models; this improved version of GNDO is called the ranking-based GNDO (RGNDO).
Experimentally, the performance of RGNDO is investigated on three PV modules and a single solar cell, and its extracted parameters on TDM are validated based on the measured I-V data. Its performance is then extensively evaluated in terms of various statistical metrics: the best, average (avg), worst, standard deviation (SD), the quartiles and Wilcoxon Rank Sum test for its outcomes, and the convergence speed toward the near-optimal solution. Finally, to check its efficacy, it was compared with a number of state-of-the-art optimization algorithms that prove the superiority of the proposed algorithm in terms of all statistical metrics and convergence speed. This paper briefly provides the following contributions:
- Improving the GNDO by the novel RUM and the premature convergence method (PCM) to produce a new variant called RGNDO for tackling the parameter estimation of the TDM.
- Comparing the performance of RGNDO with some well-established parameter estimation techniques, in addition to the standard GNDO, on five well-known commercial PV modules confirms the superiority of RGNDO over these compared algorithms in terms of convergence speed and final accuracy, in addition to its competitivity for the computational cost.
The organization of this paper is as follows: Section 2 describes the mathematical model of the TDM, Section 3 describes the standard GNDO, Section 4 extensively introduces the proposed improved RGNDO algorithm, Section 5 describes the experimental settings, Section 6 shows the numerical results of the experiments with some discussion, and Section 7 provides some conclusions along with an outline for the future work.
2. Mathematical Descriptions of the Triple-Diode Model
The performance of the PV systems under the SDM deteriorates with low irradiance and temperature deviation [11]. Therefore, DDM that employs another diode to recombine current and other non-idealities of the solar cell (SC) has been developed to get rid of this problem [41]. Unfortunately, the DDM [41] still suffers from some anomalies in the recombination process, so the TDM [12] has been suggested to overcome those drawbacks for reaching a better model. In parallel with the diodes of the DDM, the TDM used another diode to dispose of the flaws of the recombination process in DDM.
The structure of the TDM is depicted in Figure 1, in which the output current is calculated by subtracting the source current Iph or also called photo-current source, from the four currents: ID1, ID2, ID3, and Ish as described in the following equation:
where ID1 is the diffusion current, ID2 indicates the recombination current employed to recombine current and other non-idealities, and ID3 indicates the current diode element due to recombination in the flaw regions, grain boundaries, etc. [42,43]. Generally, IDi is computed by Equation (2), and Ish is the shunt current extracted using Equation (3).
Isdi indicates the reverse saturation current of the ith diode, V is the output voltage of the cell, Rs indicates the series resistance, ai expresses the ideality factor of the ith diode, K refers to Boltzmann’s Constant , q is the electron charge , and T is the temperature of the cell in kelvin (K).
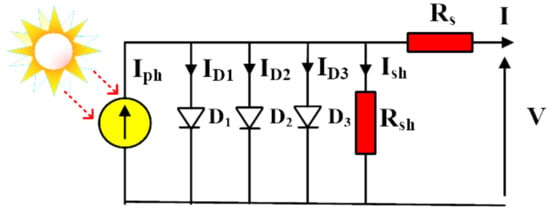
Figure 1.
The equivalent circuit of TDM.
When the solar generation unit comprises a single solar cell, the amount of electricity generated is very small. Consequently, PV modules connect Ns solar cells in series to increase the output voltage of the PV system. The PV modules can be also formulated with the previous equations with the difference that .
3. The Standard Algorithm: Generalized Normal Distribution Optimization
Recently, Zhang [40] proposed a novel optimization algorithm inspired by the Gaussian distribution theory called the GNDO algorithm for estimating efficiently and accurately the parameters of the SDM and DDM. As with other meta-heuristic algorithms, GNDO uses two operators: exploration and exploitation to search for the solution of the optimization problem. The mathematical model of GNDO is explained in the remainder of this section.
3.1. Local Exploitation
In this operator, GNDO searches for a better solution under guiding the current mean of the population, the best-so far solution, and the current solution—that is mathematically described as:
where Tit is a vector containing the next position of the ith individual at generation t. N is the population size. µi refers to the generalized mean position of the ith individual and computed using Equation (5). is the penalty factor and computed according to Equation (8).
where X* is the best-so-far solution, Xit is the current position of the ith individual at generation t, M is the current population mean estimated using Equation (6), and the generalized standard variance () is estimated according to Equation (7).
where r1, r2, , and are random numbers generated between 0 and 1.
3.2. Global Exploration
To explore the search space of the problem without becoming trapped in local minima, GNDO uses the exploration operator, which is based on three individuals selected randomly from the population and is modeled as follows:
and are two random numbers based on the standard normal distribution, β is a random number between 0 and 1 and known as the adjusting parameter, and and are two trial positions computed by:
p1, p2, and p3 are three indices selected randomly from the population where p1 ≠ p2 ≠ p3 ≠ i. The tradeoff between the exploration and exploitation in GNDO is achieved randomly.
4. The Proposed Algorithm: RGDNO
In this phase, the GNDO is improved using two strategies: a ranking method based on a novel methodology, and a PCM for tackling the parameter extraction of the TDM. The ranking method eliminates the individuals that may be unbeneficial within the next generation, due to the local optima problem or to their far distance from the optimal solution, while PCM seeks to accelerate the convergence toward the optimal solution based on a controlling factor that moves the current solution toward either two individuals selected randomly from the population or the current and the best-so-far solution. In the rest of this section, the steps of the proposed algorithm are explained in detail.
4.1. Initialization
At the start of the optimization process using GNDO, a number of N individuals are randomly created with dimension, d, equal to the number of unknown parameters (nine in our problem) that needed to be estimated. Initially, those individuals are randomly assigned values within the search ranges of the problem according to the following formula.
where and are two vectors including the upper and lower bound of the problems, respectively, and r is a vector assigned randomly between 0 and 1. The search ranges of the nine unknown parameters of the TDM according to the literature [6] are given in Table 2 and an illustrative example for representing a solution within those search ranges with ISC = 0.7605 is given in Table 3.

Table 2.
Search ranges of nine parameters.

Table 3.
An initial solution within the search ranges of nine parameters.
4.2. The Objective Function
To optimize the parameters extraction problem of the TDM using the optimization algorithm, an OF needs to be defined. This OF is established according to the root mean squared error (RMSE) between the estimated current based on the obtained parameters of the empirical mathematical model solved by the Newton–Raphson method (NPM) and the measured current given in the datasheet of a real SC [44]. The algorithm with the lowest RMSE considers the best because it could obtain the parameters that minimize the error rate between the measured and estimated. Generally, the OF for TDM is mathematically formulated as follows [20]:
where Im is the measured current, M is the length of the measured data, and Ie is the estimated current based on the mathematical model solved by NPM and computed by the following formula:
I is substituted using Equation (1) and I’ is the first derived of Equation (1) with respect to I.
4.3. Ranking-Based Novel Updating Method (RUM)
In [45], a novel method known as the ranking method was proposed to eliminate the solutions that may be unbeneficial within the rest of the optimization process and to replace them with solutions created based on a novel methodology to help the optimization algorithm, in particular, to accelerate the convergence speed and cover intractable regions.
The author in [45] sought to accelerate the convergence toward the best-so-far solution by moving the unbeneficial solutions to the region located between the current position and the best-so-far solution in the hope of finding a better solution within this region before accelerating the convergence toward the optimal solution. Within this research, a new methodology working on balancing between the exploration and exploitation operators is proposed and formulated as follows:
where tmax is the maximum generation. In this equation, within the start of the optimization process, the part taken of the best-so-far solution is very small, while the part taken by the unbeneficial solution is very high, which increases the exploration capability of the algorithm that decreases gradually as the optimization process progresses. Gradually, the part taken from the best-so-far is increased and the other part that is taken from Xit reduces, until reaching the end of the optimization process. In this case, the part taken of the best-so-far is so high compared with the part taken of the unbeneficial solution that is very small and this will encourage the exploitation capability. The unbeneficial solutions, according to [45], are extracted by calculating the number of consecutive generations (NCG) predefined by the researcher based on their experiments, in which those solutions couldn’t find a better solution than the last local best one. The flowchart of this strategy is given in Figure 2.
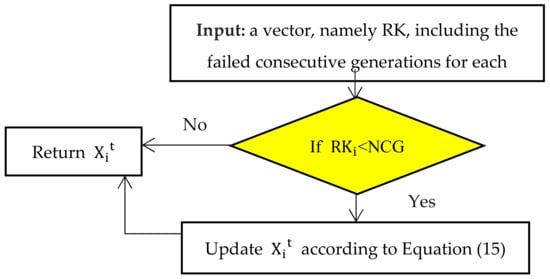
Figure 2.
The flow chart of the ranking method integrated with a novel updating method.
4.4. Premature Convergence Method (PCM)
In an attempt to accelerate the convergence toward the best-so-far solution while avoiding becoming trapped into local minima, a novel method known as the PCM has been proposed here. This method uses a controlling factor, namely , and created randomly within [0, 1] that is used to determine if the next search will be within the current and the best-so-far, or within two individuals, I1 and I2, selected randomly of the population, where I1 ≠ I2. This method will increase the exploration when < 0.5 while increasing the exploitation when and balancing between the two when . In general, the mathematical model of this method is as follows:
Finally, the two methods: the premature convergence of PCM and the ranking-based novel updating of RUM are integrated with GNDO to increase its exploration and exploitation capability to help the algorithm to reach better outcomes in fewer evaluations when estimating the unknown parameters of the TDM. The RUM is used to balancing between the exploration and exploitation capability of the algorithm in the hope of finding better solutions within the optimization process, while PCM is related to that controls the next position of the current individuals. The steps of the proposed algorithm RGNDO are listed in Table 4. The main advantages of the improved GNDO (RGNDO) as follows:

Table 4.
The steps of RGNDO Algorithm.
- Utilizing each individual in the population through the optimization process by the RUM to help in exploring more regions within the search space as possible. The RUM here aids the standard GNDO to improve the exploration operator at the start of the optimization process as an attempt to prevent stuck into local minima, while, with increasing the current function evaluation, the exploration operator is gradually converted into exploitation to search around the best-so-far solution to promote the convergence speed.
- Highly stable due to using the PCM that helps in steering the convergence speed in the right direction of the best-so-far solution to explore the promising regions that appear within the optimization process.
5. Experimental Results
In this section, the parameter settings and dataset descriptions are described in detail to illustrate all the dimensions of our experiments which are performed on an Intel(R) Core (TM) i7-4700MQ CPU @ 2.40 GHz device with 32 GB of RAM, using MATLAB R2019a to implement the algorithms.
5.1. Parameter Settings
RGNDO has a single parameter, NCG, which needs to be optimally adjusted to maximize the performance of the RNGDO. NCG is defined as the lower bound of the number of times each individual could find a worse solution than the last best one. To efficiently extract this parameter, the performance of RNGDO under different values (0, 1, 2, 3, 4, 5, 6, 7, 8, 10, and 11) within 30 independent times is depicted in Figure 3. According to this figure, the best value for NCG is 3 or 4. As a result, a value of 3 is used for NCG within our experiments. The second most important parameter with a major effect on the performance of the proposed algorithm is the population size: a large population size will increase the diversity among the members, reducing the possibility of reaching the optimal solution; a small population size skips a lot of the regions within the search space, which may include the promising solution. Hence, an extensive experiments are conducted to estimate the best value for this parameter and depicted in Figure 4 that confirms that a value of 30 is the best for the parameter N.
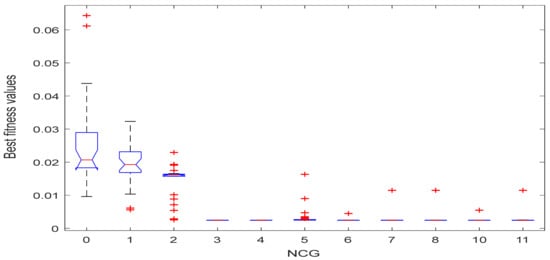
Figure 3.
Sensitivity analysis of parameter NCG.
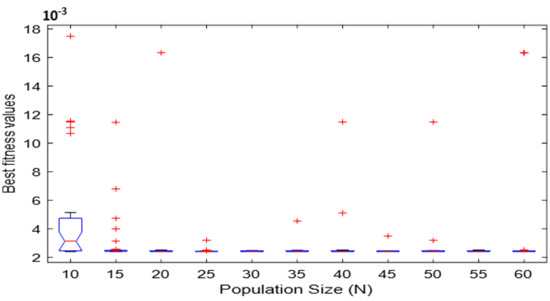
Figure 4.
Sensitivity analysis of parameter N.
In addition, to confirm the superiority of the proposed RNGDO method, it is compared with a number of the well-known algorithms proposed recently for the parameter extraction of the solar cells according to the parameters used by the authors with the exception of that is adopted at 30,000 to make a fair comparison:
- ▪
- Artificial ecosystem-based optimization (AEO) [46].
- ▪
- CPMPSO [24].
- ▪
- Improved teaching learning-based optimization (ITLBO) [31].
- ▪
- WOA [47].
- ▪
- GNDO [40].
- ▪
- Interior search algorithm (ISA) [17].
- ▪
- HHO [22].
5.2. Dataset Descriptions
To validate the efficacy of RNGDO to characterize the TDM at standard operating conditions (STC), a PV model based on RTC France [46] and consists of a PV cell will be used, in addition to two PV modules, which consists of a number of solar cells joined in series: Kyocera KC200GT [18], Ultra 85-P [48] and STP6-120/36 module [49]. Furthermore, the Ultra 85-P module is used to determine the performance of the proposed algorithm in estimating its nine parameters at dynamic irradiance and various temperature levels. RTC France comprises a single solar cell with 26 test points, experimentally extracted at T = 33 °C and G = 1000 W/m2). Additionally, ISC for RTC France is being set to 0.7605 A. For the Ultra 85-P module, ISC is equal to 5.45 A and experiments on this module are conducted on measured data of 20 test points extracted at 48.7 °C and 950 W/m2. For the STP6-120/36 module, ISC is equal to 7.48 A and 24 test points were used and extracted at 55 °C and 1000 W/m2. Regarding the Kyocera KC200GT—204.6 W module, it consists of 54 cells connected in series with , and G of at standard operating conditions.
6. Results and Discussion
6.1. Test Case 1: RTC France Cell
For this solar cell, the proposed algorithm and the seven others are executed 30 independent times and the best RMSE for each with its parameter values is displayed in Table 5. The statistical analysis, such as best, worst, avg, SD, and ranks within the independent runs are introduced in Table 6, from which it can be seen that the proposed algorithm has superior performance in terms of best, avg, worst, SD, and rank. Additionally, Figure 5a,b compares the I-V and P-V curves between the measured and estimated data that show the efficacy of RGNDO in estimating the unknown parameters accurately and efficiently to minimize the difference between the measured and estimated. In the final stage, Figure 6a shows the convergence speed of all algorithms, confirming that RGNDO is the fastest.

Table 5.
Comparison according to the best RMSE and its corresponding parameter on RTC France.

Table 6.
Comparison among algorithms on RTC France under the statistical analysis.
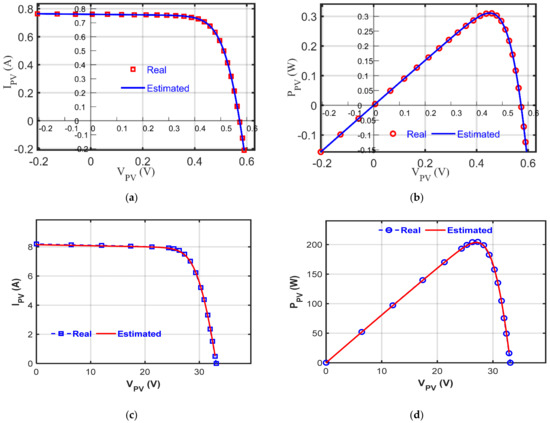
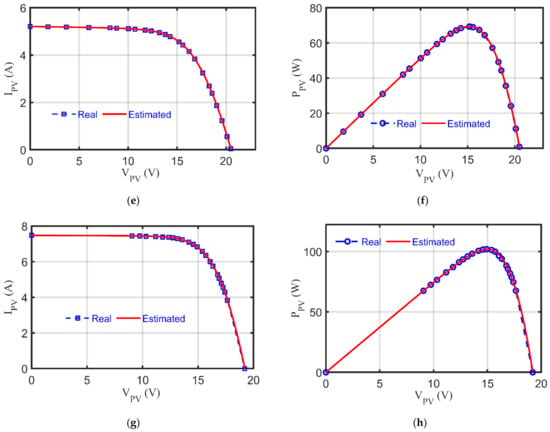
Figure 5.
Characteristics curves represented by RGNDO: (a) I−V curve of RTC France; (b) P−V curve of RTC France; (c) I-V curve of Kyocera KC200GT; (d) P-V curve of Kyocera KC200GT; (e) I−V curve of Ultra 85−P; (f) P−V curve of Ultra 85-P; (g) I−V curve of STP6−120/36 module; (h) P-V curve of STP6−120/36.
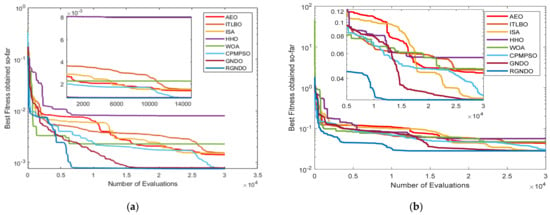
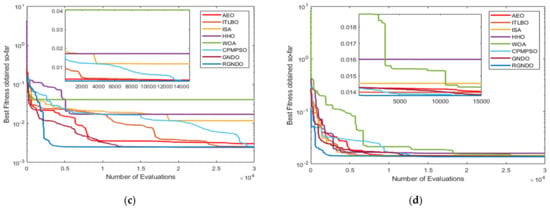
Figure 6.
Convergence curves are achieved by the algorithms: (a) Convergence on RTC France; (b) Convergence on Kyocera KC200GT; (c) Convergence on Ultra 85−P; (d) Convergence on STP6−120/36.
6.2. Test Case 2: Kyocera KC200GT—204.6 W Module
Additionally, to further affirm the superiority of RGNDO, this section presents a comparison with some of the other algorithms on another PV module called Kyocera KC200GT—204.6 W at the STC. All algorithms in this comparison are executed 30 independent times and the obtained parameters in the best time are presented with the corresponding RMSE value in Table 7, in addition to showing the other statistical analyses in Table 8. From which it is clear that GNDO fulfills the best values (indicated in bold), for all performance metrics: best, worst, avg, and rank, except for SD, where GNDO could reach better value. Further, Figure 5c,d confirms the effectiveness of RGNDO in minimizing the error between the measured and estimated data. Further, Figure 6b confirms the superiority of RGNDO in terms of convergence. It is worthy stating that the reported results in Table 7 are per cell.

Table 7.
Comparison of the best RMSE and its extracted parameter per cell on Kyocera KC200GT.

Table 8.
Comparison of the fitness on Kyocera KC200GT.
6.3. Test Case 3: Ultra 85-P
In this study, the performance of RGNDO is compared to this module at the STC. After running each algorithm 30 independent runs, the best fitness with its extracted parameters is in Table 9 and the statistical analysis is in Table 10, from which it can be seen that RGNDO achieves the best outcomes (indicated in bold), for all statistical metrics: best, worst, avg, SD, and rank. Further, Figure 5e,f confirms the effectiveness of RGNDO in minimizing the error between the measured and estimated data. Further, Figure 6c confirms the superiority of RGNDO in terms of convergence. Once again, it is worthy to mention that the resported paramters in Table 9 is per cell.

Table 9.
Comparison of the best RMSE and its extracted parameter per cell on Ultra 85-P.

Table 10.
Comparison of the fitness on Ultra 85-P.
6.4. Test Case 4: STP6-120/36 Module
In this section, RGNDO is validated on an additional module, namely STP6-120/36, with different characteristics from the previous two to determine its ability to estimate the unknown parameters under predefined setup conditions. Experimentally, each algorithm is implemented 30 independent trials, afterward, the extracted parameters for the best RMSE obtained within 30 independent runs are in Table 11. The statistical analyses of the outcomes obtained within those independent runs are in Table 12, which illustrates the superior performance of RGNDO. To indicate the consistency of RGNDO, the measured and estimated I-V and P-V curves based on the unknown parameters extracted for this module are given in Figure 5g,h. Further, Figure 6d establishes that the proposed algorithm has the best convergence speed. One more time, it is worthy to mention that the resported paramters in Table 11 is per cell.

Table 11.
Comparison of the best RMSE and its extracted parameter per cell on STP6-120/36.

Table 12.
Comparison of the fitness on STP6-120/36.
6.5. Comparison between GNDO and RGNDO
In this section, the efficacy of RGNDO over GNDO is shown in terms of the quartiles using the boxplot and the convergence speed. Figure 7 illustrates the quartiles of the outcomes obtained by each algorithm within 30 independent runs. It is obvious from this figure that RGNDO out-performs GNDO in terms of the minimum, maximum, median, first quartile, and third quartile for all PV models used in our experiments. Moreover, RGNDO has higher convergence, as shown in Figure 8.
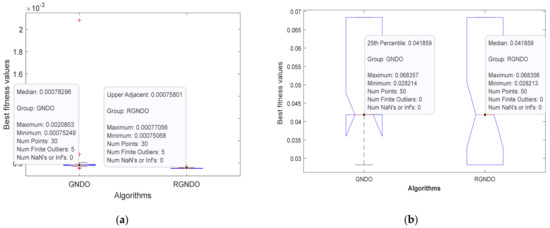
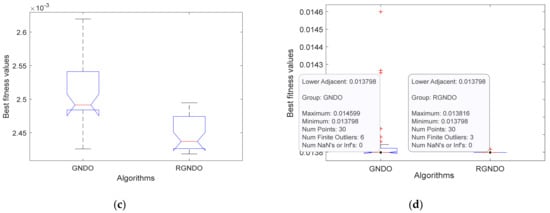
Figure 7.
Boxplot achieved by GNDO and RGNDO: (a) Boxplot on RTC France; (b) Boxplot on Kyocera KC200GT; (c) Boxplot on Ultra 85−P; (d) Boxplot on STP6−120/36.
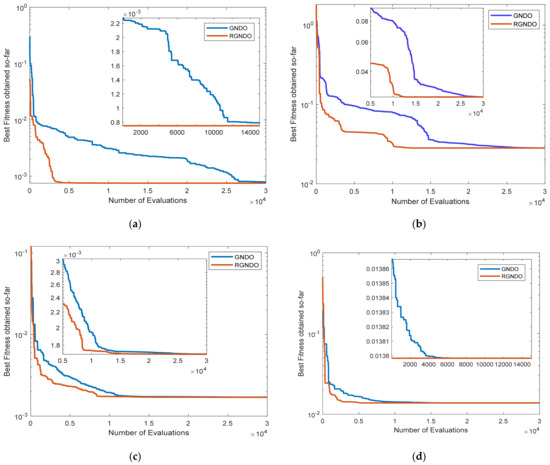
Figure 8.
Convergence curves were obtained for GNDO and RGNDO: (a) Convergence on RTC France; (b) Convergence on Kyocera KC200GT; (c) Convergence on Ultra 85−P; (d) Convergence on STP6−120/36.
6.6. CPU Time
Figure 9 shows the CPU time (in seconds) required by each algorithm on RTC France. The figure shows that the CPU time is almost the same for all algorithms, with the exception of HHO, which takes a long time, and ISA, which takes less than half the time required by the remainder. RGNDO is therefore much more superior in terms of convergence speed and quality of the outcome, with negligible difference in CPU time.
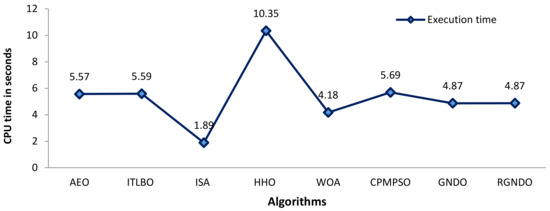
Figure 9.
CPU time required by each algorithm.
6.7. Wilcoxon Rank Sum Test
In [50], a nonparametric statistical test known as the Wilcoxon rank-sum test, also called the Mann–Whitney U Test, has been proposed to compare the outcomes obtained by each of a pair of the algorithms under two hypothesis: the null hypothesis and the alternative. In the null hypothesis, (h = 0), this test proposes that there is no difference between the outcomes of the pair, in which case the outcomes of two algorithms are with equal medians, meanwhile, the alternative (h = 1) hypothesis assumes that there is a difference between the outcomes, in which case the medians of the two are not equal. This test also supposes that the outcomes are independent.
At a significant level of 5%, the outcomes of RGNDO are compared with the outcomes of each algorithm of the compared algorithms to identify whether the null hypnosis will be accepted. Table 13 shows the h- and p-value that result from comparing RGNDO with each algorithm. According to this table, RGNDO has a p-value when compared with AEO, HHO, WOA, and CPMPSO that is less than 0.05 for all four modules, in which case the alternative hypothesis is accepted, which shows the superiority of RGNDO.

Table 13.
Comparison between the proposed with the others under the Mann–Whitney U Test.
6.8. Various Steady-State Characteristics under Varied Operating Conditions
In this final phase, non-standard conditions are simulated to generate various principal characteristics under varied cell temperature and changed levels of solar radiations. To address such changes, due to G and T variations, the adaptation of the cell parameters are [6,40,41]:
where Ki and Kv define the thermal coefficient of current and voltage, respectively, Eg denotes the semi-conductor band-energy, VOC denotes open-circuited voltage and others are the normalized parameters at STC.
Due to space limitations, STP6-20/36 is used as a representative demonstration. The values of Ki and Kv are equal to 0.065%/°C and −0.346%/°C, respectively, for this module. After passing the obtained optimal settings of the nine parameters as depicted in Table 9 generated by RGNDO, the various principal characteristics are illustrated in Figure 10, which shows the five levels of sun irradiances in Figure 10a,b at a fixed temperature of 25 °C. Figure 10c,d reveals the principal characteristics for four levels of temperature at 1000 W/m2.
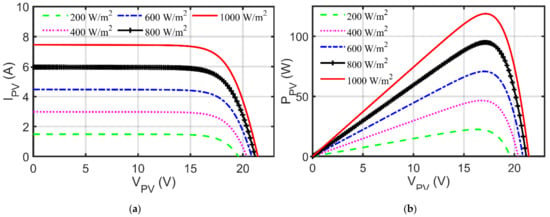
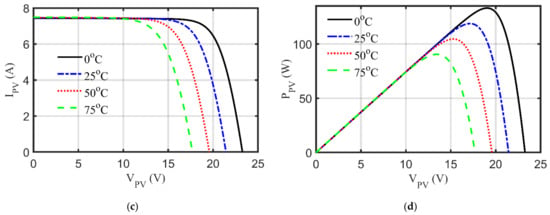
Figure 10.
Principal characteristics of STP6−120 under variables G and T: (a) I-V patterns at varied G; (b) P-V patterns at varied G; (c) I-V patterns at varied T; (d) P-V patterns at varied T.
7. Conclusions and Future Work
In this paper, the generalized normal distribution optimization (GNDO), improved by two strategies for tackling the parameter extraction of the triple-diode model, is proposed and shortened as RGNDO. The first strategy used with GNDO is called as the premature convergence method (PCM), which is used to accelerate convergence by utilizing a factor to move the current individual either between the best-so-far position and the current position or between two individuals selected randomly from the population. The second strategy known as the ranking method-based-novel updating method (RUM) is integrated with GNDO to replace the unbeneficial individuals with others created based on a novel updating method so that most regions within the search space are explored as much as possible. A single solar cell and three PV modules are used to investigate RGNDO, and its estimated parameters are validated according to the empirical dataset points. Various statistical metrics and the convergence curve are used to evaluate the performance of RGNDO that is compared with a number of recent well-known algorithms: AEO, ITLBO, CPMPSO, ISA, HHO, WOA, and GNDO. The experimental outcomes show the superiority of the proposed methodology over the other state-of-the-art, in terms of the final accuracy, where it could fulfill the following averaged RMSE values: 7.5290151 × 10−4 A, 0.0282128 A, 0.0024461773 A, and 0.0137983255 A for all observed PV models (RTC France, KC200GT, Ultra 85-P, and STP6-120/36), respectively; the Wilcoxon rank-sum test which shows that the outcomes of RGNDO are significantly different of those obtained by the compared ones; and the convergence speed. Future work includes looking for a better updating method to replace the unbeneficial individuals within the population to further improve the efficacy of the RGNDO.
Author Contributions
Conceptualization, M.A.-B., R.M., A.E.-F. and M.A.; methodology, M.A.-B., R.M., M.A. and A.E.-F.; software, A.E.-F., R.M., M.A. and M.A.-B.; validation, M.A., A.E.-F., S.S.A. and M.A.-B.; formal analysis, M.A., R.M. and M.A.-B.; investigation, S.S.A., A.E.-F. and M.A.; resources, M.A.-B., S.S.A. and R.M.; data curation, M.A.-B., R.M. and A.E.-F.; writing—original draft preparation, M.A.-B., R.M. and A.E.-F.; writing—review and editing, S.S.A., A.E.-F. and M.A.; visualization M.A.-B., A.E.-F. and R.M.; supervision, M.A., M.A.-B. and S.S.A.; project administration, A.E.-F., R.M. and M.A.-B.; funding acquisition, S.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This project is funded by King Saud University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
The study did not involve humans or animals.
Informed Consent Statement
The study did not involve humans.
Data Availability Statement
Not applicable.
Acknowledgments
Research Supporting Project number (RSP-2021/167), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alam, D.; Yousri, D.; Eteiba, M. Flower pollination algorithm based solar PV parameter estimation. Energy Convers. Manag. 2015, 101, 410–422. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Mirjalili, S.; Chakrabortty, R.K.; Ryan, M.J. Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol. Energy 2020, 209, 694–708. [Google Scholar] [CrossRef]
- Selem, S.I.; El-Fergany, A.A.; Hasanien, H.M. Artificial electric field algorithm to extract nine parameters of triple-diode photovoltaic model. Int. J. Energy Res. 2020, 45, 590–604. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Mekhilef, S.; Shamsudin, A. Parameter extraction of solar photovoltaic modules using penalty-based differential evolution. Appl. Energy 2012, 99, 297–308. [Google Scholar] [CrossRef]
- El-Hameed, M.A.; Elkholy, M.M.; El-Fergany, A.A. Three-diode model for characterization of industrial solar generating units using Manta-rays foraging optimizer: Analysis and validations. Energy Convers. Manag. 2020, 219, 113048. [Google Scholar] [CrossRef]
- Long, W.; Cai, S.; Jiao, J.; Xu, M.; Wu, T. A new hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 2020, 203, 112243. [Google Scholar] [CrossRef]
- Li, S.; Gu, Q.; Gong, W.; Ning, B. An enhanced adaptive differential evolution algorithm for parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 205, 112443. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S.; Nouh, A.S. Coyote optimization algorithm for parameters extraction of three-diode photovoltaic models of photovoltaic modules. Energy 2019, 187, 116001. [Google Scholar] [CrossRef]
- Allam, D.; Yousri, D.; Eteiba, M. Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2016, 123, 535–548. [Google Scholar] [CrossRef]
- Ahmad, T.; Sobhan, S.; Nayan, M.F. Comparative analysis between single diode and double diode model of PV cell: Concentrate different parameters effect on its efficiency. J. Power Energy Eng. 2016, 4, 31–46. [Google Scholar] [CrossRef]
- Khanna, V.; Das, B.; Bisht, D.; Singh, P. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 2015, 78, 105–113. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Chang, V.; Mohamed, R. HSMA_WOA: A hybrid novel Slime mould algorithm with whale optimization algorithm for tackling the image segmentation problem of chest X-ray images. Appl. Soft Comput. 2020, 106642. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Basset, M.; El-shahat, D.; Elhoseny, M.; Song, H. Energy-Aware Metaheuristic algorithm for Industrial Internet of Things task scheduling problems in fog computing applications. IEEE Internet Things J. 2020, 1. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Elhoseny, M.; Bashir, A.K.; Jolfaei, A.; Kumar, N. Energy-Aware Marine Predators Algorithm for Task Scheduling in IoT-based Fog Computing Applications. IEEE Trans. Ind. Inform. 2020, 17, 5068–5076. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Pillay, V.; Hirasen, D.; Sivanarain, K.; Govender, M. A Comparative study of meta-heuristic optimization algorithms for 0–1 knapsack problem: Some initial results. IEEE Access 2019, 7, 43979–44001. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Robust electrical parameter extraction methodology based on Interior Search Optimization Algorithm applied to supercapacitor. ISA Trans. 2020, 105, 86–97. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Alsaidan, I.; Abdelaziz, A.Y.; Muyeen, S. Parameter estimation of three diode photovoltaic model using grasshopper optimization algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef]
- Yousri, D.; Thanikanti, S.B.; Allam, D.; Ramachandaramurthy, V.K.; Eteiba, M. Fractional chaotic ensemble particle swarm optimizer for identifying the single, double, and three diode photovoltaic models’ parameters. Energy 2020, 195, 116979. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote optimization algorithm for parameters estimation of various models of solar cells and PV modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.; Duck, B.C.; Nadarajah, M. An improved wind driven optimization algorithm for parameters identification of a triple-diode photovoltaic cell model. Energy Convers. Manag. 2020, 213, 112872. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Parameters extraction of three-diode photovoltaic model using computation and Harris Hawks optimization. Energy 2020, 195, 117040. [Google Scholar] [CrossRef]
- Chenouard, R.; El-Sehiemy, R.A. An interval branch and bound global optimization algorithm for parameter estimation of three photovoltaic models. Energy Convers. Manag. 2020, 205, 112400. [Google Scholar] [CrossRef]
- Liang, J.; Ge, S.; Qu, B.; Yu, K.; Liu, F.; Yang, H.; Wei, P.; Li, Z. Classified perturbation mutation based particle swarm optimization algorithm for parameters extraction of photovoltaic models. Energy Convers. Manag. 2020, 203, 112138. [Google Scholar] [CrossRef]
- Long, W.; Wu, T.; Jiao, J.; Tang, M.; Xu, M. Refraction-learning-based whale optimization algorithm for high-dimensional problems and parameter estimation of PV model. Eng. Appl. Artif. Intell. 2020, 89, 103457. [Google Scholar] [CrossRef]
- Ridha, H.M.; Gomes, C.; Hizam, H. Estimation of photovoltaic module model’s parameters using an improved electromagnetic-like algorithm. Neural Comput. Appl. 2020, 32, 12627–12642. [Google Scholar] [CrossRef]
- Ridha, H.M.; Heidari, A.A.; Wang, M.; Chen, H. Boosted mutation-based Harris hawks optimizer for parameters identification of single-diode solar cell models. Energy Convers. Manag. 2020, 209, 112660. [Google Scholar] [CrossRef]
- Ram, J.P.; Pillai, D.S.; Rajasekar, N.; Chinnaiyan, V.K. Flower Pollination Based Solar PV Parameter Extraction for Double Diode Model. In Intelligent Computing Techniques for Smart Energy Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 303–312. [Google Scholar]
- Hassan, K.H.; Rashid, A.T.; Jasim, B.H. Parameters estimation of solar photovoltaic module using camel behavior search algorithm. Int. J. Electr. Comp. Eng. 2021, 11, 788–793. [Google Scholar] [CrossRef]
- Kashefi, H.; Sadegheih, A.; Mostafaeipour, A.; Omran, M.M. Parameter identification of solar cells and fuel cell using improved social spider algorithm. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2020. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L.; Gao, L. Parameter extraction of photovoltaic models using an improved teaching-learning-based optimization. Energy Convers. Manag. 2019, 186, 293–305. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Sowmya, R.; Elavarasan, R.M.; Kumar, B.S. Enhanced chaotic JAYA algorithm for parameter estimation of photovoltaic cell/modules. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Ismaeel, A.A.; Houssein, E.H.; Oliva, D.; Said, M. Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access 2021, 9, 13403–13416. [Google Scholar] [CrossRef]
- Mokeddem, D. Parameter Extraction of Solar Photovoltaic Models Using Enhanced Levy Flight Based Grasshopper Optimization Algorithm. J. Electr. Eng. Technol. 2021, 16, 171–179. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Korashy, A.; Yu, J. Photovoltaic cells parameter estimation using an enhanced teaching–learning-based optimization algorithm. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 767–779. [Google Scholar] [CrossRef]
- Kumar, C.; Raj, T.D.; Premkumar, M.; Raj, T.D. A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters. Optik 2020, 223, 165277. [Google Scholar] [CrossRef]
- Huynh, D.C.; Ho, L.D.; Dunnigan, M.W. Parameter Estimation of Solar Photovoltaic Cells Using an Improved Artificial Bee Colony Algorithm. In Proceedings of the International Conference on Green Technology and Sustainable Development, Ho Chi Minh City, Vietnam, 27–28 November 2020; pp. 281–292. [Google Scholar]
- Ćalasan, M.; Jovanović, D.; Rubežić, V.; Mujović, S.; Đukanović, S. Estimation of single-diode and two-diode solar cell parameters by using a chaotic optimization approach. Energies 2019, 12, 4209. [Google Scholar] [CrossRef]
- Nayak, B.; Mohapatra, A.; Mohanty, K.B. Parameter estimation of single diode PV module based on GWO algorithm. Renew. Energy Focus 2019, 30, 1–12. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Mirjalili, S. Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 224, 113301. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Parameter identification for solar cell models using harmony search-based algorithms. Sol. Energy 2012, 86, 3241–3249. [Google Scholar] [CrossRef]
- Fossum, J.G.; Lindholm, F.A. Theory of grain-boundary and intragrain recombination currents in polysilicon pn-junction solar cells. IEEE Trans. Electron Devices 1980, 27, 692–700. [Google Scholar] [CrossRef]
- Koohi-Kamali, S.; Rahim, N.; Mokhlis, H.; Tyagi, V. Photovoltaic electricity generator dynamic modeling methods for smart grid applications: A review. Renew. Sustain. Energy Rev. 2016, 57, 131–172. [Google Scholar] [CrossRef]
- Nunes, H.; Pombo, J.; Mariano, S.; Calado, M.; De Souza, J.F. A new high performance method for determining the parameters of PV cells and modules based on guaranteed convergence particle swarm optimization. Appl. Energy 2018, 211, 774–791. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Elhoseny, M.; Chakrabortty, R.K.; Ryan, M. A Hybrid COVID-19 Detection Model Using an Improved Marine Predators Algorithm and a Ranking-Based Diversity Reduction Strategy. IEEE Access 2020, 8, 79521–79540. [Google Scholar] [CrossRef]
- Yousri, D.; Rezk, H.; Fathy, A. Identifying the parameters of different configurations of photovoltaic models based on recent artificial ecosystem-based optimization approach. Int. J. Energy Res. 2020, 44, 11302–11322. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Parameters estimation of single-and multiple-diode photovoltaic model using whale optimisation algorithm. IET Renew. Power Gener. 2018, 12, 1755–1761. [Google Scholar] [CrossRef]
- Shell PowerMax Solar Modules for Off-Grids Markets. Available online: http://www.effectivesolar.com/PDF/shell/SQ-80-85-P.pdf (accessed on 5 March 2021).
- Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Wang, Z.; Qu, J.; Wang, H. Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 2018, 157, 460–479. [Google Scholar] [CrossRef]
- Haynes, W. Wilcoxon rank sum test. In Encyclopedia of Systems Biology; Springer: New York, NY, USA, 2013; pp. 2354–2355. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).