Packaging Process Optimization in Multihead Weighers with Double-Layered Upright and Diagonal Systems

Abstract

In multihead weighers, packaging processes seek to find the best combination of passage hoppers whose product content provides a total package weight as close as possible to its (nominal) label weight. The weighing hoppers arranged in these machines dispense the product quantity that each package contains through computer algorithms designed and executed for this purpose. For its part, in the packaging process for double-layered multihead weighers, all hoppers are arranged in two levels. The first layer comprises a group of weighing hoppers, and the second comprises a set of booster hoppers placed uprightly or diagonally to each weighing hopper based on design of the machine. In both processes, the initial machine configuration is the same; however, the hopper selection algorithm works differently. This paper proposes a new packaging process optimization algorithm for double-layer upright and diagonal machines, wherein the hopper subset combined has previously been defined, and the packaging weight is expressed as actual values. As part of its validation, product filling strategies were implemented for weighing hoppers to assess the algorithm in different scenarios. Results from the process performance metrics prove that the new algorithm improves processes by reducing variability. In addition, results reveal that some machine configurations were also able to improve their operation.

1. Introduction

Multihead weighers were first used in the 1970s and, since then, they have been used to improve industrial process performance. Currently, they are used in different packaging processes for several products, regardless of their shape or size, and have become particularly essential in the food industry [1,2]. Multihead weighers play a fundamental role in the industrial process given the accuracy and speed they provide to the packaging process. Once programmed, they can automatically package several food industry products, including products with heterogeneous characteristics. This ensures compliance with current regulatory standards while reducing production costs by maintaining an efficient, high-volume product flow and preserving process quality. Still, one of the most prominent process requirements is that package contents must match the weight printed on its label. This becomes one of the main issues that must be addressed to guarantee high-quality standards in the final product, with variability being directly related to the quality of the process [3]. In this sense, authors such as Taguchi [4] claim that product quality depends on how close its quality features are to their nominal value, in such a way that everything that deviates from said nominal value is considered as a loss to society. Hence, quality in the packaging process may be achieved by reducing variability around the target weight (T) [5]. For these purposes, processes must be streamlined trying to guarantee that package content weights are as close as possible to the weight specified on the label. Optimization techniques, new algorithms, and experiments’ design can be used as quality engineering tools for the improvement and optimization of industrial processes [6].

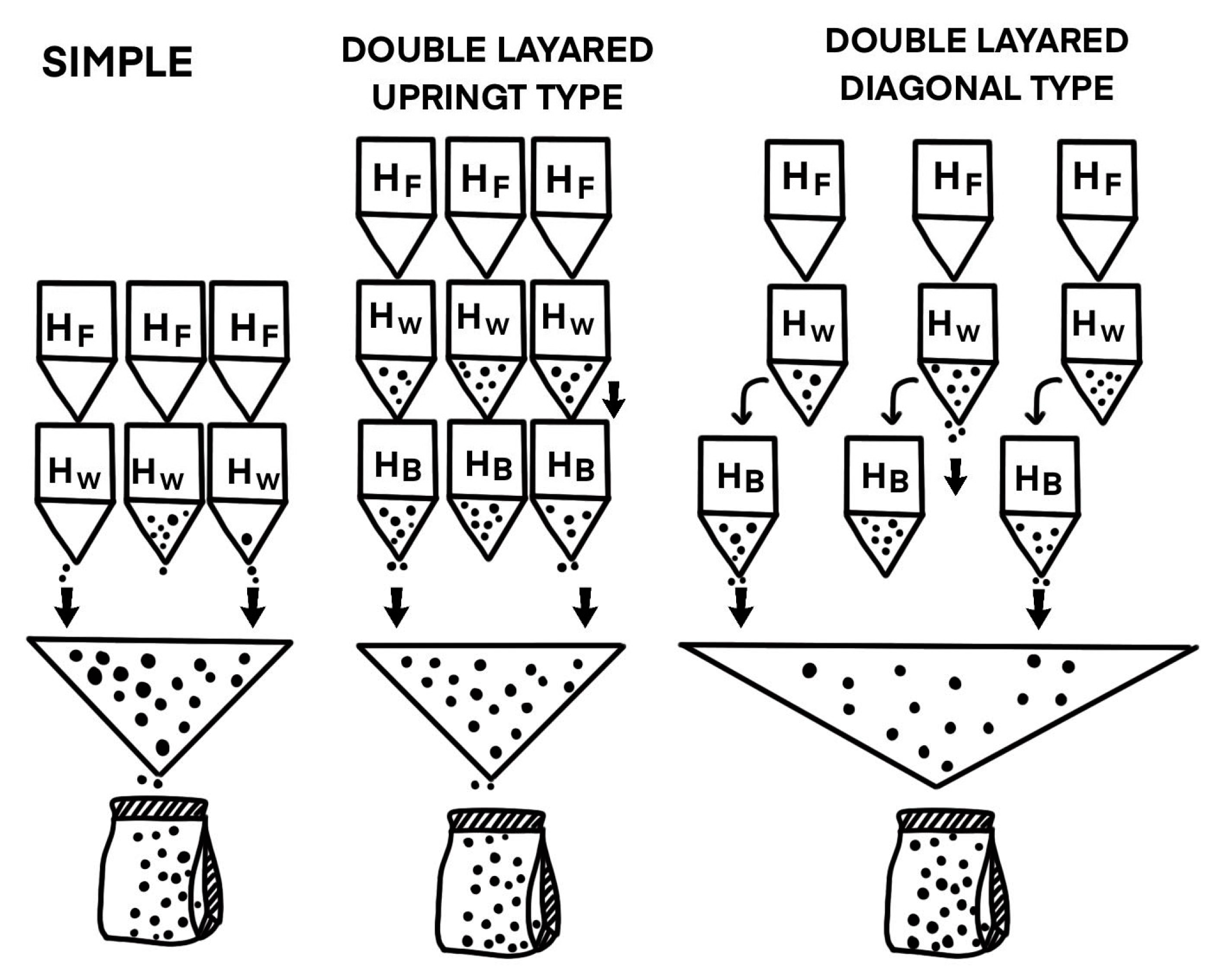
Multihead weighing systems are mainly composed of a vibrating feeder system, $n$ feeding hoppers ($H_F)$, $n$ weighing hoppers $(H_W)$, and a discharge conduit to a packaging machine. In a traditional single-layer machine (without booster hoppers), the internal algorithm combines all the n weighing hoppers in the machine to form a subgroup $H$ of $k$ hoppers and then selects a subset $H^{\prime }\in H_W$ whose sum of weights is the closest to the target weight $T$ of the package. In this sense, package content weights are obtained by combining a subgroup of $k$ hoppers from the $n$ weighing hoppers that the machine contains, with $k\le n$. However, double-layered (upright and diagonal) weighers contain an additional layer of hoppers and use a larger combination of hoppers to reach the target weight. In these double-layered machines, each of the $n$ weighing hoppers ($H_W$) has a booster hopper ($H_B$) underneath, in which a single product ration can be stored, while the weighing hoppers receive a new product ration from the feeding hoppers ($H_F$), as illustrated in Figure 1. For each package, all the hoppers must contain a certain product quantity, and the machine must combine $k$ hoppers of the $2n$ so that the system must form a subset $H^{\prime }$ of $k$ hoppers. For double-layered upright systems, this subset $H^{\prime }$ can be formed with booster hoppers or weighing hoppers as long as its corresponding booster hopper is part of the $k$ hoppers, while, for the double-layered diagonal systems, a weighing and booster hopper cannot be selected simultaneously for the same k-nuple.

This research study proposes a new optimization algorithm for double-layered upright and diagonal machines that seeks to select a subset $H^{\prime }$ of $k$ hoppers whose total weights are greater and closer to the target weight $T$. The algorithm was validated through a case study for actual products, wherein the performance characteristics of the process were measured in different scenarios. In numerical experiments, filling strategies designed and validated for three weighing hoppers in previous studies were tested. Likewise, different values from previously established $k$ combined hoppers were tested in each filling strategy.

This article is structured as follows: Section 2 presents the state of the art within the multihead machine packaging process field. In Section 3, the weighing process for double-layered upright and diagonal multihead weighers is described. Section 4 discusses the different hopper-filling strategies used in the process. Then, Section 5 explains the optimization model and the packaging algorithm proposed for double-layered weighers. Section 6 lists the results and provides a preliminary assessment of the numerical experiments. Next, Section 7 contains the results from the experimental design for the different process scenarios evaluated. Finally, Section 8 discussion and Section 9 elucidate our conclusions from this research study.

2. Background

The documented research studies of multihead machines propose diverse solutions for packaging issues. Different algorithms and solution and configuration models have been presented for these processes. For example, some authors propose an optimal scheme for determining ideal operation times for vibrating linear feeders in multihead weighers. In their corresponding studies, they found that the least-squares method can be used to reduce variability against fixed operating times [7]. A bit-operation-based weighing algorithm succeeded in proving that operation times can be reduced and that the output weight from uneven hoppers is closer to the desired target weight [8]. In other research studies, the product residence time in hoppers was introduced as a second objective. Hence, the packaging problem was formulated as a bicriteria approximation issue for discrete weights, and a dynamic programming algorithm was proposed for its solution. This algorithm aimed to reduce the maximum duration of the product in the packaging system [9] while assuring that the total weight of each package was as close as possible to its target weight. Similar work was approached for double-layered upright and diagonal machines for discrete weights in the hoppers, using a bicriteria dynamic programming algorithm for these machines [10]. Subsequently, the bicriteria model proposed by [9] was ultimately improved through algorithms designed to reduce execution times, which makes the packaging process more efficient [11]. Later, these theories were extended to duplex and quasi-duplex machines [12]. In the same sense, heuristic algorithms have been proposed to find better results in the bicriteria packaging process, targeting label weights, and priority orders [13,14]. Likewise, several optimization algorithms have been proposed to determine the optimum product flow rate for radial feeders, seeking to minimize expected production costs per each “compliant” package within a fixed period of time. In this study, the response surface methodology identified conditions of minimal process variability and lower costs, compared to an industrial solution [15]. A heuristic optimization model based on a detailed characterization of what constitutes a near-optimal solution to the multihead weigher configuration problem has also been proposed. This model reduced hopper combination response times according to each package weight, in addition to finding the right hopper feeding points to minimize the mean square error for package weights [16]. Statistical control of the packaging process has also been addressed. For example, several modified control charts have been developed and studied to monitor and control the package production process [17]. Finally, new bio-objective approaches have been developed for the optimization of actual package weights [18,19], incorporating package target weights and the priority associated with the product discharge times reported by hoppers into the model. The innovation proposed by these approaches is that the relative importance of the objectives is managed and dynamically adjusted in each packaging operation, thus determining the best operation conditions for each process [20]. These approaches are extremely useful for packaging fresh or frozen products. As evidenced, hitherto, no scientific content has been disclosed regarding diagonal and upright machines considering actual weights in hoppers with previously established $k$ values. Therefore, this study becomes quite relevant as it proposes a new optimization algorithm for double-layered upright machines that considers actual weights and preestablished $k$ values.

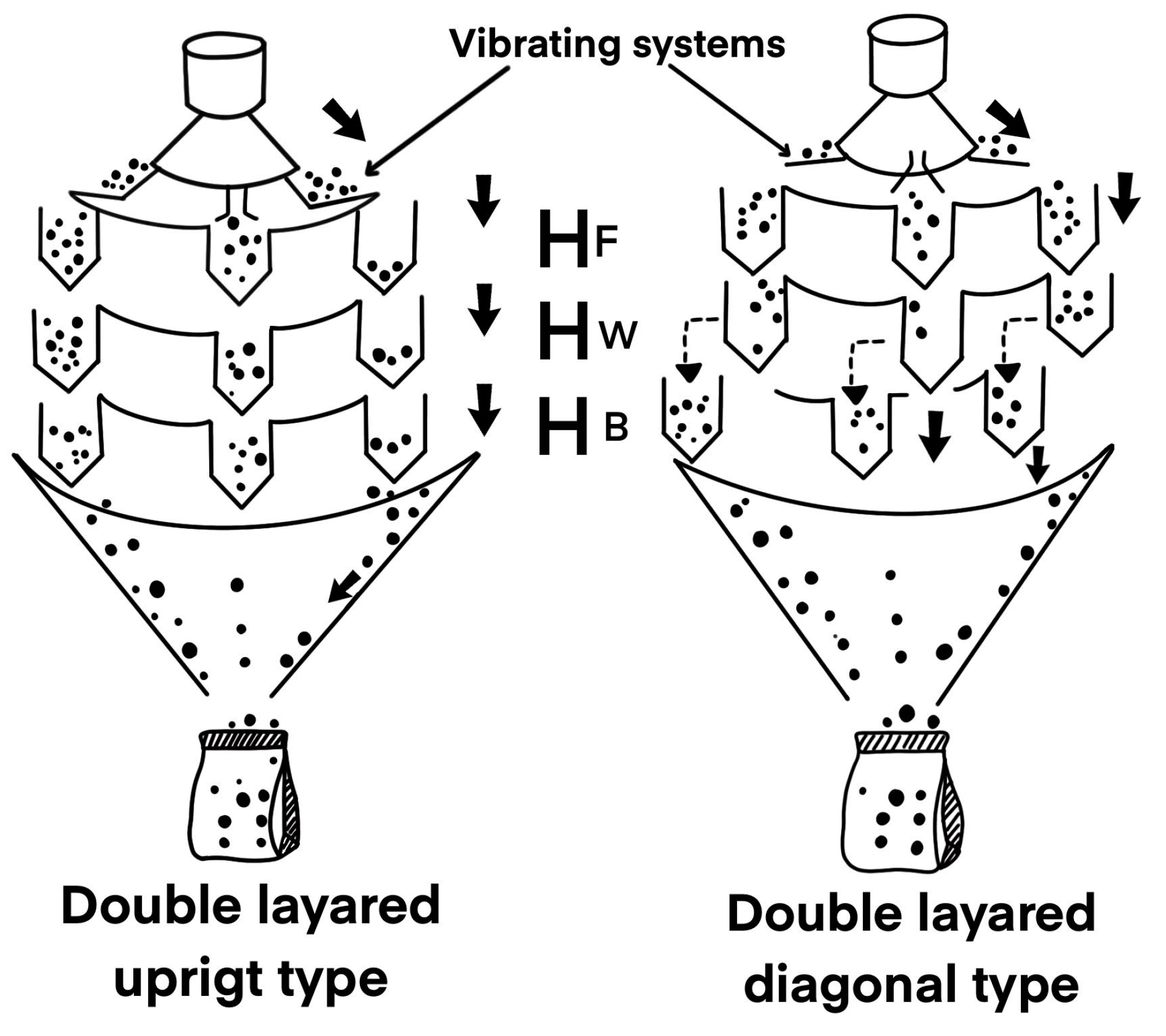
3. Weighing Process on Double-Layered Upright and Diagonal Weighers

The packaging process in double-layered multihead weighers consists of selecting a subset $H^{\prime }$ from the set $H$ of the $2n$ machine hoppers to produce each package. Initially, the product is distributed through the vibrating channels to the feeding hoppers, Then, it is discharged to the $H_{Wi}$ weighing hoppers ($i=1,2,3,\dots n)$, where the product is weighed. In double-layered upright and double-layered diagonal weighers, each of the weighing hoppers has a booster hopper, in which the content of the weighed product can be stored. For this reason, once the product is weighed, it is discharged into the corresponding $H_{Bj}$ booster hoppers ($j=n+1,n+2,\dots 2n),$ and the weighing hopper receives a new portion of the product, as denoted in Figure 2. Once all the hoppers are full (weighing and booster), the machine calculates the combinations of all the weights, selecting a subset $H^{\prime }$of $k$ hoppers whose sum of the weights is greater and closer to the target weight $T$. Then, the unloaded hoppers are filled with a new product to repeat the procedure until completing the $Q$ number of packages required.

The $w_i$ weights in the hoppers are arranged in a normal distribution $w_i~N\left(\mu ,\sigma \right)$ [14,15,16], where $\mu$ is the average weight of the product to be provided in each weighing hopper $H_{Wi}$, and $\sigma$ is the standard deviation. Previous studies have found that $\sigma$ has a direct correlation with the mean quantity $\mu$ and linearly depends on it, due to vibrating feeding systems, according to $\sigma =\gamma \mu$; where $\gamma$ is a proportionality coefficient and varies according to the characteristics of the packaging product [14,15,16,17,19].

For each discharge, the single-layer machine performs a number of combinations (NC) determined by Equation (1), where $n$ is the total number of hoppers in the system and $k$ is the hoppers to be combined. By adding the booster layers, the NCs for the double-layered upright and diagonal machines increase, being greater in the latter.

$$NC=\left(\begin{array}{c}n\\ k\end{array}\right)$$

(1)

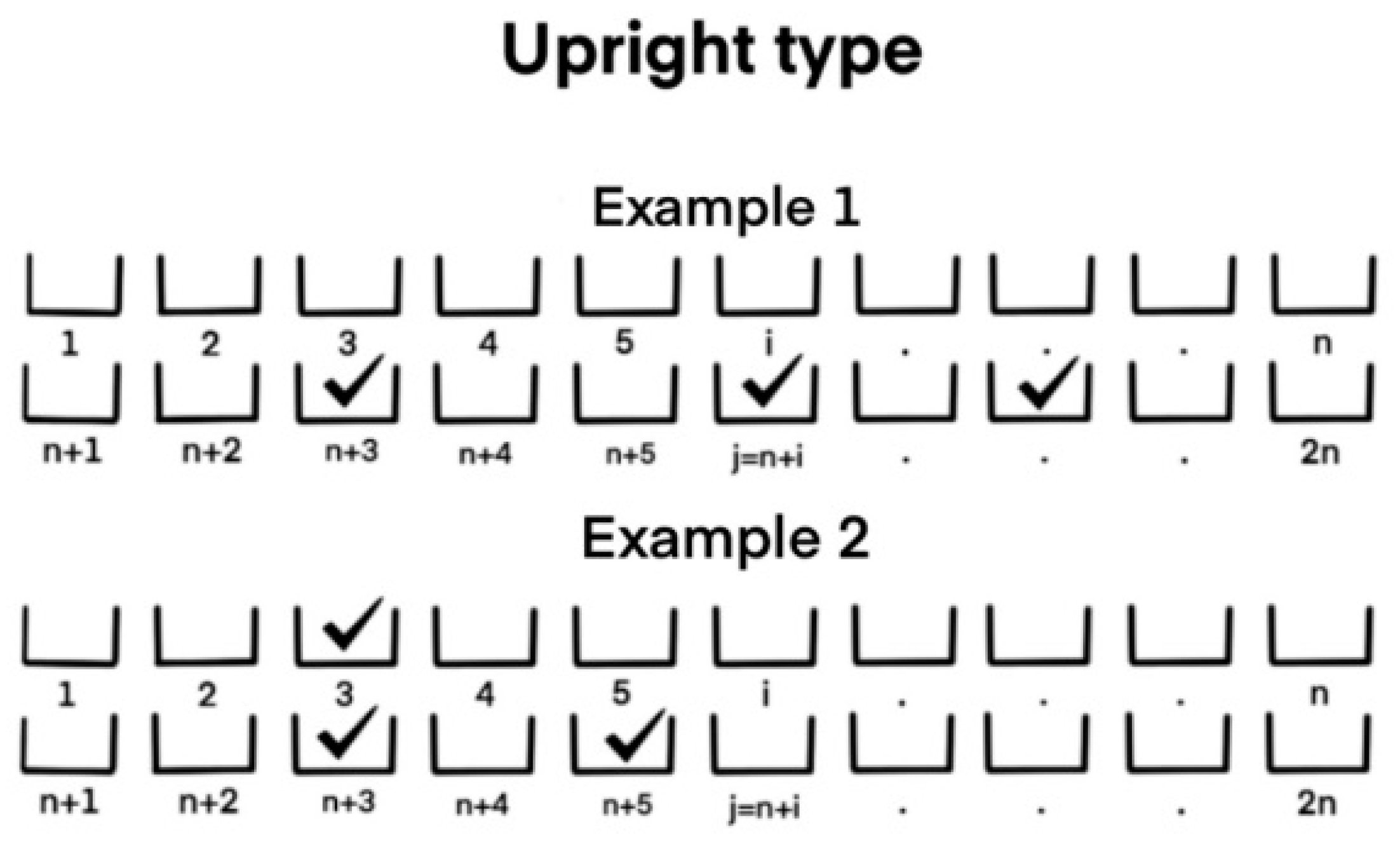
For each package produced, the double-layered upright machine can discharge booster hoppers or simultaneously discharge the weighing hopper and its corresponding booster hopper (Figure 3), making the NC greater, thus improving the possibility of finding a subset of hoppers that meet the target weight requirement. Depending on the number of weighing hoppers, we have several types of combinations. For example, the system can combine $k$ booster hoppers or $i\le \frac{k}{2}$ booster hoppers, where $i$ is an integer, with their corresponding weighing hoppers and the other $n-i$ booster hoppers.

For $k=2$, when combining the booster hoppers, $\left(\begin{array}{c}n\\ 2\end{array}\right)$ combinations are obtained, but the weighing hopper with its corresponding booster can also be combined; therefore, there are $n$ additional cases (see Equation (2)). In the same sense, for $k=3$, first, there are $\left(\begin{array}{c}n\\ 3\end{array}\right)$ booster hopper combinations. In addition, the weighing hoppers can be combined with booster hoppers, and each pair can be associated with $n-1$ hoppers, replicated $n$ times (see Equation (3)). By mathematical induction of Equations (2)–(8), it is deduced that, in general, the total NC of $k\le n$ hoppers is determined by Equation (9), where$⟦\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$2$}\right.⟧$ represents the integer part of $\frac{k}{2}$.

$$k=2,NC=\left(\begin{array}{c}n\\ 2\end{array}\right)+n$$

(2)

$$k=3,NC=\left(\begin{array}{c}n\\ 3\end{array}\right)+\left(\begin{array}{c}n-1\\ 1\end{array}\right)·n$$

(3)

$$k=4,\hspace{1em}NC=\left(\begin{array}{c}n\\ 4\end{array}\right)+\left(\begin{array}{c}n-1\\ 2\end{array}\right)·n+\left(\begin{array}{c}n\\ 2\end{array}\right)·\left(\begin{array}{c}n-2\\ 0\end{array}\right)$$

(4)

$$k=5,NC=\left(\begin{array}{c}n\\ 5\end{array}\right)+\left(\begin{array}{c}n-1\\ 3\end{array}\right)·n+\left(\begin{array}{c}n\\ 2\end{array}\right)·\left(\begin{array}{c}n-2\\ 1\end{array}\right)$$

(5)

$$k=6,NC=\left(\begin{array}{c}n\\ 6\end{array}\right)+\left(\begin{array}{c}n-1\\ 4\end{array}\right)·n+\cdots +\left(\begin{array}{c}n\\ 2\end{array}\right)·\left(\begin{array}{c}n-2\\ 2\end{array}\right)+\left(\begin{array}{c}n\\ 3\end{array}\right)·\left(\begin{array}{c}n-3\\ 0\end{array}\right)$$

(6)

$$k=7,NC=\left(\begin{array}{c}n\\ 7\end{array}\right)+\left(\begin{array}{c}n-1\\ 7-2\end{array}\right)·n+\cdots +\left(\begin{array}{c}n\\ 2\end{array}\right)·\left(\begin{array}{c}n-2\\ 7-4\end{array}\right)+\left(\begin{array}{c}n\\ 3\end{array}\right)·\left(\begin{array}{c}n-3\\ 7-6\end{array}\right)$$

(7)

$$k=8, NC=\left(\begin{array}{c}n\\ 8\end{array}\right)+\left(\begin{array}{c}n-1\\ 8-2\end{array}\right)·n+\left(\begin{array}{c}n\\ 2\end{array}\right)·\left(\begin{array}{c}n-2\\ 8-4\end{array}\right)+\cdots +\left(\begin{array}{c}n\\ 3\end{array}\right)·\left(\begin{array}{c}n-3\\ 8-6\end{array}\right)+\left(\begin{array}{c}n\\ 4\end{array}\right)·\left(\begin{array}{c}n-4\\ 8-8\end{array}\right)$$

(8)

$$NC={\displaystyle \sum }_{i=0}^{⟦\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$2$}\right.⟧}\left(\begin{array}{c}n\\ i\end{array}\right)\left(\begin{array}{c}n-i\\ k-2i\end{array}\right)$$

(9)

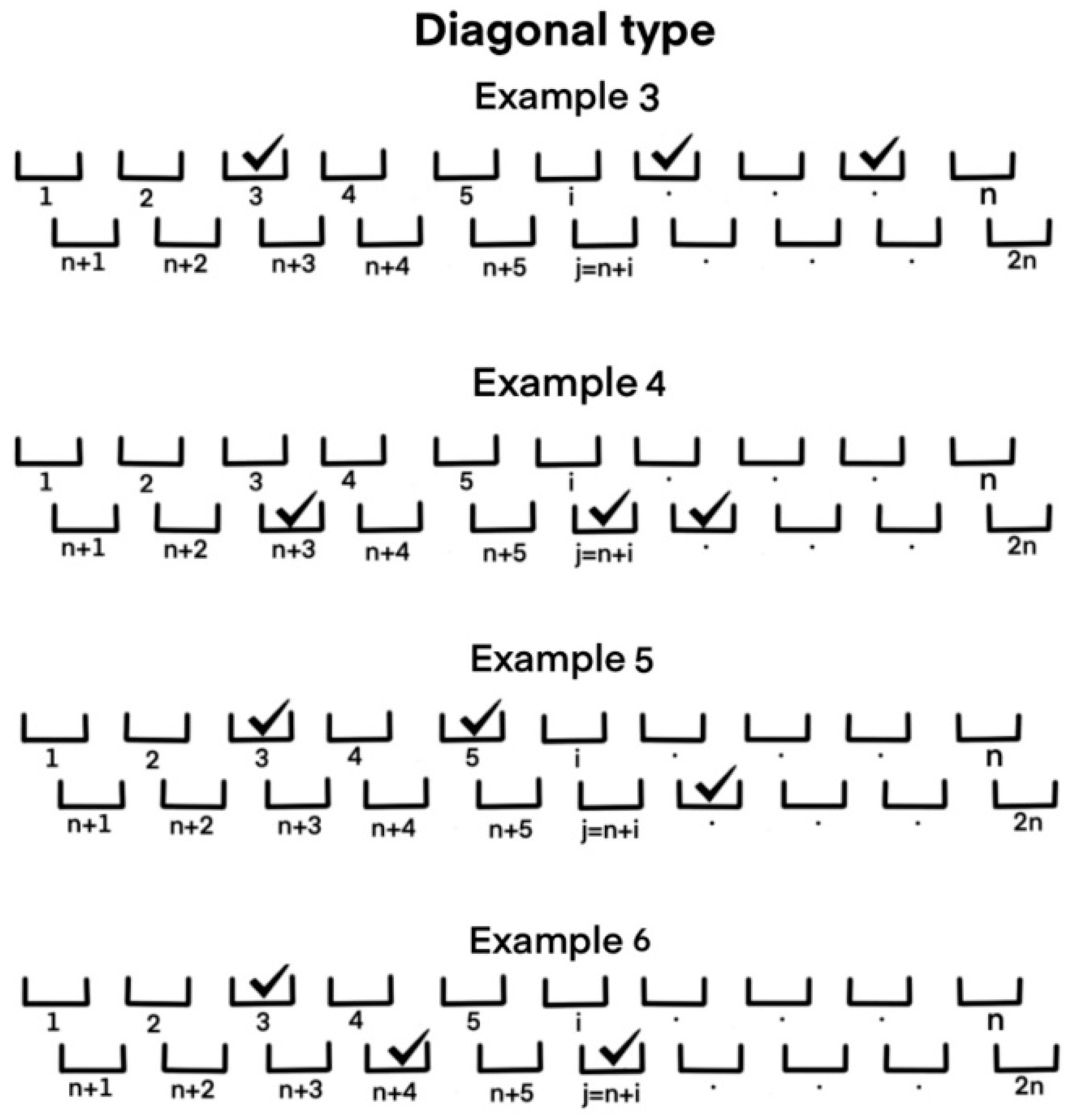
Furthermore, for double-layered diagonal machines, only booster hoppers, only weighing hoppers, or a combination of both levels can be discharged to produce each package, as long as a weighing hopper and its booster are not simultaneously unloaded, as denoted in Figure 4.

For example, for $k=2$, $\left(\begin{array}{c}n\\ 2\end{array}\right)$ weighing hopper combinations are generated, each of the weighing hoppers can be associated with $n-1$ booster hoppers replicated $n$ times and, finally, $\left(\begin{array}{c}n\\ 2\end{array}\right)$ booster hopper combinations, the mathematical expression to generate the combinations is shown in Equation (10). For $k=3$, only three booster hoppers can be combined, i.e., two booster hoppers with one of the $n-2$ remaining weighing hoppers, one booster hopper with a combination of two of the $n-1$ remaining weighing hoppers, or only three weighing hoppers. Equations (10)–(13) denote the calculation of the combinations for$k$ = 2, 3, 4, and 5. In general, by mathematical induction, the total NC of $k$ hoppers with $k\le n$ is determined by Equation (14).

Table 1. Number of combinations per package for $n$ = 16 in standard (single-layered), double-layered upright, and double-layered diagonal machines.

k	Single Layered	Double-Layered Upright	Double-Layered Diagonal
2	120	136	480
3	560	800	4480
4	1820	3620	29,120
5	4368	13,328	139,776
6	8008	41,328	512,512
7	11,440	110,448	1,464,320
8	12,870	258,570	3,294,720
9	11,440	536,640	5,857,280
10	8008	996,216	8,200,192
11	4368	1,665,456	8,945,664
12	1820	2,520,336	7,454,720
13	560	3,465,840	4,587,520
14	120	4,343,160	1,966,080
15	16	4,969,152	524,288
16	1	5,196,627	65,536

below presents an example of the NC that can be generated for each machine type for $n=16$ with $k=2$ up to $k=8$.

$$k=2, NC=\left(\begin{array}{c}n\\ 2\end{array}\right)+\left(\begin{array}{c}n\\ 1\end{array}\right)·\left(\begin{array}{c}n\\ 1\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)$$

(10)

$$k=3, NC=\left(\begin{array}{c}n\\ 3\end{array}\right)+\left(\begin{array}{c}n\\ 1\end{array}\right)·\left(\begin{array}{c}n-1\\ 2\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)·\left(\begin{array}{c}n-2\\ 1\end{array}\right)+\left(\begin{array}{c}n\\ 3\end{array}\right)$$

(11)

$$k=4, NC=\left(\begin{array}{c}n\\ 4\end{array}\right)+\left(\begin{array}{c}n\\ 1\end{array}\right)·\left(\begin{array}{c}n-1\\ 3\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)·\left(\begin{array}{c}n-2\\ 2\end{array}\right)+\cdots +\left(\begin{array}{c}n\\ 3\end{array}\right)·\left(\begin{array}{c}n-3\\ 1\end{array}\right)+\left(\begin{array}{c}n\\ 4\end{array}\right)·\left(\begin{array}{c}n-4\\ 0\end{array}\right)$$

(12)

$$\begin{gathered} k=5, NC=\left(\begin{array}{c}n\\ 5\end{array}\right)+\left(\begin{array}{c}n\\ 1\end{array}\right)·\left(\begin{array}{c}n-1\\ 4\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)·\left(\begin{array}{c}n-2\\ 3\end{array}\right)+\cdots \\ \dots +\left(\begin{array}{c}n\\ 3\end{array}\right)·\left(\begin{array}{c}n-3\\ 2\end{array}\right)+\left(\begin{array}{c}n\\ 4\end{array}\right)·\left(\begin{array}{c}n-4\\ 1\end{array}\right)+\left(\begin{array}{c}n\\ 5\end{array}\right)·\left(\begin{array}{c}n-5\\ 0\end{array}\right) \end{gathered}$$

(13)

$$NC={\displaystyle \sum }_{i=0}^k\left(\begin{array}{c}n\\ i\end{array}\right)\left(\begin{array}{c}n-i\\ k-i\end{array}\right)$$

(14)

As aforementioned, in its initial configuration, the double-layered upright machine has a restriction in the combination of the $k$ system hoppers $\left(H_m\right)$. Specifically, a hopper of $H_{Wi}$ can only be part of a $k-nupla$ of hoppers if and only if the set of the $k$hoppers contains $H_{Bj}$, with$j=n+i$. However, in the double-layered diagonal machine, all $H_{Wi}$ and $H_{Bj}$ that belong to the $k-nupla$ must meet the condition of $i\ne j-n$. 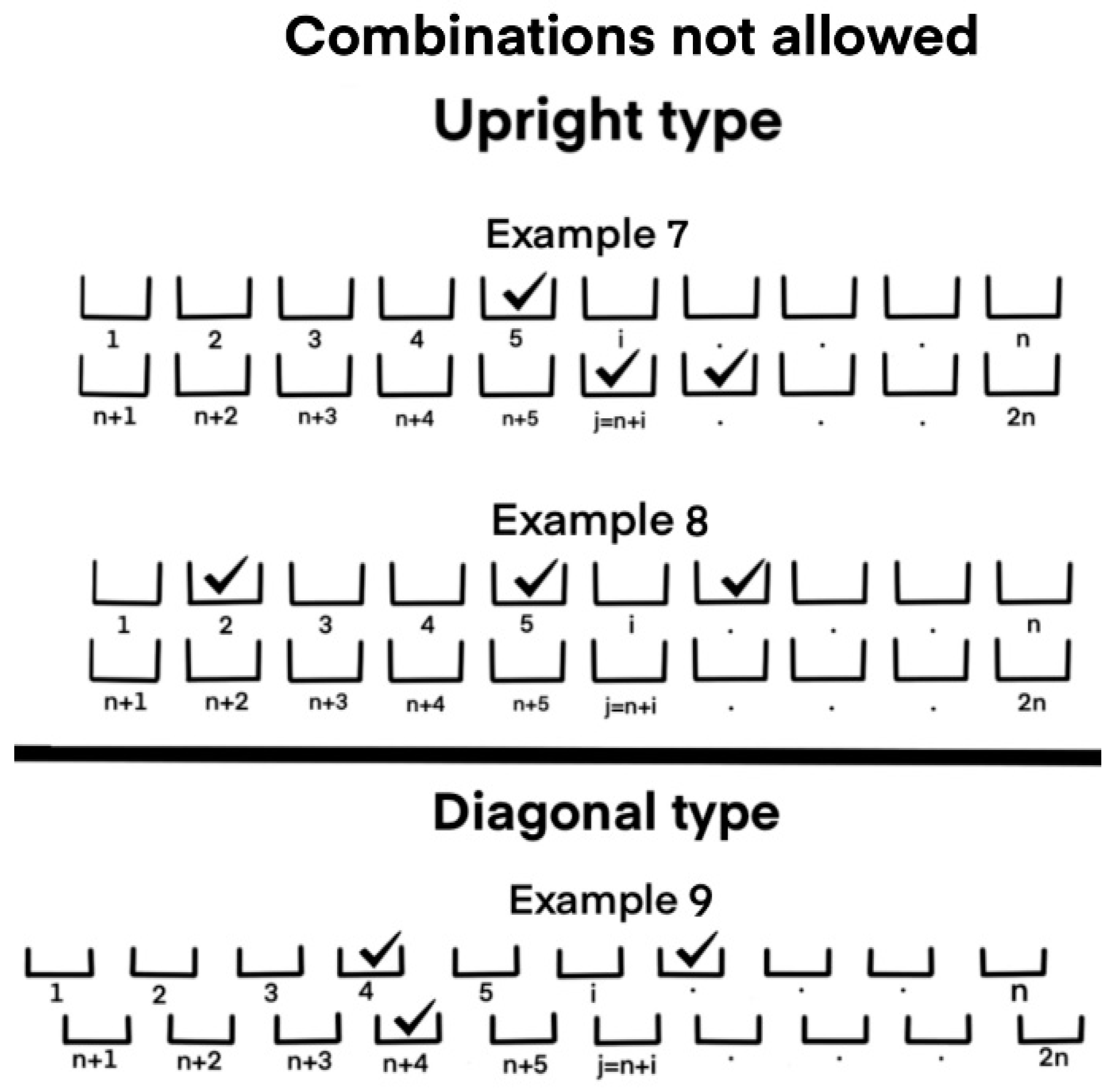Figure 3 below illustrates the invalid combinations for each machine. For example, for $n=10$ with $k=3$, Hopper 3 in a double-layered upright system is a weighing hopper, while Hopper 13 is a booster hopper. Here, Hopper 3 may be selected for combination provided that Hopper 13 is also selected, while, for the diagonal system, they cannot be selected simultaneously. Examples 7 and 8 of Figure 5 denote invalid combinations for the upright machine when trying to combine weighing hoppers without considering their corresponding booster hopper. Furthermore, Example 9 illustrates an incorrect combination in the diagonal machine when trying to simultaneously discharge the weighing hopper with their corresponding booster hopper.

4. Hopper-Filling Strategies

In the industrial field, the filling configuration of the hoppers during the multihead weighing process is made based on the experience and skill of the machine operator. This is since the machine does not have a predetermined configuration strategy for all the types of existing products that can be packaged in it. To address this fact, the present research proposes solving the packaging problem through an algorithm for different $k$ hopper combinations, with an average feed for each hopper according to the three filling strategies proposed by [14,19,20] for single-layered weighers (see

Table 2. Number of hoppers for each group according to the $S_1$, $S_2$, and $S_3$ strategies and distribution of hoppers.

Distribution	Strategy	${\mathit{n}}_1$	${\mathit{n}}_2$	${\mathit{n}}_3$	${\mathit{n}}_4$	${\mathit{n}}_5$	$\mathit{a}=\mathit{m}\mathit{o}\mathit{d}\left(\frac{\mathit{n}}{5}\right)$
Equal	S1	$\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$	$\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$	$\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$	$\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$	$\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$	$a=0$
		$⟦n/5⟧$	$⟦n/5⟧$	$⟦n/5⟧+a$	$⟦n/5⟧$	$⟦n/5⟧$	$a=1$
		$⟦n/5⟧+1$	$⟦n/5⟧$	$⟦n/5⟧$	$⟦n/5⟧$	$⟦n/5⟧+1$	$a=2$
		$⟦n/5⟧+1$	$⟦n/5⟧$	$⟦n/5⟧+1$	$⟦n/5⟧$	$⟦n/5⟧+1$	$a=3$
		$⟦n/5⟧+1$	$⟦n/5⟧+1$	$⟦n/5⟧$	$⟦n/5⟧+1$	$⟦n/5⟧+1$	$a=4$
	S2	$⟦n/3⟧$		$n-2·⟦n/3⟧$		$⟦n/3⟧$
	S3	$n$
Central	S1	1	1	$n-4$	1	1
	S2	$1,if n\le 8$ $2,if n>8$		$n-2n_1$		$1, if n\le 8$ $2, if n>8$
	S3	n
Extreme	S1	$\left(n-2\right)/2$	1	0	1	$\left(n-2\right)/2$
	S2	$\left(n-2\right)/2$		2		$\left(n-2\right)/2$
	S3	$n$

, Equations (15)–(17)). Two of these strategies consider the cases in which each hopper $i$ is filled with a different average quantity of product ${\mu }_i$ (instead of a common value $\mu =T/k$). In this sense, and considering the original concept of each filling strategy, this study will explore the cases in which hopper feeds are defined so that hopper subgroups may share the same value of ${\mu }_i$. These strategies have been implemented in single-layered machines using single-target and bio-target algorithms with good results in reducing process variability [14,18,19,20]. However, they have not yet been tested on double-layered machines. With the implementation of the strategies, it is also intended to evaluate if it is more efficient for the process to supply all hoppers with the same amount of product or uneven amount of product according to the coefficient of proportionality $\gamma$ related to the product to be packed. Hopper feed variation will depend on a change value represented by the $\delta$ parameter, which is commonly used in statistical process control to simulate out-of-control processes. Nevertheless, for the purposes hereof, it will be used to voluntarily simulate an uneven product supply for weighing hoppers. Herein, $\delta$ will take values from 0 to 3 with increments of 0.5 (these increments are represented by the ${\delta }_{min}$ parameter, as expressed in Equation (15)). In addition, the average filling value for each hopper will also be influenced by the proportionality coefficient $\gamma$ ($\sigma =\gamma \mu$), which will depend on the type of material to be packaged. In this document, proportionality coefficients are used for two different pasta products: Fusilli, with $\gamma =0.123,$ and Ravioli, with $\gamma =0.331,$ [19,20]. For example, to calculate the standard deviation for a target weight of 500 g when we want to pack a product such as Fusilli by combining three hoppers, we will have a theoretical deviation of $\sigma =0.123·\frac{500 \mathrm{g}}{3}$ = 20.5 g.

In this way, to assess the algorithm proposed for double-layered machines, the three strategies will determine the average product supply for hopper subgroups and the total number of hoppers in each subgroup. The first strategy $(S_1)$ proposes dividing the $n$ weighing hopper into five groups, $(n_1, n_2,n_3,n_4,n_5,where$ ${\displaystyle \sum }_{i=1}^5{n}_i=n)$ and feeding different average quantities to each subgroup $\left({\mu }_1, {\mu }_2,{\mu }_3,{\mu }_4,{\mu }_5\right)$, establishing the filling configuration during the packaging process according to Equation (15). The second strategy $(S_2)$ proposes diving the $n$ weighing hopper into three groups, $\left(n_1, n_3,n_5\right)$ and feeding different average quantities to each subgroup$\left({\mu }_1, {\mu }_3,{\mu }_5\right)$, as per Equation (16). Finally, in the third strategy $(S_3),$ the $n$ weighing hoppers are filled with the same amount of product, $\mu =\frac{T}{k}$ for each hopper, as expressed in Equation (17).

$$w_i~N\left({\mu }_j,\sigma =\gamma {\mu }_j\right)=\left\{\begin{array}{c}\begin{array}{c}{\mu }_1=\mu -\delta \sigma \\ {\mu }_2=\mu -\left(\delta -{\delta }_{min}\right)\sigma \end{array}\\ \begin{array}{c}{\mu }_3=\mu =\frac{T}{k}\\ {\mu }_4=\mu +\left(\delta -{\delta }_{min}\right)\sigma \\ {\mu }_5=\mu +\delta \sigma \end{array}\end{array}\right\}$$

(15)

$$w_i~N\left({\mu }_j,\sigma =\gamma {\mu }_j\right)=\left\{\begin{array}{c}\begin{array}{c}{\mu }_1=\mu -\delta \sigma \\ {\mu }_3=\mu =\frac{T}{k}\end{array}\\ {\mu }_5=\mu +\delta \sigma \end{array}\right\}$$

(16)

$$w_i~N\left(\mu ,\sigma =\gamma \mu \right)=\left\{\mu =\frac{T}{k}\right\}$$

(17)

In addition to the $S_1$, $S_2$, and $S_3$ filling strategies, in which an average product supply is established for each subgroup, we must define a distribution of hoppers, in particular, the number of hoppers that are assigned to each subgroup (see Table 2). In this sense, three types of distributions are proposed: equal, central, and extreme. In the equal distribution strategy, each group includes approximately the same number of hoppers. For example, for the $S_1$ filling strategy, the total number of hoppers $\left(n\right)$ is divided among the five groups $\left(\frac{n}{5}\right)$. Each of the $n_{i }$ ($i=1, \dots 5$) is assigned a number of hoppers equal to the largest integer multiplied by 5 that is closest to $n$(integer part $⟦\frac{n}{2}⟧$). If the remainder of the division $\left(mod\left(\frac{n}{5}\right)\right)$ is 1, the central group $\left(n_3\right)$ will have one more hopper. If it is 2, a hopper will be assigned to each extreme group. For $mod\left(\frac{n}{5}\right)=3,$ they are distributed between $n_1, n_3, and n_5$. If $mod\left(\frac{n}{5}\right)=4,$ the $n_3$ group will have one less hopper than the rest.

The central distribution consists of assigning as many hoppers as possible to the central set of hoppers. For example, in strategy $S_2$ for $n\le 8$ and $n>8,$ one and two hoppers will be assigned, respectively, to each end, and the surplus is assigned to the central group. Finally, the extreme distribution assigns the largest number of hoppers to the extreme subgroups $n_1 \mathrm{and}{n}_5$, and the least amount to $n_3$.

Table 3. Number of hoppers for each group according to the $S_1$, $S_2$, and $S_3$ strategies for equal, central, and extreme distributions with $n$ = 16.

Distribution	Strategy	${\mathit{n}}_1$	${\mathit{n}}_2$	${\mathit{n}}_3$	${\mathit{n}}_4$	${\mathit{n}}_5$
Equal	$S_1$	3	3	4	3	3
	$S_2$	5		6		5
	$S_3$	16
Central	$S_1$	1	1	12	1	1
	$S_2$	2		12		2
	$S_3$	16
Extreme	$S_1$	7	1	0	1	7
	$S_2$	7		2		7
	$S_3$	16

and

Table 4. Average filling weight according to the $S_1$, $S_2$, and $S_3$ strategies for equal, central, and extreme distributions with$n$ = 16.

Distribution	Strategy	Average Filling Weight
Equal	$S_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_2$	${\mu }_2$	${\mu }_2$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_4$	${\mu }_4$	${\mu }_4$	${\mu }_5$	${\mu }_5$	${\mu }_5$
	$S_2$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$
	$S_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$
Central	$S_1$	${\mu }_1$	${\mu }_2$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_4$	${\mu }_5$
	$S_2$	${\mu }_1$	${\mu }_1$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_5$	${\mu }_5$
	$S_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$
Extreme	$S_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_2$	${\mu }_4$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$
	$S_2$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_1$	${\mu }_3$	${\mu }_3$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$	${\mu }_5$
	$S_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$	${\mu }_3$
Weighing hoppers:$H_W$		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Booster hoppers:$H_B$		17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32

illustrate an example of the number of hoppers for each subgroup according to the$S_1$, $S_2$, and $S_3$ strategies with $n=16$ weighing hoppers, and the average supply values for central, equal, and extreme subgroup distributions.

5. Optimization Model and Packaging Algorithm

This section presents the mathematical model and the packaging algorithm for the process in double-layered upright and diagonal machines. In this work, an adaptation of the well-known backpack problem is used. For each package, a deterministic knapsack problem is solved. Some researchers have optimized this way of determining the final weight of the package [21,22,23].

The symbology, decision variables, target function, and constraints for each process are also presented.

5.1. Symbology

• $Q:$ number of packages;
• $\ell :$ iteration in which the package is packed, where $\ell \in =\left\{1,2,3.\mathrm{Q}\right\}$;
• $H_{Wi}:$ set of $n$weighing hoppers, $i=\left\{1,2,3.n\right\}$;
• $H_{Bj}:$ set of $n$ booster hoppers, $j=\left\{n+1,n+2,\dots 2n\right\}$;
• $H_m=\left\{H_{Wi}{\displaystyle \cup }{H}_{Bj}\right\}:$set of the $2n$ hoppers $m=\left\{1,2,3,\dots ,2n\right\}$;
• $H^{\prime }:$ subset of combined hoppers;
• $T:$ target label weight;
• $k:$ number of hoppers to combine;
• $w_i:$ actual weight of each hopper $i=\left\{1,2,3,\dots 2n\right\}$ based on filling strategy $\left(S_1,S_2,\mathrm{or}{S}_3\right);$
• $W_{\ell }:$ sum of the weights of the $k$ hoppers in the $\ell$ iteration.

5.2. Target Function

The target function for the packaging processes in double-layered machines seeks to minimize the difference between the effective content of the package and its target weight $T$. The binary vectors are defined for the weighing hoppers (Equation (18)) and $Y_j$ for the booster hoppers (Equation (19)), whose components $x_i$ or $y_j$ take the value of 1 if the hopper weight $H_m$ was selected, or else it takes the value of 0 (Equations (20) and (21)).

$$X_i=\left(x_1,x_2,x_3,x_4,\dots x_n\right)$$

(18)

$$Y_j=\left(y_{n+1},y_{n+2},y_{n+3},y_{n+4}\dots y_{2n}\right)$$

(19)

$$x_i=\{\begin{array}{c} 1, \mathrm{if} H_{Wi} \mathrm{is}\mathrm{the}\mathrm{selected}\mathrm{hopper}\\ 0, \mathrm{otherwise} \end{array}$$

(20)

$$y_i=\{\begin{array}{c}1, \mathrm{if} H_{Bi} \mathrm{is}\mathrm{the}\mathrm{selected}\mathrm{hopper}\hfill \\ 0,\mathrm{otherwise} \hfill \end{array}$$

(21)

To select the hoppers, whose sum of the weights are the closest and greatest to the package weight, the function will be minimized, $f=W_{\ell }-T\ge 0$.

$$\mathrm{minimize} f\left(x,y\right)=\left[{\displaystyle \sum }_{i=1}^n{x}_i{w}_i+{\displaystyle \sum }_{j=n+1}^{2n}{y}_j{w}_j\right]-T$$

(22)

The problem restrictions will be directly determined by hopper selection restrictions. For the double-layered upright machine, the operating restriction of the system is that an upper hopper cannot be selected if its corresponding booster hopper has not been selected, which means that Equation (23) must be used. For the double-layered diagonal machine, a weighing hopper and its booster cannot be selected simultaneously, which is guaranteed by Equation (24).

$$x_i-y_i\le 0$$

(23)

$$x_i+y_i\le 1$$

(24)

In each $\ell$ iteration, the best combination of $k$ hoppers from the $2n$ available must be selected. If Equation (22) and the restrictions Equations (20), (21), and (23) for the double-layered upright machine are satisfied simultaneously for the whole set of $k$ combined hoppers and Equations (20), (21), and (24) for the double-layered diagonal machine, then the combination is valid.

As an example of the description of the mathematical model adjusted to the $S_2$, first, the vectors are defined for each subgroup (Equations (25)–(30)) according to Equations (31)–(36). The mathematical model is expressed as a function to minimize (Equation (37)), subject to the restrictions from Equations (38)–(40) for the double-layered upright machine and from Equations (41)–(43) for the double-layered diagonal.

$$X_i^{S_2^{n_1}}=\left(x_i^{S_2},\dots ,x_{n_1}^{S_2}\right)$$

(25)

$$X_m^{S_2^{n_2}}=\left(x_{n_1+1}^{S_2},\dots ,x_{n_1+n_2}^{S_2}\right)$$

(26)

$$X_r^{S_2^{n_3}}=\left(x_{n_1+n_2+1}^{S_2},\dots ,x_n^{S_2}\right)$$

(27)

$$Y_j^{S_2^{n_1}}=\left(y_{1+n}^{S_2},\dots ,y_{n+n_1}^{S_2}\right)$$

(28)

$$Y_t^{S_2^{n_2}}=\left(y_{n+n_1+1}^{S_2},\dots ,y_{n+n_1+n_2}^{S_2}\right)$$

(29)

$$Y_u^{S_2^{n_3}}=\left(y_{n+n_1+n_2+1}^{S_2},\dots ,y_{2n}^{S_2}\right)$$

(30)

$$x_i=\{\begin{array}{c}1,\mathrm{if}{H}_{Wi}^{S_2^{n_1}} \mathrm{is}\mathrm{chosen}\hfill \\ 0,\mathrm{in}\mathrm{other}\mathrm{case}\hfill \end{array}$$

(31)

$$x_m=\{\begin{array}{c}1, \mathrm{if} H_{Wm}^{S_2^{n_2}} \mathrm{is}\mathrm{chosen}\hfill \\ 0,\mathrm{in}\mathrm{other}\mathrm{case}\hfill \end{array}$$

(32)

$$x_r=\{\begin{array}{c}1,\mathrm{if} H_{Wr}^{S_2^{n_3}} \mathrm{is}\mathrm{selected}\\ 0,\mathrm{in}\mathrm{other}\mathrm{case}\end{array}$$

(33)

$$y_j=\{\begin{array}{c}1,\mathrm{if} H_{Bj}^{S_2^{n_1}} \mathrm{is}\mathrm{selected}\\ 0, \mathrm{in}\mathrm{other}\mathrm{case}\end{array}$$

(34)

$$y_t=\{\begin{array}{c}1,\mathrm{if} H_{Bt}^{S_2^{n_2}} \mathrm{is}\mathrm{chosen}\\ 0,\mathrm{in}\mathrm{other}\mathrm{case}\end{array}$$

(35)

$$y_u=\{\begin{array}{c}1, \mathrm{if} H_{Bu}^{S_2^{n_3}} \mathrm{is}\mathrm{selected}\\ 0, \mathrm{in}\mathrm{other}\mathrm{case}\end{array}$$

(36)

$$\left[{\displaystyle \sum }_{l=1}^{n_1}{x}_l^1{w}_l^1+{\displaystyle \sum }_{m=n_1+1}^{n_1+n_2}{x}_m^2{w}_m^2+{\displaystyle \sum }_{r=n_1+n_2+1}^n{x}_r^3{w}_r^3+{\displaystyle \sum }_{j=l+n}^{n_1+n}{y}_j^1{w}_j^1+{\displaystyle \sum }_{t=n_1+n}^{n_1+n_2+n}{y}_t^2{w}_t^2+{\displaystyle \sum }_{u=n_1+n_2+n}^{2n}{y}_u^3{w}_u^3\right]-T\ge 0$$

(37)

$$x_i-y_j\le 0$$

(38)

$$x_m-y_t\le 0$$

(39)

$$x_r-y_r\le 0$$

(40)

$$x_i+y_j\le 1$$

(41)

$$x_m+y_t\le 1$$

(42)

$$x_r+y_r\le 1$$

(43)

5.3. Algorithm

In this subsection, we present the algorithm designed for the packaging process for double-layered upright and diagonal machines. The step-by-step process is generic for any of the $k$combinations of the $2n$hoppers of the system, with initial constants adjustable to the type of product packaged.

• Step 1. The initial values and conditions are defined.
  $Q:$ Total number of packages processed;
  $n:$ Number of weighing hoppers;
  $k:$ Number of hoppers to combine $2\le k\le n$;
  $T:$ Target weight $>0$.
• Step 2. The empty weighing hoppers $H_{Wi}$ are loaded with randomly assigned weights $w_i,i\in \left\{1,2,\dots n\right\}$ according to S1, S2, or S3 and according to the number of hoppers in each group.
• Step 3. The contents of the weighing hoppers $H_{Wi}$ are discharged into their corresponding empty booster hoppers $H_{Bj}$, with$w_{n+i}=w_i$ and $w_i=0$.
• Step 4. The weighing hoppers previously discharged are reloaded.
• Step 5. The hoppers that meet the criteria from Equation (23) or Equation (24) are combined for the upright or diagonal machines, respectively.
• Step 6. The difference between the sum of the weights of each combination and the target weight is calculated (Equation (22)).
• Step 7. The subset $H^{\prime }$ of $k$ hoppers whose difference with $T$ is minimal, from those calculated in the previous point, is selected.
• Step 8. The product is discharged and packed.
• Step 9. If the required number of Q packets has been completed, the process ends. Otherwise, it returns to Step 2.

6. Preliminary Analysis

To validate the algorithm, we used proportionality coefficients of $\gamma =0.123$ for Fusilli and $\gamma =0.331$ for Ravioli [20]. In addition, a number of $n$ = 16 weighing hoppers were assessed, at $k$ = 2, 3, 4, 5, and 7,$\delta =2,$ ${\delta }_{min}=0.5,$and a target weight of $T=250$ g. The number of hoppers in each subgroup is shown in Table 3. Combinations generated for the different values of $k$ assessed are presented in Table 1. The performance measures calculated were the average weight of the packages produced (${\mu }_{paq}$), the standard deviation of the packages produced (${\sigma }_{paq}$), and the coefficient of variation of the packages produced$\left(C{V}_{paq}=\frac{{\mu }_{paq}}{{\sigma }_{paq}}\right)$, all above for $Q$ = 10,000 packages.

Results for the double-layered upright and diagonal machine are presented in

Table 5. Results of $S_1$, $S_2$, and $S_3$ strategies, for $k=2,3,4,5,6,\mathrm{and}7$, and $\gamma =0.123$.

FUSILLI
		Vertical			Diagonal
	$\mathit{k}$	${\mathit{\mu }}_{\mathit{p}\mathit{a}\mathit{q}}$	${\mathit{\sigma }}_{\mathit{p}\mathit{a}\mathit{q}}$	$\mathit{C}{\mathit{V}}_{\mathit{p}\mathit{a}\mathit{q}}$	${\mathit{\mu }}_{\mathit{p}\mathit{a}\mathit{q}}$	${\mathit{\sigma }}_{\mathit{p}\mathit{a}\mathit{q}}$	$\mathit{C}{\mathit{V}}_{\mathit{p}\mathit{a}\mathit{q}}$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\mathit{\mu }}_3$	${\mathit{\mu }}_4$	${\mathit{\mu }}_5$
	2	254.158	2.855	0.0110	253.650	2.869	0.0110	94.25	101.94	125.00	148.06	155.75
S1	3	250.231	0.208	0.0008	250.063	0.049	0.0002	62.83	67.96	83.33	98.71	103.83
	4	250.031	0.029	0.0001	250.005	0.004	1.62e-05	47.13	50.97	62.50	74.03	77.88
	5	250.006	0.006	2.36e-05	250.001	0.001	2.48e-06	37.70	40.78	50.00	59.23	62.30
	6	250.002	0.002	6.51e-06	250.000	1.36e-04	5.47e-07	31.42	33.98	41.67	49.35	51.92
	7	250.001	0.001	2.42e-06	250.000	5.10e-05	2.04e-07	26.93	29.13	35.71	42.30	44.50
	2	253.928	2.82	0.0111	253.319	2.691	0.001	94.25		125.00		155.75
S2	3	252.181	2.158	0.0086	250.056	0.044	0.0002	62.83		83.33		103.83
	4	250.031	0.028	0.0001	250.004	0.004	1.34e-05	47.13		62.50		77.88
	5	250.006	0.006	2.42e-05	250.001	0.001	2.02e-06	37.70		50.00		62.30
	6	250.002	0.002	6.68e-06	250.001	1.21e-04	4.85e-07	31.42		41.67		51.92
	7	250.001	0.001	2.04e-06	250.000	4.21e-05	1.68e-07	26.93		35.71		44.50
	2	253.405	2.662	0.0105	252.615	2.392	0.0095			125.00
S3	3	250.414	0.82	0.0033	250.170	0.673	0.0027			83.33
	4	250.161	0.657	0.0026	250.070	0.482	0.0019			62.50
	5	250.138	0.725	0.0029	250.107	0.720	0.0029			50.00
	6	250.166	0.885	0.0040	250.060	0.556	0.0022			41.67
	7	250.084	0.623	0.0024	250.071	0.609	0.0024			35.714

and

Table 6. Results of the $S_1$, $S_2$, and $S_3$ strategies, for $k=3,4,5,6, \mathrm{and}7$, and $\gamma =0.331$.

RAVIOLI
		Vertical			Diagonal
	$\mathit{k}$	${\mathit{\mu }}_{\mathit{p}\mathit{a}\mathit{q}}$	${\mathit{\sigma }}_{\mathit{p}\mathit{a}\mathit{q}}$	$\mathit{C}{\mathit{V}}_{\mathit{p}\mathit{a}\mathit{q}}$	${\mathit{\mu }}_{\mathit{p}\mathit{a}\mathit{q}}$	${\mathit{\sigma }}_{\mathit{p}\mathit{a}\mathit{q}}$	$\mathit{C}{\mathit{V}}_{\mathit{p}\mathit{a}\mathit{q}}$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\mathit{\mu }}_3$	${\mathit{\mu }}_4$	${\mathit{\mu }}_5$
	2	254.527	2.929	0.0120	254.138	2.854	0.0110	42.25	62.94	125.00	187.06	207.75
S1	3	252.231	2.215	0.0088	251.915	2.199	0.0087	28.17	41.96	83.33	124.71	138.50
	4	250.102	0.104	0.0004	250.028	0.038	0.0002	21.13	31.47	62.50	93.53	103.88
	5	250.018	0.017	0.0001	250.002	0.002	7.47e-06	16.90	25.18	50.00	74.83	83.10
	6	250.005	0.005	1.85e-05	250.000	4.29e-04	1.69e-06	14.08	20.98	41.67	62.35	69.25
	7	250.002	0.002	6.86e-06	250.000	1.12e-04	4.84e-07	12.07	17.98	35.71	53.45	59.36
	2	254.587	2.867	0.0113	254.154	2.857	0.0112	42.25		125.00		207.75
S2	3	252.539	2.421	0.0096	251.638	2.086	0.0083	28.17		83.33		138.50
	4	250.113	0.118	0.0005	250.017	0.016	0.0001	21.13		62.50		103.88
	5	250.018	0.017	0.0001	250.002	0.002	6.85e-06	16.90		50.00		83.10
	6	250.005	0.004	1.72e-05	250.000	3.39e-04	1.35e-06	14.08		41.67		69.25
	7	250.001	0.001	5.95e-06	250.000	1.22e-04	4.88e-07	12.07		35.71		59.36
	2	254.422	2.867	0.0113	253.58	2.715	0.0107			125.00
S3	3	250.887	1.376	0.0055	250.245	0.597	0.0024			83.33
	4	250.318	0.960	0.0038	250.102	0.501	0.0020			62.50
	5	250.170	0.691	0.0028	250.053	0.410	0.0016			50.00
	6	250.160	0.793	0.0030	250.049	0.443	0.0017			41.667
	7	250.069	0.505	0.0020	250.064	0.565	0.0022			35.714

. Here, we observe that at $\gamma =0.123$, for the double-layered upright machine, the $S_3$ strategy produces a weight closer to $T$ and lower values of ${\sigma }_{paq}$ and $C{V}_{paq},$ when $k$ = 7. However, this strategy offers the highest values for ${\mu }_{paq}$ and ${\sigma }_{paq}$, thus becoming the least favorable for the process. In $S_1$ and $S_2$, the average weight closest to $T$ and lower values of ${\sigma }_{paq}$ and $C{V}_{paq}$ were obtained at $k$ = 7. However, their values were similar to $k$ = 6. These last strategies seem to be the most convenient in terms of reducing process variability. This behavior of the strategies is maintained for the double-layered diagonal machine, which also denotes lower values when compared to those obtained in the double-layered upright machine.

However, the results of the tests for $\gamma =0.331$ show that the average weight of the packages closest to the target weight and the lowest values of ${\sigma }_{paq}$ and $C{V}_{paq}$ are presented for $k=6\mathrm{and}7$ in both machines, being lower in $S_1$ and $S_2$. In general terms, we observe that when the value of the proportionality coefficient is increased to $\gamma =0.331$, the ${\mu }_{paq}$,${\sigma }_{paq},$ and $C{V}_{paq}$ values also increase. However, the behavior (operation) of the process is similar for both products. Based on these results, the design of experiments presented in Section 7 was proposed to determine which conditions decrease process variability and provide higher values and as close as possible to the target weight.

7. Experiment Design

To follow up on our preliminary analysis, an experiment design (DOE) of fixed effects factors [24] was conducted to determine the best combination of treatments that provides the least process variability. For the design, the factor levels that evidenced the best performance in their coefficient of variation are considered, discarding those that yielded the lowest levels of process variability reduction. The multifactorial design consists of eight factors, as shown in

Table 7. Experiment design factors and levels.

Factors	Factor Levels
Machine type	Upright	Diagonal
Number of weighing hoppers: $n$	10	14	16
Number of hoppers to combine$k$	5	6	7
Target weight: $T$	250	500
Material type: gamma ($\gamma$)	Fusilli = 0.123	Ravioli = 0.331
Strategy: Number of subgroups	3	5
Hopper distribution	Central	Equal	Extreme
Filling position: Delta ($\delta$)	0	0.5	1	1.5	2	2.5	3

, for a total of 1512 treatments in each machine, each of them with three replicates, finally obtaining 12,096 runs. The response variable studied is the coefficient of variation obtained in each run of 10,000 packages since it is a measure that may be used to compare different target weights $T$. In addition to analyzing the best factor combination, the upright and diagonal machines are compared against each other to determine which offers less process variability. Here, the first factor encompasses two levels, which refer to the double-layered upright or diagonal machine. A second factor is associated with the number of weighing hoppers. In this case, machines with 10, 14, and 16 weighing hoppers were assessed. The third factor is the number of hoppers to combine with values from $k=5$ to $k=7$. Another factor to consider is the target label weight, which is set at two levels: 250 g and 500 g. In addition, two packaging products, Fusilli and Ravioli, constitute the two levels of the sixth factor. The $S_1$ and $S_2$ strategies determine hopper subgroups, grouped by equal, central, and extreme levels. The filling position constitutes the eighth factor with seven levels ${\delta }_{min}=$ 0, 0.5, 1, 1.5, 2, 2.5, and 3, which simulate an out-of-control process when ${\delta }_{min}>0$.

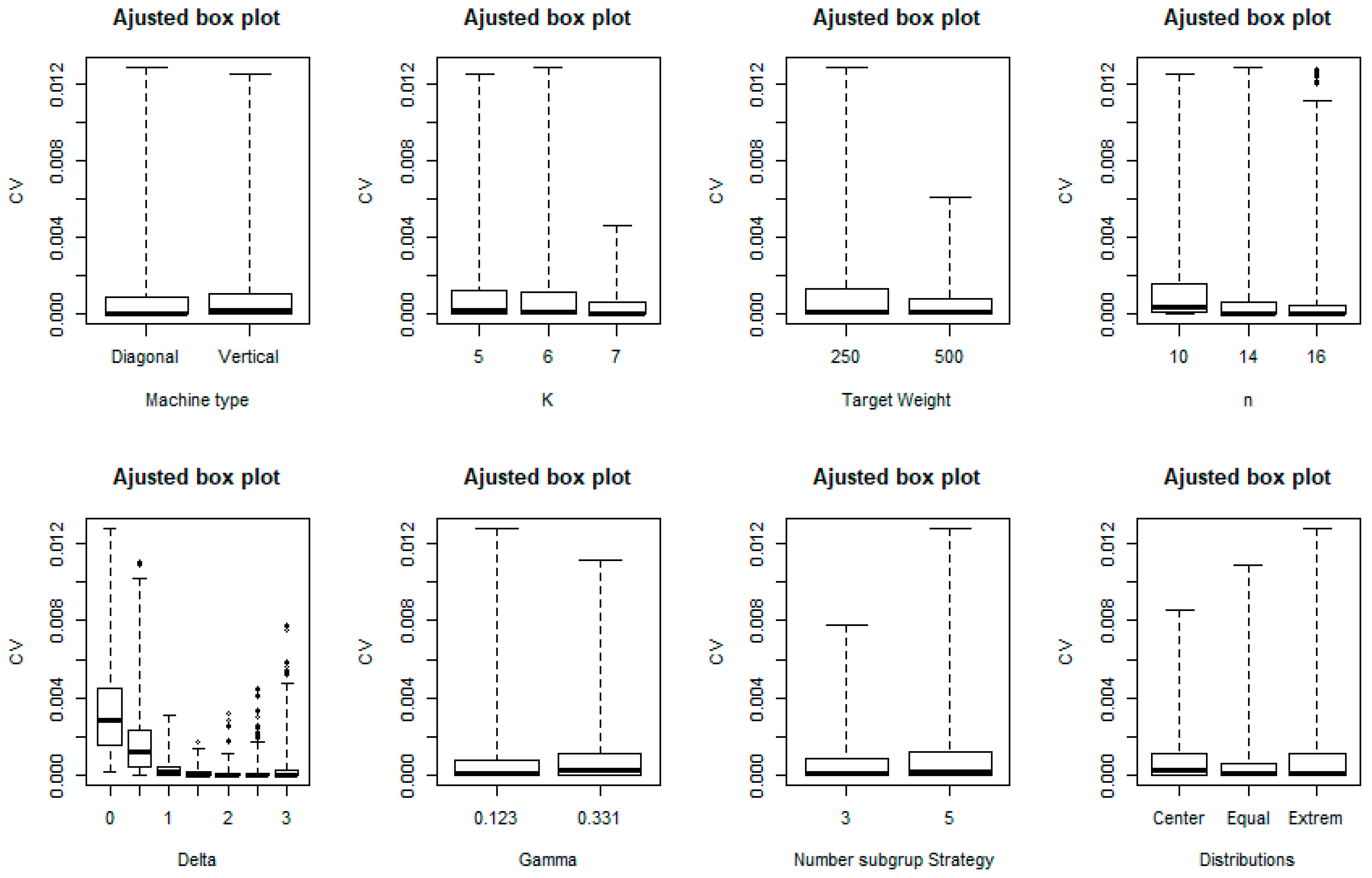
Given that the data of the response variation coefficient variable (CVpaq) are asymmetric, with a lower target weight, adjusted box plots are used to compare the levels within the same factor, as shown in Figure 6. To assess the experiment design, a transformation of the variable $CVpaq$ by Johnson’s method [25] is used to standardize the data, thus obtaining the transformed coefficient of variation ($CVpaqT$) as the response variable.

Results from the experiment design were analyzed using analysis of variance (ANOVA).

Table 8. ANOVA for CVpaqT - sum of squares type III.

Source	Sum of Squares	Df	Mean Square	F-Ratio	p-Value
MAIN EFFECTS
Machine type	1.72e14	1	1.72e14	327.78	0.0000
Target weight	2.28e14	1	2.28e14	434.55	0.0000
n	5.14e14	2	2.57e14	488.73	0.0000
k	1.90e14	2	9.52e13	181.24	0.0000
Delta	2.35e14	6	3.92e13	74.68	0.0000
Gamma	4.10e11	1	4.10e11	0.78	0.3771
Number subgroup strategy	6.17e11	1	6.17e11	1.17	0.2785
Distributions	1.25e14	2	6.26e13	119.06	0.0000
INTERACTIONS
Machine type target weight	2.83e13	1	2.83e13	53.82	0.0000
Machine Type·k	3.95e14	2	1.98e14	376.23	0.0000
Target weight·n	4.20e12	2	2.10e12	4.00	0.0184
Target weight·k	1.71e13	2	8.54e12	16.26	0.0000
n·k	8.94e13	4	2.23e13	42.53	0.0000
n·Delta	3.62e14	12	3.02e13	57.44	0.0000
n·Gamma	6.04e12	2	3.02e12	5.74	0.0032
n·Distributions	1.30e13	4	3.26e12	6.20	0.0001
k·Delta	2.69e14	12	2.24e13	42.58	0.0000
k·Number subgroup strategy	8.68e12	2	4.34e12	8.26	0.0003
k·distributions	1.46e13	4	3.65e12	6.95	0.0000
Delta·gamma	1.42e14	6	2.37e13	45.09	0.0000
Delta·number subgroup strategy	5.05e13	6	8.41e12	16.01	0.0000
Number subgroup strategy·Distributions	5.04e12	2	2.52e12	4.80	0.0083
Residual	6.32e15	12,018	5.25e11
Total (corrected)	9.19e15	12,095

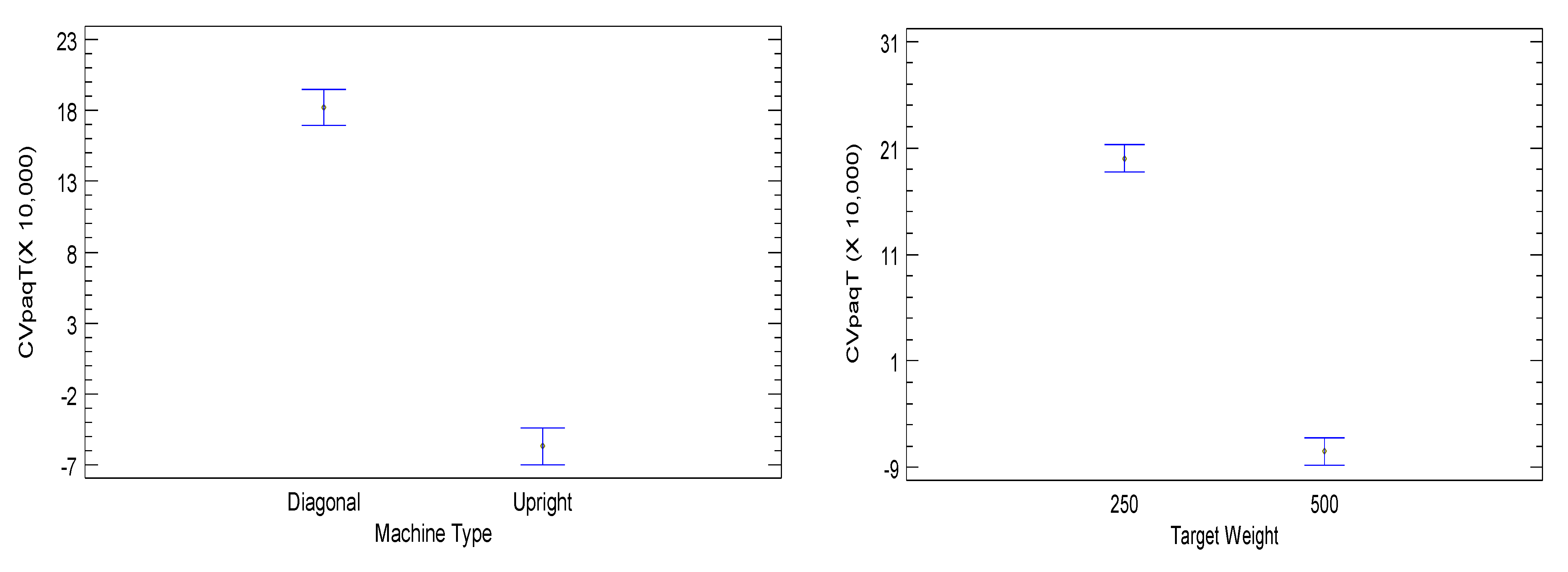
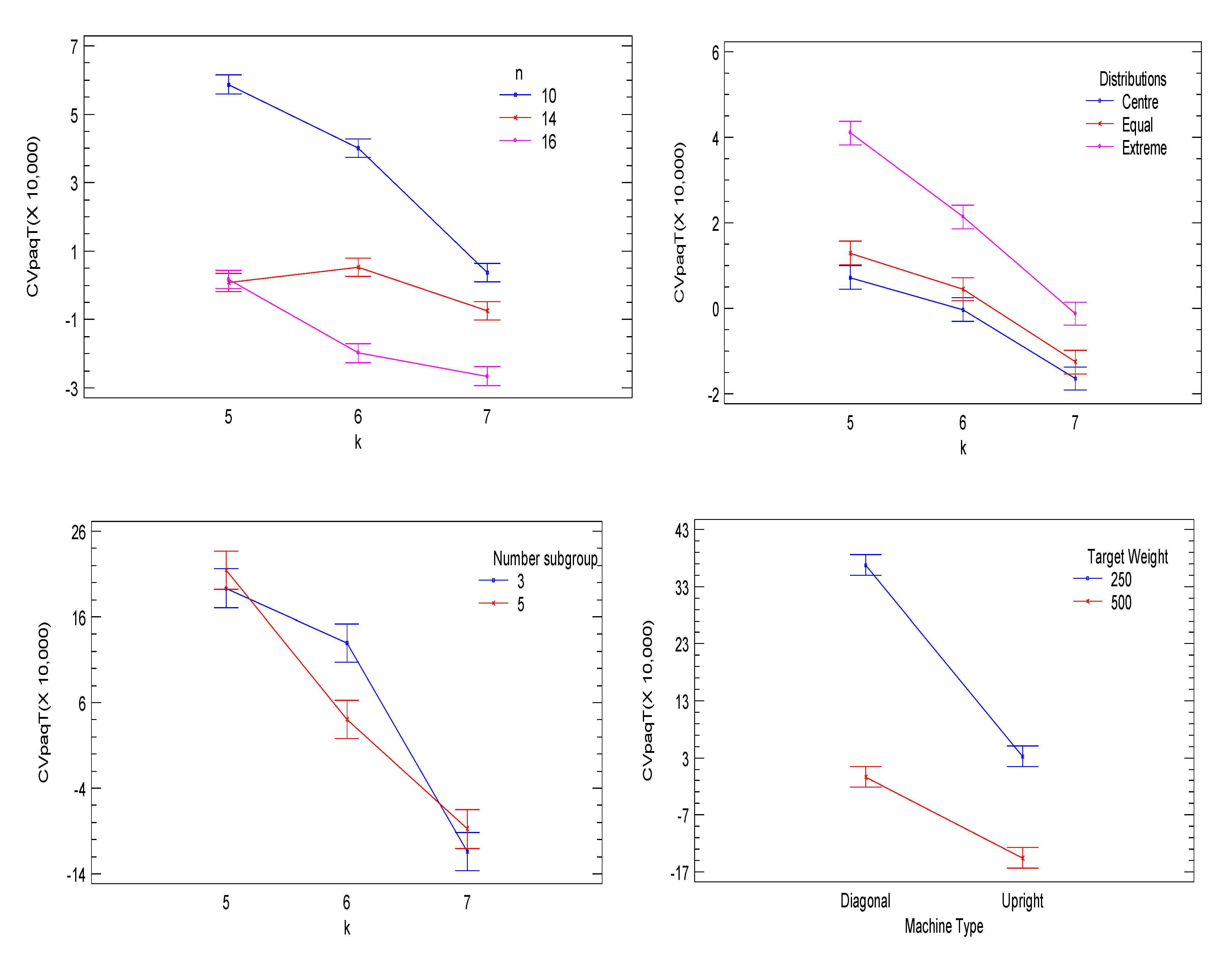
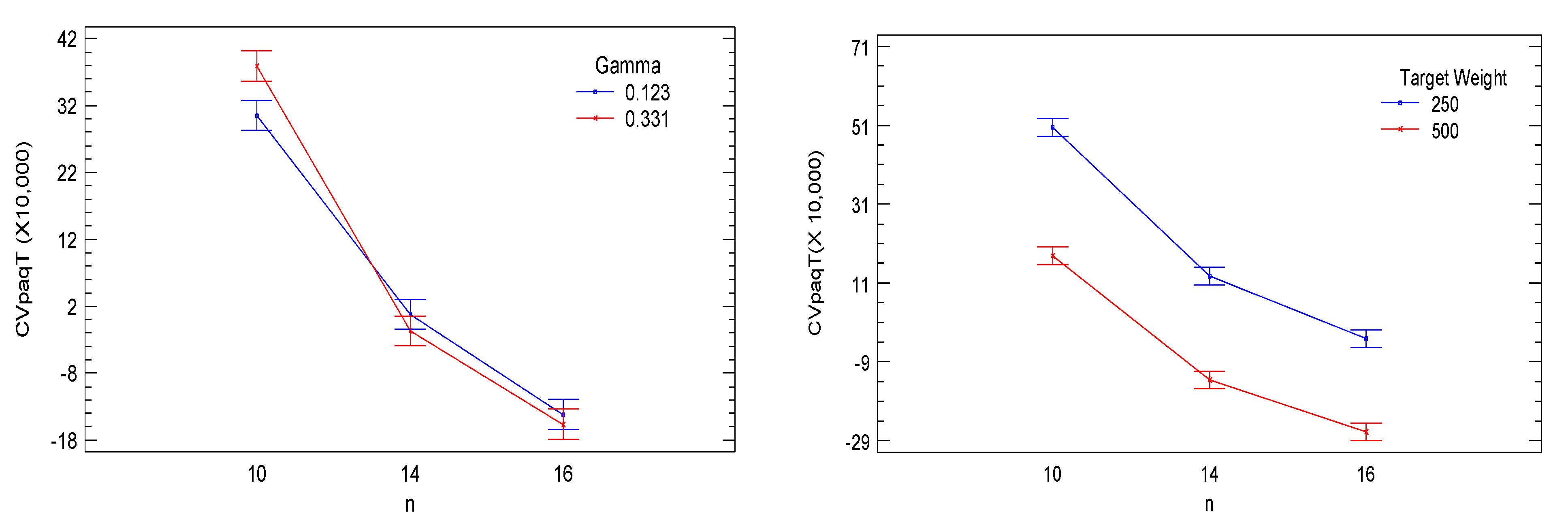
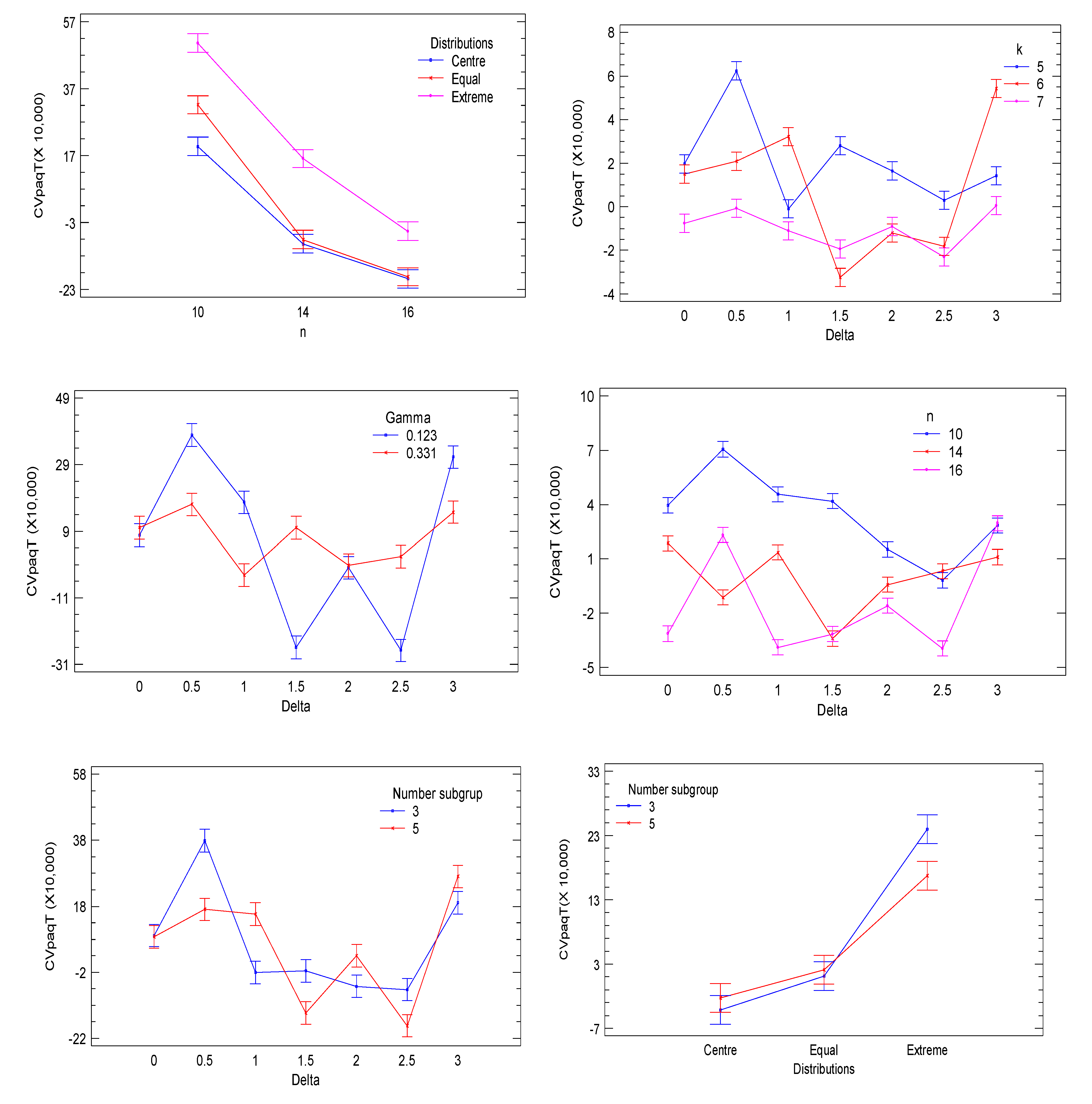
denotes the results of the ANOVA. As it may be observed, no significant differences were found in the product type and number of subgroups factors for the hopper distribution. Figure 7 denotes the significant factors. When analyzing the interactions, significant p-values were found for Machine Type Target Weight, Machine Type· k, Target Weight·n, n·k, n k, n·Delta, n·Gamma, n·Hopper Distribution, k·Delta, k·Number of Subgroups, k·Hopper Distribution, Delta·Gamma, Delta·Number of Subgroups, and Number of Subgroups·Hopper Distribution.

Based on the results of the significant interactions between the design factors (Figure 8 and Figure 9), we can infer that when comparing machine performances according to the number of weighing hoppers, $n=16$ provides greater accuracy, and it is even better when the target weight is 500 g. For the number of hoppers combined, significant differences were found between the mean values of the coefficient of variation. 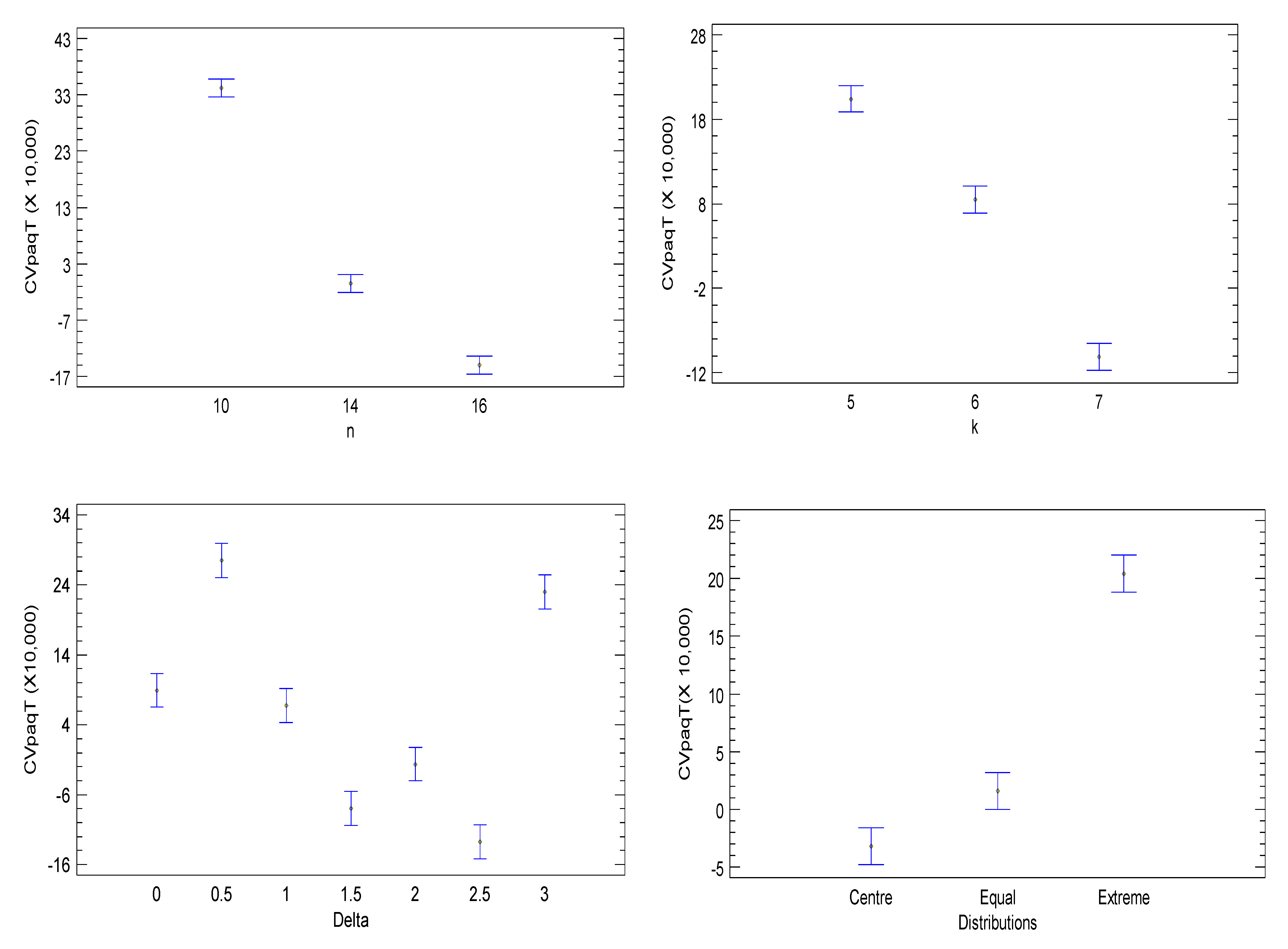Figure 6 and Figure 7 denote that for almost all interactions, $k=7$ is the ideal number of hoppers to reach the target weight, except at $\delta$ = 1.5, which suggests the use of six hopper combinations. Significant differences were also found for $CVpaqT$, according to the target weight, exhibiting better behaviors if $T=500 \mathrm{g}$. Regarding the $S_1$ and $S_2$ filling strategies, five subgroups provided better results at $\delta =2.5$. In addition, significant differences were found regarding the product type. In this aspect, better results were found when the proportionality coefficient is the lowest because lower values of $\gamma$ introduce less variability in the weights supplied to the weighing hoppers. Here, Fusilli ($\gamma =0.123$) reported less process variability with an optimum point at $\delta =2.5$. Regarding the hopper distribution for each group, the central strategy denotes better behavior for both machines. Hence, we can conclude that the optimal process uses the diagonal machine at $k=7$, $n=16$ $T=500$, $S_1=5$, central distribution, $\delta =2.5$ ($\delta =1.0$ for Ravioli), and $\gamma =0.123$.

8. Discussion

Multihead machines for their proper operation require two processes: packaging and machine configuration. The packaging process is linked to the problem of the backpack, that is, how to select the hoppers whose sum of the weights is greater and closest possible to the target weight. The new software, implemented for upright and diagonal double-layer machines with real weights according to the preliminary results (Table 5 and Table 6), shows that it is capable of responding to the problem by finding the optimal value in each package, complying with the requirements. On the other hand, the configuration of the machine is related to the amount of product that each weighing hopper receives, and in this sense, the filling strategies focus on evaluating the performance of the machine according to the amount of product supplied to each hopper. The S3 strategy provides each hopper with the same amount of product, while the S2 divides the hoppers into three groups and in the same way, S1 into five groups, which guarantees an unequal supply of product to each subset of hoppers. The preliminary results of Table 5 and Table 6 show that the configuration of the machines with the lowest performance in terms of the target weight and the variation of the process is the S3 strategy, which supplies the same quantity of product to all the hoppers; therefore, it is not taken into account for the design of the experiment (Table 7). Likewise, in the configuration process, distribution strategies (central, equal, and extreme) were tested with the number of hoppers for each subset determined in each strategy S1 and S2, according to the group to which the largest number of hoppers is assigned. In the results of the design of experiments (Table 8), it is observed that there is no difference between the strategies S1 and S2 (p-value = 0.27); however, when contrasting them in the presence of other factors, for example, the number of hoppers to combine (k) and the delta value (δ), we find that in the presence of these factors, there is a significant difference between them. In the same sense, for the type of product, significant p-values are found in the presence of a second factor such as the case of delta and the number of hoppers in the system. In accordance with the above, the type of product is an important factor to take into account when configuring the machine. When analyzing the interactions of the other factors with the delta value (δ) (Table 8, Figure 8 and Figure 9), we find that the process presents less variability in values of δ = 1.5, which suggests a group of hoppers receive content that is far away plus 1.5 standard deviations of the average content according to the target weight and the type of product to be packed. Finally, the results suggest that for k = 7, hopper combinations the packaging process achieves its optimal value.

9. Conclusions

The multihead weighing process is characterized by high product packaging performance and accuracy. The optimization of this process guarantees material savings and high levels of productivity in terms of the number of packages produced. In this document, a new packaging algorithm and its corresponding optimization model for double-layered upright and diagonal multihead weighers have been presented, considering actual weights in the weighing hoppers and a predefined number of hoppers to be combined. The algorithm was validated using three product feeding strategies ($S_1,$ $S_2,$ and $S_3$) and different numbers $k$ of hopper combinations. To assess the performance of the process, two products (Ravioli and Fusilli) were tested at different coefficients of proportionality ($\gamma$), and then an experiment design was approached to establish a comparison between different factor levels. The performance metrics used were the average weight of the packages produced, the standard deviation of the packages produced, and the coefficient of variation of the packages produced. Results revealed that the best filling configuration to reduce the process variability is the $S_1$ strategy, particularly with the five subgroups of hoppers, assigning the largest number of hoppers to the group. In addition, the number of hoppers to be combined at $k$ = 7 offered the least variability in the total weight of the packages produced in both processes. The study also concluded that process behavior or operation is better at minimum values of $\gamma$ ($\gamma =0.123$). Finally, the diagonal machine offers a greater NC for the weighing hoppers when selecting the package weight, which is reflected in lower process variability.