Flexible Time-Varying Betas in a Novel Mixture Innovation Factor Model with Latent Threshold
Abstract
1. Introduction
2. Literature Review
3. Data and Methodology
3.1. Data
3.2. Methodology
4. Empirical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- FTSE Russell. Available online: http://www2.londonstockexchangegroup.com/Smart-Beta-Results-2018-Web (accessed on 24 March 2021).
- BlackRock Investments: What is Factor Investing? Available online: https://www.blackrock.com/us/individual/investment-ideas/what-is-factor-investing (accessed on 26 March 2021).
- Melas, D.; Suryanarayanan, R.; Cavaglia, S. Efficient Replication of Factor Returns:Theory and Applications. J. Portf. Manag. 2010, 36, 39–51. [Google Scholar] [CrossRef]
- Beck, N.; Hsu, J.; Kalesnik, V.; Kostka, H. Will Your Factor Deliver? An Examination of Factor Robustness and Implementation Costs. Financ. Anal. J. 2016, 72, 58–82. [Google Scholar] [CrossRef]
- Clarke, R.; De Silva, H.; Thorley, S. Fundamentals of Efficient Factor Investing (corrected May 2017). Financ. Anal. J. 2016, 72, 9–26. [Google Scholar] [CrossRef]
- Chen, L.; Dolado, J.J.; Gonzalo, J. Detecting big structural breaks in large factor models. J. Econ. 2014, 180, 30–48. [Google Scholar] [CrossRef]
- Han, X.; Inoue, A. Tests of parameter instability in dynamic factor models. Econom. Theor. 2015, 31, 1117–1152. [Google Scholar] [CrossRef]
- Su, L.; Wang, X. On time-varying factor models: Estimation and testing. J. Econ. 2017, 198, 84–101. [Google Scholar] [CrossRef]
- Rapach, D.E.; Wohar, M.E.; Rangvid, J. Macro variables and international stock return predictability. Int. J. Forecast. 2005, 21, 137–166. [Google Scholar] [CrossRef]
- Sousa, R.M.; Vivian, A.; Wohar, M.E. Predicting asset returns in the BRICS: The role of macroeconomic and fundamental predictors. Int. Rev. Econ. Financ. 2016, 41, 122–143. [Google Scholar] [CrossRef]
- Aye, G.C.; Balcilar, M.; Gupta, R. International stock return predictability: Is the role of U.S. time-varying? Empirica 2017, 44, 121–146. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Lintner, J. The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets. Rev. Econ. Stat. 1965, 47, 13. [Google Scholar] [CrossRef]
- Jiang, C.; Du, J.; An, Y.; Zhang, J. Factor tracking: A new smart beta strategy that outperforms naïve diversification. Econ. Model. 2021, 96, 396–408. [Google Scholar] [CrossRef]
- Ang, A.; Chen, J.S. CAPM Over the Long-Run: 1926-2001. SSRN Electron. J. 2007, 14, 1–40. [Google Scholar] [CrossRef]
- Levi, Y.; Welch, I. Best Practice for Cost-of-Capital Estimates. J. Financ. Quant. Anal. 2017, 52, 427–463. [Google Scholar] [CrossRef]
- Pagan, A. Some identification and estimation results for regression models with stochastically varying coefficients. J. Econ. 1980, 13, 341–363. [Google Scholar] [CrossRef]
- Yu, H.; Fang, L.; Du, D.; Yan, P. How EPU drives long-term industry beta. Finance Res. Lett. 2017, 22, 249–258. [Google Scholar] [CrossRef]
- Aslanidis, N.; Hartigan, L. Is the assumption of constant factor loadings too strong in practice? Econ. Model. 2021, 98, 100–108. [Google Scholar] [CrossRef]
- Becker, J.; Hollstein, F.; Prokopczuk, M.; Sibbertsen, P. The memory of beta. J. Bank. Financ. 2021, 124, 106026. [Google Scholar] [CrossRef]
- Wang, L. Time-varying conditional beta, return spillovers, and dynamic bank diversification strategies. The Quart. Rev. Econ. Fin. 2021, 79, 272–280. [Google Scholar] [CrossRef]
- Hollstein, F. Estimating beta: The international evidence. J. Bank. Financ. 2020, 121, 105968. [Google Scholar] [CrossRef]
- Arshanapalli, B.; Fabozzi, F.J.; Nelson, W. The value, size, and momentum spread during distressed economic periods. Finance Res. Lett. 2006, 3, 244–252. [Google Scholar] [CrossRef]
- Ferson, W.E.; Harvey, C.R. The variation of economic risk premiums. J. Political Econ. 1991, 99, 385–415. [Google Scholar] [CrossRef]
- Jagannathan, R.; Wang, Z. The Conditional CAPM and the Cross-Section of Expected Returns. J. Financ. 1996, 51, 3–53. [Google Scholar] [CrossRef]
- Lettau, M.; Ludvigson, S. Resurrecting the (C) CAPM: A cross-sectional test when risk premia are time-varying. J. Political Econ. 2001, 109, 1238–1287. [Google Scholar] [CrossRef]
- Shanken, J. Intertemporal asset pricing: An empirical investigation. J. Econom. 1990, 45, 99–120. [Google Scholar] [CrossRef]
- Hameed, A. Time-varying factors and cross-autocorrelations in short-horizon stock returns. J. Financ. Res. 1997, 20, 435–458. [Google Scholar] [CrossRef]
- Mergner, S.; Bulla, J. Time-varying beta risk of Pan-European industry portfolios: A comparison of alternative modeling techniques. Eur. J. Finance 2008, 14, 771–802. [Google Scholar] [CrossRef]
- Moonis, S.A.; Shah, A. Testing for Time-variation in Beta in India. J. Emerg. Mark. Finance 2003, 2, 163–180. [Google Scholar] [CrossRef]
- Wells, C. Variable betas on the Stockholm exchange 1971–1989. Appl. Financ. Econ. 1994, 4, 75–92. [Google Scholar] [CrossRef]
- Zhou, J. Conditional market beta for REITs: A comparison of modeling techniques. Econ. Model. 2013, 30, 196–204. [Google Scholar] [CrossRef]
- Ang, A.; Kristensen, D. Testing conditional factor models. J. Financ. Econ. 2012, 106, 132–156. [Google Scholar] [CrossRef]
- Esteban, M.V.; Orbe-Mandaluniz, S. A nonparametric approach for estimating betas: The smoothed rolling estimator. Appl. Econ. 2010, 42, 1269–1279. [Google Scholar] [CrossRef]
- Koch, S.; Westheide, C. The conditional relation between Fama-French betas and return. Schmalenbach Bus. Rev. 2013, 65, 334–358. [Google Scholar] [CrossRef]
- Lewellen, J.; Nagel, S. The conditional CAPM does not explain asset-pricing anomalies. J. Financ. Econ. 2006, 82, 289–314. [Google Scholar] [CrossRef]
- Li, Y.; Yang, L. Testing conditional factor models: A nonparametric approach. J. Empir. Financ. 2011, 18, 972–992. [Google Scholar] [CrossRef]
- Bollerslev, T.; Engle, R.F.; Wooldridge, J.M. A Capital Asset Pricing Model with Time-Varying Covariances. J. Politi Econ. 1988, 96, 116–131. [Google Scholar] [CrossRef]
- Lee, C.F.; Chen, G.-M.; Rui, O.M. Stock returns and volatility on China’s stock markets. J. Financ. Res. 2001, 24, 523–543. [Google Scholar] [CrossRef]
- Ng, L. Tests of the CAPM with Time-Varying Covariances: A Multivariate GARCH Approach. J. Finance 1991, 46, 1507–1521. [Google Scholar] [CrossRef]
- Choudhry, T.; Wu, H. Forecasting ability of GARCH vs. Kalman filter method: Evidence from daily UK time-varying beta. J. Forecast. 2008, 27, 670–689. [Google Scholar] [CrossRef]
- Ebner, M.; Neumann, T. Time-Varying Betas of German Stock Returns. Financ. Mark. Portf. Manag. 2005, 19, 29–46. [Google Scholar] [CrossRef]
- Faff, R.W.; Hillier, D.; Hillier, J. Time Varying Beta Risk: An Analysis of Alternative Modelling Techniques. J. Bus. Finance Account. 2000, 27, 523–554. [Google Scholar] [CrossRef]
- Bauwens, L.; Laurent, S.; Rombouts, J.V.K. Multivariate GARCH models: A survey. J. Appl. Econom. 2006, 21, 79–109. [Google Scholar] [CrossRef]
- Caporin, M.; McAleer, M. Ten Things You Should Know about the Dynamic Conditional Correlation Representation. Econometrics 2013, 1, 115–126. [Google Scholar] [CrossRef]
- Ghysels, E. On Stable Factor Structures in the Pricing of Risk: Do Time-Varying Betas Help or Hurt? J. Financ. 1998, 53, 549–573. [Google Scholar] [CrossRef]
- Chan, K.S. Consistency and Limiting Distribution of the Least Squares Estimator of a Threshold Autoregressive Model. Ann. Stat. 1993, 21, 520–533. [Google Scholar] [CrossRef]
- Hansen, B.E. Sample Splitting and Threshold Estimation. Econometrica 2000, 68, 575–603. [Google Scholar] [CrossRef]
- Gonzalo, J.; Pitarakis, J.Y. Estimation and model selection based inference in single and multiple threshold models. J. Econom. 2002, 110, 319–352. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, A.; Demirer, R. Oil and Risk Premia in Equity Markets. Stud. Econ. Financ. 2020, 37, 697–723. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. The cross-section of expected stock returns. J. Financ. 1992, 47, 427–465. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. Common risk factors in the returns on stocks and bonds. J. Financ. Econ. 1993, 33, 3–56. [Google Scholar] [CrossRef]
- Fama, E.; French, K. Size and book-to-market factors in earnings and returns. J. Financ. 1995, 50, 131–155. [Google Scholar] [CrossRef]
- Jegadeesh, N.; Titman, S. Returns to buying winners and selling losers: Implications for stock market efficiency. J. Financ. 1993, 48, 65–91. [Google Scholar] [CrossRef]
- Carhart, M.M. On persistence in mutual fund performance. J. Financ. 1997, 52, 57–82. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. Size, Value, and Momentum in International Stock Returns. J. Financ. Econ. 2012, 105, 457–472. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. A five-factor asset pricing model. J. Financ. Econ. 2015, 116, 1–22. [Google Scholar] [CrossRef]
- Hou, K.; Xue, C.; Zhang, L. Digesting anomalies: An investment approach. Rev. Financ. Stud. 2015, 28, 650–705. [Google Scholar] [CrossRef]
- Chiah, M.; Chai, D.; Zhong, A.; Li, S. A Better Model? An empirical investigation of the Fama–French five-factor model in Australia. Intl. Rev. Financ. 2016, 16, 595–638. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. International tests of a five-factor asset pricing model. J. Financ. Econ. 2017, 123, 441–463. [Google Scholar] [CrossRef]
- Kubota, K.; Takehara, H. Does the Fama and French Five-Factor Model Work Well in Japan? Int. Rev. Financ. 2017, 18, 137–146. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, W.; Zhang, Y.; Zhang, H. The five-factor asset pricing model tests for the Chinese stock market. Pacific Basin Financ. J. 2017, 43, 84–106. [Google Scholar] [CrossRef]
- Cooper, M.; Gulen, H.; Schill, M. Asset growth and the cross-section of stock returns. J. Financ. 2008, 63, 1609–1651. [Google Scholar] [CrossRef]
- Ball, R.; Gerakos, J.; Linnainmaa, J.; Nikolaev, V. Accruals, cash flows, and operating profitability in the cross section of stock returns. J. Financ. Econ. 2016, 121, 28–45. [Google Scholar] [CrossRef]
- Novy-Marx, R. The other side of value: The gross profitability premium. J. Financ. Econ. 2013, 108, 1–28. [Google Scholar] [CrossRef]
- Lustig, H.N.; Verdelhan, A. Business Cycle Variation in the Risk-Return Trade-Off. SSRN Electron. J. 2011, 59, S35–S49. [Google Scholar] [CrossRef]
- Hollstein, F.; Prokopczuk, M.; Simen, C.W. Beta uncertainty. J. Bank. Financ. 2020, 116, 105834. [Google Scholar] [CrossRef]
- Kenneth, R. French: U.S. Research Returns Data. Available online: http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html (accessed on 19 January 2021).
- D’Agostino, A.A.; Gambetti, L.; Giannone, D. Macroeconomic forecasting and structural change. J. Appl. Econ. 2011, 28, 82–101. [Google Scholar] [CrossRef]
- Chib, S. Estimation and comparison of multiple change-point models. J. Econ. 1998, 86, 221–241. [Google Scholar] [CrossRef]
- Gerlach, R.; Carter, C.; Kohn, R. Efficient Bayesian inference for dynamic mixture models. J. Am. Stat. Assoc. 2000, 95, 819–828. [Google Scholar] [CrossRef]
- Giordani, P.; Kohn, R. Efficient Bayesian inference for multiple change-point and mixture innovation models. J. Bus. Econ. Stat. 2008, 26, 66–77. [Google Scholar] [CrossRef]
- Koop, G.; Leon-Gonzalez, R.; Strachan, R.W. On the evolution of the monetary policy transmission mechanism. J. Econ. Dyn. Control. 2009, 33, 997–1017. [Google Scholar] [CrossRef]
- Koop, G.; Potter, S.M. Estimation and Forecasting in Models with Multiple Breaks. Rev. Econ. Stud. 2007, 74, 763–789. [Google Scholar] [CrossRef]
- Koop, G.; Potter, S.M. Prior elicitation in multiple change-point models. Int. Econ. Rev. 2009, 50, 751–772. [Google Scholar] [CrossRef]
- McCulloch, R.E.; Tsay, R.S. Bayesian inference and prediction for mean and variance shifts in autoregressive time series. J. Am. Stat. Assoc. 1993, 88, 968–978. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Pettenuzzo, D.; Timmermann, A. Forecasting Time Series Subject to Multiple Structural Breaks. Rev. Econ. Stud. 2006, 73, 1057–1084. [Google Scholar] [CrossRef]
- Huber, F.; Kastner, G.; Feldkircher, M. Should I stay or should I go? A latent threshold approach to large-scale mixture innovation models. J. Appl. Econ. 2019, 34, 621–640. [Google Scholar] [CrossRef]
- Cuaresma, J.C.; Doppelhofer, G.; Feldkircher, M.; Huber, F. Spillovers from US monetary policy: Evidence from a time varying parameter global vector auto-regressive model. J. R. Stat. Soc. Ser. A Stat. Soc. 2019, 182, 831–861. [Google Scholar] [CrossRef]
- Balcilar, M.; Ozdemir, Z.A. The volatility effect on precious metals price returns in a stochastic volatility in mean model with time-varying parameters. Phys. A Stat. Mech. Appl. 2019, 534. [Google Scholar] [CrossRef]

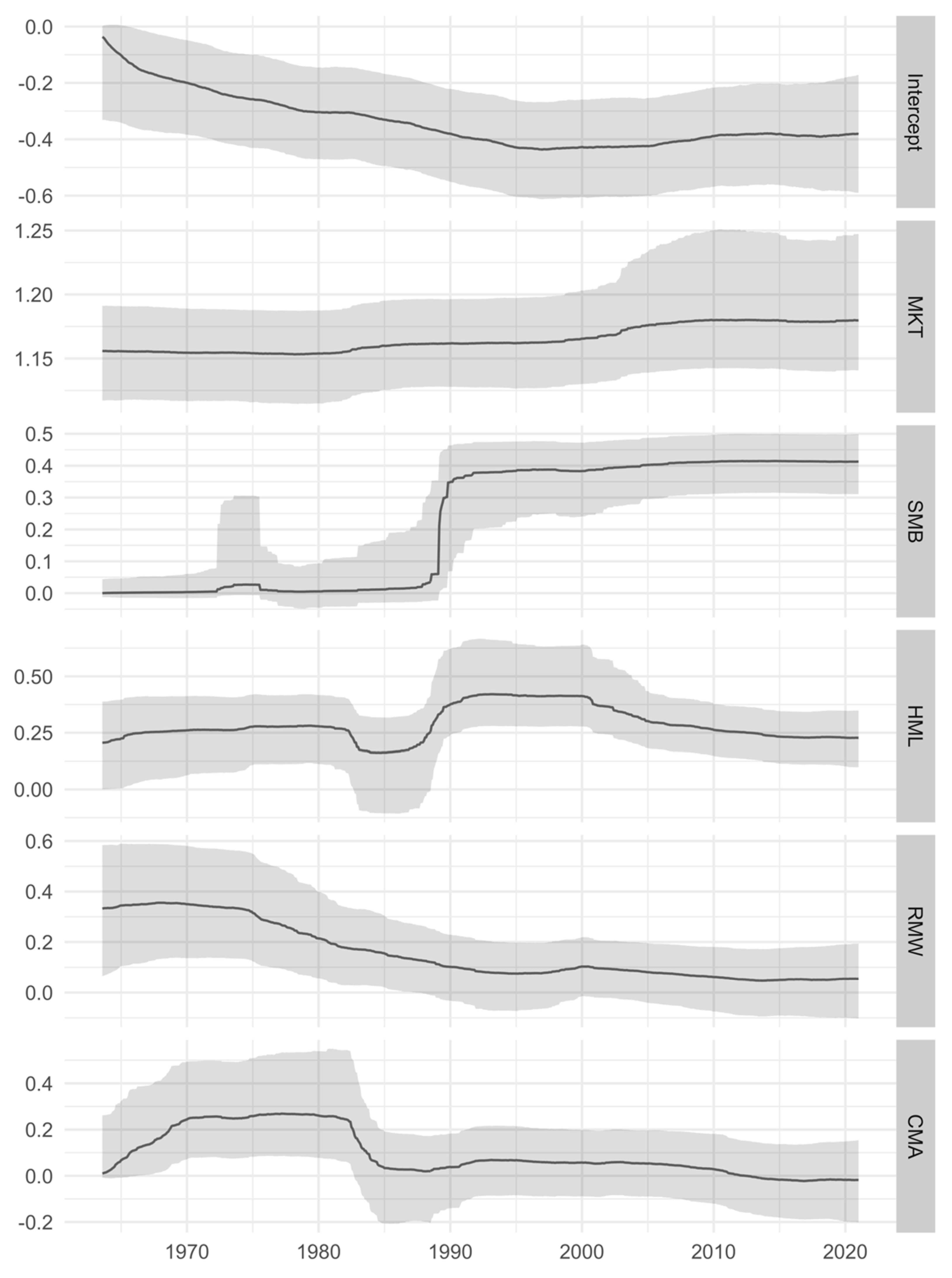

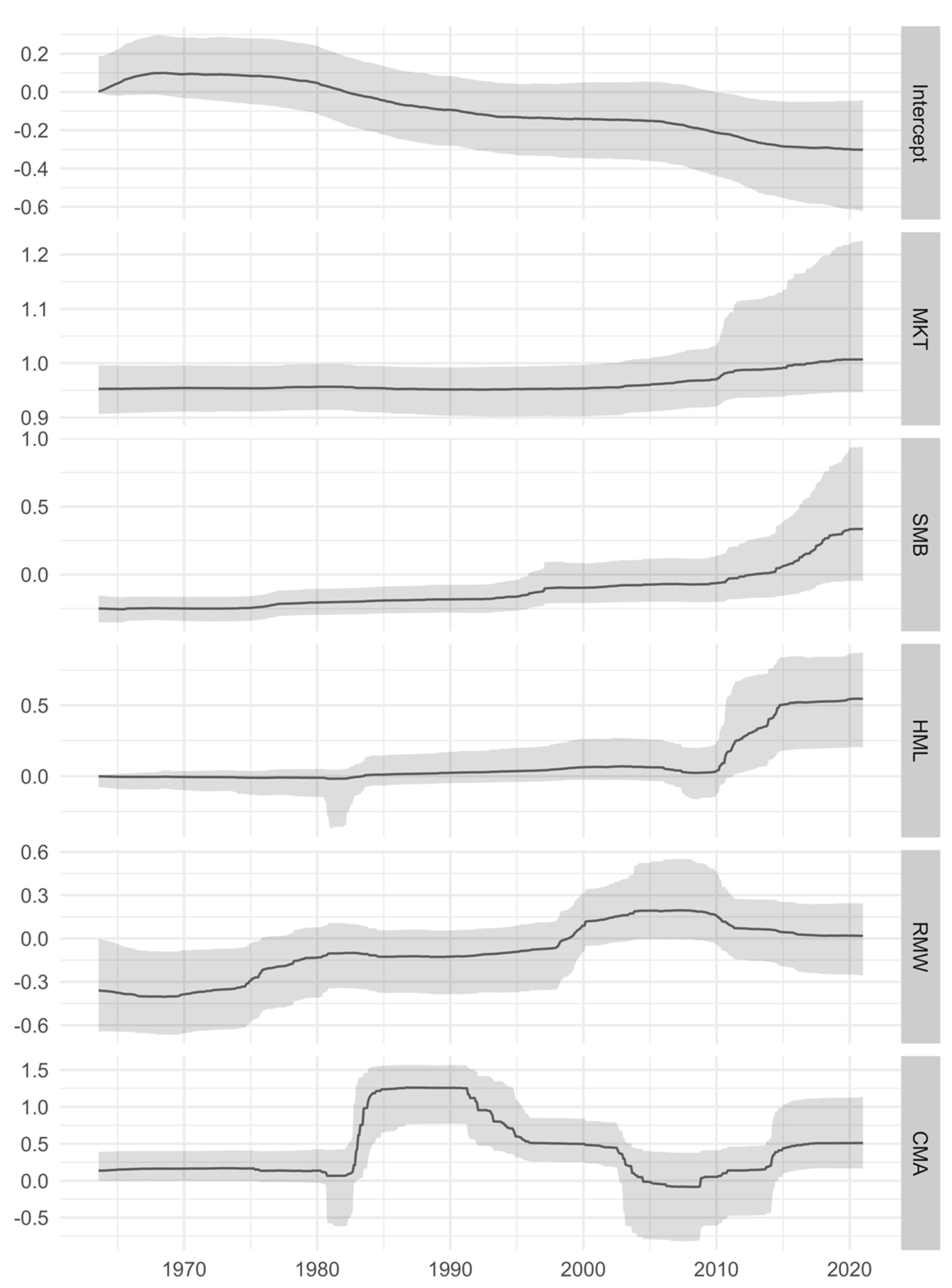
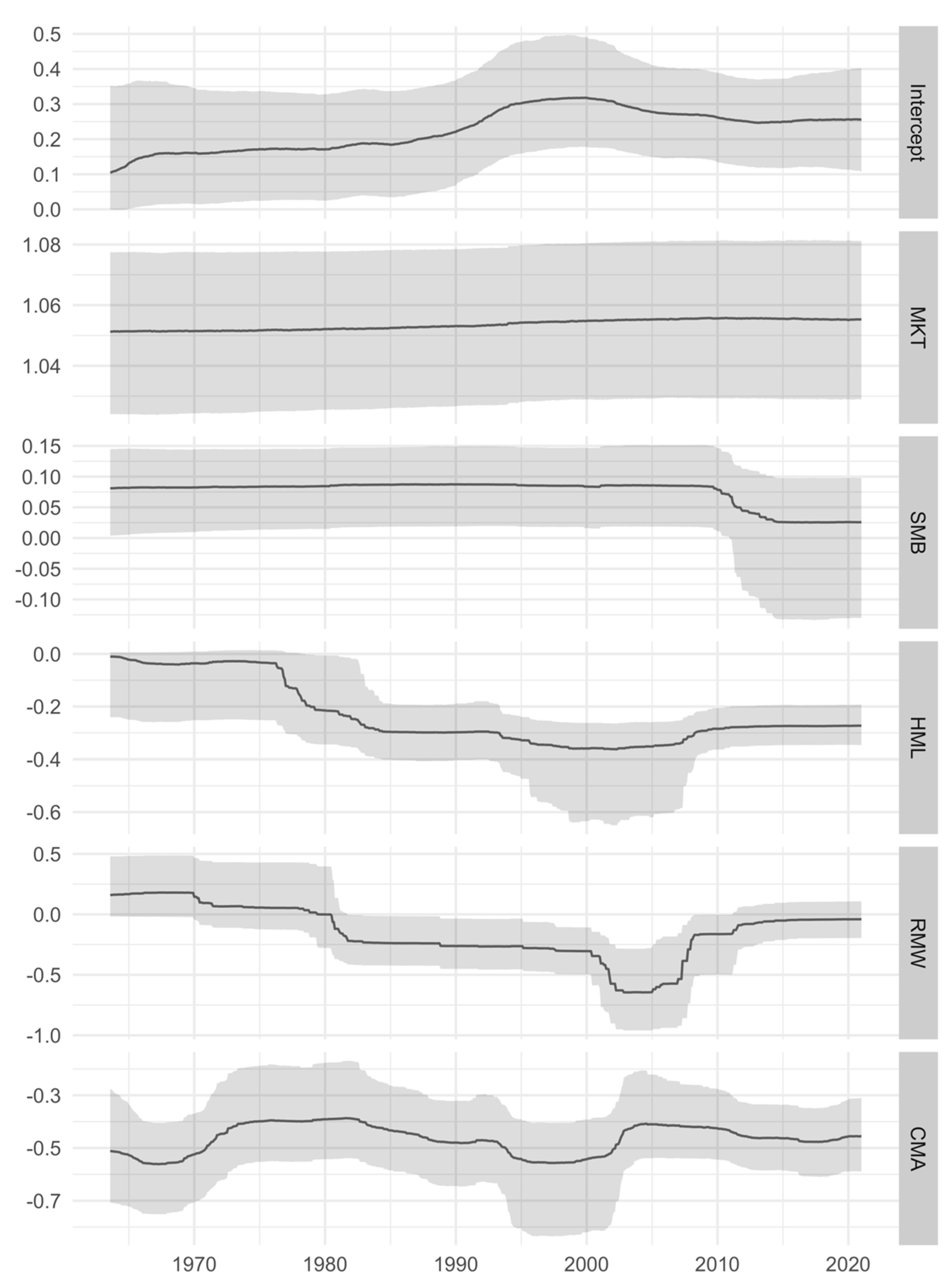
| Statistic | DURBL | MANUF | ENRGY | HITEC | MKT | SMB | HML | RMW | CMA |
|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.624 | 0.610 | 0.537 | 0.711 | 0.568 | 0.230 | 0.251 | 0.249 | 0.256 |
| S.D. | 6.726 | 4.955 | 5.901 | 6.394 | 4.468 | 3.026 | 2.867 | 2.167 | 1.988 |
| Min | −32.710 | −27.930 | −34.730 | −26.530 | −23.240 | −14.890 | −13.960 | −18.480 | −6.860 |
| Max | 42.620 | 17.500 | 32.330 | 20.320 | 16.100 | 18.080 | 12.580 | 13.380 | 9.560 |
| Skewness | 0.602 | −0.504 | 0.005 | −0.241 | −0.507 | 0.334 | 0.013 | −0.327 | 0.316 |
| Kurtosis | 5.975 | 2.506 | 4.032 | 1.290 | 1.878 | 2.947 | 2.358 | 12.238 | 1.603 |
| Jarque–Bera (JB) | 1077.237 * | 212.099 * | 472.145 * | 55.471 * | 132.675 * | 265.584 * | 161.942 * | 4349.274 * | 86.602 * |
| Q(1) | 8.152 * | 1.676 | 0.717 | 2.408 | 2.652 | 2.947 * | 21.859 * | 15.273 * | 9.901 * |
| Q(6) | 23.302 * | 7.253 | 4.158 | 4.806 | 7.417 | 10.664 * | 30.461 * | 20.396 * | 19.610 * |
| ARCH(1) | 14.192 * | 10.178 * | 83.967 * | 55.253 * | 18.336 * | 58.167 * | 40.465 * | 122.214 * | 69.473 * |
| Variable | Mean | Median | S.D. | Min | Max | 5th Percentile | 95th Percentile |
|---|---|---|---|---|---|---|---|
| Panel A: TTVP-SV Model | |||||||
| Intercept | −0.338 | −0.381 | 0.093 | −0.436 | −0.037 | −0.431 | −0.153 |
| MKT | 1.165 | 1.162 | 0.010 | 1.153 | 1.180 | 1.154 | 1.180 |
| SMB | 0.224 | 0.378 | 0.192 | 0.000 | 0.415 | 0.002 | 0.414 |
| HML | 0.287 | 0.267 | 0.073 | 0.162 | 0.421 | 0.171 | 0.416 |
| RMW | 0.157 | 0.097 | 0.110 | 0.047 | 0.356 | 0.050 | 0.350 |
| CMA | 0.094 | 0.057 | 0.098 | −0.023 | 0.269 | −0.018 | 0.266 |
| Panel B: Rolling Model | |||||||
| Intercept | −0.443 | −0.506 | 0.288 | −0.978 | 0.208 | −0.827 | 0.105 |
| MKT | 1.221 | 1.181 | 0.182 | 0.954 | 1.623 | 0.991 | 1.583 |
| SMB | 0.303 | 0.256 | 0.246 | −0.149 | 0.838 | −0.106 | 0.762 |
| HML | 0.376 | 0.406 | 0.333 | −0.408 | 1.030 | −0.277 | 0.887 |
| RMW | 0.264 | 0.198 | 0.424 | −0.382 | 1.150 | −0.287 | 1.034 |
| CMA | 0.117 | 0.071 | 0.300 | −0.575 | 0.632 | −0.340 | 0.583 |
| Panel C: Static Model | |||||||
| Intercept | −0.340 | 0.150 | −0.586 | −0.094 | |||
| MKT | 1.267 | 0.037 | 1.207 | 1.327 | |||
| SMB | 0.214 | 0.052 | 0.128 | 0.300 | |||
| HML | 0.377 | 0.069 | 0.263 | 0.491 | |||
| RMW | 0.254 | 0.072 | 0.136 | 0.373 | |||
| CMA | 0.147 | 0.106 | −0.027 | 0.320 | |||
| Variable | Mean | Median | S.D. | Min | Max | 5th Percentile | 95th Percentile |
|---|---|---|---|---|---|---|---|
| Panel A: TTVP-SV Model | |||||||
| Intercept | −0.086 | −0.083 | 0.033 | −0.135 | −0.001 | −0.133 | −0.025 |
| MKT | 1.067 | 1.067 | 0.000 | 1.066 | 1.067 | 1.066 | 1.067 |
| SMB | 0.102 | 0.102 | 0.001 | 0.101 | 0.104 | 0.101 | 0.104 |
| HML | 0.085 | 0.085 | 0.001 | 0.084 | 0.086 | 0.085 | 0.086 |
| RMW | 0.240 | 0.240 | 0.003 | 0.235 | 0.245 | 0.236 | 0.245 |
| CMA | 0.053 | 0.075 | 0.036 | 0.002 | 0.108 | 0.006 | 0.107 |
| Panel B: Rolling Model | |||||||
| Intercept | −0.118 | −0.095 | 0.148 | −0.471 | 0.120 | −0.369 | 0.078 |
| MKT | 1.105 | 1.091 | 0.058 | 0.980 | 1.265 | 1.022 | 1.200 |
| SMB | 0.103 | 0.115 | 0.062 | −0.024 | 0.258 | 0.001 | 0.198 |
| HML | 0.014 | 0.018 | 0.106 | −0.253 | 0.263 | −0.204 | 0.161 |
| RMW | 0.222 | 0.281 | 0.230 | −0.337 | 0.606 | −0.225 | 0.478 |
| CMA | 0.116 | 0.127 | 0.134 | −0.175 | 0.406 | −0.105 | 0.336 |
| Panel C: Static Model | |||||||
| Intercept | −0.164 | 0.061 | −0.265 | −0.063 | |||
| MKT | 1.084 | 0.015 | 1.059 | 1.108 | |||
| SMB | 0.110 | 0.021 | 0.074 | 0.145 | |||
| HML | 0.088 | 0.028 | 0.041 | 0.134 | |||
| RMW | 0.320 | 0.030 | 0.271 | 0.369 | |||
| CMA | 0.126 | 0.043 | 0.055 | 0.197 | |||
| Variable | Mean | Median | S.D. | Min | Max | 5th Percentile | 95th Percentile |
|---|---|---|---|---|---|---|---|
| Panel A: TTVP-SV Model | |||||||
| Intercept | −0.087 | −0.117 | 0.129 | −0.302 | 0.099 | −0.292 | 0.094 |
| MKT | 0.963 | 0.954 | 0.017 | 0.951 | 1.007 | 0.952 | 1.003 |
| SMB | −0.118 | −0.181 | 0.143 | −0.255 | 0.335 | −0.250 | 0.261 |
| HML | 0.096 | 0.026 | 0.172 | −0.018 | 0.547 | −0.011 | 0.527 |
| RMW | −0.086 | −0.103 | 0.184 | −0.404 | 0.195 | −0.400 | 0.192 |
| CMA | 0.415 | 0.168 | 0.403 | −0.084 | 1.261 | −0.047 | 1.256 |
| Panel B: Rolling Model | |||||||
| Intercept | 0.022 | 0.131 | 0.529 | −1.181 | 1.010 | −0.823 | 0.815 |
| MKT | 0.967 | 0.973 | 0.135 | 0.680 | 1.348 | 0.739 | 1.153 |
| SMB | −0.161 | −0.196 | 0.218 | −0.577 | 0.518 | −0.487 | 0.172 |
| HML | 0.031 | −0.063 | 0.261 | −0.362 | 0.733 | −0.279 | 0.563 |
| RMW | 0.042 | 0.052 | 0.545 | −0.991 | 0.921 | −0.910 | 0.773 |
| CMA | 0.304 | 0.145 | 0.605 | −0.689 | 1.748 | −0.510 | 1.675 |
| Panel C: Static Model | |||||||
| Intercept | −0.224 | 0.168 | −0.499 | 0.052 | |||
| MKT | 1.008 | 0.041 | 0.941 | 1.075 | |||
| SMB | −0.063 | 0.058 | −0.159 | 0.033 | |||
| HML | 0.230 | 0.078 | 0.102 | 0.357 | |||
| RMW | 0.209 | 0.081 | 0.076 | 0.342 | |||
| CMA | 0.365 | 0.118 | 0.170 | 0.559 | |||
| Variable | Mean | Median | S.D. | Min | Max | 5th Percentile | 95th Percentile |
|---|---|---|---|---|---|---|---|
| Panel A: TTVP-SV Model | |||||||
| Intercept | 0.227 | 0.247 | 0.057 | 0.105 | 0.318 | 0.151 | 0.315 |
| MKT | 1.054 | 1.053 | 0.002 | 1.051 | 1.056 | 1.051 | 1.056 |
| SMB | 0.075 | 0.084 | 0.021 | 0.025 | 0.088 | 0.026 | 0.087 |
| HML | −0.234 | −0.278 | 0.119 | −0.362 | −0.010 | −0.359 | −0.028 |
| RMW | −0.149 | −0.163 | 0.219 | −0.646 | 0.181 | −0.619 | 0.179 |
| CMA | −0.466 | −0.462 | 0.054 | −0.561 | −0.387 | −0.556 | −0.392 |
| Panel B: Rolling Model | |||||||
| Intercept | 0.326 | 0.178 | 0.390 | −0.150 | 1.452 | −0.104 | 1.181 |
| MKT | 1.043 | 1.032 | 0.124 | 0.835 | 1.376 | 0.873 | 1.266 |
| SMB | 0.125 | 0.107 | 0.127 | −0.222 | 0.398 | −0.035 | 0.379 |
| HML | −0.290 | −0.263 | 0.306 | −0.860 | 0.318 | −0.768 | 0.202 |
| RMW | −0.131 | −0.246 | 0.320 | −0.718 | 0.573 | −0.508 | 0.493 |
| CMA | −0.398 | −0.419 | 0.407 | −1.357 | 0.365 | −1.088 | 0.242 |
| Panel C: Static Model | |||||||
| Intercept | −0.224 | 0.168 | −0.499 | 0.052 | |||
| MKT | 1.008 | 0.041 | 0.941 | 1.075 | |||
| SMB | −0.063 | 0.058 | −0.159 | 0.033 | |||
| HML | 0.230 | 0.078 | 0.102 | 0.357 | |||
| RMW | 0.209 | 0.081 | 0.076 | 0.342 | |||
| CMA | 0.365 | 0.118 | 0.170 | 0.559 | |||
| Model | DURBL | MANUF | ENRGY | HITEC |
|---|---|---|---|---|
| TTVP-SV | 3.670 | 1.531 | 3.796 | 2.403 |
| TTVP | 3.525 | 1.520 | 3.696 | 2.372 |
| Rolling | 3.708 | 1.544 | 4.163 | 2.484 |
| Static | 3.747 | 1.533 | 4.195 | 2.575 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balcilar, M.; Demirer, R.; Bekun, F.V. Flexible Time-Varying Betas in a Novel Mixture Innovation Factor Model with Latent Threshold. Mathematics 2021, 9, 915. https://doi.org/10.3390/math9080915
Balcilar M, Demirer R, Bekun FV. Flexible Time-Varying Betas in a Novel Mixture Innovation Factor Model with Latent Threshold. Mathematics. 2021; 9(8):915. https://doi.org/10.3390/math9080915
Chicago/Turabian StyleBalcilar, Mehmet, Riza Demirer, and Festus V. Bekun. 2021. "Flexible Time-Varying Betas in a Novel Mixture Innovation Factor Model with Latent Threshold" Mathematics 9, no. 8: 915. https://doi.org/10.3390/math9080915
APA StyleBalcilar, M., Demirer, R., & Bekun, F. V. (2021). Flexible Time-Varying Betas in a Novel Mixture Innovation Factor Model with Latent Threshold. Mathematics, 9(8), 915. https://doi.org/10.3390/math9080915








