An Analytical Technique Implemented in the Fractional Clannish Random Walker’s Parabolic Equation with Nonlinear Physical Phenomena
Abstract
1. Introduction
2. Glimpse of the Technique
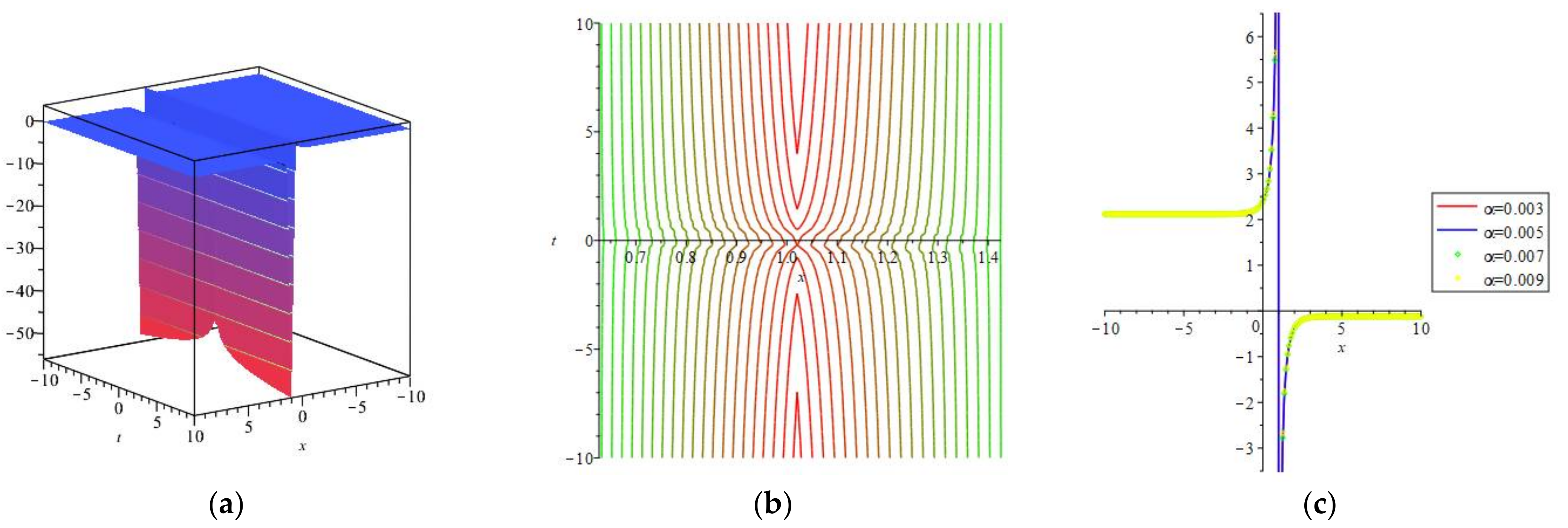
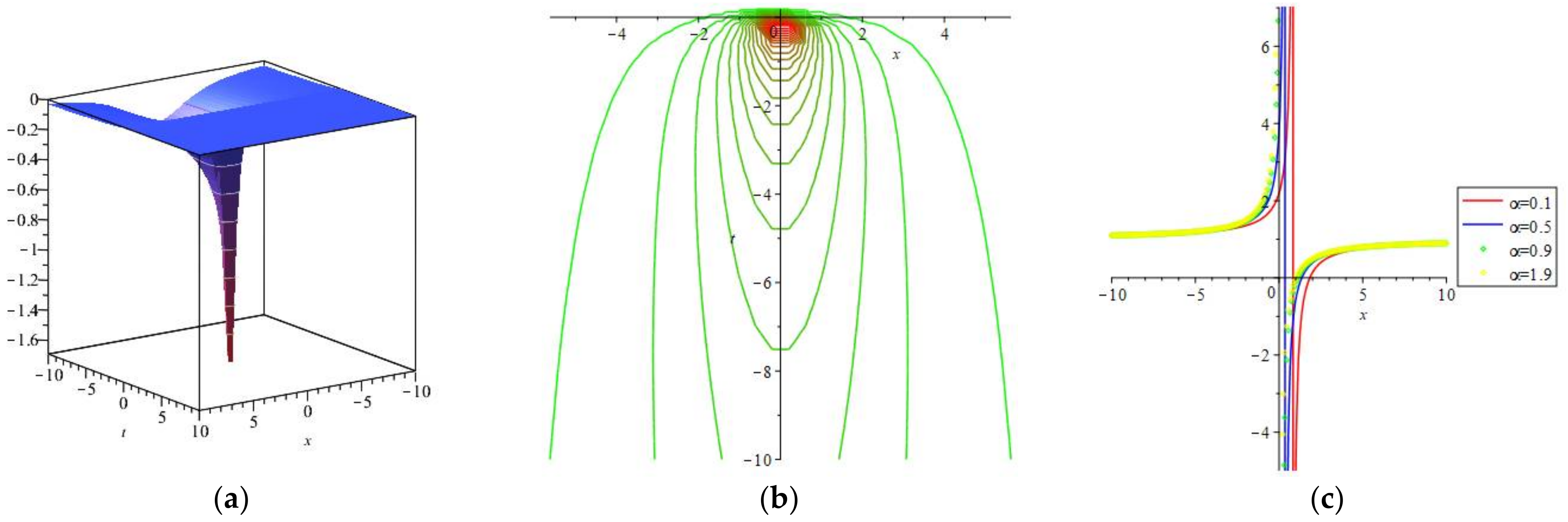
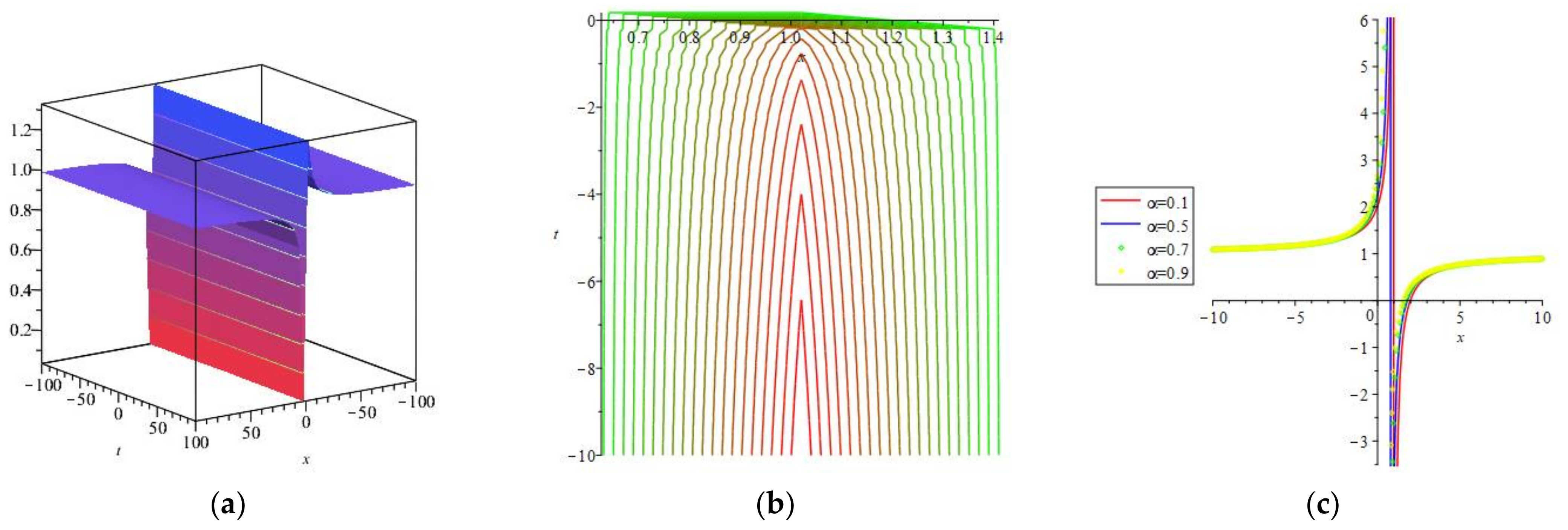
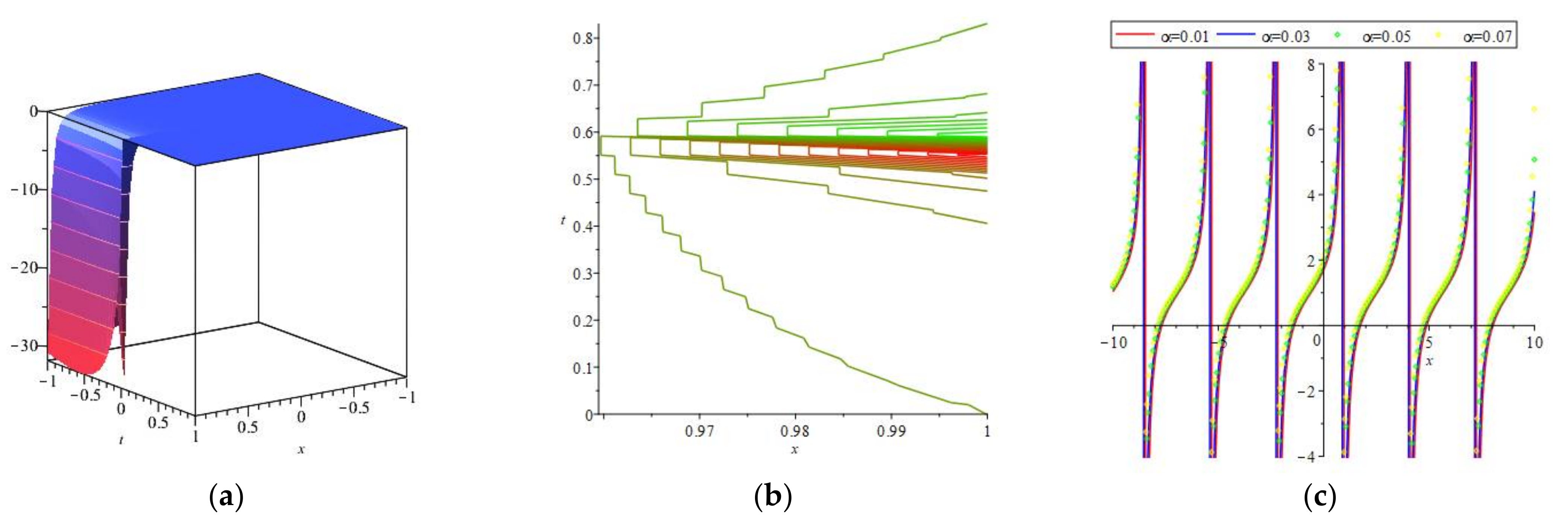
3. Mathematical Analysis
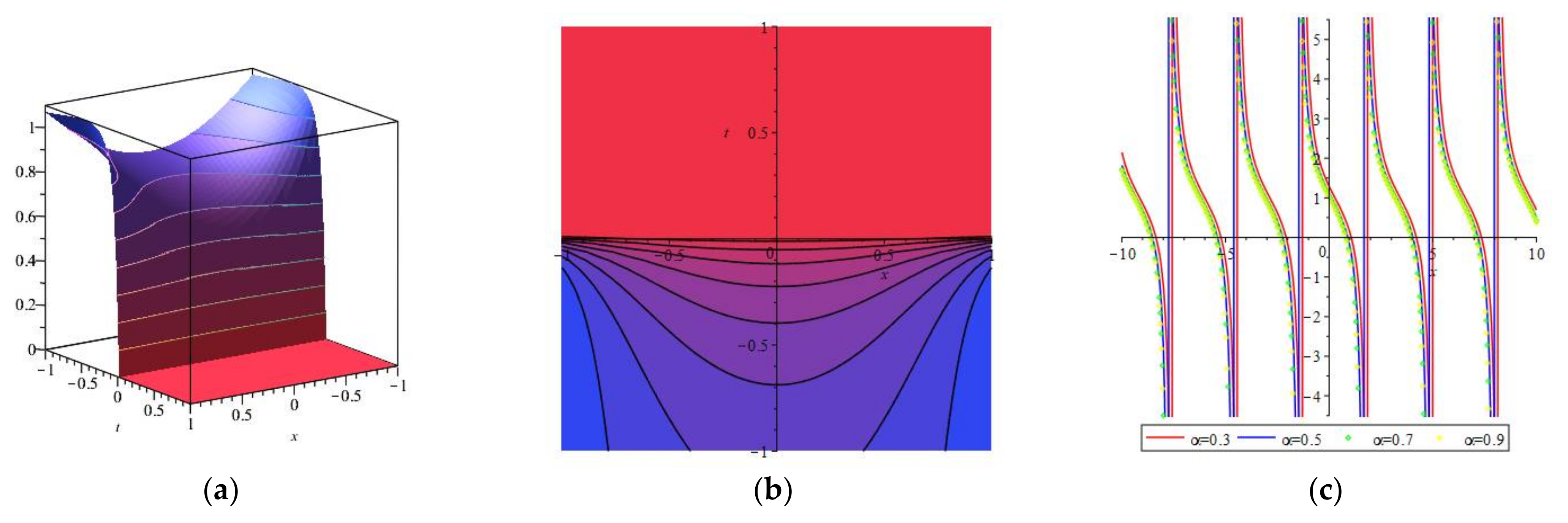
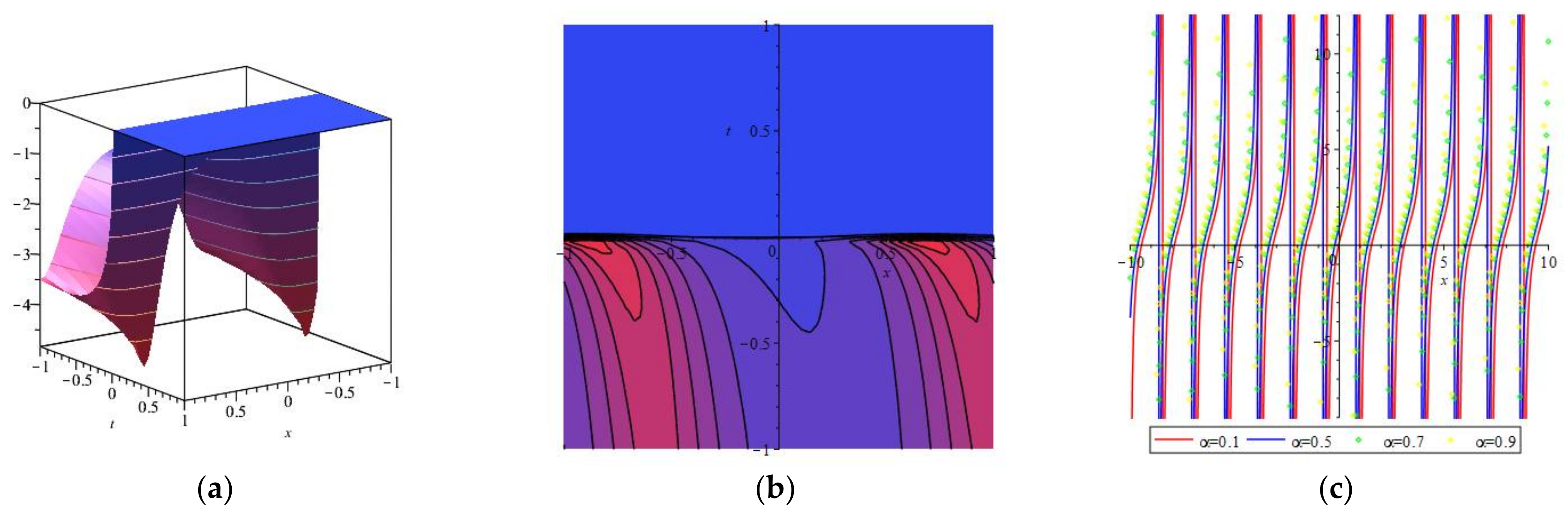
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alam, M.N.; Seadawy, A.R.; Baleanu, D. Closed-form wave structures of the space-timefractional Hirota–Satsuma coupled KdVequation with nonlinear physical phenomena. Open Phys. 2021, 18, 555–565. [Google Scholar] [CrossRef]
- Islam, S.; Alam, M.N.; Asad, M.F.A.; Tunc, C. An analytical technique for solving new computational solutions of the modified Zakharov-Kuznetsov equation arising in electrical engineering. J. Appl. Comput. Mech. 2021, 7, 715–726. [Google Scholar]
- Alam, M.N.; Tunc, C. The new solitary wave structures for the (2 + 1)-dimensional time-fractional Schrodinger equation and the space-time nonlinear conformable fractional Bogoyavlenskii equations. Alex. Eng. J. 2020, 59, 2221–2232. [Google Scholar] [CrossRef]
- Alam, M.N.; Li, X. New soliton solutions to the nonlinear complex fractional Schrödinger equation and the conformable time-fractional Klein–Gordon equation with quadratic and cubic nonlinearity. Phys. Scr. 2020, 95, 045224. [Google Scholar] [CrossRef]
- Alam, M.N.; Osman, M.S. New structures for closed-form wave solutions for the dynamical equations model related to the ion sound and Langmuir waves. Commun. Theor. Phys. 2021, 73, 035001. [Google Scholar] [CrossRef]
- Park, C.; Nuruddeen, R.I.; Ali, K.K.; Muhammad, L.; Osman, M.S.; Baleanu, D. Novel hyperbolic and exponential ansatz methods to the fractional fifth-order Korteweg-de Vries equations. Adv. Differ. Equ. 2020, 2020, 627. [Google Scholar] [CrossRef]
- Ahmad, H.; Khan, T.A.; Ahmad, I.; Stanimirović, P.S.; Chu, Y.M. A new analyzing technique for nonlinear time fractional Cauchy reaction-diffusion model equations. Results Phys. 2020, 19, 103462. [Google Scholar] [CrossRef]
- Ahmad, H.; Akgül, A.; Khan, T.A.; Stanimirović, P.S.; Chu, Y.M. New perspective on the conventional solutions of the nonlinear time fractional partial differential equations. Complexity 2020, 2020, 8829017. [Google Scholar] [CrossRef]
- Osman, M.S.; Rezazadeh, H.; Eslami, M. Traveling wave solutions for (3 + 1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity. Nonlinear Eng. 2019, 8, 559–567. [Google Scholar] [CrossRef]
- Yepez-Martınez, H.; Gomez-Aguilar, J.F.; Atangana, A. First integral method for non-linear differential equations with conformable derivative. Math. Model. Nat. Phenom. 2018, 13, 14. [Google Scholar] [CrossRef]
- Aminikhah, H.; Sheikhani, A.H.R.; Rezazadeh, H. Sub-equation method for the fractional regularized long-wave equations with conformable fractional derivatives. Sci. Iran. 2016, 23, 1048–1054. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, Y.; Li, S. Improved fractional sub-equation method and exact solutions to fractional partial differential equations. J. Funct. Sp. 2020, 2020, 5840920. [Google Scholar]
- Aslan, E.C.; Inc, M. Optical soliton solutions of the NLSE with quadratic-cubic-hamiltonian perturbations and modulation instability analysis. Optik 2019, 196, 162661. [Google Scholar] [CrossRef]
- Gurefe, Y. The generalized Kudryashov method for the nonlinear fractional partial differential equations with the beta-derivative. Rev. Mex. Fısica 2020, 66, 771–781. [Google Scholar] [CrossRef]
- Alam, M.N.; Bonyah, E.; Asad, M.F.A.; Osman, M.S.; Abualnaja, K.M. Stable and functional solutions of the Klein-Fock-Gordon equation with nonlinear physical phenomena. Phys. Scr. 2021. accepted. [Google Scholar] [CrossRef]
- Tozar, A.; Kurt, A.; Tasbozan, O. New wave solutions of time fractional integrable dispersive wave equation arising in ocean engineering models. Kuwait J. Sci. 2020, 47, 22–33. [Google Scholar]
- Ismail, G.M.; Rahim, H.R.A.; Aty, A.A.; Kharabsheh, R.; Alharbi, W.; Aty, M.A. An analytical solution for fractional oscillator in a resisting medium. Chaos Solitons Fract. 2020, 130, 109395. [Google Scholar] [CrossRef]
- Yepez-Martınez, H.; Gomez-Aguilar, J.F. Fractional sub-equation method for Hirota-Satsuma-coupled KdV equation and coupled mKdV equation using the Atangana’s conformable derivative. Waves Random Complex Media 2019, 29, 678–693. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Rabiei, F.; Baskonus, H.M.; Yel, G. Dark optical solitons to the Biswas–Arshed equation with high order dispersions and absence of the self-phase modulation. Optik 2020, 209, 164576. [Google Scholar] [CrossRef]
- Ghanbari, B.; Baleanu, D. New Optical Solutions of the Fractional Gerdjikov-Ivanov Equation with Conformable Derivative. Front. Phys. 2020, 8, 167. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Ilie, M.; Radmehr, S. Dynamics of optical solitons in the perturbed Gerdjikov–Ivanov equation. Optik 2020, 206, 164350. [Google Scholar] [CrossRef]
- Korkmaz, A.; Hepson, O.E.; Hosseini, K.; Rezazadeh, H.; Eslami, M. Sine-gordon expansion method for exact solutions to conformable time fractional equations in RLW-class. J. King Saud Univ. Sci. 2020, 32, 567–574. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Vahidi, J.; Asghari, R. Optical wave structures to the Fokas–Lenells equation. Optik 2020, 207, 164450. [Google Scholar] [CrossRef]
- Ma, X.; Pan, Y.; Chang, L. The modified (G′/G)-expansion method and its applications to KdV equation. Int. J. Nonlinear Sci. 2011, 12, 400–404. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: San Diego, CA, USA, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Kumar, A.; Vats, R.K.; Kumar, A.; Chalishajar, D.N. Numerical approach to the controllability of fractional order impulsive differential equations. Demonstr. Math. 2020, 53, 193–207. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar] [CrossRef]
- Harjani, J.; López, B.; Sadarangani, K. Existence and uniqueness of mild solutions for a fractional differential equation under Sturm-Liouville boundary conditions when the data function is of Lipschitzian type. Demonstr. Math. 2020, 53, 167–173. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 13, 889–898. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Jumarie, G. Table of some basic fractional calculus formulae derived from a modified Riemann-Liouville derivative for non-differentiable functions. Appl. Math. Lett. 2009, 22, 378–385. [Google Scholar] [CrossRef]
- Ganji, Z.; Ganji, D.; Ganji, A.D.; Rostamian, M. Analytical solution of time-fractional Navier–Stokes equation in polar coordinate by homotopy perturbation method. Numer. Methods Partial Differ. Equ. 2010, 26, 117–124. [Google Scholar] [CrossRef]
- Gunera, O.; Bekir, A.; Ünsal, Ö. Two reliable methods for solving the time fractional Clannish Random Walker’s Parabolic equation. Optik 2016, 127, 9571–9577. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.N.; Talib, I.; Bazighifan, O.; Chalishajar, D.N.; Almarri, B. An Analytical Technique Implemented in the Fractional Clannish Random Walker’s Parabolic Equation with Nonlinear Physical Phenomena. Mathematics 2021, 9, 801. https://doi.org/10.3390/math9080801
Alam MN, Talib I, Bazighifan O, Chalishajar DN, Almarri B. An Analytical Technique Implemented in the Fractional Clannish Random Walker’s Parabolic Equation with Nonlinear Physical Phenomena. Mathematics. 2021; 9(8):801. https://doi.org/10.3390/math9080801
Chicago/Turabian StyleAlam, Md. Nur, Imran Talib, Omar Bazighifan, Dimplekumar N. Chalishajar, and Barakah Almarri. 2021. "An Analytical Technique Implemented in the Fractional Clannish Random Walker’s Parabolic Equation with Nonlinear Physical Phenomena" Mathematics 9, no. 8: 801. https://doi.org/10.3390/math9080801
APA StyleAlam, M. N., Talib, I., Bazighifan, O., Chalishajar, D. N., & Almarri, B. (2021). An Analytical Technique Implemented in the Fractional Clannish Random Walker’s Parabolic Equation with Nonlinear Physical Phenomena. Mathematics, 9(8), 801. https://doi.org/10.3390/math9080801








