The Dirichlet-to-Neumann Map in a Disk with a One-Step Radial Potential: An Analytical and Numerical Study

Abstract

Herein, we considered the Schrödinger operator with a potential q on a disk and the map that associates to q the corresponding Dirichlet-to-Neumann (DtN) map. We provide some numerical and analytical results on the range of this map and its stability for the particular class of one-step radial potentials.

1. Introduction

Let $\Omega \subset {\mathbb{R}}^2$ be a bounded domain with smooth boundary $\partial \Omega$. For each $q\in L^{\infty }(\Omega )$, consider the so called Dirichlet-to-Neumann map (DtN) given by:

$$\begin{array}{ccc}\hfill {\Lambda }_q:H^{1/2}(\partial \Omega )& \to & H^{-1/2}(\partial \Omega )\hfill \\ \hfill f& \to & \frac{\partial u}{\partial n}{|}_{\partial \Omega }.\hfill \end{array}$$

(1)

where u is the solution of the following problem:

$$\left\{\begin{array}{c}\Delta u+q\left(x\right)u=0,x\in \Omega ,\hfill \\ u=f,\partial \Omega ,\hfill \end{array}\right.$$

(2)

and $\frac{\partial u}{\partial n}{|}_{\partial \Omega }$ denotes the normal derivative of u on the boundary $\partial \Omega$.

Note that the uniqueness of u as solution of (2) requires that 0 is not a Dirichlet eigenvalue of $\Delta +q$. A sufficient condition to guarantee that ${\Lambda }_q$ is well defined is to assume $q\left(x\right)<{\lambda }_1$, the first Dirichlet eigenvalue of the Laplace operator in $\Omega$, since, in this case, the solution in (2) is unique. We assume that this condition holds and lets us define the space

$$L_{<{\lambda }_1}^{\infty }(\Omega )=\{q\in L^{\infty }(\Omega ),\mathrm{s}.\mathrm{t}.q\left(x\right)<{\lambda }_1,\mathrm{a}.\mathrm{e}.\}.$$

In this work, we were interested in the following map:

$$\begin{array}{ccc}\hfill \Lambda :L_{<{\lambda }_1}^{\infty }(\Omega )& \to & \mathcal{L}(H^{1/2}(\partial \Omega );H^{-1/2}(\partial \Omega ))\hfill \\ \hfill q& \to & {\Lambda }_q.\hfill \end{array}$$

(3)

This has an important role in inverse problems, where the aim is to recover the potential q from boundary measurements. In practice, these boundary measurements correspond to the associated DtN map, and therefore, the mathematical statement of the classical inverse problem consists of the inversion of $\Lambda$.

It is known that $\Lambda$ is one-to-one as long as $q\in L^p$ with $p>2$ (see [1]). Therefore, the inverse map ${\Lambda }^{-1}$ can be defined in the range of $\Lambda$. There are, however, two related important and difficult questions that are not well understood: A characterization of the range of $\Lambda$ and its stability, i.e., a quantification of the difference of two potentials, in the $L^{\infty }$ topology in terms of the distance of their associated DtN maps. Obviously, this stability will affect the efficiency of any inversion or reconstruction algorithm to recover the potential from the DtN map (see [2] and [3]).

The first question, i.e., the characterization of the range of $\Lambda$ is widely open. Tothe best of our knowledge, the further result is due to [4], where a characterization is obtained for the adherence, with respect to the weak topology in ${\ell }_{-1}^2$, of the sequence of eigenvalues associated with the orthogonal basis of eigenvectors ${\left\{e^{ink}\right\}}_{k\in \mathbb{Z}}$. Here, ${\ell }_{\alpha }^2$ is the space of sequences ${\left\{c_n\right\}}_{n\in \mathbb{Z}}$, such that ${\sum }_{n\in \mathbb{Z}}{\left|n\right|}^{2\alpha }{\left|c_n\right|}^2<\infty .$ This topology is not the usual one in $\mathcal{L}(H^{1/2}(\partial \Omega );H^{-1/2}(\partial \Omega ))$ and it is not easy to interpret how the adherence enlarges this set. Furthermore, the characterization does not give much practical information on the range, as, for instance, the convexity or accurate bounds on the eigenvalues. In fact, characterizing such properties is one of the main motivations of this work, since we could establish easily a priori if a desired linear map in $\mathcal{L}(H^{1/2}(\partial \Omega );H^{-1/2}(\partial \Omega ))$ can be associated with a DtN map. On the contrary, we have to take into account that in practice, the DtN map is estimated from physical measurements, which are subject to errors and may provide only partial information. A precise knowledge of the range of $\Lambda$ is useful to find the best DtN map that fits the measurements and to design an inversion algorithm in such situations.

Concerning the stability, it is well known that the problem is ill posed and that the most we can expect is logarithmic stability in general (see [5]). There are more explicit results when we assume that the potential q has some smoothness. In particular, if $q\in H^s(\Omega )$ with $s>0$, the following $log-$stability condition is known (see [1]):

$$\parallel q_1-q_2{\parallel }_{L^{\infty }}\le V(\parallel {\Lambda }_{q_1}-{\Lambda }_{q_2}{\parallel }_{\mathcal{L}(H^{1/2};H^{-1/2})}),$$

(4)

where $V\left(t\right)=Clog{(1/t)}^{-\alpha }$ for some constants $C,\alpha >0$. Stronger stability conditions are known in some particular cases. For example, in [6], it was shown that when q is piecewise constant and the components where it takes a constant value are fixed and satisfy some technical conditions, the stability is Lipschitz, i.e., there exists a constant $C>0$, such that:

$$\parallel q_1-q_2{\parallel }_{L^{\infty }}\le C{\parallel {\Lambda }_{q_1}-{\Lambda }_{q_2}\parallel }_{\mathcal{L}(H^{1/2};H^{-1/2})}.$$

(5)

In this work, we tried to understand better the situation by considering the simplest case of a disk with one-step radial potentials q. More precisely, we provide some results on the range of $\Lambda$ and its stability when we restrict to the particular case $\Omega =B(0,1)=\left\{x\in {\mathbb{R}}^2:r=\left|x\right|<1\right\}$ and $q\in F\subset L^{\infty }(\Omega )$ given by:

$$F=\{q\in L^{\infty }(\Omega ):q\left(r\right)=\gamma {\chi }_{(0,b)}\left(r\right),r=|x|,b\in (0,1),\gamma \in [0,1]\},$$

(6)

where ${\chi }_{(0,b)}\left(r\right)$ is the characteristic function of the interval $(0,b)$. Note that F is a two-parametric family depending on $\gamma$ and b.

It is worth mentioning that, as we show below, the solution of (2) is unique for all $b\in (0,1)$ and $\gamma \ge 0$, and therefore, the DtN map is well defined for all of these one-step potentials. In other words, 0 is not an eigenvalue of the operator $\Delta +q$ and, in particular, we do not need to restrict ourselves to the constraint $q\left(x\right)<{\lambda }_1$. However, we still restrict ourselves to the bounded set F to simplify.

Even in this simple case, a complete analytic answer to the previous questions (range of the DtN map and sharp stability conditions) is unknown. Therefore, we also considered a numerical approach based on a discrete sampling of the set F. Given an integer $N>0$, we define $h=1/N$ and:

$$\begin{array}{ccc}\hfill F_h& =& \{q\in L^{\infty }(\Omega ):q\left(r\right)=\gamma {\chi }_{(0,b)}\left(r\right),b=hi,\gamma =hj,\hfill \\ & & i=1,\dots ,N-1,j=0,\dots ,N\}.\hfill \end{array}$$

(7)

Note that $F_h$ has $N(N-1)+1$ functions from F. As $h\to 0$, we can obtain a better description of F and, in particular, we should recover the properties for $q\in F$.

The main contributions of this paper are given below:

• Concerning the stability of $\Lambda$, we show that it fails in the sense that inequality (4) does not hold for any continuous function $V\left(t\right)$ with $V\left(0\right)=0$. The proof is an adaptation of the analogous result for the conductivity problem obtained in [7]. In fact, we consider—as potential—the same piecewise constant radial conductivity used in [7]. The stability constant blows up when the support of the inner disk where the value of the potential is constant becomes zero.
• We obtain estimates for the Lipschitz stability constant in (5), in terms of $b,\gamma \in (0,1)$. However, the stability constant in (5) depends on $b^{-4}$ and therefore blows up as $b\to 0$.
• We now consider $\gamma \in [0,1]$ fixed and we define the set $G_{\gamma }\subset F$ as:

  $$G_{\gamma }=\{q\in L^{\infty }(\Omega ):q\left(r\right)=\gamma {\chi }_{(0,b)}\left(r\right),b\in (0,1)\}.$$

  (8)
  We prove that if $b\ge b_0>0$, there is stability of the DtN map with respect to the position of the discontinuity b for potentials in $G_{\gamma }$. More precisely, we obtain a stability constant depending on ${\gamma }^{-1}{b}^{-3}$, which is uniformly bounded for $b>b_0$ and fixed $\gamma$ (see Theorem 3 below). Note, however, that this constant blows up as $\gamma \to 0$.
  This stability result does not give information about the stability with respect to the $L^{\infty }$ norm of the potentials, but it provides stability with respect to the $L^1$ norm, which is sensitive to the position of the discontinuities, when $b>b_0>0$ and $\gamma >{\gamma }_0>0$. In fact, we show numerical evidence of such stability when considering potentials in F.
• For the range of $\Lambda$, we give a characterization in terms of the first two eigenvalues of the DtN map. We also analyze the region where the stability constant is larger, and, therefore, the potentials for which any recovering algorithm for q from the DtN map will have more difficulties.

We mention that a similar analysis can be conducted for the closely related—and more classical—conductivity problem, where (2) is replaced by:

$$\left\{\begin{array}{c}-diva\left(x\right)\nabla v=0,x\in \Omega ,\hfill \\ v=f,\partial \Omega ,\hfill \end{array}\right.$$

(9)

and the Dirichlet-to-Neumann map, or voltage-to-current map, is given by:

$$\begin{array}{ccc}\hfill {\Lambda }_a:H^{1/2}(\partial \Omega )& \to & H^{-1/2}(\partial \Omega )\hfill \\ \hfill f& \to & a\frac{\partial v}{\partial n}{|}_{\partial \Omega }.\hfill \end{array}$$

(10)

In this case, the relationship between piecewise constant radial conductivities and the eigenvalues of the DtN map is known [8] through a suitable recurrence formula. However, there is not a direct transformation that relates both problems, and the analysis must be done specifically for this case.

We refer to the review paper [9] and the references therein for theoretical results on the DtN map in this case.

The rest of this paper is divided as follows: In Section 2 below, we characterize the DtN map in terms of its eigenvalues using polar coordinates. In Section 3 and Section 4, we analyze the stability and range results, respectively. In Section 5, we briefly describe the main conclusions, and finally, Section 5 contains the proofs of the theorems stated in the previous sections.

2. The Dirichlet-to-Neumann Map

In this section, we characterize the Dirichlet-to-Neumann map in the case of a disk. System (2) in polar coordinates reads:

$$\left\{\begin{array}{c}{r}^2\frac{{\partial }^{2}v}{\partial r^2}+r\frac{\partial v}{\partial r}+\frac{{\partial }^{2}v}{\partial {\theta }^2}+r^{2}q\left(r\right)v=0,(r,\theta )\in (0,1)\times [0,2\pi ),\hfill \\ \underset{r⟶0,r>0}{lim}v(r,\theta )<\infty ,\hfill \\ v(1,\theta )=g\left(\theta \right),\theta \in [0,2\pi ),\hfill \end{array}\right.$$

(11)

where $v(r,\theta )=u(rcos\theta ,rsin\theta )\mathrm{and}g\left(\theta \right)=f(cos\theta ,sin\theta )$ is a periodic function.

An orthonormal basis in $L^2(0,2\pi )$ is given by ${\left\{e^{in\theta }\right\}}_{n\in \mathbb{Z}}$. Here, we use this complex basis to simplify the notation, but in the analysis below, we only consider the subspace of real valued functions. Therefore, any function $g\in L^2(0,2\pi )$ can be written as:

$$g\left(\theta \right)=\sum _{n\in \mathbb{Z}}{g}_n{e}^{in\theta },g_n=\frac{1}{2\pi }{\int }_0^{2\pi }g\left(t\right)e^{-int}dt,$$

(12)

and ${\parallel g\parallel }_{L^2(0,2\pi )}^2={\sum }_{n\in \mathbb{Z}}{\left|g_n\right|}^2$. Associated with this basis, we define the usual Hilbert spaces: $H_{\#}^{\alpha }$, for $\alpha >0$, as

$$H_{\#}^{\alpha }={\{g:\parallel g\parallel }_{\alpha }^2=\sum _{n\in \mathbb{Z}}{(1+n^2)}^{\alpha }|g_n{|}^2<\infty \}.$$

The Dirichlet-to-Neumann map in this case is defined as:

$$\begin{array}{ccc}\hfill {\Lambda }_q:H_{\#}^{1/2}(0,2\pi )& \to & H_{\#}^{-1/2}(0,2\pi )\hfill \\ \hfill g& \to & \frac{\partial v}{\partial r}(1,·),\hfill \end{array}$$

(13)

where v is the unique solution of (11).

In the above basis, the Dirichlet-to-Neumann map turns out to be diagonal. In fact, we have the following result:

Theorem 1.

Let Ω be the unit disk and $q\in F$. Then:

$$\begin{array}{ccc}\hfill {\Lambda }_q\left(e^{in\theta }\right)& =& c_n{e}^{in\theta },n\in \mathbb{Z},\hfill \end{array}$$

(14)

where:

$$\begin{array}{ccc}\hfill c_0& =& \frac{-b\sqrt{\gamma }{J}_1\left(\sqrt{\gamma }b\right)}{blogb\sqrt{\gamma }{J}_1\left(\sqrt{\gamma }b\right)+J_0\left(\sqrt{\gamma }b\right)},\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill c_n& =& c_{-n}=n\frac{J_{n-1}\left(\sqrt{\gamma }b\right)-b^{2n}{J}_{n+1}\left(\sqrt{\gamma }b\right)}{J_{n-1}\left(\sqrt{\gamma }b\right)+b^{2n}{J}_{n+1}\left(\sqrt{\gamma }b\right)},n\in \mathbb{N},\hfill \end{array}$$

(16)

and $J_n\left(r\right)$ are the Bessel functions of the first kind.

Note that the range of $\Lambda$, when restricted to F, is characterized by the set of sequences ${\left\{c_n\right\}}_{n\ge 0}$ of the form (15) and (16) for all possible $b,\gamma$. In particular, when $q=0$, we have:

$$c_n=n,n=0,1,2,\dots ,$$

(17)

and this sequence must be in the range of $\Lambda$.

The norm of ${\Lambda }_q$, when restricted to F, is given by:

$$\parallel {\Lambda }_q{\parallel }_{\mathcal{L}(H_{\#}^{1/2};H_{\#}^{-1/2})}=\underset{n\ge 0}{sup}\frac{|c_n|}{1+n^2}.$$

(18)

Proof of Theorem 1.

We first compute $c_0$ in (14). As the boundary data at $r=1$ in (11) is the constant $g\left(\theta \right)=1$, we assume that $v(r,\theta )$ is radial, i.e., $v(r,\theta )=a_0\left(r\right)$. Then, $a_0$ should satisfy:

$$\left\{\begin{array}{c}{r}^2{a}_0^{″}+r{a}_0^{\prime }+r^{2}q\left(r\right)a_0=0,0<r<1,\hfill \\ a_0\left(1\right)=1,\underset{r⟶0,r>0}{lim}{a}_0\left(r\right)<\infty .\hfill \end{array}\right.$$

(19)

For $r\in (0,b)$, we solve the ODE with the boundary data at $r=0$, while for $r\in (b,1)$, we use the boundary data at $r=1$. In the first case, the ODE is the Bessel ODE of order 0, and therefore, we have:

$$a_0\left(r\right)=\left\{\begin{array}{cc}{A}_0{J}_0\left(\sqrt{\gamma }r\right),\hfill & r\in (0,b),\hfill \\ 1+C_{0}logr,\hfill & r\in (b,1),\hfill \end{array}\right.$$

where $J_0$ is the Bessel function of the first kind and $A_0$ and $C_0$ are constants. These are computed by imposing continuity of $a_0$ and $a_0^{\prime }$ at $r=b$. In this way, we obtain:

$$\left\{\begin{array}{c}{A}_0{J}_0\left(\sqrt{\gamma }b\right)=1+C_{0}logb\hfill \\ A_0\sqrt{\gamma }{J}_0^{\prime }\left(\sqrt{\gamma }b\right)=C_0\frac{1}{b}.\hfill \end{array}\right.$$

Solving the system for $A_0$ and $C_0$ and taking into account that ${\Lambda }_q\left(1\right)=\frac{\partial v}{\partial r}(1,\theta )=a_0^{\prime }\left(1\right)=C_0$, we easily obtain (14).

Similarly, to compute $c_n$ in (14), we have to consider $g\left(\theta \right)=e^{in\theta }$ in (11), and therefore, we assume that the solution $v(r,\theta )$ can be written in separate variables, i.e., $v(r,\theta )=a_n\left(r\right)e^{in\theta }$. Then, $a_n$ must satisfy:

$$\left\{\begin{array}{c}{r}^2{a}_n^{″}+r{a}_n^{\prime }+\left(r^{2}q\left(r\right)-n^2\right)a_n=0,0<r<1,\hfill \\ a_n\left(1\right)=1,\underset{r⟶0,r>0}{lim}{a}_n\left(r\right)<\infty ,n\ge 1.\hfill \end{array}\right.$$

(20)

As in the case of $c_0$, for $r\in (0,b)$, we solve the ODE with the boundary data at $r=0$, while for $r\in (b,1)$, we use the boundary data at $r=1$. We have:

$$a_n\left(r\right)=\left\{\begin{array}{cc}{A}_n{J}_n\left(\sqrt{\gamma }r\right),\hfill & r\in (0,b),\hfill \\ C_n(r^n-r^{-n})+r^n,\hfill & r\in (b,1),\hfill \end{array}\right.$$

where $A_n$ and $C_n$ are constants. These are computed by imposing continuity of $a_n$ and $a_n^{\prime }$ at $r=b$. In this way, we obtain:

$$\left\{\begin{array}{c}{A}_n{J}_n\left(\sqrt{\gamma }b\right)=C_n(b^n-b^{-n})+b^n\hfill \\ A_n\sqrt{\gamma }{J}_n^{\prime }\left(\sqrt{\gamma }b\right)=n{C}_n(b^{n-1}+b^{-n-1})+n{b}^{n-1}.\hfill \end{array}\right.$$

Solving the system for $A_n$ and $C_n$, we obtain, in particular:

$$C_n=\frac{-b^n{J}_n^{\prime }\left(\sqrt{\gamma }b\right)+n\frac{b^{n-1}}{\sqrt{\gamma }}{J}_n\left(\sqrt{\gamma }b\right)}{-(b^{-n-1}+b^{n-1})\frac{n}{\sqrt{\gamma }}{J}_n\left(\sqrt{\gamma }b\right)-(b^{-n}-b^n)J_n^{\prime }\left(\sqrt{\gamma }b\right)}.$$

We simplify this expression using the well-known identity:

$$2J_n^{\prime }\left(r\right)=J_{n-1}\left(r\right)-J_{n+1}\left(r\right),$$

and we obtain:

$$C_n=\frac{-J_{n+1}\left(\sqrt{\gamma }b\right)}{b^{-2n}{J}_{n-1}\left(\sqrt{\gamma }b\right)+J_{n+1}\left(\sqrt{\gamma }b\right)}.$$

Now, taking into account that ${\Lambda }_q\left(e^{in\theta }\right)=\frac{\partial v}{\partial r}(1,\theta )=a_n^{\prime }\left(1\right)e^{in\theta }=(2n{C}_n+n)e^{in\theta }$, we easily obtain (14). □

Remark 1.

In this proof of Theorem 1, we do not use the restriction $\gamma \le 1$ that satisfies the potentials in F. In fact, the statement of the theorem still holds for any step potential, as in F, but with any arbitrary large $\gamma \ge 0$.

3. Stability

In this section, we focus on the stability results for the map $\Lambda$. Some results are analytical and they are stated as theorems. The proofs are given in Appendix A. We divided this section in three subsections, where we consider the negative stability result for $q\in F$ norm, and some partial results when we consider the subsets $F_b$ defined by:

$$F_b=\left\{q\in L^{\infty }(\Omega ):q\left(r\right)={\xi }_{(0,b)}\left(r\right),\gamma \in [0,1]\right\},$$

and $G_{\gamma }$ defined in (8).

3.1. Stability for $q\in F$

The first result in this section is the lack of any stability property when $q\in F$. In particular, we prove that inequality (4) fails for any continuous function $V\left(t\right)$ with $V\left(0\right)=0$.

Theorem 2.

Given $q_0\in F$, there exists a sequence ${\left\{q_k\right\}}_{k\ge 1}\subset F$, such that $\parallel q_0-q_k{\parallel }_{L^{\infty }}=\gamma >0$ for all $k\ge 1$, while:

$$\parallel {\Lambda }_{q_0}-{\Lambda }_{q_k}{\parallel }_{\mathcal{L}(H_{\#}^{1/2};H_{\#}^{-1/2})}\to 0,ask\to \infty .$$

(21)

This result contradicts any possible stability result of the DtN map at $q_0\in F$. Roughly speaking, the idea is that the eigenvalues of $\Lambda$, given in Theorem 1 above, depend continuously on b, unlike the $L^{\infty }$ norm of the potentials. A detailed proof of the Theorem 2 is given in the Appendix A below.

3.2. Partial Stability

We now give two partial stability results when we fix b and $\gamma$, respectively.

Theorem 3.

Given $b\in (0,1)$ and $q_1,q_2\in F_b$, we have:

$$\parallel q_1-q_2{\parallel }_{L^{\infty }}\le \frac{15.0756}{b^4}{\parallel {\Lambda }_{q_1}-{\Lambda }_{q_2}\parallel }_{\mathcal{L}(H_{\#}^{1/2};H_{\#}^{-1/2})}.$$

(22)

On the contrary, given $\gamma \in (0,1]$ and $q_1,q_2\in G_{\gamma }$, we have:

$$\left|b_1-b_2\right|\le \frac{3.7489}{\gamma b^3}{\parallel {\Lambda }_{q_1}-{\Lambda }_{q_2}\parallel }_{\mathcal{L}(H_{\#}^{1/2};H_{\#}^{-1/2})},$$

(23)

where $b=min\{b_1,b_2\}$.

The proof of this theorem is in the Appendix A below.

Inequality (22) provides a Lipschitz stability result for $\Lambda$ when b is fixed. This result is not new, since this situation enters in the framework in [6], as q takes constant values in fixed regions. The contribution here is in the dependence of the Lipschitz constant on the parameter b, which is associated with the size of the region, where q takes a different constant value. An estimate (22) shows also that the lack of Lipschitz stability is related to variations in the position of the discontinuity, which is the main idea in the negative result given in Theorem 2.

A numerical quantification of this Lipschitz stability for b fixed is easily obtained. We fix $b=b_0$ and consider:

$$F_{h,b_0}=\{q\in L^{\infty }(\Omega ):q\left(r\right)=\gamma {\chi }_{(0,b)}\left(r\right),b=b_0,\gamma =hj,j=1,\dots ,1/h-1\}.$$

and for $q_0\in F_{h,b_0}$:

$$C_2(h,q_0,b_0)=\underset{\genfrac{}{}{0pt}{}{q\in F_{h,b_0}}{q\ne q_0}}{max}\frac{\parallel q_0{-q\parallel }_{L^{\infty }}}{\parallel {\Lambda }_{q_0}-{\Lambda }_q{\parallel }_{\mathcal{L}(H_{\#}^{1/2};H_{\#}^{-1/2})}},$$

(24)

then, $C_2(h,q_0,b_0)$ remains bounded as $h\to 0$ for all $q_0\in F_h$. In Figure 1, we show the behavior of $C_2(h,q_0,b_0)$ when $h={10}^{-4}$ for different values of $b_0$. To illustrate the behavior with respect to $b_0\to 0$, we plot on the left-hand side of Figure 1 the graphs of the functions:

$$C_{2,min}\left(b_0\right)=\underset{q\in F_{h,b_0}}{min}{C}_2({10}^{-4},q,b_0),\mathrm{and} C_{2,max}\left(b_0\right)=\underset{q\in F_{b_0}}{max}{C}_2({10}^{-4},q,b_0).$$

(25)

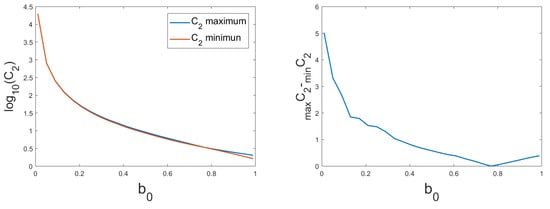
Figure 1. Numerical estimate of the stability constant $C_2$ in (24) for $h={10}^{-4}$. To illustrate the behavior on b, we plotted the maximum and minimum value when $q\in F_{h,b}$ with respect to b in logarithmic scale (left), and its range in normal scale (right).

We see that both constants become larger for small values of b. We also see that both graphs are close in this logarithmic scale. However, the range of the interval $[C_{2,min}\left(b\right),C_{2,max}\left(b\right)]$ is not small, as shown on the right-hand side of Figure 1.

Concerning inequality (23) in Theorem 3, it provides a stability result for $\Lambda$ with respect to the position of the discontinuity. In particular, this provides Lipschitz stability if we consider a norm for the potentials that is sensitive to the position of the discontinuity. This is not the case for the $L^{\infty }$ norm, but it is true for the $L^p$-norm for some $1\le p<\infty$. For example, when $p=1$:

$$\parallel q_1-q_2{\parallel }_{L^1}=\gamma \pi |b_1^2-b_2^2|\le 2\pi \gamma |b_1-b_2|\le \frac{7.4978\pi }{b^3}{\parallel {\Lambda }_{q_0}-{\Lambda }_q\parallel }_{\mathcal{L}(H_{\#}^{1/2};H_{\#}^{-1/2})}.$$

We can also check this numerically:

$$C_2(h,{\gamma }_0,b)=\underset{q\in G_{h,{\gamma }_0}}{max}\frac{\parallel q_0{-q\parallel }_{L^1}}{\parallel {\Lambda }_{q_0}-{\Lambda }_q{\parallel }_{\mathcal{L}(H_{\#}^{1/2};H_{\#}^{-1/2})}},$$

(26)

is bounded as $h\to 0$ and $b\ge b_0>0$, where:

$$G_{h,{\gamma }_0}=\{q\in L^{\infty }(\Omega ):q\left(r\right)=\gamma {\chi }_{(0,b)}\left(r\right),\gamma ={\gamma }_0,b=hj,j=1,\dots ,1/h-1\}.$$

In Figure 2, we show the values when $h={10}^{-4}$. We can observe that the constant blows up as $b\to 0$.

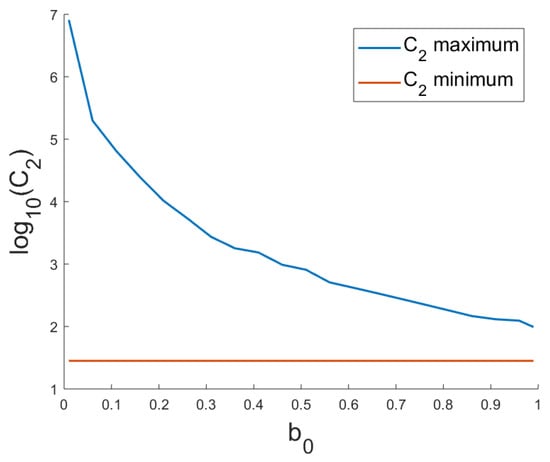
Figure 2. $C_2(h,q)$ for $b>b_0$ when $h={10}^{-4}$.

4. Range of the DtN Map

In this section, we are interested in the range of $\Lambda$ when $q\in F$, i.e., the set of sequences ${\left\{c_n\right\}}_{n\ge 0}$ of the form (15) and (16) for all possible $b,\gamma \in [0,1]\times [0,1]$.

As F is a bi-parametric family of potentials, it is natural to check if we can characterize the family ${\left\{c_n\right\}}_{n\ge 0}$ with only the first two coefficients $c_0$ and $c_1$. In this section, we give numerical evidence of the following facts:

• The first two coefficients, $c_0$ and $c_1$, in (15) and (16) are the most sensitive with respect to $(b,\gamma )$ and, therefore, are the more relevant ones to identify b and $\gamma$ from the DtN map.
• The function:

  $$\begin{array}{ccc}\hfill {\Lambda }^h:F_h& \to & {\mathbb{R}}^2\hfill \\ \hfill q& \to & (c_0,c_1),\hfill \end{array}$$

  (27)

  is injective. This means, in particular, that the DtN map can be characterized by the coefficients $c_0$ and $c_1$, when restricted to functions in $F_h$. We also illustrate the set of possible coefficients $c_0,c_1$.
• The lack of stability for $\Lambda$ is associated with a higher density of points in the range of ${\Lambda }^h$. This occurs when either b or $\gamma$ is close to zero.

4.1. Sensitivity of $c_n$

To analyze the relevance and sensitivity of the coefficients $c_n=c_n(b,\gamma )$ to identify the parameters $(b,\gamma )$, we computed their range when $(b,\gamma )\in [0,1]\times [0,1]$, and the norm of their gradients. As we can see in Table 1, the range decreases for large n. This means that, for larger values of n, the variability of $c_n$ is smaller and they are likely to be less relevant to identify q.

Table 1. Range of the coefficients, i.e., for each $c_n$, the range is defined as ${max}_{q\in F_h}{c}_n-{min}_{q\in F_h}{c}_n$.

Coefficient	Range
$c{}_0$	0.5523
$c{}_1$	0.2486
$c{}_2$	0.1588
$c{}_3$	0.1157
$c{}_4$	0.0904
$c_5$	0.0736

However, even if the range of $c_n$ becomes smaller for large n, they could be more sensitive to small perturbations in $(b,\gamma )$ and this would make them useful to distinguish different potentials. However, this is not the case. In Figure 3, we show that for the given values of $\gamma =0.1,0.34,0.67,0.99$ and $b\in (0,1]$, the gradients of the first two coefficients, with respect to $(b,\gamma )$, are larger than the others. Therefore, we conclude that the two first coefficients, $c_0$ and $c_1$, are the most sensitive and, therefore relevant to identify the potential q.

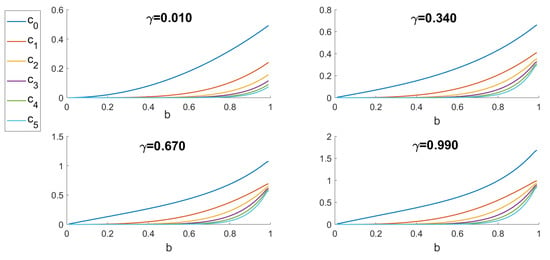
Figure 3. Norm of the gradient of the coefficients $c_n(\gamma ,b)$ in terms of $b\in (0,1)$ for different values of $\gamma$. We can see that the gradients of higher coefficients $n\ge 2$ are smaller than those of the first two. We can also observe that these gradients become small for small values of b.

We also see in Figure 3 that these gradients are very small for $b<<1$. This means, in particular, that identifying potentials with small b from the DtN map should be more difficult.

4.2. Range of the DtN in Terms of $c_0,c_1$

Now, we focus on the range of the DtN in terms of the relevant coefficients $(c_0,c_1)$, i.e., the range of the map ${\Lambda }^h$ in (27): $R\left({\Lambda }^h\right)$. In Figure 4, we show this range.

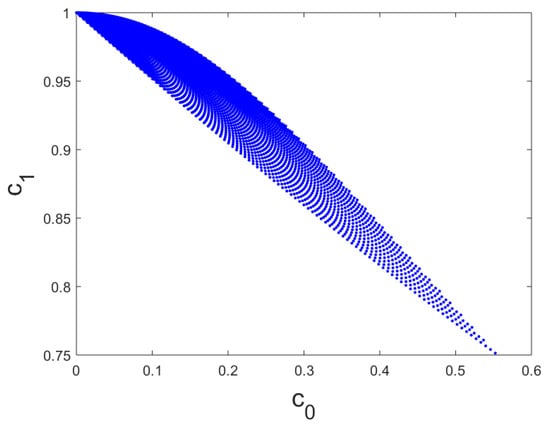
Figure 4. Range of the discrete Dirichlet-to-Neumann (DtN) map in (27) ($h={10}^{-2})$.

Coordinate lines for fixed $\gamma$ and b are given in Figure 5. We can observe that $R\left({\Lambda }^h\right)$ is a convex set between the curves:

$$\begin{array}{ccc}& & r_{low}:\{(c_0(\gamma ,1),c_1(\gamma ,1)),with \gamma \in [0,1]\},\hfill \\ & & r_{up}:\{(c_0(1,b),c_1(1,b)),with b\in [0,1]\}.\hfill \end{array}$$

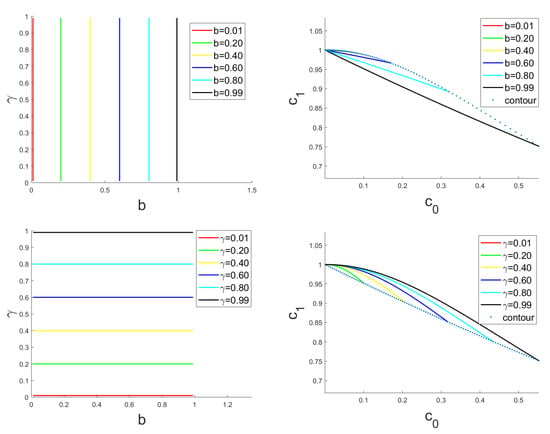
Figure 5. Coordinate lines of the map ${\Lambda }^h$ defined in (27) ($h={10}^{-2})$. The upper figure contains the coordinate lines associated with b constant, while the lower one corresponds to $\gamma$ constant.

Note also that in the $c_0,c_1$ plane, the length of the coordinate lines associated with b constant are segments that become smaller as $b\to 0$. Analogously, the length of those associated with constant $\gamma$ become smaller as $\gamma \to 0$. Thus, the region where either b or $\gamma$ are small produces a higher density of points in the range of ${\Lambda }^h$. This corresponds to the upper left part of its range (see Figure 4). On the contrary, this Figure provides numerical evidence of the injectivity of ${\Lambda }^h$ as well. In fact, any point inside $R\left({\Lambda }^h\right)$ is the intersection of two coordinate lines associated with some unique $b_0$ and ${\gamma }_0$.

The higher density of points in the upper left hand-side of the range of ${\Lambda }^h$ should correspond to potentials q with a large stability constant $C_2(h,q)$, defined as:

$$C_2(h,q)=\underset{q\in F}{max}\frac{\parallel q_0{-q\parallel }_{L^1}}{\parallel {\Lambda }_{q_0}-{\Lambda }_q{\parallel }_{\mathcal{L}(H_{\#}^{1/2};H_{\#}^{-1/2})}}.$$

In Figure 6, we show the level sets of $C_2(h,q)$ for $h={10}^{-4}$ and different $q\in F_h$. The region with a larger constant corresponds to small values of b (upper right figure) and larger values of $c_1$ (upper left and lower figures). On the contrary, the region with a lower stability constant is for b close to $b=1$, which corresponds to the lower part of the range of ${\Lambda }^h$ when $c_0$ is small.

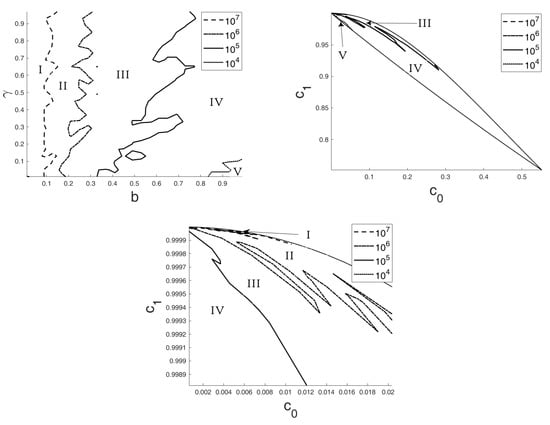
Figure 6. Level sets of the $C_2(b,\gamma )$ for $q\in F_h$ and $h={10}^{-4}$ in terms of $(b,\gamma )$ (upper left) and in terms of $(c_0,c_1)$ (upper right), and a close up of the upper left region in this last figure is in the lower figure. Regions separated by level sets are indicated: Region I corresponds to the potentials with a stability constant larger that ${10}^7$, region II corresponds to those with a stability constant lower that ${10}^7$ but larger than ${10}^6$, and so on.

It is interesting to analyze the set of potentials with the same coefficient $c_0$ or $c_1$. We provide, in Figure 7, the coordinate lines of the inverse map ${\left({\Lambda }^h\right)}^{-1}$. When increasing the value of either $c_0$ (light lines) or $c_1$ (dark lines), we obtain lines closer to the left part of the $(b,\gamma )$ region. We can see that the angle between coordinate lines becomes very small for small b. In this region, close points could be the intersection of the coordinate lines associated with not so close parameters $(b,\gamma )$. This agrees with the region where the stability constant is larger.

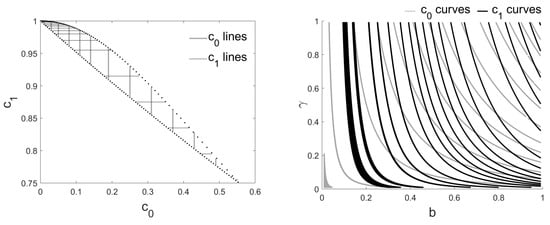
Figure 7. Coordinate lines of the map ${\left({\Lambda }^h\right)}^{-1}$ defined in (27).

5. Conclusions

We considered the relationship between the potential in the Schrödinger equation and the associated DtN map in one of the simplest situations, i.e., for a subset of radial one-step potentials in two-dimension. In particular, we focused on two difficult problems: The stability of the map $\Lambda$ (defined in (3)) and its range. In this case, the map $\Lambda$ is easily characterized in terms of the Bessel functions and this allows us to give some analytical and numerical results for these problems. We proved the lack of any possible stability result by adapting the argument in [7] [Alessandrini, 1988] for the conductivity problem. We also obtained some partial Lipschitz stability when the position of the discontinuity is fixed in the potential, as well as numerical evidence of the stability with respect to the $L^1$ norm. Finally, we characterized numerically the range of $\Lambda$ in terms of the first two eigenvalues of the DtN map and provided some insight into the regions where the stability of $\Lambda$ is worse. As a future line of work, it could be interesting to consider the problem in a more complicated stage, for instance, one can study not only one-step radial potentials q in the problem, but could add more steps into the definition of the potentials.