Partial Anti-Synchronization of the Fractional-Order Chaotic Systems through Dynamic Feedback Control

Abstract

This paper investigates the partial anti-synchronization problem of fractional-order chaotic systems through the dynamic feedback control method. Firstly, a necessary and sufficient condition is proposed, by which the existence of the partial anti-synchronization problem is proved. Then, an algorithm is given and used to obtain all solutions of this problem. Moreover, the partial anti-synchronization problem of the fractional-order chaotic systems is realized through the dynamic feedback control method. It is noted that the designed controllers are single-input controllers. Finally, two illustrative examples with numerical simulations are used to verify the correctness and effectiveness of the proposed results.

1. Introduction

It is well known that Lorenz first found the chaos attractor [1] in 1963. From then on, chaotic systems and their control problems have been widely studied by scholars. With the development of chaos theory, many new chaotic systems were derived, and a lot of important results were applied in several scientific areas, such as economics, robotics, automatic control, signal detection and processing (see [2,3,4,5,6,7] and the references therein). As we know that the control problems of chaotic systems include stabilization, complete synchronization, anti-synchronization, simultaneous synchronization and anti-synchronization, lag synchronization, and projective synchronization, numerous valuable conclusions have been drawn from the study of these problems (for details, please see [8,9,10,11,12,13,14]). The anti-synchronization problem of chaotic systems has been a hot topic in recent years, and a variety of results have been published. In [12], it is pointed out for the first time that the anti-synchronization problem of a given chaotic system $\dot{x}=f\left(x\right)$ exists if and only if $f(-x)=-f\left(x\right)$. That is to say, the slave system $\dot{y}=f\left(y\right)+Bu$ and the master system $\dot{x}=f\left(x\right)$ can achieve anti-synchronization through the designed controller u, which is described as $u=u(x,e)$ and meets the condition $u(x,0)\equiv 0$, where $e=x+y$ and B is a constant matrix. Only when this necessary and sufficient condition is met can a simple and physical controller be designed. It is noted that only a few chaotic or hyper-chaotic systems can meet the above condition: $f(-x)=-f\left(x\right)$. A natural question arises: If this condition is not met, can the part variables of the given chaotic system $\dot{x}=f\left(x\right)$ realize anti-synchronization or not? If yes, this type of anti-synchronization is called the partial anti-synchronization problem, which will be introduced in Section 2.1. However, to the best of our knowledge, there are no relative results that have been published so far.

It is well known that chaotic systems can generally be divided into two categories: integer-order chaotic systems and fractional-order chaotic systems. Integer-order chaotic systems and fractional-order chaotic systems are closely related, and the difference between them lies mainly in the order of the differential equation. For any given chaotic system $D_t^{{\alpha }_i}x=f\left(x\right)$, where $x\in R^n$ is the state and $f\left(x\right)\in R^n$ is the continuous function, the system is a fractional-order chaotic system when $0<{\alpha }_i<1$, $i=1,2,\cdots ,n$. Compared with integer-order chaotic systems, fractional-order chaotic systems develop later. Until now, lots of both important and useful results have been obtained (see [15,16,17,18,19,20,21,22,23,24]). However, there are no published results about the partial anti-synchronization problem of fractional-order chaotic systems. Therefore, we shall investigate the partial anti-synchronization problem of fractional-order chaotic systems in this paper.

Motivated by the above conclusions, we study the partial anti-synchronization problem of fractional-order chaotic systems through the dynamic feedback control method. The main contributions of this paper are summarized as follows:

(a)

A necessary and sufficient condition is presented to determine the existence of the partial anti-synchronization problem;

(b)

An algorithm is proposed to obtain all solutions of this partial anti-synchronization problem;

(c)

This partial anti-synchronization problem is realized through the dynamic feedback control method, and the designed controllers are single-input controllers.

The rest of this paper is organized as follows. Section 2 introduces the preliminary knowledge and the problem formation, Section 3 presents the main results of this paper, Section 4 provides illustrative examples with numerical simulations, and Section 5 gives the conclusions.

2. Preliminaries and Problem Formation

2.1. Preliminaries

The Caputo derivative of order $\alpha$ is defined as

$$D_t^{\alpha }f\left(x\right)=\frac{D^{\alpha }f\left(x\right)}{d{t}^{\alpha }}=\left\{\begin{array}{cc}\frac{1}{\Gamma (\alpha -n)}{\int }_{\alpha }^t\frac{f^{\left(n\right)}\left(\varsigma \right)}{{(t-\varsigma )}^{\alpha +1-n}}d\varsigma ,\hfill & n-1<\alpha <n\hfill \\ \\ \frac{d^{n}f\left(t\right)}{d{t}^n},\hfill & \alpha =n\hfill \end{array}\right.$$

where $n=\left[\alpha \right]$, $\Gamma (.)$ is a function with the following expression:

$$\Gamma \left(z\right)={\int }_0^{\infty }{e}^{-t}{t}^{z-1}dt.$$

Consider the following fractional-order nonlinear system:

$$D_t^{\alpha }x=f\left(x\right),$$

(1)

where $x\in R^n$ is the state, and $f\left(x\right)\in R^n$ is a continuous function.

Let the system (1) be the master system; then, the corresponding slave system is

$$D_t^{\alpha }y=f\left(y\right)+bu,$$

(2)

where $y\in R^n$ is the state, $f\left(y\right)\in R^n$ is a continuous function, $b\in R^{n\times l}$ is a constant matrix, $\left(f\right(x),b)$ is assumed to be controllable, $u\in R^l$, and $l\ge 1$ is the controller to be designed.

Set $e=x+y$; then, the sum system (i.e., the addition between system (1) and the system (2)) is given as

$$D_t^{\alpha }e=f\left(x\right)+f\left(y\right)+bu,$$

(3)

where $e\in R^n$ is the state, and $b,u$ are given in Equation (2).

Definition 1.

Consider the system (3). If ${\displaystyle \underset{t\to \infty }{lim}\parallel e\parallel =0}$, then the master system (1) and slave system (2) are called to realize anti-synchronization through the controller u.

Remark 1.

In [12], we pointed out that the master system (1) and slave system (2) realize anti-synchronization through the controller u, which is expressed as $u=u(x,e)$ and meets the condition $u(x,0)\equiv 0$ if and only if $f(-x)=-f\left(x\right)$, i.e., $f\left(x\right)$ is an odd function.

It is well known that only a few chaotic systems can meet the condition $f(-x)=-f\left(x\right)$, such as the modified Chua system. However, the famous Lorenz system does not satisfy that condition. When the whole chaotic system does not achieve anti-synchronization, a natural question arises of whether the part variables of a given chaotic system can realize anti-synchronization or not. Moreover, if yes, how can those part variables of that given chaotic system be found? In the following, we firstly give a definition of partial anti-synchronization.

Consider the system (1). If there exists a non-singular transformation:

$$p=\left(\begin{array}{c}X\\ Z\end{array}\right)=Tx$$

(4)

where $X\in R^m$, $1\le m<n$, $Z\in R^{n-m}$, and $T\in R^{n\times n}$ is a constant matrix, then the system (1) is divided into the following two subsystems:

$$D_t^{\alpha }X=F(X,Z)$$

(5)

$$D_t^{\alpha }Z=G(X,Z)$$

(6)

where $F(-X,Z)=-F(X,Z)$.

According to Remark 1, the subsystem (5) satisfies the condition of anti-synchronization. Therefore, let the system (5) be the master subsystem; then, the slave subsystem is presented as follows:

$$D_t^{\alpha }Y=F(Y,Z)+BU,$$

(7)

where $Y\in R^m$ and Z is given in Equation (6), $B\in R^{n\times r}$ is a constant matrix, $\left(F\right(Y,Z),B)$ is assumed to be controllable, $U\in R^r$, and $r\ge 1$ is the controller to be designed.

Let $E=X+Y$; then, the sum subsystem (i.e., the addition between the subsystem (5) and the subsystem (7)) is given as

$$D_t^{\alpha }E=F(Y,Z)+F(X,Z)+BU,$$

(8)

where $E\in R^{m\times m}$ is the state, and $B,U$ are given in Equation (7).

Definition 2.

Consider the sum subsystem (8). If ${\displaystyle \underset{t\to \infty }{lim}\parallel E\parallel =0}$, then the master subsystem (5) and slave subsystem (7) are called to realize anti-synchronization through the controller U. That is to say, the master system (1) and the slave system (2) achieve partial anti-synchronization.

For the stabilization problem of the sum subsystem (8), there are many methods to deal with it. Here, we choose the dynamic feedback control method, and introduce it in the following.

Lemma 1

([15]). Consider the system (2). If $\left(f\right(x),b)$ is stabilized, then the designed controller u is proposed as follows:

$$u=K\left(t\right)x,$$

(9)

where $K\left(t\right)=k\left(t\right)b^T$, ${\displaystyle D_t^{\alpha }k\left(t\right)\le -\sum _{i=1}^n{x}_i^2}$, and 

$$\dot{k}\left(t\right)=-x^{T}x=-{\parallel x\left(t\right)\parallel }^2=-\sum _{i=1}^n{x}_i^2.$$

(10)

2.2. Problem Formulation

The system (1) with $f\left(x\right)$ is not an odd function; there are three problems to be solved.

(1)

Whether the partial anti-synchronization problem exists or not;

(2)

If the partial anti-synchronization problem exists, how can the non-singular transformation matrix T in Equation (4) be found, and how many matrices in the form T can be obtained?

(3)

How can a simple and physical controller U be designed to realize this type anti-synchronization?

3. Main Results

3.1. The Existence of the Partial Anti-Synchronization Problem

In this section, the existence of the partial anti-synchronization problem for the system (1) is investigated, and a conclusion is derived as follows.

Theorem 1.

Consider the system (1). If the following linear equations about β

$$\left\{\begin{array}{c}{f}_{i_1}\left(\beta x\right)\equiv {\beta }_{i_1}{f}_{i_1}\left(x\right)\hfill \\ f_{i_2}\left(\beta x\right)\equiv {\beta }_{i_2}{f}_{i_2}\left(x\right)\hfill \\ ⋮\hfill \\ f_{i_m-1}\left(\beta x\right)\equiv {\beta }_{i_m-1}{f}_{i_m-1}\left(x\right)\hfill \\ f_{i_m}\left(\beta x\right)\equiv {\beta }_{i_m}{f}_{i_m}\left(x\right)\hfill \end{array}\right.$$

(11)

have a solution in the following form

$${\gamma }^{\left(m\right)}=\left(\begin{array}{c}-1\\ ⋮\\ -1\\ -1\\ 1\\ ⋮\\ 1\end{array}\right)\leftarrow m$$

(12)

where m is the last position of $-1$, 

$$\beta =\left(\begin{array}{cccc}{\beta }_{i_1}& 0& \cdots & 0\\ 0& {\beta }_{i_2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\beta }_{i_n}\end{array}\right),$$

(13)

and $|{\beta }_{i_j}|=1,i_j\in \Lambda =\{1,2,\cdots ,n\}$ with $i_j\ne i_l$ if $j\ne l$, $j=1,2,\cdots ,n$, then the partial anti-synchronization problem for the system (1) exists, and the matrix T given in Equation (4) is obtained as:

$$T=\left(\begin{array}{c}{\delta }_n^{i_1}\\ ⋮\\ {\delta }_n^{i_k-1}\\ {\delta }_n^{i_m}\\ {\delta }_n^{i_m+1}\\ ⋮\\ {\delta }_n^{i_n}\end{array}\right),$$

(14)

where

$$\begin{gathered} {\delta }_n^k=\left(\begin{array}{ccccccc}0& \cdots & 0& 1& 0& \cdots & 0\end{array}\right)\in R^n \\ \uparrow \\ k \end{gathered}$$

(15)

$k\in \Lambda$.

Proof. 

Since ${\gamma }^{\left(m\right)}$ in Equation (12) is a solution of the equations in Equation (11), we let

$$F(X,Z)=\left(\begin{array}{c}{f}_{i_1}\left(x\right)\\ f_{i_2}\left(x\right)\\ ⋮\\ f_{i_m}\left(x\right)\end{array}\right),G(X,Z)=\left(\begin{array}{c}{f}_{i_m+1}\left(x\right)\\ f_{i_m+2}\left(x\right)\\ ⋮\\ f_{i_n}\left(x\right)\end{array}\right),$$

(16)

where

$$X=\left(\begin{array}{c}{x}_{i_1}\\ x_{i_2}\\ ⋮\\ x_{i_m}\end{array}\right),Z=\left(\begin{array}{c}{x}_{i_m+1}\\ x_{i_m+2}\\ ⋮\\ x_{i_n}\end{array}\right).$$

(17)

Obviously, $F(-X,Z)=-F(X,Z)$, and the matrix T is given in Equation (4); we conclude that the partial anti-synchronization problem of the system (1) exists. □

3.2. All Solutions of the Partial Anti-Synchronization Problem

From Section 3.1, we know that the partial anti-synchronization problem exists if the matrix T given in Equation (4) is obtained. How to get this matrix T and how many matrices in the form T are important in this problem. A flowchart is shown in the Figure 1, and an algorithm is proposed in the next.

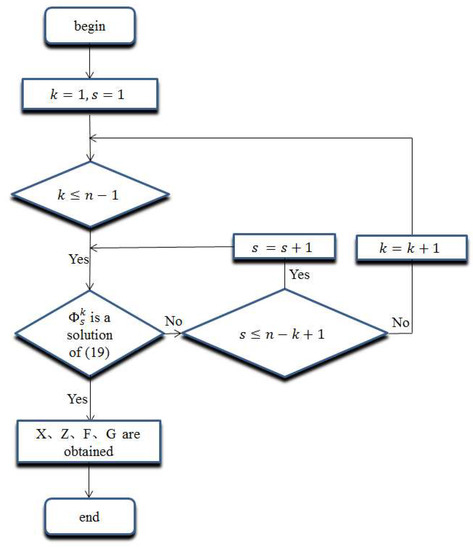
Figure 1. Flowchart of the algorithm.

In conclusion, we can obtain all of the transformation matrices in the form T given in Equation (4) by Algorithm 1 if the partial anti-synchronization problem of the system (1) exists.

Algorithm 1 Consider the system (1).

Input: Step 1: Let $k=1$, where k is the number of ${\beta }_j=1$,  $j\in \Lambda$, s is the first position where ${\beta }_j=1$, and $1\le s\le n$; we verify if the vector $${\mathsf{\Phi }}_s^k=\left(\begin{array}{c}{\mathsf{\Phi }}_{s,1}^k\\ ⋮\\ {\mathsf{\Phi }}_{s,s-1}^k\\ {\mathsf{\Phi }}_{s,s}^k\\ {\mathsf{\Phi }}_{s,s+1}^k\\ ⋮\\ {\mathsf{\Phi }}_{s,n}^k\end{array}\right)=\left(\begin{array}{c}-1\\ ⋮\\ -1\\ 1\\ -1\\ ⋮\\ -1\end{array}\right)\leftarrow s$$ (18) is a solution of the following linear equations about $\beta$: $$\left\{\begin{array}{c}{f}_1\left(\beta x\right)\equiv {\beta }_1{f}_1\left(x\right)\hfill \\ ⋮\\ f_{s-1}\left(\beta x\right)\equiv {\beta }_{s-1}{f}_{s-1}\left(x\right)\hfill \\ f_{s+1}\left(\beta x\right)\equiv {\beta }_{s+1}{f}_{s+1}\left(x\right)\hfill \\ ⋮\\ f_n\left(\beta x\right)\equiv {\beta }_n{f}_n\left(x\right)\hfill \end{array}\right.$$ (19) or not. If yes, then the transformation matrix T is given as $$T=\left(\begin{array}{c}{\delta }_n^1\\ ⋮\\ {\delta }_n^{s-1}\\ {\delta }_n^n\\ {\delta }_n^{s+1}\\ ⋮\\ {\delta }_n^s\end{array}\right),$$ (20) where ${\delta }_n^k$ is given in Equation (15), $k\in \Lambda$. 1: If not, please go to the second step.   Step 2: $k=2$. k is also the number of ${\beta }_j=1$, s is also the first position where ${\beta }_j=1$, $s+1$ is the second position where ${\beta }_j=1$, and $1\le s\le n-1$; we verify if the vector $${\mathsf{\Phi }}_s^k=\left(\begin{array}{c}{\mathsf{\Phi }}_{s,1}^k\\ {\mathsf{\Phi }}_{s,2}^k\\ ⋮\\ {\mathsf{\Phi }}_{s,s-1}^k\\ {\mathsf{\Phi }}_{s,s}^k\\ {\mathsf{\Phi }}_{s,s+1}^k\\ {\mathsf{\Phi }}_{s,s+2}^k\\ ⋮\\ {\mathsf{\Phi }}_{s,n}^k\end{array}\right)=\left(\begin{array}{c}-1\\ -1\\ ⋮\\ -1\\ 1\\ 1\\ -1\\ ⋮\\ -1\end{array}\right)\leftarrow s$$ (21) is a solution of the following linear equations about $\beta$: $$\left\{\begin{array}{c}{f}_1\left(\beta x\right)\equiv {\beta }_1{f}_1\left(x\right)\hfill \\ ⋮\\ f_{s-1}\left(\beta x\right)\equiv {\beta }_{s-1}{f}_{s-1}\left(x\right)\hfill \\ f_{s+2}\left(\beta x\right)\equiv {\beta }_{s+2}fs+2\left(x\right)\hfill \\ ⋮\\ f_n\left(\beta x\right)\equiv {\beta }_n{f}_n\left(x\right)\hfill \end{array}\right.$$ (22) or not. If yes, then the transformation matrix T is given as $$T=\left(\begin{array}{c}{\delta }_n^1\\ ⋮\\ {\delta }_n^{s-1}\\ {\delta }_n^{n-1}\\ {\delta }_n^n\\ {\delta }_n^{s+2}\\ ⋮\\ {\delta }_n^s\\ {\delta }_n^{s+1}\end{array}\right).$$ (23) If not, please go to the third step. Step 3: $k=3$, and a similar procedure is done until $s=n-k+1$.

3.3. Controller Design

For the sum subsystem (8), there are many control methods for realizing its stabilization problem. The dynamic feedback control method for the stabilization problem for fractional=order chaotic systems was proposed in [15]. As we know, the partial anti-synchronization problem of the system (1) and the system (2) is equivalent to the stabilization of the sum subsystem (8). Thus, we present the following conclusion without a proof.

Theorem 2.

Consider the sum subsystem (8). If $\left(F\right(X,Z)+F(Y,Z),B)$ can be stabilized, then the designed controller U is proposed as follows:

$$U=K\left(t\right)E,$$

(24)

where $K\left(t\right)=k\left(t\right)B^T$, ${\displaystyle D_t^{\alpha }k\left(t\right)\le -\sum _{i=1}^n{E}_i^2}$, and

$$\dot{k}\left(t\right)=-E^{T}E=-{\parallel E\left(t\right)\parallel }^2=-\sum _{i=1}^m{E}_i^2.$$

(25)

4. Illustrative Examples with Numerical Simulations

In this section, two examples are used to verify the correctness and effectiveness of the proposed results.

Example 1.

Consider a fractional-order Lorenz system [25]:

$$\left\{\begin{array}{c}{D}_t^{\alpha }{x}_1=10(x_2-x_1)\hfill \\ D_t^{\alpha }{x}_2=28x_1-x_1{x}_3-x_2\hfill \\ D_t^{\alpha }{x}_3=x_1{x}_2-\frac{8}{3}{x}_3\hfill \end{array}\right.,$$

(26)

where $0<\alpha <1$.

According to Algorithm 1, it is easy to verify that

$${\mathsf{\Phi }}_1^3=\left(\begin{array}{c}-1\\ -1\\ 1\end{array}\right)$$

(27)

is the only solution of the following linear equations about $\beta$:

$$\left\{\begin{array}{c}{f}_1\left(\beta x\right)\equiv {\beta }_{1}f\left(x\right)\hfill \\ f_2\left(\beta x\right)\equiv {\beta }_{2}f\left(x\right)\hfill \end{array}\right.,$$

(28)

i.e.,

$$\left\{\begin{array}{c}{\beta }_2={\beta }_1\hfill \\ {\beta }_1{\beta }_3={\beta }_2\hfill \end{array}\right..$$

(29)

Thus,

$$T=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right).$$

(30)

According to Theorem 1,

$$X=\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right),Z=x_3.$$

(31)

The master subsystem is given as

$$D_t^{\alpha }X=F(X,Z),$$

(32)

where

$$F(X,Z)=\left(\begin{array}{c}10(X_2-X_1)\\ -28X_1+X_{1}Z-10X_2\end{array}\right).$$

(33)

The slave subsystem is presented as

$$D_t^{\alpha }Y=F(Y,Z)+BU,$$

(34)

where

$$F(Y,Z)=\left(\begin{array}{c}10(Y_2-Y_1)\\ -28Y_1+Y_{1}Z-10Y_2\end{array}\right),B=\left(\begin{array}{c}0\\ 1\end{array}\right),$$

(35)

and then the sum subsystem is expressed as

$$\left\{\begin{array}{c}{D}_t^{\alpha }{E}_1=10(E_2-E_1)\hfill \\ D_t^{\alpha }{E}_2=28E_1-E_{1}Z-E_2+U\hfill \end{array}\right..$$

(36)

According to Theorem 2, the designed controller U is

$$U=k\left(t\right)E_2,$$

(37)

where $\dot{k}\left(t\right)=-E_2^2$.

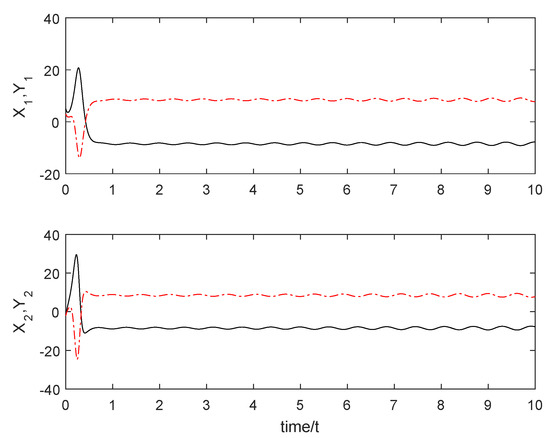
The initial conditions are selected as: $X_1\left(0\right)=5$, $X_2\left(0\right)=-2$, $Y_1\left(0\right)=-3$, $Y_2\left(0\right)=3$, and $Z\left(0\right)=-2$ with $\alpha =0.9$. Using the simulation tool in Matlab, the numerical simulations were performed. From Figure 2, we observe that the sum subsystem (36) is asymptotically stable through the controller U, which implies that the master subsystem (32) and the slave subsystem (34) achieve anti-synchronization. Figure 3 show the states of the master subsystem (32) and the slave subsystem (34). It can be seen that the state vectors of the slave subsystem (34) have the same amplitude but opposite signs compared to those of the master subsystem (32).

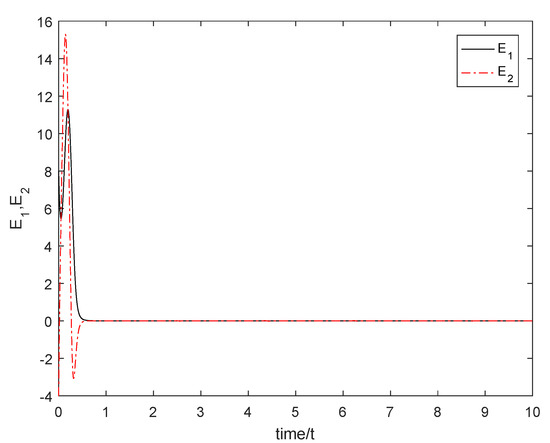
Figure 2. The sum subsystem (36) is asymptotically stable.

Figure 3. The states of the master subsystem (32) and the slave subsystem (34).

Example 2. 

Fractional-order hyper-Chen system [26]

$$\left\{\begin{array}{c}{D}_t^{\alpha }{x}_1=-37x_1+37x_2\hfill \\ D_t^{\alpha }{x}_2=-9x_1-x_1{x}_3+26x_2\hfill \\ D_t^{\alpha }{x}_3=-3x_3+x_1{x}_2+x_1{x}_3-x_4\hfill \\ D_t^{\alpha }{x}_4=-8x_4+x_2{x}_3-x_1{x}_3\hfill \end{array}\right.,$$

(38)

where $0<\alpha <1$.

According to Algorithm 1, we conclude that

$${\mathsf{\Phi }}_2^3=\left(\begin{array}{c}-1\\ -1\\ 1\\ 1\end{array}\right)$$

(39)

is the unique solution of the following linear equations about $\beta$:

$$\left\{\begin{array}{c}{f}_1\left(\beta x\right)-{\beta }_{1}f\left(x\right)=({\beta }_2-{\beta }_1)x_2\equiv 0\hfill \\ f_2\left(\beta x\right)-{\beta }_{2}f\left(x\right)=-9({\beta }_2-{\beta }_1)x_2-({\beta }_1{\beta }_3-{\beta }_2)x_1{x}_3\equiv 0\hfill \end{array}\right.,$$

(40)

i.e.,

$$\left\{\begin{array}{c}{\beta }_2\equiv {\beta }_1\hfill \\ {\beta }_1{\beta }_3\equiv {\beta }_2\hfill \end{array}\right..$$

(41)

Thus,

$$T=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right).$$

(42)

According to Theorem 1,

$$X=\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right),Z=\left(\begin{array}{c}{x}_3\\ x_4\end{array}\right).$$

(43)

The master subsystem is given as

$$D_t^{\alpha }X=F(X,Z),$$

(44)

where

$$F(X,Z)=\left(\begin{array}{c}37(X_2-X_1)\\ -9X_1-X_1{Z}_1+26X_2\end{array}\right).$$

(45)

The slave subsystem is presented as

$$D_t^{\alpha }Y=F(Y,Z)+BU,$$

(46)

where

$$F(Y,Z)=\left(\begin{array}{c}37(Y_2-Y_1)\\ -9Y_1-Y_1{Z}_1+26Y_2\end{array}\right),B=\left(\begin{array}{c}0\\ 1\end{array}\right),$$

(47)

and then the sum subsystem is expressed as

$$\left\{\begin{array}{c}{D}_t^{\alpha }{E}_1=37(E_2-E_1)\hfill \\ D_t^{\alpha }{E}_2=-9E_1-E_1{Z}_1+26E_2+U\hfill \end{array}\right..$$

(48)

According to Theorem 2, the designed controller U is

$$U=k\left(t\right)E_2,$$

(49)

where $\dot{k}\left(t\right)=-E_2^2$.

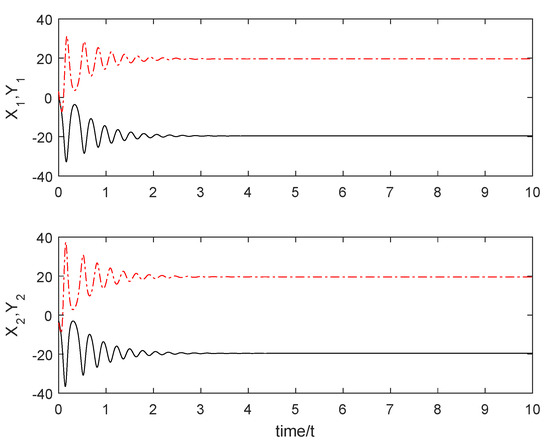
The initial conditions are selected as: $X_1\left(0\right)=1$, $X_2\left(0\right)=-3$, $Y_1\left(0\right)=-3$, $Y_2\left(0\right)=-2$, $Z_3\left(0\right)=3$, and $Z_4\left(0\right)=-4$ with $\alpha =0.8$. Using the simulation tool in Matlab, the numerical simulations were performed. From Figure 4, we notice that the sum subsystem (48) is asymptotically stable through the controller U, which implies that the master subsystem (44) and the slave subsystem (46) achieve anti-synchronization. Figure 5 shows the states of the master subsystem (44) and the slave subsystem (46). It can be seen that the state vectors of the slave subsystem (46) have the same amplitude but opposite signs compared to those of the master subsystem (44).

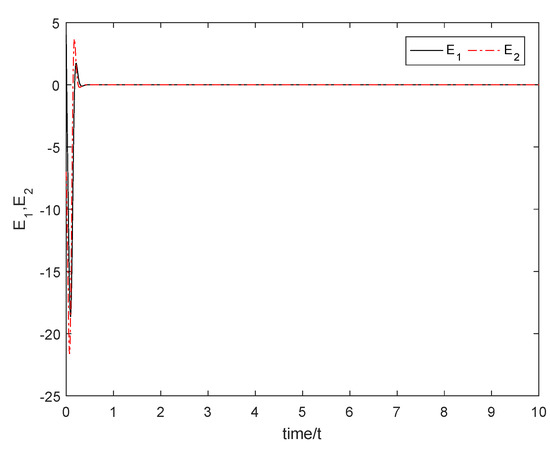
Figure 4. The sum subsystem (48) is asymptotically stable.

Figure 5. The states of the master subsystem (44) and the slave subsystem (46).

5. Conclusions

The partial anti-synchronization problem of fractional-order chaotic systems was investigated through the dynamic feedback control method. Firstly, the existence of the partial anti-synchronization problem was proved, and a necessary and sufficient condition was proposed. Secondly, an algorithm was derived, through which all solutions of this anti-synchronization problem could be obtained. Moreover, the partial anti-synchronization problem for fractional-order chaotic systems was realized through the dynamic feedback control method. Finally, two illustrative examples with numerical simulations were applied in order to verify the correctness and effectiveness of the proposed method.