State Estimation for a Class of Distributed Parameter Systems with Time-Varying Delay over Mobile Sensor–Actuator Networks with Missing Measurements
Abstract
1. Introduction
- (1)
- The proposed estimation strategy is based on a class of distributed parameter systems with time-varying delay, which is complex and challenging and has not been studied, the achievements complement the existing results and are valuable for the development of engineering practice.
- (2)
- A new kind of distributed estimators has been constructed in order to address the problem about mobile sensor–actuator networks occurring missing measurement, the distributed estimators involve consistency component and gain component and approximate the original system state well.
- (3)
- The control forces of mobile sensor–actuator have been designed by utilizing mobile sensor–actuator networks and Lyapunov functional technology, which have enhanced the estimators performance and made the state of estimation error systems converge to zero faster than that of fixed sensor–actuator networks.
2. Problem Formulation and Estimator Design
2.1. Problem Formulation and Preliminaries
2.2. System Evolution and Estimator Design
3. Main Results
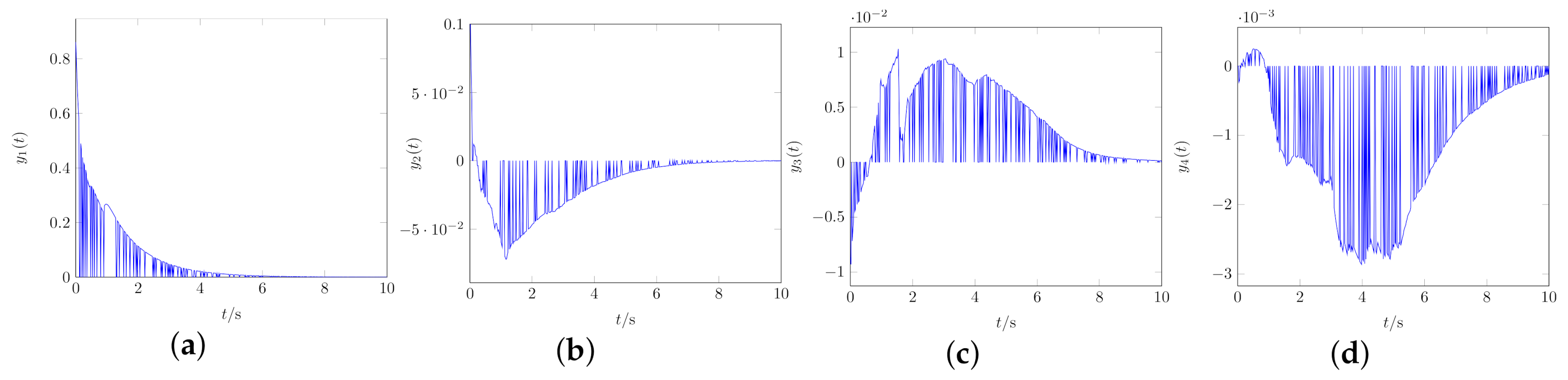
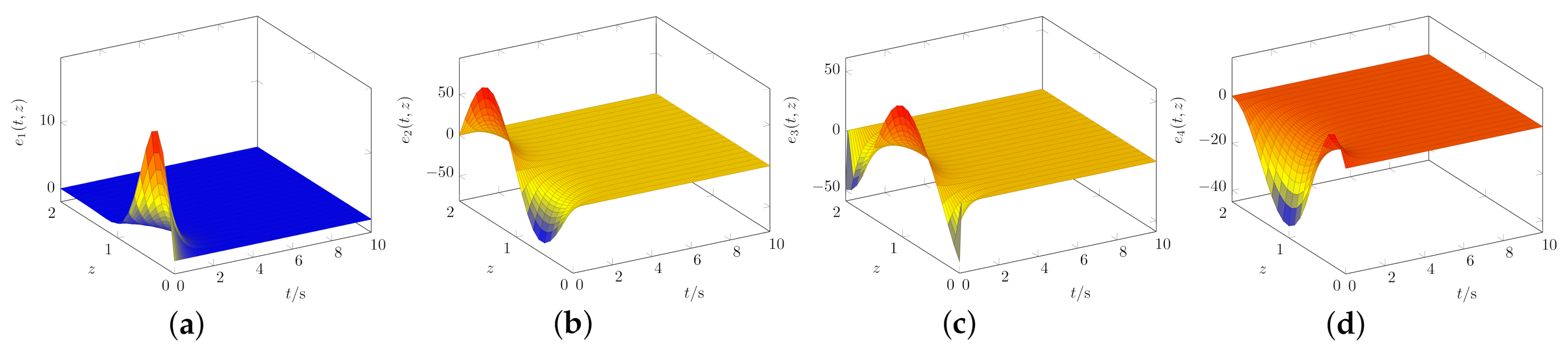
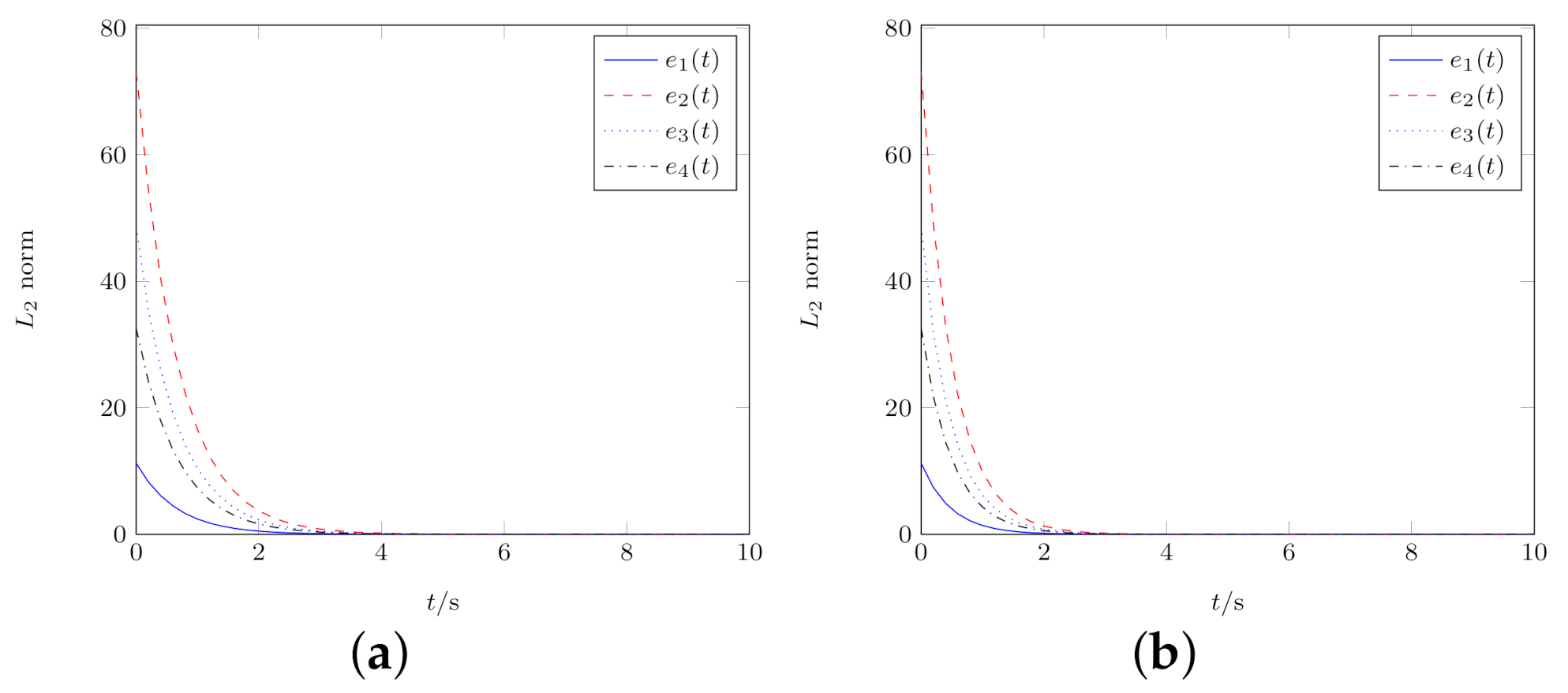
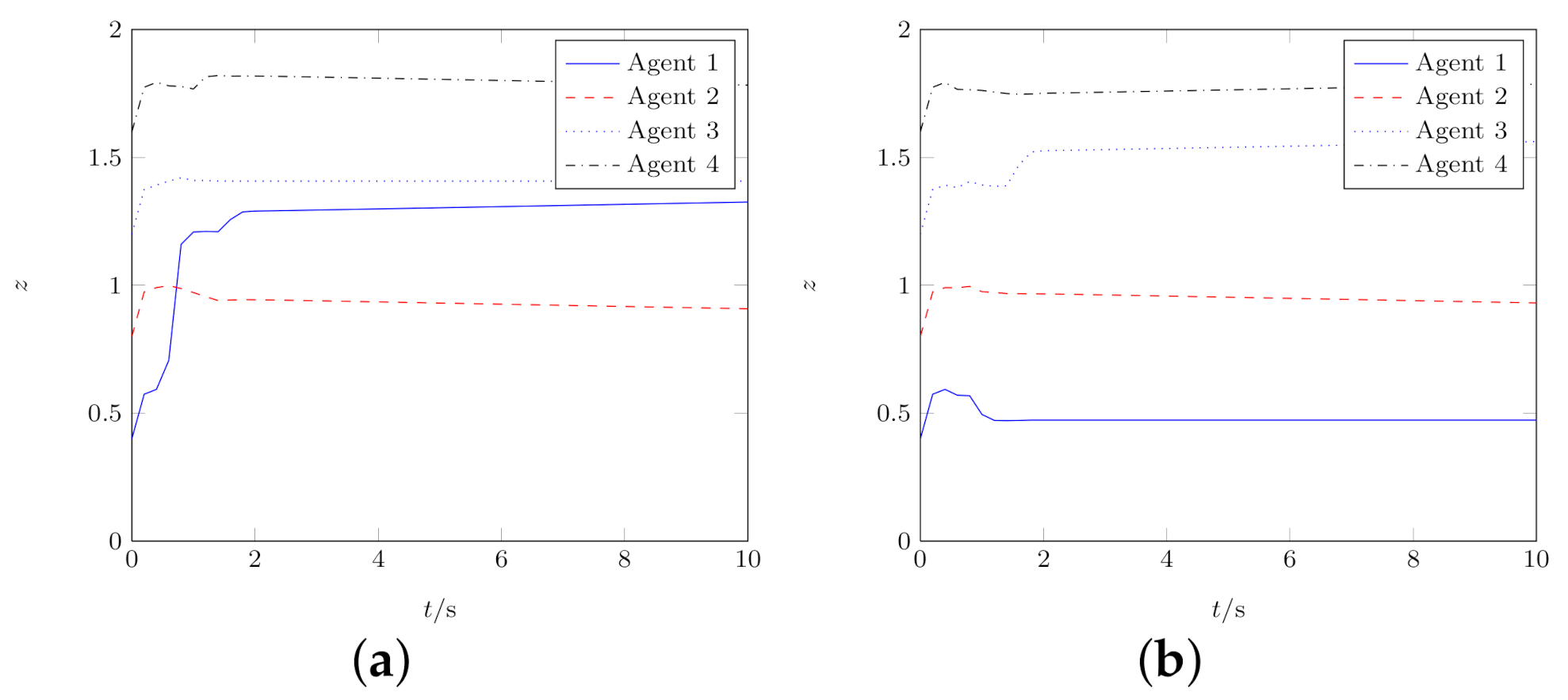
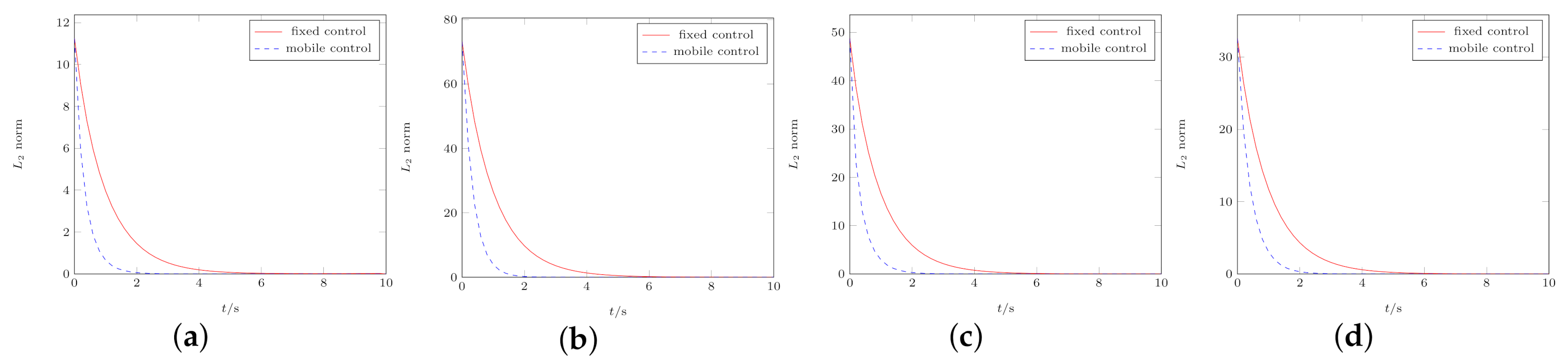
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stafrace, S.K.; Antonopoulos, N. Military tactics in agent-based sinkhole attack detection for wireless ad hoc networks. Comput. Commun. 2010, 33, 619–638. [Google Scholar] [CrossRef]
- Rehman, A.; Abbasi, A.Z.; Islam, N.; Shaikh, Z.A. A review of wireless sensors and networks applications in agriculture. Comput. Stand. Interfaces 2014, 36, 263–270. [Google Scholar] [CrossRef]
- Aalsalem, M.Y.; Khan, W.Z.; Gharibi, W.; Khan, M.K.; Arshad, Q. Wireless Sensor Networks in oil and gas industry: Recent advances, taxonomy, requirements, and open challenges. J. Netw. Comput. Appl. 2018, 113, 87–97. [Google Scholar] [CrossRef]
- Wu, H.F.; Xian, J.F.; Wang, J.; Khandge, S.; Mohapatra, P. Missing data recovery using reconstruction in ocean wireless sensor networks. Comput. Commun. 2018, 132, 1–9. [Google Scholar] [CrossRef]
- Jenabzadeh, A.; Safarinejadian, B.; Binazadeh, T. Distributed tracking control of multiple nonholonomic mobile agents with input delay. Trans. Inst. Meas. Control 2018, 41, 805–815. [Google Scholar] [CrossRef]
- Safarinejadian, B.; Kianpour, N.; Asad, M. State estimation in fractional-order systems with coloured measurement noise. Trans. Inst. Meas. Control 2017, 40, 1819–1835. [Google Scholar] [CrossRef]
- Bounoua, W.; Benkara, A.B.; Kouadri, A.; Bakdi, A. Online monitoring scheme using principal component analysis through Kullback-Leibler divergence analysis technique for fault detection. Trans. Inst. Meas. Control 2019, 42, 1225–1238. [Google Scholar] [CrossRef]
- Bu, X.H.; Tian, S.P.; Cui, L.Z.; Yang, J.Q. Stability and stabilization of 2-D Roesser systems with time-varying delays subject to missing measurements. Trans. Inst. Meas. Control 2017, 40, 1999–2010. [Google Scholar]
- Ali, K.; Tahir, M. Maximum likelihood-based robust state estimation over a horizon length during measurement outliers. Trans. Inst. Meas. Control 2020. [Google Scholar] [CrossRef]
- Lin, J.X.; Jiang, G.P.; Gao, Z.F.; Rong, L.N. State and input simultaneous estimation for discrete-time switched singular delay systems with missing measurements. Int. J. Robust Nonlinear Control 2016, 27, 2749–2772. [Google Scholar] [CrossRef]
- Song, X.; Zheng, W.X. Linear estimation for discrete-time periodic systems with unknown measurement input and missing measurements. ISA Trans. 2019, 95, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Li, L.; Su, X. Finite-region dissipative dynamic output feedback control for 2-D FM systems with missing measurements. Inf. Sci. 2020, 514, 1–14. [Google Scholar] [CrossRef]
- Liu, W.; Tao, G.; Shen, C. Robust measurement fusion steady-state estimator design for multisensor networked systems with random two-step transmission delays and missing measurements. Math. Comput. Simul. 2021, 181, 242–283. [Google Scholar] [CrossRef]
- Behrooz, H.A.; Boozarjomehry, R.B. Distributed and decentralized state estimation in gas networks as distributed parameter systems. ISA Trans. 2015, 58, 552–566. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xue, A. Adaptive event-triggered H∞ filtering for discrete-time delayed neural networks with randomly occurring missing measurements. Signal Process. 2018, 153, 221–230. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, S.; Liu, F. Identification of jump Markov autoregressive exogenous systems with missing measurements. J. Frankl. Inst. 2020, 357, 3498–3523. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, S.; Li, G.; Xia, J.; Qi, X.; Gao, B. Distributed recursive filtering for multi-sensor networked systems with multi-step sensor delays, missing measurements and correlated noise. Signal Process. 2021, 181, 107868. [Google Scholar] [CrossRef]
- Liang, J.L.; Wang, Z.Z.; Liu, X.H. Distributed State Estimation for Discrete-Time Sensor Networks With Randomly Varying Nonlinearities and Missing Measurements. IEEE Trans. Neural Netw. 2011, 22, 486–496. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.D.; Ding, D.R.; Liu, X.H. H∞state estimation for discrete-time delayed neural networks with randomly occurring quantizations and missing measurements. Neurocomputing 2015, 148, 388–396. [Google Scholar] [CrossRef]
- Shu, H.S.; Zhang, S.J.; Shen, B.; Liu, Y. Unknown input and state estimation for linear discrete-time systems with missing measurements and correlated noises. Int. J. Gen. Syst. 2016, 45, 648–661. [Google Scholar] [CrossRef]
- Wang, Z.G.; Chen, D.Y.; Du, J.H. Distributed variance-constrained robust filtering with randomly occurring nonlinearities and missing measurements over sensor networks. Neurocomputing 2019, 329, 397–406. [Google Scholar] [CrossRef]
- Zhang, H.X.; Hu, J.; Liu, H.J.; Yu, X.Y.; Liu, F.Q. Recursive state estimation for time-varying complex networks subject to missing measurements and stochastic inner coupling under random access protocol. Neurocomputing 2019, 346, 48–57. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Z.; Liu, G.P.; Jia, C.; Williams, J. Event-triggered recursive state estimation for dynamical networks under randomly switching topologies and multiple missing measurements. Automatica 2020, 115, 108908. [Google Scholar] [CrossRef]
- Ran, C.J.; Deng, Z.L. Robust fusion Kalman estimators for networked mixed uncertain systems with random one-step measurement delays, missing measurements, multiplicative noises and uncertain noise variances. Inf. Sci. 2020, 534, 27–52. [Google Scholar] [CrossRef]
- Bolic, M.; Djuric, P.; Hong, S. Resampling algorithms and architectures for distributed particle filters. IEEE Trans. Signal Process. 2005, 53, 2442–2450. [Google Scholar] [CrossRef]
- Read, J.; Achutegui, K.; Míguez, J. A distributed particle filter for nonlinear tracking in wireless sensor networks. Signal Process. 2014, 98, 121–134. [Google Scholar] [CrossRef]
- Míguez, J.; Vázquez, M.A. A proof of uniform convergence over time for a distributed particle filter. Signal Process. 2016, 122, 152–163. [Google Scholar] [CrossRef]
- Martino, L.; Elvira, V. Compressed Monte Carlo with application in particle filtering. Inf. Sci. 2021, 553, 331–352. [Google Scholar] [CrossRef]
- Dai, X.S.; Tu, X.M.; Zhao, Y.; Tan, G.X.; Zhou, X.Y. Iterative learning control for MIMO parabolic partial difference systems with time delay. Adv. Differ. Equ. 2018, 2018, 344. [Google Scholar] [CrossRef]
- Dai, X.S.; Mei, S.G.; Tian, S.P.; Yu, L. D-type iterative learning control for a class of parabolic partial difference systems. Trans. Inst. Meas. Control 2018, 40, 3105–3114. [Google Scholar] [CrossRef]
- Dai, X.S.; Wang, C.; Tian, S.P.; Huang, Q.N. Consensus control via iterative learning for distributed parameter models multi-agent systems with time-delay. J. Frankl. Inst. 2019, 356, 5240–5259. [Google Scholar] [CrossRef]
- Patan, M.; Uciński, D. Configuration of sensor network with uncertain location of nodes for parameter estimation in distributed parameter systems. IFAC Proc. Vol. 2009, 42, 31–36. [Google Scholar] [CrossRef]
- Studener, S.; Habaieb, K.; Lohmann, B.; Wolf, R. Estimation of process parameters on a moving horizon for a class of distributed parameter systems. J. Process Control 2010, 20, 58–62. [Google Scholar] [CrossRef]
- Cai, J.; Ferdowsi, H.; Sarangapani, J. Model-based fault detection, estimation, and prediction for a class of linear distributed parameter systems. Automatica 2016, 66, 122–131. [Google Scholar] [CrossRef]
- Hu, W.; Wen, G.; Rahmani, A.; Yu, Y. Parameters estimation using mABC algorithm applied to distributed tracking control of unknown nonlinear fractional-order multi-agent systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104933. [Google Scholar] [CrossRef]
- Dash, M.; Panigrahi, T.; Sharma, R. Distributed parameter estimation of IIR system using diffusion particle swarm optimization algorithm. J. King Saud Univ. Eng. Sci. 2019, 31, 345–354. [Google Scholar] [CrossRef]
- Demetriou, M.A.; Hussein, I.I. Estimation of spatially distributed processes using mobile spatially distributed sensor network. SIAM J. Control Optim. 2009, 48, 266–291. [Google Scholar] [CrossRef]
- Demetriou, M.A. Guidance of Mobile Actuator-Plus-Sensor Networks for Improved Control and Estimation of Distributed Parameter Systems. IEEE Trans. Autom. Control 2010, 55, 1570–1584. [Google Scholar] [CrossRef]
- Demetriou, M.A.; Ucinski, D. State estimation of spatially distributed processes using mobile sensing agents. In Proceedings of the 2011 American Control Conference, Orlando, FL, USA, 12–15 December 2011; IEEE: San Francisco, CA, USA, 2011; pp. 1770–1776. [Google Scholar]
- Demetriou, M.A. Guidance of a moving sensor used in state estimation of a flexible beam. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; IEEE: Los Angeles, CA, USA, 2014; pp. 557–562. [Google Scholar]
- Egorova, T.; Demetriou, M.A.; Gatsonis, N.A. Estimation of a gaseous release into the atmosphere using an unmanned aerial vehicle. In Proceedings of the 2015 European Control Conference, Linz, Austria, 15–17 July 2015; IEEE: Linz, Austria, 2015; pp. 873–878. [Google Scholar]
- Mu, W.Y.; Cui, B.T.; Li, W.; Jiang, Z. Improving control and estimation for distributed parameter systems utilizing mobile actuator–sensor network. ISA Trans. 2014, 53, 1087–1095. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.X.; Cui, B.T. Estimation of spatially distributed processes using mobile sensor networks with missing measurements. Chin. Phys. B 2015, 24, 113–119. [Google Scholar] [CrossRef]
- Jiang, Z.X.; Cui, B.T.; Lou, X.Y. Distributed consensus estimation for diffusion systems with missing measurements over sensor networks. Int. J. Syst. Sci. 2016, 47, 2753–2761. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Cui, B.T. Controlling a class of stochastic distributed parameter systems using mobile sensor-actuator networks with missing measurements. In Proceedings of the 2017 Chinese Automation Congress, Jinan, China, 20–22 October 2017; IEEE: Jinan, China, 2017; pp. 451–455. [Google Scholar]
- Zhang, J.Z.; Cui, B.T. Mobile observation for distributed parameter system with moving boundary over mobile sensor networks. J. Control Decis. 2019, 1–18. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Lv, G.L.; Jiang, Z.X. State estimation for parabolic PDE system with moving boundary utilizing mobile sensor networks with missing measurements. In Proceedings of the 20th Chinese Control And Decision Conference, Hefei, China, 20–21 June 2020; IEEE: Hefei, China, 2020; pp. 2262–2267. [Google Scholar]
- Zhang, J.Z.; Cui, B.T.; Zhuang, B. Improved control for distributed parameter systems with time-dependent spatial domains utilizing mobile sensor–actuator networks. Chin. Phys. B 2017, 26, 11–20. [Google Scholar] [CrossRef]
- Jiang, Z.X.; Cui, B.T.; Lou, X.Y. Improved Control of Distributed Parameter Systems with Time-Varying Delay Based on Mobile Actuator-Sensor Networks. In Proceedings of the 19th World Congress of the International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014; IEEE: Cape Town, South Africa, 2014; pp. 24–29. [Google Scholar]
- Dai, L.; Cao, Q.; Xia, Y.; Gao, Y. Distributed MPC for formation of multi-agent systems with collision avoidance and obstacle avoidance. J. Frankl. Inst. 2017, 354, 2068–2085. [Google Scholar] [CrossRef]
- Slotine, J.J.; Li, W.; Hall, P. Applied Nonlinear Control: United States Edition; Pearson Education Inc.: Prentice-Hall, NJ, USA, 1991. [Google Scholar]
Short Biography of Authors
 | Huansen Fu received his B.S. degree in Electrical Engineering and Automation in 2006 and his M.S. degree in 2008 in Power Electronics and Power Drives from Jiangnan University, Wuxi, Jiangsu, China. He is currently pursuing the Ph.D. degree in Control Theory and Control Engineering from Jiangnan University, and he is currently an associate professor of Taizhou University, Taizhou, Jiangsu, China. His interests include distributed parameter systems, intelligent automation and application, process control. |
 | Baotong Cui received his Ph.D. degree in Control Theory and Control Engineering from the College of Automation Science and Engineering, South China University of Technology, in 2003. He was a post-doctoral fellow at Shanghai Jiaotong University from July 2003 to September 2005, and a visiting scholar at Department of Electrical and Computer Engineering, National University of Singapore from August 2007 to February 2008. He is now a professor in the School of IoT Engineering, Jiangnan University. His current research interests include systems analysis, stability theory, artificial neural networks and chaos synchronization. |
 | Bo Zhuang received his B.S. degree in Computer Science and Education and his M.S. degree in Computer Science and Technology from Shandong Normal University in 1999 and 2008, respectively. He received his Ph.D. degree in Control Theory and Control Engineering from School of IoT Engineering in 2019, Jiangnan University, Wuxi, Jiangsu, China. His current research interests include distributed parameter systems, and multi-agent systems. |
 | Jianzhong Zhang received the B.S. and M.S. degrees in Mathematics in 2005 and 2008 from Shandong University of Science and Technology, Tsingtao, Shandong, China, and the Ph.D. degree in Control Science and Engineering in 2019 from Jiangnan University, Wuxi, Jiangsu, China. He is currently a lecturer in School of Mathematics and Statistics, Taishan University. His current research interests include distributed parameter systems, networked control systems, mobile control and stability theory. |


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.; Cui, B.; Zhuang, B.; Zhang, J. State Estimation for a Class of Distributed Parameter Systems with Time-Varying Delay over Mobile Sensor–Actuator Networks with Missing Measurements. Mathematics 2021, 9, 661. https://doi.org/10.3390/math9060661
Fu H, Cui B, Zhuang B, Zhang J. State Estimation for a Class of Distributed Parameter Systems with Time-Varying Delay over Mobile Sensor–Actuator Networks with Missing Measurements. Mathematics. 2021; 9(6):661. https://doi.org/10.3390/math9060661
Chicago/Turabian StyleFu, Huansen, Baotong Cui, Bo Zhuang, and Jianzhong Zhang. 2021. "State Estimation for a Class of Distributed Parameter Systems with Time-Varying Delay over Mobile Sensor–Actuator Networks with Missing Measurements" Mathematics 9, no. 6: 661. https://doi.org/10.3390/math9060661
APA StyleFu, H., Cui, B., Zhuang, B., & Zhang, J. (2021). State Estimation for a Class of Distributed Parameter Systems with Time-Varying Delay over Mobile Sensor–Actuator Networks with Missing Measurements. Mathematics, 9(6), 661. https://doi.org/10.3390/math9060661





