GMM Estimation of a Partially Linear Additive Spatial Error Model

Abstract

This article presents a partially linear additive spatial error model (PLASEM) specification and its corresponding generalized method of moments (GMM). It also derives consistency and asymptotic normality of estimators for the case with a single nonparametric term and an arbitrary number of nonparametric additive terms under some regular conditions. In addition, the finite sample performance for our estimates is assessed by Monte Carlo simulations. Lastly, the proposed method is illustrated by analyzing Boston housing data.

1. Introduction

Linear regression is one of the most classic and widely used techniques in statistics. Linear regression models usually assume that the mean response is linear; however, this assumption is not always granted Fan and Gijbels [1]. A nonparametric model was proposed to more flexibly solve nonlinear problems encountered in practice. Partially linear additive regression model (PLARM) can be used to study the linear and nonlinear relationship between a response and its covariates simultaneously. Opsomer and Ruppert [2] first proposed the PLARM and presented consistent backfitting estimators for the parametric part. Manzan and Zerom [3] introduced a kernel estimator of the finite dimensional parameter in the PLARM and derived consistency and asymptotic normality of the estimators under some regular conditions. Zhou et al. [4] considered variable selection for PLARM with measurement error. Wei et al. [5] investigated the empirical likelihood method for the PLARM. Hoshino [6] proposed a two-step estimation approach of partially linear additive quantile regression model. Lou et al. [7] introduced sparse PLARM and discussed the model selection problem through convex relaxation. Liu et al. [8] presented the spline–backfitted kernel estimator of PLARM and studied statistical inference properties of the estimator. Manghi et al. [9] also discussed the statistical inference of the generalized PLARM.

The linear spatial autoregressive model, which extends the ordinary linear regression model in view of a spatially lagged term of the response variable, has been one of the most important statistical tools for modeling spatial dependence among the spatial units (Li and Mei [10]). Theories and estimation methods based on linear autoregressive models have attracted widespread attention and have been extensively studied (Anselin [11], Kelejian and Prucha [12], Elhorst [13], et al.). In the real world, highly nonlinear practice problems commonly exist between response variables and regressors, especially for spatial data. Su and Jin [14] investigated profile quasi-maximum likelihood estimation of a partially linear spatial autoregressive model. Su [15] proposed generalized method of moments (GMM) estimation of nonparametric spatial autoregressive (SAR) model, which included heteroscedasticity and spatial dependence in the error terms. Li and Mei [10] studied statistical inference of a profile quasi-maximum likelihood estimator based on the partially linear spatial autoregressive model in Su and Jin [14]. However, these models face the problem of “curse of dimensionality”, namely, their nonparametric estimation precision decreases rapidly as the dimension of explanatory variables increases. In order to overcome this drawback, some useful semiparametric SAR models with dimensional reduction functions, which include partially linear single-index, varying coefficient, and additive SAR models, have been developed in recent years. Sun [16] studied GMM estimators of single-index SAR models and their asymptotic distributions. Cheng et al. [17] not only extended the single-index SAR model to partially linear single-index SAR models, but they also explored GMM estimation of the model and asymptotic properties of estimators. Wei and Sun [18] proposed GMM estimation of varying coefficients in the SAR model and obtained asymptotic properties of estimators. Dai et al. [19] considered a quantile regression approach for partially linear varying coefficients in the SAR model and established asymptotic properties of estimators and test statistics. Du et al. [20] presented a partially linear additive SAR model, constructed GMM estimation of the model, and proved the asymptotic properties of estimators. To our best knowledge, research on the statistical inference of partially linear additive spatial error model (PLASEM) is still lacking. In this paper, we attempt to study GMM estimation of this model and statistical properties of estimators.

The remainder of this paper is organized as follows. In Section 2, we present the PLASEM and its corresponding estimation method. In Section 3, we derive the large sample properties under some regular assumptions. Some Monte Carlo simulations are conducted in Section 4 to assess the finite sample performance of estimates. The developed method is illustrated with the Boston housing price data in Section 5. Conclusions are summarized in Section 6. The detailed proofs are given in Appendix A.

2. Model and Estimation

2.1. Model Specification

Consider the following PLASEM:

$$\left\{\begin{array}{c}{y}_{n,i}={\mathit{\beta }}^T{\mathit{x}}_{n,i}+{\displaystyle \sum _{j=1}^d}{m}_j\left(z_{n,ij}\right)+{\eta }_{n,i},\hfill \\ {\eta }_{n,i}=\lambda {\displaystyle \sum _{k=1}^n}{w}_{n,ik}{\eta }_{n,k}+{\epsilon }_{n,i},\hfill \end{array}\right.i=1,2,\cdots ,n,$$

(1)

where $y_{n,i}$ is the ith observation of response variable $y_n$, ${\mathit{x}}_{n,i}$ is the ith observation of p dimensional exogenous regressor ${\mathit{x}}_n$, $z_{n,ij}$ is the jth observation of exogenous regressor ${\mathit{z}}_{n,i}$, $\mathit{\beta }$ is a p dimensional linear regression coefficient, $\lambda$ is a spatial auto-correlation coefficient, $m_j(·)(j=1,2,\cdots ,d)$ is an unknown smooth function, ${\eta }_{n,i}$ is regression disturbance, $w_{n,ij}$ is non-stochastic spatial weight, and the ith innovation ${\epsilon }_{n,i}$ is independent with E$\left(e_{n,i}\right)=0$ and E${\left(e_{n,i}\right)}^2={\sigma }^2$. Furthermore, we assume E$\left(m_j\left(z_{n,ij}\right)\right)=0(j=1,2,\cdots ,d)$ for identification purposes. Denote ${\mathit{Y}}_n={(y_{n,1},y_{n,2},\cdots ,y_{n,n})}^T$, and similarly for ${\mathit{X}}_n$, ${\mathit{\eta }}_n$ and ${\mathit{\epsilon }}_n$. We write the spatial weight matrix and the vectors of additive functions as ${\mathit{W}}_n={\left(w_{n,ij}\right)}_{1\le i,j\le n}$ and ${\mathit{m}}_j={\left(m_j\left(z_{n,1j}\right),m_j\left(z_{n,2j}\right),\cdots ,m_j\left(z_{n,nj}\right)\right)}^T$ respectively. In matrix notation, Model (1) can be rewritten as

$$\left\{\begin{array}{c}{\mathit{Y}}_n={\mathit{X}}_n\mathit{\beta }+{\mathit{m}}_1+{\mathit{m}}_2+\cdots +{\mathit{m}}_d+{\mathit{\eta }}_n,\hfill \\ {\mathit{\eta }}_n=\lambda {\mathit{W}}_n{\mathit{\eta }}_n+{\mathit{\epsilon }}_n.\hfill \end{array}\right.$$

(2)

2.2. Estimation Procedures

We first study the simple case with $d=1$, so Model (2) under consideration is

$$\left\{\begin{array}{c}{\mathit{Y}}_n={\mathit{X}}_n\mathit{\beta }+\mathit{m}+{\mathit{\eta }}_n,\hfill \\ {\mathit{\eta }}_n=\lambda {\mathit{W}}_n{\mathit{\eta }}_n+{\mathit{\epsilon }}_n,\hfill \end{array}\right.$$

(3)

where $\mathit{m}={\left(m\left(z_{n,1}\right),\cdots ,m\left(z_{n,n}\right)\right)}^T$. The specific estimation procedures are as follows:

• Step 1. The initial estimation of unknown function $m(·)$. Following the idea of “working independence” in Lin and Carroll, [21], the correlation structure of ${\mathit{\eta }}_n$ can be ignored when we estimate $m(·)$. Next, a local linear estimation method is used to fit unknown function $m(·)$. Let ${\mathit{s}}_z$ represent the equivalent kernels for the local linear regression at z, it can be written as ${\mathit{s}}_z={\mathit{e}}_1^T{\left({\mathit{Z}}^T\mathit{K}\mathit{Z}\right)}^{-1}{\mathit{Z}}^T\mathit{K}$, where ${\mathit{e}}_1={(1,0)}^T$, $\mathit{Z}={\left(\begin{array}{ccc}1& \cdots & 1\\ \frac{z_{n,1}-z}{h}& \cdots & \frac{z_{n,n}-z}{h}\end{array}\right)}^T$, $\mathit{K}=\mathrm{diag}\left\{k_h(z_{n,1}-z),\cdots ,k_h(z_{n,n}-z)\right\}$ with $k_h(·)=\frac{1}{h}k(·/h)$ for kernel function $k(·)$ and bandwidth h. Thus, we can obtain the initial estimator of $m(·)$:

  $$\tilde{m}\left(z\right)={\mathit{s}}_z\left({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }\right).$$
  Let $\mathit{S}={\left({\mathit{s}}_{z,1}^T,\cdots ,{\mathit{s}}_{z,n}^T\right)}^T$ be the smoother matrix whose rows are the equivalent kernels; we have

  $$\tilde{\mathit{m}}=\mathit{S}\left({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }\right).$$

  (4)
• Step 2. The initial GMM estimation of $\mathit{\beta }$. Let ${\mathit{H}}_n={({\mathit{h}}_{n,1},\cdots ,{\mathit{h}}_{n,n})}^T$ be an $n\times r(r\ge p+1)$ matrix of instrumental variables, where ${\mathit{h}}_{n,i}={(h_{n,i1},h_{n,i2},\cdots ,h_{n,ir})}^T$, and we have the moment conditions E$\left({\mathit{H}}_n^T{\mathit{\eta }}_n\right)=0$. Now we replace $\mathit{m}$ in Model (3) by $\tilde{\mathit{m}}$ and get the corresponding moment functions:

  $$l_n\left(\mathit{\beta }\right)={\mathit{H}}_n^T\left({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }-\tilde{\mathit{m}}\right)={\mathit{H}}_n^T\left({\tilde{\mathit{Y}}}_n-{\tilde{\mathit{X}}}_n\mathit{\beta }\right),$$

  where ${\tilde{\mathit{Y}}}_n=({\mathit{I}}_n-\mathit{S}){\mathit{Y}}_n$, ${\tilde{\mathit{X}}}_n=({\mathit{I}}_n-\mathit{S}){\mathit{X}}_n$. Let ${\mathit{A}}_r$ be a $r\times r$ positive definite constant matrix, we can choose initial estimator of $\mathit{\beta }$ by minimizing object function

  $$\begin{array}{c}\hfill Q_n\left(\mathit{\beta }\right)=l_n^T\left(\mathit{\beta }\right){\mathit{A}}_r{l}_n\left(\mathit{\beta }\right)={\left({\tilde{\mathit{Y}}}_n-{\tilde{\mathit{X}}}_n\mathit{\beta }\right)}^T{\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T\left({\tilde{\mathit{Y}}}_n-{\tilde{\mathit{X}}}_n\mathit{\beta }\right),\end{array}$$
  It is easy to see that

  $$\tilde{\mathit{\beta }}=\arg \underset{\mathit{\beta }}{min}{Q}_n\left(\mathit{\beta }\right)={\left({\tilde{\mathit{X}}}_n^T{\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T{\tilde{\mathit{X}}}_n\right)}^{-1}{\tilde{\mathit{X}}}_n^T{\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T{\tilde{\mathit{Y}}}_n.$$
• Step 3. The estimation of parameters $\lambda$ and ${\sigma }^2$. For notational convenience, let ${\overline{\mathit{\eta }}}_n={\mathit{W}}_n{\mathit{\eta }}_n$, ${\stackrel{=}{\mathit{\eta }}}_n={\mathit{W}}_n^2{\mathit{\eta }}_n$, ${\overline{\mathit{\epsilon }}}_n={\mathit{W}}_n{\mathit{\epsilon }}_n$, similarly, we have ${\mathit{\eta }}_n=\lambda {\overline{\mathit{\eta }}}_n+{\mathit{\epsilon }}_n$ and ${\overline{\mathit{\eta }}}_n=\lambda {\stackrel{=}{\mathit{\eta }}}_n+{\overline{\mathit{\epsilon }}}_n$, where ${\overline{\eta }}_{n,i}$, ${\stackrel{=}{\eta }}_{n,i}$, ${\overline{\epsilon }}_{n,i}$ are the ith element of ${\overline{\mathit{\eta }}}_n$, ${\stackrel{=}{\mathit{\eta }}}_n$, ${\overline{\mathit{\epsilon }}}_n$ respectively. Therefore, we get the following equations

  $$\begin{array}{c}\hfill {\eta }_{n,i}-\lambda {\overline{\eta }}_{n,i}={\epsilon }_{n,i},\end{array}$$

  (5)

  $$\begin{array}{c}\hfill {\overline{\eta }}_{n,i}-\lambda {\overline{\overline{\eta }}}_{n,i}={\overline{\epsilon }}_{n,i}.\end{array}$$

  (6)
  By squaring (5) and then summing, squaring (6) and summing, multiplying (5) by (6), and summing, we obtain the following equations:

  $$\begin{array}{cc}\hfill & \frac{1}{n}\sum _{i=1}^n{\eta }_{n,i}^2=\frac{2\lambda }{n}\sum _{i=1}^n{\eta }_{n,i}{\overline{\eta }}_{n,i}-\frac{{\lambda }^2}{n}\sum _{i=1}^n{\overline{\eta }}_{n,i}^2+\frac{1}{n}\sum _{i=1}^n{\epsilon }_{n,i}^2,\hfill \\ \hfill & \frac{1}{n}\sum _{i=1}^n{\overline{\eta }}_{n,i}^2=\frac{2\lambda }{n}\sum _{i=1}^n{\overline{\eta }}_{n,i}{\overline{\overline{\eta }}}_{n,i}-\frac{{\lambda }^2}{n}\sum _{i=1}^n{\overline{\overline{\eta }}}_{n,i}^2+\frac{1}{n}\sum _{i=1}^n{\overline{\epsilon }}_{n,i}^2,\hfill \\ \hfill & \frac{1}{n}\sum _{i=1}^n{\eta }_{n,i}{\overline{\eta }}_{n,i}=\frac{\lambda }{n}\sum _{i=1}^n({\eta }_{n,i}{\overline{\overline{\eta }}}_{n,i}+{\overline{\eta }}_{n,i}^2)-\frac{{\lambda }^2}{n}\sum _{i=1}^n{\overline{\eta }}_{n,i}{\overline{\overline{\eta }}}_{n,i}+\frac{1}{n}\sum _{i=1}^n{\epsilon }_{n,i}{\overline{\epsilon }}_{n,i}.\hfill \end{array}$$

  (7)
  Assumption 2 implies $\mathrm{E}(\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\epsilon }_{n,i}^2)={\sigma }^2$, noting that $\mathrm{E}(\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\epsilon }_{n,i}{\overline{\epsilon }}_{n,i})=0$ and $\mathrm{E}(\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\overline{\epsilon }}_{n,i}^2)=\frac{{\sigma }^2}{n}\mathrm{tr}\left({\mathit{W}}_n^T{\mathit{W}}_n\right)$, where $\mathrm{tr}(·)$ denotes the trace operator, let $\mathit{\theta }={(\lambda ,{\lambda }^2,{\sigma }^2)}^T$, taking the expectations of Equation (7), we have

  $${\mathrm{\Gamma }}_n\mathit{\theta }={\mathit{\gamma }}_n,$$

  (8)

  where ${\mathrm{\Gamma }}_n=\frac{1}{n}\left(\begin{array}{ccc}2\mathrm{E}\left({\mathit{\eta }}_n^T{\overline{\mathit{\eta }}}_n\right)& -\mathrm{E}\left({\overline{\mathit{\eta }}}_n^T{\overline{\mathit{\eta }}}_n\right)& 1\\ 2\mathrm{E}\left({\overline{\mathit{\eta }}}_n^T{\stackrel{=}{\mathit{\eta }}}_n\right)& -\mathrm{E}\left({\stackrel{=}{\mathit{\eta }}}_n^T{\stackrel{=}{\mathit{\eta }}}_n\right)& \mathrm{tr}\left({\mathit{W}}_n^T{\mathit{W}}_n\right)\\ \mathrm{E}({\mathit{\eta }}_n^T{\stackrel{=}{\mathit{\eta }}}_n+{\overline{\mathit{\eta }}}_n^T{\overline{\mathit{\eta }}}_n)& -\mathrm{E}\left({\overline{\mathit{\eta }}}_n^T{\stackrel{=}{\mathit{\eta }}}_n\right)& 0\end{array}\right)$, ${\mathit{\gamma }}_n=\frac{1}{n}\left(\begin{array}{c}\mathrm{E}\left({\mathit{\eta }}_n^T{\mathit{\eta }}_n\right)\\ \mathrm{E}\left({\overline{\mathit{\eta }}}_n^T{\overline{\mathit{\eta }}}_n\right)\\ \mathrm{E}\left({\mathit{\eta }}_n^T{\overline{\mathit{\eta }}}_n\right)\end{array}\right)$.
  If ${\mathrm{\Gamma }}_n$ and ${\mathit{\gamma }}_n$ are known, Equations (7) implies that (8) determines estimator of $\mathit{\theta }$ as

  $$\widehat{\mathit{\theta }}={\mathrm{\Gamma }}_n^{-1}{\mathit{\gamma }}_n.$$

  (9)
  In general, ${\mathrm{\Gamma }}_n$ and ${\mathit{\gamma }}_n$ are unknown, we present the estimator of $\mathit{\theta }$ by the two-stage estimation in Kelejian and Prucha [12]. Let ${\widetilde{\overline{\mathit{\eta }}}}_n={\mathit{W}}_n{\tilde{\mathit{\eta }}}_n$ and ${\widetilde{\stackrel{=}{\mathit{\eta }}}}_n={\mathit{W}}_n^2{\tilde{\mathit{\eta }}}_n$, where ${\tilde{\mathit{\eta }}}_n={\tilde{\mathit{Y}}}_n-{\tilde{\mathit{X}}}_n\tilde{\mathit{\beta }}$ is obtained from ${\tilde{\mathit{\eta }}}_n$ in the second step, and denote ${\tilde{\eta }}_{n,i}$, ${\tilde{\overline{\eta }}}_{n,i}$, ${\widetilde{\overline{\overline{\eta }}}}_{n,i}$ as the ith element of ${\tilde{\mathit{\eta }}}_n$, ${\widetilde{\overline{\mathit{\eta }}}}_n$, ${\widetilde{\stackrel{=}{\mathit{\eta }}}}_n$ respectively. Thus, the estimators of ${\mathrm{\Gamma }}_n$ and ${\mathit{\gamma }}_n$ can be obtained respectively as follows:
  ${\mathit{G}}_n=\frac{1}{n}\left(\begin{array}{ccc}2{\displaystyle \sum _{i=1}^n}{\tilde{\eta }}_{n,i}{\tilde{\overline{\eta }}}_{n,i}& -{\displaystyle \sum _{i=1}^n}{\tilde{\overline{\eta }}}_{n,i}^2& 1\\ 2{\displaystyle \sum _{i=1}^n}{\tilde{\overline{\eta }}}_{n,i}{\widetilde{\overline{\overline{\eta }}}}_{n,i}& -{\displaystyle \sum _{i=1}^n}{\widetilde{\overline{\overline{\eta }}}}_{n,i}^2& \mathrm{tr}\left({\mathit{W}}_n^T{\mathit{W}}_n\right)\\ {\displaystyle \sum _{i=1}^n}({\tilde{\eta }}_{n,i}{\widetilde{\overline{\overline{\eta }}}}_{n,i}+{\tilde{\overline{\eta }}}_{n,i}^2)& -{\displaystyle \sum _{i=1}^n}{\tilde{\overline{\eta }}}_{n,i}{\widetilde{\overline{\overline{\eta }}}}_{n,i}& 0\end{array}\right)$, ${\mathit{g}}_n=\frac{1}{n}\left(\begin{array}{c}{\displaystyle \sum _{i=1}^n}{\tilde{\eta }}_{n,i}^2\\ {\displaystyle \sum _{i=1}^n}{\tilde{\overline{\eta }}}_{n,i}^2\\ {\displaystyle \sum _{i=1}^n}{\tilde{\eta }}_{n,i}{\tilde{\overline{\eta }}}_{n,i}\end{array}\right)$.
  Then, the empirical form of Formula (8) is

  $${\mathit{g}}_n={\mathit{G}}_n\mathit{\theta }+{\mathit{v}}_n,$$

  (10)

  where ${\mathit{v}}_n$ can be viewed as a vector of regression residuals. It follows from Formula (9) that the empirical estimator of $\mathit{\theta }$ can be given by

  $$\widehat{\mathit{\theta }}={\mathit{G}}_n^{-1}{\mathit{g}}_n.$$

  (11)
  Based on Formula (10), the nonlinear least square estimator can also be defined by Kelejian and Prucha [12]

  $$\begin{array}{c}\hfill \tilde{\mathit{\theta }}=\arg \underset{\mathit{\theta }}{min}{\left({\mathit{g}}_n-{\mathit{G}}_n\mathit{\theta }\right)}^T\left({\mathit{g}}_n-{\mathit{G}}_n\mathit{\theta }\right)={\left({\mathit{G}}_n^T{\mathit{G}}_n\right)}^{-1}{\mathit{G}}_n^T{\mathit{g}}_n.\end{array}$$

  (12)
  Kelejian and Prucha [12] proved that both $\widehat{\mathit{\theta }}$ and $\tilde{\mathit{\theta }}$ are consistent estimators of $\mathit{\theta }$. Hence, it does not matter which one is chosen as the estimator of $\mathit{\theta }$. In the following study, we need only consider $\tilde{\mathit{\theta }}$ as an estimator of $\mathit{\theta }$.
• Step 4. The final estimation of $\mathit{\beta }$ and $\mathit{m}$. Applying a Cochrane–Orcutt type transformation to Model (3) yields

  $${\mathit{Y}}_n^{*}={\mathit{X}}_n^{*}\mathit{\beta }+{\mathit{\epsilon }}_n,$$

  where ${\mathit{Y}}_n^{*}={\tilde{\mathit{Y}}}_n-\lambda {\mathit{W}}_n{\tilde{\mathit{Y}}}_n$ and ${\mathit{X}}_n^{*}={\tilde{\mathit{X}}}_n-\lambda {\mathit{W}}_n{\tilde{\mathit{X}}}_n$. Therefore, we get the final estimator of $\mathit{\beta }$ as follows:

  $$\widehat{\mathit{\beta }}={\left({\mathit{X}}_n^{*T}(\tilde{\lambda }){\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T{\mathit{X}}_n^{*}(\tilde{\lambda })\right)}^{-1}{\mathit{X}}_n^{*T}(\tilde{\lambda }){\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T{\mathit{Y}}_n^{*}(\tilde{\lambda }),$$

  (13)

  where ${\mathit{X}}_n^{*}(\tilde{\lambda })={\tilde{\mathit{X}}}_n-\tilde{\lambda }{\mathit{W}}_n{\tilde{\mathit{X}}}_n$ and ${\mathit{Y}}_n^{*}(\tilde{\lambda })={\tilde{\mathit{Y}}}_n-\tilde{\lambda }{\mathit{W}}_n{\tilde{\mathit{Y}}}_n$.
  Finally, we replace $\mathit{\beta }$ in Formula (4) by $\widehat{\mathit{\beta }}$ and obtain the final estimator of $\mathit{m}$ as

  $$\widehat{\mathit{m}}=\mathit{S}({\mathit{Y}}_n-{\mathit{X}}_n\widehat{\mathit{\beta }}).$$

Now, let us discuss the case $d>1$. We estimate unknown functions by the popular “backfitting” method (Buja et al. [22], Härdle and Hall, [23]), and estimation of unknown parameters is similar to the case $d=1$. The detailed steps are described as follows:

• Step 1. The initial estimation of $m_j,j\in \{1,\cdots ,d\}$ is fixed. Suppose that $\mathit{\beta }$ and ${\mathit{m}}_i(i\ne j)$ are given, for any given $z_j$, we can fit unknown function $m_j\left(z_{n,ij}\right)$ and its derivative $m_j^{\prime }\left(z_{n,ij}\right)$ by using local linear estimation method:

  $$\left(\begin{array}{c}{\tilde{m}}_j\left(z_j\right)\\ h{\tilde{m}}_j^{\prime }\left(z_j\right)\end{array}\right)={\left({\mathit{Z}}_j^T{\mathit{K}}_j{\mathit{Z}}_j\right)}^{-1}{\mathit{Z}}_j^T{\mathit{K}}_j({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }-\sum _{k\ne j}{\mathit{m}}_k),$$

  where ${\mathit{Z}}_j={\left(\begin{array}{ccc}1& \cdots & 1\\ \frac{z_{n,1j}-z_j}{h_j}& \cdots & \frac{z_{n,nj}-z_j}{h_j}\end{array}\right)}^T$ and ${\mathit{K}}_j=\mathrm{diag}\left\{k_{h_j}(z_{n,1j}-z_j),\cdots ,k_{h_j}(z_{n,nj}-z_j)\right\}$. Let ${\mathit{s}}_{j,z_j}={\mathit{e}}_1^T{\left({\mathit{Z}}_j^T{\mathit{K}}_j{\mathit{Z}}_j\right)}^{-1}{\mathit{Z}}_j^T{\mathit{K}}_j$, then ${\mathit{S}}_j={({\mathit{s}}_{j,z_{n,1j}}^T,\cdots ,{\mathit{s}}_{j,z_{n,nj}}^T)}^T$ represents the smoother matrix for the local linear regression at observation $z_j$. Like Opsomer and Ruppert [2], the smoother matrix ${\mathit{S}}_j$ is replaced by ${\mathit{S}}_j^{*}=({\mathit{I}}_n-\mathbf{1}{\mathbf{1}}^T/n){\mathit{S}}_j$, where ${\mathit{I}}_n$ is an $n\times n$ unit matrix and $\mathbf{1}={(1,1,\cdots ,1)}^T$. Therefore, we get

  $${\tilde{\mathit{m}}}_j={\mathit{S}}_j^{*}({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }-\sum _{k\ne j}{\mathit{m}}_k).$$
• Step 2. The initial estimation of $m_k\left(z_{n,ik}\right)$ ($k\ne j$). Based on backfitting algorithm, we choose the common Gauss–Seidel iteration, it schemes update one component at a time, based on the most recent components available Buja et al.( [22]). Let ${\tilde{\mathit{m}}}_s^{\left(l\right)}$ be estimation of the lth update for ${\mathit{m}}_s$. Therefore, we have

  $${\tilde{\mathit{m}}}_s^{\left(l\right)}={\mathit{S}}_s^{*}\left({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }-\sum _{i=1}^{s-1}{\tilde{\mathit{m}}}_i^{\left(l\right)}-\sum _{i=s+1}^d{\mathit{m}}_i^{(l-1)}\right).$$
  Iterate the above equation until convergence. Therefore, we obtain

  $${\tilde{\mathit{m}}}_j={\mathit{S}}_j^{*}\left({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }-\sum _{k\ne j}{\tilde{\mathit{m}}}_k\right),j=1,2,\cdots ,d.$$

  (14)
  Hastie and Tibshirani [24], Opsomer and Ruppert [25] proposed the backfitting estimator of ${\mathit{m}}_j$ in the bivariate additive model ${\mathit{Y}}_n=\mathit{\alpha }+{\mathit{m}}_1+{\mathit{m}}_2+\mathit{\epsilon }$. Similar to Opsomer and Ruppert [2], Opsomer [26], we can get the estimators of additive part functions by solving the following normal equations:

  $$\begin{array}{c}\hfill \left(\begin{array}{cccc}{\mathit{I}}_n& {\mathit{S}}_1^{*}& \cdots & {\mathit{S}}_1^{*}\\ {\mathit{S}}_2^{*}& {\mathit{I}}_n& \cdots & {\mathit{S}}_2^{*}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{S}}_d^{*}& {\mathit{S}}_d^{*}& \cdots & {\mathit{I}}_n\end{array}\right)\left(\begin{array}{c}{\tilde{\mathit{m}}}_1\\ {\tilde{\mathit{m}}}_2\\ ⋮\\ {\tilde{\mathit{m}}}_d\end{array}\right)=\left(\begin{array}{c}{\mathit{S}}_1^{*}({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta })\\ {\mathit{S}}_2^{*}({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta })\\ ⋮\\ {\mathit{S}}_d^{*}({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta })\end{array}\right),\end{array}$$
  Generally, if the matrix ${\mathit{M}}_n=\left(\begin{array}{cccc}{\mathit{I}}_n& {\mathit{S}}_1^{*}& \cdots & {\mathit{S}}_1^{*}\\ {\mathit{S}}_2^{*}& {\mathit{I}}_n& \cdots & {\mathit{S}}_2^{*}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{S}}_d^{*}& {\mathit{S}}_d^{*}& \cdots & {\mathit{I}}_n\end{array}\right)$ is invertible, we may write the above estimators directly as

  $$\begin{array}{c}\hfill \left(\begin{array}{c}{\tilde{\mathit{m}}}_1\\ {\tilde{\mathit{m}}}_2\\ ⋮\\ {\tilde{\mathit{m}}}_d\end{array}\right)={\mathit{M}}_n^{-1}{\mathit{C}}_n({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }),\end{array}$$

  (15)

  where ${\mathit{C}}_n=\left(\begin{array}{c}{\mathit{S}}_1^{*}\\ {\mathit{S}}_2^{*}\\ \cdots \\ {\mathit{S}}_d^{*}\end{array}\right)$. Let ${\mathit{E}}_j={({\mathbf{0}}_n,\cdots ,{\mathit{I}}_n,\cdots ,{\mathbf{0}}_n)}_{n\times nd}$ is a partitioned matrix with an $n\times n$ identity matrix as the jth “block” and zeros elsewhere. Then, we have

  $$\begin{array}{cc}\hfill {\tilde{\mathit{m}}}_j=& {\mathit{E}}_j{\mathit{M}}_n^{-1}{\mathit{C}}_n({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta })={\mathit{F}}_j({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }),\hfill \\ \hfill {\tilde{\mathit{m}}}_{+}=& \sum _{j=1}^d{\tilde{\mathit{m}}}_j=\sum _{j=1}^d{\mathit{F}}_j({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta })={\mathit{F}}_n({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }),\hfill \end{array}$$

  (16)

  where ${\mathit{F}}_j={\mathit{E}}_j{\mathit{M}}_n^{-1}{\mathit{C}}_n$ and ${\mathit{F}}_n={\displaystyle \sum _{j=1}^d}{\mathit{F}}_j$. Next, we need the $d-1$ dimensional smoother matrix ${\mathit{F}}_n^{[-j]}$, which can be derived from the data generated by the model

  $$y_{n,i}^{†}={\mathit{\beta }}_0^T{\mathit{x}}_{n,i}+\sum _{k=1}^{j-1}{m}_k\left(z_{n,ik}\right)+\sum _{k=j+1}^d{m}_k\left(z_{n,ik}\right)+{\epsilon }_{n,i}$$
  Based on Lemma 2.1 in Opsomer [26], we know that the backfitting estimators convergence to a unique solution if $\parallel {\mathit{S}}_j^{*}{\mathit{F}}_n^{[-j]}\parallel <1$ for some $j(1\le j\le d)$. In this case, ${\mathit{F}}_j$ can be rewritten as

  $${\mathit{F}}_j={\mathit{I}}_n-{\left({\mathit{I}}_n-{\mathit{S}}_j^{*}{\mathit{F}}_n^{[-j]}\right)}^{-1}({\mathit{I}}_n-{\mathit{S}}_j^{*})={\left({\mathit{I}}_n-{\mathit{S}}_j^{*}{\mathit{F}}_n^{[-j]}\right)}^{-1}{\mathit{S}}_j^{*}({\mathit{I}}_n-{\mathit{F}}_n^{[-j]}).$$
• Step 3. The initial GMM estimation of $\mathit{\beta }$. Let ${\mathit{H}}_n={({\mathit{h}}_{n,1},{\mathit{h}}_{n,2},\cdots ,{\mathit{h}}_{n,n})}^T$ be an $n\times r(r\ge p+1)$ matrix of instrumental variables (IV), ${\overline{\mathit{Y}}}_n=({\mathit{I}}_n-{\mathit{F}}_n){\mathit{Y}}_n$ and ${\overline{\mathit{X}}}_n=({\mathit{I}}_n-{\mathit{F}}_n){\mathit{X}}_n$, we have the corresponding moment functions

  $$l_n\left(\mathit{\beta }\right)={\mathit{H}}_n^T\left({\mathit{Y}}_n-{\mathit{X}}_n\mathit{\beta }-{\tilde{\mathit{m}}}_{+}\right)={\mathit{H}}_n^T\left({\overline{\mathit{Y}}}_n-{\overline{\mathit{X}}}_n\mathit{\beta }\right),$$
  Let ${\mathit{A}}_r$ be a $r\times r$ positive definite constant matrix; we can obtain the initial estimator of $\mathit{\beta }$ by minimizing

  $$\begin{array}{c}\hfill Q_n\left(\mathit{\beta }\right)=l_n^T\left(\mathit{\beta }\right){\mathit{A}}_r{l}_n\left(\mathit{\beta }\right)={\left({\overline{\mathit{Y}}}_n-{\overline{\mathit{X}}}_n\mathit{\beta }\right)}^T{\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T\left({\overline{\mathit{Y}}}_n-{\overline{\mathit{X}}}_n\mathit{\beta }\right),\end{array}$$
  It is easy to know that

  $$\tilde{\mathit{\beta }}=\arg \underset{\mathit{\beta }}{min}{Q}_n\left(\mathit{\beta }\right)={\left({\overline{\mathit{X}}}_n^T{\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T{\overline{\mathit{X}}}_n\right)}^{-1}{\overline{\mathit{X}}}_n^T{\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T{\overline{\mathit{Y}}}_n.$$
• Step 4. The estimation of parameter of $\mathit{\theta }$. Similar to Step 3 in the case $d=1$, we get the estimator of $\mathit{\theta }$ by two-stage estimation in Kelejian and Prucha [12]. Denote ${\tilde{\mathit{\eta }}}_n={\overline{\mathit{Y}}}_n-{\overline{\mathit{X}}}_n\tilde{\mathit{\beta }}$ as estimator of ${\mathit{\eta }}_n$, we have

  $$\tilde{\mathit{\theta }}={\left({\mathit{G}}_n^T{\mathit{G}}_n\right)}^{-1}{\mathit{G}}_n^T{\mathit{g}}_n.$$
• Step 5. The final estimator of $\mathit{\beta }$ and $\mathit{m}$. Applying a Cochrane–Orcutt type transformation to Model (2). Let ${\mathit{Y}}_n^{*}={\overline{\mathit{Y}}}_n-\lambda {\mathit{W}}_n{\overline{\mathit{Y}}}_n$ and ${\mathit{X}}_n^{*}={\overline{\mathit{X}}}_n-\lambda {\mathit{W}}_n{\overline{\mathit{X}}}_n$ We can get the final estimator of $\mathit{\beta }$

  $$\widehat{\mathit{\beta }}={\left({\mathit{X}}_n^{*T}\left(\tilde{\lambda }\right){\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T{\mathit{X}}_n^{*}\left(\tilde{\lambda }\right)\right)}^{-1}{\mathit{X}}_n^{*T}\left(\tilde{\lambda }\right){\mathit{H}}_n{\mathit{A}}_r{\mathit{H}}_n^T{\mathit{Y}}_n^{*}\left(\tilde{\lambda }\right),$$

  (17)

  where ${\mathit{X}}_n^{*}\left(\tilde{\lambda }\right)={\overline{\mathit{X}}}_n-\tilde{\lambda }{\mathit{W}}_n{\overline{\mathit{X}}}_n$ and ${\mathit{Y}}_n^{*}\left(\tilde{\lambda }\right)={\overline{\mathit{Y}}}_n-\tilde{\lambda }{\mathit{W}}_n{\overline{\mathit{Y}}}_n$.
  By substituting $\widehat{\mathit{\beta }}$ into the expression (16), we obtain the final estimator of ${\mathit{m}}_j$ and ${\mathit{m}}_{+}$ respectively as

  $$\begin{array}{ccc}\hfill & {\widehat{\mathit{m}}}_j={\mathit{F}}_j({\mathit{Y}}_n-{\mathit{X}}_n\widehat{\mathit{\beta }}),\hfill & \hfill {\widehat{\mathit{m}}}_{+}={\mathit{F}}_n({\mathit{Y}}_n-{\mathit{X}}_n\widehat{\mathit{\beta }}).\end{array}$$

3. Asymptotic Properties

To provide a rigorous consistency and asymptotic normality of parametric and nonparametric components, we state the following basic regular assumptions.

3.1. Assumptions

Assumption 1.

(1) 

The elements of spatial weight matrix ${\mathit{W}}_n$ are non-random, and all elements on the primary diagonal satisfy $w_{n,ii}=0$ $(i=1,2,\cdots ,n)$.

(2)

The matrix ${\mathit{I}}_n-\lambda {\mathit{W}}_n$ is nonsingular for all $\left|\lambda \right|<1$.

(3) 

The matrices ${\mathit{W}}_n$ and ${\left({\mathit{I}}_n-\lambda {\mathit{W}}_n\right)}^{-1}$ are uniformly bounded in both row and column sums in absolute value for all $\left|\lambda \right|<1$.

Assumption 2.

(1) 

The covariate ${\mathit{X}}_n$ is a non-stochastic matrix and has full row rank, and the elements of ${\mathit{X}}_n$ are uniformly bounded in absolute value.

(2) 

The column vectors of covariate ${\mathit{Z}}_n$ are i.i.d. random variables.

(3) 

The instrumental variables matrix ${\mathit{H}}_n$ is uniformly bounded in both row and column sums in absolute value.

(4) 

The innovation sequence satisfies $\mathrm{E}|{\epsilon }_{n,i}{|}^{2+\delta }=c_{\delta }<\infty$ for some small δ, where $c_{\delta }$ is a positive constant.

(5) 

The density $f(·)$ of random variable z is positive and uniformly bounded away from zero on its compact support set. Furthermore, both $f^{\prime }(·)$ and $f^{″}(·)$ are bounded on their support sets.

Assumption 3.

(1) 

The kernel function $k(·)$ is a bounded and continuous nonnegative symmetric function on its closed support set.

(2) 

Let ${\mu }_l=\int v^{l}k\left(v\right)dv$ and ${\nu }_l=\int v^l{k}^2\left(v\right)dv$, where l is a nonnegative integer.

(3) 

The second derivative of $m(·)$ exists and is bounded and continuous.

Assumption 4.

For notational simplicity, denote

(1) 

${\mathit{A}}_r=\mathit{A}+o_P\left(1\right)$, where $\mathit{A}$ is a positive semidefinite matrix.

(2) 

$\frac{1}{n}{\mathit{H}}_n^T({\mathit{I}}_n-\mathit{S}){\mathit{X}}_n={\mathit{Q}}_{HX}+o_P\left(1\right)$.

(3) 

$\frac{1}{n}{\mathit{H}}_n^T{\mathit{W}}_n({\mathit{I}}_n-\mathit{S}){\mathit{X}}_n={\mathit{Q}}_{HWX}+o_P\left(1\right)$.

(4) 

$\frac{1}{n}{\mathit{H}}_n^T{\mathit{H}}_n={\mathit{Q}}_{HH}+o_P\left(1\right)$.

(5) 

${\Sigma }_1=\underset{n\to \infty }{lim}\frac{1}{n}{\mathit{H}}_n^T({\mathit{I}}_n-\mathit{S}){({\mathit{I}}_n-{\lambda }_0{\mathit{W}}_n)}^{-1}{({\mathit{I}}_n-{\lambda }_0{\mathit{W}}_n^T)}^{-1}{({\mathit{I}}_n-\mathit{S})}^T{\mathit{H}}_n$.

Assumption 5.

As $n\to \infty$, $h\to 0$ and $n{h}^4\to \infty$, $n{h}^5\to 0$.

Assumption 6.

(1) 

The kernel function $k_j(·)$ $(j=1,2,\cdots ,d)$ is a bounded and continuous nonnegative symmetric function on its closed support set.

(2) 

Let ${\mu }_l^j=\int v^l{k}_j\left(v\right)dv$ and ${\nu }_l^j=\int v^l{k}_j^2\left(v\right)dv$ $(j=1,2,\cdots ,d)$, where l is a nonnegative integer.

(3) 

The second derivative of $m_j(·)$ $(j=1,2,\cdots ,d)$ exists and is bounded and continuous.

Assumption 7.

Denote

(1) 

$\frac{1}{n}{\mathit{H}}_n^T({\mathit{I}}_n-{\mathit{F}}_n){\mathit{X}}_n={\mathit{R}}_{HX}+o_P\left(1\right)$.

(2) 

$\frac{1}{n}{\mathit{H}}_n^T{\mathit{W}}_n({\mathit{I}}_n-{\mathit{F}}_n){\mathit{X}}_n={\mathit{R}}_{HWX}+o_P\left(1\right)$.

(3) 

$\frac{1}{n}{\mathit{H}}_n^T{\mathit{H}}_n={\mathit{Q}}_{HH}+o_P\left(1\right)$.

(4) 

${\Sigma }_2=\underset{n\to \infty }{lim}\frac{1}{n}{\mathit{H}}_n^T({\mathit{I}}_n-{\mathit{F}}_n){({\mathit{I}}_n-{\lambda }_0{\mathit{W}}_n)}^{-1}{({\mathit{I}}_n-{\lambda }_0{\mathit{W}}_n^T)}^{-1}{({\mathit{I}}_n-{\mathit{F}}_n)}^T{\mathit{H}}_n$.

Assumption 8.

As $n\to \infty$, $h_j\to 0$ and $n{h}_j^4\to \infty$, $n{h}_j^5\to 0$, $j=1,2,\cdots ,d$.

Remark 1.

Assumption 1 provides the basic features of the spatial weight matrix. In some empirical applications, it is a practice to have ${\mathit{W}}_n$ be row normalized, namely, ${\displaystyle \sum _{j=1}^n}{w}_{n,ij}=1$. Assumption 2 concerns the features of the regressors, error term, instrumental variables and density function for the model. Assumption 3 concerns the kernel function and nonparametric function for the case $d=1$. Assumptions 4–5 are necessary for the asymptotic properties of the estimator for the case $d=1$. Assumptions 6–8 are corresponding conditions of kernel functions, bandwidths and asymptotic properties of the estimator for arbitrary nonparametric additive terms.

3.2. Asymptotic Properties

In the next subsection, we first discuss the asymptotic normality of estimators for the case with a single nonparametric term. We then study the asymptotic properties of estimators for an arbitrary number of nonparametric additive terms.

Theorem 1.

Suppose that Assumptions 1–4 hold, $\mathit{\beta }$ has a consistent estimator $\tilde{\mathit{\beta }}$. Furthermore, we have

$$\sqrt{n}(\tilde{\mathit{\beta }}-\mathit{\beta })\stackrel{D}{\to }N(\mathbf{0},{\mathrm{\Omega }}_1),$$

where ${\mathrm{\Omega }}_1={\sigma }^2{\left({\mathit{Q}}_{HX}^T\mathit{A}{\mathit{Q}}_{HX}\right)}^{-1}{\mathit{Q}}_{HX}^T\mathit{A}{\Sigma }_1\mathit{A}{\mathit{Q}}_{HX}{\left({\mathit{Q}}_{HX}^T\mathit{A}{\mathit{Q}}_{HX}\right)}^{-1}$.

Theorem 2.

Suppose that Assumptions 1–5 hold, we have

$$\tilde{\mathit{\theta }}\stackrel{P}{\to }\mathit{\theta }.$$

Theorem 3.

Suppose that Assumptions 1–5 hold and ${\mathit{A}}_r={\left(\frac{1}{n}{\mathit{H}}_n^T{\mathit{H}}_n\right)}^{-1}$, we have

$$\sqrt{n}(\widehat{\mathit{\beta }}-\mathit{\beta })\stackrel{D}{\to }N(\mathbf{0},{\sigma }^2{\overline{\mathit{Q}}}^{-1}),$$

where $\overline{\mathit{Q}}={({\mathit{Q}}_{HX}-\lambda {\mathit{Q}}_{HWX})}^T{\mathit{Q}}_{HH}^{-1}({\mathit{Q}}_{HX}-\lambda {\mathit{Q}}_{HWX})$.

Theorem 4.

Suppose that Assumptions 1–5 hold, we have

$$\sqrt{nh}\left(\widehat{m}\left(z\right)-m\left(z\right)\right)\stackrel{D}{\to }N\left(0,f^{-2}\left(z\right){\mathrm{\Gamma }}_{11}\right),$$

where ${\mathrm{\Gamma }}_{11}$ is the (1,1)$th$ element of Γ and $\mathrm{\Gamma }={\mathit{Z}}^T\mathit{K}{(\mathit{I}-\lambda {\mathit{W}}_n)}^{-1}{(\mathit{I}-\lambda {\mathit{W}}_n^T)}^{-1}\mathit{K}\mathit{Z}$.

Theorem 5.

Suppose that Assumptions 1–2 and Assumptions 6–8 hold, we have

$$\sqrt{n}(\tilde{\mathit{\beta }}-\mathit{\beta })\stackrel{D}{\to }N(\mathbf{0},{\mathrm{\Omega }}_2),$$

where ${\mathrm{\Omega }}_2={\sigma }^2{\left({\mathit{R}}_{HX}^T\mathit{A}{\mathit{R}}_{HX}\right)}^{-1}{\mathit{R}}_{HX}^T\mathit{A}{\Sigma }_2\mathit{A}{\mathit{R}}_{HX}{\left({\mathit{R}}_{HX}^T\mathit{A}{\mathit{R}}_{HX}\right)}^{-1}$.

Theorem 6.

Suppose that Assumptions 1–2 and Assumptions 6–8 hold, we have

$$\tilde{\mathit{\theta }}\stackrel{P}{\to }\mathit{\theta }.$$

Theorem 7.

Suppose that Assumptions 1–2 and Assumptions 6–8 hold and ${\mathit{A}}_r={\left(\frac{1}{n}{\mathit{H}}_n^T{\mathit{H}}_n\right)}^{-1}$, we have

$$\sqrt{n}(\widehat{\mathit{\beta }}-\mathit{\beta })\stackrel{D}{\to }N(\mathbf{0},{\sigma }^2{\overline{\mathit{R}}}^{-1}),$$

where $\overline{\mathit{R}}={({\mathit{R}}_{HX}-\lambda {\mathit{R}}_{HWX})}^T{\mathit{Q}}_{HH}^{-1}({\mathit{R}}_{HX}-\lambda {\mathit{R}}_{HWX})$.

Theorem 8.

Suppose that Assumptions 1–2 and Assumptions 6–8 hold, we have

$$\begin{array}{cc}\hfill & E({\widehat{\mathit{m}}}_j-{\mathit{m}}_j)=\frac{1}{2}{h}_j^2{\mu }_2^j({\mathit{m}}_j^{″}-\mathrm{E}\left({\mathit{m}}_j^{″}\right))-{\mathit{S}}_j^{*}{\mathit{B}}_{-j}+O_P\left(\frac{1}{\sqrt{n}}\right)+o_P\left(h_j^2\right),\hfill \\ \hfill & Var({\widehat{\mathit{m}}}_j-{\mathit{m}}_j)={\sigma }^2{\mathit{F}}_j{({\mathit{I}}_n-{\lambda }_0{\mathit{W}}_n)}^{-1}{({\mathit{I}}_n-\lambda {\mathit{W}}_n^T)}^{-1}{\mathit{F}}_j^T,\hfill \end{array}$$

where ${\mathit{B}}_{-j}=({\mathit{F}}_n^{[-j]}-{\mathit{I}}_n){\mathit{m}}_{(-j)}$ with ${\mathit{m}}_{(-j)}={\mathit{m}}_1+\cdots +{\mathit{m}}_{j-1}+{\mathit{m}}_{j+1}+\cdots +{\mathit{m}}_d$.

4. Simulation Studies

In this section, we will illustrate the finite sample performance of our GMM estimators by Monte Carlo experiment results. Similar to Cheng et al. [15], we generate the spatial weight matrix according to Rook contiguity (Anselin [11], pp. 17–18). The data generating process comes from the following model:

$$\left\{\begin{array}{c}{y}_{n,i}={\displaystyle \sum _{k=1}^2}{x}_{n,ik}{\beta }_k+m_1\left(z_{n,i1}\right)+m_2\left(z_{n,i2}\right)+{\eta }_{n,i},\hfill \\ {\eta }_{n,i}=\lambda {\displaystyle \sum _{k=1}^n}{w}_{n,ik}{\eta }_{n,k}+{\epsilon }_{n,i},\hfill \end{array}\right.$$

(18)

where covariate $x_{n,ik}(k=1,2)$ is independently generated from multivariate normal distribution $N(\mathbf{0},\Sigma )$ with $\mathbf{0}={(0,0)}^T$ and $\Sigma =\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$. Covariates $z_{n,i1}$ and $z_{n,i2}$ are independently generated from uniform distributions $U(-1,1)$ and $U(0,1)$, respectively. $m_1\left(z_{n,i1}\right)$$=2sin\left(\pi z_{n,i1}\right)$ and $m_2\left(z_{n,i2}\right)=z_{n,i2}^3+3z_{n,i2}^2-2z_{n,i2}-1$. The innovations ${\epsilon }_{n,i}$ are independently generated from normal distribution $N(0,1)$. The true value $\mathit{\beta }={(1,1.5)}^T$. For comparison, three different values $\lambda =0.25$, $\lambda =0.5$ and $\lambda =0.75$, which represent from weak to strong spatial dependence of the error terms, are investigated.

For the parametric estimates, the sample mean (MEAN), the sample standard deviation (SD) and mean square error (MSE) are used as the evaluation criteria. For the nonparametric function, we use the root of average squared error (RASE, as in Fan and Wu [27]) as the evaluation criterion

$${\mathrm{RASE}}_q=\sqrt{Q^{-1}\sum _{q=1}^Q{\left({\widehat{m}}_j\left(z_q\right)-m_j\left(z_q\right)\right)}^2},q=1,2,\cdots ,Q,$$

where grid point $Q=40$ is fixed.

For bandwidth sequences, we use cross-validation to choose the optimal bandwidth. For all estimators, we use the standardized Epanechikov kernel $k\left(u\right)=\frac{3}{4}\sqrt{5}(1-\frac{1}{5}{u}^2)I(u^2\le 5)$. Furthermore, we select the instrumental variables matrix as set to ${\mathit{H}}_n=({\mathit{X}}_n,{\mathit{W}}_n{\mathit{X}}_n)$. The sample sizes under investigation are $n=49,64,81,100,225,400$. For each case, there are 500 repetitions using Matlab software.

Table 1, Table 2 and Table 3 report the finite sample performance for all estimates under three cases of spatial correlation coefficient $\lambda$, respectively. First, the biases of $\lambda$ are slightly larger when sample size $n=49$, but they decrease as sample size increases. SDs and MSEs for estimates of $\lambda$ are small for all cases and have a downward trend as sample size increases. Second, the biases, SDs and MSEs for estimates of ${\beta }_1$, ${\beta }_2$ and ${\sigma }^2$ are small for all cases and decrease as sample size increases. Third, the MEANs and SDs of 500 RASEs fairly rapidly decrease as sample size increases.

Table 1. The results of parametric estimates in Model (18) with $\lambda =0.25$.

Parameter	True Value	MEAN	SD	MSE	MEAN	SD	MSE
		$\mathit{n}=\mathbf{49}$			$\mathit{n}=\mathbf{64}$
$\lambda$	0.2500	0.2838	0.0560	0.0043	0.2837	0.0201	0.0015
${\beta }_1$	1.0000	1.0067	0.1318	0.0174	1.0020	0.1057	0.0112
${\beta }_2$	1.5000	1.4828	0.1256	0.0161	1.4996	0.1071	0.0115
${\sigma }^2$	0.0100	0.0535	0.0678	0.0065	0.0335	0.0469	0.0028
$m_1$	-	1.1696	0.7665	-	0.5390	0.4070	-
$m_2$	-	3.4316	0.4778	-	2.9212	0.3052	-
		$n=81$			$n=100$
$\lambda$	0.2500	0.2733	0.0172	0.0008	0.2730	0.0133	0.0007
${\beta }_1$	1.0000	0.9974	0.0923	0.0085	0.9934	0.0824	0.0068
${\beta }_2$	1.5000	1.4974	0.0905	0.0082	1.5025	0.0823	0.0068
${\sigma }^2$	0.0100	0.0181	0.0276	0.0008	0.0132	0.0204	0.0004
$m_1$	-	0.5216	0.4050	-	0.3775	0.2905	-
$m_2$	-	2.7251	0.2396	-	2.3652	0.1914	-
		$n=225$			$n=400$
$\lambda$	0.2500	0.2618	0.0053	0.0002	0.2614	0.0033	0.0001
${\beta }_1$	1.0000	1.0013	0.0573	0.0033	0.9979	0.0373	0.0014
${\beta }_2$	1.5000	1.5009	0.0546	0.0030	1.5026	0.0409	0.0017
${\sigma }^2$	0.0100	0.0116	0.0049	2.66E-5	0.0113	0.0035	1.39E-5
$m_1$	-	0.1673	0.1303	-	0.0858	0.0654	-
$m_2$	-	1.5636	0.0852	-	1.1394	0.0473	-

Table 2. The results of parametric estimates in Model (18) with $\lambda =0.5$.

Parameter	True Value	MEAN	SD	MSE	MEAN	SD	MSE
		$\mathit{n}=\mathbf{49}$			$\mathit{n}=\mathbf{64}$
$\lambda$	0.5000	0.5438	0.0341	0.0031	0.5366	0.0209	0.0018
${\beta }_1$	1.0000	1.0019	0.1289	0.0166	0.9948	0.1147	0.0132
${\beta }_2$	1.5000	1.5015	0.1236	0.0153	1.4997	0.1106	0.0122
${\sigma }^2$	0.0100	0.0477	0.0652	0.0057	0.0319	0.0434	0.0024
$m_1$	-	1.1397	0.7554	-	0.5453	0.4035	-
$m_2$	-	3.4167	0.4098	-	2.9159	0.3232	-
		$n=81$			$n=100$
$\lambda$	0.5000	0.5348	0.0208	0.0016	0.5295	0.0129	0.0010
${\beta }_1$	1.0000	0.9979	0.0919	0.0085	0.9999	0.0824	0.0068
${\beta }_2$	1.5000	1.5027	0.0901	0.0081	1.4992	0.0877	0.0077
${\sigma }^2$	0.0100	0.0200	0.0309	0.0011	0.0149	0.0228	0.0005
$m_1$	-	0.5001	0.4017	-	0.3653	0.2852	-
$m_2$	-	2.7182	0.2304	-	2.3661	0.1948	-
		$n=225$			$n=400$
$\lambda$	0.5000	0.5184	0.0049	0.0004	0.5137	0.0028	0.0002
${\beta }_1$	1.0000	1.0013	0.0566	0.0032	1.0024	0.0414	0.0017
${\beta }_2$	1.5000	1.5005	0.0572	0.0033	1.4998	0.0408	0.0017
${\sigma }^2$	0.0100	0.0032	0.0043	0.0001	0.0031	0.0031	0.0001
$m_1$	-	0.1689	0.1238	-	0.0872	0.0645	-
$m_2$	-	1.5603	0.0897	-	1.1407	0.0501	-

Table 3. The results of parametric estimates in Model (18) with $\lambda =0.75$.

Parameter	True Value	MEAN	SD	MSE	MEAN	SD	MSE
		$\mathit{n}=\mathbf{49}$			$\mathit{n}=\mathbf{64}$
$\lambda$	0.7500	0.7838	0.0559	0.0043	0.7837	0.0194	0.0015
${\beta }_1$	1.0000	0.9926	0.1317	0.0174	0.9894	0.1093	0.0121
${\beta }_2$	1.5000	1.5051	0.1252	0.0157	1.4942	0.1070	0.0115
${\sigma }^2$	0.0100	0.0548	0.0735	0.0074	0.0343	0.0470	0.0028
$m_1$	-	1.2188	0.8086	-	0.5739	0.4374	-
$m_2$	-	3.4220	0.4281	-	2.9343	0.2837	-
		$n=81$			$n=100$
$\lambda$	0.7500	0.7734	0.0187	0.0009	0.7730	0.0139	0.0007
${\beta }_1$	1.0000	0.9945	0.0940	0.0089	1.0052	0.0842	0.0071
${\beta }_2$	1.5000	1.4976	0.1030	0.0106	1.4965	0.0853	0.0073
${\sigma }^2$	0.0100	0.0226	0.0340	0.0013	0.0131	0.0201	0.0004
$m_1$	-	0.5159	0.3918	-	0.4090	0.2959	-
$m_2$	-	2.7176	0.2388	-	2.3667	0.1983	-
		$n=225$			$n=400$
$\lambda$	0.7500	0.7618	0.0049	0.0002	0.7614	0.0031	0.0001
${\beta }_1$	1.0000	1.0010	0.0564	0.0032	0.9997	0.0390	0.0015
${\beta }_2$	1.5000	1.5030	0.0538	0.0029	1.5013	0.0402	0.0016
${\sigma }^2$	0.0100	0.0124	0.0046	2.69E-5	0.0103	0.0033	1.09E-5
$m_1$	-	0.1671	0.1265	-	0.0818	0.0615	-
$m_2$	-	1.5586	0.0850	-	1.1395	0.0471	-

Figure 1 shows the fitted results and 95% confidence intervals of unknown function $m_1$ for three cases of $\lambda$ when $n=225$ and $n=400$, respectively. The short dashed and solid curves display the true unknown function $m_1$ and its estimates, respectively. The long dashed curves describe the corresponding 95% confidence intervals. Figure 2 shows the corresponding fitted results of unknown function $m_2$. By observing the fitting effect and confidence intervals of unknown functions in Figure 1 and Figure 2, we find that the small sample performances of nonparametric functions are good.

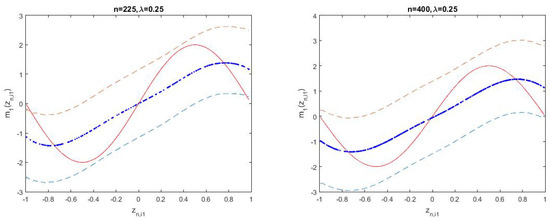
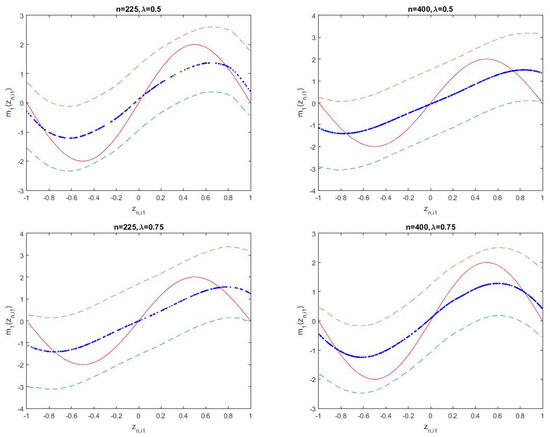
Figure 1. The fitting results of $m_1$ in Model (18).

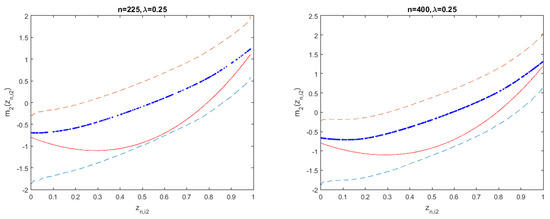
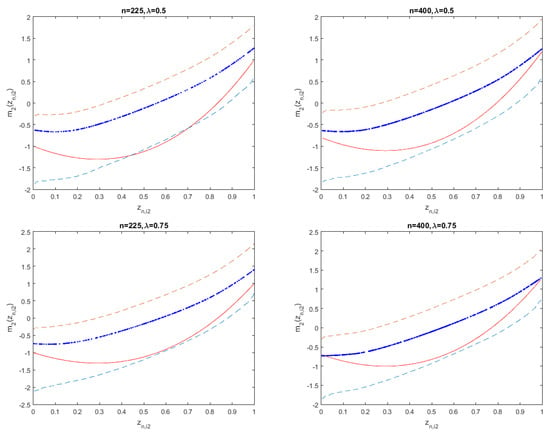
Figure 2. The fitting results of $m_2$ in Model (18).

5. A Real Data Example

In this section, we will analyze the well-known Boston housing data in 1970 using the proposed estimation procedures in Section 2. The data set has 506 observations, 15 exogenous regressors and 1 response variable. It includes the following variables:

• MEDV: The median value of owner-occupied homes in USD 1000s.
• LON: Longitude coordinates.
• LAT: Lattitude coordinates.
• CRIM: Per capita crime rate by town.
• ZN: Proportion of residential land zoned for lots over 25,000 sq.ft.
• INDUS: Proportion of non-retail business acres per town.
• CHAS: Charles river dummy variable.
• NOX: Nitric oxides concentration.
• RM: Average number of rooms per dwelling.
• AGE: Proportion of owner-occupied units built prior to 1940.
• DIS: Weighted distances to five Boston employment centers.
• RAD: Index of accessibility to radial highways.
• TAX: Full-value property tax per USD 10,000.
• PTRATIO: Pupil–teacher ratio by town.
• B: 1000(B-0.63)${}^2$ where B is the proportion of blacks by town.
• LSTAT: Percentage of lower status of the population.

Zhang et al. [28] analyzed these data via the partially linear additive model. Moreover, they investigated this data set by using variable selection and concluded that variables RAD and PTRATIO have linear effects on the response variable MEDV; variables CRIM, NOX, RM, DIS, TAX and LSTAT have nonlinear effects on the response variable MEDV; and the other variables are insignificant and were removed from the final model. Based on the conclusion drawn by Du et al. [28] and Zhang et al. [20], the spatial effect was considered using the partially linear additive spatial autoregressive model. Cheng et al. [17] investigated these data using the partially linear single-index spatial autoregressive model.

In our real data analysis, based on the conclusions drawn by Cheng et al. [17] and Du et al. [20], we consider that the dependent variable is MEDV; variables RAD and PTRATIO have linear effects on the response variable MEDV; and variables CRIM, NOX, RM, DIS and LSTAT have nonlinear effects on the response variable MEDV. We consider the partially linear additive spatial error model as follows:

$$\left\{\begin{array}{c}{y}_{n,i}=x_{n,1i}{\beta }_1+x_{n,2i}{\beta }_2+{\displaystyle \sum _{k=1}^5}{m}_k\left(z_{n,ki}\right)+{\eta }_{n,i},\hfill \\ {\eta }_{n,i}=\lambda {\displaystyle \sum _{k=1}^n}{w}_{n,ik}{\eta }_{n,k}+{\epsilon }_{n,i},\hfill \end{array}\right.$$

(19)

where the response variable $y_{n,i}=log\left(MED{V}_i\right)$, the covariates $x_{n,1i}=log\left(RA{D}_i\right)$ and $x_{n,2i}=log\left(PTRATI{O}_i\right)$, $z_{n,1i},\cdots ,z_{n,5i}$ are the ith element of CRIM, NOX, RM, DIS and log(LSTAT), respectively. As in Cheng et al. [17] and Du et al. [20], logarithmic transformation of variables is taken to relieve the trouble caused by big gaps in the domain. The spatial weight matrix $w_{n,ij}$ is calculated by the Euclidean distance in the light of longitude and latitude coordinates of any two houses. Moreover, the spatial weight matrix is normalized. Table 4 lists analysis results for the estimation of unknown parametric coefficients and their corresponding 95% confidence intervals. The function estimates of nonparametric components are displayed in Figure 3.

Table 4. Estimation results of unknown parameters in Model (19).

	Estimate	SD	MSE	Lower Bound	Upper Bound
$\lambda$	0.4689	0.0916	0.0085	0.3797	0.5216
${\beta }_1$	0.1625	0.0468	0.0023	0.0708	0.2105
${\beta }_2$	−0.3455	0.0790	0.0065	−0.4336	−0.1831

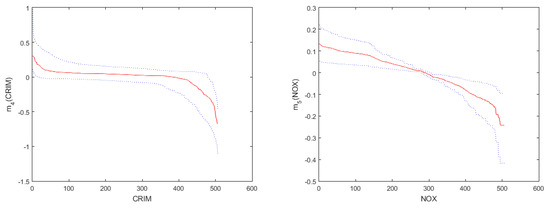
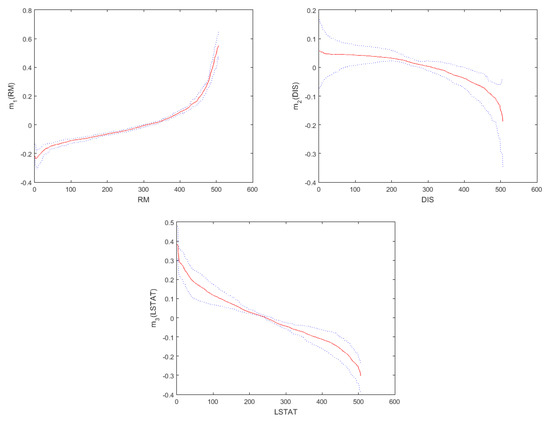
Figure 3. The estimates of the nonparametric functions in Model (19).

From Table 4, we can get the conclusions as follows. Firstly, the estimate of the spatial coefficient is 0.4689, the standard deviation 0.0916, and the mean square error is 0.0085 with a confidence interval that does not include 0, which shows that there exists a positive spatial relation among the regression disturbance term. Secondly, for the linear part, the regression coefficient for RAD is positive, which indicates that the housing price increases as the index of accessibility to radial highways increasing. The regression coefficient for PTRATIO is negative, which reveals that the pupil–teacher ratio by town has a negative effect on the housing price. Thirdly, for the nonlinear part, by observing Figure 3, we can obtain that the housing price would decrease as the other variables increase except RM. The variables CRIM, NOX, RM, DIS and log(LSTAT) have non-linear effects on the response, which is slightly different from the conclusion obtained by Du et al. [20]. The main reason is that our model has a different spatial structure compared with the model given in Du et al. [20].

6. Conclusions

In this paper, we present a partially linear additive spatial error model. This model not only can effectively avoid the “curse of dimensionality” in the nonparametric spatial autoregressive model and enhance the robustness of estimation, but it also investigates the spatial autocorrelation of error terms, and captures the linearity and nonlinearity between the response variable and the interesting regressors simultaneously. The local linear estimators of nonparametric additive components and GMM estimators of unknown parameters are constructed for the cases $d=1$ and $d>1$, respectively. The consistency and asymptotic normality of estimators under some regular conditions are developed for both cases. Meanwhile, Monte Carlo simulation illustrates the good finite sample performance of estimators. The real data analysis implies that our proposed methodology can be used to fit Boston data well and is easy to perform in practice.

This paper focuses only on the independent errors with homoscedasticity. However, many real spatial data sets do not satisfy the conditions, and it is significant to extend this model to cases with heteroscedasticity. Furthermore, we have not considered the issue of variable selection in the model. These scenarios will be studied as future topics.