Abstract
Finite mixtures normal regression (FMNR) models are widely used to investigate the relationship between a response variable and a set of explanatory variables from several unknown latent homogeneous groups. However, the classical EM algorithm and Gibbs sampling to deal with this model have several weak points. In this paper, a non-iterative sampling algorithm for fitting FMNR model is proposed from a Bayesian perspective. The procedure can generate independently and identically distributed samples from the posterior distributions of the parameters and produce more reliable estimations than the EM algorithm and Gibbs sampling. Simulation studies are conducted to illustrate the performance of the algorithm with supporting results. Finally, a real data is analyzed to show the usefulness of the methodology.
1. Introduction
Finite mixtures regression (FMR) models are powerful statistical tools to explore the relationship between a response variable and a set of explanatory variables from several latent homogeneous groups. The aim of FMR is to discriminate the group an observation belongs to, and reveal the dependent relationship between the response and predictor variables in the same group after classification. Finite mixture regression model with normal error assumption (FMNR) is the earliest and most used mixture regression model in practice, see Quandt and Ramsey [1], De Veaux [2], Jones and McLachlan [3], Turner [4], McLachlan [5], Frühwirth–Schnatter [6] and Faria and Soromenho [7] et al. for early literatures. In recent years, many authors have extended the finite mixture normal regression models to other error distribution based mixture regression models, such as mixture Student’s t regression (Peel [8]), mixture Laplace regression (Song et al. [9,10]), mixture regression based on scale mixture of skew-normal distribution (Zeller et al. [11]), and mixture quantile regression model (Tian et al. [12], Yang et al. [13]). The classical methods to deal with these mixture models are mainly based on Gibbs sampling for Bayesian analysis and EM algorithm (Dempster [14]) for finding the maximum likelihood estimator (MLE) from frequentist perspective, and the crucial technique in these methods is to employ a group of latent variables to indicate the group an observation belongs to, and formulate a missing data structure. Although EM algorithm and Markov Chain Monte Carlo (MCMC) based algorithm are widely used in dealing with mixture models, there are still some weak points in these algorithms, which should not be omitted. As to EM algorithm, the standard error of estimated parameter is always calculated as the square root of the diagonal element of the asymptotic covariance matrix motivated by the central limit theorem, but when the size of samples is small or even medium, this approximation may be unreasonable. In the case of Gibbs or other MCMC based sampling algorithms, the samples used for statistical inferences are iteratively generated, thus the accuracy of parameter estimation may decrease due to the dependency in samples. Besides, although there are several tests and methods to study the convergence of the generated Markov Chain, no procedure can check convincingly whether the stage of convergence has been reached upon termination of iteration. So it would be a beneficial attempt to develop some algorithm with more effectiveness and computationally feasibility to deal with complex missing data problems.
Tan et al. [15,16] proposed a kind of non-iterative sampling algorithm (named IBF algorithm after Inverse Bayesian Formula) for missing data models, which can draw independently and identically distributed (i.i.d.) samples from posterior distribution. Without convergence diagnosis, the i.i.d. samples can be directly used to estimate model parameters and their standard errors, thus avoids the shortcomings in EM algorithm and Gibbs sampling. Recently, extensive applications of IBF algorithm have seen prosperous development in documents, to name a few, Yuan and Yang [17] developed a IBF algorithm for Student’s t regression with censoring, Yang and Yuan [18] applied the idea of IBF sampling to quantile regression models, also Yang and Yuan [19] designed a IBF algorithm for robust regression models with scale mixture of normal distribution, which includes normal, Student’s t, Slash, and contaminated normal as special cases. Tsionas [20] applied the idea to financial area and proposed a non-iterative method for posterior inference in stochastic volatility models.
Inspired by Tian et al. [15,16], in this paper, we propose an effective Bayesian statistical inference for FMNR model from a non-iterative perspective. We first introduce a group of latent multinomial distributed mixture component variables to formulate a missing data structure, and then combine the EM algorithm, inverse Bayes Formula, and sampling/importance resampling (SIR) ([21,22]) algorithm into a non-iterative sampling algorithm. Finally, we implement the IBF sampling to generate i.i.d. samples from posterior distributions and use these samples directly to estimate the parameters. We conduct simulation studies to assess the performance of the procedure by comparison with the EM algorithm and Gibbs sampling, and apply it to a classical data set with supporting results. The IBF sampling procedure can be directly extended to other mixture regression models, such as mixture regression model driven by Student’s t or Laplace error distributions.
2. Finite Mixture Normal Regression (FMNR) Model
In this subsection, we first introduce the usual FMNR model, and then display the complete likelihood function for observations and a set of latent variables, which are the mixture component variables, indicating the group an observation belongs to.
Let represent the ith observation of a response variable and be the ith observation of a set of explanatory variables. The FMNR model is described as follows
therefore, the distribution of response variables is modeled as finite mixture normal distributions with g components. Here, is the mixture proportion with , and , is the p-dimension regression coefficient vector in jth group with the first element denoting the intercept, represents the variance of the error distribution in group j, and represents the normal distribution with mean and variance .
Denote parameters
and observation vector , the likelihood of in the FMNR model is that
where denotes the density function of distribution evaluated at . It is challenging to get the maximum likelihood estimations of the parameters by directly maximizing the above likelihood function, and it is also difficult to get the full conditional distributions used in Bayesian analysis. In documents, one effective approach to deal with mixture models is to introduce a group of latent variables which establishes a missing data structure, in this way, some data augmentation algorithms, such as EM algorithm and Gibbs sampling can be easily performed, besides, by taking advantage of the missing data structure, a new non-iterative sampling algorithm can be smoothly carried out.
Here, we introduce a group of latent membership-indicators , such that
with for and . Given the mixing probabilities , the latent variables are independent of each other, with multinomial densities,
Note that given , we have , and thus get the following complete likelihood of observations and latent variables :
The above complete likelihood is crucial to implement EM algorighm, Gibbs sampling and IBF algorithm.
3. Bayesian Inference Using IBF Algorithm
3.1. The Prior and Conditional Distributions
In Bayesian framework, suitable prior distributions should be adopted for the parameters. With the purpose to emphasize the importance of data and for simplicity, a set of independent non-informative prior distributions are used, which are
In fact, the prior of is Dirichlet distribution with concentration equals to 1, also known as a uniform prior over the space . These priors are improper and noninformative, but the posterior distributions are proper and meaningful. Then given complete data , the posterior density of is shown as
In order to implement the IBF sampling in FMNR model, we now present several required conditional posterior distributions, which are all proportional to the complete posterior density .
1. Conditional distribution
For , the conditional posterior distribution of is
the right side of (1) is the kernel of the probability density function of multimomial distribution, thus we obtain that
where
with standing for the multinomial distribution with parameters .
2. Conditional distribution
The conditional density of is given by
Let
and
then, we have
consequently,
3. Conditional distribution
The conditional density of is obtained as
noticing that the right side of Equation (4) is the kernel of inverse-Gamma density, we get
4. Conditional distribution
Finally, we obtain the conditional density of , that is
the right side of (6) is the kernel of Dirichlet distribution, thus
3.2. IBF Sampler
Based on the following expression
and
in order to draw i.i.d. samples from , we should first get i.i.d. samples from . According to Tan et al. [15,16], and based on the inverse Bayes formula, the posterior distribution of can be expressed as
where is the posterior mode of obtained by EM algorithm. The idea of IBF sampler in the EM framework is to use EM algorithm to obtain , an optimal important sampling density which can best approximate , thus by implementing SIR algorithm, i.i.d. samples can be generated approximately from .
Specifically, the IBF algorithm for FMNR model includes the following four steps:
Step 1. Based on (2), draw i.i.d. samples
for , where is the same as in (3), with replaced by . Denote
Step 2. Calculate the weights
where is calculated as with replaced by .
Step 3. Choose a subset from via resampling without replacement from the discrete distribution on with probabilities to obtain an i.i.d. sample of size approximately from , denoted by
Step 4. Based on (8), generate
For , based on (6), generate
and based on (4), generate
where
and
Finally, are the i.i.d. samples approximately generated from .
In this section, we employ a non-informative prior setting for the FMNR model and develop a IBF sampler. We will extend this procedure to the conjugate prior situation in the supplement.
4. Results
4.1. Simulation Studies
To investigate the performance of the proposed algorithm, we conduct some simulations under different situations by means of four criteria such as the mean, mean square error, mean absolute deviance, and the coverage probability to evaluate the method by comparison with the classical EM and Gibbs sampling.
The data are generated from the following mixture model
where is a group indicator of with . Here, is generated from the uniform distribution on interval , and is the random error. We consider the following symmetric distributions to describe error:
- 1.
- Normal distribution: ;
- 2.
- Student’s t distribution: ;
- 3.
- Laplace distribution: ;
- 4.
- Logistic distribution:
In these error distributions, cases 2–4 are heavy-tailed symmetric distributions and often used in the literature to mimic the outlier situations. We use these distributions to illustrate the robustness and effectiveness of the procedure, and implement a 2-components mixture normal regression model with IBF sampling algorithm, EM algorithm and Gibbs sampling to fit these simulated data. The prior setting is the same as in Section 3.1.
To evaluate the finite sample performance of the proposed methods, the experiment is replicated for 200 times with sample size and 300, respectively, for each error distribution. In the i-th replication, we set and , then get 3000 i.i.d samples from the posterior distributions using the proposed non-iterative sampling algorithm. Similarly, when performing Gibbs sampling, we generate 6000 Gibbs samples and discard the first 3000 as burn-in samples, then use the later 3000 after burn-in samples as effective samples to estimate the parameters. We record the mean of these samples as , for , and calculate the means (Mean), mean squared errors (MSE) and mean absolute deviances (MAD) of , which are expressed as
Besides, we calculate the coverage probability (CP) of 200 intervals with confidence level which cover the true values of parameters. The evaluation criteria for EM algorithm are the same as the above four statistics, with denoting posterior mode instead of posterior mean in the i-th replication. These four statistics are used to assess the performance of the three algorithms.
Simulation results are presented in Table 1, Table 2 and Table 3. From these tables, we are delighted to see that:

Table 1.
Monte Carlo simulation results for IBF sampler.

Table 2.
Monte Carlo simulation results for Gibbs sampling.

Table 3.
Monte Carlo simulation results for EM algortim.
- 1.
- All the three algorithms recover the true parameters successfully, since most of the Means based on the 200 replications are very close to the corresponding true values of parameters, and the MSEs and MADs are rather small. Besides, almost all of the coverage probabilities are around 0.95, which is the true level of confidence interval. We also see that as sample size increases from 100 to 300, the MSEs and MADs decrease and fluctuate steadily in a small range;
- 2.
- In general, for fixed size of samples, the MSEs and MADs in IBF algorithm are smaller than the ones in EM algorithm and Gibbs sampling, which show that the IBF sampling algorithm can produce more accurate estimators.
Thus, from these simulation studies, we can draw the conclusion that the IBF sampling algorithm is comparable to, and in most cases more effective than the EM algorithm and Gibbs sampling when modelling mixture regression data. Besides that, the IBF algorithm is much faster that the iterative Gibbs sampling, for example, when , the mean running time is 6 s for IBF and 10.39 s for Gibbs, and when , it is 19.58 for IBF and 31.16 s for Gibbs.
4.2. Real Data Analysis
The tone perception data stem from an experiment of Cohen [23] on the perception of musical tones by musicians. In this study, a pure fundamental tone was played to a trained musician with electronically generated overtones added, which is determined by a stretch ratio. The predictor variable is stretch ratio (X) and the response variable is the tuning ratio (Y), which is defined as the ratio of the adjusted tone to the fundamental tone. 150 pairs of observations with the same musician were recorded. The data is typically suitable for mixture regression modelling for that two separate trends clearly emerge in the scatter plot Figure 1. The dataset “tonedata” can be found in the R package mixtools authored by Benaglia et al. [24]. Many articles have analyzed this dataset using a mixture of mean regressions framework, see Cohen [23], Viele and Tong [25], Hunter and Young [26], and Young [27]. Recently, Song et al. [20], Wu and Yao [28] analyzed the data using a 2-component mixtures median regression models from parametric and semi-parametric perspective, respectively.
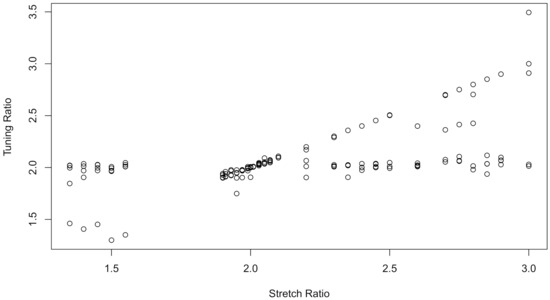
Figure 1.
Scatter plot of tone perception data.
Now we re-analyze this data with the following 2-components FMNR model:
and implenment IBF algorithm by comparison with the EM and Gibbs sampling. For EM algorithm, we let as initial values, and use the R function mixreg and covmix in R package mixreg (authored by Turner [29]) to estimate the parameters and calculate the standard deviance. As to IBF algorithm, we set and , thus get 6000 posterior samples. Similarly, in Gibbs sampling, we generate 10,000 Gibbs samples and discard the first 4000 as burn-in samples, then use the later 6000 after burn-in samples as effective samples to estimate the parameters.
Table 4 reports the estimated means and standard deviances of the parameters based on the above three algorithms. Clearly, the IBF algorithm are comparable to the EM and Gibbs sampling with very slight differences in means and standard deviances. We should notice that, although EM algorithm is effective for parameter estimation in mixture models, the standard deviances in EM algorithm are calculated as the square roots of the diagonal elements for the observed inverse information matrix, which are based on the asymptotic theory of MLE, however when the sample size is small or moderate, the estimated standard deviances may be unreliable. Therefore, compared with EM algorithm, we prefer to IBF sampling, for that the standard deviances can be directly estimated based on the i.i.d. posterior samples without extra effort. Figure 2 is the scatter plot with fitted mixture regression lines based on IBF, which clearly describes the linear relationship between turning ratio and stretch ratio in two different groups. In this figure, the observations are shown in different symbols, and classified using the mean of by comparison with 0.5, when the i-element of the mean vector is greater than 0.5, the i observation is classified to group one. In the supplement, we present the plots of ergodic means of posterior samples for all parameters based on IBF sampler and Gibbs sampler. We can see from theses plots that for each parameter, the ergodic means based on IBF algorithm converge much faster than the ones based on Gibbs sampling, which is not surprising for that the IBF samples are i.i.d generated from the posterior distributions. Considering this point, the IBF sampling outperforms the Gibbs sampler.

Table 4.
Estimations with EM, Gibbs, and IBF in Tone data analysis.
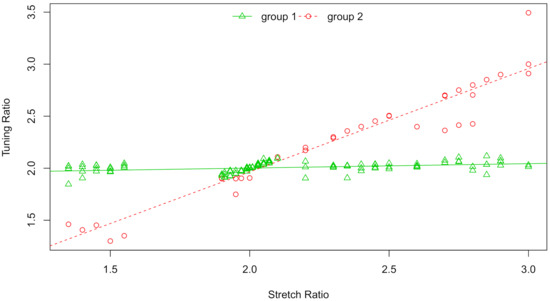
Figure 2.
Scatter plot of tone perception data with estimated mixture regression lines by IBF algorithm.
For illustrating purpose, in the supplement, the histograms with kernel density estimation curves based on 6000 IBF samples and 6000 Gibbs samples are plotted in Figures S5–S8, with the red lines denoting the posterior means. In general, the posterior distributions of each parameter based on IBF algorithm and Gibbs sampler are very similar. These plots vividly depict the posterior distributions of the parameters, for example, the distributions of regression coefficients are nearly symmetric, resemble normal distributions, but the distributions of variances and are both right skewed with a long tail at the right side of the distributions, which cannot be spotted by the asymptotically normality theory for MLE (or posterior mode).
Therefore, the IBF sampling algorithm provides an access to estimate the posterior distributions of parameters with more accuracy than the EM algorithm and Gibbs sampling by utilizing the i.i.d. posterior samples.
4.3. Algorithm Selection
There are several Bayesian model selection criteria to compare different models in fitting the same data set, here we take advantage of the idea of model selection to help determine which sampling algorithm is the “best”, the IBF algorithm or the Gibbs sampling. The deviance information criterion (DIC), proposed by Spiegelhalter et al. [30], was used as a measure of fit and complexity. The deviance is defined as
where is the likelihood function for FMNR model given by (2), and is the log-likelihood. The DIC statistic is defined as
with and . Here, are the posterior samples obtained by IBF sampler or Gibbs sampling, and are the estimated posterior means.
In Bayesian framework, the Akaike information criterion (AIC) proposed by Brooks [31] and the Bayesian information criterion (BIC) proposed by Carlin and Louis [32], can be estimated by
where s is the number of the model parameters. We choose the algorithm with smaller , and as a better algorithm to fit the model.
In the tone data study, the estimated measures based on FMNR model are given in Table 5. This table tells us that for all the three criteria, the values based on IBF are slightly smaller than the Gibbs counterparts, which justifies the superiority of the IBF sampler over the Gibbs sampler, although this superiority is not significant.

Table 5.
Model selection criteria for FHNR model with IBF sampler and Gibbs algorithm in the tone data analysis.
5. Discussion
This paper propose an effective Bayesian inference procedures for fitting FMNR models. With the in-complete data structure introduced by a group of multinomial distributed mixture component variables, a non-iterative sampling algorithms named IBF under a non-informative prior settings is developed. The algorithm combines the EM algorithm, inverse Bayesian formula and SIR algorithm to obtain i.i.d samples approximately from the observed posterior distributions of parameters. Simulation studies show that the IBF algorithm can estimate the parameters with more accuracy than the EM algorithm and Gibbs sampling, and runs much faster than Gibbs sampling. Real data analysis shows the usefulness of the methodology, also illustrates the advantages of the IBF sampler, for example, the ergodic means of samples from IBF sampling converge much faster than the ones from Gibbs sampling, and density estimation based on i.i.d. IBF samples are more reliable than the asymptotically normal distribution from EM algorithm. The IBF sampling algorithm can be viewed as an important supplement of the classical EM, Gibbs sampling and other missing data algorithms. The procedure can be extended to other error distribution based finite mixture regression models, such as mixture Student’s t regression. In this case, the Student’s t distribution should be firstly represented as a mixture of normal distribution with the latent mixture variable following a gamma distribution, and the IBF algorithm should be carried out twice. In this paper, the number of component is known, when g is unknown, the Reversible-jump MCMC method (Green [33], Richardson and Green [34]) may be used to estimate g, and this point is under consideration.e. Future research directions may also be highlighted.
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-7390/9/6/590/s1.
Author Contributions
Conceptualization, S.A. and F.Y.; methodology, S.A. and F.Y.; investigation, S.A. and F.Y.; software, S.A.; writing-original draft preparation, S.A. and F.Y.; writing-review and editing, S.A. and F.Y.; Both authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of Shandong province of China under grant ZR2019MA026.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The “tonedata” used in this paper are availabe from the free R package mixtools authored by Benaglia et al. [24].
Acknowledgments
The authors would like to express their gratitude to Benaglia et al. [24] for providing the “tonedata” in the free R package mixtools.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Quandt, R.; Ramsey, J. Estimating mixtures of normal distributions and switching regression. J. Am. Stat. Assoc. 1978, 73, 730–738. [Google Scholar] [CrossRef]
- De Veaux, R.D. Mixtures of linear regressions. Comput. Stat. Data Anal. 1989, 8, 227–245. [Google Scholar] [CrossRef]
- Jones, P.N.; McLachlan, G.J. Fitting finite mixture models in a regression context. Aust. J. Stat. 1992, 34, 233–240. [Google Scholar] [CrossRef]
- Turner, T.R. Estimating the propagation rate of a viral infection of potato plants via mixtures of regressions. J. R. Stat. Soc. C-Appl. 2000, 49, 371–384. [Google Scholar] [CrossRef]
- McLachlan, J.; Peel, D. Finite Mixture Models, 1st ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Frühwirth-Schnatter, S. Finite Mixture and Markov Switching Models, 1st ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Faria, S.; Soromenho, G. Fitting mixtures of linear regressions. J. Stat. Comput. Simul. 2010, 80, 201–225. [Google Scholar] [CrossRef]
- Peel, D.; Mclachlan, G.J. Roubust mixture modelling using the t distribution. Stat. Comput. 2000, 10, 339–348. [Google Scholar] [CrossRef]
- Song, W.X.; Yao, W.X.; Xing, Y.R. Robust mixture regression model fitting by Laplace distribution. Comput. Stat. Data Anal. 2014, 71, 128–137. [Google Scholar] [CrossRef]
- Song, W.X.; Yao, W.X.; Xing, Y.R. Robust mixture multivariate linear regression by multivariate Laplace distribution. Stat. Probab. Lett. 2017, 43, 2162–2172. [Google Scholar]
- Zeller, C.B.; Cabral, C.R.B.; Lachos, V.H. Robust mixture regression modelling based on scale mixtures of skew-normal distributions. Test 2016, 25, 375–396. [Google Scholar] [CrossRef]
- Tian, Y.Z.; Tang, M.L.; Tian, M.Z. A class of finite mixture of quantile regressions with its applications. J. Appl. Stat. 2016, 43, 1240–1252. [Google Scholar] [CrossRef]
- Yang, F.K.; Shan, A.; Yuan, H.J. Gibbs sampling for mixture quantile regression based on asymmetric Laplace distribution. Commun. Stat. Simul. Comput. 2019, 48, 1560–1573. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Robin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 1977, 39, 1–38. [Google Scholar]
- Tan, M.; Tian, G.L.; Ng, K. A non-iterative sampling algorithm for computing posteriors in the structure of em-type algorithms. Stat. Sin. 2003, 43, 2162–2172. [Google Scholar]
- Tan, M.; Tian, G.L.; Ng, K. Bayesian Missing Data Problems: EM, Data Augmentation and Noniterative Computation, 1st ed.; Chapman & Hall/CRC: New York, NY, USA, 2010. [Google Scholar]
- Yuan, H.J.; Yang, F.K. A non-iterative Bayesian sampling algorithm for censored Student-t linear regression models. J. Stat. Comput. Simul. 2016, 86, 3337–3355. [Google Scholar]
- Yang, F.K.; Yuan, H.J. A non-iterative posterior sampling algorithm for linear quantile regression model. Commun. Stat. Simul. Comput. 2017, 46, 5861–5878. [Google Scholar] [CrossRef]
- Yang, F.K.; Yuan, H.J. A Non-iterative Bayesian Sampling Algorithm for Linear Regression Models with Scale Mixtures of Normal Distributions. Comput. Econ. 2017, 45, 579–597. [Google Scholar] [CrossRef]
- Tsionas, M.G. A non-iterative (trivial) method for posterior inference in stochastic volatility models. Stat. Probab. Lett. 2017, 126, 83–87. [Google Scholar] [CrossRef][Green Version]
- Rubin, D.B. Comments on “The calculation of posterior distributions by data augmentation,” by M.A. Tanner and W.H. Wong. J. Am. Statist. Assoc. 1987, 82, 543–546. [Google Scholar]
- Rubin, D.B. Using the SIR algorithm to simulate posterior distributions. In Bayesian Statistics; Bernardo, J.M., DeGroot, M.H., Lindley, D.V.A., Simith, A.F.M., Eds.; Oxford University Press: Oxford, UK, 1988; Volume 3, pp. 395–402. [Google Scholar]
- Cohen, E. The Influence of Nonharmonic Partials on Tone Perception. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1980. [Google Scholar]
- Benaglia, T.; Chauveau, D.; Hunter, D.R.; Yong, D. mixtools: An R package for analyzing finite mixture models. J. Stat. Softw. 2009, 32, 1–19. [Google Scholar] [CrossRef]
- Viele, K.; Tong, B. Modeling with mixtures of linear regressions. Stat. Comput. 2002, 12, 315–330. [Google Scholar] [CrossRef]
- Hunter, D.R.; Young, D.S. Semiparametric Mixtures of regressions. J. Nonparametr. Stat. 2012, 24, 19–38. [Google Scholar] [CrossRef]
- Young, D.S. Mixtures of regressions with change points. Stat. Comput. 2014, 24, 265–281. [Google Scholar] [CrossRef]
- Wu, Q.; Yao, W.X. Mixtures of quantile regressions. Comput. Stat. Data Anal. 2016, 93, 162–176. [Google Scholar] [CrossRef]
- Turner, R. Mixreg: Functions to Fit Mixtures of Regressions. R Package Version 0.0-6. 2018. Available online: http://CRAN.R-project.org/package=mixreg (accessed on 30 March 2018).
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. B 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Brooks, S.P. Discussion on the paper by Spiegelhalter, Best, Carlin, and van der Linde. J. R. Stat. Soc. B 2002, 64, 616–618. [Google Scholar]
- Carlin, B.P.; Louis, T.A. Bayes and Empirical Bayes Methods for Data Analysis, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Green, P.J. Reversible jump markov chain monte carlo computation and Bayesian model determination. Biometrika 1995, 82, 711–732. [Google Scholar] [CrossRef]
- Richardson, S.; Green, P.J. On bayesian analysis of mixtures with an unknown number of components. J. R. Stat. Soc. B 1997, 59, 731–784. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).