Fibonacci, Golden Ratio, and Vector Bundles

Abstract

There is a family of vector bundles over the moduli space of stable curves that, while first appearing in theoretical physics, has been an active topic of study for algebraic geometers since the 1990s. By computing the rank of the exceptional Lie algebra ${\mathfrak{g}}_2$ case of these bundles in three different ways, a family of summation formulas for Fibonacci numbers in terms of the golden ratio is derived.

1. Introduction

The purpose of this note is to establish the following elementary summation formulas involving the famous Fibonacci numbers:

Theorem 1.

For all integers $n\ge 0$ and $g\ge 2$,

$$\sum _{i=0}^g\left(\genfrac{}{}{0pt}{}{g}{i}\right)F_{2i+n-1}={\phi }^n{(\phi +2)}^{g-1}+{\overline{\phi }}^n{(\overline{\phi }+2)}^{g-1}=\sum _{i=0}^g\left(\genfrac{}{}{0pt}{}{g}{i}\right)2^{g-i}{F}_{i+n-1},$$

(1)

where $F_k$ is the $kth$ Fibonacci number, $\phi =\frac{1+\sqrt{5}}{2}$ is the golden ratio, and $\overline{\phi }=\frac{1-\sqrt{5}}{2}$ is the conjugate root of its minimal polynomial $x^2-x-1$.

These formulas naturally emerge from an ostensibly unrelated setting. Indeed, by computing the rank of a certain vector bundle, for each n and g, in three different ways, we arrive at the above formulas. The relevant vector bundles here are the exceptional Lie algebra ${\mathfrak{g}}_2$ case of a more general construction, occurring for each simple complex Lie algebra, of the so-called vector bundle of conformal blocks on the Deligne–Mumford moduli space ${\overline{\mathcal{M}}}_{g,n}$ of stable n-pointed genus g curves. These vector bundles first appeared in mathematical physics [1,2] and they have been studied from the perspectives of both infinite-dimensional representation theory [3,4,5] and algebraic geometry [6,7,8,9,10,11]; these citations are just a sample of the vast literature. One of the most significant properties of these bundles is their recursive structure reflecting the boundary stratification of ${\overline{\mathcal{M}}}_{g,n}$. This property, known as factorization, was cleverly used by Mukhopadhyay to compute the rank of the ${\mathfrak{g}}_2$, level 1, case of these bundles and the formula he obtained [12] is the middle expression in Equation (1) involving the golden ratio; by using factorization in two different ways, we obtain the two Fibonacci summation expressions in that equation. The details of this assertion are the content of this paper.

Remark 1.

The author learned from the Online Encyclopedia of Integer Sequences that in the case $n=0$, the formulas in Theorem 1 count the number of no-leaf edge-subgraphs in the Möbius ladder $M_{g-1}$ [13] (see ([14], Theorem 16.1)).

2. Conformal Blocks Vector Bundles

2.1. Notation

Given a simple complex Lie algebra $\mathfrak{g}$ and an integer $\ell \ge 1$ called the level, let $P_{\ell }$ denote the set of dominant integral weights for $\mathfrak{g}$ of level ℓ. For any weight $\mu \in P_{\ell }$, the dual weight ${\mu }^{*}\in P_{\ell }$ is the highest weight of the dual of the irreducible representation corresponding to $\mu$. For each n-tuple of weights

$$\underline{\mu }=({\mu }_1,\dots ,{\mu }_n)\in P_{\ell }^n,$$

there is a vector bundle of conformal blocks on the moduli stack ${\overline{\mathcal{M}}}_{g,n}$ of stable n-pointed genus g curves that we denote by ${\mathbb{V}}_{g,n}^{\mathfrak{g},\ell }\left(\underline{\mu }\right)$, or by ${\mathbb{V}}_g^{\mathfrak{g},\ell }$ when $n=0$ [3,4,10]. The construction of this vector bundle is immaterial for our purposes, and we shall only need some standard properties well-established in the literature.

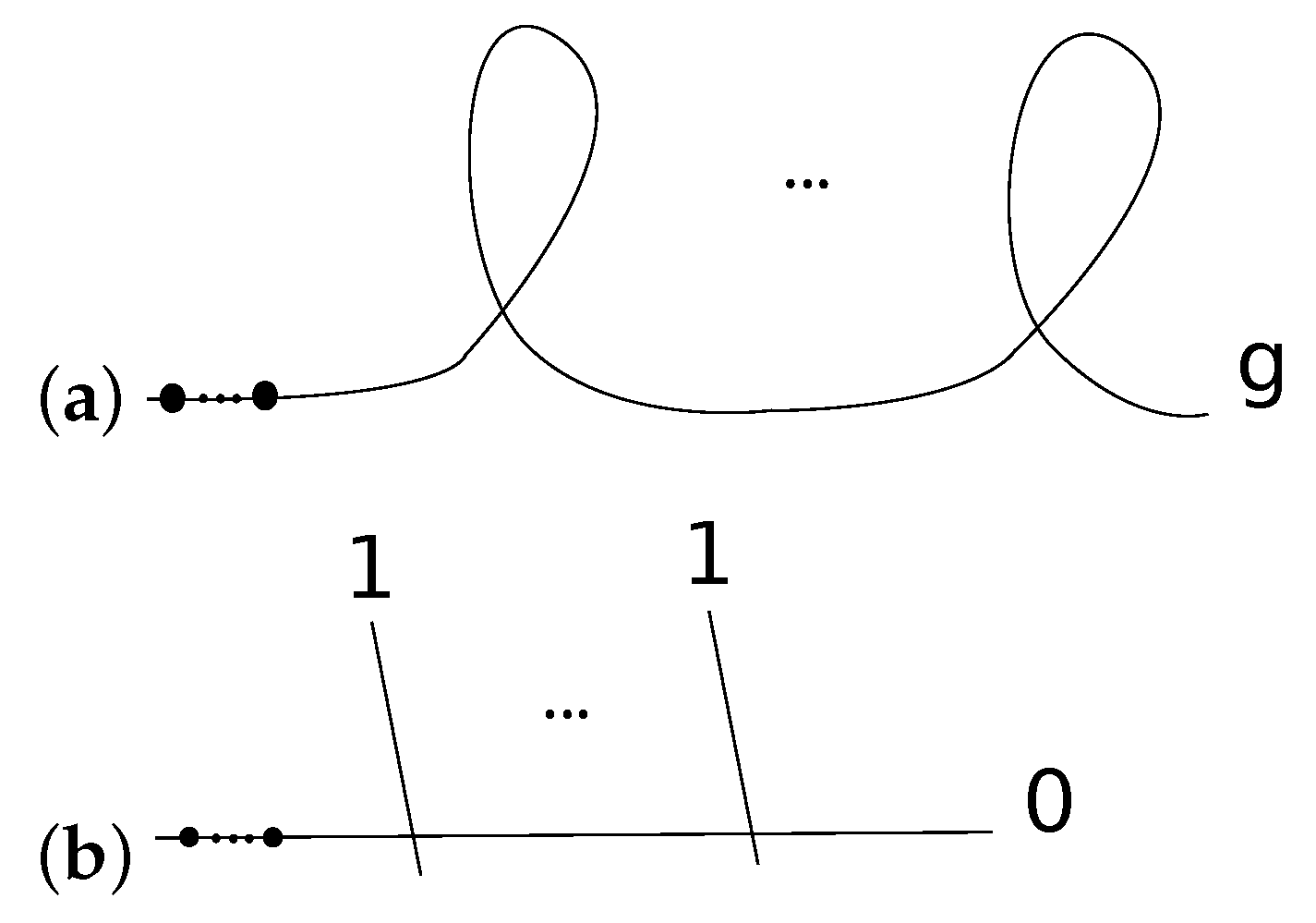
2.2. Factorization, Fusion Rules, Propagation of Vacua

The main property of conformal blocks vector bundles we will need is their rank. One way to compute the rank is via factorization, which describes the behavior of the fibers over a curve as the curve degenerates from smooth to nodal [3]. Fakhruddin has nicely expressed this in terms of boundary divisors in the moduli space ([10], Proposition 2.4): if

$$\gamma :{\overline{\mathcal{M}}}_{g_1,n_1+1}\times {\overline{\mathcal{M}}}_{g_2,n_2+1}\to {\overline{\mathcal{M}}}_{g_1+g_2,n_1+n_2}$$

is the gluing map attaching the pair of points given by the last marked point on each component, then

$${\gamma }^{*}{\mathbb{V}}_{g_1+g_2,n_1+n_2}^{\mathfrak{g},\ell }({\mu }_1,\dots ,{\mu }_{n_1+n_2})\cong \underset{\mu \in P_{\ell }}{⨁}{\mathbb{V}}_{g_1,n_1+1}^{\mathfrak{g},\ell }({\mu }_1,\dots ,{\mu }_{n_1},\mu )\otimes {\mathbb{V}}_{g_2,n_2+1}^{\mathfrak{g},\ell }({\mu }_{n_1+1},\dots ,{\mu }_{n_1+n_2},{\mu }^{*}).$$

Taking ranks, this says

$$rk{\mathbb{V}}_{g_1+g_2,n_1+n_2}^{\mathfrak{g},\ell }({\mu }_1,\dots ,{\mu }_{n_1+n_2})=\sum _{\mu \in P_{\ell }}rk{\mathbb{V}}_{g_1,n_1+1}^{\mathfrak{g},\ell }({\mu }_1,\dots ,{\mu }_{n_1},\mu )rk{\mathbb{V}}_{g_2,n_2+1}^{\mathfrak{g},\ell }({\mu }_{n_1+1},\dots ,{\mu }_{n_1+n_2},{\mu }^{*})$$

(2)

Similarly, if

$$\gamma :{\overline{\mathcal{M}}}_{g-1,n+2}\to {\overline{\mathcal{M}}}_{g,n}$$

is the clutching map attaching the last two marked points to create a loop, then

$${\gamma }^{*}{\mathbb{V}}_{g,n}^{\mathfrak{g},\ell }({\mu }_1,\dots ,{\mu }_n)\cong \underset{\mu \in P_{\ell }}{⨁}{\mathbb{V}}_{g-1,n+2}^{\mathfrak{g},\ell }({\mu }_1,\dots ,{\mu }_n,\mu ,{\mu }^{*})$$

and so

$$rk{\mathbb{V}}_{g,n}^{\mathfrak{g},\ell }({\mu }_1,\dots ,{\mu }_n)=\sum _{\mu \in P_{\ell }}rk{\mathbb{V}}_{g-1,n+2}^{\mathfrak{g},\ell }({\mu }_1,\dots ,{\mu }_n,\mu ,{\mu }^{*}).$$

(3)

Another ingredient we shall need is the propagation of vacua property (also first proven in [3] then expressed in modular terms in ([10], Proposition 2.4)), which says that if a weight ${\mu }_i$ in $\underline{\mu }$ is zero, then

$${\mathbb{V}}_{g,n}^{\mathfrak{g},\ell }\left(\underline{\mu }\right)\cong {\pi }_i^{*}{\mathbb{V}}_{g,n-1}^{\mathfrak{g},\ell }({\mu }_1,\dots ,\widehat{{\mu }_i},\dots ,{\mu }_n),$$

where ${\pi }_i$ is the map forgetting the ith marked point and the hat ∧ over a weight indicates that weight is omitted from the tuple. This says that all points marked by the zero weight can be ignored when computing the rank of a conformal blocks vector bundle.

The final ingredient we shall need is the fusion rules, which are computations of the rank when $g=0$ and $n=3$. The special case of this that we require is the following ([4], Corollary 3.5.2):

$$rk{\mathbb{V}}_{0,3}^{\mathfrak{g},\ell }({\mu }_1,{\mu }_2,0)=\left\{\begin{array}{cc}1\hfill & {\mu }_2={\mu }_1^{*}\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(4)

2.3. The Verlinde Formula

There is a famous closed formula for the rank of conformal blocks vector bundles, called the Verlinde formula, that was established using factorization (see [15] for a nice survey). For $n=0$ and $\mathfrak{g}$ of classical type or ${\mathfrak{g}}_2$, the Verlinde formula reads as follows (see ([16], Proposition B.1)):

$$rk{\mathbb{V}}_g^{\mathfrak{g},\ell }={\left({(\ell +h^{\vee })}^{rk\left(\mathfrak{g}\right)}\#(P/Q)\#(Q/Q_{lg})\right)}^{g-1}\sum _{\mu \in P_{\ell }}\prod _{\alpha \in {\Delta }_{+}}2sin\left(\frac{\pi \langle \alpha ,\mu +\rho \rangle }{\ell +h^{\vee }}\right),$$

(5)

where $P_{\ell }$ is the set of dominant integral weights for $\mathfrak{g}$ of level ℓ, ${\Delta }_{+}$ is the set of positive roots, $\langle ·,·\rangle$ is the Killing form, $\rho =\frac{1}{2}{\sum }_{{\alpha }_j\in {\Delta }_{+}}{\alpha }_j$, $h^{\vee }$ is the dual Coxeter number, P is the weight lattice, Q is the root lattice, and $Q_{lg}$ is the long root lattice.

2.4. Specializing to an Exceptional Lie Algebra

Our focus is on the conformal blocks vector bundles for the exceptional Lie algebra $\mathfrak{g}={\mathfrak{g}}_2$ and level $\ell =1$, for curves of genus $g\ge 2$. Here, there is only one nontrivial representation, and it is self-dual, so we can write $P_1=\{0,\mu \}$ where ${\mu }^{*}=\mu$.

Gregoire evaluated the Verlinde formula explicitly in this special case ([16], Appendix B) (see also [17]):

$$rk{\mathbb{V}}_g^{{\mathfrak{g}}_2,1}={\left(\frac{5+\sqrt{5}}{2}\right)}^{g-1}+{\left(\frac{5-\sqrt{5}}{2}\right)}^{g-1}$$

(6)

Mukhopadhyay used factorization and induction to generalize this formula from $n=0$ to all $n\ge 0$ [12]:

$$rk{\mathbb{V}}_{g,n}^{{\mathfrak{g}}_2,1}\left({\mu }^{\underline{n}}\right)={\left(\frac{1+\sqrt{5}}{2}\right)}^n{\left(\frac{5+\sqrt{5}}{2}\right)}^{g-1}+{\left(\frac{1-\sqrt{5}}{2}\right)}^n{\left(\frac{5-\sqrt{5}}{2}\right)}^{g-1},$$

(7)

where

$${\mu }^{\underline{n}}:=\underset{n}{\underbrace{(\mu ,\dots ,\mu )}}\in P_1^n.$$

This provides the middle expression in Equation (1) for all $n\ge 0$ and $g\ge 2$.

3. Fibonacci Formulas from Factorization

Consider an n-pointed genus $g\ge 2$ curve with g irreducible nodes, as in Figure 1a. This curve represents the generic point of a stratum deep in the stratification of the boundary of ${\overline{\mathcal{M}}}_{g,n}$. A repeated application of factorization (the clutching type described in Equation (3)) yields the following, for any $\underline{\mu }\in P_{\ell }^n$:

$$rk{\mathbb{V}}_{g,n}^{\mathfrak{g},\ell }\left(\underline{\mu }\right)=\sum _{({\lambda }_1,\dots ,{\lambda }_g)\in P_{\ell }^g}rk{\mathbb{V}}_{0,n+2g}^{\mathfrak{g},\ell }(\underline{\mu },{\lambda }_1,{\lambda }_1^{*},\dots ,{\lambda }_g,{\lambda }_g^{*})$$

(8)

Specializing to $\mathfrak{g}={\mathfrak{g}}_2$ and $\ell =1$, so that $P_1=\{0,\mu \}$ with ${\mu }^{*}=\mu$, we then have

$$\begin{array}{cc}\hfill rk{\mathbb{V}}_{g,n}^{{\mathfrak{g}}_2,1}\left({\mu }^{\underline{n}}\right)& =\sum _{({\lambda }_1,\dots ,{\lambda }_g)\in {\{0,\mu \}}^g}rk{\mathbb{V}}_{0,n+2g}^{{\mathfrak{g}}_2,1}({\mu }^{\underline{n}},{\lambda }_1,{\lambda }_1,\dots ,{\lambda }_g,{\lambda }_g)\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & =\sum _{i=0}^g\left(\genfrac{}{}{0pt}{}{g}{i}\right)rk{\mathbb{V}}_{0,n+2i}^{{\mathfrak{g}}_2,1}\left({\mu }^{\underline{n+2i}}\right),\hfill \end{array}$$

(10)

where for the last equality we used propagation of vacua, that is, weight zero points can be dropped. Fakhruddin has used factorization, together with the three-point fusion rule $rk{\mathbb{V}}_{0,3}^{{\mathfrak{g}}_2,1}(\mu ,\mu ,\mu )=1$, to show ([10], §5.2.8) that

$$rk{\mathbb{V}}_{0,m}^{{\mathfrak{g}}_2,1}\left({\mu }^{\underline{m}}\right)=F_{m-1},$$

(11)

the $(m-1)$th Fibonacci number, and this turns the preceding formula into the left expression in (1).

To get the right expression in Equation (1), we apply the reducible gluing type of factorization rather than the irreducible clutching applied above. Specifically, consider the n-pointed genus g curve in Figure 1b where there is a single irreducible “spine” component isomorphic to ${\mathbb{P}}^1$ carrying all n marked points, and attached to this spine are g irreducible elliptic tails. The factorization formula (2), for any $\underline{\mu }\in P_{\ell }^n$, yields

$$rk{\mathbb{V}}_{g,n}^{\mathfrak{g},\ell }\left(\underline{\mu }\right)=\sum _{({\lambda }_1,\dots ,{\lambda }_g)\in P_{\ell }^g}rk{\mathbb{V}}_{0,n+g}^{\mathfrak{g},\ell }(\underline{\mu },{\lambda }_1,\dots ,{\lambda }_g)\prod _{i=1}^{g}rk{\mathbb{V}}_{1,1}^{\mathfrak{g},\ell }\left({\lambda }_i^{*}\right).$$

(12)

Now specializing to $\mathfrak{g}={\mathfrak{g}}_2$ and $\ell =1$, so that $P_1=\{0,\mu \}$ with ${\mu }^{*}=\mu$, we have

$$\begin{array}{cc}\hfill rk{\mathbb{V}}_{g,n}^{{\mathfrak{g}}_2,1}\left({\mu }^{\underline{n}}\right)& =\sum _{({\lambda }_1,\dots ,{\lambda }_g)\in {\{0,\mu \}}^g}rk{\mathbb{V}}_{0,n+g}^{{\mathfrak{g}}_2,1}({\mu }^{\underline{n}},{\lambda }_1,\dots ,{\lambda }_g)\prod _{i=1}^{g}rk{\mathbb{V}}_{1,1}^{\mathfrak{g},\ell }\left({\lambda }_i\right)\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & =\sum _{i=0}^g\left(\genfrac{}{}{0pt}{}{g}{i}\right)rk{\mathbb{V}}_{0,n+i}^{{\mathfrak{g}}_2,1}\left({\mu }^{\underline{n+i}}\right){\left(rk{\mathbb{V}}_{1,1}^{\mathfrak{g},\ell }\left(\mu \right)\right)}^i{\left(rk{\mathbb{V}}_{1,1}^{\mathfrak{g},\ell }\left(0\right)\right)}^{g-i}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & =\sum _{i=0}^g\left(\genfrac{}{}{0pt}{}{g}{i}\right)F_{n+i-1}{2}^{g-i}.\hfill \end{array}$$

(15)

For the last equality we used that $rk{\mathbb{V}}_{1,1}^{{\mathfrak{g}}_2,1}\left(\mu \right)=1$ and $rk{\mathbb{V}}_{1,1}^{{\mathfrak{g}}_2,1}\left(0\right)=2$, which follow, for instance, from clutching factorization and the fusion rule stated in Equation (4):

$$\begin{array}{cc}\hfill rk{\mathbb{V}}_{1,1}^{{\mathfrak{g}}_2,1}\left(\mu \right)& =rk{\mathbb{V}}_{0,3}^{{\mathfrak{g}}_2,1}(\mu ,0,0)+rk{\mathbb{V}}_{0,3}^{{\mathfrak{g}}_2,1}(\mu ,\mu ,\mu )\hfill \\ \hfill & =0+1,\hfill \\ \hfill rk{\mathbb{V}}_{1,1}^{{\mathfrak{g}}_2,1}\left(0\right)& =rk{\mathbb{V}}_{0,3}^{{\mathfrak{g}}_2,1}(0,0,0)+rk{\mathbb{V}}_{0,3}^{{\mathfrak{g}}_2,1}(0,\mu ,\mu )\hfill \\ \hfill & =1+1.\hfill \end{array}$$

This completes the proof of Theorem 1.