Abstract
Biological systems are commonly constituted by a high number of interacting agents. This great dimensionality hinders biological modelling due to the high computational cost. Therefore, new modelling methods are needed to reduce computation time while preserving the properties of the depicted systems. At this point, Boolean Networks have been revealed as a modelling tool with high expressiveness and reduced computing times. The aim of this work has been to introduce an automatic and coherent procedure to model systems through Boolean Networks. A synergy that harnesses the strengths of both approaches is obtained by combining an existing approach to managing information from biological pathways with the so-called Nested Canalising Boolean Functions (NCBF). In order to show the power of the developed method, two examples of an application with systems studied in the bibliography are provided: The epithelial-mesenchymal transition and the lac operon. Due to the fact that this method relies on directed graphs as a primary representation of the systems, its applications exceed life sciences into areas such as traffic management or machine learning, in which these graphs are the main expression of the systems handled.
1. Introduction
Biological systems are commonly constituted by a high number of interacting agents. This great dimensionality hinders biological modelling due to the high computational cost. Therefore, new modelling methods are needed to reduce computation time while preserving the properties of the depicted systems. At this point, Boolean Networks have been revealed as a modelling tool with high expressiveness and reduced computing times. The aim of this work is to introduce an automatic and coherent procedure to model systems through Boolean Networks.
Systems’ biology rely on accurate descriptions of the systems to depict. However, these systems are commonly made of hundreds, even thousands of different entities and agents to consider. Due to the high dimensionality of the systems that are to be conveyed, the modelling of its dynamics requires alternative approaches to differential equations. In this context, Boolean Networks have reaped achievements since the beginning of the 1960s [1,2]. Boolean Networks (BN) have been widely developed in the last few decades [3,4,5,6,7] and, among these advancements, new inference algorithms have taken place [8,9,10,11,12,13].
Since there are a great variety of techniques to infer BN models, two independent theoretical approaches have been selected: Nested Canalising Boolean Functions (NCBF) and what we will denote as Conflicts Strategy (CS). NCBF are a special kind of Canalizing Boolean Functions (CBF), where CBF is a mathematical representation of the canalisation phenomenon [14], a mechanism by which biological systems buffer variability in key features [15]. Canalisation enables species to preserve and develop sophisticated structures, e.g., eyes, throughout evolution. Since NCBF represent this phenomenon, they have been proven effective to model biological systems [12,14,16].
On the other hand, Conflicts Strategy (CS) constitutes a theoretical framework built upon biological deduction [8]. CS is based on the imposition of biological restrictions to which the system is subjected, i.e., biochemical relations among the system agents. Some of these restrictions are not mutually compatible, e.g., a simultaneous imposition of high and low concentration for a protein. In consequence, they must be adapted to the nature of the model (BN) because it is to be an accurate representation of all the system dynamics, even if they seem contradictory. These incompatibilities are what is denoted as conflicts [8]. It is precisely the conflicts resolution that drives the modelling procedure performed during the CS.
In this analysis, an algorithm based on a new theoretical framework that combines the best of CS and NCBF is proposed. It is a modification of the one explained in [8]. To clarify the logic behind the algorithm and how it has been obtained, we explain the basis of CS and NCBF (Section 2) to immediately expose the theoretical model (Section 3) upon which the algorithm has been developed. In fact, the algorithm can be divided in two different sections: The general algorithm (Section 3.4), which introduces the system dynamics, and the conflicts algorithm, which solves the contradictions among those dynamics (Section 3.5). Once the algorithm has been explained, its power is shown by means of two systems: The Epithelial-Mesenchymal Transition (EMT) [12] (Section 4.1) and the lac operon [17] (Section 4.2). These two systems, expressed in the form of genetic circuits through graphs, illustrate the modelling capabilities of the algorithm. For each example, the nature of the system is first explained, and then the results of the modelling (Section 5). Finally, the current limitations of the algorithm are discussed, and how it will be improved in further works (Section 6). It should be noted that this work is accompanied by a Supplementary Materials file showing all the boolean functions used for each of the examples in Section 4, as well as the pathways and conflicts between them. The resulting NCBFs in each of the two examples are also shown.
It is essential to emphasise that, although this framework has been devised to be applied in biological systems, its applications exceed life sciences. The reason is that its foundations rely on principles of Graph Theory which are not exclusive to living systems. On the contrary, they can be found in other structures such as underground maps or airlines networks. In other words, the theory shown in this work can be applied upon every organisation susceptible of being depicted through a graph. Hence, it can unravel hidden relationships not only in biology but in a wide range of disciplines.
2. Theoretical Framework
The method shown in this analysis is based on two theoretical cornerstones: Nested Canalising Boolean Functions (NCBF) and Conflicts Strategy (CS).
2.1. Nested Canalising Boolean Functions
In the 1940s, C. H. Waddington observed that despite great genetic and environmental variability, individuals tend to manifest highly specialised characteristics [18]. He introduced the concept of canalisation: A property of systems to buffer variability [15]. The idea is that variability is a key concept for life that allows species benefit from it throughout evolution to achieve unique features and skills to succeed in their respective environments. However, once a useful feature has been acquired, variability could provoke its loss, e.g., a mutation could erase the effects of another mutation. At this point, it can be concluded that variability is not enough, a mechanism is needed to prioritise those variations worth obtaining and discard the rest. Canalisation is such a mechanism, operating as a selection process. It permits the development of sophisticated structures, such as fins or teeth, through the filtering of those alterations worth preserving. The development of these structures would be impossible without this phenomenon because the need for many changes towards the same direction.
In a mathematical context, canalisation can be defined through Canalised Boolean Functions (CBF) [19]. A CBF is a function f with n variables, in which at least one of its variables is capable of imposing a certain result. For example, independent of the remaining of variables. In other words, the individual f with genotype is bound to manifest the phenotype b, regardless of any perturbation of the system (other variables in f). In this case, is a canalising variable because it imposes a value (b) on f. In this sense, the canalising depth is the number of canalising variables in f. It has been proven that non-canalising functions, whose depth equals zero, are notably more unstable than those whose canalising depth is greater than 0 [20], which is coherent with Waddington’s notion of canalisation.
At this point, a NCBF is every CBF with a maximum canalising depth. This is a function like the one shown in Equation (1) [19], a function in which all its variables are canalising:
Genetic systems exhibit canalising behaviour according to this variability buffer. Consequently, NCBF have reported numerous successes in the modelling of Gene Regulatory Networks (GRN) [4,5,12]. According to [19], every NCBF can be uniquely represented under the form of Equation (2). The relationship between both Equations (1) and (2) is illustrated in the example of canalisation of Section 2.1.
where . Note that Equation (2) is structured in r layers. Every layer consists of a product () and the other side of the module 2 operation denoted with the symbol ⊕ (where for example ). For instance, the first layer is made of the terms and b. The index i denotes the layer, j indicates the variable within a layer i, is the number of variables in each product, and r is the number of products. Every variable has a canalising value and a canalised value. For example, the canalised value of the canalising variables in is b. If a variable is thought as an action or phenomenon, the canalising value is the trigger of the action whilst the canalised value is the effect of the action. For example, in the expression , the canalising and canalised values for the variable are 0 and 1 respectively.
Consequently, the variables in the products of outer layers have priority over the variables in the products of inner layers. This is because at the moment in which any variable equals its canalising value, its product becomes 0 along with all the nested products, no matter the values of their variables. This is the way in which the canalising behaviour of Equation (1) is represented in Equation (2).
On the other hand, the number of layers (r) will not necessarily equal the number of variables (n), this will be in the case in which every layer is made of one variable (). It can be appreciated in Equation (2) that all the variables in the same layer have the same canalised value. Moreover, the only canalised value that is specified is the value for the first layer (), that is b. It is not necessary to specify more in Equation (2) due to the fact that in boolean algebra – they are just different notations. Consequently, the nested negations in Equation (2) bring about the canalised values to alternate along the layers. In other words, , , and so on. In a mathematical context, variables must be ordered by their priority according to this pattern.
In practice, the advantage of employing NCBF in relation to other approaches is that the search for boolean functions is restricted to only NCBF. This strategy is based on combinatorics restricted by biological information and by models that depict the phenomenon of canalisation, which highly reduces computation time. However, the total time destined for the obtaining and validation of networks is still huge.
Example of Canalisation
In order to depict this phenomenon, a simplified example of eye colour inheritance is considered. Let us consider a couple of homozygous individuals for a particular gene, for example the gene responsible for eye colour. Assuming that one individual has blue eyes and the other brown eyes, all their descendants will be heterozygous for this gene, holding two different alleles, one from each parent. This case shows an example of eye colour inheritance. The brown allele (B) dominates over the blue allele (L) because when an individual manifests heterozygosity, the exhibited phenotype is the one determined by the brown allele. Nature allows variability through mutations (blue allele) although it prioritises those features with better adaptive outcomes (brown allele). Thus, only a few variants (phenotypes) are exhibited in the majority of individuals despite having numerous alternatives (alleles) for each feature.
This is a simplified example of canalisation. In order to model it, a function is defined to answer the question: Will the phenotype manifest a brown colour? The answer can be either yes (1) or no (0). The behaviour of this function is exposed in Equation (3) according to Equation (1). A NCBF with this performance is shown in Equation (4) according to the structures shown in Equation (2):
According to Equation (4), possessing the brown allele implies that and, similarly, possessing the blue allele implies that . Consequently, the only case in which the blue allele manifests is in homozygosity, that is to say, 25% of all the possible cases, whereas the prioritised allele will determine the rest (75%). Note that, in case that and , and, although this is mathematically correct, such an arguments combination is impossible because every individual is, at least, to hold one type of allele. Thus, canalisation can be expressed through NCBF.
2.2. Conflicts Strategy
In this work, Conflicts Strategy (CS) is the name given to the theory developed in [8]. In CS, the basic unit is what we will refer to as pathway, the relationship between two nodes of a directed graph. These relationships establish either activation or inhibition dependencies among nodes. This definition of pathway is mathematically represented according to Equation (5):
Q and P are the functions that drive the behaviour of two nodes in a given graph, u represents the time steps required to meet the relation between Q and P, v is the value to which Q must be equal to trigger the action, and b is the value to which P must be equal, the effect of the action. Thus, the pathways used in CS are like the ones shown in Equation (6), where D, H, T, and R are graph nodes, and ∨, ∧, and ¬ denote the OR, AND, and NOT operators respectively:
The objective of the inference process is to obtain the expressions which best show the nodes behaviour, in other words, the nodes expressions are unknown during the inference. For instance, the graph in Figure 1a can be separated in the pathways of Figure 1b. In the second pathway of the set, , the dependency conveyed is as follows: “If the function which controls the node X equals 1, after 1 time step the function which controls the node Y must equal 1”.
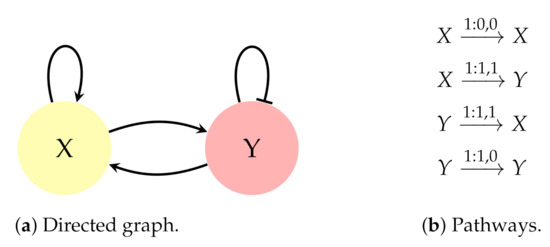
Figure 1.
Example of genetic circuit with two genes X and Y. (a) Directed graph. Each node represents an agent in the circuit. These agents are often genes although they can also be inputs or metabolites. The edges convey relationships among nodes. The arrows indicate activation dependencies and the plain-ended links represent inhibition connections. (b) Set of pathways.
Since boolean logic admits only 2 values, nodes can be either active (1) or inactive (0). In the same way, every node in a graph divides its linked nodes in activators and inhibitors. For example, in relation to the graph in Figure 1, the node Y has one activator (node X) and one inhibitor (node Y). The reason is that the pathway establishes an activation dependency from X to Y. In other words, X activates Y because it makes Y equal to 1. Thus, X is an activator of Y and, for the same reason, Y is an inhibitor of Y.
Then, what is depicted in ? It is represented that at the moment in which there is not concentration of X, there will not be concentration of X on the following time step. Consequently, attending this pathway, X is a necessary condition for X, which is coherent with the behaviour of an activator. Therefore, throughout this work, it is considered a node to be activator when it manifests one of the pairs {(0, 0), (1, 1)} through at least one pathway, otherwise it is considered an inhibitor. In consequence, the same graph can give rise to several combinations of pathways, what influences the obtained model. It is important to emphasise that this is the definition of an activator and inhibitor in this analysis for both CS and NCBF.
Then, what happens when one activator and one inhibitor coincide in the same node? This is what occurs in Figure 1a for node Y, when X and Y are simultaneously active (). According to the pathways, there is a contradiction because Y would have to be active () and inactive () at the following time step. These contradictions are called conflicts. In this case, the conditions (left side) of the pathways of Equation (7) overlap in a region called , where . Therefore, the conflict emerges when :
Since conflicts must be solved in order to build BN models, a method of conflict resolution is proposed. This procedure is a modification of the one explained in [8] as it will be made explicit later.
For this purpose, two concepts are to be introduced. The first one is the support (supp), according to [8] of a boolean function f is the set of arguments combinations that make the function 1. For example, given the function (Equation (6)), , where the order of the arguments in the tuples is D, H. The second concept is the antecedent and consequent of a pathway that are their left and right sides respectively.
In order to avoid conflict, the idea is to prioritise one pathway over the other. It should be noticed that the priority between pathways is very close to the concept of canalisation, that is to say, the canalisation is the prioritised expression of certain genes over the others, and consequently, it can be obtained through CS.
Let us consider Figure 2a, in which the supports of the antecedents of both pathways before any modification are represented. It can be observed that both supports overlap in a region , the conditions in which the system manifests the conflict.

Figure 2.
Graphic representation of the conflict avoidance. Each circle symbolise the support of the antecedent of a pathway. The red region indicates the overlap between the two supports, that in this case is .
The procedure, explained briefly (more details are in Section 3.1 and Section 3.5) consist of three steps:
- Step 1.
- Prioritisation of one pathway over the other. In this example, the pathway is arbitrarily prioritised, although a priority criterion will be explained in the next section.
- Step 2.
- Modification of the non-prioritised pathway to avoid the conflict. The modified expression is obtained through the intersection of the original support of the non-prioritised pathway with the region of the space that does not belong to the prioritised pathway: , what is equivalent to (green regions in Figure 2). Then, the modification consists of multiplying the negated antecedent of the prioritised pathway by the antecedent of the non-prioritised pathway. In our example, since and , the second pathway becomes , so there is no overlapping region.
- Step 3.
- Introduction of a new pathway. Finally, we introduce a pathway to conserve the dynamics underlying . Note that the effect of the non-prioritised pathway represents a dynamic that cannot be ignored due to its biological meaning. In order to preserve this dynamic, a new pathway is introduced, which obtains the non-prioritised value in the node but in two time steps whereas the prioritised one is obtained in one time step. In our example the new pathway is: .
It is important to mention that, as noted in [8], through CS, it is not always possible to find a solution to the problem. A reason for this is that the modifications over the pathways are performed according to the information that is already known about the BN, namely, just those same pathways. Since they form a partial representation of the system, the inference process is limited to a fraction of all the solutions that could be obtained. Hence, the methodology described in [8] avoids potential solutions as a consequence of this problem of partial information.
3. The Model
NCBF and CS are independent theoretical frameworks used for the inference of BN, that is to say, to represent the dynamics of a given system. Both approaches will be convergent given that the nature of a system is unique by definition. For example, in the system of Figure 3 (modification of the one found in [8]), the solutions obtained with both theoretical frameworks, CS (through the method described in [8]) and NCBF [12,19] approaches are shown in Table 1 and Figure 4 (see Supplementary Materials).
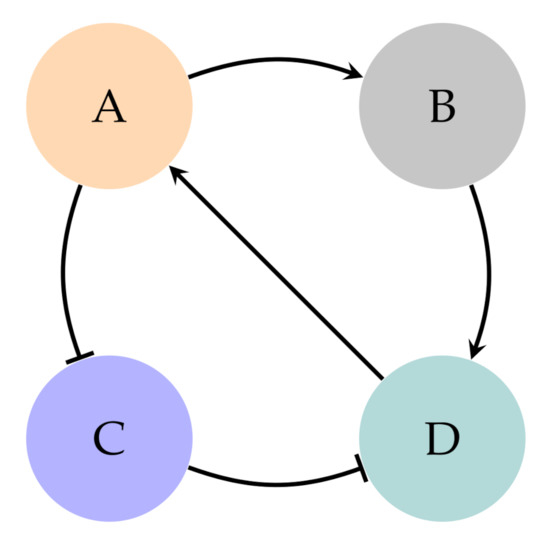
Figure 3.
Directed graph to represent the system composed of four nodes (genes): A, B, C, and D with dependencies conveyed according to the standard set in Figure 1a.

Table 1.
Truth tables of the functions of the networks obtained through Conflicts Strategy (CS) and Nested Canalising Boolean Functions (NCBF). The letter x indicates an undefined value. The red cells show (by node) the discrepancies among the solutions of both methods. An undefined value can never be considered discrepancy given that it can be any value.

Figure 4.
Expressions of the networks obtained through CS and NCBF.
The truth tables in Table 1 show that both networks have a similarity of 92.18%. Therefore, discrepancies may exist between the NCBF and CS solutions. Nonetheless, this result is coherent with the idea of convergence explained before. In Figure 4 note that all the expressions of the CS solution include all their equivalents of the NCBF solution. The difference is that in three out of four expressions, the CS solution incorporates an extra term. This is in line with the hypothesis stated in [18], in which canalisation is not the absolute rule that drives systems. On the contrary, canalisation would play a modulating function over the system dynamics, allowing some non-canalising features. Since the example shown in Figure 3 does not represent any biological system, this result suggests that maybe this hypothesis can be applied to graphs in general and not only to biological graphs, however, this affirmation needs further work in order to be proven.
It is reasonable to think that both approaches converge at a high degree, according to the results shown in Table 1 and Figure 4. In the same way, canalisation explains the most of system dynamics. At this point, it is relevant to question if both approaches can be combined to overcome their own limitations: (1) Extended computation time in NCBF search and (2) missing information in CS.
In this section, a new algorithm based on CS including NCBF is shown. This algorithm constitutes an efficient procedure of BN inference capable of representing the non-canalising dynamics of the modelled systems. Actually, this algorithm is a modification of the one explained in [8]. The extent of the modifications have been explicitly described in Section 3.1 and Section 3.2. Essentially, the idea behind this work is to complement the pathway-based approach exposed in [8] with the information provided by the NCBF. The alterations performed over the initial algorithm address three issues: Priority criterion, missing information, and pathways application. Additionally, in this work, a mechanism has been included to filter the obtained networks so as to gather only those with biological coherence. We call it validation and it will be further developed in Section 3.3.
3.1. Priority Criterion
The conflicts resolution procedure needs to distinguish between the prioritised pathway and the non-prioritised one. In [8], a mathematical criterion to solve this problem is proposed. In our opinion this criterion cannot be entirely based on mathematical principles because its aim is to solve a biological problem. Therefore, it should include biological information. In this work, an alternative method is proposed: A rule based on experimental data, the priority matrix. The priority matrix aims to provide a feasible mechanism to set the pathways priority, and at the same time, the matrix is to enhance the inference procedure through an introduction of experimental data.
Let us suppose a conflict between two pathways and , there are two conflicting nodes: X and Y. The conflict would be addressed through the values of the priority matrix, that we will denote as . Thus, and , where . If , the prioritised pathway is to be . Analogously, if the prioritised pathway should be .
The objective with the priority matrix is to gather a big quantity of experimental data in a synthetic manner. The numbers in the matrix explain the priority among the system nodes and their combinations. Therefore, a priority criterion based on experimental data through this matrix is performed. Due to the lack of such data, all the matrices exposed and employed along this article have been randomly generated although the idea is to use experimental data.
For example, in the graph of Figure 3, there are two conflicting pathways: and . In Table 2, as P(B,C)=3 whereas P(C,B)=2, then and the prioritised pathway should be . Note that pathways with more complex expressions are generated during the inference process, although the procedure would be the same. For example, given the pathways and , the prioritised pathway should be because .

Table 2.
Priority matrix for the graph of Figure 3 nodes A, B, C, and D.
Since the expressions of the pathways are made of different genes, the priority matrices are to give an answer for every possible conflict. Therefore, if a graph with 4 nodes is evaluated (as is the case in Figure 3), the priority matrix should be a matrix of 15 × 15 because there are 15 possible groupings employing the nodes of the graph. In Table 2 a smaller matrix is shown for the sake of clarity although with the examples exposed there would have not been any difference in the case of using a bigger matrix. Note that it has been considered implicitly that the priority of and a is the same. For example, let us suppose the pathways and , the priority of the matrix is (for the first value in the comparison). However, for the pair of pathways, and , the priority is also . This is because there are no entries in the matrix for negative nodes, nonetheless, alternative implementations of this matrix can be developed to consider this possibility.
Assumptions like these and the matrices employed may vary depending on the problem tackled and the available data. Nonetheless, the key concept is the introduction of external information so as to obtain a more accurate inference. In this work, the priority matrix is proposed as a way of introducing such information.
3.2. Missing Information
According to the conflict between the pathways and (Figure 3), the conflict-solving procedure generates a new pathway: , where is the region of conflict between the two pathways (). Let us denote the right side of that pathway, where b is the value that we are imposing (1, because the prioritised pathway is ). Likewise, S is a function that returns the combinations of nodes that should be activated in time t to make the conflicting node (D) equal to the non-imposed value . In this case, , and consequently, if in time t, , in time , .
The key concept to solve the conflict is the function S, which returns the arguments combinations of the inferred function that fulfils the selected value, in this case . In other words, taking the example above, represents the conditions needed to make . Thus, the pathway is imposing the non-prioritised value () in the step after (). This stage relates not only to the inferred function but to the whole network. It is the imposition of this stage that generates new, non predicted, relationships among the nodes.
In this way, iteration by iteration, new pathways are inferred and, consequently, the truth table of every node is progressively fulfilled. However, there are empty entries, especially at the beginning of the inference. These entries correspond to information not provided by the pathways assessed. For this reason, at a given time step, S will not return all the possible conditions, which are all that actually provoke the desired effect. On the contrary, it will only return those conditions, whose effect is known to be the desired one. Consequently, at a given time step, CS will obtain a subset of all the possible solutions. This is what is called in this analysis the problem of missing information, the main limitation of CS.
In this work, in order to solve the problem of missing information, we propose the use of a network made of NCBF to approximate the true network. It has been shown before that canalisation explains the most of the sysem dynamics. Consequently, it is reasonable to assume that NCBF constitute a good approximation for the real dynamics of the system. Moreover, as we exhibite in the example of Figure 3, both methodologies converge at a high degree. For all these reasons, it can be stated that NCBF make a good approximation for the inferred functions. Therefore, in this work the employment of NCBF is proposed so as to estimate function S. The use of NCBF as an approximation brings two benefits: (1) The total amount of combinations returned from S increases, which expands the solutions set reached through CS, and (2) the total quantity of NCBF to be analysed decreases because not all the NCBF converge during the inference process. In this manner, CS constitutes a filter for the NCBF-based networks. Eventually, this behaviour provokes that the total number of networks to be checked is lower compared with a pure NCBF-based inference.
On the other hand, the obtained functions might not be restricted to NCBF but to CBF. The rationale for this idea relies on the stability of the very functions. According to [20], networks made with functions of low canalising depth exhibit a much more stable behaviour than those made of non-canalising functions. Nonetheless, these stability improvements are considerably smaller, employing functions of a high depth in relation to functions of a low depth. For this reason, due to the fact that CBF combine stability with the possibility of non-canalising behaviour in some variables, CBF could be employed for canalisation modelling.
3.3. Validation
It could be possible to obtain several solutions for the same problem due to the nature of CS. Besides, several networks made of NCBF might explain the same system. Then, the algorithm exposed in this analysis obtains different solutions with each execution. Therefore, it is necessary to have a mechanism to separate those networks with biological meaning from those that lack any sense. This mechanism has been called validation in this work. The objetive of validation is to assess whether an obtained network is biologically coherent or not. It can be based in different properties such as the structure of the network, the presence of some states in its topography, or in the nature of attractors of the obtained model, as it is the case of this analysis.
BN are finite systems, which means that their topology is made of a group of finite states, conveyed in the truth table of every network. Since the number of possible states is a finite set, there must be a time in which every network expresses a state that was expressed previously. Consequently, after a number of time steps the network will enter in a cyclic series of repeating states, a loop. This loop is called an attractor and it can be constituted by one state (steady-state attractor) or by multiple states (simple cycle) [21,22]. In practice, these attractors hold biological correspondence with the system, for example, if the system models the transition between cell types, each of these types will be expressed through a different attractor. Furthermore, the attractor related to a cell type should show the most paradigmatic nature of that type. Only the meaningful models will show a behaviour coherent with the biology to depict. Therefore, what it called validation in this analysis is just the filtering of the obtained models based on this criterion. It is a way of introducing available knowledge in the inference.
3.4. Algorithm of Inference of Boolean Networks Based on Both Conflicts Strategy and Nested Canalising Boolean Functions
In this section, we expose an algorithm based on [8] with the modifications described in previous sections. For the sake of clarity, every step is explained according to the example of Figure 3.
Starting from a graph that represents the system to be modelled:
- Calculate all possible networks made of NCBF which are compatible with the graph.From now on, the selected network used along the example will be the one shown in Equation (8). It is called a “prenetwork” to distinguish it from the final network. We will say a NCBF is compatible with a graph when the pairs of canalising/canalised values related to its variables convey the biological meaning underlying the edges of the graph. That meaning is the same that was stated for pathways in CS. For example, the function of Equation (8) is compatible with the graph of Figure 3 because the pairs depict the behaviour of an activator for B (first pair), and the behaviour of an inhibitor for C (second pair). Indeed, this is the nature expressed in Figure 3. This process is the one employed to obtain models through combinatorics with NCBF. It is completely explained in the Supplementary Materials:Several networks will be obtained according to combinatorics with NCBF. Therefore, to develop all the possible models, every further step described is to be applied to all these prenetworks, not only to the selected one. Consequently, at the end of the algorithm, a set of networks will be obtained.
- Represent the graph in the form of independent pathways.The graph in Figure 3 represents the set of pathways conveyed in Equation (9). There are two possible pairs of canalising/canalised values for activators () and for inhibitors () according to Section 2.2. Therefore, given n pathways in the network, there are groupings like the one shown in Equation (9). Hence, there are several solutions attending the chosen group. For the example developed along this section, the chosen group is the one shown in Equation (9). In this example, this group has been selected for the sake of clarity, however, all the possible groups should be studied:
- Set a priority criterion to the pathways when there are existing conflicts among them.In Section 3.1, a priority matrix was stated for the existence of conflicts between pathways. Nonetheless, other criteria can be used, such as the one set out in [8]. In the example of Section 3.1, the pathway’s priority has been established arbitrarily.
- Apply the Conflicts Resolution Algorithm in every node.All the steps needed to solve the conflicts of a given node are described in Section 3.5, the Conflicts Resolution Algorithm. The first node in being assessed will be the node D given that it is the node which best exposes the nature of the algorithm.
- Iterate over the network nodes until there is no conflict found in the total set of pathways.The algorithm iterates over the nodes until there is no conflict. Since new pathways appear through the conflicts solution, contradictions among pathways may propagate to different nodes. At the end of the process, there will not be any conflict among pathways.
- Impose the set of pathways on the prenetwork of step 1.It is the process described in Table 3 (step 3e in Section 3.5) applied over the whole set of nodes in the network. The result is the truth tables of every node.
 Table 3. Truth tables for the node D. It is conveyed the information stored in the Pathway Information (PI), Prenetwork (PN), and Resulting Network (RN). The red rows indicate the arguments combinations to which the value in the pathways information is not the same to the one expressed in the prenetwork. The x represents undefined values that, consequently, cannot be imposed over the prenetwork.
Table 3. Truth tables for the node D. It is conveyed the information stored in the Pathway Information (PI), Prenetwork (PN), and Resulting Network (RN). The red rows indicate the arguments combinations to which the value in the pathways information is not the same to the one expressed in the prenetwork. The x represents undefined values that, consequently, cannot be imposed over the prenetwork. - Filter the total amount of networks to only retain those with biological meaning.Since different executions of the algorithm may drive to different solutions, the results that are biologically coherent are to be selected. In other words, this is the scenario described in Section 3.3, where the principles behind this filtering are described.
3.5. Conflicts Resolution Algorithm
This algorithm solves the conflicts of a given node. The example developed in this section takes the node D given that it is the node that best shows the nature of the method.
- Take all the pathways which have the selected node in the right side of the graph.In this case, the selected pathways are and . Both pathways impose conditions over the node D. Note that in this example there are only two pathways, nevertheless, usually there will be more.
- Pair the pathways up in couples of one activator and one inhibitor.There are only two pathways in conflict, one couple. The activator is and the inhibitor is . If all the pathways in the system, related to a node, were either activators or inhibitors, the algorithm would be finished because there cannot be conflicts among pathways of the same nature.On the other hand, regarding this example, there is not any unpaired pathway. If there were unpaired pathways, these would be left apart (we will refer to them as the isolated group). They will be reincorporated to the whole set in following steps.
- For each couple (development of the Section 2.2):
- (a)
- Check if there is any conflict among the two members of the couple.The couple of the example has a conflict because the pathways have an overlapping region;
- (b)
- If there is no conflict, go to the following couple and apply the previous step. Otherwise define the region of the conflict, Ψ, and continue.In the example of these two pathways .Nonetheless, it may occur that in some pairs . For instance, the pair and could never bring any conflict because the regions of action do not overlap, that is to say, because (note that the couple with nodes Z and T does not belong to the example of the Figure 3);
- (c)
- Obtain the prioritised pathway in relation to the priority criterion and make no modification upon the prioritised pathway.Owing to the lack of experimental data (Section 3.1), priority matrices are generated randomly. In this example, the prioritised pathway is according to Table 2. It has been prioritised this pathway to make the example clearer;
- (d)
- Modify the non-prioritised pathway to avoid the conflict.In this example, the non-prioritised pathway is . Since the prioritised one is , to avoid the conflict the negation of () in the antecedent of the non-prioritised pathway is introduced. This modification is shown in Equation (10):
- (e)
- Impose all the information given by the pathways over the function of the treated node in the prenetwork.The pathways are introduced through truth tables according to their antecedents. In this example, there are two pathways: and . For the second pathway, it means that . On the contrary, . The values of the truth table in the Pathway Information (PI) column are imposed over the truth table of the Prenetwork (PN), to obtain the Resulting Network (RN). All this process is depicted in Table 3.This is the process referenced in step 4 in Section 3.4 to obtain the truth tables of the final network obtained the pathways, the final set without conflicts;
- (f)
- Take the resulting network to calculate .In relation to the example, equals a boolean expression. In order to obtain this expression, the attention is to be focused on the truth table of RN in Table 3. The combinations of arguments are to be taken that make the node function equal to 1, because the aim is to obtain . Consequently, this set of combinations is , 0001, 0100, 0101, 1000, 1001, 1100, .Every combination of the set corresponds to a minterm. Recall that a minterm is a product of all the variables in the function, in which no variable appears twice or is paired with its negation. Therefore, equals the sum of the related minterms of the set. Thus, equals the sum of all the minterms in Equation (11), whose simplified expression is :There is a minterm for every combination. Likewise, given a minterm, every node appears negated if in the combination it equals 0. For instance, the combination 0101 becomes . In other words, the objective is to obtain the disjunctive normal form of the function from its results in Table 3, that is the sum of the products depicted in Equation (11);
- (g)
- Compute the solution pathway.In previous steps, it was already obtained that and . On the other hand, the solution pathway obeys the formula . Therefore, the new pathway to be introduced is depicted in Equation (12), which is equivalent to Equation (13). For the sake of clarity, all along the article, the notation described in Equation (13) is employed:In this case, S has only one term although it may have several terms. For instance, let us suppose the previous pathway to be the one conveyed in Equation (14), then there are several terms (every term is enclosed by a parenthesis). Moreover, every term has 2 factors:According to [8], it is enough with fulfilling the requirements of one term to make the whole statement true. This is coherent with Boolean Logic. In case of two or more terms, one has to be chosen. The conditions established by the selected one will be the only conditions to be met. In addition, since there is no way of knowing the result of choosing a given term, its election is taken randomly. In this example, the second is elected. For this reason, Equation (14) becomes Equation (15):
- Join all the pathways of each couple in a group together with the ones of the isolated group, if there were unpaired pathways in point 2.Since in this example there were no pathways in the isolated group, the current pathways for the node D are shown in Equation (17):
- Repeat the previous two steps until all the pathways have been compared and there are no conflicts among the pathways of the node.It can be seen in Equation (17) that all the pathways are compatible in relation to node D. Consequently, the iteration would continue to the next node.
4. Results
The algorithm developed in this article has been applied over two biological systems: The EMT and the lac operon.
4.1. Epithelial-Mesenchymal Transition
4.1.1. System Modelled
The EMT is the process by which epithelial cells lose their polarity and cell-cell bindings to gain mobility in the form of mesenchymal cells. This is a key process implicated in metastasis [12], represented in the gene circuit of Figure 5 [12,23,24,25]. In addition to the epithelial and mesenchymal cell states, it is considered a third state in EMT, the hybrid state [24,25], although its nature remains uncertain [12].
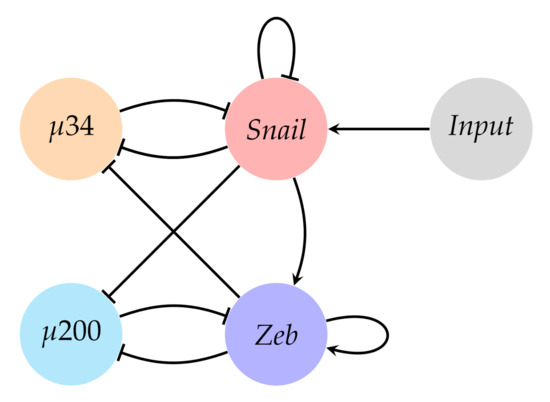
Figure 5.
Gene circuit of the Epithelial-Mesenchymal Transition (EMT).
This circuit is made of two microRNAs ( and ) and two genes (Snail and Zeb). The network is divided in two mutually inhibitory toggle switches (34 vs. Snail and 200 vs. Zeb) [12]. Conversely, Snail and Zeb constitute a feed-forward loop through both 34 and 200 [12]. On the other hand, EMT is triggered through several transcription factors and signalling pathways summarised through the Input node, which indicates the beginning of EMT. According to these features, there have been searched systems with the attractors defined in Table 4 [12] based on the idea that Zeb is a mesenchymal marker and 200 is an epithelial marker. In this approach, it has been considered that every cell state refers to a steady attractor, which is a one-state attractor.

Table 4.
Relationship between attractors and cell states in the EMT.
4.1.2. Result
Since the priority matrix was randomly generated, the analysis was repeated several times to perform the inference with multiple matrices. Likewise, the nature of the algorithm is an important source of variability since there is no criteria to minterms selection, which increases the total number of results obtained for the system of Figure 5. From all these networks, it has been selected the one exposed in Equation (18) whose attractors are shown in Table 5.

Table 5.
Attractors of the network of Equation (18). Every row represents a state of an attractor. In the cyclic attractors (epithelial), states are ordered from top to bottom.
Regarding the result of Equation (18), the conflicts solved during the inference, and the pathways developed through the process, may be found in the Supplementary Materials. The results are explored in the Discussion section.
4.2. Lac Operon
4.2.1. System Modelled
The lac operon was the first genetic circuit characterised [26]. This mechanism regulates the lactose metabolism and, due to its simplicity, has been widely studied. That is the reason for its suitability in testing new modelling methods, and the reason why it has been analysed in this work. In the presence of lactose, the lac operon starts the transcription of -galactosidase, an enzyme that turns lactose into allolactose, to degrade allolactose in glucose and galactose thereafter. Owing to the fact that glucose is the product of lactose metabolism, in the presence of glucose the execution of the lac operon would not make any sense. Therefore, if there is glucose available in the cytoplasm, this system avoids its activation through the cAMP-CAP complex, which blocks the synthesis of mRNA. In this analysis, used as a simplified model to represent the lac operon [17], this model neither includes the cAMP-CAP complex nor other dynamics. Nevertheless, it still conveys the overall nature of the lac operon with its strong bistability, representing two possible scenarios: The absence and presence of lactose.
The lac operon dynamics are conveyed in the graph of Figure 6. This graph has been developed from the reduced model of 3 variables shown in Equation (19) [17]. In this model there are three system variables: Allolactose (A), -galactosidase (B), and messenger RNA (M). The rest of parameters are constants [17] except lactose (L), which is an input variable.
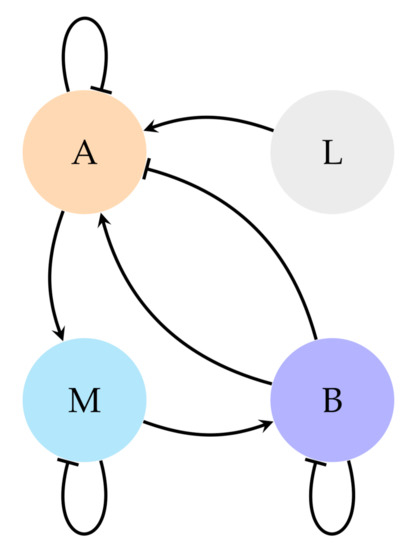
Figure 6.
Gene circuit of the lac operon.
The lac operon manifests a bistable behaviour whose two states correspond with the absence and saturation of lactose [27,28]. This bistability is the feature upon which validation has been centred. They have been searched systems with the attractors depicted in Table 6, one attractor per state.

Table 6.
Relationship between attractors and environmental scenarios in the lac operon. There is one attractor per scenario and every row conveys an attractor.
In this way, the movement between attraction basins could only be achieved through changes in the input variable (lactose, L) or by stochastic events [29,30]. Nonetheless, given a situation of changing lactose concentration, the transition from one stationary regime to the other is not instant. On the contrary, a little transitional regime associated with a situation of middle lactose concentration is developed. In BN, this transitional regime can be represented through a third basin of attraction [29]. Nevertheless, because it is hard to define the middle lactose concentration, we have focused on the attractors defined in Table 6 to perform the validation.
4.2.2. Result
According to these conditions, from all the networks obtained by the algorithm, the one described in Equation (20) was selected. There were many different networks obtained, nevertheless, several patterns repeated all along them. This network was selected because it was considered to depict all these common features. The attractors of this network are shown in Table 7:

Table 7.
Attractors of the network of Equation (20). Every row represents an attractor state.
Regarding the result of Equation (20), the pathways developed during the inference and the conflicts solved are in the Supplementary Materials.
5. Discussion
In this section, the differences between the obtained models and those found in bibliography are exposed, as well as how they explain the biology of each system. Despite the uncertain nature of the priority matrices, the selected networks are archetypical of the whole set of BN produced by the algorithm, and have not been reached by chance. On the contrary, they are accurate representations of the logic behind the inference process.
5.1. Epithelial-Mesenchymal Transition
There are some differences between the model exposed in Equation (18) and the one shown in [12]. In relation to the epithelial attractor, our solution shows a cyclic attractor of two states, whereas the network exposed in [12] obtains a steady-state attractor. Firstly, this may suggest that our algorithm is to be depurated in further versions to obtain better results. However, as it will be explained in the case of the lac operon, results like these might expose other lines of research to unravel hidden phenomena. Regarding the hybrid state, the biology of its attractor is not completely explained [12]. Therefore, although the hybrid attractor of the network in Equation (18) is not the same as the one in [12], its biology is coherent in the sense that it gathers mesenchymal and epithelial characteristics.
Finally, regarding the basins of the mesenchymal and hybrid states, the problem lies in the size and topology of the attractor basins. In [12], the hybrid and mesenchymal basins are different than those in the network of Equation (18), which is the main difference between both solutions. Its explanation should rely upon biological data, which exceeds the scope of this work. Nevertheless, the basins are correct in relation to the algorithm.
5.2. Lac Operon
The main difference between this system and the EMT is the relationship between nodes A and B (allolactose and -galactosidase). It can be seen in the graph in Figure 6 that B simultaneously activates and inhibits A. This contradiction is difficult to symbolise through NCBF because they can only convey one canalising value for a variable.
Nevertheless, this structural problem of the NCBF does not exist in CS because the conflict allows the imposition of the value with a higher priority (what would be the value placed in the outer layers of the NCBF) and redirects the dynamics of the non prioritised to be fulfilled in the following time steps through the solution pathway (Section 2.2). In other words, provided a situation like the one depicted in Figure 6, in CS the question is about which pathway is delayed, when in NBCF the question is about which pathway is ignored.Therefore, the algorithm exposed in this article exceeds the expression possibilities provided by a pure NCBF approach.
Regarding the obtained model depicted in Equation (20), the attractors in Table 7 are not the same as those in Table 6. Nonetheless, the network represents the biology depicted in the model of Equation (19). Firstly, the lactose absence attractor. According to Table 7, this is a cyclic attractor which contains the state of the steady attractor conveyed in Table 6. At first sight, the appearance of the second state may be disturbing. The reason is that, in line with its structure, this attractor provokes the generation of -galactosidase and mRNA from a situation of absence of all the metabolites implied in the system. Surprisingly, it is documented [27] that the lac operon system is not “perfect”. Every once in a while, the repressor protein falls down from the DNA strand, resulting in the production of some mRNA which produce -galactosidase traces. These “imperfections” are crucial for the bistability behaviour of the system [27]. Consequently, the cyclic attractor for lactose absence is an accurate representation of the system behaviour when lacking lactose.
Secondly, the attractor of the middle lactose concentration. Despite its form not being defined, the one shown in Table 7 is a valid expression due to two reasons: (1) It is coherent with the dynamics of the system, and (2) it may be a valid representation of middle concentration. Nonetheless, due to the switching between active and inactive allolactose, it indeed may be a good characterisation. Notice that lactose cannot change because it is an input and allolactose is the first product of lactose metabolism in the lac operon system. In consequence, this attractor is valid in relation to the system’s biology. Finally, the lactose saturation attractor does not present any inconvenience, it is exactly the one searched.
In summary, the model obtained represents the system, insofar as it manifests the lac operon nature.
5.3. Further Steps
In this article models of two different systems have been exposed: EMT and lac operon. It has been stated that there are discrepancies between the results obtained and the previous assumptions based on the bibliography. However, they do not compromise the modelled nature in the network. However, such differences point the way forward. Even though it has been demonstrated the ability of the algorithm to elucidate non-contemplated features, such as the -galactosidase traces in the lac operon model. The final objective is the achievement of accurate models in perfect accordance with previous results.
Therefore, this is the first version of an algorithm that is necessary to improve based on two principles: (1) Accuracy of the obtained models and (2) inference time. In relation to the first point, this algorithm overcomes both NCBF and CS, however, the theoretical basis is to be further extended regarding the canalising and canalised values. These values are present in both NCBF and CS, although their connection between one framework and the other remains unclear. For example, attending the definitions of the activator and inhibitor, they can be achieved different groups of pathways from the same graph. These groups correspond with combinations of value pairs that can be employed as canalising/canalised pairs to define a prenetwork. In consequence, there are prenetworks as groups of pathways. At this point, it is questionable that employing the same pairs for pathways and prenetwork improves convergence. This can be appreciated in the EMT result, which implements the same combination in both. Nevertheless, the lac-operon result changes the pair of the -galactosidase between pathways and prenetwork in relation to the allolactose expression.
Regarding inference time, according to the analyses shown in this work, it took 1 h and 20 min to launch the algorithm between 800,000 and 1,200,000 times depending on 2 aspects: Hardware and system complexity. The later is provided by the number of pathways of the system. Likewise, the presence of contradictory pathways significantly increases computation time. In relation to the hardware, all computing was performed on a system with an Intel Core i7-1065G7 (1.3 GHz) and 8 GB of RAM. Finally, the algorithm exposed in this analysis were coded in Python employing the multiprocessing module and five processes. Future versions of the algorithm aspire to decrease this computation time.
On the other hand, despite employing different priority matrices (randomly generated), attractors tend to repeat. In other words, priority seems to have limited influence over the inference process. On the contrary, the canalising/canalised pairs appear to be related to the attractors obtained. Furthermore, the pairs combination employed in pathways and prenetwork seems to be related to the whole attractors set of the resulting network. Altogether, it may be due to the fact that nodes manifest different variants of the same behaviour depending on the position of its activity. In other words, the same node might have different pairs for its action in the prenetwork (general behaviour) in relation to its pathways-defined performance (specific behaviour).
Additionally, it is convenient to consider the appeareance of contradictory nodes in our approach to NCBF. For all the reasons stated before, NCBF seems to manifest poor performance when handling relationships like the one exposed between the nodes A and B in Figure 6. In the simulations performed during this work, they have not been introduced in the prenetworks, or what is to say, all the prenetworks employed in the lac operon were generated without one of the two contradictory dynamics. Nonetheless, how NCBF deal with this kind of behaviour deserves further study so as to obtain more accurate prenetworks.
Finally, note that in the definition of pathway, it is not stated that the time steps are to be always 1, although in practice they are always 1. This restriction has two effects: (1) Loss of dynamics and (2) loss of solutions. Regarding the first point, note that, in the conflicts, sometimes they are obtained pathways whose domain is the empty set. Thus, the dynamics conveyed in those pathways are lost. In relation to the second, the modification of the pathway definition to express a wider range of time steps is necessary to expand the region of reachable solutions, increasing the method’s expressiveness.
Summarising, there are multiple possibilities to improve the algorithm explained in this work. Firstly, the theory employed can be extensively developed through the study of the canalising/canalised pairs and their relationship between the CS and NCBF. Secondly, there are several aspects such as priority or contradictory links among nodes whose management can be improved through alternative mechanisms still to devise.
6. Conclusions
In this analysis a new algorithm for the inference of Boolean Networks models was proposed. This algorithm was developed from a new framework built upon the theory of Nested Canalising Boolean Functions (NCBF), called in this work Conflicts Strategy (CS). In order to show the power of the algorithm, it was applied to model two biological processes: EMT and the lac operon. The reasoning behind the inference could be assessed by means of the analysis of the pathways and conflicts solved during the execution of the method. This assessment is of great interest to: (1) Validate the obtained models and (2) evaluate the coherence of the inferred knowledge through new pathways.
However, we plan to improve the algorithm in further versions so as to enhance two aspects: (1) Accuracy of the obtained models, and (2) inference time. The new framework devised through the combination of NCBF with CS remains incomplete. Even so, this algorithm could, as it has been demonstrated in both examples, represent satisfactorily the nature of the modelled systems, driving into the obtention of valuable conclusions. For all these reasons, this method is a state-of-the-art procedure to infer knowledge from every system subject to be expressed through a directed graph. Therefore, its applications, although rooted in life sciences, can comprehend areas such as underground design or airlines management.
Supplementary Materials
The following are available at https://www.mdpi.com/2227-7390/9/4/373/s1.
Author Contributions
Design and development of the Mathematical model, M.R.-C.; Formal analysis, M.R.-C., C.S. and B.G.-M.; computational framework, M.R.-C.; implementation of the simulations, M.R.-C.; performance of the calculations, M.R.-C. and G.R.; application to the EMT-Transition and Lac Operon, M.R.-C. and G.R.; writing—original draft, M.R.-C., C.S. and B.G.-M.; writing—review and editing, M.R.-C., B.G.-M., C.S. and G.R.; supervision, M.R.-C., B.G.-M., C.S. and G.R.; funding acquisition, G.R. All authors have read and agreed to the published version of the manuscript.
Funding
This paper has been supported by the Generalitat Valenciana grant AICO/2020/114.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kauffman, S. Homeostasis and differentiation in random genetic control networks. Nature 1969, 224, 177–178. [Google Scholar] [CrossRef]
- Thomas, R. Boolean formalization of genetic control circuits. J. Theor. Biol. 1973, 42, 563–585. [Google Scholar] [CrossRef]
- Akutsu, T. Algorithms for Analysis, Inference, and Control of Boolean Networks; World Scientific: Singapore, 2018. [Google Scholar]
- Kauffman, S.; Peterson, C.; Samuelsson, B.; Troein, C. Random Boolean Network Models and the Yeast Transcriptional Network. Proc. Natl. Acad. Sci. USA 2003, 100, 14796–14799. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.; Peterson, C.; Samuelsson, B.; Troein, C. Genetic Networks with Canalyzing Boolean Rules Are Always Stable. Proc. Natl. Acad. Sci. USA 2004, 101, 17102–17107. [Google Scholar] [CrossRef] [PubMed]
- Thieffry, D.; Kaufman, M. Regulatory circuits: From living systems to hyper-chaos. A special issue dedicated to the memory of René Thomas. J. Theor. Biol. 2019, 474, 42–47. [Google Scholar] [CrossRef]
- Huang, S.; Kauffman, S. Complex gene regulatory networks—From structure to biological observables: Cell fate determination. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: Cham, Switzerland, 2009. [Google Scholar]
- Layek, R. Pathways, Networks and Therapy: A Boolean Approach to Systems Biology. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2012. [Google Scholar]
- Das, H.; Deshpande, A.; Layek, R.K. A Linear Formulation of Asynchronous Boolean Networks. IEEE Control Syst. Lett. 2019, 3, 284–289. [Google Scholar] [CrossRef]
- Maheshwari, P.; Albert, R. A framework to find the logic backbone of a biological network. BMC Syst. Biol. 2017, 11, 122. [Google Scholar] [CrossRef] [PubMed]
- Kourou, K.; Rigas, G.; Papaloukas, C.; Mitsis, M.; Fotiadis, D.I. Cancer classification from time series microarray data through regulatory Dynamic Bayesian Networks. Comput. Biol. Med. 2020, 116, 103577. [Google Scholar] [CrossRef]
- Joo, J.I.; Zhou, J.X.; Huang, S.; Cho, K.H. Determining Relative Dynamic Stability of Cell States Using Boolean Network Model. Sci. Rep. 2018, 8, 12077. [Google Scholar] [CrossRef]
- Layek, R.K.; Datta, A.; Dougherty, E.R. From biological pathways to regulatory networks. Mol. BioSyst. 2011, 7, 843–851. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.X.; Samal, A.; d’Hérouël, A.F.; Price, N.D.; Huang, S. Relative Stability of Network States in Boolean Network Models of Gene Regulation in Development. Biosystems 2016, 142–143, 15–24. [Google Scholar] [CrossRef]
- Hallgrimsson, B.; Green, R.M.; Katz, D.C.; Fish, J.L.; Bernier, F.P.; Roseman, C.C.; Young, N.M.; Cheverud, J.M.; Marcucio, R.S. The developmental-genetics of canalization. Canalization, a central concept in biology. Semin. Cell Dev. Biol. 2019, 88, 67–79. [Google Scholar] [CrossRef] [PubMed]
- Robeva, R.; Kirkwood, B.; Davies, R. Mechanisms of Gene Regulation: Boolean Network Models of the Lactose Operon in Escherichia Coli. In Mathematical Concepts and Methods in Modern Biology; Elsevier: Amsterdam, The Netherlands, 2013; pp. 1–35. [Google Scholar] [CrossRef]
- Yildirim, N.; Santillán, M.; Horike, D.; Mackey, M.C. Dynamics and bistability in a reduced model of the lac operon. Chaos 2004, 14, 279–292. [Google Scholar] [CrossRef] [PubMed]
- Waddington, C.H. Canalization of Development and the Inheritance of Acquired Characters. Nature 1942, 150, 563–565. [Google Scholar] [CrossRef]
- Li, Y.; Adeyeye, J.O.; Murrugarra, D.; Aguilar, B.; Laubenbacher, R. Boolean Nested Canalizing Functions: A Comprehensive Analysis. Theor. Comput. Sci. 2013, 481, 24–36. [Google Scholar] [CrossRef]
- Paul, E.; Pogudin, G.; Qin, W.; Laubenbacher, R. The Dynamics of Canalizing Boolean Networks. Complexity 2020, 2020, 3687961. [Google Scholar] [CrossRef]
- Hopfensitz, M.; Müssel, C.; Maucher, M.; Kestler, H.A. Attractors in Boolean networks: A tutorial. Comput. Stat. 2013, 28, 19–36. [Google Scholar] [CrossRef]
- Schwab, J.D.; Kühlwein, S.D.; Ikonomi, N.; Kühl, M.; Kestler, H.A. Concepts in Boolean network modeling: What do they all mean? Comput. Struct. Biotechnol. J. 2020, 18, 571–582. [Google Scholar] [CrossRef] [PubMed]
- Grosse-Wilde, A.; Fouquier d’Hérouël, A.; McIntosh, E.; Ertaylan, G.; Skupin, A.; Kuestner, R.E.; Del Sol, A.; Walters, K.A.; Huang, S. Stemness of the hybrid Epithelial Mesenchymal State in Breast Cancer and Its Association with Poor Survival. PLoS ONE 2015, 10, e0126522. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; Jolly, M.K.; Levine, H.; Onuchic, J.N.; Ben-Jacob, E. MicroRNA-based regulation of epithelial–hybrid–mesenchymal fate determination. Proc. Natl. Acad. Sci. USA 2013, 110, 18144–18149. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, X.J.; Zhang, H.; Teng, Y.; Li, R.; Bai, F.; Elankumaran, S.; Xing, J. TGF-Induced epithelial-to-mesenchymal transition proceeds through stepwise activation of multiple feedback loops. Sci. Signal. 2014, 7, ra91. [Google Scholar] [CrossRef] [PubMed]
- Jacob, F.; Monod, J. Genetic regulatory mechanisms in the synthesis of proteins. J. Mol. Biol. 1961, 3, 318–356. [Google Scholar] [CrossRef]
- Robeva, R.S.; Macauley, M.; Chen, G. Algebraic and Combinatorial Computational Biology; OCLC: 1066055671; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Novick, A.; Weiner, M. Enzyme Induction as an All-or-None Phenomenon. Proc. Natl. Acad. Sci. USA 1957, 43, 553–566. [Google Scholar] [CrossRef] [PubMed]
- Veliz-Cuba, A.; Stigler, B. Boolean Models Can Explain Bistability in the Lac Operon. J. Comput. Biol. 2011, 18, 783–794. [Google Scholar] [CrossRef] [PubMed]
- Santillán, M.; Mackey, M.C. Quantitative approaches to the study of bistability in the Lac Operon Escherichia coli. J. R. Soc. Interface 2008, 5, S29–S39. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).