Nonlocal Reaction–Diffusion Models of Heterogeneous Wealth Distribution
Abstract
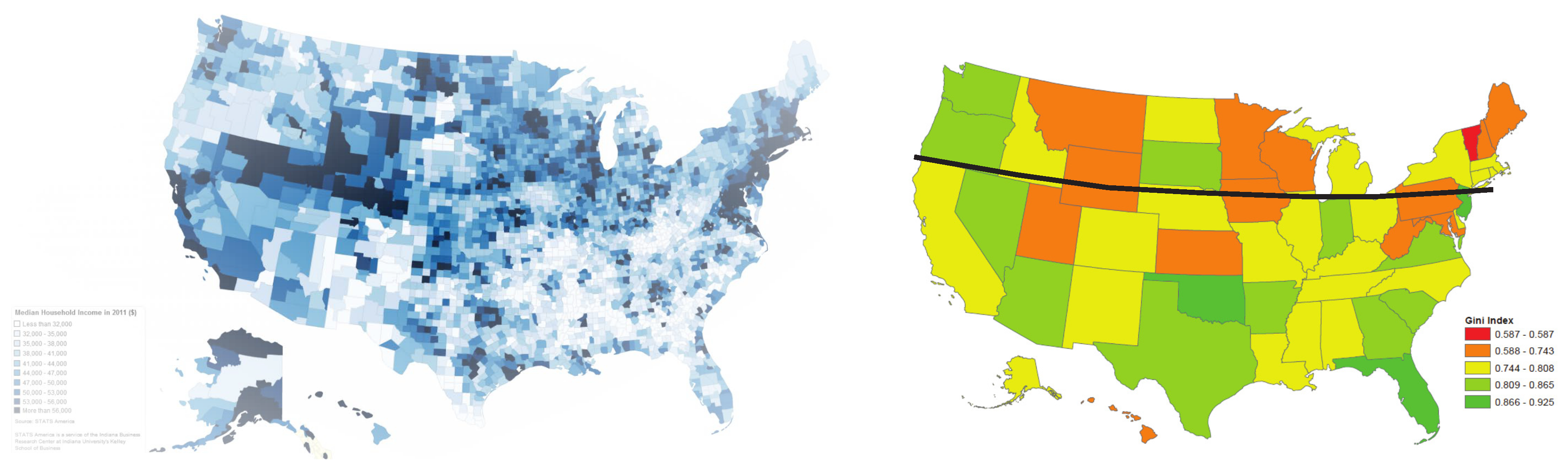
1. Introduction
2. Reaction–Diffusion Model of Population-Wealth Distribution
2.1. Basic Model with Constant Resources
2.2. Variable Resources
- Local dependence on wealth: . The first factor shows that extraction of resources depends on wealth, and the second factor that resources are consumed proportionally to wealth. Here , , and k are some positive parameters.
- Nonlocal dependence on wealth: , where , where the kernel shows how the consumption of resources depends on the distance . The kernel function is even and non-negative. It can take into account the cost of transportation and other factors limiting the usage of distant resources.
- Global dependence on wealth: , where . In this case, resources are available independently of their location. In particular, this may be the case of intellectual property, software, and other “immaterial” resources, or the cases where the cost of transportation and other distance-related expenses can be neglected.
3. Wealth Distribution in Excess of Human Resources
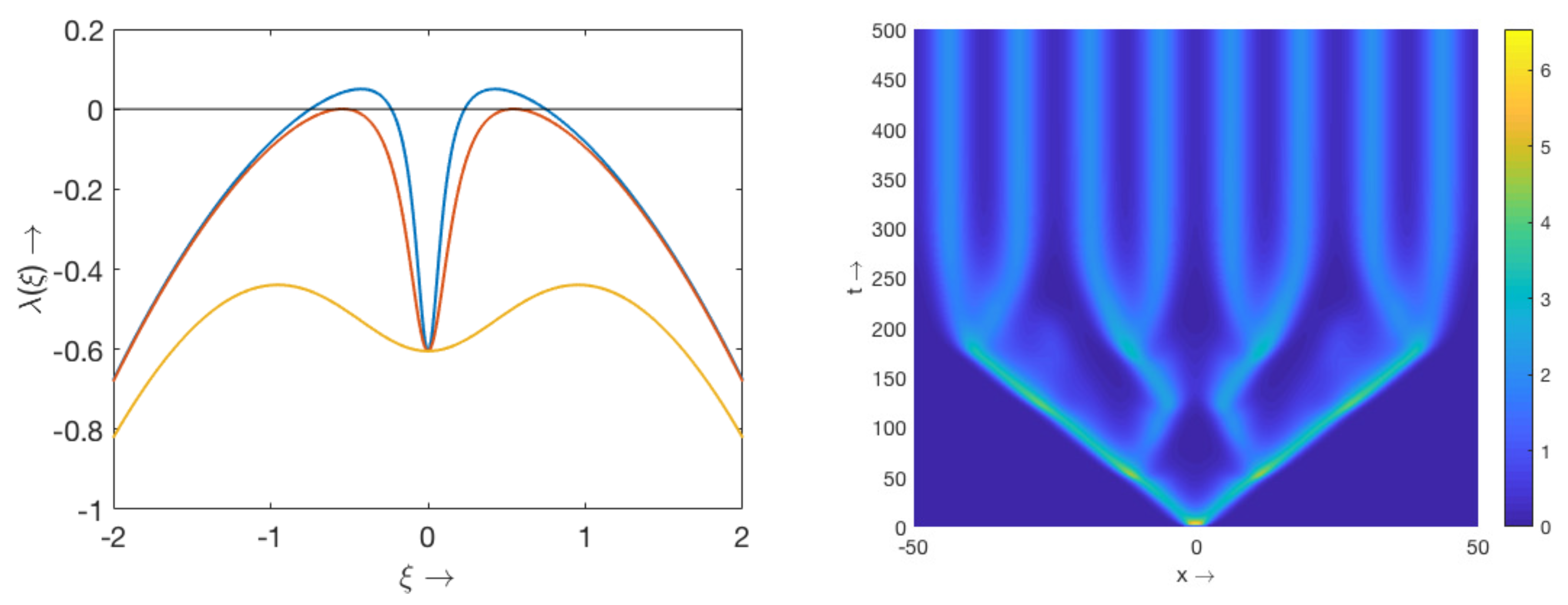
3.1. Nonlocal Consumption of Resources
3.2. Global Consumption of Resources
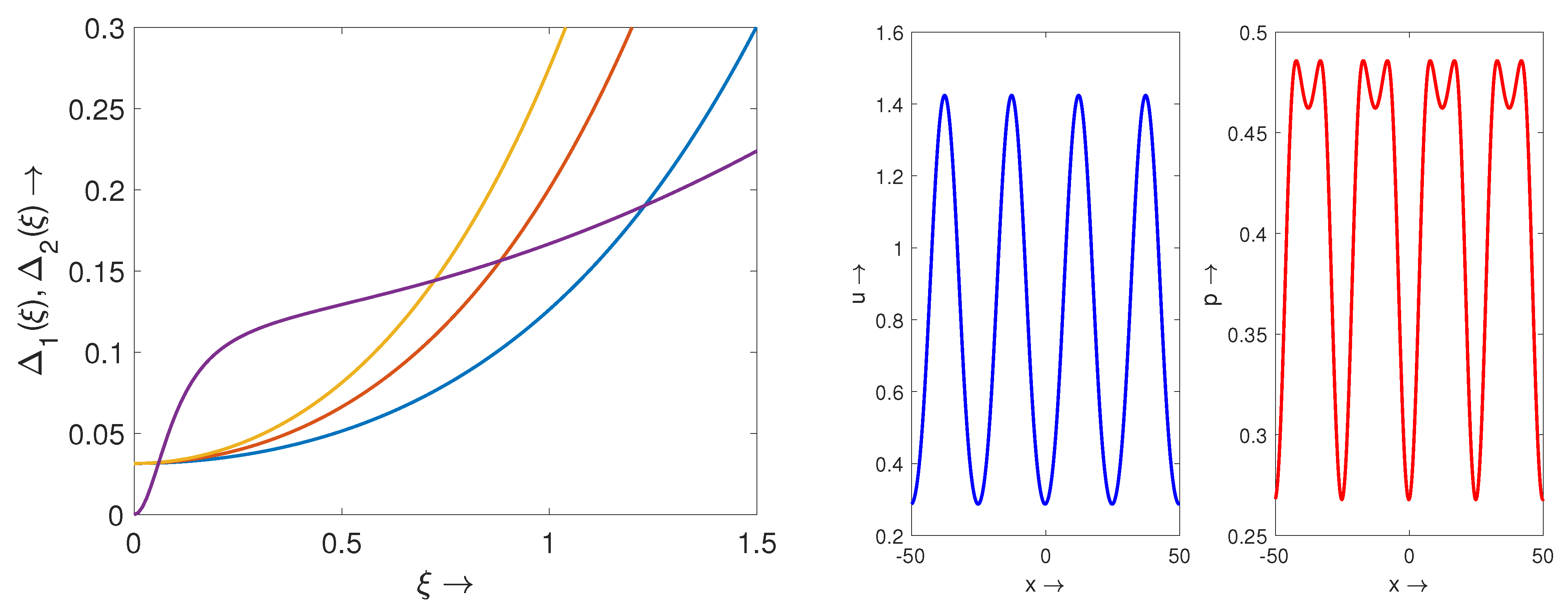
4. Periodic Structures and Pulses for the Wealth-Population System
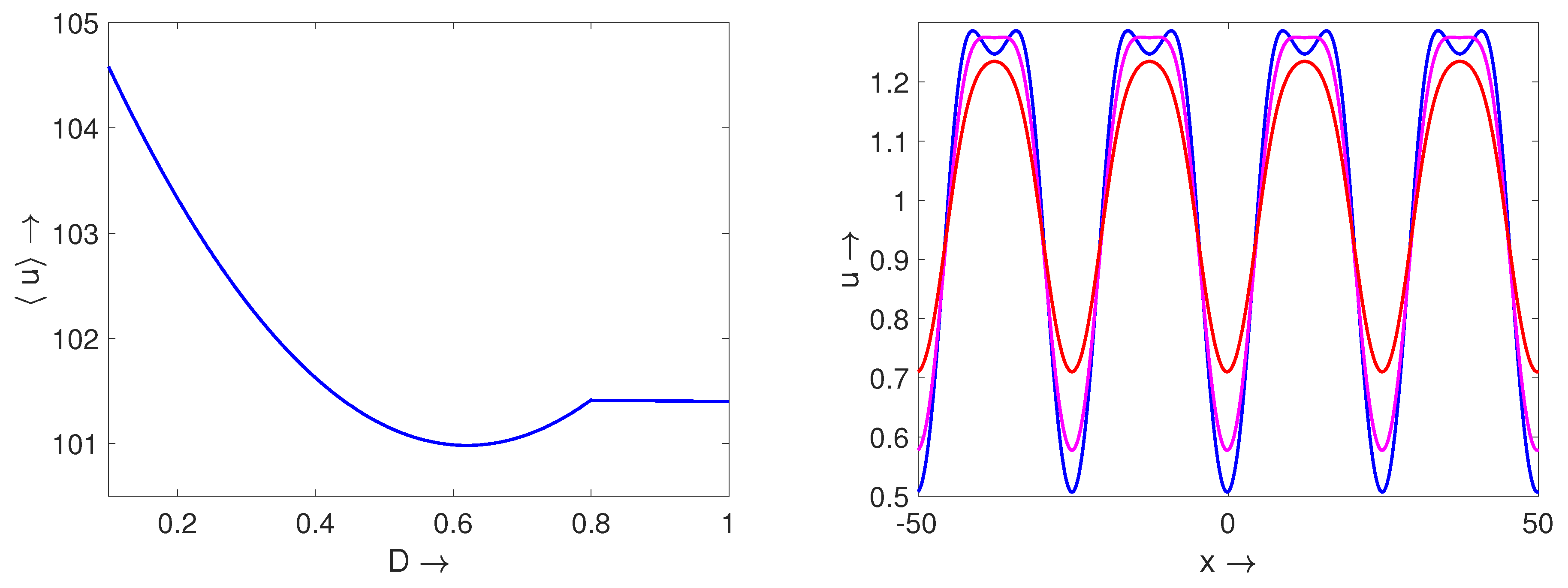
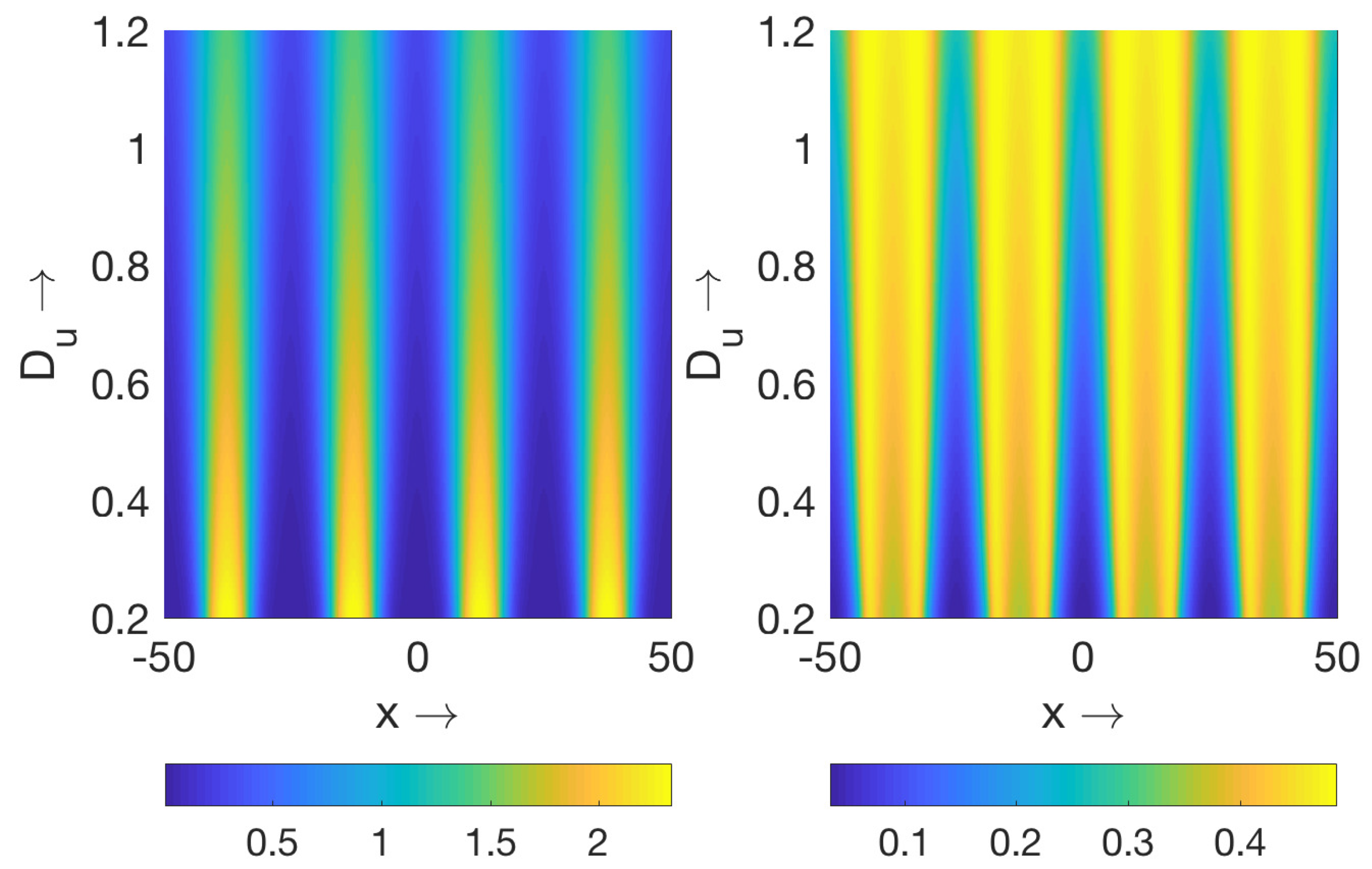
4.1. Periodic Structures for Nonlocal Consumption
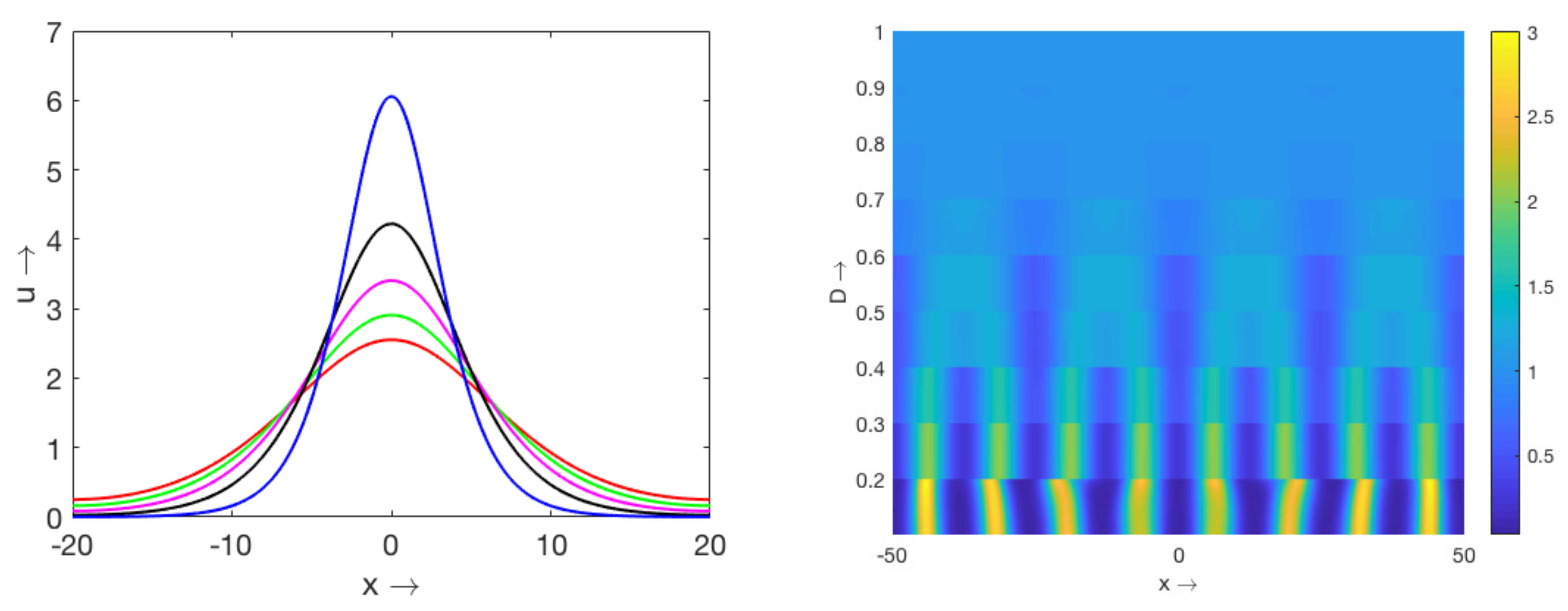
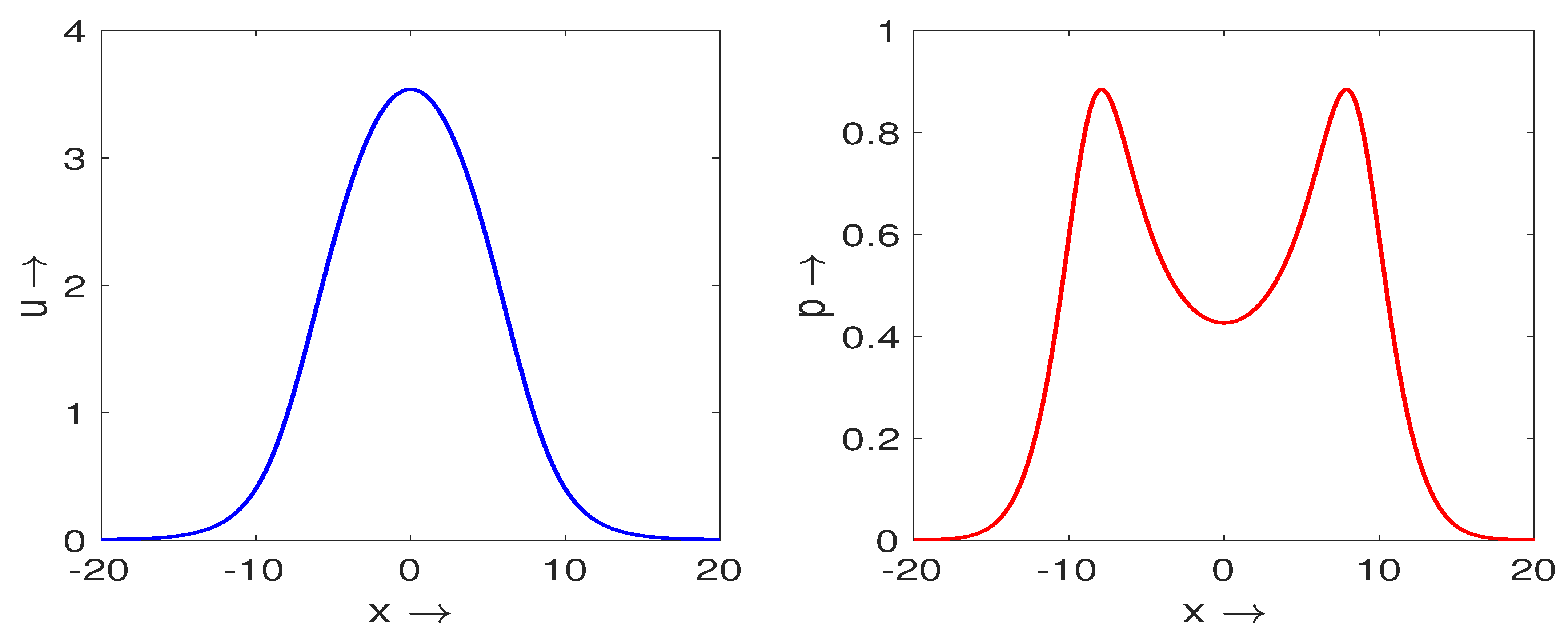
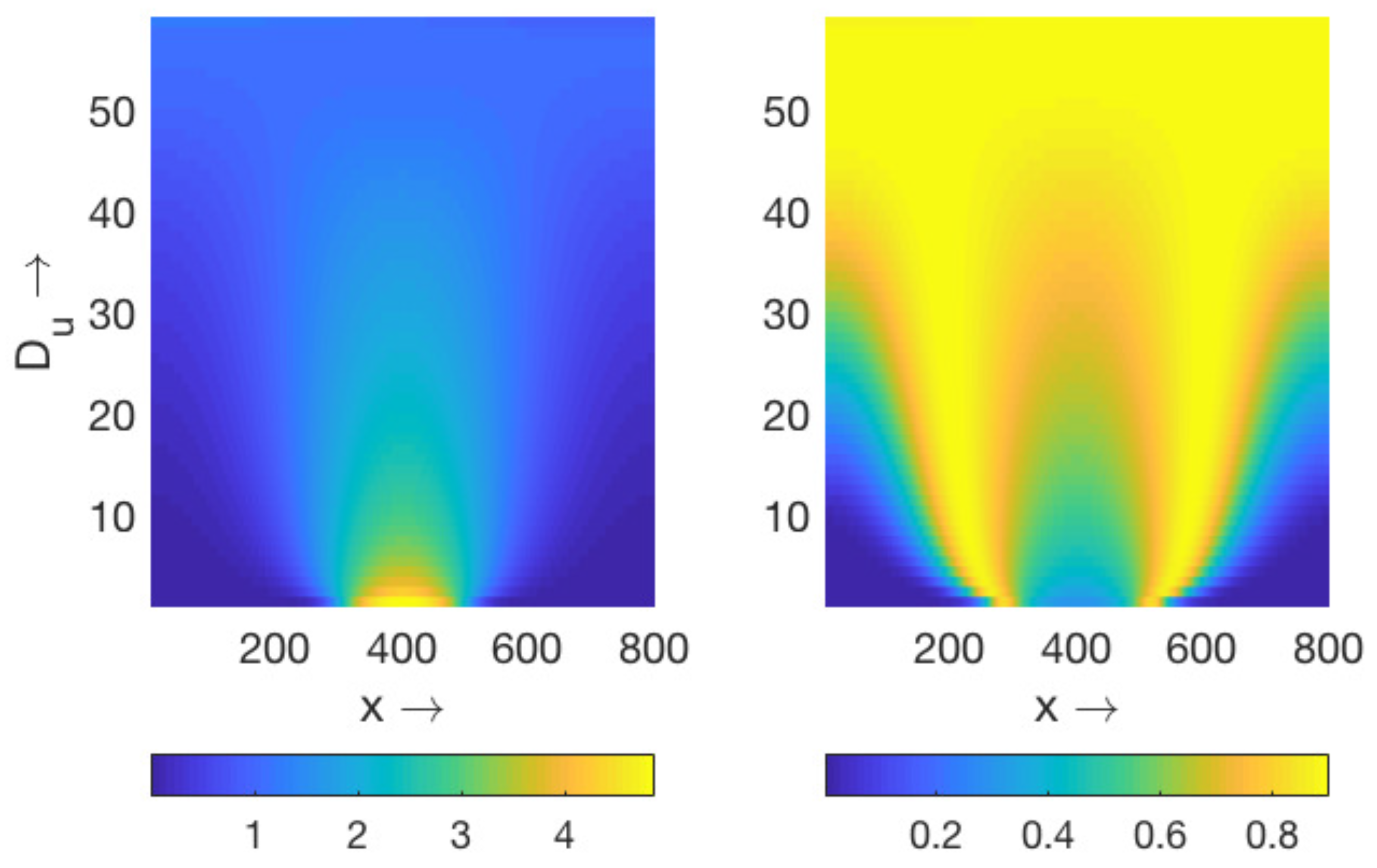
4.2. Pulses for Global Consumption
5. Discussion and Conclusions
5.1. On the Mechanisms of Pattern Formation
5.2. Properties of the Nonlocal Economy
5.3. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Posner, R.A. Equality, Wealth, and Political Stability. J. Law, Econ. Organ. 1997, 13, 344–365. [Google Scholar] [CrossRef]
- Von Mises, L. Ideas on Liberty; Foundation for Economic Education: Irvington, NJ, USA, 1955. [Google Scholar]
- Okun, A. Equality and Efficiency: The Big Tradeoff; Brookings Institute Press: Washington, DC, USA, 1975. [Google Scholar]
- Lansley, S. Inequality and instability: Why more equal societies have more stable economies. Poverty 2012, 142, 10–13. [Google Scholar]
- Pareto, V. Cours d’Economie Politique; Librairie Droz: Geneva, Switzerland, 1964. [Google Scholar]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Quadrini, V.; Rios-Rull, J.-V. Understanding the U.S. Distribution of Wealth. Fed. Reserve Bank Minneap. Q. Rev. 1997, 21, 22–36. [Google Scholar]
- Davies, J.B.; Shorrocks, A.F. The distribution of wealth. In Handbook of Income Distribution; Elsevier: Amsterdam, the Netherlands, 2000; Volume 1, pp. 605–675. [Google Scholar]
- Epstein, J.M. Nonlinear Dynamics, Mathematical Biology, and Social Science; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Turchin, P. Historical Dynamics: Why States Rise and Fall; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Krugman, P. Confronting the mistery of urban hierarchy. J. Japan. Intern. Econ. 1996, 10, 399–418. [Google Scholar] [CrossRef]
- Fujita, M.; Krugman, P.R.; Venables, A. The Spatial Economy: Cities, Regions, and International Trade; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Bouchaud, J.-P.; Mézard, M. Wealth condensation in a simple model of economy. Physica 2000, 282, 536–545. [Google Scholar] [CrossRef]
- Wang, N. An equilibrium model of wealth distribution. J. Monet. Econ. 2007, 54, 1882–1904. [Google Scholar] [CrossRef]
- Ikeda, K.; Murota, K. Bifurcation Theory for Hexagonal Agglomeration in Economic Geography; Springer: Tokyo, Japan, 2014. [Google Scholar]
- Torregrossa, M.; Toscani, G. On a Fokker-Planck equation for wealth distribution. Kinet. Relat. Model. 2018, 11, 337–355. [Google Scholar] [CrossRef]
- Chenevert, R.; Gottschalck, A.; Klee, M.; Zhang, X. Where the Wealth Is: The Geographic Distribution of Wealth in the United States. US Census Bureau, 2017. Available online: https://www.census.gov/content/dam/Census/newsroom/press-kits/2017/assa-geographic-distr-wealth.pdf (accessed on 10 October 2020).
- Rammelt, C.F.; van Schie, M.; Tegabu, F.N.; Leung, M. Vaguely Right or Exactly Wrong: Measuring the (Spatial) Distribution of Land Resources, Income and Wealth in Rural Ethiopia. Sustainability 2017, 9, 962. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Cantrell, R.S.; Cosner, C. Spatial Ecology via Reaction-Diffusion Equations; John Wiley & Son: London, UK, 1989. [Google Scholar]
- Malchow, H.; Petrovskii, S.V.; Venturino, E. Spatiotemporal Patterns in Ecology and Epidemiology: Theory, Models, and Simulation; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Meron, E. Nonlinear Physics of Ecosystems; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Volpert, V.; Petrovskii, S.; Zincenko, A. Interaction of human migration and wealth distribution. Nonlinear Anal. 2017, 159, 408–423. [Google Scholar] [CrossRef]
- Zincenko, A.; Petrovskii, S.; Volpert, V. Turing Instability in an Economic-Demographic Dynamical System Can Lead to Pattern Formation on Geographical Scale. arXiv 2020, arXiv:2006.01664v1. [Google Scholar]
- Deaton, A. The Great Escape—Health, Wealth, and the Origins of Inequality; Princeton Univ Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Rees, W.E. Ecological footprints and appropriated carrying capacity: What urban economics leaves out. Environ. Urban. 1992, 4, 121–130. [Google Scholar] [CrossRef]
- Small, M.L.; Harding, D.J.; Lamont, M. Reconsidering culture and poverty. Ann. Am. Acad. Political Soc. Sci. 2010, 629, 6–27. [Google Scholar] [CrossRef]
- Groth, C. Lecture Notes in Macroeconomics; Mimeo: New York, NY, USA, 2015. [Google Scholar]
- The Digital Economist. Available online: http://www.digitaleconomist.org/dmacro.html (accessed on 10 October 2020).
- Volpert, V. Elliptic partial differential equations. In Reaction-Diffusion Equations; Birkhäuser: Basel, Switzerland, 2014; Volume 2. [Google Scholar]
- Genieys, S.; Volpert, V.; Auger, P. Pattern and waves for a model in population dynamics with nonlocal consumption of resources. Math. Model. Nat. Phenom. 2006, 1, 63–80. [Google Scholar] [CrossRef]
- Zincenko, A.; Petrovskii, S.; Volpert, V. An economic-demographic dynamical system. Math. Model. Nat. Phenom. 2018, 13, 27. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banerjee, M.; Petrovskii, S.V.; Volpert, V. Nonlocal Reaction–Diffusion Models of Heterogeneous Wealth Distribution. Mathematics 2021, 9, 351. https://doi.org/10.3390/math9040351
Banerjee M, Petrovskii SV, Volpert V. Nonlocal Reaction–Diffusion Models of Heterogeneous Wealth Distribution. Mathematics. 2021; 9(4):351. https://doi.org/10.3390/math9040351
Chicago/Turabian StyleBanerjee, Malay, Sergei V. Petrovskii, and Vitaly Volpert. 2021. "Nonlocal Reaction–Diffusion Models of Heterogeneous Wealth Distribution" Mathematics 9, no. 4: 351. https://doi.org/10.3390/math9040351
APA StyleBanerjee, M., Petrovskii, S. V., & Volpert, V. (2021). Nonlocal Reaction–Diffusion Models of Heterogeneous Wealth Distribution. Mathematics, 9(4), 351. https://doi.org/10.3390/math9040351







