Abstract
The main objective of our paper is to focus on the study of sequences (finite or countable) of groups and hypergroups of linear differential operators of decreasing orders. By using a suitable ordering or preordering of groups linear differential operators we construct hypercompositional structures of linear differential operators. Moreover, we construct actions of groups of differential operators on rings of polynomials of one real variable including diagrams of actions–considered as special automata. Finally, we obtain sequences of hypergroups and automata. The examples, we choose to explain our theoretical results with, fall within the theory of artificial neurons and infinite cyclic groups.
1. Introduction
This paper discusses sequences of groups, hypergroups and automata of linear differential operators. It is based on the algebraic approach to the study of linear ordinary differential equations. Its roots lie in the work of Otakar Borůvka, a Czech mathematician, who tied the algebraic, geometrical and topological approaches, and his successor, František Neuman, who advocated the algebraic approach in his book [1]. Both of them (and their students) used the classical group theory in their considerations. In several papers, published mainly as conference proceedings such as [2,3,4], the existing theory was extended by the use of hypercompositional structures in place of the usual algebraic structures. The use of hypercompositional generalizations has been tested in the automata theory, where it has brought several interesting results; see, e.g., [5,6,7,8]. Naturally, this approach is not the only possible one. For another possible approach, investigations of differential operators by means of orthognal polynomials, see, e.g., [9,10].
Therefore, in this present paper we continue in the direction of [2,4] presenting results parallel to [11]. Our constructions, no matter how theoretical they may seem, are motivated by various practical issues of signal processing [12,13,14,15,16]. We construct sequences of groups and hypergroups of linear differential operators. This is because, in signal processing (but also in other real-life contexts), two or more connecting systems create a standing higher system, characteristics of which can be determined using characteristics of the original systems. Cascade (serial) and parallel connecting of systems of signal transfers are used in this. Moreover, series of groups motivated by the Galois theory of solvability of algebraic equations and the modern theory of extensions of fields, are often discussed in literature. Notice also paper [11] where the theory of artificial neurons, used further on in some examples, has been studied.
Another motivation for the study of sequences of hypergroups and their homomorphisms can be traced to ideas of classical homological algebra which comes from the algebraic description of topological spaces. A homological algebra assigns to any topological space a family of abelian groups and to any continuous mapping of topological spaces a family of group homomorphisms. This allows us to express properties of spaces and their mappings (morphisms) by means of properties of the groups or modules or their homomorphisms. Notice that a substantial part of homology theory is devoted to the study of exact short and long sequences of the above mentiones structures.
2. Sequences of Groups and Hypergroups: Definitions and Theorems
2.1. Notation and Preliminaries
It is crucial that one understands the notation used in this paper. Recall that we study, by means of algebra, linear ordinary differential equations. Therefore, our notation, which follows the original model of Borůvka and Neuman [1], uses a mix of algebraic and functional notation.
First, we denote intervals by J and regard open intervals (bounded or unbounded). Systems of functions with continuous derivatives of order k on J are denoted by ; for we write instead of . We treat as a ring with respect to the usual addition and multiplication of functions. We denote by the Kronecker delta, i.e., and , whenever ; by we mean . Since we will be using some notions from the theory of hypercompositional structures, recall that by one means the power set of X while means .
We regard linear homogeneous differential equations of order with coefficients, which are real and continuous on J, and–for convenience reasons–such that for all , i.e., equations
By we, adopting the notation of Neuman [1], mean the set of all such equations.
Example 1.
The above notation can be explained on an example taken from [17], in which Neuman considers the third-order linear homogeneous differential equation
on the open interval . One obtains this equation from the system
Here satisfies the condition on J. In the above differential equation we have , , and . It is to be noted that the above three equations form what is known as set of global canonical forms for the third-order equation on the interval J.
Denote the above linear differential operator defined by
where and for all . Further, denote by the set of all such operators, i.e.,
By we mean subsets of such that , i.e., there is for all . If we want to explicitly emphasize the variable, we write , , etc. However, if there is no specific need to do this, we write y, , etc. Using vector notation , we can write
Writing (or ) is a shortcut for writing (or, ).
On the sets of linear differential operators, i.e., on sets , or their subsets , we define some binary operations, hyperoperations or binary relations. This is possible because our considerations happen within a ring (of functions).
For an arbitrary pair of operators , where , , we define an operation “” with respect to the m-th component by , where and
for all , and all . Obviously, such an operation is not commutative.
Moreover, apart from the above binary operation we can define also a relation “” comparing the operators by their m-th component, putting whenever, for all , there is
for all . Obviously, is a partially ordered set.
At this stage, in order to simplify the notation, we write instead of because the lower index m is kept in the operation and relation. The following lemma is proved in [2].
Lemma 1.
Triads are partially ordered (noncommutative) groups.
Now we can use Lemma 1 to construct a (noncommutative) hypergroup. In order to do this, we will need the following lemma, known as Ends lemma; for details see, e.g., [18,19,20]. Notice that a join space is a special case of a hypergroup–in this paper we speak of hypergroups because we want to stress the parallel with groups.
Lemma 2.
Let be a partially ordered semigroup. Then , where is defined, for all by
is a semihypergroup, which is commutative if and only if “·” is commutative. Moreover, if is a group, then is a hypergroup.
Thus, to be more precise, defining
by
for all pairs , lets us state the following lemma.
Lemma 3.
Triads are (noncommutative) hypergroups.
Notation 1.
Hypergroups will be denoted by for an easier distinction.
Remark 1.
As a parallel to (2) and (3) we define
and
and, by defining the binary operation “” and “” in the same way as for , it is easy to verify that also are noncommutative partially ordered groups. Moreover, given a hyperoperation defined in a way parallel to (8), we obtain hypergroups , which will be, in line with Notation 1, denoted .
2.2. Results
In this subsection we will construct certain mappings between groups or hypergroups of linear differential operators of various orders. The result will have a form of sequences of groups or hypergroups.
Define mappings by
and by
It can be easily verify that both and are, for an arbitrary , group homomorphisms.
Evidently, for all admissible Thus we obtain two complete sequences of ordinary linear differential operators with linking homomorphisms and
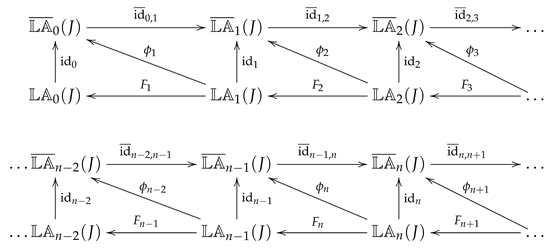 where , are corresponding inclusion embeddings.
where , are corresponding inclusion embeddings.

Notice that this diagram, presented at the level of groups, can be lifted to the level of hypergroups. In order to do this, one can use Lemma 3 and Remark 1. However, this is not enough. Yet, as Lemma 4 suggests, it is possible to show that the below presented assignment is functorial, i.e., not only objects are mapped onto objects but also morphisms (isotone group homomorphisms) are mapped onto morphisms (hypergroup homomorphisms). Notice that Lemma 4 was originally proved in [4]. However, given the minimal impact of the proceedings and its very limited availability and accessibility, we include it here with a complete proof.
Lemma 4.
Let be preordered groups and a group homomorphism, which is isotone, i.e., the mapping is order-preserving. Let be hypergroups constructed from by Lemma 2, respectively. Then is a homomorphism, i.e., for any pair of elements
Proof.
Let be a pair of elements and be an arbitrary element. Then there is i.e., such that Since the mapping f is an isotone homomorphism, we have thus . Hence
□
Consider a sequence of partially ordered groups of linear differential operators
given above with their linking group homomorphisms for . Since mappings , or rather
for all , are group homomorphisms and obviously mappings isotone with respect to the corresponding orderings, we immediately get the following theorem.
Theorem 1.
Suppose is an open interval, is an integer such that Let be the hypergroup obtained from the group by Lemma 2. Suppose that are the above defined surjective group-homomorphisms, Then are surjective homomorphisms of hypergroups.
Proof.
See the reasoning preceding the theorem. □
Remark 2.
It is easy to see that the second sequence from (11) can be mapped onto the sequence of hypergroups
This mapping is bijective and the linking mappings are surjective homomorphisms . Thus this mapping is functorial.
3. Automata and Related Concepts
3.1. Notation and Preliminaries
The concept of an automaton is mathematical interpretation of diverse real-life systems that work on a discrete time-scale. Various types of automata, called also machines, are applied and used in numerous forms such as money changing devices, various calculating machines, computers, telephone switch boards, selectors or lift switchings and other technical objects. All the above mentioned devices have one aspect in common–states are switched from one to another based on outside influences (such as electrical or mechanical impulses), called inputs. Using the binary operation of concatenation of chains of input symbols one obtains automata with input alphabets in the form of semigroups or a groups. In the case of our paper we work with input sets in the form of hypercompositional structures. When focusing on the structure given by transition function and simultaneously neglecting the output functions and output sets, one reaches a generalization of automata–quasi-automata (or semiautomata); see classical works such as, e.g., [3,18,21,22,23,24].
To be more precise, a quasi-automaton is a system which consists of a non-void set A, an arbitrary semigroup S and a mapping such that
for arbitrary and . Notice that the concept of quasi-automaton has been introduced by S. Ginsberg as quasi-machine and was meant to be a generalization of the Mealy-type automaton. Condition (12) is sometimes called Mixed Associativity Condition (MAC). With most authors it is nameless, though.
For further reading on automata theory and its links to the theory of hypercompositional structures (also known as algebraic hyperstructures), see, e.g., [24,25,26]. Furthermore, for clarification and evolution of terminology, see [8]. For results obtained by means of quasi-multiautomata, see, e.g., [5,6,7,8,27].
Definition 1.
Let A be a nonempty set, be a semihypergroup and a mapping satisfying the condition
for any triad , where . Then the triad is called quasi-multiautomaton with the state set A and the input semihypergroups . The mapping is called the transition function (or the next-state function) of the quasi-multiautomaton . Condition (13) is called Generalized Mixed Associativity Condition (or GMAC).
In this section, means, as usually, the ring of polynomials of degree at most n.
3.2. Results
Now, consider linear differential operators defined by
Denote by the additive abelian group of differential operators where for we define
where
Suppose that and define
by
Theorem 2.
Let , be structures and the mapping defined above. Then the triad is a quasi-automaton, i.e., an action of the group on the group .
Proof.
We are going to verify the mixed associativity condition (MAC) which should satisfy the above defined action:
Suppose Then
thus the mixed associativity condition is satisfied. □
Since are endowed with naturally defined orderings, Lemma 2 can be straightforwardly applied to construct semihypergroups from them.
Indeed, for a pair of polynomials we put whenever In such a case is a partially ordered abelian group. Now we define a binary hyperoperation
by
By Lemma 2 we have that is a hypergroup.
Moreover, defining
by which means
where we obtain, again by Lemma 2 that the hypergroupoid is a commutative semihypergroup.
Finally, define a mapping
by
Below, in the proof of Theorem 3, we show that the mapping satisfies the GMAC condition.
This allows us to construct a quasi-multiautomaton.
Theorem 3.
Suppose are hypergroups constructed above and is the above defined mapping. Then the structure
is a quasi-multiautomaton.
Proof.
Suppose Then
hence the GMAC condition is satisfied. □
Now let us discuss actions on objects of different dimensions. Recall that a homomorphism of automaton into the automaton is a mapping such that is a mapping and is a homomorphism (of semigroups or groups) such that for any pair we have
In order to define homomorphisms of our considered actions and especially in order to construct a sequence of quasi-automata with decreasing dimensions of the corresponding objects, we need a different construction of a quasiautomaton.
If and , we define
Now, if we have
Hence is the transition function (satisfying MAC) of the automaton
Consider now two automata– and the above one. Define mappings
in the following way: For put
and for define
Evidently, there is for any pair of polynomials
Theorem 4.
Let be mappings defined above. Define as mapping
Then the following diagram
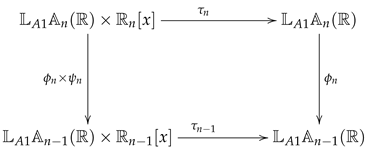 is commutative, thus the mapping is a homomorphism of the automaton into the automaton
is commutative, thus the mapping is a homomorphism of the automaton into the automaton

Proof.
Let Then
Thus the diagram (32) is commutative. □
Using the above defined homomorphism of automata we obtain the sequence of automata with linking homomorphisms
Here, for we have
for any and any it holds
The obtained sequence of automata can be transformed into a countable sequence of quasi-multiautomata. We already know that the transition function
satisfies GMAC. Further, suppose . Then
here for any polynomial Thus the mapping is a good homomorphism of corresponding hypergroups.
Now we are going to construct a sequence of automata with increasing dimensions, i.e., in a certain sense sequence “dual” to the previous sequence. First of all, we need a certain “reduction” member to the definition of a transition function
namely whenever In detail, if then
Further, is acting by
whereas i.e.,
Then for any pair where , we obtain
and
thus the mapping is well defined. We should verify validity of MAC and commutativity of the square diagram determining a homomorphism between automata.
Suppose Then
thus MAC is satisfied.
Further, we are going to verify commutativity of this diagram
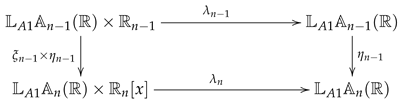 where i.e.,
and
where i.e.,
and

Considering and the polynomial similarly as above, we have
Thus the above diagram is commutative. Now, denoting by the pair of mappings , we obtain that is a homomorphism of the given automata. Finally, using as connecting homomorphism, we obtain the sequence
4. Practical Applications of the Sequences
In this section, we will include several examples of the above reasoning. We will apply the theoretical results in the area of artificial neurons, i.e., in a way, continue with the paper [11] which focuses on artificial neurons. For notation, recall [11]. Further on we consider a generalization of the usual concept of artificial neurons. We assume that the inputs u and weight are functions of an argument t, which belongs into a linearly ordered (tempus) set T with the least element The index set is, in our case, the set of all continuous functions defined on an open interval . Now, denote by W the set of all non-negative functions . Obviously W is a subsemiring of the ring of all real functions of one real variable . Further, denote by for , the mapping
which will be called the artificial neuron with the bias By we denote the collection of all such artificial neurons.
4.1. Cascades of Neurons Determined by Right Translations
Similarly as in the group of linear differential operators we will define a binary operation in the system of artificial neurons and construct a non-commutative group.
Suppose such that and , , where . Let be a such an integer that We define
where
and, of course, the neuron is defined as the mapping
The algebraic structure is a non-commutative group. We proceed to the construction of the cascade of neurons. Let be the additive group of all integers. Let be an arbitrary but fixed chosen artificial neuron with the output function
Denote by the right translation within the group of time varying neurons determined by , i.e.,
for any neuron . In what follows, denote by the r-th iteration of for Define the projection by
One easily observes that we get a usual (discrete) transformation group, i.e., the action of (as the phase group) on the group . Thus the following two requirements are satisfied:
- for any neuron .
- for any integers and any artificial neuron . Notice that the just obtained structure is called a cascade within the framework of the dynamical system theory.
4.2. An Additive Group of Differential Neurons
As usually denote by the ring of polynomials of variable t over of the grade at most Suppose be the fixed vector of continuous functions be the bias for any polynomial For any such polynomial we define a differential neuron given by the action
Considering the additive group of we obtain an additive commutative group of differential neurons which is assigned to the group of . Thus for , with actions
and
we have with the action
Considering the chain of inclusions
we obtain the corresponding sequence of commutative groups of differential neurons.
4.3. A Cyclic Subgroup of the Group Generated by Neuron
First of all recall that if , where , are vector function of weights such that with outputs (with inputs ), then the product has the vector of weights
The binary operation “” is defined under the assumption that all values of functions which are m-th components of corresponding vectors of weights are different from zero.
Let us denote by the cyclic subgroup of the group generated by the neuron Then denoting the neutral element by we have
Now we describe in detail objects
i.e., the inverse element to the neuron .
Let us denote with then
Then the vector of weights of the neuron is
the output function is of the form
It is easy to calculate the vector of weights of the neuron
Finally, putting for the vector of weights of this neuron is
Now, consider the neutral element (the unit) of the cyclic group Here the vector of weights is where and for each Moreover the bias
We calculate products . Denote results of corresponding products, respectively–we have where
if and for . Since the bias is , we obtain . Thus Similarly, denoting we obtain for and if thus consequently again.
Consider the inverse element to the element Denote We have Then
From the above equalities we obtain
Hence, for , we get
where the number 1 is on the m-th position. Of course, the bias of the neuron is where is the bias of the neuron
5. Conclusions
The scientific school of O. Borůvka and F. Neuman used, in their study of ordinary differencial equations and their transformations [1,28,29,30], the algebraic approach with the group theory as a main tool. In our study, we extended this existing theory with the employment of hypercomposiional structures—semihypergroups and hypergroups. We constructed hypergroups of ordinary linear differential operators and certain sequences of such structures. This served as a background to investigate systems of artificial neurons and neural networks.
Author Contributions
Investigation, J.C., M.N., B.S.; writing—original draft preparation, J.C., M.N., D.S.; writing—review and editing, M.N., B.S.; supervision, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Neuman, F. Global Properties of Linear Ordinary Differential Equations; Academia Praha-Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1991. [Google Scholar]
- Chvalina, J.; Chvalinová, L. Modelling of join spaces by n-th order linear ordinary differential operators. In Proceedings of the Fourth International Conference APLIMAT 2005, Bratislava, Slovakia, 1–4 February 2005; Slovak University of Technology: Bratislava, Slovakia, 2005; pp. 279–284. [Google Scholar]
- Chvalina, J.; Moučka, J. Actions of join spaces of continuous functions on hypergroups of second-order linear differential operators. In Proc. 6th Math. Workshop with International Attendance, FCI Univ. of Tech. Brno 2007. [CD-ROM]. Available online: https://math.fce.vutbr.cz/pribyl/workshop_2007/prispevky/ChvalinaMoucka.pdf (accessed on 4 February 2021).
- Chvalina, J.; Novák, M. Laplace-type transformation of a centralizer semihypergroup of Volterra integral operators with translation kernel. In XXIV International Colloquium on the Acquisition Process Management; University of Defense: Brno, Czech Republic, 2006. [Google Scholar]
- Chvalina, J.; Křehlík, Š.; Novák, M. Cartesian composition and the problem of generalising the MAC condition to quasi-multiautomata. Analele Universitatii “Ovidius" Constanta-Seria Matematica 2016, 24, 79–100. [Google Scholar] [CrossRef]
- Křehlík, Š.; Vyroubalová, J. The Symmetry of Lower and Upper Approximations, Determined by a Cyclic Hypergroup, Applicable in Control Theory. Symmetry 2020, 12, 54. [Google Scholar] [CrossRef]
- Novák, M.; Křehlík, Š. EL–hyperstructures revisited. Soft Comput. 2018, 22, 7269–7280. [Google Scholar] [CrossRef]
- Novák, M.; Křehlík, Š.; Staněk, D. n-ary Cartesian composition of automata. Soft Comput. 2020, 24, 1837–1849. [Google Scholar]
- Cesarano, C. A Note on Bi-orthogonal Polynomials and Functions. Fluids 2020, 5, 105. [Google Scholar] [CrossRef]
- Cesarano, C. Multi-dimensional Chebyshev polynomials: A non-conventional approach. Commun. Appl. Ind. Math. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Chvalina, J.; Smetana, B. Series of Semihypergroups of Time-Varying Artificial Neurons and Related Hyperstructures. Symmetry 2019, 11, 927. [Google Scholar] [CrossRef]
- Jan, J. Digital Signal Filtering, Analysis and Restoration; IEEE Publishing: London, UK, 2000. [Google Scholar]
- Koudelka, V.; Raida, Z.; Tobola, P. Simple electromagnetic modeling of small airplanes: Neural network approach. Radioengineering 2009, 18, 38–41. [Google Scholar]
- Krenker, A.; Bešter, J.; Kos, A. Introduction to the artificial neural networks. In Artificial Neural Networks: Methodological Advances and Biomedical Applications; Suzuki, K., Ed.; InTech: Rijeka, Croatia, 2011; pp. 3–18. [Google Scholar]
- Raida, Z.; Lukeš, Z.; Otevřel, V. Modeling broadband microwave structures by artificial neural networks. Radioengineering 2004, 13, 3–11. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Neuman, F. Global theory of ordinary linear homogeneous differential equations in the ral domain. Aequationes Math. 1987, 34, 1–22. [Google Scholar] [CrossRef]
- Křehlík, Š.; Novák, M. From lattices to Hv–matrices. An. Şt. Univ. Ovidius Constanţa 2016, 24, 209–222. [Google Scholar] [CrossRef]
- Novák, M. On EL-semihypergroups. Eur. J. Comb. 2015, 44, 274–286. [Google Scholar] [CrossRef]
- Novák, M. Some basic properties of EL-hyperstructures. Eur. J. Comb. 2013, 34, 446–459. [Google Scholar] [CrossRef]
- Bavel, Z. The source as a tool in automata. Inf. Control 1971, 18, 140–155. [Google Scholar] [CrossRef][Green Version]
- Dörfler, W. The cartesian composition of automata. Math. Syst. Theory 1978, 11, 239–257. [Google Scholar] [CrossRef]
- Gécseg, F.; Peák, I. Algebraic Theory of Automata; Akadémia Kiadó: Budapest, Hungary, 1972. [Google Scholar]
- Massouros, G.G. Hypercompositional structures in the theory of languages and automata. An. Şt. Univ. A.I. Çuza Iaşi, Sect. Inform. 1994, III, 65–73. [Google Scholar]
- Massouros, G.G.; Mittas, J.D. Languages, Automata and Hypercompositional Structures. In Proceedings of the 4th International Congress on Algebraic Hyperstructures and Applications, Xanthi, Greece, 27–30 June 1990. [Google Scholar]
- Massouros, C.; Massouros, G. Hypercompositional Algebra, Computer Science and Geometry. Mathematics 2020, 8, 138. [Google Scholar] [CrossRef]
- Křehlík, Š. n-Ary Cartesian Composition of Multiautomata with Internal Link for Autonomous Control of Lane Shifting. Mathematics 2020, 8, 835. [Google Scholar] [CrossRef]
- Borůvka, O. Lineare Differentialtransformationen 2. Ordnung; VEB Deutscher Verlager der Wissenschaften: Berlin, Germany, 1967. [Google Scholar]
- Borůvka, O. Linear Differential Transformations of the Second Order; The English University Press: London, UK, 1971. [Google Scholar]
- Borůvka, O. Foundations of the Theory of Groupoids and Groups; VEB Deutscher Verlager der Wissenschaften: Berlin, Germany, 1974. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).