Algebraic Solution to Constrained Bi-Criteria Decision Problem of Rating Alternatives through Pairwise Comparisons
Abstract
1. Introduction
2. Constrained Bi-Criteria Decision Problem
2.1. Unconstrained Pairwise Comparisons under Single Criterion
2.2. Constrained Pairwise Comparisons under Two Criteria
3. Preliminary Algebraic Definitions and Results
3.1. Idempotent Semifields
3.2. Matrices and Vectors
3.3. Vector Inequalities
- 1.
- 2.
- If , then there is only the trivial solution .
3.4. Identities for Traces
4. Constrained Bi-Objective Optimization Problem
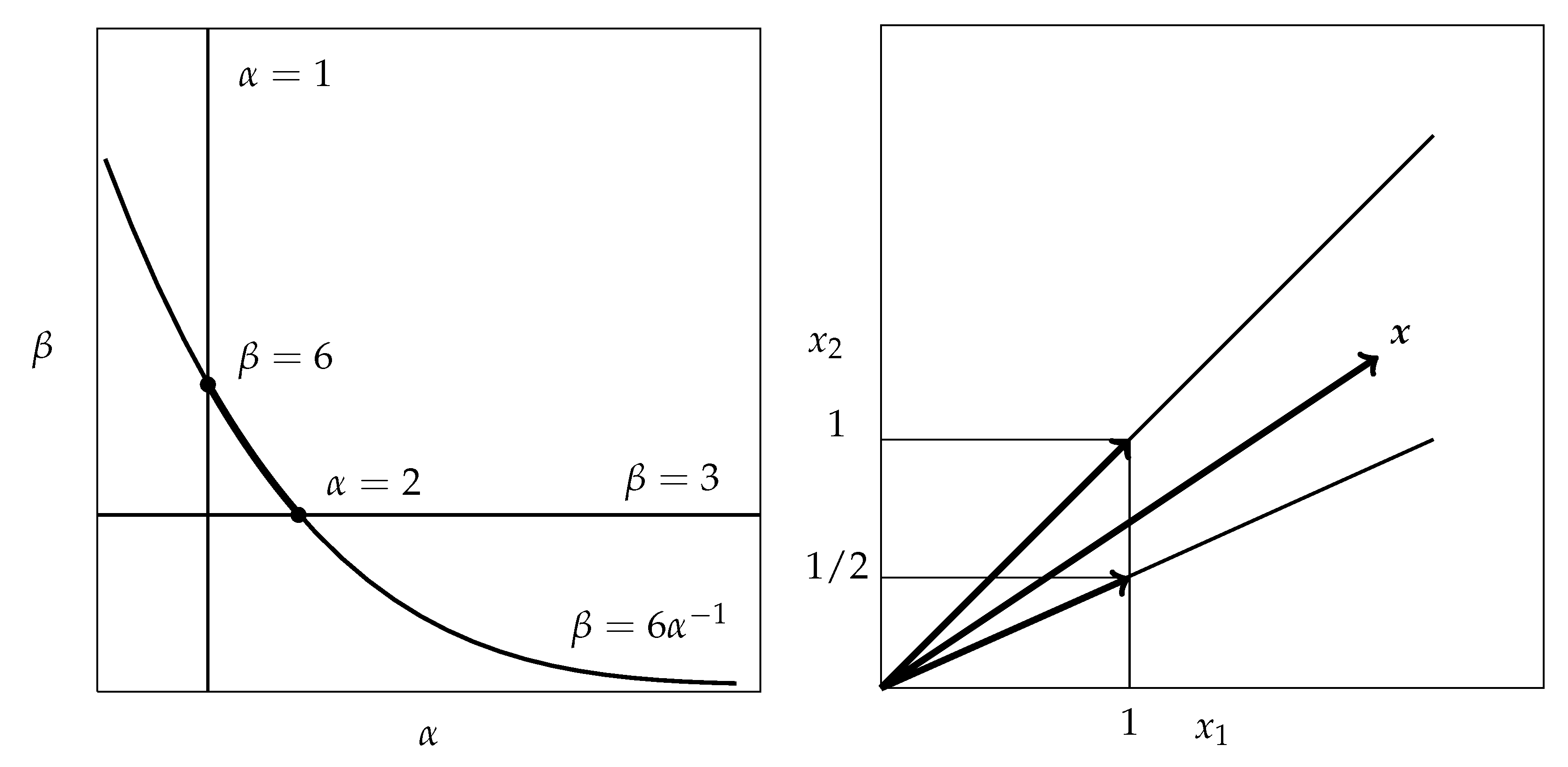
5. Application to Constrained Bi-Criteria Decision Problem
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baccelli, F.L.; Cohen, G.; Olsder, G.J.; Quadrat, J.P. Synchronization and Linearity; Wiley Series in Probability and Statistics; Wiley: Chichester, UK, 1993. [Google Scholar]
- Kolokoltsov, V.N.; Maslov, V.P. Idempotent Analysis and Its Applications; Mathematics and Its Applications; Springer: Dordrecht, The Netherlands, 1997; Volume 401. [Google Scholar] [CrossRef]
- Golan, J.S. Semirings and Affine Equations Over Them; Mathematics and Its Applications; Springer: Dordrecht, The Netherlands, 2003; Volume 556. [Google Scholar] [CrossRef]
- Heidergott, B.; Olsder, G.J.; van der Woude, J. Max Plus at Work; Princeton Series in Applied Mathematics; Princeton Univeristy Press: Princeton, NJ, USA, 2006. [Google Scholar]
- McEneaney, W.M. Max-Plus Methods for Nonlinear Control and Estimation; Systems and Control: Foundations and Applications; Birkhäuser: Boston, MA, USA, 2006. [Google Scholar] [CrossRef]
- Gondran, M.; Minoux, M. Graphs, Dioids and Semirings; Operations Research/ Computer Science Interfaces; Springer: Boston, MA, USA, 2008; Volume 41. [Google Scholar] [CrossRef]
- Maclagan, D.; Sturmfels, B. Introduction to Tropical Geometry; Graduate Studies in Mathematics; AMS: Providence, RI, USA, 2015; Volume 161. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process, 2nd ed.; RWS Publications: Pittsburgh, PA, USA, 1990. [Google Scholar]
- Gavalec, M.; Ramík, J.; Zimmermann, K. Decision Making and Optimization; Lecture Notes in Economics and Mathematical Systems; Springer: Cham, Switzerland, 2015; Volume 677. [Google Scholar] [CrossRef]
- Saaty, T.L. On the measurement of intangibles: A principal eigenvector approach to relative measurement derived from paired comparisons. Not. Am. Math. Soc. 2013, 60, 192–208. [Google Scholar] [CrossRef]
- Crawford, G.; Williams, C. A note on the analysis of subjective judgment matrices. J. Math. Psych. 1985, 29, 387–405. [Google Scholar] [CrossRef]
- Barzilai, J. Deriving weights from pairwise comparison matrices. J. Oper. Res. Soc. 1997, 48, 1226–1232. [Google Scholar] [CrossRef]
- Elsner, L.; van den Driessche, P. Max-algebra and pairwise comparison matrices. Linear Algebra Appl. 2004, 385, 47–62. [Google Scholar] [CrossRef][Green Version]
- Elsner, L.; van den Driessche, P. Max-algebra and pairwise comparison matrices, II. Linear Algebra Appl. 2010, 432, 927–935. [Google Scholar] [CrossRef][Green Version]
- Gursoy, B.B.; Mason, O.; Sergeev, S. The analytic hierarchy process, max algebra and multi-objective optimisation. Linear Algebra Appl. 2013, 438, 2911–2928. [Google Scholar] [CrossRef]
- Tran, N.M. Pairwise ranking: Choice of method can produce arbitrarily different rank order. Linear Algebra Appl. 2013, 438, 1012–1024. [Google Scholar] [CrossRef]
- Goto, H.; Wang, S. Polyad inconsistency measure for pairwise comparisons matrices: Max-plus algebraic approach. Oper. Res. Int. J. 2020. [Google Scholar] [CrossRef]
- Krivulin, N. Rating alternatives from pairwise comparisons by solving tropical optimization problems. In Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD); Tang, Z., Du, J., Yin, S., He, L., Li, R., Eds.; IEEE: Piscataway, NJ, USA, 2015; pp. 162–167. [Google Scholar] [CrossRef]
- Krivulin, N. Using tropical optimization techniques to evaluate alternatives via pairwise comparisons. In Proceedings of the 2016 Proc. 7th SIAM Workshop on Combinatorial Scientific Computing; Gebremedhin, A.H., Boman, E.G., Ucar, B., Eds.; SIAM: Philadelphia, PA, USA, 2016; pp. 62–72. [Google Scholar] [CrossRef]
- Krivulin, N. Using tropical optimization techniques in bi-criteria decision problems. Comput. Manag. Sci. 2020, 17, 79–104. [Google Scholar] [CrossRef]
- Krivulin, N.; Sergeev, S. Tropical implementation of the Analytical Hierarchy Process decision method. Fuzzy Sets Syst. 2019, 377, 31–51. [Google Scholar] [CrossRef]
- Thurstone, L.L. A law of comparative judgment. Psychol. Rev. 1927, 34, 273–286. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Comparison of eigenvalue, logarithmic least squares and least squares methods in estimating ratios. Math. Model. 1984, 5, 309–324. [Google Scholar] [CrossRef]
- Choo, E.U.; Wedley, W.C. A common framework for deriving preference values from pairwise comparison matrices. Comput. Oper. Res. 2004, 31, 893–908. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psych. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Portugal, R.D.; Svaiter, B.F. Weber-Fechner law and the optimality of the logarithmic scale. Minds Mach. 2011, 21, 73–81. [Google Scholar] [CrossRef]
- Ehrgott, M. Multicriteria Optimization, 2nd ed.; Springer: Berlin, Germany, 2005. [Google Scholar] [CrossRef]
- Luc, D.T. Pareto optimality. In Pareto Optimality, Game Theory and Equilibria; Chinchuluun, A., Pardalos, P.M., Migdalas, A., Pitsoulis, L., Eds.; Springer: New York, NY, USA, 2008; pp. 481–515. [Google Scholar] [CrossRef]
- Benson, H.P. Multi-objective optimization: Pareto optimal solutions, properties. In Encyclopedia of Optimization, 2nd ed.; Floudas, C.A., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 2009; pp. 2478–2481. [Google Scholar] [CrossRef]
- Pappalardo, M. Multiobjective optimization: A brief overview. In Pareto Optimality, Game Theory and Equilibria; Chinchuluun, A., Pardalos, P.M., Migdalas, A., Pitsoulis, L., Eds.; Springer: New York, NY, USA, 2008; pp. 517–528. [Google Scholar] [CrossRef]
- Ruzika, S.; Wiecek, M.M. Approximation methods in multiobjective programming. J. Optim. Theory Appl. 2005, 126, 473–501. [Google Scholar] [CrossRef]
- Krivulin, N. Extremal properties of tropical eigenvalues and solutions to tropical optimization problems. Linear Algebra Appl. 2015, 468, 211–232. [Google Scholar] [CrossRef]
- Krivulin, N. A multidimensional tropical optimization problem with nonlinear objective function and linear constraints. Optimization 2015, 64, 1107–1129. [Google Scholar] [CrossRef]
- Krivulin, N. Direct solution to constrained tropical optimization problems with application to project scheduling. Comput. Manag. Sci. 2017, 14, 91–113. [Google Scholar] [CrossRef]
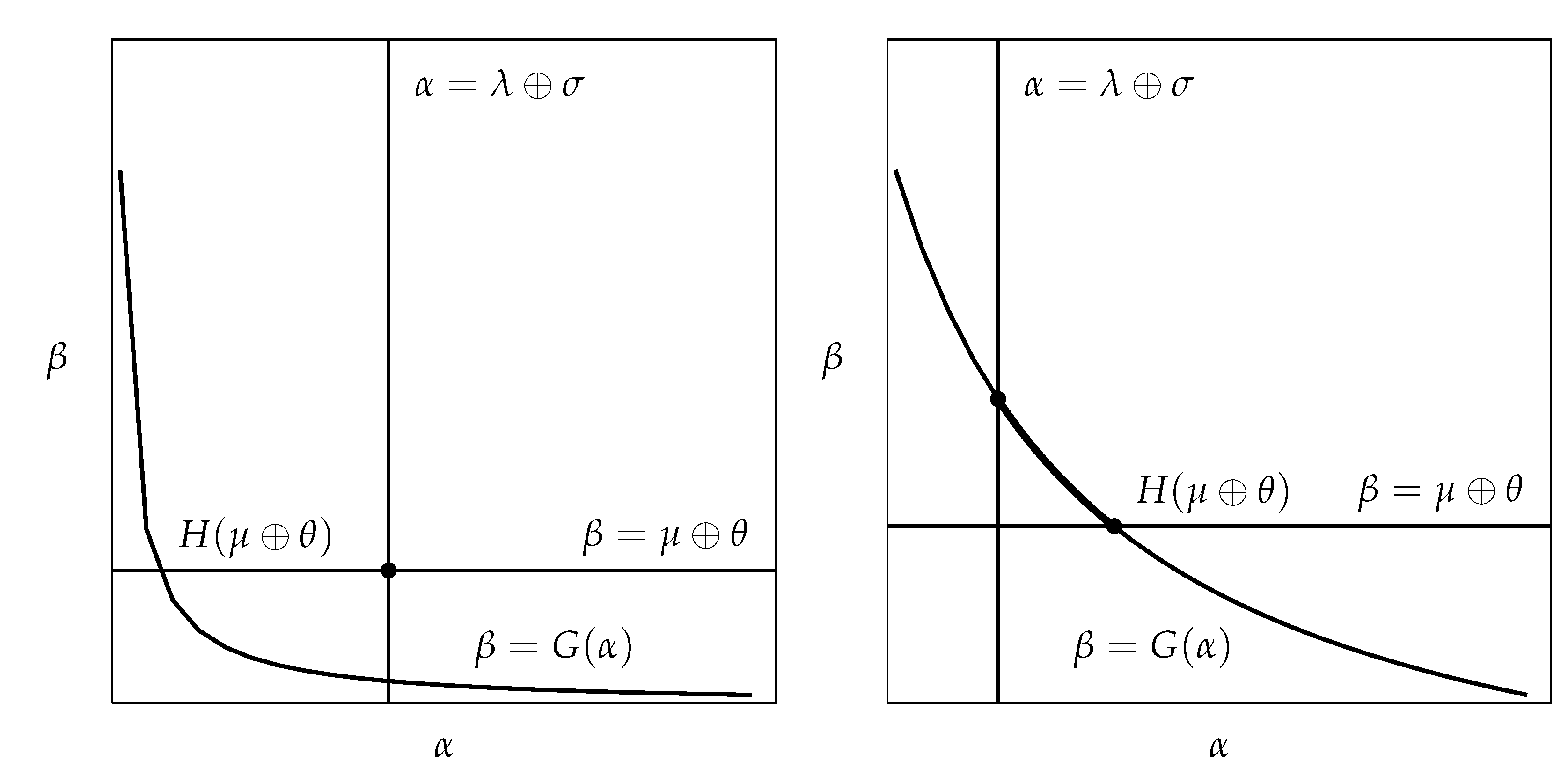
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krivulin, N. Algebraic Solution to Constrained Bi-Criteria Decision Problem of Rating Alternatives through Pairwise Comparisons. Mathematics 2021, 9, 303. https://doi.org/10.3390/math9040303
Krivulin N. Algebraic Solution to Constrained Bi-Criteria Decision Problem of Rating Alternatives through Pairwise Comparisons. Mathematics. 2021; 9(4):303. https://doi.org/10.3390/math9040303
Chicago/Turabian StyleKrivulin, Nikolai. 2021. "Algebraic Solution to Constrained Bi-Criteria Decision Problem of Rating Alternatives through Pairwise Comparisons" Mathematics 9, no. 4: 303. https://doi.org/10.3390/math9040303
APA StyleKrivulin, N. (2021). Algebraic Solution to Constrained Bi-Criteria Decision Problem of Rating Alternatives through Pairwise Comparisons. Mathematics, 9(4), 303. https://doi.org/10.3390/math9040303





