Optimal Reinsurance Problem under Fixed Cost and Exponential Preferences
Abstract
1. Introduction
2. Problem Formulation
2.1. Model Formulation
2.2. The Utility Maximization Problem
3. The Pure Reinsurance Problem
4. Reduction to an Optimal Stopping Problem
5. The Optimal Stopping Problem
- If the stopping region is not empty, that is , , we know that , hence , which implies and is optimal for problem (24).
- If the stopping region is not empty, for , we have that , otherwise, by continuity of both the functions, if (or ), the same inequality holds in a neighborhood of , which contradicts that , . Then, and is optimal for problem (24).
- If the continuation region is not empty, that is , , repeating the localization argument with the stopping time , we getas a consequence and is optimal for problem (24).
- Finally, for , by assumption, , , is optimal for problem (24) and this concludes the proof.
- 1.
- Ifthen and , so that , implying that .
- 2.
- Ifthen and ; in this case .
- 3.
- Ifthen and , so that .
- If , then .
- If , then there exists such that and .
- (i)
- When , we have that by Remark 3 and it easy to verify that H is increasing in , while it is decreasing in . Hence, it takes the maximum value at . As a consequence, if we have that , being .Otherwise, if there exists such that , that is , and , that is .
- (ii)
- When , by Lemma 2 we get that H is increasing in and we can repeat the same arguments as in the previous case to distinguish the two casese and , obtaining the same results.
- (iii)
- When , by Remark 3, we know that H is decreasing in , so that , that is , . Moreover, in this case, .
- If , then .
- If , then , where is the unique solution to equation
- (1)
- If , then the continuation region is , the value function isand is an optimal stopping time.
- (2)
- If , then , where is the unique solution to , the value function isand , given byis an optimal stopping time.
6. Solution to the Original Problem
- (1)
- If , then , that is no reinsurance is purchased.
- (2)
- If , then , that is the optimal choice for the insurer consists in stipulating the contract at the initial time, selecting the optimal retention level (as in the pure reinsurance problem).
- If , thenand , that is no reinsurance is purchased.
7. Numerical Simulations
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Finetti, B. Il problema dei “pieni”. G. Ist. Ital. Attuari 1940, 11, 1–88. [Google Scholar]
- Bühlmann, H. Mathematical Methods in Risk Theory; Springer: Berlin/Heidelberg, Germany, 1970. [Google Scholar]
- Gerber, H. Entscheidungskriterien für den zusammengesetzten Poisson-Prozess. Schweiz. Verein. Versicherungsmath. Mitt. 1969, 69, 185–228. [Google Scholar]
- Irgens, C.; Paulsen, J. Optimal control of risk exposure, reinsurance and investments for insurance portfolios. Insur. Math. Econ. 2004, 35, 21–51. [Google Scholar] [CrossRef]
- Brachetta, M.; Ceci, C. Optimal proportional reinsurance and investment for stochastic factor models. Insur. Math. Econ. 2019, 87, 15–33. [Google Scholar] [CrossRef]
- Brachetta, M.; Ceci, C. Optimal Excess-of-Loss Reinsurance for Stochastic Factor Risk Models. Risks 2019, 7, 48. [Google Scholar] [CrossRef]
- Skogh, G. The Transactions Cost Theory of Insurance: Contracting Impediments and Costs. J. Risk Insur. 1989, 56, 726–732. [Google Scholar] [CrossRef]
- Braouezec, Y. Public versus private insurance system with (and without) transaction costs: Optimal segmentation policy of an informed monopolist. Appl. Econ. 2019, 51, 1907–1928. [Google Scholar] [CrossRef]
- Egami, M.; Young, V.R. Optimal reinsurance strategy under fixed cost and delay. Stoch. Process. Their Appl. 2009, 119, 1015–1034. [Google Scholar] [CrossRef]
- Li, P.; Zhou, M.; Yin, C. Optimal reinsurance with both proportional and fixed costs. Stat. Probab. Lett. 2015, 106, 134–141. [Google Scholar] [CrossRef]
- Schmidli, H. Risk Theory; Springer Actuarial, Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Karatzas, I.; Wang, H. Utility maximization with discretionary stopping. Siam J. Control. Optim. 2000, 39, 306–329. [Google Scholar] [CrossRef]
- Ceci, C.; Bassan, B. Mixed Optimal Stopping and Stochastic Control Problems with Semicontinuous Final Reward for Diffusion Processes. Stochastics Stoch. Rep. 2004, 76, 323–337. [Google Scholar] [CrossRef]
- Bouchard, B.; Touzi, N. Weak Dynamic Programming Principle for Viscosity Solutions. Siam J. Control. Optim. 2011, 49, 948–962. [Google Scholar] [CrossRef]
- Chen, M.; Yuen, K.C.; Wang, W. Optimal reinsurance and dividends with transaction costs and taxes under thinning structure. Scand. Actuar. J. 2020, 1–20. [Google Scholar] [CrossRef]
- Grandell, J. Aspects of Risk Theory; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Eisenberg, J.; Schmidli, H. Optimal control of capital injections by reinsurance in a diffusion approximation. Blätter DGVFM 2009, 30, 1–13. [Google Scholar] [CrossRef]
- ∅ksendal, B. Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]

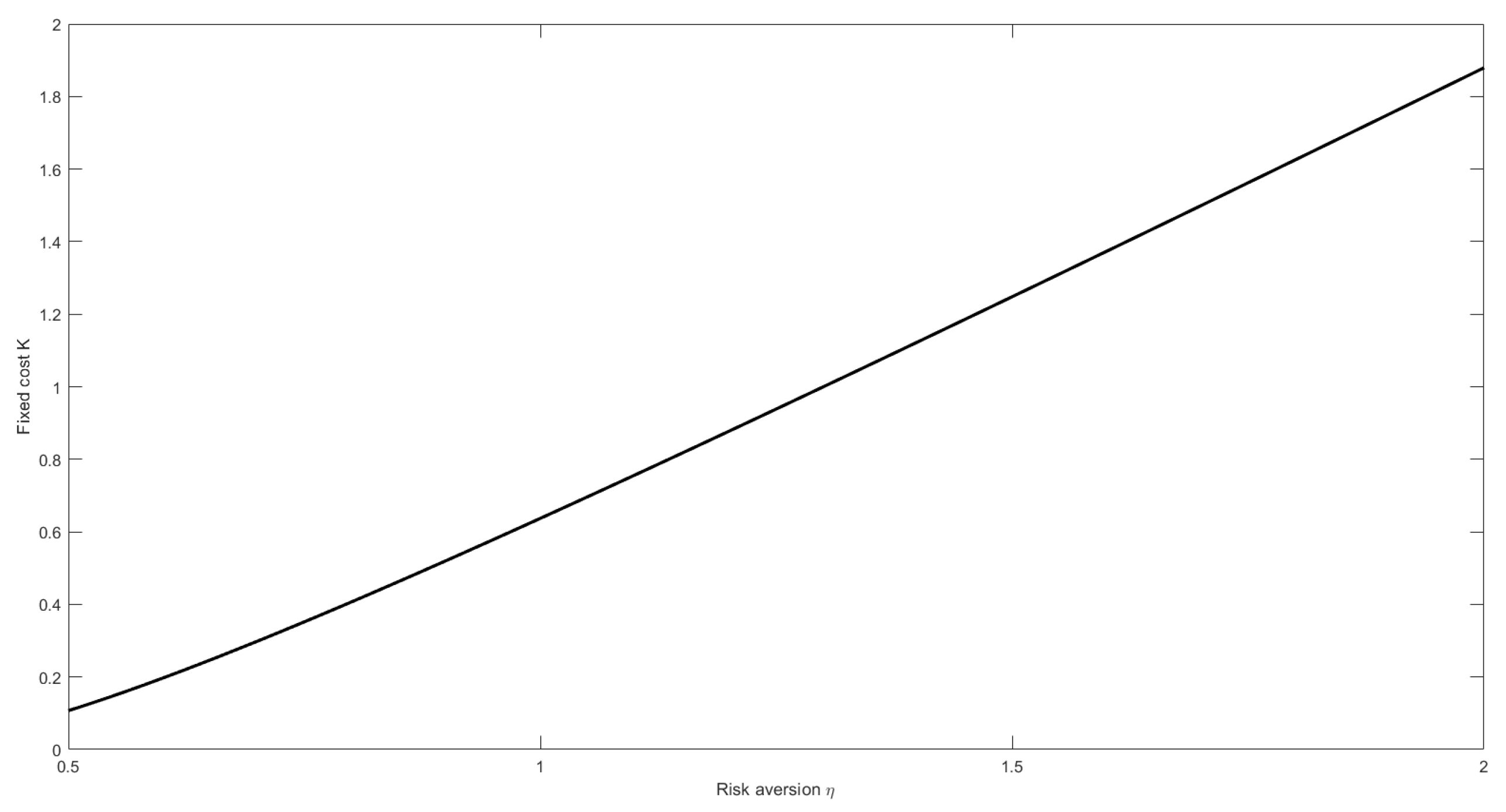

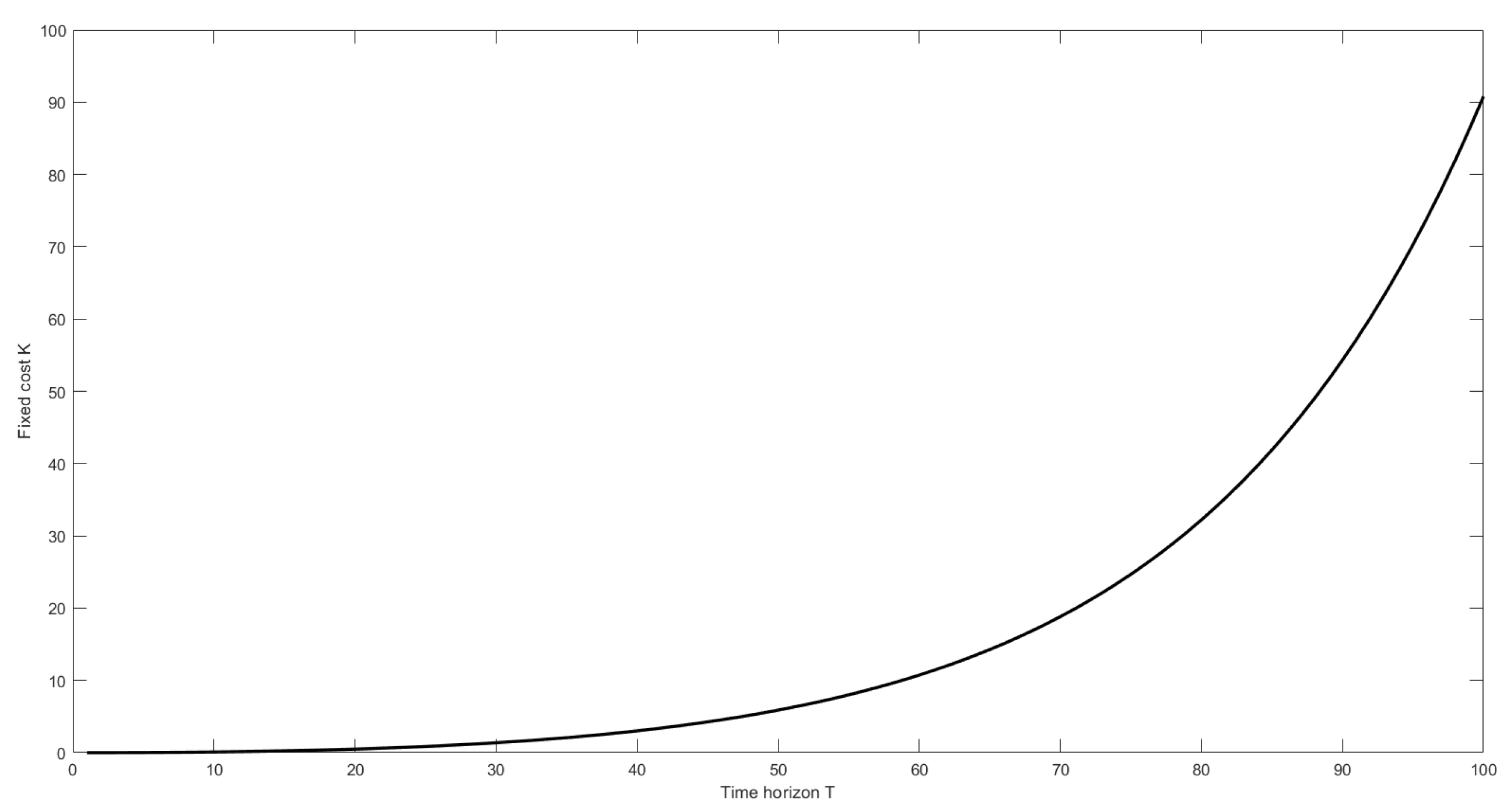
| Parameter | Value |
|---|---|
| T | 10 |
| q | |
| R |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brachetta, M.; Ceci, C. Optimal Reinsurance Problem under Fixed Cost and Exponential Preferences. Mathematics 2021, 9, 295. https://doi.org/10.3390/math9040295
Brachetta M, Ceci C. Optimal Reinsurance Problem under Fixed Cost and Exponential Preferences. Mathematics. 2021; 9(4):295. https://doi.org/10.3390/math9040295
Chicago/Turabian StyleBrachetta, Matteo, and Claudia Ceci. 2021. "Optimal Reinsurance Problem under Fixed Cost and Exponential Preferences" Mathematics 9, no. 4: 295. https://doi.org/10.3390/math9040295
APA StyleBrachetta, M., & Ceci, C. (2021). Optimal Reinsurance Problem under Fixed Cost and Exponential Preferences. Mathematics, 9(4), 295. https://doi.org/10.3390/math9040295






